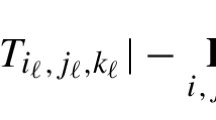Tensor theta norms and low rank recovery

Abstract

We study extensions of compressive sensing and low rank matrix recovery to the recovery of tensors of low rank from incomplete linear information. While the reconstruction of low rank matrices via nuclear norm minimization is rather well-understand by now, almost no theory is available so far for the extension to higher order tensors due to various theoretical and computational difficulties arising for tensor decompositions. In fact, nuclear norm minimization for matrix recovery is a tractable convex relaxation approach, but the extension of the nuclear norm to tensors is in general NP-hard to compute. In this article, we introduce convex relaxations of the tensor nuclear norm which are computable in polynomial time via semidefinite programming. Our approach is based on theta bodies, a concept from real computational algebraic geometry which is similar to the one of the better known Lasserre relaxations. We introduce polynomial ideals which are generated by the second-order minors corresponding to different matricizations of the tensor (where the tensor entries are treated as variables) such that the nuclear norm ball is the convex hull of the algebraic variety of the ideal. The theta body of order k for such an ideal generates a new norm which we call the θ_k-norm. We show that in the matrix case, these norms reduce to the standard nuclear norm. For tensors of order three or higher however, we indeed obtain new norms. The sequence of the corresponding unit-θ_k-norm balls converges asymptotically to the unit tensor nuclear norm ball. By providing the Gröbner basis for the ideals, we explicitly give semidefinite programs for the computation of the θ_k-norm and for the minimization of the θ_k-norm under an affine constraint. Finally, numerical experiments for order-three tensor recovery via θ₁-norm minimization suggest that our approach successfully reconstructs tensors of low rank from incomplete linear (random) measurements.

1 Introduction and motivation

Compressive sensing predicts that sparse vectors can be recovered from underdetermined linear measurements via efficient methods such as ℓ₁-minimization [10, 20, 23]. This finding has various applications in signal and image processing and beyond. It has recently been observed that the principles of this theory can be transferred to the problem of recovering a low rank matrix from underdetermined linear measurements. One prominent choice of recovery method consists in minimizing the nuclear norm subject to the given linear constraint [22, 55]. This convex optimization problem can be solved efficiently and recovery results for certain random measurement maps have been provided, which quantify the minimal number of measurements required for successful recovery [6, 7, 31, 32, 43, 55].

There is significant interest in going one step further and to extend the theory to the recovery of low rank tensors (higher-dimensional arrays) from incomplete linear measurements. Applications include image and video inpainting [46], reflectance data recovery [46] (e.g., for use in photo-realistic raytracers), machine learning [56], and seismic data processing [41]. Several approaches have already been introduced [25, 39, 46, 52, 53], but unfortunately, so far, for none of them a completely satisfactory theory is available. Either the method is not tractable [63], or no (complete) rigorous recovery results quantifying the minimal number of measurements are available [17, 25, 40, 42, 46, 52, 53], or the available bounds are highly nonoptimal [21, 39, 47]. For instance, the computation (and therefore, also the minimization) of the tensor nuclear norm ([19, 57, 61]) for higher order tensors is in general NP-hard [24]—nevertheless, some recovery results for tensor completion via nuclear norm minimization are available in [63]. Moreover, versions of iterative hard thresholding for various tensor formats have been introduced [52, 53]. This approach leads to a computationally tractable algorithm, which empirically works well. However, only a partial analysis based on the tensor restricted isometry property has been provided, which so far only shows convergence under a condition on the iterates that cannot be checked a priori. Nevertheless, the tensor restricted isometry property (TRIP) has been analyzed for certain random measurement maps [52,53,54]. These near optimal bounds on the number of measurements ensuring the TRIP, however, provide only a hint on how many measurements are required because the link between the TRIP and recovery is so far only partial [53, 54].

This article introduces a new approach for tensor recovery based on convex relaxation, initially suggested in slightly different form (but not worked out) in [12]. The idea is to further relax the nuclear norm in order to arrive at a norm which can be computed (and minimized under a linear constraint) in polynomial time. The hope is that the new norm is only a slight relaxation and possesses very similar properties as the nuclear norm. Our approach is based on theta bodies, a concept from computational algebraic geometry [2, 27, 48] which is similar to the better known Lasserre relaxations [45]. We arrive at a whole family of convex bodies (indexed by a polynomial degree), which form convex relaxations of the unit nuclear norm ball. The resulting norms are called theta norms. The corresponding unit norm balls are nested and contain the unit nuclear norm ball. Even more, the sequence of the unit-θ_k-norm balls converges asymptotically to the unit tensor nuclear norm ball. The θ_k-norm as well as its minimization subject to an affine constraint can be computed via semidefinite optimization, and also the minimization of the θ_k-norm subject to a linear constraint is a semidefinite program (SDP), whose solution can be computed in polynomial time—the complexity growing with k.

The tensor nuclear norm may be defined for both base fields $\mathbb {R}$ and $\mathbb {C}$. In general the resulting norms may differ for a real tensor. In this article, we restrict to relaxations of the real tensor nuclear norm because the concept of theta bodies is based on real algebraic geometry and not well-defined for the complex case.

The basic idea for the construction of these new norms is to define polynomial ideals, where each variable corresponds to an entry of the tensor, such that its algebraic variety consists of the rank-one tensors of unit Frobenius norm. The convex hull of this set is the tensor nuclear norm ball. The ideals that we propose are generated by the minors of order two of all matricizations of the tensor (or at least of a subset of the possible matricizations) together with the polynomial corresponding to the squared Frobenius norm minus one. Here, a matricization denotes a matrix which is generated from the tensor by combining several indices to a row index, and the remaining indices to a column index. In fact, all such minors being zero simultaneously means that the tensor has rank one. The k-theta body of the ideal corresponds then to a relaxation of the convex hull of its algebraic variety, i.e., to a further relaxation of the tensor nuclear norm. The index $k \in \mathbb {N}$ corresponds to a polynomial degree involved in the construction of the theta bodies (a certain polynomial is required to be k-sos modulo the ideal, see below), and k = 1 leads to the largest theta body in a family of convex relaxations.

Our investigations have been strongly motivated by [12], where theta bodies have first been suggested for low rank tensor recovery. The approach in [12] has not been worked out in detail, however. It suggests a slightly different polynomial ideal that requires additional auxiliary variables. The corresponding Gröbner basis and, hence, also the theta basis, become much more complicated (see also Remark 2). This would lead to very technical computations on the theoretical side and to less efficient algorithms on the practical side.

We show that for the matrix case (tensors of order 2), our relaxation approach does not lead to new norms. All resulting theta norms are rather equal to the matrix nuclear norm. This fact suggests that the theta norms in the higher order tensor case are all natural generalizations of the matrix nuclear norm.

The derivation of the semidefinite program for calculating the θ_k-norm requires to compute the so-called theta basis of the related polynomial ideal which in turn needs the reduced Gröbner basis. We prove the somewhat surprising fact that the Gröbner basis is given by the generating set defining the polynomial ideal, i.e., the order two minors and the polynomial related to the Frobenius norm. This is one of the core results of this paper. Its proof is somewhat technical (and therefore we separate the simpler order three case from the case of tensors of general order d), but it allows us to explicitly compute the theta basis and the so-called moment matrix, which finally defines the semidefinite program.

We present numerical experiments which show that θ₁-norm minimization successfully recovers tensors of low rank from few random linear measurements. We remark that we use a standard semidefinite solver which limits the size of tensors as computation time becomes too large (despite formally being polynomial) for tensors whose size is of the order 10 × 10 × 10, say. This may seem a severe limitation, but we emphasize that the focus of this paper is a first investigation of the tensor θ_k-norms with a derivation of the corresponding semidefinite programs and first (promising) numerical tests on the recovery performance. We expect that specialized algorithms for θ_k-norm minimization, for instance based on proximal splitting methods [14] such as ADMM, may lead to significantly increased computation speed with respect to standard semidefinite solvers. A second main motivation of our work is that the θ_k-norm minimization approach seems like a promising polynomially tractable approach that allows for a theoretical analysis of the required number of random linear measurement ensuring recovery—improving over presently available bounds for tractable algorithms. As outlined above, optimal estimates of the required number of measurements are presently available only for tensor recovery approaches that are NP-hard. Unfortunately, such a theoretical analysis is still missing for θ_k-norm minimization, but will be the subject of future work. In this sense, the present article may be seen as a contribution that hopefully paves the way for a better understanding of the theory of low rank tensor recovery.

Contributions

We summarize the main contributions of this article below.

• We show that the θ_k-norm reduces to nuclear norm in the matrix case for all $k \in \mathbb {N}$. This fact suggest that the θ_k-norms are natural generalizations of the matrix nuclear norm to the tensor case.

• We provide semidefinite programs for the calculation of the θ_k-norms in the case of general tensors of order d ≥ 3. We present numerical experiments for low rank tensor recovery from a small number of random Gaussian linear measurements which show that our approach is successful in practice.

• The derivation of the semidefinite programs requires to compute a moment matrix based on a theta basis of the vector space of real polynomials modulo the ideal. The computation of the theta basis in turn needs a reduced Gröbner basis of the polynomial ideal whose real algebraic variety corresponds to the (canonical) rank one, unit norm tensors. We prove the remarkable fact of potential independent interest that the generating set of minors of order 2 and the squared Frobenius norm minus 1 is already a Gröbner with respect to the graded reverse lexicographic (grevlex) ordering (Section 4.1 for third-order tensors, and Section 4.2 for general d th-order tensors).

• We show in addition that no matter which notion of tensor rank (canonical, TT, HOSVD) we consider, the polynomial ideal generated by the rank one (in the corresponding notion), unit norm tensors are all the same. As a consequence, the θ_k-norms corresponding to the different notions will all coincide (Section 4.2).

• Due to the fact that the theta norms are built from the polynomial ideal whose real algebraic variety contains all rank-one unit norm tensors, it is a natural question to ask whether the resulting θ_k-norms coincide with the weighted sum of the nuclear norms of the matricizations. In Remark 3 (Section 4.1) we show that this is not the case at least for the largest relaxation, i.e., for the θ₁-norm.

• We prove that the sequence of θ_k-norms convergence asymptotically to the (real) tensor nuclear norm as $k \to \infty$ (Section 5).

The last point should be seen as a rather theoretical result because in practice one would rather choose k = 1 or k = 2 due to computational constraints. Therefore, one cannot easily transfer theoretical results for tensor nuclear norm minimization to θ_k-norm minimization, but one rather requires a direct analysis of our approach which is postponed to future contributions.

1.1 Low rank matrix recovery

Before passing to tensor recovery, we recall some basics on matrix recovery. Let $\mathbf {X} \in \mathbb {R}^{n_{1} \times n_{2}}$ of rank at most $r \ll \min \limits \{n_{1},n_{2}\}$, and suppose we are given linear measurements $\mathbf {y} = {\mathcal{A}}(\mathbf {X})$, where ${\mathcal{A}} : \mathbb {R}^{n_{1} \times n_{2}} \to \mathbb {R}^{m}$ is a linear map with m ≪ n₁n₂. Reconstructing X from y amounts to solving an underdetermined linear system. Unfortunately, the rank minimization problem of computing the minimizer of

$$ \min_{\mathbf{Z} \in \mathbb{R}^{n_{1} \times n_{2}}} \operatorname{rank}(\mathbf{Z}) \quad \text{ subject to } \mathcal{A}(\mathbf{Z}) = \mathbf{y} $$

is NP-hard in general. As a tractable alternative, the convex optimization problem

$$ \min_{\mathbf{Z} \in \mathbb{R}^{n_{1} \times n_{2}}} \| \mathbf{Z} \|_{*} \quad \text{ subject to } \mathcal{A}(\mathbf{Z}) = \mathbf{y} $$

(1)

has been suggested [22, 55], where the nuclear norm $\|\mathbf {Z} \|_{*} = {\sum }_{j} \sigma _{j}(\mathbf {Z})$ is the sum of the singular values of Z. This problem can be solved efficiently by various methods [3]. For instance, it can be reformulated as a semidefinite program [22], but splitting methods may be more efficient [14, 51, 59].

A by-now standard result [6, 12] states that a matrix X of rank r can be stably recovered from $\mathbf {y} = {\mathcal{A}}(\mathbf {X})$, where ${\mathcal{A}}$ is a Gaussian measurement map, via nuclear norm minimization (1) with probability at least 1 − e^−cm provided that

$$ m \geq C r (n_{1}+n_{2}), $$

(2)

where the constants c, C > 0 are universal. Other interesting measurement maps (matrix completion and rank-one measurements) have been studied in [7,8,9, 13, 31, 43].

1.2 Tensor recovery

An order-d tensor (or mode-d-tensor) is an element $\mathbf {X} \in \mathbb {R}^{n_{1} \times n_{2} \times {\cdots } \times n_{d}}$ indexed by [n₁] × [n₂] ×⋯ × [n_d]. Of course, the case d = 2 corresponds to matrices. For d ≥ 3, several notions and computational tasks become much more involved than for the matrix case. Already the notion of rank requires some clarification, and in fact, several different definitions are available (see, for instance, [30, 36, 37, 44]). We will mainly work with the canonical rank or CP-rank in the following. A d th-order tensor $\mathbf {X} \in \mathbb {R}^{n_{1} \times n_{2} \times {\cdots } \times n_{d}}$ is of rank one if there exist vectors $\mathbf {u}^{1} \in \mathbb {R}^{n_{1}}, \mathbf {u}^{2} \in \mathbb {R}^{n_{2}}, \ldots , \mathbf {u}^{d} \in \mathbb {R}^{n_{d}}$ such that X = u¹ ⊗u² ⊗⋯ ⊗u^d or elementwise

$$ X_{i_{1} i_{2} {\ldots} i_{d}}=u_{i_{1}}^{1} u_{i_{2}}^{2} {\cdots} u_{i_{d}}^{d}. $$

The CP-rank (or canonical rank and in the following just rank) of a tensor $\mathbf {X} \in \mathbb {R}^{n_{1} \times n_{2} \times {\cdots } \times n_{d}}$, similarly as in the matrix case, is the smallest number of rank-one tensors that sum up to X.

Given a linear measurement map ${\mathcal{A}} : \mathbb {R}^{n_{1} \times {\cdots } \times n_{d}} \to \mathbb {R}^{m}$ (which can represented as a (d + 1)th-order tensor), our aim is to recover a tensor $\mathbf {X} \in \mathbb {R}^{n_{1} \times {\cdots } \times n_{d}}$ from $\mathbf {y} = {\mathcal{A}}(\mathbf {X})$ when m ≪ n₁ ⋅ n₂⋯n_d. The matrix case d = 2 suggests to consider minimization of the tensor nuclear norm for this task,

$$ \min_{\mathbf{Z}} \|\mathbf{Z}\|_{*} \quad \text{ subject to } {\mathcal{A}}(\mathbf{Z}) = \mathbf{y}, $$

where the nuclear norm is defined as

$$ \begin{array}{@{}rcl@{}} \left\|\mathbf{X}\right\|_{*}&=&\min \Big\{\sum\limits_{k=1}^{r} \left|c_{k}\right|: \mathbf{X} =\sum\limits_{k=1}^{r} c_{k} \mathbf{u}^{1,k} \otimes \mathbf{u}^{2,k} \otimes {\cdots} \otimes \mathbf{u}^{d,k}, r \in \mathbb{N}, \\ &&\left\|\mathbf{u}^{i,k}\right\|_{\ell_{2}}=1, i \in \left[d\right], k \in \left[r\right]\Big\}. \end{array} $$

Unfortunately, in the tensor case, computing the canonical rank of a tensor, as well as computing the nuclear norm of a tensor is NP-hard in general (see [24, 35, 38]). Let us nevertheless mention that some theoretical results for tensor recovery via nuclear norm minimization are contained in [63].

We remark that, unlike in the matrix scenario, the tensor rank and consequently the tensor nuclear norm are dependent on the choice of base field (see, for example, [4, 18, 24]). In other words, the rank (and the nuclear norm) of a given tensor with real entries depends on whether we regard it as a real tensor or as a complex tensor. In this paper, we focus only on tensors with real-valued entries, i.e., we work over the field $\mathbb {R}$.

The aim of this article is to introduce relaxations of the tensor nuclear norm, based on theta bodies, which is both computationally tractable and whose minimization allows for exact recovery of low rank tensors from incomplete linear measurements.

Let us remark that one may reorganize (flatten) a low rank tensor $\mathbf {X} \in \mathbb {R}^{n \times n \times n}$ into a low rank matrix $\tilde {\mathbf {X}} \in \mathbb {R}^{n \times n^{2}}$ and simply apply concepts from matrix recovery. However, the bound (2) on the required number of measurements then reads

$$ m \geq C r n^{2}. $$

(3)

Moreover, it has been suggested in [25, 46, 60] to minimize the sum of nuclear norms of the unfoldings (different reorganizations of the tensor as a matrix) subject to the linear constraint matching the measurements. Although this seems to be a reasonable approach at first sight, it has been shown in [50], that it cannot work with less measurements than stated by the estimate in (3). This is essentially due to the fact that the tensor structure is not represented. That is, instead of solving a tensor nuclear norm minimization problem under the assumption that the tensor is of low rank, the matrix nuclear norm minimization problem is being solved under the assumption that a particular matricization of a tensor is of low rank.

A version of the restricted isometry property for certain tensor formats in [54] is satisfied for

$$ m \geq C r^{2} n $$

(4)

Gaussian random measurements with high probability—precisely, this bound uses the tensor train format [49]. (Possibly, the term r² may even be lowered to r when using the “right” tensor format.) Unfortunately, up to the authors knowledge, it is open to show that an efficient (polynomial time) algorithm can recover rank r tensors if the restricted isometry property is satisfied. Only partial results are known [53, 54]: a tensor iterative hard thresholding algorithm is shown to converge to the original rank r tensor if on top of the restricted isometry property a certain inequality is satisfied for the approximate projection of each iterate onto the rank r tensors. Unfortunately, that inequality cannot be guaranteed for the approximate projection and also cannot be checked throughout the iterations. The exact projection would satisfy it, but is NP-hard to compute, which is the reason why one resorts to an efficient approximate projection. (Given the empirical success of the algorithm, it seems that the inequality usually holds at least starting from a certain iteration.) A local convergence result for tensor iterative hard thresholding has been given in [53], but one cannot guarantee that the iterates get close enough to the original low rank tensor ensuring convergence to the original tensor by the local result.

In any case, considering that the bound (4) for an RIP adapted to certain tensor formats is significantly better than (3) suggests that one should exploit the tensor structure of the problem rather than reducing to a matrix recovery problem in order to recover a low rank tensor using the minimal number of measurements. Of course, similar considerations apply to tensors of order higher than three, where the difference between the reduction to the matrix case and working directly with the tensor structure will become even stronger.

Unlike in the previously mentioned contributions, we consider the canonical tensor rank and the corresponding tensor nuclear norm, which respects the tensor structure. It may be expected that the bound on the minimal number of measurements needed for low rank tensor recovery via tensor nuclear norm minimization is optimal. We conjecture that such optimal bound is of the form m ≥ Crn or possibly $m \geq C r n \log (n)$. (Our numerical experiments suggest that at least the latter is true, see Fig. 3.) We note that it has been shown in [63] that tensor completion via tensor nuclear norm minimization is successful in recovering (incoherent) n × n × n tensors of rank r if $m \geq C \sqrt {r} (n \log (n))^{3/2}$, which is slightly worse than the conjectured bound (in particular, $\sqrt {rn}$ instead of r). This deficiency may be due to the fact that tensor completion is harder than recovery from Gaussian random matrices or that the proof given in [63] does not give the optimal bound (or both). In any case, the drawback of tensor nuclear norm minimization is that the tensor nuclear norm is NP-hard to compute so that this approach is intractable. In fact, [63] only gives a theoretical analysis and no algorithm (not even a heuristic one) for solving tensor nuclear norm minimization problems.

To overcome this difficulty, we introduce what we call the tensor θ_k-norms in this paper—new tensor norms which can be computed via semidefinite programming. These norms are tightly related to the tensor nuclear norm. That is, the unit θ_k-norm balls (which are defined for $k\in \mathbb {N}$) satisfy

$$ \begin{array}{@{}rcl@{}} \left\{\mathbf{X}: \left\|\mathbf{X}\right\|_{\theta_{1}}\leq 1\right\} \supseteq {\cdots} \supseteq \left\{\mathbf{X}: \left\|\mathbf{X}\right\|_{\theta_{k}}\leq 1\right\}&& \supseteq \left\{\mathbf{X}: \left\|\mathbf{X}\right\|_{\theta_{k+1}}\leq 1\right\} \\&& \supseteq {\cdots} \supseteq \left\{\mathbf{X}: \left\|\mathbf{X}\right\|_{*}\leq 1\right\}. \end{array} $$

In particular, we show that in the matrix scenario all θ_k-norms coincide with the matrix nuclear norm. In case of order-d tensors (d ≥ 3), we prove that the sequence of the unit-θ_k-norm balls converges asymptotically to the unit tensor nuclear norm ball. Next, we provide numerical experiments on low rank tensor recovery via θ₁-norm minimization. We provide numerical experiments for θ₁-minimization that indicate that this is a very promising approach for low rank tensor recovery. However, we note that standard solvers for semidefinite programs only allow us to test our method on small to moderate size problems. Nevertheless, it is likely that specialized efficient algorithms can be developed. Indeed, recall that θ_k-norms all coincide with the matrix nuclear norm and the state-of-the-art algorithms allow us computing the nuclear norm of matrices of large dimensions. This suggests the possibility that new algorithms could be developed which would allow us to apply our method on larger tensors. Thus, this paper presents the first step in a new convex optimization approach to low rank tensor recovery.

1.3 Some notation

We write vectors with small bold letters, matrices and tensors with capital bold letters and sets with capital calligraphic letters. The cardinality of a set ${\mathcal{S}}$ is denoted by $|{\mathcal{S}}|$.

For a matrix $\mathbf {A} \in \mathbb {R}^{m \times n}$ and subsets ${\mathcal{I}} \subset \left [m\right ]$, ${\mathcal{J}} \subset \left [n\right ]$ the submatrix of A with columns indexed by ${\mathcal{I}}$ and rows indexed by ${\mathcal{J}}$ is denoted by $\mathbf {A}_{{\mathcal{I}}, {\mathcal{J}}}$.

The Frobenius norm of a d th-order tensor $\mathbf {X} \in \mathbb {R}^{n_{1} \times n_{2} \times {\cdots } \times n_{d}}$ is defined as $\left \|\mathbf {X}\right \|_{F}= \left ({\sum }_{i_{1}=1}^{n_{1}} {\sum }_{i_{2}=1}^{n_{2}} {\cdots } {\sum }_{i_{d}=1}^{n_{d}} X_{i_{1} i_{2} {\cdots } i_{d}}^{2}\right )^{1/2}.$ The vectorization of a tensor $\mathbf {X} \in \mathbb {R}^{n_{1} \times n_{2} \times \cdots \times n_{d}}$ is denoted by $(\mathbf {X}) \in \mathbb {R}^{n_{1} n_{2} {\cdots } n_{d}}$. For $k \in \left [d\right ]$, the mode-k fiber of a d th-order tensor is obtained by fixing every index except for the k th one. For a tensor $\mathbf {X} \in \mathbb {R}^{n_{1} \times n_{2} \times {\cdots } \times n_{d}}$ and an ordered subset ${\mathcal{S}} \subseteq \left [d\right ]$, an ${\mathcal{S}}$-matricization $\mathbf {X}^{{\mathcal{S}}} \in \mathbb {R}^{{\prod }_{k \in {\mathcal{S}}} n_{k} \times {\prod }_{\ell \in {\mathcal{S}}^{c}}n_{\ell }}$ is defined as ${X}^{{\mathcal{S}}}_{(i_{k})_{k \in {\mathcal{S}}}, (i_{\ell })_{\ell \in {\mathcal{S}}^{c}}}={X}_{i_{1} i_{2} {\ldots } i_{d}},$ i.e., the indices in the set ${\mathcal{S}}$ define the rows of the matrix $\mathbf {X}^{{\mathcal{S}}}$ and the indices in the set ${\mathcal{S}}^{c}=\left [d\right ]\backslash {\mathcal{S}}$ define the columns. For a singleton set ${\mathcal{S}}=\{i\}$, for $i \in \left [d\right ]$, we call the ${\mathcal{S}}$-matricization the i th unfolding.

For a tensor $\mathbf {X} \in \mathbb {R}^{n_{1} \times n_{2} \times {\cdots } \times n_{d}}$ of order d, we write X(:,:,…,:,k) for the order (d − 1) subtensor in $\mathbb {R}^{n_{1} \times n_{2} \times {\cdots } \times n_{d-1}}$ obtained by fixing the last index α_d to k. Instead of writing $x_{\alpha _{1}\alpha _{2}{\ldots } \alpha _{d}}x_{\beta _{1}\beta _{2}\ldots \beta _{d}}$, we often use the simpler notation x_αx_β. We will use the grevlex ordering of monomials: $x_{11{\ldots } 11} > x_{11 {\ldots } 12} > {\cdots } > x_{11{\ldots } 1 n_{d}} > x_{111 {\ldots } 21}> {\ldots } > x_{n_{1} n_{2} {\ldots } n_{d}}$.

1.4 Structure of the paper

In Section 2 we will review the basic definition and properties of theta bodies. Section 3 considers the matrix case. We introduce a suitable polynomial ideal whose algebraic variety is the set of rank-one unit Frobenius norm matrices. We discuss the corresponding θ_k-norms and show that they all coincide with the matrix nuclear norm. The case of 2 × 2-matrices is described in detail. In Section 4 we pass to the tensor case and discuss first the case of order-three tensors. We introduce a suitable polynomial ideal, provide its reduced Gröbner basis and define the corresponding θ_k-norms. We additionally show that considering matricizations corresponding to the TT-format will lead to the same polynomial ideal and thus to the same θ_k-norms. The general d th-order case is discussed at the end of Section 4. Here, we define the polynomial ideal J_d which corresponds to the set of all possible matricizations of the tensor. We show that a certain set of order-two minors forms the reduced Gröbner basis for this ideal, which is key for defining the θ_k-norms. We additionally show that polynomial ideals corresponding to different tensor formats (such as TT format or Tucker/HOSVD format) coincide with the ideal J_d and consequently, they lead to the same θ_k-norms. In Section 5 we discuss the convergence of the sequence of the unit-θ_k-norm balls to the unit tensor nuclear norm ball. Section 6 briefly discusses the polynomial runtime of the algorithms for computing and minimizing the θ_k-norms showing that our approach is tractable. Numerical experiments for low rank recovery of third-order tensors are presented in Section 7, which show that our approach successfully recovers a low rank tensor from incomplete Gaussian random measurements. Appendix discusses some background from computer algebra (monomial orderings and Gröbner bases) that is required throughout the main body of the article.

2 Theta bodies

As outlined above, we will introduce new tensor norms as relaxations of the nuclear norm in order to come up with a new convex optimization approach for low rank tensor recovery. Our approach builds on theta bodies, a recent concept from computational algebraic geometry, which is similar to Lasserre relaxations [45]. In order to introduce it, we first discuss the necessary basics from computational commutative algebra. For more information, we refer to [15, 16] and to the Appendix.

For a non-zero polynomial $f={\sum }_{\mathbf {\alpha }}a_{\mathbf {\alpha }} {\mathbf {x}}^{\mathbf {\alpha }}$ in $\mathbb {R}\left [\mathbf {x}\right ]=\mathbb {R}\left [x_{1},x_{2},\ldots ,x_{n}\right ]$ and a monomial order >, we denote

• a) the multidegree of f by multideg $\left (f\right )=\max \limits \left (\mathbf {\alpha } \in \mathbb {Z}_{\geq 0}^{n}: a_{\mathbf {\alpha }} \neq 0\right )$,

• b) the leading coefficient of f by LC $\left (f\right )=a_{\text {multideg} \left (f\right )} \in \mathbb {R}$,

• c) the leading monomial of f by LM $\left (f\right )=\mathbf {x}^{\text {multideg} \left (f\right )}$,

• d) the leading term of f by LT $\left (f\right )=LC\left (f\right ) LM\left (f\right ).$

Let $J \subset \mathbb {R}\left [\mathbf {x}\right ]$ be a polynomial ideal. Its real algebraic variety is the set of all points in $\mathbf {x} \in \mathbb {R}^{n}$ where all polynomials in the ideal vanish, i.e.,

$$\nu_{\mathbb{R}}\left( J\right)=\{\mathbf{x} \in \mathbb{R}^{n}: f(\mathbf{x})=0, \text{ for all } f \in J \}.$$

By Hilbert’s basis theorem [16] every polynomial ideal in $\mathbb {R}\left [\mathbf {x}\right ]$ has a finite generating set. Thus, we may assume that J is generated by a set ${\mathcal{F}}=\{f_{1},f_{2},\ldots ,f_{k}\}$ of polynomials in $\mathbb {R}[x]$ and write

$$J=\left<f_{1},f_{2},\ldots,f_{k}\right>=\left<\left\{f_{i}\right\}_{i \in \left[k\right]}\right> \quad \text{or simply} \quad J=\left<\mathcal{F}\right>.$$

Its real algebraic variety is the set

$$\nu_{\mathbb{R}}\left( J\right)=\{\mathbf{x} \in \mathbb{R}^{n}: f_{i}(\mathbf{x})=0 \text{ for all } i \in \left[k\right] \}.$$

Throughout the paper, $\mathbb {R}\left [\mathbf {x}\right ]_{k}$ denotes the set of polynomials of degree at most k. A degree one polynomial is also called linear polynomial. A very useful certificate for positivity of polynomials is contained in the following definition [27].

Definition 1

Let J be an ideal in $\mathbb {R}\left [\mathbf {x}\right ]$. A polynomial $f \in \mathbb {R}\left [\mathbf {x}\right ]$ is k-sos mod J if there exists a finite set of polynomials $h_{1},h_{2},\ldots ,h_{t} \in \mathbb {R}\left [\mathbf {x}\right ]_{k}$ such that $f \equiv {\sum }_{j=1}^{t} {h_{j}^{2}}$ mod J, i.e., if $f-{\sum }_{j=1}^{t} {h_{j}^{2}} \in J$.

A special case of theta bodies was first introduced by Lovász in [48] and in full generality they appeared in [27]. Later, they have been analyzed in [26, 28]. The definitions and theorems in the remainder of the section are taken from [27].

Definition 2 (Theta body)

Let $J \subseteq \mathbb {R}\left [\mathbf {x}\right ]$ be an ideal. For a positive integer k, the k th theta body of J is defined as

$$ TH_{k}\left( J\right):=\left\{\mathbf{x} \in \mathbb{R}^{n} : f\left( \mathbf{x}\right)\geq 0 \text{ for every linear } f \text{ that is \textit{k}-sos mod }J \right\}. $$

We say that an ideal $J \subseteq \mathbb {R}\left [\mathbf {x}\right ]$ is TH_k-exact if $TH_{k}\left (J\right )$ equals $\overline {\text {conv}\left (\nu _{\mathbb {R}}({J})\right )}$, the closure of the convex hull of $\nu _{\mathbb {R}}\left (J\right )$.

Theta bodies are closed convex sets, while $\text {conv}\left (\nu _{\mathbb {R}}({J})\right )$ may not necessarily be closed and by definition,

$$ TH_{1}\left( J\right) \supseteq TH_{2}\left( J\right) \supseteq {\cdots} \supseteq \text{conv}\left( \nu_{\mathbb{R}}({J}\right)). $$

(5)

The theta body sequence of J can converge (finitely or asymptotically), if at all, only to $\overline {\text {conv}\left (\nu _{\mathbb {R}}({J})\right )}$. More on guarantees on convergence can be found in [27, 28]. However, to our knowledge, none of the existing guarantees applies to the cases discussed below.

Given any polynomial, it is possible to check whether it is k-sos mod J using a Gröbner basis and semidefinite programming. However, using this definition in practice requires knowledge of all linear polynomials (possibly infinitely many) that are k-sos mod J. To overcome this difficulty, we need an alternative description of TH_k(J) discussed next.

As in [2], we assume that there are no linear polynomials in the ideal J. Otherwise, some variable x_i would be congruent to a linear combination of other variables modulo J and we could work in a smaller polynomial ring $\mathbb {R}[{x}^{i}]=\mathbb {R}[x_{1},x_{2},\ldots ,x_{i-1},x_{i+1},\ldots ,x_{n}]$. Therefore, $\mathbb {R}[{x}]_{1}/J \cong \mathbb {R}[{x}]_{1}$ and {1 + J, x₁ + J,…,x_n + J} can be completed to a basis ${\mathcal{B}}$ of $\mathbb {R}[{x}]/J$. Recall that the degree of an equivalence class f + J, denoted by $\deg ({f+J})$, is the smallest degree of an element in the class. We assume that each element in the basis ${\mathcal{B}}=\{f_{i}+J\}$ of $\mathbb {R}[{x}]/J$ is represented by the polynomial whose degree equals the degree of its equivalence class, i.e., $\deg {f_{i}+J}=\deg {f_{i}}$. In addition, we assume that ${\mathcal{B}}=\{f_{i}+J\}$ is ordered so that f_i+ 1 > f_i, where > is a fixed monomial ordering. Further, we define the set ${\mathcal{B}}_{k}$

$$ \mathcal{B}_{k}:=\{ f+J \in \mathcal{B}: deg(f+J) \leq k\}. $$

Definition 3 (Theta basis)

Let $J \subseteq \mathbb {R}\left [\mathbf {x}\right ]$ be an ideal. A basis ${\mathcal{B}}=\{f_{0}+J, f_{1}+J, \ldots \}$ of the vector space $\mathbb {R}\left [\mathbf {x}\right ]/J$ is a θ-basis if it has the following properties

• 1) ${\mathcal{B}}_{1}=\left \{1+J, x_{1} +J, \ldots , x_{n}+J\right \}$,

• 2) if $deg\left (f_{i}+J\right ), deg\left (f_{j}+J\right ) \leq k$ then f_if_j + J is in the $\mathbb {R}$-span of ${\mathcal{B}}_{2k}$.

As in [2, 27] we consider only monomial bases ${\mathcal{B}}$ of $\mathbb {R}\left [\mathbf {x}\right ]/J$, i.e., bases ${\mathcal{B}}$ such that f_i is a monomial, for all $f_{i}+J \in {\mathcal{B}}$.

For determining a θ-basis, we first need to compute the reduced Gröbner basis ${\mathcal{G}}$ of the ideal J (see Definitions 8 and 9). The set ${{\mathcal{B}}}$ will satisfy the second property in the definition of the theta basis if the reduced Gröbner basis is with respect to an ordering which first compares the total degree. Therefore, throughout the paper we use the graded reverse monomial ordering (Definition 7) or simply grevlex ordering, although also the graded lexicographic ordering would be appropriate.

A technique to compute a θ-basis ${\mathcal{B}}$ of $\mathbb {R}\left [\mathbf {x}\right ]/J$ consists in taking ${\mathcal{B}}$ to be the set of equivalence classes of the standard monomials of the corresponding initial ideal

$$J_{\text{initial}}=\left<\left\{LT(f)\right\}_{f \in J}\right>=\left<\left\{LT(g_{i})\right\}_{i \in \left[s\right]}\right>, $$

where ${\mathcal{G}}=\left <g_{1},g_{2},\ldots ,g_{s}\right >$ is the reduced Gröbner basis of the ideal J. In other words, a set ${\mathcal{B}}=\{f_{0}+J,f_{1}+J,\ldots \}$ will be a θ-basis of $\mathbb {R}[{x}]/J$ if it contains all f_i + J such that

• 1. f_i is a monomial

• 2. f_i is not divisible by any of the monomials in the set $\left \{LT(g_{i}): i \in \left [s\right ]\right \}$.

The next important tool we need is the combinatorial moment matrix of J. To this end, we fix a θ-basis ${\mathcal{B}}=\left \{f_{i} +J\right \}$ of $\mathbb {R}\left [\mathbf {x}\right ]/J$ and define $\left [\mathbf {x}\right ]_{{\mathcal{B}}_{k}}$ to be the column vector formed by all elements of ${\mathcal{B}}_{k}$ in order. Then $\left [\mathbf {x}\right ]_{{\mathcal{B}}_{k}}\left [\mathbf {x}\right ]_{{\mathcal{B}}_{k}}^{T}$ is a square matrix indexed by ${\mathcal{B}}_{k}$ and its $\left (i,j\right )$-entry is equal to f_if_j + J. By hypothesis, the entries of $\left [\mathbf {x}\right ]_{{\mathcal{B}}_{k}}\left [\mathbf {x}\right ]_{{\mathcal{B}}_{k}}^{T}$ lie in the $\mathbb {R}$-span of ${\mathcal{B}}_{2k}$. Let $\{\lambda _{i,j}^{l}\}$ be the unique set of real numbers such that $f_{i} f_{j} + J={\sum }_{f_{l} + J \in {\mathcal{B}}_{2k}}\lambda _{i,j}^{l} \left (f_{l}+J\right )$.

The theta bodies can be characterized via the combinatorial moment matrix as stated in the next result from [27], which will be the basis for computing and minimization the new tensor norm introduced below via semidefinite programming.

Definition 4

Let $J, {\mathcal{B}}$ and $\{\lambda _{i,j}^{l}\}$ be as above. Let y be a real vector indexed by ${\mathcal{B}}_{2k}$ with y₀ = 1, where y₀ is the first entry of y, indexed by the basis element 1 + J. The k th combinatorial moment matrix $\textbf {M}_{{\mathcal{B}}_{k}}({y})$ of J is the real matrix indexed by ${\mathcal{B}}_{k}$ whose (i, j)-entry is $[{M}_{{\mathcal{B}}_{k}}(\textbf {y})]_{i,j}={\sum }_{f_{l}+J \in {\mathcal{B}}_{2k}} \lambda _{i,j}^{l} y_{l}$.

Theorem 1

The k th theta body of J, $\text {TH}_{k}\left (J\right )$, is the closure of

$$ \mathbf{Q}_{\mathcal{B}_{k}}\left( J\right)=\pi_{\mathbb{R}^{n}} \left\{\mathbf{y} \in \mathbb{R}^{\mathcal{B}_{2k}} : \mathbf{M}_{\mathcal{B}_{k}}\left( \mathbf{y}\right) \succeq 0, y_{0}=1\right\}, $$

where $\pi _{\mathbb {R}^{n}}$ denotes the projection onto the variables $y_{1}=y_{x_{1} + J},\ldots ,y_{n}=y_{x_{n} + J}$.

Algorithm 1 shows a step-by-step procedure for computing TH_k(J).

3 The matrix case

As a start, we consider the matrix nuclear unit norm ball and provide hierarchical relaxations via theta bodies. The k th relaxation defines a matrix unit θ_k-norm ball with the property

$$ \left\|\mathbf{X}\right\|_{\theta_{k}} \leq \left\|\mathbf{X}\right\|_{\theta_{k+1}} \quad \text{ for all } \mathbf{X} \in \mathbb{R}^{m \times n} \text{ and all } k \in \mathbb{N} . $$

However, we will show that all these θ_k-norms coincide with the matrix nuclear norm.

The first step in computing hierarchical relaxations of the unit nuclear norm ball consists in finding a polynomial ideal J such that its algebraic variety (the set of points for which the ideal vanishes) coincides with the set of all rank-one, unit Frobenius norm matrices

$$ \nu_{\mathbb{R}}(J) = \left\{\mathbf{X} \in \mathbb{R}^{m \times n}: \left\|\mathbf{X}\right\|_{F}=1, \text{rank}\left( \mathbf{X}\right)=1\right\}. $$

(6)

Recall that the convex hull of this set is the nuclear norm ball. The following lemma states the elementary fact that a non-zero matrix is a rank-one matrix if and only if all its minors of order two are zero.

For notational purposes, we define the following polynomials in $\mathbb {R}\left [\mathbf {x}\right ]=\mathbb {R}\left [x_{11},x_{12},\ldots ,x_{mn}\right ]$

$$ \begin{array}{@{}rcl@{}} g(\mathbf{x})&=&\sum\limits_{i=1}^{m} \sum\limits_{j=1}^{n} x_{ij}^{2}-1 \text{ and }f_{ijkl}(\mathbf{x})=x_{il}x_{kj}-x_{ij}x_{kl} \\ && \quad \text{ for } 1\leq i<k \leq m, 1\leq j <l \leq n. \end{array} $$

(7)

Lemma 1

Let $\mathbf {X} \in \mathbb {R}^{m \times n} \backslash \left \{\mathbf {0}\right \}$. Then X is a rank-one, unit Frobenius norm matrix if and only if

$$ \mathbf{X} \in \mathcal{R}:=\{\mathbf{X}: g(\mathbf{X})=0 \text{ and } f_{ijkl}(\mathbf{X})=0 \text{ for all } i<k, j<l \}. $$

(8)

Proof

If $\mathbf {X} \in \mathbb {R}^{m \times n}$ is a rank-one matrix with ∥X∥_F = 1, then by definition there exist two vectors $\mathbf {u} \in \mathbb {R}^{m}$ and $\mathbf {v} \in \mathbb {R}^{n}$ such that X_ij = u_iv_j for all $i \in \left [m\right ]$, $j \in \left [n\right ]$ and $\left \|\mathbf {u}\right \|_{2}=\left \|\mathbf {v}\right \|_{2}=1$. Thus

$$ \begin{array}{@{}rcl@{}} & X_{ij}X_{kl}-X_{il}X_{kj}= u_{i} v_{j} u_{k} v_{l} - u_{i} v_{l} u_{k} v_{j} = 0 \\ \text{and} \quad &\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{n} X_{ij}^{2}=\sum\limits_{i=1}^{m} {u_{i}^{2}} \sum\limits_{j=1}^{n} {v_{j}^{2}}=1. \end{array} $$

For the converse, let X_⋅i represent the i th column of a matrix $\mathbf {X} \in {\mathcal{R}}$. Then, for all $j,l \in \left [n\right ]$ with j < l, it holds

$$ X_{ml} \cdot \mathbf{X}_{\cdot j} - X_{mj} \cdot \mathbf{X}_{\cdot l}= \begin{bmatrix} X_{1j}X_{ml} - X_{1l}X_{mj} \\ X_{2j}X_{ml} -X_{2l}X_{mj} \\ {\vdots} \\ X_{mj}X_{ml} -X_{mj}X_{ml} \end{bmatrix}= \mathbf{0}, $$

since X_ijX_ml = X_ilX_mj for all $i \in \left [m-1\right ]$ by definition of ${\mathcal{R}}$. Thus, the columns of the matrix X span a space of dimension one, i.e., the matrix X is a rank-one matrix. From ${\sum }_{i=1}^{m} {\sum }_{j=1}^{n} X_{ij}^{2}-1=0$ it follows that the matrix X is normalized, i.e., $\left \|\mathbf {X}\right \|_{F}=1$. □

It follows from Lemma 1 that the set of rank-one, unit Frobenius norm matrices coincides with the algebraic variety $\nu _{\mathbb {R}}\left (J_{M_{mn}}\right )$ for the ideal $J_{M_{mn}}$ generated by the polynomials g and f_ijkl, i.e.,

$$ \begin{array}{@{}rcl@{}} J_{M_{mn}}&=&\langle\mathcal{G}_{M_{mn}}\rangle\quad \text{with}\\ \mathcal{G}_{M_{mn}}&=&\{g(x)\}\cup\{f_{ijkl}(x):1\leq{i}<{k}\leq{m},1\leq{j}<{l}\leq{n}\} \end{array} $$

(9)

Recall that the convex hull of the set ${\mathcal{R}}$ in (8) forms the unit nuclear norm ball and by definition of the theta bodies,

$$\overline{\text{conv}(\nu_{\mathbb{R}}(J_{M_{mn}}))} \subseteq {\cdots} \subseteq TH_{k+1}(J_{M_{mn}}) \subseteq TH_{k}(J_{M_{mn}}) \subseteq {\cdots} \subseteq TH_{1}(J_{M_{mn}}).$$

Therefore, the theta bodies form closed, convex hierarchical relaxations of the matrix nuclear norm ball. In addition, the theta body $TH_{k}(J_{M_{mn}})$ is symmetric, $TH_{k}(J_{M_{mn}}) = - TH_{k}(J_{M_{mn}})$. Therefore, it defines a unit ball of a norm that we call the θ_k-norm.

The next result shows that the generating set of the ideal $J_{M_{mn}}$ introduced above is a Gröbner basis.

Lemma 2

The set ${\mathcal{G}}_{M_{mn}}$ forms the reduced Gröbner basis of the ideal $J_{M_{mn}}$ with respect to the grevlex order.

Proof

The set ${\mathcal{G}}_{M_{m n}}$ is clearly a basis for the ideal $J_{M_{m n}}$. By Proposition 1 in the Appendix, we only need to check whether the S-polynomial (see Definition 11) satisfies $S\left (p,q\right ) \rightarrow _{{\mathcal{G}}_{M_{mn}}} 0$ for all $p,q \in {\mathcal{G}}_{M_{m n}}$ whenever the leading monomials $LM\left (p\right )$ and LM(q) are not relatively prime. Here, $S\left (p,q\right ) \rightarrow _{{\mathcal{G}}_{M_{mn}}} 0$ means that $S\left (p,q\right )$ reduces to 0 modulo ${{\mathcal{G}}_{M_{mn}}}$ (see Definition 10).

Notice that $LM\left (g\right )=x_{11}^{2}$ and $LM\left (f_{ijkl}\right )=x_{il}x_{kj}$ are relatively prime, for all 1 ≤ i < k ≤ m and 1 ≤ j < l ≤ n. Therefore, we only need to show that $S(f_{ijkl},f_{\hat {i}\hat {j}\hat {k}\hat {l}}) \rightarrow _{{\mathcal{G}}_{M_{mn}}} 0$ whenever the leading monomials LM(f_ijkl) and $LM(f_{\hat {i}\hat {j}\hat {k}\hat {l}})$ are not relatively prime. First we consider

$$ f_{ijkl}(\mathbf{x})=x_{il} x_{kj} - x_{ij}x_{kl} \quad \text { and } \quad f_{i\hat{j}\hat{k}l}(\mathbf{x})= x_{il} x_{\hat{k}\hat{j}} - x_{i\hat{j}}x_{\hat{k}l} $$

for $1 \leq i < k < \hat {k} \leq m, 1 \leq j < \hat {j} <l \leq n$. The S-polynomial is then of the form

$$ \begin{array}{@{}rcl@{}} S(f_{ijkl},f_{i\hat{j}\hat{k}l}) = x_{\hat{k}\hat{j}}f_{ijkl}(\mathbf{x}) - x_{kj}f_{i\hat{j}\hat{k}l}(\mathbf{x})&=& - x_{ij}x_{kl}x_{\hat{k}\hat{j}} + x_{i\hat{j}}x_{\hat{k}l}x_{kj}\\&=&x_{\hat{k}l} f_{ijk\hat{j}}(\mathbf{x}) - x_{ij} f_{k\hat{j}\hat{k}l}(\mathbf{x}) \in J_{M_{mn}} \end{array} $$

so that $S(f_{ijkl},f_{i\hat {j}\hat {k}l}) \rightarrow _{{\mathcal{G}}_{M_{mn}}} 0$. The remaining cases are treated with similar arguments.

In order to show that ${\mathcal{G}}_{M_{mn}}$ is a reduced Gröbner basis (see Definition 9), we first notice that LC(f) = 1 for all $f \in {\mathcal{G}}_{M_{m n}}$. In addition, the leading monomial of $f \in {\mathcal{G}}_{M_{mn}}$ is always of degree two and there are no two different polynomials $f_{i},f_{j} \in {\mathcal{G}}_{M_{m n}}$ such that LM(f_i) = LM(f_j). Therefore, ${\mathcal{G}}_{M_{mn}}$ is the reduced Gröbner basis of the ideal $J_{M_{mn}}$ with respect to the grevlex order. □

The Gröbner basis ${\mathcal{G}}_{M_{m n}}$ of $J_{M_{mn}}=\left <{\mathcal{G}}_{M_{mn}}\right >$ yields the θ-basis of $\mathbb {R}[\mathbf {x}]/J_{M_{mn}}$. For the sake of simplicity, we only provide its elements up to degree two,

$$ \begin{array}{@{}rcl@{}} \mathcal{B}_{1}&=&\left\{1+J_{M_{mn}}, x_{11}+J_{M_{mn}}, x_{12}+J_{M_{mn}}, \ldots, x_{mn}+J_{M_{mn}} \right\} \\ \mathcal{B}_{2}&=&\mathcal{B}_{1} \cup \left\{x_{ij}x_{kl}+J_{M_{mn}}: \left( i,j,k,l\right) \in \mathcal{S}_{\mathcal{B}_{2}}\right\}, \end{array} $$

where ${\mathcal{S}}_{{\mathcal{B}}_{2}}=\left \{\left (i,j,k,l\right ): 1 \leq i \leq k \leq m, 1 \leq j \leq l \leq n\right \} \backslash \left (1,1,1,1\right )$. Given the θ-basis, the theta body $TH_{k}(J_{M_{mn}})$ is well-defined. We formally introduce an associated norm next.

Definition 5

The matrix θ_k-norm, denoted by $\left \|\cdot \right \|_{\theta _{k}}$, is the norm induced by the k-theta body $TH_{k}\left (J_{M_{mn}}\right )$, i.e.,

$$ \left\|\mathbf{X}\right\|_{\theta_{k}}=\inf \left\{r: \mathbf{X} \in r TH_{k}\left( J_{M_{mn}}\right)\right\}. $$

The θ_k-norm can be computed with the help of Theorem 1, i.e., as

$$ \left\|\mathbf{X}\right\|_{\theta_{k}} = \min t \quad \text{ subject to } \mathbf{X} \in t \mathbf{Q}_{\mathcal{B}_{k}}(J_{M_{mn}}). $$

Given the moment matrix $\mathbf {M}_{{\mathcal{B}}_{k}}[\mathbf {y}]$ associated with $J_{M_{mn}}$, this minimization program is equivalent to the semidefinite program

$$ \min_{t \in \mathbb{R} , \mathbf{y} \in \mathbb{R}^{\mathcal{B}_{k}}} t \quad \text{ subject to } \quad \mathbf{M}_{\mathcal{B}_{k}}[\mathbf{y}] \succcurlyeq 0, y_{0} = t, \mathbf{y}_{\mathcal{B}_{1}} = \mathbf{X}. $$

(10)

The last constraint might require some explanation. The vector $\mathbf {y}_{{\mathcal{B}}_{1}}$ denotes the restriction of y to the indices in ${\mathcal{B}}_{1}$, where the latter can be identified with the set [m] × [n] indexing the matrix entries. Therefore, $\mathbf {y}_{{\mathcal{B}}_{1}} = \mathbf {X}$ means componentwise $y_{x_{11}+J} = X_{11}, y_{x_{12}+J} = X_{12}, \hdots , y_{x_{mn} + J} = X_{mn}$. For the purpose of illustration, we focus on the θ₁-norm in $\mathbb {R}^{2 \times 2}$ in Section 3.1 below, and provide a step-by-step procedure for building the corresponding semidefinite program in (10).

Notice that the number of elements in ${\mathcal{B}}_{1}$ is mn + 1, and in ${\mathcal{B}}_{2} \backslash {\mathcal{B}}_{1}$ is $\frac {m\cdot (m+1)}{2} \cdot \frac {n \cdot (n+1)}{2} -1\sim \frac {\left (mn\right )^{2}}{2}$, i.e., the number of elements of the θ-basis restricted to the degree 2 scales polynomially in the total number of matrix entries mn. Therefore, the computational complexity of the SDP in (10) is polynomial in mn.

We will show next that the theta body TH₁(J) and hence, all TH_k(J) for $k \in \mathbb {N}$, coincide with the nuclear norm ball. To this end, the following lemma provides expressions for the boundary of the matrix nuclear unit norm ball.

Lemma 3

Let ${\mathcal{O}}_{c}$ (${\mathcal{O}}_{r}$) denote the set of all matrices $\mathbf {M} \in \mathbb {R}^{n \times m}$ with orthonormal columns (rows), i.e., ${\mathcal{O}}_{c}=\left \{\mathbf {M} \in \mathbb {R}^{n \times m}: \mathbf {M}^{T}\mathbf {M}=\mathbf {I}_{m}\right \}$ and ${\mathcal{O}}_{r}=\left \{\mathbf {M} \in \mathbb {R}^{n \times m}: \mathbf {M}\mathbf {M}^{T}=\mathbf {I}_{n}\right \}$. Then

$$ \left\{\mathbf{X} \in \mathbb{R}^{m \times n}: \left\|\mathbf{X}\right\|_{*}\leq 1\right\}=\left\{\mathbf{X} \in \mathbb{R}^{m \times n}:tr\left( \mathbf{M}\mathbf{X}\right) \leq 1, \text{ for all } \mathbf{M} \in \mathcal{O}_{c} \cup \mathcal{O}_{r}\right\}. $$

(11)

Remark 1

Notice that ${\mathcal{O}}_{c}=\emptyset$ for m > n and ${\mathcal{O}}_{r}=\emptyset$ for m < n.

Proof

If suffices to treat the case m ≤ n because $\left \|\mathbf {X}\right \|_{*}=\left \|\mathbf {X}^{T}\right \|_{*}$ for all matrices X, and $\mathbf {M} \in {\mathcal{O}}_{r}$ if and only if $\textbf {M}^{T} \in {\mathcal{O}}_{c}$. Let $\mathbf {X} \in \mathbb {R}^{m \times n}$ such that $\left \|\mathbf {X}\right \|_{*}\leq 1$ and let $\mathbf {X}=\mathbf {U}_{\Sigma }\mathbf {V}^{T}$ be its singular value decomposition. For $\mathbf {M} \in {\mathcal{O}}_{c}$, the spectral norm satisfies ∥M∥≤ 1 and therefore, using that the nuclear norm is the dual of the spectral norm (see e.g., [1, p. 96]),

$$ \begin{array}{@{}rcl@{}} tr\left( \mathbf{M}\mathbf{X}\right) \leq \|\mathbf{M}\| \cdot \|\mathbf{X}\|_{*} \leq \left\|\mathbf{X}\right\|_{*} \leq 1. \end{array} $$

For the converse, let $\mathbf {X} \in \mathbb {R}^{m \times n}$ be such that $tr\left (\mathbf {M}\mathbf {X}\right ) \leq 1$, for all $\mathbf {M} \in {\mathcal{O}}_{c}$. Let $\mathbf {X}=\mathbf {U}_{\bar {\Sigma }} \overline {\mathbf {V}}^{T}$ denote its reduced singular value decomposition, i.e., $\mathbf {U},_{\bar {\Sigma }} \in \mathbb {R}^{m \times m}$ and $\overline {\mathbf {V}} \in \mathbb {R}^{n \times m}$ with $\mathbf {U}^{T}\mathbf {U}=\mathbf {U}\mathbf {U}^{T}=\overline {\mathbf {V}}^{T}\overline {\mathbf {V}}=\mathbf {I}_{m}$. Since $\mathbf {M}:=\overline {\mathbf {V}}\mathbf {U}^{T} \in {\mathcal{O}}_{c}$, it follows that

$$ 1\geq tr(\mathbf{MX})=tr(\overline{\mathbf{V}}\mathbf{U}^{T}\mathbf{U}_{\bar{\Sigma}} \overline{\mathbf{V}}^{T})=tr_{({\bar{\Sigma})}}=\left\|\mathbf{X}\right\|_{*}.$$

This completes the proof. □

Next, using Lemma 3, we show that the theta body TH₁(J) equals the nuclear norm ball. This result is related to Theorem 4.4 in [28].

Theorem 2

The polynomial ideal $J_{M_{m n}}$ defined in (9) is TH₁-exact, i.e.,

$$TH_{1}\left( J_{M_{m n}}\right)=\text{conv}\left( \mathbf{x} : g(\mathbf{x})=0, f_{ijkl}(\mathbf{x})=0 \text{ for all }i<k, j<l\right).$$

In other words,

$$ \left\{\mathbf{X} \in \mathbb{R}^{m \times n}: \mathbf{X} \in TH_{1}\left( J_{M_{mn}}\right)\right\}=\left\{\mathbf{X} \in \mathbb{R}^{m \times n}: \left\|\mathbf{X}\right\|_{*} \leq 1\right\}. $$

Proof

By definition of $TH_{1}(J_{M_{mn}})$, it is enough to show that the boundary of the unit nuclear norm can be written as 1-sos mod $J_{M_{mn}}$, which by Lemma 3 means that the polynomial $1-{\sum }_{i=1}^{m}{\sum }_{j=1}^{n}{x_{ij}M_{ji}}$ is 1-sos mod $J_{M_{mn}}$ for all $\mathbf {M} \in {\mathcal{O}}_{c} \cup {\mathcal{O}}_{r}$. We start by fixing $\mathbf {M}=\begin {pmatrix} \mathbf {I}_{m} \\ \mathbf {0} \end {pmatrix}$ in case m ≤ n and $\mathbf {M}=\begin {pmatrix} \mathbf {I}_{n} & \mathbf {0} \end {pmatrix}$ in case m > n, where $\mathbf {I}_{k} \in \mathbb {R}^{k \times k}$ is the identity matrix. For this choice of M, we need to show that $1-{\sum }_{i=1}^{\ell } x_{ii}$ is 1-sos mod $J_{M_{mn}}$, where $\ell ={\min \limits } \left \{m,n\right \}$. Note that

$$ \begin{array}{@{}rcl@{}} 1-{\sum}_{i=1}^{\ell}x_{ii}&=&\frac{1}{2}\left[\left( 1-{\sum}_{i=1}^{\ell} x_{ii}\right)^{2} + \left( 1-{\sum}_{i=1}^{m}{\sum}_{j=1}^{n} x_{ij}^{2}\right)+{\sum}_{i<j\leq {\ell}}\left( x_{ij}-x_{ji}\right)^{2} \right.\\ && \left. -2{\sum}_{i<j\leq {\ell}}\left( x_{ii}x_{jj}-x_{ij}x_{ji}\right) +{\sum}_{i=1}^{m}{\sum}_{j=m+1}^{n} x_{ij}^{2} + {\sum}_{i=n+1}^{m}{\sum}_{j=1}^{n} x_{ij}^{2}\right], \end{array} $$

since

$$ \begin{array}{@{}rcl@{}} \left( 1-{\sum}_{i=1}^{\ell} x_{ii}\right)^{2}&=&1-2{\sum}_{i=1}^{\ell} x_{ii}+{\sum}_{i=1}^{\ell}{\sum}_{j=1}^{\ell} x_{ii}x_{jj} \\ &=& 1-2{\sum}_{i=1}^{\ell} x_{ii}+2{\sum}_{i<j\leq {\ell}}x_{ii}x_{jj} +{\sum}_{i=1}^{\ell} x_{ii}^{2}, \end{array} $$

$$ \begin{array}{@{}rcl@{}} 1-{\sum}_{i=1}^{m}{\sum}_{j=1}^{n} x_{ij}^{2}+{\sum}_{i=1}^{m}{\sum}_{j=m+1}^{n} x_{ij}^{2} + &&{\sum}_{i=n+1}^{m} {\sum}_{j=1}^{n} x_{ij}^{2} =1-{\sum}_{i=1}^{\ell} {\sum}_{j=1}^{\ell} x_{ij}^{2} \\ &=&1-{\sum}_{i<j\leq {\ell}}\left( x_{ij}^{2}+x_{ji}^{2}\right)-{\sum}_{i=1}^{\ell} x_{ii}^{2}, \end{array} $$

and

$$ \begin{array}{@{}rcl@{}} {\sum}_{i<j\leq {\ell}}\left( x_{ij}-x_{ji}\right)^{2}- && 2{\sum}_{i<j\leq {\ell}}\left( x_{ii}x_{jj}-x_{ij}x_{ji}\right)\\&=&{\sum}_{i<j\leq {\ell}} \left( x_{ij}^{2}+x_{ji}^{2}-2x_{ij}x_{ji}-2 x_{ii}x_{jj}+2 x_{ij}x_{ji}\right) \\ &=&{\sum}_{i<j\leq {\ell}} \left( x_{ij}^{2}+x_{ji}^{2}\right)-2{\sum}_{i<j \leq {\ell}}x_{ii}x_{jj}. \end{array} $$

Therefore, $1-{\sum }_{i=1}^{\ell } x_{ii}$ is 1-sos mod $J_{M_{mn}}$, since the polynomials $1-{\sum }_{i=1}^{\ell } x_{ii}$, x_ij − x_ji, x_ij, and x_ji are linear and the polynomials $1-{\sum }_{i=1}^{m}{\sum }_{j=1}^{n} x_{ij}^{2}$ and $2\left (x_{ii}x_{jj}-x_{ij}x_{ji}\right )$ are contained in the ideal, for all i < j ≤ ℓ.

Next, we define transformed variables

$$x^{\prime}_{ij}= \begin{cases} {\sum}_{k=1}^{m} M_{ik} x_{kj} & \text{if } m \leq n, \\ {\sum}_{k=1}^{n} x_{ik} M_{kj} & \text{if } m> n. \end{cases} $$

Since $x^{\prime }_{ij}$ is a linear combination of $\{ x_{kj}\}_{k=1}^{m} \cup \{ x_{ik}\}_{k=1}^{n}$, for every $i \in \left [m\right ]$ and $j \in \left [n\right ]$, linearity of the polynomials $1-{\sum }_{i=1}^{\ell } x^{\prime }_{ii}$, $x^{\prime }_{ij}-x^{\prime }_{ji}$, $x^{\prime }_{ij}$, and $x^{\prime }_{ji}$ is preserved, for all i < j. It remains to show that the ideal is invariant under this transformation. For the polynomial $1-{\sum }_{i=1}^{m}{\sum }_{j=1}^{n} {x^{\prime }_{ij}}^{2}$ this is clear since $\textbf {M} \in \mathbb {R}^{n \times m}$ has unitary columns in case when m ≤ n and unitary rows in case m ≥ n. In the case of m ≤ n the polynomial $x^{\prime }_{ii}x^{\prime }_{jj}-x^{\prime }_{ij}x^{\prime }_{ji}$ is contained in the ideal J since

$$ x^{\prime}_{ii}x^{\prime}_{jj}-x^{\prime}_{ij}x^{\prime}_{ji}={\sum}_{k=1}^{m}{\sum}_{l=1}^{m} M_{ik}M_{jl}\left( x_{ki} x_{lj}-x_{kj}x_{li}\right) $$

and the polynomials x_kix_lj − x_kjx_li are contained in J for all i < j ≤ m. Similarly, in case m ≥ n the polynomial $x^{\prime }_{ii}x^{\prime }_{jj}-x^{\prime }_{ij}x^{\prime }_{ji}$ is in the ideal since

$$x^{\prime}_{ii}x^{\prime}_{jj}-x^{\prime}_{ij}x^{\prime}_{ji}={\sum}_{k=1}^{n}{\sum}_{l=1}^{n} M_{ki}M_{lj}\left( x_{ik} x_{jl}-x_{il}x_{jk}\right) $$

and polynomials x_ikx_jl − x_ilx_jk are in the ideal, for all i < j ≤ n. □

The following corollary is a direct consequence of Theorem 2 and the nestedness property (5) of theta bodies.

Corollary 1

The matrix θ₁-norm coincides with the matrix nuclear norm, i.e.,

$$ \left\|\mathbf{X}\right\|_{*}=\left\|\mathbf{X}\right\|_{\theta_{1}}, \quad \text{ for all } \mathbf{X} \in \mathbb{R}^{m \times n}. $$

Moreover,

$$ TH_{1}\left( J_{M_{m n}}\right) = TH_{2}\left( J_{M_{m n}}\right) = {\cdots} = \text{conv}\left( \nu_{\mathbb{R}}(J_{M_{m n}})\right).$$

Remark 2

The ideal (9) is not the only choice that satisfies (6). The following polynomial ideal was suggested in [12],

$$ J=\left<\left\{x_{ij}-u_{i}v_{j}\right\}_{i \in \left[m\right],j \in \left[n\right]}, {\sum}_{i=1}^{m} {u_{i}^{2}}-1, {\sum}_{j=1}^{n} {v_{j}^{2}}-1\right> $$

(12)

in $\mathbb {R}\left [\mathbf {x}, \mathbf {u},\mathbf {v}\right ]=\mathbb {R}\left [x_{11},\ldots ,x_{mn},u_{1},\ldots ,u_{m},v_{1},\ldots ,u_{n}\right ]$. Some tedious computations reveal the reduced Gröbner basis ${\mathcal{G}}$ of the ideal J with respect to the grevlex (and grlex) ordering,

$$ \begin{array}{@{}rcl@{}} \mathcal{G}&=&\left\{ g_{1}^{ij}= x_{ij} - u_{i}v_{j} : i\in\left[m\right], j\in\left[n\right]\right\} \bigcup \left\{ g_{2} = {\sum}_{i=1}^{m} {u_{i}^{2}} - 1, g_{3} = {\sum}_{j=1}^{n} {v_{j}^{2}} -1\right\} \\ &\bigcup& \left\{ g_{4}^{i,j,k} = x_{ij}u_{k}-x_{kj}u_{i} : 1\leq i <k \leq m, j \in \left[n\right]\right\} \\ &\bigcup & \left\{ g_{5}^{i,j,k} = x_{ij}v_{k}-x_{ik}v_{j} : i \in \left[m\right] , 1\leq j <k \leq n \right\} \end{array} $$

$$ \begin{array}{@{}rcl@{}} &\bigcup & \left\{ {g_{6}^{i}} = {\sum}_{j=1}^{n} x_{ij}v_{j}-u_{i} : i \in \left[m\right]\right\} \bigcup \left\{ {g_{7}^{j}} = {\sum}_{i=1}^{m} x_{ij}u_{i}-v_{j}: j \in \left[n\right] \right\} \\ &\bigcup & \left\{ g_{8}^{i,j} = {\sum}_{k=1}^{n} x_{ik}x_{jk}-u_{i} u_{j} : 1 \leq i < j \leq m\right\} \\ &\bigcup & \left\{ g_{9}^{i,j} = {\sum}_{k=1}^{m} x_{ki} x_{kj}-v_{i} v_{j} : 1 \leq i < j \leq n \right\} \\ &\bigcup & \left\{ g_{10}^{i} = {\sum}_{j=1}^{n} x_{ij}^{2}-{u_{i}^{2}} : 2 \leq i \leq m \right\} \bigcup \left\{ g_{11}^{j} = {\sum}_{i=1}^{m} x_{ij}^{2}-{v_{j}^{2}} : 2 \leq j \leq n \right\} \\ &\bigcup & \left\{ g_{12}^{i,j,k,l} = x_{ij}x_{kl}- x_{il}x_{kj} : 1\leq i <k \leq m, 1\leq j <l \leq n \right\} \\ &\bigcup &\left\{ g_{13} = x_{11}^{2}-{\sum}_{i=2}^{m}{\sum}_{j=2}^{n}x_{ij}^{2}+ {\sum}_{i=2}^{m} {u_{i}^{2}} + {\sum}_{j=2}^{n} {v_{j}^{2}}-1 \right\}. \end{array} $$

(13)

Obviously, this Gröbner basis is much more complicated than the one of the ideal $J_{M_{mn}}$ introduced above. Therefore, computations (both theoretical and numerical) with this alternative ideal seem to be more demanding. In any case, the variables $\left \{u_{i}\right \}_{i=1}^{m}$ and $\left \{v_{j}\right \}_{j=1}^{n}$ are only auxiliary ones, so one would like to eliminate these from the above Gröbner basis. By doing so, one obtains the Gröbner basis ${\mathcal{G}}_{M_{mn}}$ defined in (9). Notice that ${\sum }_{i=1}^{m}{\sum }_{j=1}^{n} x_{ij}^{2}-1=g_{13}+{\sum }_{i=2}^{m} g_{10}^{i} + {\sum }_{j=2}^{n} g_{11}^{j}$ together with $\{g_{12}^{i,j,k,l}\}$ form the basis ${\mathcal{G}}_{M_{m n}}$.

3.1 The θ ₁-norm in $\mathbb {R}^{2 \times 2}$

For the sake of illustration, we consider the specific example of 2 × 2 matrices and provide the corresponding semidefinite program for the computation of the θ₁-norm explicitly. Let us denote the corresponding polynomial ideal in $\mathbb {R}\left [\mathbf {x}\right ]=\mathbb {R}\left [x_{11},x_{12},x_{21},x_{22}\right ]$ simply by

$$ J = J_{M_{22}} = \left<x_{12}x_{21}-x_{11}x_{22}, x_{11}^{2}+x_{12}^{2}+x_{21}^{2}+x_{22}^{2}-1\right> $$

(14)

The associated algebraic variety is of the form

$$ \nu_{\mathbb{R}}\left( J\right)=\left\{\mathbf{x}: x_{12}x_{21}=x_{11}x_{22},x_{11}^{2}+x_{12}^{2}+x_{21}^{2}+x_{22}^{2}=1\right\} $$

and corresponds to the set of rank-one matrices with ∥X∥_F = 1. Its convex hull consists of matrices $\mathbf {X} \in \mathbb {R}^{2 \times 2}$ with ∥X∥_∗≤ 1. According to Lemma 2, the Gröbner basis ${\mathcal{G}}$ of J with respect to the grevlex order is

$$ \mathcal{G}=\left\{g_{1} = x_{12}x_{21}-x_{11}x_{22} , g_{2} = x_{11}^{2}+x_{12}^{2}+x_{21}^{2}+x_{22}^{2}-1\right\} $$

with the corresponding θ-basis ${\mathcal{B}}$ of $\mathbb {R}\left [\mathbf {x}\right ]/J$ restricted to the degree two given as

$$ \begin{array}{@{}rcl@{}} \mathcal{B}_{1}&=&\left\{1+J, x_{11}+J, x_{12}+J, x_{21}+J, x_{22}+J \right\} \\ \mathcal{B}_{2}&=&\mathcal{B}_{1} \cup \{x_{11}x_{12}+J, x_{11}x_{21}+J, x_{11}x_{22}+J, x_{12}^{2}+J, x_{12}x_{22}+J, \\ && \quad \quad x_{21}^{2}+J, x_{21}x_{22}+J, x_{22}^{2}+J \}. \end{array} $$

The set ${\mathcal{B}}_{2}$ consists of all monomials of degree at most two which are not divisible by a leading term of any of the polynomials inside the Gröbner basis ${\mathcal{G}}$. For example, x₁₁x₁₂ + J is an element of the theta basis ${\mathcal{B}}$, but $x_{11}^{2}+J$ is not since $x_{11}^{2}$ is divisible by LT(g₂).

Linearizing the elements of ${\mathcal{B}}_{2}$ results in Table 1, where the monomials f in the first row stand for an element $f+J \in {\mathcal{B}}_{2}$.

Table 1 Linearization of the elements of ${\mathcal{B}}_{2}=\{f+J\}$ for matrix 2 × 2 case

Therefore, $\left [\mathbf {x}\right ]_{{\mathcal{B}}_{1}}=\left (1, x_{11}, x_{12}, x_{21}, x_{22}\right )^{T}$ and the following combinatorial moment matrix $\mathbf {M}_{{\mathcal{B}}_{1}}\left (\mathbf {x},\mathbf {y}\right )$ (see Definition 4) is given as

$$ \mathbf{M}_{\mathcal{B}_{1}}\left( \mathbf{x},\mathbf{y}\right)= \begin{bmatrix} y_{0} & x_{11} & x_{12} & x_{21} & x_{22} \\ x_{11} & -y_{4}-y_{6}-y_{8}+y_{0} & y_{1} & y_{2} & y_{3} \\ x_{12} & y_{1} & y_{4} & y_{3} & y_{5} \\ x_{21} & y_{2} & y_{3} & y_{6} & y_{7} \\ x_{22} & y_{3} & y_{5} & y_{7} & y_{8} \end{bmatrix}. $$

For instance, the entry (2,2) of $\left [\mathbf {x}\right ]_{{\mathcal{B}}_{1}}\left [\mathbf {x}\right ]_{{\mathcal{B}}_{1}}^{T}$ is of the form $x_{11}^{2}+J = -x_{12}^{2}-x_{21}^{2}-x_{22}^{2}+1+J$, where we exploit the second property in Definition 3 and the fact that g₂ ∈ J. Replacing $x_{12}^{2}+J$ by y₄ etc., as in Table 1, yields the stated expression for $\textbf {M}_{{\mathcal{B}}_{1}}(\textbf {x},\textbf {y})_{2,2}$.

By Theorem 1, the first theta body $TH_{1}\left (J\right )$ is the closure of

$$ \mathbf{Q}_{\mathcal{B}_{1}}\left( J\right)=\pi_{\mathbf{x}}\left\{\left( \mathbf{x},\mathbf{y}\right) \in \mathbb{R}^{\mathcal{B}_{2}}: \mathbf{M}_{\mathcal{B}_{1}}\left( \mathbf{x},\mathbf{y}\right) \succeq 0, y_{0}=1\right\}, $$

where π_x represents the projection onto the variables x, i.e., the projection onto x₁₁, x₁₂, x₂₁, x₂₂. Furthermore, θ₁-norm of a matrix $\mathbf {X} \in \mathbb {R}^{2 \times 2}$ induced by the $TH_{1}\left (J\right )$ and denoted as $\left \|\cdot \right \|_{\theta _{1}}$ can be computed as

$$ \left\|\mathbf{X}\right\|_{\theta_{1}}=\inf t \text{ s.t. } \mathbf{X} \in t\mathbf{Q}_{\mathcal{B}_{1}}\left( J\right) $$

(15)

which is equivalent to

$$ \inf_{t \in \mathbb{R},\mathbf{y} \in \mathbb{R}^{8}} t \quad \text{ s.t. } \quad \mathbf{M}= \begin{bmatrix} t & X_{11} & X_{12} & X_{21} & X_{22} \\ X_{11} & -y_{4}-y_{6}-y_{8}+t & y_{1} & y_{2} & y_{3} \\ X_{12} & y_{1} & y_{4} & y_{3} & y_{5} \\ X_{21} & y_{2} & y_{3} & y_{6} & y_{7} \\ X_{22} & y_{3} & y_{5} & y_{7} & y_{8} \\ \end{bmatrix} \succeq 0. $$

(16)

Notice that trace(M) = 2t. By Theorem 2, the above program is equivalent to the standard semidefinite program for computing the nuclear norm of a given matrix $\mathbf {X} \in \mathbb {R}^{m \times n}$

$$ \min_{\mathbf{W},\mathbf{Z}} \frac{1}{2}\left( trace(\mathbf{W})+trace(\mathbf{Z})\right) \quad \text{ s.t. } \quad \begin{bmatrix} W_{11} & W_{12} & X_{11} & X_{12} \\ W_{12} & W_{22} & X_{21} & X_{22} \\ X_{11} & X_{21} & Z_{11} & Z_{12} \\ X_{22} & X_{22} & Z_{12} & Z_{22} \\ \end{bmatrix} \succeq 0. $$

Remark 3

In compressive sensing, reconstruction of sparse signals via ℓ₁-norm minimization is well-understood (see, for example, [10, 20, 23]). It is possible to provide hierarchical relaxations via theta bodies of the unit ℓ₁-norm ball. However, as in the matrix scenario discussed above, all these relaxations coincide with the unit ℓ₁-norm ball, [58].

4 The tensor θ _k-norm

Let us now turn to the tensor case and study the hierarchical closed convex relaxations of the unit tensor nuclear norm ball defined via theta bodies. Since in the matrix case all θ_k-norms are equal to the matrix nuclear norm, their generalization to the tensor case may all be viewed as natural generalizations of the nuclear norm. We focus mostly on the θ₁-norm whose unit norm ball is the largest in a hierarchical sequence of relaxations. Unlike in the matrix case, the θ₁-norm defines a new tensor norm, that up to the best of our knowledge has not been studied before.

The polynomial ideal will be generated by the minors of order two of the unfoldings—and matricizations in the case d ≥ 4 – of the tensors, where each variable corresponds to one entry in the tensor. As we will see, a tensor is of rank one if and only if all order-two minors of the unfoldings (matricizations) vanish. While the order-three case requires to consider all three unfoldings, there are several possibilities for the order-d case when d ≥ 4. In fact, a d th-order tensor is of rank one if all minors of all unfoldings vanish so that it may be enough to consider only the unfoldings. However, one may as well consider the ideal generated by all minors of all matricizations or one may consider a subset of matricizations including all unfoldings. Indeed, any tensor format—and thereby any notion of tensor rank—corresponds to a set of matricizations and in this way, one may associate a θ_k-norm to a certain tensor format. We refer to, e.g., [33, 53] for some background on various tensor formats. However, as we will show later, the corresponding reduced Gröbner basis with respect to the grevlex order does not depend on the choice of the tensor format. We will mainly concentrate on the case that all matricizations are taken into account for defining the ideal. Only for the case d = 4, we will briefly discuss the case, that the ideal is generated only by the minors corresponding to the four unfoldings.

Below, we consider first the special case of third-order tensors and continue then with fourth-order tensors. In Section 4.2 we will treat the general d th-order case.

4.1 Third-order tensors

As described above, we will consider the order-two minors of all the unfoldings of a third-order tensor. Our notation requires the following sets of subscripts

$$ \begin{array}{@{}rcl@{}} \mathcal{S}_{1} & = \left\{\left( \mathbf{\alpha},\mathbf{\beta}\right) : 1 \leq \alpha_{1} < \beta_{1} \leq n_{1}, 1 \leq \beta_{2} < \alpha_{2} \leq n_{2}, 1 \leq \beta_{3} \leq \alpha_{3} \leq n_{3}\right\}, \\ \mathcal{S}_{2} & = \left\{\left( \mathbf{\alpha},\mathbf{\beta}\right) : 1 \leq \alpha_{1} \leq \beta_{1} \leq n_{1}, 1 \leq \beta_{2} < \alpha_{2} \leq n_{2}, 1 \leq \alpha_{3} < \beta_{3} \leq n_{3}\right\}, \\ \mathcal{S}_{3} & = \left\{ \left( \mathbf{\alpha},\mathbf{\beta}\right) : 1 \leq \alpha_{1} < \beta_{1} \leq n_{1}, 1 \leq \alpha_{2} \leq \beta_{2} \leq n_{2}, 1 \leq \beta_{3} < \alpha_{3} \leq n_{3}\right\}, \\ \overline{\mathcal{S}}_{i} &=\left\{\left( \mathbf{\alpha},\mathbf{\beta}\right): \left( \mathbf{\alpha},\mathbf{\beta}\right) \in \mathcal{S}_{i} \text{ and } \alpha_{j}\neq\beta_{j}, \text{ for all } j \in \left[3\right]\right\}, \quad \text{for all } i \in \left[3\right]. \end{array} $$

The following polynomials $f^{\left (\mathbf {\alpha },\mathbf {\beta }\right )}$ in $\mathbb {R}\left [\mathbf {x}\right ]=\mathbb {R}\left [x_{111},x_{112},\ldots ,x_{n_{1}n_{2}n_{3}}\right ]$ correspond to a subset of all order-two minors of all tensor unfoldings,

$$ \begin{array}{@{}rcl@{}} f^{\left( \mathbf{\alpha}, \mathbf{\beta}\right)}(\mathbf{x})&=&x_{\mathbf{\alpha}} x_{\mathbf{\beta}}-x_{\mathbf{\alpha} \vee \mathbf{\beta}} x_{\mathbf{\alpha} \wedge \mathbf{\beta}}, \quad \left( \mathbf{\alpha},\mathbf{\beta}\right) \in \mathcal{S}:=\mathcal{S}_{1} \cup \mathcal{S}_{2} \cup \mathcal{S}_{3} \\g_{3}(\mathbf{x})&=& {\sum}_{i=1}^{n_{1}} {\sum}_{j=1}^{n_{2}} {\sum}_{k=1}^{n_{3}} x_{ijk}^{2}-1, \end{array} $$

where $\left [\mathbf {\alpha } \vee \mathbf {\beta }\right ]_{i}=\max \limits \left \{\alpha _{i},\beta _{i}\right \}$ and $\left [\mathbf {\alpha } \wedge \mathbf {\beta }\right ]_{i}=\min \limits \left \{\alpha _{i},\beta _{i}\right \}$. In particular, the following order-two minor of X^{1} is not contained in $\left \{f^{({\alpha },{\beta }}): ({\alpha },{\beta }) \in {\mathcal{S}}\right \}$

$$f=x_{\mathbf{\alpha}}x_{\mathbf{\beta}}-x_{\hat{\mathbf{\alpha}}}x_{\hat{\mathbf{\beta}}}, \quad \text{where } \hat{\mathbf{\alpha}}=\left( \alpha_{1},\beta_{2},\beta_{3}\right), \hat{{\beta}}=(\beta_{1},\alpha_{2},\alpha_{3}) \text{ and } ({\alpha},{\beta}) \in \overline{\mathcal{S}}_{3}. $$

We remark that in real algebraic geometry and commutative algebra, polynomials $f^{\left (\mathbf {\alpha },\mathbf {\beta }\right )}$ are known as Hibi relations (see [34]).

Lemma 4

A tensor $\mathbf {X} \in \mathbb {R}^{n_{1} \times n_{2} \times n_{3}}$ is a rank-one, unit Frobenius norm tensor if and only if

$$ g_{3}(\mathbf{X})=0 \text{ and } f^{\left( \mathbf{\alpha},\mathbf{\beta}\right)}(\mathbf{X})=0 \quad \text{for all} \quad \left( \mathbf{\alpha},\mathbf{\beta}\right) \in \mathcal{S}. $$

(17)

Proof

Sufficiency of (17) follows directly from the definition of the rank-one unit Frobenius norm tensors. For necessity, the first step is to show that mode-1 fibers (columns) span one-dimensional space in $\mathbb {R}^{n_{1}}$. To this end, we note that for β₂ ≤ α₂ and β₃ ≤ α₃, the fibers $\mathbf {X}_{\cdot \alpha _{2}\alpha _{3}}$ and $\mathbf {X}_{\cdot {\beta }_{2} {\beta }_{3}}$ satisfy

$$ \begin{array}{@{}rcl@{}} -X_{n_{1}\alpha_{2}\alpha_{3}} \begin{bmatrix} X_{1\beta_{2}\beta_{3}} \\ X_{2\beta_{2}\beta_{3}} \\ {\vdots} \\ X_{n_{1}\beta_{2}\beta_{3}} \end{bmatrix}&+& X_{n_{1}\beta_{2}\beta_{3}} \begin{bmatrix} X_{1\alpha_{2}\alpha_{3}} \\ X_{2\alpha_{2}\alpha_{3}} \\ {\vdots} \\ X_{n_{1}\alpha_{2}\alpha_{3}} \end{bmatrix}\\ &=& \begin{bmatrix} -X_{1\beta_{2}\beta_{3}}X_{n_{1}\alpha_{2}\alpha_{3}} + X_{1\beta_{2}\beta_{3}}X_{n_{1}\alpha_{2}\alpha_{3}} \\ -X_{2\beta_{2}\beta_{3}}X_{n_{1}\alpha_{2}\alpha_{3}} + X_{2\beta_{2}\beta_{3}}X_{n_{1}\alpha_{2}\alpha_{3}} \\ {\vdots} \\ -X_{n_{1}\beta_{2}\beta_{3}}X_{n_{1}\alpha_{2}\alpha_{3}} + X_{n_{1}\beta_{2} \beta_{3}}X_{n_{1}\alpha_{2}\alpha_{3}} \end{bmatrix}=\mathbf{0}, \end{array} $$

where we used that $f^{\left (\mathbf {\alpha },\mathbf {\beta }\right )}(\mathbf {X})=0$ for all $\left (\mathbf {\alpha },\mathbf {\beta }\right ) \in {\mathcal{S}}$. From $g_{3}\left (\mathbf {X}\right )=0$ it follows that the tensor X is normalized.

Using similar arguments, one argues that mode-2 fibers (rows) and mode-3 fibers span one dimensional spaces in $\mathbb {R}^{n_{2}}$ and $\mathbb {R}^{n_{3}}$, respectively. This completes the proof. □

A third-order tensor $\mathbf {X} \in \mathbb {R}^{n_{1} \times n_{2} \times n_{3}}$ is rank one if and only if all three unfoldings $\mathbf {X}^{\{1\}} \in \mathbb {R}^{n_{1} \times n_{2} n_{3}}$, $\mathbf {X}^{\{2\}} \in \mathbb {R}^{n_{2} \times n_{1} n_{3}}$, and $\mathbf {X}^{\{3\}} \in \mathbb {R}^{n_{3} \times n_{1} n_{2}}$ are rank-one matrices. Notice that $f^{\left (\mathbf {\alpha },\mathbf {\beta }\right )}(\mathbf {X})=0$ for all $\left (\mathbf {\alpha },\mathbf {\beta }\right ) \in {\mathcal{S}}_{\ell }$ is equivalent to the statement that the ℓ-th unfolding X^{ℓ} is a rank-one matrix, i.e., that all its order-two minors vanish, for all $\ell \in \left [3\right ]$.

In order to define relaxations of the unit tensor nuclear norm ball we introduce the polynomial ideal ${J}_{3} \subset \mathbb {R}\left [\mathbf {x}\right ]=\mathbb {R}\left [x_{111},x_{112,}\ldots , x_{n_{1} n_{2} n_{3}}\right ]$ as the one generated by

$$ \mathcal{G}_{3}= \left\{f^{\left( \mathbf{\alpha},\mathbf{\beta}\right)}\left( \mathbf{x}\right) : \left( \mathbf{\alpha},\mathbf{\beta}\right) \in \mathcal{S}\right\} \cup \left\{g_{3}\left( \mathbf{x}\right)\right\}, $$

(18)

i.e., ${J}_{3}=\left <{\mathcal{G}}_{3}\right >$. Its real algebraic variety equals the set of rank-one third-order tensors with unit Frobenius norm and its convex hull coincides with the unit tensor nuclear norm ball. The next result provides the Gröbner basis of J₃.

Theorem 3

The basis ${\mathcal{G}}_{3}$ defined in (18) forms the reduced Gröbner basis of the ideal ${J}_{3}=\left <{\mathcal{G}}_{3}\right >$ with respect to the grevlex order.

Proof

Similarly to the proof of Theorem 2 we need to show that $S\left (p,q\right ) \rightarrow _{{\mathcal{G}}_{3}} 0$ for all polynomials $p,q \in {\mathcal{G}}_{3}$ whose leading terms are not relatively prime. The leading monomials with respect to the grevlex ordering are given by

$$ \begin{array}{@{}rcl@{}} &&LM(g_{3}) = x_{111}^{2} \\ \text{and } && LM(f^{\left( \mathbf{\alpha},\mathbf{\beta}\right)})=x_{\mathbf{\alpha}}x_{\mathbf{\beta}}, \quad \left( \mathbf{\alpha},\mathbf{\beta}\right) \in \mathcal{S}. \end{array} $$

The leading terms of g₃ and $f^{\left (\mathbf {\alpha },\mathbf {\beta }\right )}$ are always relatively prime. First we consider two distinct polynomials $f,g \in \{f^{\left (\mathbf {\alpha },\mathbf {\beta }\right )}: \left (\mathbf {\alpha },\mathbf {\beta }\right ) \in {\mathcal{S}}_{3}\}$. Let $f=f^{\left (\mathbf {\alpha },\mathbf {\beta }\right )}$ and $g=f^{\left (\mathbf {\alpha },\overline {\mathbf {\beta }}\right )}$ for $\left (\mathbf {\alpha },\mathbf {\beta }\right ) \in \overline {{\mathcal{S}}}_{3}$, where $\overline {\mathbf {\beta }}=\left (\beta _{1},\alpha _{2},\beta _{3}\right )$. That is,

$$ \begin{array}{@{}rcl@{}} f(\mathbf{x})=x_{\mathbf{\alpha}}x_{\mathbf{\beta}} - x_{\mathbf{\alpha} \vee \mathbf{\beta}}x_{\mathbf{\alpha} \wedge \mathbf{\beta}}, \quad\quad g(\mathbf{x})=x_{\mathbf{\alpha}}x_{\overline{\mathbf{\beta}}} - x_{\mathbf{\alpha} \vee \overline{\mathbf{\beta}}}x_{\mathbf{\alpha} \wedge \overline{\mathbf{\beta}}}. \end{array} $$

Since $\mathbf {\alpha } \wedge \mathbf {\beta }=\mathbf {\alpha } \wedge \overline {\mathbf {\beta }}$ and $f^{\left (\mathbf {\beta },\mathbf {\alpha } \vee \overline {\mathbf {\beta }}\right )} \in \{f^{({\alpha },{\beta })}: ({\alpha },{\beta }) \in {\mathcal{S}}_{2}\}$, then

$$S\left( f,g\right)=x_{\mathbf{\alpha} \wedge \mathbf{\beta}}\left( -x_{\overline{\mathbf{\beta}}}x_{\mathbf{\alpha} \vee \mathbf{\beta}} + x_{\mathbf{\beta}}x_{\mathbf{\alpha} \vee \overline{\mathbf{\beta}}}\right) = x_{{\alpha} \wedge {\beta}} f^{({\beta},{\alpha} \vee \overline{{\beta})}} \rightarrow_{\mathcal{G}_{3}} 0.$$

Next we show that $S\left (f,g\right )\in {J}_{3}$, for $f \in \left \{f^{\left (\mathbf {\alpha },\mathbf {\beta }\right )}: \left (\mathbf {\alpha },\mathbf {\beta }\right ) \in {\mathcal{S}}_{2}\right \}$ and $g \in \left \{f^{\left (\mathbf {\alpha },\mathbf {\beta }\right )}: \left (\mathbf {\alpha },\mathbf {\beta }\right ) \in {\mathcal{S}}_{1}\right \}$. Let $f=f^{\left (\mathbf {\alpha },\hat {\mathbf {\beta }}\right )}$ with $\hat {\mathbf {\beta }}=\left (\alpha _{1},\beta _{2},\beta _{3}\right )$ and $g = f^{\left (\mathbf {\alpha },\tilde {\mathbf {\beta }}\right )}$ with $\tilde { {\beta }}=(\beta _{1},\beta _{2},\alpha _{3})$, where $\left (\mathbf {\alpha },\mathbf {\beta }\right ) \in \overline {{\mathcal{S}}}_{2}$. Since $x_{\mathbf {\alpha } \wedge \hat {\mathbf {\beta }}}=x_{\mathbf {\alpha } \wedge \tilde {\mathbf {\beta }}}$, $f^{\left (\hat {\mathbf {\beta }}, \mathbf {\alpha } \vee \tilde {\mathbf {\beta }}\right )} \in \left \{f^{\left (\mathbf {\alpha },\mathbf {\beta }\right )}:\left (\mathbf {\alpha },\mathbf {\beta }\right ) \in {\mathcal{S}}_{3}\right \}$, and $f^{\left (\mathbf {\alpha } \vee \hat {\mathbf {\beta }}, \tilde {\mathbf {\beta }} \right )} \in \left \{f^{\left (\mathbf {\alpha },\mathbf {\beta }\right )}:\left (\mathbf {\alpha },\mathbf {\beta }\right ) \in {\mathcal{S}}_{1}\right \}$

$$S\left( f,g\right)=x_{\mathbf{\alpha} \wedge \hat{\mathbf{\beta}}}\left( -x_{\tilde{\mathbf{\beta}}}x_{\mathbf{\alpha} \vee \hat{\mathbf{\beta}}}+x_{\hat{\mathbf{\beta}}}x_{\mathbf{\alpha} \vee \tilde{\mathbf{\beta}}}\right)=x_{\mathbf{\alpha} \wedge \hat{\mathbf{\beta}}}\left( f^{(\hat{\mathbf{\beta}}, \mathbf{\alpha} \vee \tilde{\mathbf{\beta}} )} - f^{(\mathbf{\alpha} \vee \hat{\mathbf{\beta}}, \tilde{\mathbf{\beta}} )}\right) \rightarrow_{\mathcal{G}_{3}} 0.$$

For the remaining cases one proceeds similarly. In order to show that ${\mathcal{G}}_{3}$ is the reduced Gröbner basis, one uses the same arguments as in the proof of Theorem 2. □

Remark 4

The above Gröbner basis ${\mathcal{G}}_{3}$ is obtained by taking a particular subset of all order-two minors of all three unfoldings of the tensor $\mathbf {X} \in \mathbb {R}^{n_{1} \times n_{2} \times n_{3}}$ (not considering the same minor twice). One might think that the θ₁-norm obtained in this way corresponds to a (weighted) sum of the nuclear norms of the unfoldings, which has been used in [25, 39] for tensor recovery. The examples of cubic tensors $\mathbf {X} \in \mathbb {R}^{2 \times 2 \times 2}$ presented in Table 2 show that this is not the case. Assuming that θ₁-norm is a linear combination of the nuclear norm of the unfoldings, there exist α, β, $\gamma \in \mathbb {R}$ such that $\alpha \|\mathbf {X}^{\{1\}}\|_{*}+ \beta \|\mathbf {X}^{\{2\}}\|_{*} +\gamma \|\mathbf {X}^{\{3\}}\|_{*}=\|\mathbf {X}\|_{\theta _{1}}.$ From the first and the second tensors in Table 2 we obtain γ = 0. Similarly, the first and the third tensors and the first and the fourth tensors give β = 0 and α = 0, respectively. Thus, the θ₁-norm does not coincide with a weighted sum of the nuclear norms of the unfoldings. In addition, the last tensor shows that the θ₁-norm does not equal maximum of the norms of the unfoldings.

Table 2 Matrix nuclear norms of unfoldings and θ₁-norm of tensors $\mathbf {X} \in \mathbb {R}^{2 \times 2 \times 2}$, which are represented in the second column as $\mathbf {X}=\left [\mathbf {X}\left (:,:,1\right ) \middle \vert \mathbf {X}\left (:,:,2\right )\right ]$. The third, fourth and fifth columns represent the nuclear norms of the first, second and the third unfolding of a tensor X, respectively. The last column contains the numerically computed θ₁-norm

Theorem 3 states that ${\mathcal{G}}_{3}$ is the reduced Gröbner basis of the ideal J₃ generated by all order-two minors of all matricizations of an order-three tensor. That is, J₃ is generated by the following polynomials

$$ \begin{array}{@{}rcl@{}} f_{\left( \mathbf{\alpha},\mathbf{\beta}\right)}^{\{1\}}(\mathbf{x})&=-x_{\alpha_{1} \alpha_{2} \alpha_{3}} x_{\beta_{1} \beta_{2} \beta_{3}} + x_{\alpha_{1} \beta_{2} \beta_{3}} x_{\beta_{1} \alpha_{2} \alpha_{3}}, \quad \text{for } (\mathbf{\alpha},\mathbf{\beta}) \in \mathbf{\mathcal{T}}^{\{1\}} \\ f_{\left( \mathbf{\alpha},\mathbf{\beta}\right)}^{\{2\}}(\mathbf{x})&=-x_{\alpha_{1} \alpha_{2} \alpha_{3}} x_{\beta_{1} \beta_{2} \beta_{3}} + x_{\beta_{1} \alpha_{2} \beta_{3}} x_{\alpha_{1} \beta_{2} \alpha_{3}}, \quad \text{for } (\mathbf{\alpha},\mathbf{\beta}) \in \mathbf{\mathcal{T}}^{\{2\}}\\ f_{\left( \mathbf{\alpha},\mathbf{\beta}\right)}^{\{3\}}(\mathbf{x})&=-x_{\alpha_{1} \alpha_{2} \alpha_{3}} x_{\beta_{1} \beta_{2} \beta_{3}} + x_{\beta_{1} \beta_{2} \alpha_{3}} x_{\alpha_{1} \alpha_{2} \beta_{3}}, \quad \text{for } (\mathbf{\alpha},\mathbf{\beta}) \in \mathbf{\mathcal{T}}^{\{3\}}, \end{array} $$

where $\left \{f_{\left (\mathbf {\alpha },\mathbf {\beta }\right )}^{\{k\}}(\mathbf {x}):\left (\mathbf {\alpha },\mathbf {\beta }\right ) \in \mathbf {{\mathcal{T}}}^{\{k\}}\right \}$ is the set of all order-two minors of the k th unfolding and

$$ \begin{array}{@{}rcl@{}} \mathbf{\mathcal{T}}^{\{k\}}&=\left\{(\mathbf{\alpha},\mathbf{\beta}): \alpha_{k}\neq\beta_{k}, \overline{\mathbf{\alpha}} \neq\overline{\mathbf{\beta}}, \text{where } \overline{\alpha}_{k}=\overline{\beta}_{k}=0, \overline{\alpha}_{\ell}=\alpha_{\ell}, \overline{\beta}_{\ell}=\beta_{\ell}\right\}. \end{array} $$

For $\left (\mathbf {\alpha },\mathbf {\beta }\right )$, $x_{\mathbf {\alpha }^{\{k\}}} x_{\mathbf {\beta }^{\{k\}}}$ denotes a monomial where $\alpha _{k}^{\{k\}}=\alpha _{k}$, $\beta _{k}^{\{k\}}=\beta _{k}$, and $\alpha _{\ell }^{\{k\}}=\beta _{\ell }$, $\beta _{\ell }^{\{k\}}=\alpha _{\ell }$, for all $\ell \in \left [d\right ]\backslash \{k\}$. Notice that $f_{\left (\mathbf {\alpha },\mathbf {\beta }\right )}^{\{k\}}(\mathbf {x})=f_{\left (\mathbf {\beta },\mathbf {\alpha }\right )}^{\{k\}}(\mathbf {x})=-f_{\left (\mathbf {\alpha }^{\{k\}},\mathbf {\beta }^{\{k\}}\right )}^{\{k\}}(\mathbf {x})=-f_{\left (\mathbf {\beta }^{\{k\}},\mathbf {\alpha }^{\{k\}}\right )}^{\{k\}}(\mathbf {x})$, for all $\left (\mathbf {\alpha },\mathbf {\beta }\right ) \in \mathbf {{\mathcal{T}}}^{\{k\}}$, and all $k \in \left [3\right ]$. Let us now consider a TT-format and a corresponding notion of tensor rank. Recall that a TT-rank of an order three tensor is a vector r = (r₁, r₂) where $r_{1}=\text {rank}(\mathbf {X}^{\{1\}})$ and $r_{2}=\text {rank}(\mathbf {X}^{\{1,2\}})$. Consequently, we consider an ideal J_3,TT generated by all order-two minors of matricizations X^{1} and X^{1,2} of the order-3 tensor. That is, the ideal J_3,TT is generated by the polynomials

$$ \begin{array}{@{}rcl@{}} f_{\left( \mathbf{\alpha},\mathbf{\beta}\right)}^{\{1\}}(\mathbf{x})&=-x_{\alpha_{1} \alpha_{2} \alpha_{3}} x_{\beta_{1} \beta_{2} \beta_{3}} + x_{\alpha_{1} \beta_{2} \beta_{3}} x_{\beta_{1} \alpha_{2} \alpha_{3}}, \quad\!\! \text{for } (\mathbf{\alpha},\mathbf{\beta}) \in \mathbf{\mathcal{T}}^{\{1\}}, \\ f_{\left( \mathbf{\alpha},\mathbf{\beta}\right)}^{\{1,2\}}(\mathbf{x})&=-x_{\alpha_{1} \alpha_{2} \alpha_{3}} x_{\beta_{1} \beta_{2} \beta_{3}} + x_{\alpha_{1} \alpha_{2} \beta_{3}} x_{\beta_{1} \beta_{2} \alpha_{3}} , \quad\ \text{for } (\mathbf{\alpha},\mathbf{\beta}) \in \mathbf{\mathcal{T}}^{\{1,2\}}, \end{array} $$

where $\mathbf {{\mathcal{T}}}^{\{1,2\}}=\left \{(\mathbf {\alpha },\mathbf {\beta }): \left (\alpha _{1},\alpha _{2},0\right ) \neq \left (\beta _{1},\beta _{2},0\right ), \alpha _{3} \neq \beta _{3}\right \}$.

Theorem 4

The polynomial ideals J₃ and J_3,TT are equal.

Remark 5

As a consequence, ${\mathcal{G}}_{3}$ is also the reduced Gröbner basis for the ideal J_3,TT with respect to the grevlex ordering.

Proof

Notice that $\left (\mathbf {X}^{\{3\}}\right )^{T}=\mathbf {X}^{\{1,2\}}$ and therefore

$$\left\{f_{\left( \mathbf{\alpha},\mathbf{\beta}\right)}^{\{3\}}(\mathbf{x}):\left( \mathbf{\alpha},\mathbf{\beta}\right) \in \mathbf{\mathcal{T}}^{\{3\}}\right\} = \left\{f_{\left( \mathbf{\alpha},\mathbf{\beta}\right)}^{\{1,2\}}(\mathbf{x}):\left( \mathbf{\alpha},\mathbf{\beta}\right) \in \mathbf{\mathcal{T}}^{\{1,2\}}\right\}.$$

Hence, it is enough to show that $f_{\left (\mathbf {\alpha },\mathbf {\beta }\right )}^{\{2\}} \in J_{3,\text {TT}}$, for all $\left (\mathbf {\alpha },\mathbf {\beta }\right ) \in \mathbf {{\mathcal{T}}}^{\{2\}}$. By definition of $\mathbf {{\mathcal{T}}}^{\{2\}}$, we have that α₂≠β₂ and (α₁,0,α₃)≠(β₁,0,β₃). We can assume that α₃≠β₃, since otherwise $f_{\left (\mathbf {\alpha },\mathbf {\beta }\right )}^{\{2\}} = f_{\left (\mathbf {\alpha },\mathbf {\beta }\right )}^{\{1\}}$. Analogously, α₁≠β₁ since otherwise $f_{\left (\mathbf {\alpha },\mathbf {\beta }\right )}^{\{2\}} = f_{\left (\mathbf {\alpha },\mathbf {\beta }\right )}^{\{1,2\}}$. Consider the following polynomials

$$ \begin{array}{@{}rcl@{}} f(\mathbf{x})&=&-x_{\alpha_{1} \alpha_{2} \alpha_{3}} x_{\beta_{1} \beta_{2} \beta_{3}} + x_{\beta_{1} \alpha_{2} \beta_{3}} x_{\alpha_{1} \beta_{2} \alpha_{3}}, \quad (\mathbf{\alpha},\mathbf{\beta}) \in\mathbf{\mathcal{T}}^{\{2\}}\\ g(\mathbf{x})&=&-x_{\beta_{1} \beta_{2} \alpha_{3}} x_{\alpha_{1} \alpha_{2} \beta_{3}} + x_{\beta_{1} \alpha_{2} \beta_{3}} x_{\alpha_{1} \beta_{2} \alpha_{3}} ,\quad (\beta_{1},\beta_{2},\alpha_{3},\alpha_{1},\alpha_{2},\beta_{3}) \in\mathbf{\mathcal{T}}^{\{1\}}\\ h(\mathbf{x})&=&-x_{\alpha_{1} \alpha_{2} \alpha_{3}} x_{\beta_{1} \beta_{2} \beta_{3}} + x_{\alpha_{1} \alpha_{2} \beta_{3}} x_{\beta_{1} \beta_{2} \alpha_{3}} ,\quad (\mathbf{\alpha},\mathbf{\beta}) \in\mathbf{\mathcal{T}}^{\{1,2\}}. \end{array} $$

Thus, we have that f(x) = g(x) + h(x) ∈ J_3,TT. □

4.2 The theta norm for general d th-order tensors

Let us now consider d th-order tensors in $\mathbb {R}^{n_{1}\times n_{2} \times {\cdots } \times n_{d}}$ for general d ≥ 4. Our approach relies again on the fact that a tensor $\mathbf {X} \in \mathbb {R}^{n_1 \times n_2 \times {\cdots } \times n_d}$ is of rank-one if and only if all its matricizations are rank-one matrices, or equivalently, if all minors of order two of each matricization vanish.

The description of the polynomial ideal generated by the second-order minors of all matricizations of a tensor $\mathbf {X} \in \mathbb {R}^{n_1 \times n_2 \times {\cdots } \times n_d}$ unfortunately requires some technical notation. Again, we do not need all such minors in the generating set that we introduce next. In fact, this generating set will turn out to be the reduced Gröbner basis of the ideal.

Similarly to before, the entry $\left (\alpha _{1},\alpha _{2},\ldots ,\alpha _{d}\right )$ of a tensor $\mathbf {X} \in \mathbb {R}^{n_1 \times n_2 \times {\cdots } \times n_d}$ corresponds to the variable $x_{\alpha _{1}\alpha _{2} {\cdots } \alpha _{d}}$ or simply x_α. We aim at introducing a set of polynomials of the form

$$ f_{d}^{\left( \mathbf{\alpha},\mathbf{\beta}\right)}(\mathbf{x}):= -x_{\mathbf{\alpha} \wedge \mathbf{\beta}}x_{\mathbf{\alpha} \vee \mathbf{\beta}}+x_{\mathbf{\alpha}}x_{\mathbf{\beta}} $$

(19)

which will generate the desired polynomial ideal. These polynomials correspond to a subset of all order-two minors of all the possible d th-order tensor matricizations. The set ${\mathcal{S}}$ denotes the indices where α and β differ. Since for an order-two minor of a matricization $\mathbf {X}^{{\mathcal{M}}}$ the sets α and β need to differ in at least two indices, ${\mathcal{S}}$ is contained in

$$ \mathcal{S}_{\left[d\right]}:=\{\mathcal{S} \subset \left[d\right]: 2\leq | \mathcal{S} | \leq d\}.$$

Given the set ${\mathcal{S}}$ of different indices, we require all non-empty subsets ${\mathcal{M}} \subset {\mathcal{S}}$ of possible indices which are “switched” between α and β for forming the minors in (19). This implies that, without loss of generality,

$$ \begin{array}{@{}rcl@{}} &&\alpha_{j} > \beta_{j}, \quad \text{ for all } j \in \mathcal{M}\\ &&\alpha_{k} < \beta_{k}, \quad \text{ for all } k \in \mathcal{S} \backslash \mathcal{M}. \end{array} $$

That is, the same minor is obtained if we require that α_j < β_j for all $j \in {\mathcal{M}}$ and α_k > β_k for all $k \in {\mathcal{S}}\backslash {\mathcal{M}}$ since the set of all two-minors of $\textbf {X}^{{\mathcal{M}}}$ coincides with the set of all two-minors of $\textbf {X}^{{\mathcal{S}}\backslash {\mathcal{M}}}$.

For ${\mathcal{S}} \in {\mathcal{S}}_{\left [d\right ]}$, we define $e_{{\mathcal{S}}}:=\min \limits \{p: p \in {\mathcal{S}}\}$. The set ${\mathcal{M}}$ corresponds to an associated matricization $\mathbf {X}^{{\mathcal{M}}}$. The set of possible subsets ${\mathcal{M}}$ is given as

$$ \mathcal{P}_{\mathcal{S}} = \begin{cases} \left\{\mathcal{M} \subset \mathcal{S}: |\mathcal{M}| \leq \lfloor\frac{|\mathcal{S}|}{2}\rfloor\right\}\backslash\{\emptyset\}, \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \text{if } |\mathcal{S}| \text{ is odd}, \\ \left\{\mathcal{M} \subset \mathcal{S}: |\mathcal{M}| \leq \lfloor\frac{|\mathcal{S}|-1}{2}\rfloor\right\} \cup \left\{ \mathcal{M} \subset \mathcal{S}: | \mathcal{M}| = \frac{|\mathcal{S}|}{2}, e_{\mathcal{S}} \in \mathcal{M}\right\}\backslash\{\emptyset\},\quad\text{otherwise}. \end{cases} $$

Notice that ${\mathcal{P}}_{{\mathcal{S}}} \cup {\mathcal{P}}_{{\mathcal{S}}^{c}} \cup \{\emptyset \} \cup {\mathcal{S}}$ with ${\mathcal{P}}_{{\mathcal{S}}^{c}}:=\{{\mathcal{M}}: {\mathcal{S}} \backslash {\mathcal{M}} \in {\mathcal{P}}_{{\mathcal{S}}}\}$ forms the power set of ${\mathcal{S}}$. The constraint on the size of ${\mathcal{M}}$ in the definition of ${\mathcal{P}}_{{\mathcal{S}}}$ is motivated by the fact that the role of α and β can be switched and lead to the same polynomial $f_{d}^{(\mathbf {\alpha },\mathbf {\beta })}$.

Thus, for ${\mathcal{S}} \in {\mathcal{S}}_{\left [d\right ]}$ and ${\mathcal{M}} \in {\mathcal{P}}_{{\mathcal{S}}}$, we define a set

$$ \begin{array}{@{}rcl@{}} \mathcal{T}_{d}^{\mathcal{S},\mathcal{M}}:=\{\left( \mathbf{\alpha},\mathbf{\beta}\right): \alpha_{i}&=&\beta_{i}, \text{ for all } i \notin \mathcal{S} \\ \alpha_{j} &>& \beta_{j} , \text{ for all } j \in \mathcal{M} \\ \alpha_{k} &<& \beta_{k} , \text{ for all } k \in \mathcal{S}\backslash\mathcal{M} \} . \end{array} $$

For notational purposes, we define

$$\{f_{d}^{\mathcal{S}}\}=\cup_{\mathcal{M} \in \mathcal{P}_{\mathcal{S}}}\{f_{d}^{\left( \mathbf{\alpha},\mathbf{\beta}\right)}: \left( \mathbf{\alpha},\mathbf{\beta}\right) \in \mathcal{T}_{d}^{\mathcal{S},\mathcal{M}}\} \quad \text{ for } \mathcal{S} \in \mathcal{S}_{[d]}. $$

Since we are interested in unit Frobenius norm tensors, we also introduce the polynomial

$$ g_{d}\left( \mathbf{x}\right)={\sum}_{i_{1}=1}^{n_{1}}{\sum}_{i_{2}=1}^{n_{2}}{\ldots} {\sum}_{i_{d}=1}^{n_{d}}x_{i_{1} i_{2} {\ldots} i_{d}}^{2}-1. $$

Our polynomial ideal is then the one generated by the polynomials in

$$ \mathcal{G}_{d} = \bigcup_{\mathcal{S}\in \mathcal{S}_{\left[d\right]}} \{f_{d}^{\mathcal{S}}\} \cup \{g_{d}\} \subset \mathbb{R}\left[\mathbf{x}\right]=\mathbb{R}\left[x_{11\ldots1}, x_{11 {\ldots} 2}, \ldots, x_{n_{1} n_{2} {\ldots} n_{d}}\right], $$

i.e., $J_{d} = \langle {\mathcal{G}}_{d} \rangle$. As in the special case of the third-order tensors, not all second-order minors corresponding to all matricizations are contained in the generating set ${\mathcal{G}}_{d}$ due to the condition $i_{k} < \hat {i}_{k}$ for all $k \in {\mathcal{S}}$ in the definition of ${\mathcal{T}}_{d}^{{\mathcal{S}}}$. Nevertheless all second-order minors are contained in the ideal J_d as will also be revealed by the proof of Theorem 5 below. For instance, h(x) = −x₁₂₃₄x₂₃₄₃ + x₁₂₄₃x₂₃₃₄—corresponding to a minor of the matricization $\mathbf {X}^{{\mathcal{M}}}$ for ${\mathcal{M}} = \{1,2\}$—does not belong to ${\mathcal{G}}_{4}$, but it does belong to the ideal J₄. Moreover, it is straightforward to verify that all polynomials in ${\mathcal{G}}_{d}$ differ from each other.

The algebraic variety of J_d consists of all rank-one unit Frobenius norm order-d tensors as desired, and its convex hull yields the tensor nuclear norm ball.

Theorem 5

The set ${\mathcal{G}}_{d}$ forms the reduced Gröbner basis of the ideal J_d with respect to the grevlex order.

Proof

Again, we use Buchberger’s criterion stated in Theorem 9. First notice that the polynomials g_d and $f_{d}^{\left (\mathbf {\alpha },\mathbf {\beta }\right )}$ are always relatively prime, since $LM(g_{d})=x_{11{\ldots } 1}^{2}$ and $LM(f_{d}^{\left (\mathbf {\alpha },\mathbf {\beta }\right )})=x_{\mathbf {\alpha }} x_{\mathbf {\beta }}$ for $(\mathbf {\alpha },\mathbf {\beta }) \in {\mathcal{T}}_{d}^{{\mathcal{M}},{\mathcal{S}}}$, where ${\mathcal{S}} \in {\mathcal{S}}_{\left [d\right ]}$ and ${\mathcal{M}} \in {\mathcal{P}}_{{\mathcal{S}}}$. Therefore, we need to show that $S(f_{1},f_{2}) \rightarrow _{{\mathcal{G}}_{d}} 0$, for all $f_{1},f_{2} \in {\mathcal{G}}_{d}\backslash \{g_{d}\}$ with f₁≠f₂. To this end, we analyze the division algorithm on $\left \langle {\mathcal{G}}_{d}\right \rangle$.

Let $f_{1},f_{2} \in {\mathcal{G}}_{d}$ with f₁≠f₂. Then it holds LM(f₁)≠LM(f₂). If these leading monomials are not relatively prime, the S-polynomial is of the form

$$S(f_{1},f_{2})=x_{\mathbf{\alpha}^{1}} x_{\mathbf{\alpha}^{2}} x_{\mathbf{\alpha}^{3}} - x_{\bar{\mathbf{\alpha}}^{1}} x_{\bar{\mathbf{\alpha}}^{2}}x_{\bar{\mathbf{\alpha}}^{3}} $$

with $\left \{{\alpha _{k}^{1}}, {\alpha _{k}^{2}}, {\alpha _{k}^{3}}\right \}= \left \{\bar {\alpha }_{k}^{1},\bar {\alpha }_{k}^{2}, \bar {\alpha }_{k}^{3}\right \}$ for all $k \in \left [d\right ]$.

The step-by-step procedure of the division algorithm for our scenario is presented in Algorithm 2. We will show that the algorithm eventually stops and that step 2) is feasible, i.e., that there always exist k and ℓ such that line 7 of Algorithm 2 holds—provided that Sⁱ≠ 0. (In fact, the purpose of the algorithm is to achieve the condition that in the i th iteration of the algorithm $\hat {\alpha }_{k}^{1,i} \leq \hat {\alpha }_{k}^{2,i} \leq \hat {\alpha }_{k}^{3,i}$, for all $k \in \left [d\right ]$.) This will show then that $S(f_{1},f_{2}) \rightarrow _{{\mathcal{G}}_{d}} 0$.

Before passing to the general proof, we illustrate the division algorithm on an example for d = 4. The experienced reader may skip this example.

Let $f_{1}(\mathbf {x}):=f_{4}^{(1212,2123)}(\mathbf {x})=-x_{1112}x_{2223}+x_{1212}x_{2123} \in {\mathcal{G}}_{4}$ (with the corresponding sets ${\mathcal{S}}=\{1,2,3,4\}$, ${\mathcal{M}}=\{2\}$) and $f_{2}(\mathbf {x}):=f_{4}^{(3311,2123)}(\mathbf {x})=-x_{2111}x_{3323}+x_{3311}x_{2123} \in {\mathcal{G}}_{4}$ (with the corresponding sets ${\mathcal{S}}=\{1,2,3,4\}$, ${\mathcal{M}}=\{1,2\}$). We will show that $S(f_{1},f_{2})=-x_{1112}x_{2223}x_{3311}+x_{1212}x_{2111}x_{3323} \rightarrow _{{\mathcal{G}}_{4}} 0$ by going through the division algorithm.

In iteration i = 0 we set S⁰ = S(f₁, f₂) = −x₁₁₁₂x₂₂₂₃x₃₃₁₁ + x₁₂₁₂x₂₁₁₁x₃₃₂₃. The leading monomial is LM(S⁰) = x₁₁₁₂x₂₂₂₃x₃₃₁₁, the leading coefficient is LC(S⁰) = − 1, and the non-leading monomial is $\mathbb {N}LM(S^{0})=x_{1212}x_{2111}x_{3323}$. Among the two options for choosing a pair of indexes (α^1,0, α^2,0) in step 2), we decide to take α^1,0 = 1112 and α^2,0 = 3311 which leads to the set ${\mathcal{M}}_{0} =\{4\}$. The polynomial $x_{\mathbf {\alpha }^{1,0}}x_{\mathbf {\alpha }^{2,0}}-x_{\mathbf {\alpha }^{1,0} \wedge \mathbf {\alpha }^{2,0}}x_{\mathbf {\alpha }^{1,0} \vee \mathbf {\alpha }^{2,0}}$ then equals the polynomial $f_{4}^{(1112,3311)}(\mathbf {x})=-x_{1111}x_{3312}+x_{1112}x_{3311} \in {\mathcal{G}}_{4}$ and we can write

$$S^{0}=-1\cdot \Big(x_{2223}\left( -x_{1111}x_{3312}+x_{1112}x_{3311}\right)+\underbrace{x_{1111}x_{2223}x_{3312}-x_{1212}x_{2111}x_{3323}}_{\displaystyle =S^{1}}\Big) .$$

The leading and non-leading monomials of S¹ are LM(S¹) = x₁₁₁₁x₂₂₂₃x₃₃₁₂ and $\mathbb {N}LM(S^{1})=x_{1212}x_{2111}x_{3323}$, respectively, while LC(S¹) = 1. The only option for a pair of indices as in line 7 of Algorithm 2 is α^1,1 = 3312,α^2,1 = 2223, so that the set ${\mathcal{M}}_{1}=\{1,2\}$. The divisor $x_{\mathbf {\alpha }^{1,1}}x_{\mathbf {\alpha }^{2,1}}-x_{\mathbf {\alpha }^{1,1} \wedge \mathbf {\alpha }^{2,1}}x_{\mathbf {\alpha }^{1,1} \vee \mathbf {\alpha }^{2,1}}$ in the step 4) equals $f_{4}^{(3312,2223)}(\mathbf {x})= -x_{2212}x_{3323}+x_{3312}x_{2223}\in {\mathcal{G}}_{4}$ and we obtain

$$ S^{1}=1\cdot \Big(x_{1111}\left( -x_{2212}x_{3323}+x_{2223}x_{3312}\right)+ \underbrace{x_{1111}x_{2212}x_{3323}-x_{1212}x_{2111}x_{3323}}_{\displaystyle = S^{2}}\Big) . $$

The index sets of the monomial $x_{\mathbf {\alpha }^{1}}x_{\mathbf {\alpha }^{2}}x_{\mathbf {\alpha }^{3}}=x_{1111}x_{2212}x_{3323}$ in S² satisfy

$${\alpha_{k}^{1}} \leq {\alpha_{k}^{2}} \leq {\alpha_{k}^{3}} \quad \text{ for all } k \in \left[4\right] $$

and therefore it is the non-leading monomial of S², i.e., $\mathbb {N}LM(S^{2})=x_{1111}x_{2212}x_{3323}$. Thus, LM(S²) = x₁₂₁₂x₂₁₁₁x₃₃₂₃ and LC(S²(f₁, f₂)) = − 1. Now the only option for a pair of indices as in step 2) is α^1,2 = 2111, α^2,2 = 1212 with ${\mathcal{M}}_{2}=\{1\}$. This yields

$$ S^{2}=-1 \cdot \Big(x_{3323}\left( -x_{1111}x_{2212}+x_{2111}x_{1212}\right)+ \underbrace{x_{1111}x_{2212}x_{3323} -x_{1111}x_{2212}x_{3323}}_{\displaystyle = S^{3} = 0}\Big). $$

Thus, the division algorithm stops and we obtained after three steps

$$ \begin{array}{@{}rcl@{}} {S}(f_{1},f_{2}) = S^{0}& = LC(S^{0})x_{2223}f_{4}^{(1112,3311)}(\mathbf{x})+LC(S^{0}) LC(S^{1})x_{1111} f_{4}^{(3312,2223)}(\mathbf{x}) \\ & +LC(S^{0})LC(S^{1})LC(S^{2}) x_{3323}f_{4}^{(2111,1212)}(\mathbf{x}). \end{array} $$

Thus, $S(f_{1},f_{2}) \rightarrow _{{\mathcal{G}}_{4}} 0$.

Let us now return to the general proof. We first show that there always exist indices α^1,i, α^2,i satisfying line 7 of Algorithm 2 unless Sⁱ = 0. We start by setting $\mathbf {x}^{\mathbf {\alpha }_{i}}=x_{\hat {\mathbf {\alpha }}^{1,i}}x_{\hat {\mathbf {\alpha }}^{2,i}}x_{\hat {\mathbf {\alpha }}^{3,i}}$ with $x_{\hat {\mathbf {\alpha }}^{1,i}} \geq x_{\hat {\mathbf {\alpha }}^{2,i}} \geq x_{\hat {\mathbf {\alpha }}^{3,i}}$ to be the leading monomial and $\mathbf {x}^{\mathbf {\beta }_{{i}}}$ to be the non-leading monomial of Sⁱ. The existence of a polynomial $h \in {\mathcal{G}}_{d}$ such that LM(h) divides $LM(S^{i})=x_{\hat { {\alpha }}^{1,i}}x_{\hat { {\alpha }}^{2,i}}x_{\hat { {\alpha }}^{3,i}}=\mathbf {x}^{ {\alpha }_{i}}$ is equivalent to the existence of $\mathbf {\alpha }^{1,i},\mathbf {\alpha }^{2,i} \in \left \{\hat {\mathbf {\alpha }}^{1,i},\hat {\mathbf {\alpha }}^{2,i},\hat {\mathbf {\alpha }}^{3,i}\right \}$ such that there exists at least one k and at least one ℓ for which ${\alpha }_{k}^{1,i} < {\alpha }_{k}^{2,i}$ and ${\alpha }_{\ell }^{1,i}>{\alpha }_{\ell }^{2,i}$. If such pair does not exist in iteration i, we have

$$ \hat{\alpha}_{k}^{1,i} \leq \hat{\alpha}_{k}^{2,i} \leq \hat{\alpha}_{k}^{3,i} \quad \text{ for all } k \in \left[d\right]. $$

(20)

We claim that this cannot happen if Sⁱ≠ 0. In fact, (20) would imply that the monomial $\mathbf {x}^{ {\alpha }_{i}}=x_{\hat { {\alpha }}^{1,i}}x_{\hat { {\alpha }}^{2,i}}x_{\hat { {\alpha }}^{3,i}}$ is the smallest monomial x_βx_γx_η (with respect to the grevlex order) which satisfies

$$ \left\{\beta_{k}, \gamma_{k}, \eta_{k}\right\}=\{ \hat{\alpha}_{k}^{1,i},\hat{\alpha}_{k}^{2,i},\hat{\alpha}_{k}^{3,i}\} \quad \text{for all } k \in \left[d\right].$$

However, then $\mathbf {x}^{ {\alpha }_{i}}$ would not be the leading monomial by definition of the grevlex order, which leads to a contradiction. Hence, we can always find indices α^1,i, α^2,i satisfying line 7 in step 2) of Algorithm 2 unless Sⁱ = 0.

Next we show that the division algorithm always stops in a finite number of steps. We start with iteration i = 0 and assume that S⁰≠ 0. We choose α^1,0, α^2,0, α^3,0 as in step 2) of Algorithm 2. Then we divide the polynomial S⁰ by a polynomial $h \in {\mathcal{G}}_{d}$ such that $LM(h)=x_{\mathbf {\alpha }^{1,0}}x_{\mathbf {\alpha }^{2,0}}$. The polynomial $h \in {\mathcal{G}}_{d}$ is defined as in step 3) of the algorithm, i.e.,

$$h(\mathbf{x}) =f_{d}^{\left( \mathbf{\alpha}^{1,0}, \mathbf{\alpha}^{2,0}\right)}=x_{\mathbf{\alpha}^{1,0}}x_{\mathbf{\alpha}^{2,0}}- x_{\mathbf{\alpha}^{1,0} \wedge \mathbf{\alpha}^{2,0}}x_{\mathbf{\alpha}^{1,0} \vee \mathbf{\alpha}^{2,0}}\in \mathcal{G}_{d}.$$

The division of S⁰ by h results in

$$ S^{0} =LC(S^{0}) \Big(x_{{\mathbf{\alpha}}^{3,0}} \cdot f_{d}^{\left( \mathbf{\alpha}^{1,0}, \mathbf{\alpha}^{2,0}\right)} +\underbrace{x_{\mathbf{\alpha}^{1,0} \wedge \mathbf{\alpha}^{2,0}}x_{\mathbf{\alpha}^{1,0} \vee \mathbf{\alpha}^{2,0}}x_{\mathbf{\alpha}^{3,0}}- \text{NLM}(S^{0})}_{\displaystyle = S^{1}}\Big).$$

Note that by construction

$$ \left[\mathbf{\alpha}^{1,0} \wedge \mathbf{\alpha}^{2,0}\right]_{k} \leq \left[\mathbf{\alpha}^{1,0} \vee \mathbf{\alpha}^{2,0}\right]_{k} \quad \text{ for all } k \in \left[d\right]. $$

(21)

If S¹≠ 0, then in the following iteration i = 1 we can assume $LM(S^{1})=x_{\mathbf {\alpha }^{1,0} \wedge \mathbf {\alpha }^{2,0}} x_{\mathbf {\alpha }^{1,0} \wedge \mathbf {\alpha }^{2,0}} x_{\mathbf {\alpha }^{3,0}}$. Due to (21), a pair α^1,1, α^2,1 as in line 7 of Algorithm 2 can be either α^1,0 ∧α^2,0, α^3,0 or α^1,0 ∨α^2,0, α^3,0. Let us assume the former. Then this iteration results in

$$ S^{1}=LC(S^{1})\Big(x_{\mathbf{\alpha}^{3,1}}\cdot f_{d}^{\left( \mathbf{\alpha}^{1,1},\mathbf{\alpha}^{2,1}\right)} +\underbrace{x_{\mathbf{\alpha}^{1,1} \wedge \mathbf{\alpha}^{2,1}} x_{\mathbf{\alpha}^{1,1} \vee {\alpha}^{2,1}} x_{{\alpha}^{3,1}} -\text{NLM}(S^{0})}_{\displaystyle=S^{2}}\Big) $$

with

$$ \left[\mathbf{\alpha}^{1,1} \wedge \mathbf{\alpha}^{2,1}\right]_{k} \leq \left[\mathbf{\alpha}^{3,1}\right]_{k} , \left[\mathbf{\alpha}^{1,1} \vee \mathbf{\alpha}^{2,1}\right]_{k} \quad \text{ for all } k \in \left[d\right], \text{ and } x_{\mathbf{\alpha}^{3,1}}=x_{\mathbf{\alpha}^{1,0} \vee \mathbf{\alpha}^{2,0}}. $$

Next, if S²≠ 0 and $LM(S^{2})=x_{\mathbf {\alpha }^{1,1} \wedge \mathbf {\alpha }^{2,1}} x_{\mathbf {\alpha }^{1,1} \vee \mathbf {\alpha }^{2,1}} x_{\mathbf {\alpha }^{3,1}}$ then a pair of indices satisfying line 7 of Algorithm 2 must be α^1,1 ∨ α^2,1, α^3,1 so that the iteration ends up with

$$ S^{2}=LC(S^{2})\Big(x_{\mathbf{\alpha}^{3,2}} \cdot f_{d}^{\left( \mathbf{\alpha}^{1,2},\mathbf{\alpha}^{2,2}\right)}+\underbrace{x_{\mathbf{\alpha}^{1,2} \wedge \mathbf{\alpha}^{2,2}} x_{\mathbf{\alpha}^{1,2} \vee {\alpha}^{2,2}}x_{{\alpha}^{3,2}}-\text{NLM}(S^{0})}_{\displaystyle=S^{3}}\Big) $$

such that

$$ \left[\mathbf{\alpha}^{3,2}\right]_{k} \leq \left[\mathbf{\alpha}^{1,2} \wedge \mathbf{\alpha}^{2,2}\right]_{k} \leq \left[\mathbf{\alpha}^{1,2} \vee \mathbf{\alpha}^{2,2}\right]_{k} \quad \text{ for all } k \in \left[d\right], \text{ and } x_{\mathbf{\alpha}^{3,2}}=x_{\mathbf{\alpha}^{1,1}\wedge \mathbf{\alpha}^{2,1}}. $$

Thus, in iteration i = 3 the leading monomial LM(S³) must be NLM(S⁰) (unless S³ = 0).

A similar analysis can be performed on the monomial NLM(S⁰) and therefore the algorithm stops after at most 6 iterations. The division algorithm results in

$$ S(f_{1},f_{2})=\sum\limits_{i=0}^{p} \left( \prod\limits_{j=0}^{i} LC(S^{j})\right) x_{\mathbf{\alpha}^{3,i}}\cdot f_{d}^{\left( \mathbf{\alpha}^{1,i}, \mathbf{\alpha}^{2,i}\right)}, $$

where $f_{d}^{\left (\mathbf {\alpha }^{1,i}, \mathbf {\alpha }^{2,i}\right )}=-x_{\mathbf {\alpha }^{1,i} \wedge \mathbf {\alpha }^{2,i}}x_{\mathbf {\alpha }^{1,i} \vee \mathbf {\alpha }^{2,i}}+x_{\mathbf {\alpha }^{1,i}}x_{\mathbf {\alpha }^{2,i}} \in {\mathcal{G}}_{d}$ and p ≤ 5. All the cases that we left out above are treated in a similar way. This shows that ${\mathcal{G}}_{d}$ is a Gröbner basis of J_d.

In order to show that ${\mathcal{G}}_{d}$ is the reduced Gröbner basis of J_d, first notice that LC(g) = 1 for all $g \in {\mathcal{G}}_{d}$. Furthermore, the leading term of any polynomial in ${\mathcal{G}}_{d}$ is of degree two. Thus, it is enough to show that for every pair of different polynomials $f_{d}^{(\mathbf {\alpha }^{1},\mathbf {\beta }^{1})},f_{d}^{(\mathbf {\alpha }^{2},\mathbf {\beta }^{2})} \in {\mathcal{G}}_{d}$ (related to ${\mathcal{S}}_{1}, {\mathcal{M}}_{1}$ and ${\mathcal{S}}_{2},{\mathcal{M}}_{2}$, respectively) it holds that $LM(f_{d}^{(\mathbf {\alpha }^{1},\mathbf {\beta }^{1})})\neq LM(f_{d}^{(\mathbf {\alpha }^{2},\mathbf {\beta }^{2})})$ with $(\mathbf {\alpha }^{k},\mathbf {\beta }^{k}) \in {\mathcal{T}}_{d}^{{\mathcal{S}}_{k},{\mathcal{M}}_{k}}$ for k = 1,2. But this follows from the fact that all elements of ${\mathcal{G}}_{d}$ are different as remarked before the statement of the theorem. □

We define the tensor θ_k-norm analogously to the matrix scenario.

Definition 6

The tensor θ_k-norm, denoted by $\left \|\cdot \right \|_{\theta _{k}}$, is the norm induced by the k-theta body $TH_{k}\left (J_{d}\right )$, i.e.,

$$ \left\|\mathbf{X}\right\|_{\theta_{k}}=\inf \left\{r: \mathbf{X} \in rTH_{k}\left( J_{d}\right)\right\}. $$

The θ_k-norm can be computed with the help of Theorem 1, i.e., as

$$ \left\|\mathbf{X}\right\|_{\theta_{k}} = \min t \quad \text{ subject to } \mathbf{X} \in t \mathbf{Q}_{\mathcal{B}_{k}}(J_{d}). $$

Given the moment matrix $\mathbf {M}_{{\mathcal{B}}_{k}}[\mathbf {y}]$ associated with J_d, this minimization program is equivalent to the semidefinite program

$$ \min_{t \in \mathbb{R} , \mathbf{y} \in \mathbb{R}^{\mathcal{B}_{k}}} t \quad \text{ subject to } \quad \mathbf{M}_{\mathcal{B}_{k}}[\mathbf{y}] \succcurlyeq 0, y_{0} = t, \mathbf{y}_{\mathcal{B}_{1}} = \mathbf{X}. $$

(22)

We have focused on the polynomial ideal generated by all second-order minors of all matricizations of the tensor. One may also consider a subset of all possible matricizations corresponding to various tensor decompositions and notions of tensor rank. For example, the Tucker(HOSVD)-rank (corresponding to the Tucker or HOSVD decomposition) of a d th-order tensor X is a d-dimensional vector r_{HOSV D} = (r₁, r₂,…,r_d) such that $r_{i}=rank\left (\mathbf {X}^{\{i\}}\right )$ for all $i \in \left [d\right ]$ (see [29]). Thus, we can define an ideal J_d,HOSVD generated by all second-order minors of unfoldings X^{k}, for $k \in \left [d\right ]$.

The tensor train (TT) decomposition is another popular approach for tensor computations. The corresponding TT-rank of a d th-order tensor X is a (d − 1)-dimensional vector r_TT = (r₁, r₂,…,r_d− 1) such that $r_{i}=rank\left (\mathbf {X}^{\{1,\ldots ,i\}}\right )$, $i \in \left [d-1\right ]$ (see [49] for details). By taking into account only minors of order two of the matricizations $\mathbf {\tau } \in \left \{\{1\},\{1,2\},\ldots ,\{1,2,\ldots ,d-1\}\right \}$, one may introduce a corresponding polynomial ideal J_d,TT.

Theorem 6

The polynomial ideals J_d, J_d,HOSVD, and J_d,TT are equal, for all d ≥ 3.

Proof

Let $\mathbf {\tau } \subset \left [d\right ]$ represent a matricization. Similarly to the case of order-three tensors, for $\left (\mathbf {\alpha },\mathbf {\beta }\right ) \in \mathbb {N}^{2d}$, $x_{\mathbf {\alpha }^{\mathbf {\tau }}}x_{\mathbf {\beta }^{\mathbf {\tau }}}$ denotes the monomial where $\alpha _{k}^{\mathbf {\tau }}=\alpha _{k}$, $\beta _{k}^{\mathbf {\tau }}=\beta _{k}$ for all k ∈τ and $\alpha _{\ell }^{\mathbf {\tau }}=\beta _{\ell }$, $\beta _{\ell }^{\mathbf {\tau }}=\alpha _{\ell }$ for all $\ell \in \mathbf {\tau }^{c}=\left [d\right ]\backslash \mathbf {\tau }$. Moreover, $x_{\mathbf {\alpha }^{\mathbf {\tau },\mathbf {0}}}x_{\mathbf {\beta }^{\mathbf {\tau },\mathbf {0}}}$ denotes the monomial where $\alpha _{k}^{\mathbf {\tau },\mathbf {0}}=\alpha _{k}$, $\beta _{k}^{\mathbf {\tau },\mathbf {0}}=\beta _{k}$ for all k ∈τ and $\alpha _{\ell }^{\mathbf {\tau },\mathbf {0}}=\beta _{\ell }^{\mathbf {\tau },\mathbf {0}}=0$ for all $\ell \in \mathbf {\tau }^{c}=\left [d\right ]\backslash \mathbf {\tau }$. The corresponding order-two minors are defined as

$$ f_{(\mathbf{\alpha},\mathbf{\beta})}^{\mathbf{\tau}}(\mathbf{x})=-x_{\mathbf{\alpha}} x_{\mathbf{\beta}} + x_{\mathbf{\alpha}^{\mathbf{\tau}}} x_{\mathbf{\beta}^{\mathbf{\tau}}}, \quad (\mathbf{\alpha},\mathbf{\beta}) \in\mathbf{\mathcal{T}}^{\mathbf{\tau}}. $$

We define the set $\mathbf {{\mathcal{T}}}^{\mathbf {\tau }}$ as

$$\mathbf{\mathcal{T}}^{\mathbf{\tau}}= \left\{\left( \mathbf{\alpha},\mathbf{\beta}\right): \mathbf{\alpha}^{\mathbf{\tau},\mathbf{0}}\neq\mathbf{\beta}^{\mathbf{\tau},\mathbf{0}}, \mathbf{\alpha}^{\mathbf{\tau}^{c},\mathbf{0}}\neq\mathbf{\beta}^{\mathbf{\tau}^{c},\mathbf{0}}\right\}.$$

Similarly as in the case of order-three tensors, notice that $f_{( {\alpha }, {\beta })}^{ {\tau }}(\mathbf {x})= f_{( {\beta }, {\alpha })}^{ {\tau }}(\mathbf {x})=-f_{( {\alpha }^{ {\tau }}, {\beta }^{ {\tau }})}^{ {\tau }}(\mathbf {x}) = -f_{( {\beta }^{ {\tau }}, {\alpha }^{ {\tau }})}^{ {\tau }}(\mathbf {x})$, for all $( {\alpha }, {\beta }) \in {{\mathcal{T}}}^{ {\tau }}$. First, we show that J_d = J_d,HOSVD by showing that $f_{( {\alpha }, {\beta })}^{ {\tau }}(\mathbf {x}) \in J_{d,\text {HOSVD}}$, for all $( {\alpha }, {\beta }) \in {{\mathcal{T}}}^{ {\tau }}$ and all |τ|≥ 2. Without loss of generality, we can assume that α_i≠β_i, for all i ∈ τ since otherwise we can consider the matricization τ∖{i : α_i = β_i}. Additionally, by definition of ${{\mathcal{T}}}^{ {\tau }}$, there exists at least one ℓ ∈ τ^c such that α_ℓ≠β_ℓ. Let τ = {t₁, t₂,…,t_k} with t_i < t_i+ 1, for all i ∈ [k − 1] and k ≥ 2. Next, fix $({\alpha },{\beta }) \in {\mathcal{T}}^{ {\tau }}$ and define α⁰ = α and β⁰ = β. Algorithm 3 results in polynomials g_k ∈ J_3,TT such that $f_{( {\alpha }, {\beta })}^{ {\tau }}(\mathbf {x})={\sum }_{i=1}^{k} g_{i}(\mathbf {x})$. This follows from

$${\sum}_{i=1}^{k} g_{i} = {\sum}_{i=1}^{k} \left( -x_{\mathbf{\alpha}^{i-1}} x_{\mathbf{\beta}^{i-1}}+x_{\mathbf{\alpha}^{i}} x_{\mathbf{\beta}^{i}}\right)= -x_{\mathbf{\alpha}^{0}} x_{\mathbf{\beta}^{0}} + x_{{\alpha}^{k}} x_{{\beta}^{k}}=f_{({\alpha},{\beta})}^{{\tau}}(\mathbf{x}). $$

By the definition of polynomials g_k it is obvious that

$$g_{i} \in \left\{f_{({\alpha},{\beta})}^{\{i\}}(\mathbf{x}): ({\alpha},{\beta}) \in {\mathcal{T}}^{\{i\}}\right\}, \text{ for all } i \in[k].$$

Next, we show that J_d = J_d,TT. Since J_d = J_d,HOSVD, it is enough to show that $f_{(\mathbf {\alpha },\mathbf {\beta })}^{\{k\}} \!\in \! J_{d,\text {TT}}$, for all $(\mathbf {\alpha },\mathbf {\beta }) \!\in \! \mathbf {{\mathcal{T}}}^{\{k\}}$ and all $k \!\in \! \left [d\right ]$. By definition of J_d,TT this is true for k = 1. Fix k ∈{2,3,…,d}, $(\mathbf {\alpha },\mathbf {\beta }) \in \mathbf {{\mathcal{T}}}^{\{k\}}$ and consider a polynomial $f(\mathbf {x})=f_{(\mathbf {\alpha },\mathbf {\beta })}^{\{k\}}(\mathbf {x})$ corresponding to the second-order minor of the matricization X^{k}. By definition of $\mathbf {{\mathcal{T}}}^{\{k\}}$, α_k≠β_k and there exists an index $i \in \left [d\right ]\backslash \{k\}$ such that α_i≠β_i. Assume that i > k. Define the polynomials $g(\mathbf {x}) \in \mathbf {{\mathcal{R}}}^{\{1,2,\ldots ,k\}}:=\left \{f_{(\mathbf {\alpha },\mathbf {\beta })}^{\{1,2,\ldots ,k\}}(\mathbf {x}): \left (\mathbf {\alpha },\mathbf {\beta }\right ) \in \mathbf {{\mathcal{T}}}^{\{1,2,\ldots ,k\}}\right \}$ and $h(\mathbf {x}) \in \mathbf {{\mathcal{R}}}^{\{1,2,\ldots ,k-1\}}:=\left \{f_{(\mathbf {\alpha },\mathbf {\beta })}^{\{1,2,\ldots ,k-1\}}(\mathbf {x}): \left (\mathbf {\alpha },\mathbf {\beta }\right ) \in \mathbf {{\mathcal{T}}}^{\{1,2,\ldots ,k-1\}}\right \}$ as

$$ \begin{array}{@{}rcl@{}} g(\mathbf{x})& =& -x_{\mathbf{\alpha}} x_{\mathbf{\beta}} + x_{\mathbf{\alpha}^{\{1,2,\ldots,k\}}} x_{\mathbf{\beta}^{\{1,2,\ldots,k\}}} \\ h(\mathbf{x})& =& - x_{\mathbf{\alpha}^{\{1,2,\ldots,k\}}} x_{\mathbf{\beta}^{\{1,2,\ldots,k\}}} + x_{{\mathbf{\alpha}^{\{1,2,\ldots,k\}}}^{\{1,2,\ldots,k-1\}}} x_{{\mathbf{\beta}^{\{1,2,\ldots,k\}}}^{\{1,2,\ldots,k-1\}}} \end{array} $$

Since $x_{{\mathbf {\alpha }^{\{1,2,\ldots ,k\}}}^{\{1,2,\ldots ,k-1\}}} x_{{\mathbf {\beta }^{\{1,2,\ldots ,k\}}}^{\{1,2,\ldots ,k-1\}}}=x_{\mathbf {\alpha }^{\{k\}}} x_{\mathbf {\beta }^{\{k\}}}$, we have f(x) = g(x) + h(x) and thus f ∈ J_d,TT. If i < k notice that f(x) = g₁(x) + h₁(x), where

$$ \begin{array}{@{}rcl@{}} g_{1}(\mathbf{x})& =& -x_{\mathbf{\alpha}} x_{\mathbf{\beta}} + x_{\mathbf{\alpha}^{\{1,2,\ldots,k-1\}}} x_{\mathbf{\beta}^{\{1,2,\ldots,k-1\}}} \in \mathbf{\mathcal{R}}^{\{1,2,\ldots,k-1\}}\\ h_{1}(\mathbf{x})& =& - x_{{\alpha}^{\{1,2,\ldots,k-1\}}} x_{{\beta}^{\{1,2,\ldots,k-1\}}} + x_{{{\alpha}^{\{1,2,\ldots,k-1\}}}^{\{1,2,\ldots,k\}}} x_{{{\beta}^{\{1,2,\ldots,k-1\}}}^{\{1,2,\ldots,k\}}}\\ &=&-x_{\mathbf{\alpha}^{\{1,2,\ldots,k\}}} x_{\mathbf{\beta}^{\{1,2,\ldots,k\}}} + x_{\mathbf{\alpha}^{\{k\}}} x_{\mathbf{\beta}^{\{k\}}} \in \mathbf{\mathcal{R}}^{\{1,2,\ldots,k\}}. \end{array} $$

□

Remark 6

Fix a decomposition tree T_I which generates a particular HT-decomposition and consider the ideal $J_{d,\text {HT},T_{I}}$ generated by all second-order minors corresponding to the matricizations induced by the tree T_I. In a similar way as above, one can obtain that $J_{d,\text {HT},T_{I}}$ equals to J_d.

5 Convergence of the unit θ _k-norm balls

In this section we show the following result on the convergence of the unit θ_k-balls .

Theorem 7

The theta body sequence of J_d converges asymptotically to the $\text {conv}\left (\nu _{\mathbb {R}}(J)\right )$, i.e.,

$$ \bigcap_{k=1}^{\infty} TH_{k}(J_{d})=\text{conv}\left( \nu_{\mathbb{R}}(J_{d})\right).$$

To prove Theorem 7 we use the following result presented in [2] which is a consequence of Schmüdgen’s Positivstellensatz.

Theorem 8

Let J be an ideal such that $\nu _{\mathbb {R}}(J)$ is compact. Then the theta body sequence of J converges to the convex hull of the variety $\nu _{\mathbb {R}}(J)$, in the sense that

$$ \bigcap_{k=1}^{\infty} TH_{k}(J)=\text{conv}\left( \nu_{\mathbb{R}}(J)\right).$$

Proof Proof of Theorem 7

The set $\nu _{\mathbb {R}}(J_{d})$ is the set of rank-one tensors with unit Frobenius norm which can be written as $\nu _{\mathbb {R}}(J_{d})={\mathcal{A}}_{1} \bigcap {\mathcal{A}}_{2}$ where

$$ \begin{array}{@{}rcl@{}} \mathcal{A}_{1}&=&\left\{\mathbf{X} \in \mathbb{R}^{n_1 \times n_2 \times {\cdots} \times n_d}: \text{rank}(\mathbf{X})=1\right\}, \\ \text{and }\mathcal{A}_{2}&=&\left\{\mathbf{X} \in \mathbb{R}^{n_1 \times n_2 \times {\cdots} \times n_d}: \left\|\mathbf{X}\right\|_{F}=1\right\}. \end{array} $$

It is well-known that ${\mathcal{A}}_{1}$ is closed [11, discussion before Definition 2.2] and since ${\mathcal{A}}_{2}$ is clearly compact, $\nu _{\mathbb {R}}(J_{d})$ is compact. Therefore, the result follows from Theorem 8. □

6 Computational complexity

The computational complexity of the semidefinite programs for computing the θ₁-norm of a tensor or for minimizing the θ₁-norm subject to a linear constraint depends polynomially on the number of variables, i.e., on the size of ${\mathcal B}_{2k}$, and on the dimension of the moment matrix M. We claim that the overall complexity scales polynomially in n, where for simplicity we consider d th-order tensors in $\mathbb {R}^{n \times n \times {\cdots } \times n}$. Therefore, in contrast to tensor nuclear norm minimization which is NP-hard for d ≥ 3, tensor recovery via θ₁-norm minimization is tractable.

Indeed, the moment matrix M is of dimension (1 + n^d) × (1 + n^d) (see also (16) for matrices in $\mathbb {R}^{2 \times 2}$) and if a = n^d denotes the total number of entries of a tensor $\mathbf {X} \in \mathbb {R}^{n \times {\cdots } \times n}$, then the number of the variables is at most $\frac {a\cdot (a+1)}{2} \sim {\mathcal{O}}(a^{2})$ which is polynomial in a. (A more precise counting does not give a substantially better estimate.)

7 Numerical experiments

Let us now empirically study the performance of low rank tensor recovery via θ₁-norm minimization via numerical experiments, where we concentrate on third-order tensors. Due to large computation times with standard semidefinite solvers, we focus only on small tensors and leave the optimization of the algorithm for future work. Given measurements $\mathbf {b} = {\mathcal{A}}(\mathbf {X})$ of a low rank tensor $\mathbf {X} \in \mathbb {R}^{n_{1} \times n_{2} \times n_{3}}$, where ${\mathcal{A}} : \mathbb {R}^{n_{1} \times n_{2} \times n_{3}} \to \mathbb {R}^{m}$ is a linear measurement map, we aim at reconstructing X as the solution of the minimization program

$$ \min \| \mathbf{Z} \|_{\theta_{1}} \quad \text{ subject to } \mathcal{A}(\mathbf{Z}) = \mathbf{b}. $$

(23)

As outlined in Section 2, the θ₁-norm of a tensor Z can be computed as the minimizer of the semidefinite program

$$ \min_{t, \mathbf{y}} t \quad \text{ subject to } \quad \mathbf{M}(t,\mathbf{y}, \mathbf{Z}) \succcurlyeq 0, $$

where $\mathbf {M}(t,\mathbf {y},\mathbf {X}) = \mathbf {M}_{{\mathcal{B}}_{1}}(t, \mathbf {X}, \mathbf {y})$ is the moment matrix of order 1 associated to the ideal J₃ (see Theorem 3). This moment matrix for J₃ is explicitly given by

$$ \mathbf{M}\left( t,\mathbf{y},\mathbf{X}\right)=t\mathbf{M}_{0}+{\sum}_{i=1}^{n_{1}}{\sum}_{j=1}^{n_{2}}{\sum}_{k=1}^{n_{3}} X_{ijk}\mathbf{M}_{ijk}+{\sum}_{p=2}^{9}{\sum}_{q=1}^{|\mathbf{M}^{p}|}y_{\ell}\mathbf{M}_{h_{p}(q)}^{p}, $$

where $\ell ={\sum }_{r=2}^{p-1}\left |\mathbf {M}^{r}\right |+q$, $\mathbf {M}^{p}=\{\mathbf {M}_{\widetilde {I}}^{p}\}$, and the matrices M₀, M_ijk and $\mathbf {M}_{\widetilde {I}}^{p}$ are provided in Table 3. For p ∈{2,3,…,9}, the function h_p denotes an arbitrary but fixed bijection $\left \{1,2,\ldots ,\left |\mathbf {M}^{p}\right |\right \} \mapsto \{(i,\hat {i},j,\hat {j},k,\hat {k})\}$, where $\widetilde {I}=(i,\hat {i},j,\hat {j},k,\hat {k})$ is in the range of the last column of Table 3. As discussed in Section 2 for the general case, the θ₁-norm minimization problem (23) is then equivalent to the semidefinite program

$$ \min_{t, \mathbf{y}, \mathbf{Z}} t \quad \text{ subject to }\quad \mathbf{M}\left( t, \mathbf{y}, \mathbf{Z}\right)\succeq 0 \quad \text{ and } \quad \mathcal{A}(\mathbf{Z}) = \mathbf{b}. $$

(24)

Table 3 The matrices involved in the definition of the moment matrix $\mathbf {M}\left (t,\mathbf {y},\mathbf {X}\right )$. Due to the symmetry only the upper triangle part of the matrices is specified

For our experiments, the linear mapping is defined as $({\mathcal{A}}\left (\mathbf {X}\right ))_{k}=\left <\mathbf {X},{\mathcal{A}}_{k}\right >$, k ∈ [m], with independent Gaussian random tensors ${\mathcal{A}}_{k} \in \mathbb {R}^{n_{1} \times n_{2} \times n_{3}}$, i.e., all entries of ${\mathcal{A}}_{k}$ are independent ${\mathcal{N}}\left (0,\frac {1}{m}\right )$ random variables. We choose tensors $\mathbf {X} \in \mathbb {R}^{n_{1} \times n_{2} \times n_{3}}$ of rank one as X = u ⊗v ⊗w, where each entry of the vectors u, v, and w is taken independently from the normal distribution ${\mathcal{N}}\left (0,1\right )$. Tensors $\mathbf {X} \in \mathbb {R}^{n_{1} \times n_{2} \times n_{3}}$ of rank two are generated as the sum of two random rank-one tensors. With ${\mathcal{A}}$ and X given, we compute $\mathbf {b} = {\mathcal{A}}(\mathbf {X})$, run the semidefinite program (24) and compare its minimizer with the original low rank tensor X. For a given set of parameters, i.e., dimensions n₁, n₂, n₃, number of measurements m and rank r, we repeat this experiment 200 times and record the empirical success rate of recovering the original tensor, where we say that recovery is successful if the elementwise reconstruction error is at most 10^− 6. We use MATLAB (R2008b) for these numerical experiments, including SeDuMi_1.3 for solving the semidefinite programs.

Table 4 summarizes the results of our numerical tests for cubic and non-cubic tensors of rank one and two and several choices of the dimensions. Here, the number m₀ denotes the maximal number of measurements for which not even one out of 200 generated tensors is recovered and m₁ denotes the minimal number of measurements for which all 200 tensors are recovered. The fifth column in Table 4 represents the number of independent measurements which are always sufficient for the recovery of a tensor of an arbitrary rank. For illustration, we present the average cpu time (in seconds) for solving the semidefinite programs via SeDuMi_1.3 in the last column. Alternatively, the SDPNAL+ MATLAB toolbox (version 0.5 beta) for semidefinite programming [62, 64] allows to perform low rank tensor recovery via θ₁-norm minimization for even higher-dimensional tensors. For example, with m = 95 measurement we managed to recover all rank-one 9 × 9 × 9 tensors out of 200 (each simulation taking about 5 min). Similarly, rank-one 11 × 11 × 11 tensors are recovered from m = 125 measurements with one simulation lasting about 50 min. Due to these large computation times, more elaborate numerical experiments have not been conducted in these scenarios. We remark that no attempt of accelerating the optimization algorithm has been made. This task is left for future research.

Table 4 Numerical results for low rank tensor recovery in $\mathbb {R}^{n_{1} \times n_{2} \times n_{3}}$

Except for very small tensor dimensions, we can always recover tensors of rank-one or two from a number of measurements which is significantly smaller than the dimension of the corresponding tensor space. Therefore, low rank tensor recovery via θ₁-minimization seems to be a promising approach. Of course, it remains to investigate the recovery performance theoretically.

Figures 1 and 2 present the numerical results for low rank tensor recovery via θ₁-norm minimization for Gaussian measurement maps, conducted with the SDPNAL+ toolbox. For fixed tensor dimensions n × n × n, fixed tensor rank r, and fixed number m of measurements 50 simulations are performed. We say that recovery is successful if the elementwise reconstruction error is smaller than 10^− 3. Figures 1a, 2a, and 3a and 1b, 2b, and 3b present experiments for rank-one and rank-two tensors, respectively. The vertical axis in all three figures represents the empirical success rate. In Fig. 1 the horizontal axis represents the relative number of measurements, to be more precise, for a tensor of size n × n × n, the number $\bar {n}$ on the horizontal axis represents $m=\bar {n} \frac {n^{3}}{100}$ measurements. In Fig. 2 for a rank-r tensor of size n × n × n and the number of measurements m, the horizontal axis represents the number m/(3nr). Notice that 3nr represents the degrees of freedom in the corresponding CP-decomposition. In particular, if the number of measurements necessary for tensor recovery is m ≥ 3Crn, for an universal constant C, Fig. 2 suggests that the constant C depends on the size of the tensor. In particular, it seems to grow slightly with n (although it is still possible that there exists C > 0 such that m ≥ 3Crn would always be enough for the recovery). With C = 3.3 we would always be able to recover a low rank tensor of size n × n × n with n ≤ 7. The horizontal axis in Fig. 3 represents the number $m/\left (3nr\cdot \log (n)\right )$. The figure suggests that with the number of measurements $m \geq 6rn\cdot \log (n)$ we would always be able to recover a low rank tensor and therefore it may be possible that a logarithmic factor is necessary.

Fig. 1

Recovery of rank-1 and rank-2 tensors via θ₁-norm minimization

Fig. 2

Recovery of rank-1 and rank-2 tensors via θ₁-norm minimization

Fig. 3

Recovery of rank-1 and rank-2 tensors via θ₁-norm minimization

We remark that we have used standard MATLAB packages for convex optimization to perform the numerical experiments. To obtain better performance, new optimization methods should be developed specifically to solve our optimization problem, or more generally, to solve the sum-of-squares polynomial problems. We expect this to be possible and the resulting algorithms to give much better performance results since we have shown that in the matrix scenario all theta norms correspond to the matrix nuclear norm. The state-of-the-art algorithms developed for the matrix scenario can compute the matrix nuclear norm and can solve the matrix nuclear norm minimization problem for matrices of large dimensions. The theory developed in this paper together with the first numerical results should encourage the development into this direction.

Appendix: Monomial orderings and Gröbner bases

An ordering on the set of monomials $\mathbf {x}^{\alpha } \in \mathbb {R}[\mathbf {x}]$, $\mathbf {x}^{\alpha } = x_{1}^{\alpha _{1}}\cdot x_{2}^{\alpha _{2}} {\cdots } x_{n}^{\alpha _{n}}$, is essential for dealing with polynomial ideals. For instance, it determines an order in a multivariate polynomial division algorithm. Of particular interest is the graded reverse lexicographic (grevlex) ordering.

Definition 7

For $\mathbf {\alpha }=\left (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n}\right )$, $\mathbf {\beta }=\left (\beta _{1},\beta _{2}, \ldots , \beta _{n}\right ) \in \mathbb {Z}_{\geq 0}^{n}$, we write $\mathbf {x}^{\mathbf {\alpha }}>_{grevlex}\mathbf {x}^{\mathbf {\beta }}$ (or α >_grevlexβ) if $\left |\mathbf {\alpha }\right |> \left |\mathbf {\beta }\right |$ or $\left |\mathbf {\alpha }\right |= \left |\mathbf {\beta }\right |$ and the rightmost nonzero entry of α −β is negative.

Once a monomial ordering is fixed, the meaning of leading monomial, leading term and leading coefficient of a polynomial (see Section 2) is well-defined. For more information on monomial orderings, we refer the interested reader to [15, 16].

A Gröbner basis is a particular kind of generating set of a polynomial ideal. It was first introduced in 1965 in the Phd thesis of Buchberger [5].

Definition 8 (Gröbner basis)

For a fixed monomial order, a basis ${\mathcal{G}}=\left \{g_{1}, g_{2}, \ldots , g_{s}\right \}$ of a polynomial ideal $J \subset \mathbb {R}\left [\mathbf {x}\right ]$ is a Gröbner basis (or standard basis) if for all $f \in \mathbb {R}[\mathbf {x}]$ there exist a unique $r \in \mathbb {R}[\mathbf {x}]$ and g ∈ J such that f = g + r and no monomial of r is divisible by any of the leading monomials in ${\mathcal{G}}$, i.e., by any of the monomials LM(g₁),LM(g₂),…,LM(g_s).

A Gröbner basis is not unique, but the reduced version defined next is.

Definition 9

The reduced Gröbner basis for a polynomial ideal $J \in \mathbb {R}\left [\mathbf {x}\right ]$ is a Gröbner basis ${\mathcal{G}}=\left \{g_{1},g_{2},\ldots ,g_{s}\right \}$ for J such that

• 1) LC(g_i) = 1, for all $i \in \left [s\right ]$.

• 2) g_i does not belong to $\left <LT({\mathcal{G}}\backslash \{g_{i}\})\right >$ for all $i \in \left [s\right ]$.

In other words, a Gröbner basis ${\mathcal{G}}$ is the reduced Gröbner basis if for all $i \in \left [s\right ]$ the polynomial $g_{i} \in {\mathcal{G}}$ is monic (i.e., LC(g_i) = 1) and the leading monomial LM(g_i) does not divide any monomial of g_j, j≠i.

Many important properties of the ideal and the corresponding algebraic variety can be deduced via its (reduced) Gröbner basis. For example, a polynomial belongs to a given ideal if and only if the unique r from the Definition 8 equals zero. Gröbner bases are also one of the main computational tools in solving systems of polynomial equations [16].

With $\overline {f}^{F}$ we denote the remainder on division of f by the ordered k-tuple $F=\left (f_{1},f_{2},\ldots ,f_{k}\right )$. If F is a Gröbner basis for an ideal $\left <f_{1},f_{2},\ldots ,f_{k}\right >$, then we can regard F as a set without any particular order by Definition 8, or in other words, the result of the division algorithm does not depend on the order of the polynomials. Therefore, $\overline {f}^{{\mathcal{G}}}=r$ in Definition 8.

The following result follows directly from Definition 8 and the polynomial division algorithm [16].

Corollary 2

Fix a monomial ordering and let ${\mathcal{G}}=\{g_{1},g_{2},\ldots ,g_{s}\} \subset \mathbb {R}\left [\mathbf {x}\right ]$ be a Gröbner basis of a polynomial ideal J. A polynomial $f \in \mathbb {R}[\mathbf {x}]$ is in the ideal J if it can be written in the form f = a₁g₁ + a₂g₂ + … + a_sg_s, where $a_{i} \in \mathbb {R}[\mathbf {x}]$, for all i ∈ [s], s.t. whenever a_ig_i≠ 0 we have

$$multideg(f) \geq multideg(a_{i}g_{i}).$$

Definition 10

Fix a monomial order and let ${\mathcal{G}}=\left \{g_{1},g_{2},\ldots ,g_{s}\right \} \subset \mathbb {R}\left [\mathbf {x}\right ]$. Given $f \in \mathbb {R}\left [\mathbf {x}\right ]$, we say that f reduces to zero modulo ${\mathcal{G}}$ and write

$$ f \rightarrow_{\mathcal{G}} 0$$

if it can be written in the form f = a₁g₁ + a₂g₂ + … + a_kg_k with $a_{i} \in \mathbb {R}[\mathbf {x}]$ for all i ∈ [k] s.t. whenever a_ig_i≠ 0 we have multideg(f) ≥ multideg(a_ig_i).

Assume that ${\mathcal{G}}$ in the above definition is a Gröbner basis of a given ideal J. Then a polynomial f is in the ideal J if and only if f reduces to zero modulo ${\mathcal{G}}$. In other words, for a Gröbner basis ${\mathcal{G}}$,

$$f \rightarrow_{\mathcal{G}} 0 \text{ if and only if } \overline{f}^{\mathcal{G}}=0.$$

The Gröbner basis of a polynomial ideal always exists and can be computed in a finite number of steps via Buchberger’s algorithm [5, 15, 16].

Next we define the S-polynomial of given polynomials f and g which is important for checking whether a given basis of the ideal is a Gröbner basis.

Definition 11

Let $f,g \in \mathbb {R}\left [\mathbf {x}\right ]$ be a non-zero polynomials.

• 1. If $multideg\left (f\right )=\mathbf {\alpha }$ and $multideg\left (g\right )=\mathbf {\beta }$, then let $\mathbf {\gamma }=\left (\gamma _{1},\gamma _{2},\ldots , \gamma _{n}\right )$, where $\gamma _{i}=\max \limits \{\alpha _{i},\beta _{i}\}$, for every i. We call x^γ the least common multiple of LM(f) and LM(g) written x^γ = LCM(LM(f),LM(g)).

• 2. The S-polynomial of f and g is the combination

  $$ S\left( f,g\right)=\frac{\mathbf{x}^{\mathbf{\gamma}}}{LT\left( f\right)}f - \frac{\mathbf{x}^{\mathbf{\gamma}}}{LT\left( g\right)}g. $$

The following theorem gives a criterion for checking whether a given basis of a polynomial ideal is a Gröbner basis.

Theorem 9 (Buchberger’s criterion)

A basis ${\mathcal{G}}=\left \{g_{1},g_{2},\ldots ,g_{s}\right \}$ for a polynomial ideal $J \subset \mathbb {R}\left [\mathbf {x}\right ]$ is a Gröbner basis if and only if $S\left (g_{i},g_{j}\right ) \rightarrow _{{\mathcal{G}}} 0$ for all i≠j.

Computing whether $S\left (g_{i},g_{j}\right ) \rightarrow _{{\mathcal{G}}} 0$ for all possible pairs of polynomials in the basis ${\mathcal{G}}$ can be a tedious task. The following proposition tells us for which pairs of polynomials this is not needed.

Proposition 1

Given a finite set ${\mathcal{G}} \subset \mathbb {R}\left [\mathbf {x}\right ]$, suppose that the leading monomials of $f,g \in {\mathcal{G}}$ are relatively prime, i.e.,

$$ LCM\left( LM(f), LM(g)\right)=LM(f)LM(g), $$

then $S\left (f,g\right )\rightarrow _{{\mathcal{G}}} 0$.

Therefore, to prove that the set ${\mathcal{G}} \subset \mathbb {R}\left [\mathbf {x}\right ]$ is a Gröbner basis, it is enough to show that $S\left (g_{i},g_{j}\right )\rightarrow _{{\mathcal{G}}} 0$ for those i < j where LM(g_i) and LM(g_j) are not relatively prime.