A new stable collocation method for solving a class of nonlinear fractional delay differential equations

Abstract

In this paper, a stable collocation method for solving the nonlinear fractional delay differential equations is proposed by constructing a new set of multiscale orthonormal bases of $W^{1}_{2,0}$. Error estimations of approximate solutions are given and the highest convergence order can reach four in the sense of the norm of $W_{2,0}^{1}$. To overcome the nonlinear condition, we make use of Newton’s method to transform the nonlinear equation into a sequence of linear equations. For the linear equations, a rigorous theory is given for obtaining their ε-approximate solutions by solving a system of equations or searching the minimum value. Stability analysis is also obtained. Some examples are discussed to illustrate the efficiency of the proposed method.

1 Introduction

Nowadays, fractional differential equations have been a hot topic in the field of differential equations for their widespread applications in many science fields [1, 2]. Among them, fractional delay differential equations begin to arouse attentions of many researchers. These equations have also many applications in various areas such as control theory, biology, and economy [3, 4]. Since some models have a great deal to do with past condition, the insertion of a time delay makes these models more realistic. Therefore, the development of theory and numerical algorithms about fractional delay differential equations is of importance. For example, Hu and Zhao [5] give the condition of asymptotical stability of nonlinear fractional system with distributed time delay by utilizing the function monotonous properties and the stability theorem of the fractional linear system. Pimenov et al. [6] use a BDF difference scheme based on approximations of Clenshaw and Curtis type to get the numerical solution of the following equation:

$$ \left\{ \begin{array}{ll} D^{\beta}_{C}y(t)=f[t,y(t),y(t-\tau)], ~0\leq t\leq L,~ 0<\beta\leq 1,\\ y(t)=\phi(t),~~~-\tau\leq t\leq 0. & \end{array} \right. $$

(1)

For (1), Moghaddam and Mostaghim [4] use the fractional finite difference method to obtain its numerical solutions. Saeed et al. [7] draw on the steps method and Chebyshev wavelet method to solve the nonlinear fractional delay differential equation:

$$ \left\{ \begin{array}{ll} D^{\alpha}_{C}y(x)=h(x) + f[y(x),y^{\prime}(x),y(px - \tau),y^{\prime}(px-\tau)], ~0\!\leq\! x\leq b,~1\!<\!\alpha\!\leq\! 2,\\ y(x)=\phi(x),~~~-b\leq x\leq 0, & \end{array} \right. $$

(2)

and get their approximate solutions. However, to our best knowledge, there are few articles about the study of fractional delay differential equations especially with regard to nonlinear fractional delay differential equations.

Newton’s iterative method is a very powerful tool to solve the nonlinear problems. Many researchers have been studying and generalizing Newton’s iterative method and they use it to solve nonlinear problems. Deuflhard [8] in his monograph constructs adaptive Newton algorithms for some specific nonlinear problems. Krasnosel’skii et al. [9] in their monograph study the Newton-Kantorovich’s method, give a modified Newton-Kantorovich’s method and solve the problem of the choice of initial approximations. Xu et al. [10] use quasi-Newton’s method to linearize a nonlinear operator equation, and so on. Theoretical analysis shows that the convergence order of Newton’s iterative formula is order 2.

Motivated greatly by the abovementioned excellent works, in this paper, we deal with the nonlinear fractional delay differential (2) in the condition p = 1, that is the following equation:

$$ \left\{ \begin{array}{ll} D^{\alpha}_{C}y(x)=g(x)+f[x,y(x),y^{\prime}(x),y(x-\tau),y^{\prime}(x - \tau)], ~0\leq x\leq 1,~1\!<\!\alpha\!\leq\! 2,\\ y(x)=y_{0}(x),~~~-\tau\leq x\leq 0, & \ \end{array} \right. $$

(3)

where f has continuous second order partial derivative, g(x) ∈ C[0, 1] and y₀(x) ∈ C² [−τ, 0] which are known functions. τ > 0 is a constant delay. The fractional derivative is in the sense of Caputo and y(x) ∈ C¹ [−τ,1] is the unknown function.

In this article, we develop a stable and effective collocation method to solve (3). The collocation method is one of the most efficient methods for obtaining accurate numerical solutions of differential equations including variable coefficients and nonlinear differential equations [11,12,13,14]. The stability of collocation methods has always been an important topic. At present, the definition of its stability is that when there are many collocation nodes, the resulting equations are not ill conditioned and the results are still valid. For a stable collocation method, we can improve the accuracy by increasing the number of approximation terms. Accordingly, it is particularly important to establish a high-precision and stable collocation method.

The choice of bases of a space is important for a collocation method. Approximate solutions with different accuracy can be derived by using different bases for the same equation. For obtaining higher accuracy solution of the nonlinear fractional differential equation, we construct a new set of multiscale orthonormal bases of $W^{1}_{2,0}$, give error estimations of approximate solutions, and prove in Section 3 that the highest convergence order can reach four in the sense of $W_{2,0}^{1}$.

Noting that the problem of initial value selection of the Newton’s iterative method has been well solved in [9], so in this paper we transform (3) into a list of linear equations by using Newton’s iterative method. Then a new stable collocation method is proposed to solve these equations. Compared with [15], the final numerical experiments show that our method is better in dealing with this kind of equations.

The remainder of this paper is organized as follows: In Section 2, some relevant definitions and properties of the fractional calculus and the space ${W_{2}^{1}}$ and $W_{2,0}^{1}$ are introduced. In Section 3, we construct a set of multiscale orthonormal bases of $W^{1}_{2,0}$ and give an error estimation of the approximate solution. In Section 4, we construct the ε −approximate solution method and apply this method to solve the linear fractional delay differential equation. In Section 5, we analyze the stability of the ε −approximate solution method. In Section 6, we make use of Newton’s method to transform the nonlinear equation into a sequence of linear equations. In Section 7, we give the algorithm implementation of Newton’s iterative formula for solving the nonlinear fractional delay differential equation. In Section 8, three numerical examples are given to clarify the effectiveness of the algorithm. In the last section, the conclusions are prensented.

2 Preliminaries and notations

In this section, some preliminary results about the fractional calculus operators and reproducing kernel spaces are recalled [16,17,18].

Definition 2.1

The Riemann-Liouville (R-L) fractional integral operator $J_{0}^{\alpha }$ is given by

$$J_{0}^{\alpha}u(x)=\frac{1}{\Gamma(\alpha)}{{\int}_{0}^{x}}(x-s)^{\alpha-1}u(s)\mathrm{d}s,~\alpha>0,$$

where ${\Gamma }(\alpha )={\int \limits }_{0}^{\infty }x^{\alpha -1}e^{-x}\mathrm {d}x.$

Definition 2.2

The Caputo fractional differential operator $D_{C}^{\alpha }$ is given by

$$D_{C}^{\alpha}u(x)=\frac{1}{\Gamma(n-\alpha)}{{\int}_{0}^{x}}(x-s)^{n-\alpha-1}u^{(n)}(s)\mathrm{d}s, n-1<\alpha<{n,~n}=\lceil\alpha\rceil.$$

Theorem 2.1

Let u(x) be the exact solution of (3), then $D^{\alpha }_{C}u(x)\in C[0, 1].$

Proof

By the assumption, one has

$$ |D^{\alpha}_{C}u(x)|=|J_{0}^{2-\alpha}u^{\prime\prime}(x)|<\infty. $$

Since integrability of a function is equivalent to its absolute integrability, one has

$$\frac{x^{1-\alpha}}{\Gamma(2-\alpha)}{{\int}_{0}^{x}}|u^{\prime\prime}(s)|\mathrm{d}s\leq\frac{1}{\Gamma(2-\alpha)}{{\int}_{0}^{x}}(x-s)^{1-\alpha}|u^{\prime\prime}(s)|\mathrm{d}s<\infty.$$

Taking x = 1, we obtain $u^{\prime \prime }(x)\in L^{1}[0, 1]$. Thus, u(x) and $u^{\prime }(x)$ are absolutely continuous on [0, 1]. Hence, $D^{\alpha }_{C}u=g(x)+f[x,u(x),u^{\prime }(x),u(x-\tau ),u^{\prime }(x-\tau )]\in C[0, 1]$. □

Definition 2.3

Assume that n is a positive integer, then we denote

$$ AC^{n}[0, 1]=\left.\{u(x)|u^{(n-1)}(x)~is~absolute~continuous~in ~[0, 1]\right.\}.$$

$$ {W^{1}_{2}}={W^{1}_{2}}[0, 1]=\{u(x)|u(x)\in AC[0, 1],u^{\prime}\in L^{2}[0, 1]\}.$$

The inner product (⋅,⋅)₁ and the norm ∥⋅∥₁ of ${W^{1}_{2}}$ are given by

$$ \begin{array}{@{}rcl@{}} (u,v)_{1}\!\!\!&=\!\!\!& u(0)v(0)+{{\int}_{0}^{1}}u^{\prime}(x)v^{\prime}(x)\mathrm{d}x, \|u(x)\|_{1}=\sqrt{(u(x),u(x))_{1}}~,~~\forall u,v \in {W^{1}_{2}}. \end{array} $$

It is easy to see that ${W^{1}_{2}}\subset C[0, 1]$. Similar to [17], we can prove that ${W^{1}_{2}}$ is not only a Hilbert space, but also a reproducing kernel space with the reproducing kernel

$$r(x,y)= \left\{ \begin{array}{ll} 1+x, ~ x\leq y,\\ 1+y, ~ x>y. \end{array} \right. $$

Definition 2.4

The inner product space $W^{1}_{2,0}$ is defined as $W^{1}_{2,0}\triangleq W^{1}_{2,0}[0, 1]=\{u(x)\in {W^{1}_{2}}|u(0)=0 \}$ with the inner product

$$(u,v)_{1}= {{\int}_{0}^{1}}u^{\prime}(x)v^{\prime}(x)\mathrm{d}x,~~\forall u,v\in W^{1}_{2,0}.$$

Lemma 2.1

$$ \|u(x)\|_{C}\leq \sqrt{2}\|u(x)\|_{1},~~\forall u(x)\in {W^{1}_{2}}, $$

where $\|u(x)\|_{C}\triangleq \underset {\left .x\in [0, 1]\right .}{\max \limits }|u(x)|.$

Proof

For any $u(x)\in {W^{1}_{2}}$, we have

$$ \begin{array}{@{}rcl@{}} |u(x)|&=&\mid (u(y),r(x,y))_{1}\mid\leq\|u(x)\|_{1}\cdot\|r(x,y)\|_{1}=\|u(x)\|_{1}\cdot\sqrt{r(x,x)}\\ &=&\|u(x)\|_{1} \sqrt{1+x}\leq\sqrt{2}\|u(x)\|_{1}. \end{array} $$

Thus $\|u(x)\|_{C}\leq \sqrt {2}\|u(x)\|_{1}.$□

The following definition will be used in Section 6.

Definition 2.5

The inner product space $W^{\alpha }_{2}$ is defined as $W^{\alpha }_{2}\triangleq W^{\alpha }_{2}[0, 1]=\{J_{0}^{\alpha }u(s)|u(s)\in W^{1}_{2,0}[0, 1]\}$. And the inner product and the norm of $W^{\alpha }_{2}$ are given by

$$ \begin{array}{@{}rcl@{}} (u,v)_{\alpha}&=&(D_{C}^{\alpha}u(s),D_{C}^{\alpha}v(s))_{1}\\ &=&{{\int}_{0}^{1}}(D_{C}^{\alpha}u)'(s)(D_{C}^{\alpha}v)'(s)\mathrm{d}s, \|u(x)\|_{\alpha}=\sqrt{(u(x),u(x))_{\alpha}}~, \end{array} $$

where $u,v\in W^{\alpha }_{2}.$

Remark 2.1

Similar to [19], one can prove that $W^{\alpha }_{2}$ is not only a Hilbert space, but also a reproducing kernel space.

3 Construction of the multiscale orthonormal bases of $W^{1}_{2,0}$ and error estimations

In this section, we construct the multiscale orthonormal bases of $W^{1}_{2,0}$ by the famous Legendre multiwavelets, and give error estimations of approximate solutions.

Define the cubic Legendre scaling functions in the interval [0, 1] [20],

$$ \begin{array}{@{}rcl@{}} \eta^{0}(x)&=&1,\\ \eta^{1}(x)&=&\sqrt{3}(2x-1),\\ \eta^{2}(x)&=&\sqrt{5}(6x^{2}-6x+1),\\ \eta^{3}(x)&=&\sqrt{7}(20x^{3}-30x^{2}+12x-1), \end{array} $$

and then cubic Legendre multiwavelets are given as

$$ \begin{array}{@{}rcl@{}} \phi^{0}(x)&=&\left\{ \begin{array}{ll} k_{1}(x)=-\sqrt{\frac{15}{17}}(224x^{3}-216x^{2}+56x-3), & x\in[0,\frac{1}{2}),\\ k_{2}(x)=\sqrt{\frac{15}{17}}(224x^{3}-456x^{2}+296x-61), & x\in[\frac{1}{2},1], \end{array} \right. \\ \phi^{1}(x)&=&\left\{ \begin{array}{ll} k_{3}(x)=\sqrt{\frac{1}{21}}(1680x^{3}-1320x^{2}+270x-11), & x\in[0,\frac{1}{2}),\\ k_{4}(x)=\sqrt{\frac{1}{21}}(1680x^{3}-3720x^{2}+2670x-619), & x\in[\frac{1}{2},1], \end{array} \right. \\ \phi^{2}(x)&=&\left\{ \begin{array}{ll} k_{5}(x)=-\sqrt{\frac{35}{17}}(256x^{3}-174x^{2}+30x-1), & x\in[0,\frac{1}{2}),\\ k_{6}(x)=\sqrt{\frac{35}{17}}(256x^{3}-594x^{2}+450x-111), & x\in[\frac{1}{2},1], \end{array} \right. \\ \phi^{3}(x)&=&\left\{ \begin{array}{ll} k_{7}(x)=\sqrt{\frac{5}{42}}(420x^{3}-246x^{2}+36x-1), & x\in[0,\frac{1}{2}),\\ k_{8}(x)=\sqrt{\frac{5}{42}}(420x^{3}-1014x^{2}+804x-209), & x\in[\frac{1}{2},1], \end{array} \right. \end{array} $$

$$ \begin{array}{@{}rcl@{}} \phi^{0}_{ik}(x)&=&\sqrt{2}^{i-1}\phi^{0}(2^{i-1}x-k)=\sqrt{2}^{i-1}\left\{ \begin{array}{ll} k_{1}(2^{i-1}x-k), & x\in[\frac{k}{2^{i-1}},\frac{k+\frac{1}{2}}{2^{i-1}}),\\ k_{2}(2^{i-1}x-k), & x\in[\frac{k+\frac{1}{2}}{2^{i-1}},\frac{k+1}{2^{i-1}}],\\ 0, & \text{else,} \end{array} \right. \\ \phi^{1}_{ik}(x)&=&\sqrt{2}^{i-1}\phi^{1}(2^{i-1}x-k)=\sqrt{2}^{i-1}\left\{ \begin{array}{ll} k_{3}(2^{i-1}x-k), & x\in[\frac{k}{2^{i-1}},\frac{k+\frac{1}{2}}{2^{i-1}}),\\ k_{4}(2^{i-1}x-k), & x\in[\frac{k+\frac{1}{2}}{2^{i-1}},\frac{k+1}{2^{i-1}}],\\ 0, & \text{else,} \end{array} \right. \\ \phi^{2}_{ik}(x)&=&\sqrt{2}^{i-1}\phi^{2}(2^{i-1}x-k)=\sqrt{2}^{i-1}\left\{ \begin{array}{ll} k_{5}(2^{i-1}x-k), & x\in[\frac{k}{2^{i-1}},\frac{k+\frac{1}{2}}{2^{i-1}}),\\ k_{6}(2^{i-1}x-k), & x\in[\frac{k+\frac{1}{2}}{2^{i-1}},\frac{k+1}{2^{i-1}}],\\ 0, & \text{else,} \end{array} \right. \\ \phi^{3}_{ik}(x)&=&\sqrt{2}^{i-1}\phi^{3}(2^{i-1}x-k)=\sqrt{2}^{i-1}\left\{ \begin{array}{ll} k_{7}(2^{i-1}x-k), & x\in[\frac{k}{2^{i-1}},\frac{k+\frac{1}{2}}{2^{i-1}}),\\ k_{8}(2^{i-1}x-k), & x\in[\frac{k+\frac{1}{2}}{2^{i-1}},\frac{k+1}{2^{i-1}}],\\ 0, & \text{else,} \end{array} \right. \end{array} $$

where i = 1, 2, ⋯ , k = 0, 1, 2, ⋯ , 2^{i− 1} − 1.

Denote

$$ \begin{array}{@{}rcl@{}} \{\varphi_{i}(x)\}^{\infty}_{i=1}&\triangleq&\{\eta^{0}(x),\eta^{1}(x),\eta^{2}(x),\eta^{3}(x),\phi^{0}(x),\phi^{1}(x),\phi^{2}(x),\phi^{3}(x),\phi^{0}_{20}(x),\\ && \phi^{0}_{21}(x),\phi^{1}_{20}(x),\phi^{1}_{21}(x),\phi^{2}_{20}(x),\\ && \phi^{2}_{21}(x),\phi^{3}_{20}(x),\phi^{3}_{21}(x),\phi^{0}_{30}(x),\cdots\}. \end{array} $$

Lemma 3.1

$\{\varphi _{i}(x)\}^{\infty }_{i=1}$ is a set of multiscale orthonormal bases of L² [0, 1].

Proof

For the proof one can refer to [21]. □

Theorem 3.1

$\{\psi _{i}(x)\}^{\infty }_{i=1}\!\triangleq \!\{{J_{0}^{1}}\varphi _{i}(x)\}^{\infty }_{i=1}=\{{J_{0}^{1}}\eta ^{0}(x),{J_{0}^{1}}\eta ^{1}(x),{J_{0}^{1}}\eta ^{2}(x),{J_{0}^{1}}\eta ^{3}(x)$, ${J_{0}^{1}}\phi ^{0}(x)$, ${J_{0}^{1}}\phi ^{1}(x)$, ${J_{0}^{1}}\phi ^{2}(x)$, ${J_{0}^{1}}\phi ^{3}(x)$, ${J_{0}^{1}}\phi ^{0}_{20}(x)$, ${J_{0}^{1}}\phi ^{0}_{21}(x)$, ${J_{0}^{1}}\phi ^{1}_{20}(x)$, ${J_{0}^{1}}\phi ^{1}_{21}(x)$, ${J_{0}^{1}}\phi ^{2}_{20}(x),{J_{0}^{1}}\phi ^{2}_{21}(x),{J_{0}^{1}}\phi ^{3}_{20}(x)$, ${J_{0}^{1}}\phi ^{3}_{21}(x),{J_{0}^{1}}\phi ^{0}_{30}(x),\cdots \}$ is a set of orthonormal bases of $W^{1}_{2,0}[0, 1]$.

Proof

Firstly, we show that $\{\psi _{i}(x)\}^{\infty }_{i=1}$ is orthonormal in $W^{1}_{2,0}$.

$$ \begin{array}{@{}rcl@{}} (\psi_{i}(x),\psi_{j}(x))_{1}&=&({J_{0}^{1}}\varphi_{i}(x),{J_{0}^{1}}\varphi_{j}(x))_{1}=(\varphi_{i}(x),\varphi_{j}(x))_{L^{2}}=\delta_{ij}, \end{array} $$

where $\delta _{ij}=\left \{ \begin {array}{ll} 1, & i=j\\ 0, & i\neq j \end {array} \right ..$ So $\{\psi _{i}(x)\}^{\infty }_{i=1}$ is orthonormal in $W^{1}_{2,0}$.

Next, we prove that $\{\psi _{i}(x)\}^{\infty }_{i=1}$ is complete in $W^{1}_{2,0}$. Let $\xi (x)\in W^{1}_{2,0}$ and (ξ(x), ψ_i(x))₁ = 0, i = 1,2,⋯ . That is,

$$ \begin{array}{@{}rcl@{}} (\xi(x),\psi_{i}(x))_{1} = (\xi(x),{J_{0}^{1}}\varphi_{i}(x))_{1} = (\xi^{\prime}(x),\varphi_{i}(x))_{L^{2}} = {{\int}_{0}^{1}}\xi^{\prime}(x)\cdot\varphi_{i}(x)\mathrm{d}x = 0. \end{array} $$

(4)

By Lemma 3.1, $\{\varphi _{i}(x)\}^{\infty }_{i=1}$ is a set of multiscale orthonormal bases of L² [0, 1], and we obtain $\xi ^{\prime }(x)=0$. Noting that $\xi (x)\in W^{1}_{2,0}$, we have ξ(0) = 0. So $\xi (x)=\xi (0)+{{{\int \limits }_{0}^{x}}\xi ^{\prime }(t)\mathrm {d}t}=0$. Thus, $\{\psi _{i}(x)\}^{\infty }_{i=1}$ is complete in $W^{1}_{2,0}$ and $\{\psi _{i}(x)\}^{\infty }_{i=1}$ is a set of orthonormal bases of $W^{1}_{2,0}$. □

Remark 3.1

Noting that

$$ \begin{array}{@{}rcl@{}} {J_{0}^{1}}\phi^{m}_{ik}(x)&=&{{\int}_{0}^{1}}\phi^{m}_{ik}(x){\mathrm{d}}x=\left\{ \begin{array}{ll} 0, & x\in[0,\frac{k}{2^{i-1}}){,}\\ 2^{\frac{i-1}{2}}{\int}_{\frac{k}{2^{i-1}}}^{x} \phi^{m}(2^{i-1}t-k){\mathrm{d}}t, & x\in[\frac{k}{2^{i-1}},\frac{k+1}{2^{i-1}}],\\ 2^{\frac{i-1}{2}}{\int}_{\frac{k}{2^{i-1}}}^{\frac{k+1}{2^{i-1}}}\phi^{m}(2^{i-1}t-k){\mathrm{d}}t, & x\in(\frac{k+1}{2^{i-1}},1], \end{array} \right.\\ &=&\left\{ \begin{array}{ll} 0, & x\in[0,\frac{k}{2^{i-1}}),\\ 2^{-\frac{i-1}{2}}{\int}_{0}^{2^{i-1}x-k} \phi^{m}(t){\mathrm{d}}t, & x\in[\frac{k}{2^{i-1}},\frac{k+1}{2^{i-1}}], \\ 2^{-\frac{i-1}{2}}{{\int}_{0}^{1}}\phi^{m}(t){\mathrm{d}}t, & x\in(\frac{k+1}{2^{i-1}},1]{,} \end{array} \right.\\ &=&\left\{ \begin{array}{ll} 0, & x\in[0,\frac{k}{2^{i-1}}),\\ 2^{-\frac{i-1}{2}}({J_{0}^{1}}\phi^{m})(2^{i-1}x-k), & x\in[\frac{k}{2^{i-1}},\frac{k+1}{2^{i-1}}], \\ 0, & x\in(\frac{k+1}{2^{i-1}},1], \end{array} \right.\\ &=&2^{-\frac{i-1}{2}}({J_{0}^{1}}\phi^{m})(2^{i-1}x-k), \end{array} $$

and we can see that ${J_{0}^{1}}\phi ^{m}(x),~m=0,1,2,3$ is multiwavelets in $W^{1}_{2,0}.$

Definition 3.1

Let μ(x) ∈ L² [0, 1]. If μ(x) satisfies the following conditions

$$ {{\int}_{0}^{1}}\mu(x)\cdot x^{j}\mathrm{d}x=0,~~j=0,1,2,\cdots,r;~~{{\int}_{0}^{1}}\mu(x)\cdot x^{r+1}\mathrm{d}x\neq 0, $$

we call the Vanishing Moment of μ(x) is r + 1.

Property 3.1

The Vanishing Moment of ϕⁱ(x) is i + 4, i = 0, 1, 2, 3.

Proof

By specific calculation, we can reach that

$$ {{\int}_{0}^{1}}\phi^{i}(x)\cdot x^{j}\mathrm{d}x=0,~i=0,1,2,3;~j=0,1,\cdots,i+3, $$

and ${{\int \limits }_{0}^{1}}\phi ^{i}(x)\cdot x^{i+4}{\mathrm {d}}x\neq {0,~i}=0,1,2,3$. So the conclusion holds. □

Remark 3.2

According to Property 3.1, we obtain that the Vanishing Moment of $\{\phi ^{i}(x)\}_{i=0}^{3}$ is at least 4.

Property 3.2

For any $v(x)\in W_{2,0}^{1}[0, 1]$ and $N\in \mathbb {N}_{+}$, we have

$$ \parallel v(x)-\sum\limits_{i=1}^{N}a_{i}\psi_{i}(x){\parallel_{1}^{2}}=\sum\limits_{i=N+1}^{\infty}{a_{i}^{2}}, $$

where a_i = (v(x), ψ_i(x))₁.

Proof

According to Theorem 3.1, $\{\psi _{i}(x)\}^{\infty }_{i=1}$ is a set of orthonormal bases of $W^{1}_{2,0}[0, 1]$. Hence,

$$ v(x)=\sum\limits_{i=1}^{\infty}a_{i}\psi_{i}(x), $$

where a_i = (v(x), ψ_i(x))₁. Thus,

$$ \begin{array}{@{}rcl@{}} \parallel v(x)-\sum\limits_{i=1}^{N}a_{i}\psi_{i}(x){\parallel_{1}^{2}}&=&\parallel \sum\limits_{i=1}^{\infty}a_{i}\psi_{i}(x)-\sum\limits_{i=1}^{N}a_{i}\psi_{i}(x){\parallel_{1}^{2}}\\ &=&\parallel\sum\limits_{i=N+1}^{\infty}a_{i}\psi_{i}(x){\parallel_{1}^{2}}=\sum\limits_{i=N+1}^{\infty}{a_{i}^{2}}. \end{array} $$

□

Let y(x) and y_J(x) be an exact solution and an approximate solution of (3), respectively. Denote

$$y(x)=\sum\limits_{i=0}^{3}a_{i}{J_{0}^{1}}\eta^{i}(x)+\sum\limits_{i=1}^{\infty}\sum\limits_{l=0}^{3}\sum\limits_{k=0}^{2^{i-1}-1}c_{ik}^{l}{J_{0}^{1}}\phi_{ik}^{l}(x),$$

$$y_{J}(x)=\sum\limits_{i=0}^{3}a_{i}{J_{0}^{1}}\eta^{i}(x)+\sum\limits_{i=1}^{J}\sum\limits_{l=0}^{3}\sum\limits_{k=0}^{2^{i-1}-1}c_{ik}^{l}{J_{0}^{1}}\phi_{ik}^{l}(x),$$

where $a_{i}=(y(x),{J_{0}^{1}}\eta ^{i}(x))_{1}$, $c_{ik}^{l}=(y(x),{J_{0}^{1}}\phi _{ik}^{l}(x))_{1}$.

Lemma 3.2

Let $y(x)\in W_{2,0}^{1},\mid y^{(j)}(x)\mid \leq M,~{\forall ~x}\in [0, 1], {\text {for some } }j\in \{2,3,4,5\}$. Then $|c_{ik}^{l}|\leq 2^{-(i-1)(j-1/2)}AM,~l=0,1,2,3$ where A is a constant.

Proof

Without loss of generality, we first consider $|c_{ik}^{0}|$.

$$ |c_{ik}^{0}|=\left|\left( y(x),{J_{0}^{1}}\phi_{ik}^{0}(x)\right)_{1}\right|=\left|{{\int}_{0}^{1}}y^{\prime}(x)\phi_{ik}^{0}(x){\mathrm{d}}x\right|=\left|{\int}_{\frac{k}{2^{i-1}}}^{\frac{k+1}{2^{i-1}}}y^{\prime}(x)\phi_{ik}^{0}(x){\mathrm{d}}x\right|. $$

Expand $y^{\prime }(x)$ at $x=\frac {k}{2^{i-1}}$:

$$ \begin{array}{@{}rcl@{}} y^{\prime}(x)&=&y^{\prime}\left( \frac{k}{2^{i-1}}\right)+y^{\prime\prime}\left( \frac{k}{2^{i-1}}\right)\left( x-\frac{k}{2^{i-1}}\right)+\cdots\\&&+\frac{y^{(j)}(\xi)}{(j-1)!}\left( x-\frac{k}{2^{i-1}}\right)^{j-1},~\xi\in\left( \frac{k}{2^{i-1}},\frac{k+1}{2^{i-1}}\right). \end{array} $$

Thus, we have

$$ \begin{array}{@{}rcl@{}} \left|c_{ik}^{0}\right|&\leq&\left|y^{\prime}\left( \frac{k}{2^{i-1}}\right){\int}_{\frac{k}{2^{i-1}}}^{\frac{k+1}{2^{i-1}}}\phi_{ik}^{0}(x){\mathrm{d}}x\right|+\left|y^{\prime\prime}\left( \frac{k}{2^{i-1}}\right){\int}_{\frac{k}{2^{i-1}}}^{\frac{k+1}{2^{i-1}}}\left( x-\frac{k}{2^{i-1}}\right)\phi_{ik}^{0}(x){\mathrm{d}}x\right|\\ &&+\cdots+\left|{\int}_{\frac{k}{2^{i-1}}}^{\frac{k+1}{2^{i-1}}}\frac{y^{(j)}(\xi)}{(j-1)!}\left( x-\frac{k}{2^{i-1}}\right)^{j-1}\phi_{ik}^{0}(x){\mathrm{d}}x\right|. \end{array} $$

The first integral of the above inequality

$$ \begin{array}{@{}rcl@{}} {\int}_{\frac{k}{2^{i-1}}}^{\frac{k+1}{2^{i-1}}}\phi_{ik}^{0}(x){\mathrm{d}}x&=&\sqrt{2}^{i-1}{\int}_{\frac{k}{2^{i-1}}}^{\frac{k+1}{2^{i-1}}}\phi^{0}(2^{i-1}x-k){\mathrm{d}}x~~\underline{\underline{t=2^{i-1}x-k}}~~\sqrt{2}^{i-1}\\ &&\times{{\int}_{0}^{1}}\phi^{0}(t)\left( \frac{1}{2}\right)^{i-1}{\mathrm{d}}t=\left( \frac{1}{\sqrt{2}}\right)^{i-1}{{\int}_{0}^{1}}\phi^{0}(t){\mathrm{d}}t=0, \end{array} $$

by using Property 3.1.

Similarly, one can obtain that

$$ \begin{array}{@{}rcl@{}} {\int}_{\frac{k}{2^{i-1}}}^{\frac{k+1}{2^{i-1}}}\left( x-\frac{k}{2^{i-1}}\right)\phi_{ik}^{0}(x){\mathrm{d}}x&=&0,~~ {\int}_{\frac{k}{2^{i-1}}}^{\frac{k+1}{2^{i-1}}}\left( x-\frac{k}{2^{i-1}}\right)^{2}\phi_{ik}^{0}(x){\mathrm{d}}x\\&=&0,~~ {\int}_{\frac{k}{2^{i-1}}}^{\frac{k+1}{2^{i-1}}}\left( x-\frac{k}{2^{i-1}}\right)^{3}\phi_{ik}^{0}(x){\mathrm{d}}x=0. \end{array} $$

while

$$ \begin{array}{@{}rcl@{}} &&\left|{\int}_{\frac{k}{2^{i-1}}}^{\frac{k+1}{2^{i-1}}}\frac{y^{(j)}(\xi)}{(j-1)!}\left( x-\frac{k}{2^{i-1}}\right)^{j-1}\phi_{ik}^{0}(x){\mathrm{d}}x\right|\leq\frac{M}{(j-1)!}{\int}_{\frac{k}{2^{i-1}}}^{\frac{k+1}{2^{i-1}}}\left( x-\frac{k}{2^{i-1}}\right)^{j-1}\left|\phi_{ik}^{0}(x)\right|{\mathrm{d}}x\\ &&\quad=\frac{M}{(j-1)!}\sqrt{2}^{i-1}{\int}_{\frac{k}{2^{i-1}}}^{\frac{k+1}{2^{i-1}}}\left( x-\frac{k}{2^{i-1}}\right)^{j-1}\left|\phi^{0}(2^{i-1}x-k)\right|{\mathrm{d}}x\\ &&\quad=\frac{M}{(j-1)!}\sqrt{2}^{i-1}{{\int}_{0}^{1}}\left( \frac{t}{2^{i-1}}\right)^{j-1}\left|\phi^{0}(t)\right|\left( \frac{1}{2}\right)^{i-1}{\mathrm{d}}t~~(t=2^{i-1}x-k)\\ &&\quad=\frac{M}{(j-1)!}\frac{1}{2^{(i-1)(j-1/2)}}{{\int}_{0}^{1}}t^{j-1}\left|\phi^{0}(t)\right|{\mathrm{d}}t\\ &&\quad{\leq}2^{-(i-1)(j-1/2)}AM, \end{array} $$

where $A=\underset {\left .l=0,1,2,3\right .}{\max \limits }\left \{\frac {1}{(j-1)!}{{\int \limits }_{0}^{1}}t^{j-1}\big |\phi ^{l}(t)\big |\mathrm {d}t\right \}$. one has

$$|c_{ik}^{0}|\leq 2^{-(i-1)(j-1/2)}AM.$$

In the same way, one can derive that $|c_{ik}^{l}|\leq 2^{-(i-1)(j-1/2)}AM,~l=1,2,3$. So the conclusion holds. □

Theorem 3.2

Assume $y(x)\in W_{2,0}^{1},~|y^{(j)}(x)|\leq M,~\forall ~x\in [0, 1], {\text { for some }}~j\in \{2,3,4,5\}$. Then ∥ y(x) − y_J(x) ∥₁ ≤ C ⋅ 2^{−(j− 1)J} where C is a constant.

Proof

Using Property 3.2 and Lemma 3.2, we can derive

$$ \begin{array}{@{}rcl@{}} \parallel y(x)-y_{J}(x)\parallel_{1}&=&\left\|\sum\limits_{i=J+1}^{\infty}\sum\limits_{l=0}^{3}\sum\limits_{k=0}^{2^{i-1}-1}c_{ik}^{l}{J_{0}^{1}}\phi_{ik}^{l}(x)\right\|_{1}=\sqrt{\sum\limits_{i=J+1}^{\infty}\sum\limits_{l=0}^{3}\sum\limits_{k=0}^{2^{i-1}-1}(c_{ik}^{l})^{2}}\\ &\leq& AM\sqrt{\sum\limits_{i=J+1}^{\infty}\sum\limits_{l=0}^{3}\sum\limits_{k=0}^{2^{i-1}-1}(2^{-(i-1)(j-1/2)})^{2}}\\&=&AM\sqrt{\sum\limits_{i=J+1}^{\infty}2^{-2(i-1)(j-1)}\cdot 4}\leq C\cdot2^{-(j-1)J}, \end{array} $$

where $C=AM\sqrt {\frac {4}{1-2^{-2(j-1)}}}$. □

4 Linear fractional delay differential equations

In this section, we construct the ε-approximate solution method for solving (3) with f being linear, i.e.,

$$ \left\{ \begin{array}{ll} D^{\alpha}_{C}y(x)=h(x)+a(x)y(x)+b(x)y^{\prime}(x)+c(x)y(x-\tau)+d(x)y^{\prime}(x-\tau), ~0\leq x\leq 1, 1<\alpha\leq 2,\\ y(x)=y_{0}(x),~~~-\tau\leq x\leq 0, & \end{array} \right. $$

(5)

and analyze the convergence order of the ε-approximate solutions. $a(x),b(x),c(x),d(x),h(x)\in {W^{1}_{2}}[0, 1]$, y₀(x) ∈ C² [−τ,0] are known functions and y(x) is an unknown function. τ > 0 is a constant delay. Similar to Theorem 2.1, we can prove $D^{\alpha }_{C} y(x)\in C[0, 1]$. Here, we further assume $D^{\alpha }_{C}y(x)\in {W^{1}_{2}}$.

Let

$$\zeta (x)=\left\{ \begin{array}{ll} y_{0}(x), ~~~~~~~~~-\tau\leq x\leq 0,\\ y_{0}(0)+xy^{\prime}_{0}(0), ~0\leq x\leq 1, \end{array} \right. $$

and

$$v(x)=y(x)-\zeta(x).$$

Then (5) is equivalently transformed into

$$ \left\{ \begin{array}{ll} D^{\alpha}_{C}v=g(x)+a(x)v(x)+b(x)v^{\prime}(x)+c(x)v(x-\tau)+d(x)v^{\prime}(x-\tau), ~0\leq x\leq 1, \\ v(x)=0,~~~-\tau\leq x\leq 0, & \end{array} \right. $$

(6)

where

$$ g(x)=h(x)+a(x)\zeta(x)+b(x)\zeta^{\prime}(x)+c(x)\zeta(x-\tau)+d(x)\zeta^{\prime}(x-\tau). $$

Introducing the symbols ${~}^{-\tau }D_{C}^{\alpha }$ and $J_{-\tau }^{\alpha }$, we have $^{-\tau }D_{C}^{\alpha }=D_{C}^{\alpha },~J_{-\tau }^{\alpha }=J_{0}^{\alpha }$ due to the fact that ${~}^{-\tau }D_{C}^{\alpha }v(x)=\frac {1}{\Gamma (2-\alpha )}{\int \limits }_{-\tau }^{x}(x-t)^{1-\alpha }v^{\prime \prime }(t){\mathrm {d}}t=\frac {1}{\Gamma (2-\alpha )}{{\int \limits }_{0}^{x}}(x-t)^{1-\alpha }v^{\prime \prime }(t){\mathrm {d}}t=D_{C}^{\alpha }v(x)$ and $J_{-\tau }^{\alpha }v(x)=\frac {1}{\Gamma (\alpha )}{\int \limits }_{-\tau }^{x}(x-t)^{\alpha -1}v(t){\mathrm {d}}t=\frac {1}{\Gamma (\alpha )}{{\int \limits }_{0}^{x}}(x-t)^{\alpha -1}v(t){\mathrm {d}}t=J_{0}^{\alpha }v(x)$. So we use the denotation $D_{C}^{\alpha }$ and $J_{0}^{\alpha }$ below.

Let $\omega (x)={~}^{-\tau }\!D^{\alpha }_{C}v(x)=D^{\alpha }_{C}v(x)$. Thus, (6) is transformed into

$$ \left\{ \begin{array}{ll} \omega(x)=g(x)+a(x)J^{\alpha}_{0}\omega(x)+b(x)J^{\alpha-1}_{0}\omega(x)+c(x)J^{\alpha}_{0}\omega(x-\tau)+d(x)J^{\alpha-1}_{0}\omega(x-\tau), ~0\leq x\leq 1, \\ \omega(x)=0,~~~-\tau\leq x\leq 0. & \end{array} \right. $$

And $v(x)=J^{\alpha }_{-\tau }{{~}^{-\tau }\!D}^{\alpha }_{C}v(x)=J^{\alpha }_{-\tau }\omega (x)=J^{\alpha }_{0}\omega (x).$

Defining an operator $L: W^{1}_{2,0}\rightarrow W^{1}_{2,0}$,

$$ L(\omega(x))\triangleq \omega(x)-a(x)J^{\alpha}_{0}\omega(x)-b(x)J^{\alpha-1}_{0}\omega(x)-c(x)J^{\alpha}_{0}\omega(x-\tau)-d(x)J^{\alpha-1}_{0}\omega(x-\tau), $$

(7)

then (6) is equivalent to

$$ L(\omega(x)) =g(x). $$

(8)

Therefore, the solution y(x) of (5) can be obtained by

$$ y(x)=v(x)+\zeta(x)=J^{\alpha}_{0}\omega(x)+\zeta(x). $$

(9)

We need the following Lemmas for our aims.

Lemma 4.1

$(J_{0}^{\alpha }\omega (x))_{x}^{\prime }\in L^{1}[0, 1]$ for any $\omega (x)\in W^{1}_{2,0}[0, 1]$ with α > 0.

Proof

It is easy to see that

$$ \begin{array}{@{}rcl@{}} J_{0}^{\alpha}\omega(x)&=&\frac{1}{\Gamma(\alpha)}{{\int}_{0}^{x}}(x-t)^{\alpha-1}\omega(t){\mathrm{d}}t=\frac{1}{\Gamma(\alpha)}{{\int}_{0}^{x}}s^{\alpha-1}\omega(x-s){\mathrm{d}}s. \end{array} $$

So we can derive

$$ \begin{array}{@{}rcl@{}} (J_{0}^{\alpha}\omega)_{x}^{\prime}&=&\frac{1}{\Gamma(\alpha)}{{\int}_{0}^{x}}s^{\alpha-1}\omega^{\prime}(x-s){\mathrm{d}}s=\frac{1}{\Gamma(\alpha)}{{\int}_{0}^{x}}(x-t)^{\alpha-1}\omega^{\prime}(t){\mathrm{d}}t. \end{array} $$

Thus,

$$ \begin{array}{@{}rcl@{}} {{\int}_{0}^{1}}\left|(J_{0}^{\alpha}\omega)_{t}^{\prime}\right|{\mathrm{d}}t &\leq& \frac{1}{\Gamma(\alpha)}{{\int}_{0}^{1}}\left|{{\int}_{0}^{t}}(t-s)^{\alpha-1}\omega^{\prime}(s){\mathrm{d}}s\right|{\mathrm{d}}t\\ &\leq&\frac{1}{\Gamma(\alpha)}{{\int}_{0}^{1}}{{\int}_{0}^{t}}(t-s)^{\alpha-1}\left|\omega^{\prime}(s)\right|{\mathrm{d}}s{\mathrm{d}}t\\ &=&\frac{1}{\Gamma(\alpha)}{{\int}_{0}^{1}}{{\int}_{s}^{1}}(t-s)^{\alpha-1}\left|\omega^{\prime}(s)\right|{\mathrm{d}}t{\mathrm{d}}s\\ &=&\frac{1}{\Gamma(\alpha+1)}{{\int}_{0}^{1}}\left|\omega^{\prime}(s)\right|(1-s)^{\alpha}{\mathrm{d}}s\\ &\leq&\frac{1}{\Gamma(\alpha+1)}{{\int}_{0}^{1}}\left|\omega^{\prime}(s)\right|{\mathrm{d}}s<\infty. \end{array} $$

This implies $(J_{0}^{\alpha }\omega (x))_{x}^{\prime }\in L^{1}[0, 1].$□

Lemma 4.2

Let α > 0. Then

$$J_{0}^{\alpha}\omega\in W^{1}_{2,0}~\text{and}~\|J_{0}^{\alpha}\omega\|_{1}\leq \sqrt{\tilde{M}_{\alpha}}\|\omega\|_{1},$$

hold for any $\omega (x)\in W^{1}_{2,0}$ where $\tilde {M}_{\alpha }=\frac {1}{\alpha ^{2}{\Gamma }^{2}(\alpha )}$.

Proof

We can find that

$$ \begin{array}{@{}rcl@{}} {{\int}_{0}^{x}}(J_{0}^{\alpha}\omega)_{t}^{\prime}{\mathrm{d}}t&=&\frac{1}{\Gamma(\alpha)}{{\int}_{0}^{x}}{{\int}_{0}^{t}}(t-s)^{\alpha-1}\omega^{\prime}(s){\mathrm{d}}s{\mathrm{d}}t\\ &=&\frac{1}{\Gamma(\alpha)}{{\int}_{0}^{x}}{{\int}_{s}^{x}}(t-s)^{\alpha-1}\omega^{\prime}(s){\mathrm{d}}t{\mathrm{d}}s\\ &=&\frac{1}{\Gamma(\alpha)}{{\int}_{0}^{x}}\omega^{\prime}(s)\left( {{\int}_{s}^{x}}(t-s)^{\alpha-1}{\mathrm{d}}t\right){\mathrm{d}}s\\ &=&\frac{1}{\Gamma(\alpha+1)}{{\int}_{0}^{x}}\omega^{\prime}(s)(x-s)^{\alpha}{\mathrm{d}}s{,} \end{array} $$

hold for any $\omega (x)\in W^{1}_{2,0}$. On the other hand, we obtain

$$ \begin{array}{@{}rcl@{}} J_{0}^{\alpha}\omega(x)=\frac{1}{\Gamma(\alpha)}{{\int}_{0}^{x}}\omega(t)(x-t)^{\alpha-1}{\mathrm{d}}t=\frac{1}{\Gamma(\alpha+1)}{{\int}_{0}^{x}}\omega^{\prime}(t)(x-t)^{\alpha}{\mathrm{d}}t, \end{array} $$

by using the integration by parts. Hence, we have $J_{0}^{\alpha }\omega (x)={{\int \limits }_{0}^{x}}(J_{0}^{\alpha }\omega )_{t}^{\prime }{\mathrm {d}}t$ and $J_{0}^{\alpha }\omega (x)\in AC[0, 1].$

Moreover, we have

$$ \begin{array}{@{}rcl@{}} {{\int}_{0}^{1}}\left( (J_{0}^{\alpha}\omega(x))_{x}^{\prime}\right)^{2}{\mathrm{d}}x&=&\frac{1}{{\Gamma}^{2}(\alpha)}{{\int}_{0}^{1}}\left( {{\int}_{0}^{x}}(x-t)^{\alpha-1}\omega^{\prime}(t){\mathrm{d}}t\right)^{2}{\mathrm{d}}x\\ &\leq&\frac{1}{{\Gamma}^{2}(\alpha)}{{\int}_{0}^{1}}\left( {{\int}_{0}^{x}}(x-t)^{\alpha-1}{\mathrm{d}}t{\cdot{\int}_{0}^{x}}(x-t)^{\alpha-1}\omega^{\prime2}(t){\mathrm{d}}t\right){\mathrm{d}}x\\ &=&\frac{1}{{\Gamma}^{2}(\alpha)}{{\int}_{0}^{1}}\frac{x^{\alpha}}{\alpha}\left( {{\int}_{0}^{x}}(x-t)^{\alpha-1}\omega^{\prime2}(t){\mathrm{d}}t\right){\mathrm{d}}x\\ &\leq&\frac{1}{\alpha{\Gamma}^{2}(\alpha)}{{\int}_{0}^{1}}{{\int}_{0}^{x}}(x-t)^{\alpha-1}\omega^{\prime2}(t){\mathrm{d}}t{\mathrm{d}}x\\ &=&\frac{1}{\alpha{\Gamma}^{2}(\alpha)}{{\int}_{0}^{1}}{{\int}_{t}^{1}}(x-t)^{\alpha-1}\omega^{\prime2}(t){\mathrm{d}}x{\mathrm{d}}t\\ &=&\frac{1}{\alpha^{2}{\Gamma}^{2}(\alpha)}{{\int}_{0}^{1}}\omega^{\prime2}(t)(1-t)^{\alpha}{\mathrm{d}}t\\ &\leq&\frac{1}{\alpha^{2}{\Gamma}^{2}(\alpha)}{{\int}_{0}^{1}}\omega^{\prime2}(t){\mathrm{d}}t.\\ \end{array} $$

Let $\tilde {M}_{\alpha }=\frac {1}{\alpha ^{2}{\Gamma }^{2}(\alpha )}$. Then

$${{\int}_{0}^{1}}\left( (J_{0}^{\alpha}\omega(x))_{x}^{\prime}\right)^{2}\mathrm{d}x\leq\tilde{M}_{\alpha}{{\int}_{0}^{1}}\omega^{\prime2}(t){\mathrm{d}}t=\tilde{M}_{\alpha}\|\omega\|_{1}^{2}<\infty,$$

holds. So $(J_{0}^{\alpha }\omega (x))_{x}^{\prime }\in L^{2}[0, 1]$. Noting that $J_{0}^{\alpha }\omega (0)=0$, we have $J_{0}^{\alpha }\omega (x)\in W^{1}_{2,0}$ and

$$ \left\|J_{0}^{\alpha}\omega\right\|_{1}\leq \sqrt{\tilde{M}_{\alpha}}\|\omega\|_{1}. $$

□

Lemma 4.3

Let $a(x)\in {W^{1}_{2}}[0, 1],\omega (x)\in W^{1}_{2,0}[0, 1],\alpha >0.$ Then

$$\|a(x)J_{0}^{\alpha}\omega(x)\|_{1}^{2}\leq 4\|a(x)\|_{1}^{2}\left[\frac{1}{{\Gamma}^{2}(\alpha+1)}+\tilde{M}_{\alpha}\right]\|\omega\|_{1}^{2},$$

holds.

Proof

Using Lemmas 2.1 and 4.2, we have

$$ \begin{array}{@{}rcl@{}} \|a(x)J_{0}^{\alpha}\omega(x)\|_{1}^{2}&=&\left( a(x)J_{0}^{\alpha}\omega(x),a(x)J_{0}^{\alpha}\omega(x)\right)_{1}\\ &=&{{\int}_{0}^{1}}\left[\left( a(x)J_{0}^{\alpha}\omega(x)\right)^{\prime}\right]^{2}{\mathrm{d}}x\\ &=&{{\int}_{0}^{1}}\left[a^{\prime}(x)J_{0}^{\alpha}\omega(x)+a(x){(J_{0}^{\alpha}\omega(x))^{\prime}}\right]^{2}{\mathrm{d}}x\\ &\leq&2{{\int}_{0}^{1}}\left[a^{\prime}(x)J_{0}^{\alpha}\omega(x)\right]^{2}{\mathrm{d}}x+2{{\int}_{0}^{1}}\left[a(x){(J_{0}^{\alpha}\omega(x))^{\prime}}\right]^{2}{\mathrm{d}}x\\ &\leq&2\|J_{0}^{\alpha}\omega(x)\|_{C}^{2}{{\int}_{0}^{1}}a^{\prime2}(x){\mathrm{d}}x+2\|a(x)\|_{C}^{2}{{\int}_{0}^{1}}\left[(J_{0}^{\alpha}\omega(x))^{\prime}\right]^{2}{\mathrm{d}}x\\ &\leq&\frac{2\|a(x)\|_{1}^{2}}{{{\Gamma}^{2}(\alpha)}}\left\|{{\int}_{0}^{x}}(x-t)^{\alpha-1}\omega(t){\mathrm{d}}t\right\|^{2}_{C}+4\|a(x)\|_{1}^{2}\tilde{M}_{\alpha}\|\omega\|_{1}^{2}\\ &\leq&\frac{2\|a(x)\|_{1}^{2}}{{\Gamma}^{2}(\alpha)}\|\omega(x)\|_{C}^{2}\left|{{\int}_{0}^{x}}(x-t)^{\alpha-1}{\mathrm{d}}t\right|^{2}+4\|a(x)\|_{1}^{2}\tilde{M}_{\alpha}\|\omega\|_{1}^{2}\\ &=&\frac{2\|a(x)\|_{1}^{2}}{{\Gamma}^{2}(\alpha+1)}\|\omega(x)\|_{C}^{2}x^{2\alpha}+4\|a(x)\|_{1}^{2}\tilde{M}_{\alpha}\|\omega\|_{1}^{2}\\ &\leq&\frac{4\|a(x)\|_{1}^{2}}{{\Gamma}^{2}(\alpha+1)}\|\omega(x)\|_{1}^{2}+4\|a(x)\|_{1}^{2}\tilde{M}_{\alpha}\|\omega\|_{1}^{2}\\ &=&4\|a(x)\|_{1}^{2}\left[\frac{1}{{\Gamma}^{2}(\alpha+1)}+\tilde{M}_{\alpha}\right]\|\omega\|_{1}^{2}. \end{array} $$

So the conclusion holds. □

Theorem 4.1

The operator L defined by (7) is a bounded linear operator from $W^{1}_{2,0}$ to $W^{1}_{2,0}$.

Proof

Obviously, L is a linear operator. Noting that $a(x),b(x),c(x),d(x)\in {W^{1}_{2}}[0, 1]$, thus we know a(x), b(x), c(x), d(x) ∈ AC[0, 1]. Denote $M_{1}=\max \limits \{\|a(x)\|_{1},\|b(x)\|_{1},\|c(x)\|_{1},\|d(x)\|_{1}\}.$

Let $\omega (x)\in W^{1}_{2,0}[0, 1]$, according to Lemma 4.2 and 4.3, and we have $J_{0}^{\alpha }\omega \in W^{1}_{2,0}$, and there exists an $\tilde {M}_{\alpha }$ such that

$$\|J_{0}^{\alpha}\omega\|_{1}\leq \sqrt{\tilde{M}_{\alpha}}\|\omega\|_{1}, $$

$$ \|a(x)J_{0}^{\alpha}\omega(x)\|_{1}^{2}\leq 4\|a(x)\|_{1}^{2}\left[\frac{1}{{\Gamma}^{2}(\alpha+1)}+\tilde{M}_{\alpha}\right]\|\omega\|_{1}^{2}\leq 4{M_{1}^{2}}\left[\frac{1}{{\Gamma}^{2}(\alpha+1)}+\tilde{M}_{\alpha}\right]\|\omega\|_{1}^{2}, $$

$$ \|c(x)J_{0}^{\alpha}\omega(x-\tau)\|_{1}^{2}\leq 4\|c(x)\|_{1}^{2}\left[\frac{1}{{\Gamma}^{2}(\alpha+1)}+\tilde{M}_{\alpha}\right]\|\omega\|_{1}^{2}\leq 4{M_{1}^{2}}\left[\frac{1}{{\Gamma}^{2}(\alpha+1)}+\tilde{M}_{\alpha}\right]\|\omega\|_{1}^{2}. $$

Similarly, there exists an $\tilde {M}_{\alpha -1}$ such that

$$ \|b(x)J_{0}^{\alpha-1}\omega(x)\|_{1}^{2}\leq 4\|b(x)\|_{1}^{2}\left[\frac{1}{{\Gamma}^{2}(\alpha)}+\tilde{M}_{\alpha-1}\right]\|\omega\|_{1}^{2}\leq 4{M_{1}^{2}}\left[\frac{1}{{\Gamma}^{2}(\alpha)}+\tilde{M}_{\alpha-1}\right]\|\omega\|_{1}^{2}, $$

$$ \|d(x)J_{0}^{\alpha-1}\omega(x-\tau)\|_{1}^{2}\leq 4\|d(x)\|_{1}^{2}\left[\frac{1}{{\Gamma}^{2}(\alpha)}+\tilde{M}_{\alpha-1}\right]\|\omega\|_{1}^{2}\leq 4{M_{1}^{2}}\left[\frac{1}{{\Gamma}^{2}(\alpha)}+\tilde{M}_{\alpha-1}\right]\|\omega\|_{1}^{2}. $$

Therefore,

$$ \begin{array}{@{}rcl@{}} \|L(\omega(x))\|_{1}&=&\|\omega(x)-a(x)J^{\alpha}_{0}\omega(x)-b(x)J^{\alpha-1}_{0}\omega(x)-c(x)J^{\alpha}_{0}\omega(x-\tau)-d(x)J^{\alpha-1}_{0}\omega(x-\tau)\|_{1}\\ &\leq&\|\omega(x)\|_{1}+4M_{1}\|\omega\|_{1}\sqrt{\frac{1}{{\Gamma}^{2}(\alpha+1)}+\tilde{M}_{\alpha}}+4M_{1}\|\omega\|_{1}\sqrt{\frac{1}{{\Gamma}^{2}(\alpha)}+\tilde{M}_{\alpha-1}}\\ &=&\left[1+4M_{1}\sqrt{\frac{1}{{\Gamma}^{2}(\alpha+1)}+\tilde{M}_{\alpha}}+4M_{1}\sqrt{\frac{1}{{\Gamma}^{2}(\alpha)}+\tilde{M}_{\alpha-1}}\right]\|\omega(x)\|_{1}, \end{array} $$

which implies L is a bounded linear operator from $W^{1}_{2,0}$ to $W^{1}_{2,0}$. □

Theorem 4.2

Suppose there exists a unique solution of the equation defined by (8), then L is a bijection from $W^{1}_{2,0}$ to $L(W^{1}_{2,0})$ and $L^{-1}:L(W^{1}_{2,0})\rightarrow W^{1}_{2,0}$ does not only exist but is also bounded.

Remark 4.1

It is easy to see that L is a bijection from $W^{1}_{2,0}$ to $L(W^{1}_{2,0})$. For the latter part of the conclusion, we can define an operator $J:W^{1}_{2,0}\rightarrow W^{1}_{2,0},~J(\omega (x))=J^{\alpha }_{0}\omega (x),~\omega (x)\in W^{1}_{2,0}$. One can prove that the operator J is compact. Since the sum of finite compact operators is still compact and $\{(I-J)\omega (x)|\omega (x)\in W^{1}_{2,0}\}$ is closed, one can obtain that $L^{-1}:L(W^{1}_{2,0})\rightarrow W^{1}_{2,0}$ is bounded by the Inverse Operator Theorem in the Banach spaces.

Definition 4.1

y(x) is called an ε −approximate solution of (8) if ∥ L(y) − g ∥₁ < ε for any given ε > 0.

Theorem 4.3

For any ε > 0, there exists a positive integer N such that for every fixed n ≥ N, $\omega ^{*}_{n}(x)={\sum }^{n}_{i=0}c_{i}^{*}\psi _{i}(x)$ is an ε −approximate solution of (8), where $\{c_{i}^{*}\}_{i=0}^{n}$ satisfies

$$ \|g(x)-\sum\limits^{n}_{i=0}c_{i}^{*}f_{i}(x)\|_{1}=\underset{\left.c_{i}\in \mathrm{R}\right.}{\mathrm{\min}}{\|g(x)-\sum\limits^{n}_{i=0}c_{i}f_{i}(x)\|_{1}} $$

(10)

and

$$ f_{i}(x)=L(\psi_{i}(x)),~~i=0,1,2,3,\cdots. $$

Proof

Suppose ω(x) is the exact solution of (8). By Theorem 3.1, there exists a positive integer N such that for any n > N, there exists $\omega _{n}(x)={\sum }_{i=0}^{n}c_{i}\psi _{i}(x)$ such that

$$\|\omega(x)-\omega_{n}(x)\|_{1}=\|\omega(x)-\sum\limits_{i=0}^{n}c_{i}\psi_{i}(x)\|_{1}<\frac{\varepsilon}{\|L\|}.$$

So we can derive

$$ \begin{array}{@{}rcl@{}} \|L(\omega(x))-L(\omega_{n}(x))\|_{1}\leq \|L\|\|\omega(x)-\omega_{n}(x)\|_{1}<\varepsilon. \end{array} $$

Noting that L(ω(x)) = g(x), we have $\|g(x)-L(\omega _{n}(x))\|_{1}=\|g(x)-{\sum }_{i=0}^{n}c_{i}f_{i}(x)\|_{1}<\varepsilon .$ Thus, we obtain

$$ \begin{array}{@{}rcl@{}} \|g(x)-L(\omega_{n}^{*}(x))\|_{1}&=&\|g(x)-L\left( \sum\limits_{i=0}^{n}c_{i}^{*}\psi_{i}(x)\right)\|_{1}=\|g(x)-\sum\limits_{i=0}^{n}c_{i}^{*}f_{i}(x)\|_{1}\\ &=&\underset{\left.c_{i}\in \mathrm{R}\right.}{\mathrm{\min}}{\|g(x)-{\sum}^{n}_{i=0}c_{i}f_{i}(x)\|_{1}}<\varepsilon. \end{array} $$

That is, $\omega ^{*}_{n}(x)$ is an ε −approximate solution of (8). □

Next, we find the ε −approximate solution of (8). Denote

$$ S(c_{1},c_{2},\cdots,c_{n})=\|g(x)-\sum\limits_{i=0}^{n}c_{i}f_{i}(x)\|_{1}^{2}. $$

(11)

According to the norm definition, we have

$$ \begin{array}{@{}rcl@{}} S(c_{1},c_{2},\cdots,c_{n})&=&(g(x)-\sum\limits_{i=0}^{n}c_{i}f_{i}(x),g(x)-\sum\limits_{j=0}^{n}c_{j}f_{j}(x))_{1}\\ &=&(g(x),g(x))_{1}-2(g(x),\sum\limits_{i=0}^{n}c_{i}f_{i}(x))_{1}+\left( \sum\limits_{i=0}^{n}c_{i}f_{i}(x),\sum\limits_{j=0}^{n}c_{j}f_{j}(x)\right)_{1}\\ &=&(g(x),g(x))_{1}-2\sum\limits_{i=0}^{n}c_{i}(g(x),f_{i}(x))_{1}+\sum\limits_{i=0}^{n}\sum\limits_{j=0}^{n}c_{i}c_{j}(f_{i}(x),f_{j}(x))_{1}{.} \end{array} $$

(12)

For obtaining the minimum of the S(c₁, c₂, ⋯ , c_n), we solve the normal equations of (12)

$$ \frac{\partial S}{\partial c_{k}}=-2(g(x),f_{k}(x))_{1}+2\sum\limits_{i=0}^{n}c_{i}(f_{i}(x),f_{k}(x))_{1}=0,~~k=0,1,\cdots,n. $$

(13)

Theorem 4.4

The system of normal (13) has a unique solution.

Proof

The system of normal (13) can be rewritten as:

$$ \left( \begin{array}{cccc} (f_{0}(x),f_{0}(x))_{1} & (f_{0}(x),f_{1}(x))_{1} & {\cdots} & (f_{0}(x),f_{n}(x))_{1}\\ (f_{1}(x),f_{0}(x))_{1} & (f_{1}(x),f_{1}(x))_{1} & {\cdots} & (f_{1}(x),f_{n}(x))_{1} \\ \vdots& {\vdots} & {\vdots} & {\vdots} \\ (f_{n}(x),f_{0}(x))_{1} & (f_{n}(x),f_{1}(x))_{1} & {\cdots} & (f_{n}(x),f_{n}(x))_{1} \end{array} \right) \left( \begin{array}{c} c_{0} \\ c_{1} \\ {\vdots} \\ c_{n} \end{array} \right) = \left( \begin{array}{c} (g(x),f_{0}(x))_{1} \\ (g(x),f_{1}(x))_{1} \\ {\vdots} \\ (g(x),f_{n}(x))_{1} \end{array} \right) $$

Denote

$$ G=\left( \begin{array}{cccc} (f_{0}(x),f_{0}(x))_{1} & (f_{0}(x),f_{1}(x))_{1} & {\cdots} & (f_{0}(x),f_{n}(x))_{1}\\ (f_{1}(x),f_{0}(x))_{1} & (f_{1}(x),f_{1}(x))_{1} & {\cdots} & (f_{1}(x),f_{n}(x))_{1} \\ \vdots& {\vdots} & {\vdots} & {\vdots} \\ (f_{n}(x),f_{0}(x))_{1} & (f_{n}(x),f_{1}(x))_{1} & {\cdots} & (f_{n}(x),f_{n}(x))_{1} \end{array} \right), $$

then G is a Gram matrix. So G is a nonsingular matrix if and only if f₀(x), f₁(x), ⋯ , f_n(x) are linearly independent.

We prove that f₀(x), f₁(x), ⋯ , f_n(x) are linearly independent. Let

$$ l_{0}f_{0}(x)+l_{1}f_{1}(x)+\cdots+l_{n}f_{n}(x)\equiv 0. $$

We derive ${\sum }_{i=0}^{n}l_{i}L(\psi _{i}(x))\equiv 0$, or $L({\sum }_{i=0}^{n}l_{i}\psi _{i}(x))\equiv 0.$ Since L is injective, thus ${\sum }_{i=0}^{n}l_{i}\psi _{i}(x)\equiv 0.$ Noting that $\{\psi _{i}(x)\}_{i=0}^{n}$ are linearly independent, we obtain l_i = 0, i = 0,1, ⋯ , n. Therefore, f₀(x), f₁(x), ⋯ , f_n(x) are linearly independent, G is nonsingular, and the system of normal (13) has a unique solution. □

Remark 4.2

The unique solution of normal (13) is denoted as $(c_{0}^{*},c_{1}^{*},\cdots ,c_{n}^{*})$. Similar to [22], we can prove $S(c_{1},c_{2},\cdots ,c_{n})\geq S(c_{0}^{*},c_{1}^{*},\cdots ,c_{n}^{*}).$ Thus, (10) has a unique solution determined by (13). The desired approximate solution y^∗(x) of (5) can be obtained by (9).

Theorem 4.5

Assume that $\omega ^{*}_{n}({\kern -.4pt}x{\kern -.4pt})\! =\! {\sum }_{i=0}^{3}{\kern -.4pt}a_{i}{\kern -.4pt}{J_{0}^{1}}\eta ^{i}\!({\kern -.4pt}x{\kern -.4pt}){\kern -.4pt}+\!{\sum }_{i=1}^{n}\!{\sum }_{l=0}^{3}\!{\sum }_{k=0}^{2^{i-1}-1}\!c_{ik}^{l}{\kern -.5pt}{J_{0}^{1}}{\kern -.5pt}\phi _{ik}^{l}{\kern -.5pt}({\kern -.5pt}x{\kern -.5pt})$ obtained by Theorem 6 is an ε-approximate solution of Eq.(8), ω(x) is the exact solution of Eq.(8) and |ω^(j)(x)| ≤ M, ∀ x ∈ [0, 1], for some j ∈ {2, 3, 4, 5}. Then $\parallel \omega (x)-\omega ^{*}_{n}(x)\parallel _{1}\leq C\cdot 2^{-(j-1)n}$, where C is a constant.

Proof

According to Theorem 3.2, one has $\parallel \omega (x)-\omega _{n}(x)\parallel _{1}\leq \bar {C}\cdot 2^{-(j-1)n}$ where $\bar {C}$ is a constant. Thus, one can derive that

$$ \begin{array}{@{}rcl@{}} \| \omega(x)-\omega^{*}_{n}(x)\|_{1}&\leq&\|L^{-1}\|\cdot\|L(\omega(x))-L(\omega^{*}_{n}(x))\|_{1}=\|L^{-1}\|\cdot\|g(x)-L(\omega^{*}_{n}(x))\|_{1}\\ &\leq&\|L^{-1}\|\|g(x)-L(\omega_{n}(x))\|_{1}=\|L^{-1}\|\|L(\omega(x))-L(\omega_{n}(x))\|_{1}\\ &\leq& \|L^{-1}\|\|L\|\|\omega(x)-\omega_{n}(x)\|_{1}\leq \bar{C}\|L^{-1}\|\|L\|\cdot2^{-(j-1)n}=C\cdot2^{-(j-1)n}, \end{array} $$

where $C=\bar {C}\|L^{-1}\|\|L\|$. □

5 Stability analysis

In this section, we consider the stability of our proposed method.

Assume λ is a eigenvalue of the matrix G which is defined in the proof of Theorem 4.4, that is, there exists an $X=[x_{0},x_{1},\cdots ,x_{n}]^{T}\in \mathbb {R}^{n+1},~X\neq 0,$ such that GX = λX. Hence,

$$ \left\{ \begin{array}{ll} \lambda x_{0}={\sum}_{j=0}^{n}(f_{0},f_{j})_{1}\cdot x_{j}, \\ {\vdots} \\ \lambda x_{i}={\sum}_{j=0}^{n}(f_{i},f_{j})_{1}\cdot x_{j}, \\ {\vdots} \\ \lambda x_{n}={\sum}_{j=0}^{n}(f_{n},f_{j})_{1}\cdot x_{j}. \end{array} \right. $$

So we derive that

$$ \begin{array}{@{}rcl@{}} \lambda x_{i}&=&\sum\limits_{j=0}^{n}(f_{i},f_{j})_{1}\cdot x_{j}=\sum\limits_{j=0}^{n}(L(\psi_{i}(x)),L(\psi_{j}(x)))_{1}\cdot x_{j}\\&=&(L(\psi_{i}(x)),\sum\limits_{j=0}^{n}L(\psi_{j}(x)))_{1}\cdot x_{j}=(L(\psi_{i}(x)),\sum\limits_{j=0}^{n}L(\psi_{j}(x))\cdot x_{j})_{1}, \end{array} $$

$$ \lambda {x_{i}^{2}}=(L(\psi_{i}(x))\cdot x_{i},\sum\limits_{j=0}^{n}L(\psi_{j}(x))\cdot x_{j})_{1}, $$

and

$$ \lambda \sum\limits_{i=0}^{n}{x_{i}^{2}}=\left( \sum\limits_{i=0}^{n}x_{i}L(\psi_{i}(x)\right),\sum\limits_{j=0}^{n}x_{j}L(\psi_{j}(x)))_{1}. $$

Thus, we have

$$ \lambda\|X\|_{\mathbb{R}^{n+1}}^{2}=\left\|L\left( \sum\limits_{i=0}^{n}x_{i}\psi_{i}(x)\right)\right\|_{1}^{2}, $$

or

$$ \begin{array}{@{}rcl@{}} \lambda&=&\frac{\left\|L\left( {\sum}_{i=0}^{n}x_{i}\psi_{i}(x)\right)\right\|_{1}^{2}}{\|X\|_{\mathbb{R}^{n+1}}^{2}}\\ &=&\left\|L\left( {\sum}_{i=0}^{n}\frac{x_{i}}{\|X\|_{\mathbb{R}^{n+1}}}\psi_{i}(x)\right)\right\|_{1}^{2}\\ &=&\left\|L\left( {\sum}_{i=0}^{n}y_{i}\psi_{i}(x)\right)\right\|_{1}^{2}~~~~~~~~~~~~~~~\left( y_{i}\triangleq\frac{x_{i}}{\|X\|_{\mathbb{R}^{n+1}}}\right)\\ &=&\left\|L(u)\right\|_{1}^{2}~~~~~~~~~~~~~~~~~~~~~~~~\left( u\triangleq{\sum}_{i=0}^{n}y_{i}\psi_{i}(x)\right). \end{array} $$

Noting that $\{\psi _{i}(x)\}^{\infty }_{i=0}$ is a set of orthonormal bases of $W^{1}_{2,0}$, we have

$$ \begin{array}{@{}rcl@{}} \|u\|_{1}^{2}=\left\|\sum\limits_{i=0}^{n}y_{i}\psi_{i}(x)\right\|_{1}^{2}=\sum\limits_{i=0}^{n}\left\|y_{i}\psi_{i}(x)\right\|_{1}^{2}=\sum\limits_{i=0}^{n}|y_{i}|^{2}\cdot\|\psi_{i}(x)\|_{1}^{2}=\sum\limits_{i=0}^{n}|y_{i}|^{2}=1. \end{array} $$

Hence, we can obtain that

$$ \begin{array}{@{}rcl@{}} \lambda=\big\|L(u)\big\|_{1}^{2}\leq\|L\|^{2}\cdot\|u\|_{1}^{2}=\|L\|^{2}. \end{array} $$

Thus, the largest eigenvalue λ_max of G satisfies λ_max ≤∥L∥².

On the other hand, we prove that the least eigenvalue of G satisfies $\lambda _{min}\geq \frac {1}{\|L^{-1}\|^{2}}.$

Otherwise, there exists {u_n}, ∥u_n∥₁ = 1 such that $\|L(u_{n})\|_{1}<\frac {1}{\|L^{-1}\|}$.

Denote ω_n = L(u_n). Hence, $\|\omega _{n}\|_{1}<\frac {1}{\|L^{-1}\|}$ and u_n = L^{− 1}(ω_n). So we can derive

$$ 1=\|u_{n}\|_{1}=\|L^{-1}(\omega_{n})\|_{1}\leq\|L^{-1}\|\cdot\|\omega_{n}\|_{1}<\|L^{-1}\|\cdot\frac{1}{\|L^{-1}\|}=1. $$

It is a contradiction. So we obtain $\lambda _{min}\geq \frac {1}{\|L^{-1}\|^{2}}.$

Therefore, we have

$$ 1\leq Cond(G)_{2}=\frac{\lambda_{max}}{\lambda_{min}}\leq \frac{\|L\|^{2}}{\frac{1}{\|L^{-1}\|^{2}}}=(\|L\|\cdot\|L^{-1}\|)^{2}. $$

That is, Cond(G)₂ ≤ (∥L∥⋅∥L^{− 1}∥)², which implies that the spectral condition number [23] of the matrix G is bounded, and the algorithm is stable.

6 Nonlinear fractional delay differential equations

In this section, we solve (3) when f is nonlinear. In order to obtain high-accuracy approximate solutions, we employ F-derivative and Newton’s iterative formula.

Similar to the linear case, we denote

$$\zeta (x)=\left\{ \begin{array}{ll} y_{0}(x), ~~~~~~~~~-\tau\leq x\leq 0,\\ y_{0}(0)+xy^{\prime}_{0}(0), ~0\leq x\leq 1, \end{array} \right. $$

and

$$z(x)=y(x)-\zeta(x).$$

Then, (3) can be written as

$$ \left\{ \begin{array}{ll} D^{\alpha}_{C}z(x)=g(x)+f[x,(z+\zeta)(x),(z+\zeta)^{\prime}(x),(z+\zeta)(x-\tau),(z+\zeta)^{\prime}(x-\tau)],~0\leq x\leq {1,~}1<\alpha\leq 2,\\ z(x)=0,~~~-\tau\leq x\leq 0. & \end{array} \right. $$

Hence, there is no harm in supposing that the equation to be solved is

$$ \left\{ \begin{array}{ll} D^{\alpha}_{C}u(x) = g(x) + f[x,u(x),u^{\prime}(x),u(x - \tau),u^{\prime}(x-\tau)], ~0\leq x\leq {1,~}1<\alpha\leq 2,\\ u(x)=0,~~~-\tau\leq x\leq 0. & \end{array} \right. $$

(14)

Let u be the exact solution of the above equation and assume that $D^{\alpha }_{C}u(x)=\omega (x)$. At the beginning of Section 4, we have proved that $u(x)=J_{0}^{\alpha } \omega (x)$ and $\omega \in W_{2,0}^{1}$. So $u(x)\in W_{2}^{\alpha }$.

Define an operator $F: W_{2}^{\alpha }[0, 1]\rightarrow {W_{2}^{1}}[0, 1]$,

$$ F(u)= D^{\alpha}_{C}u-f[x,u(x),u^{\prime}(x),u(x-\tau),u^{\prime}(x-\tau)]-g(x), $$

(15)

(14) is equivalent to the following equation

$$ \left\{ \begin{array}{ll} F(u)=0, ~0\leq x\leq 1,~1<\alpha\leq 2,\\ u(x)=0,~~~-\tau\leq x\leq 0. & \end{array} \right. $$

(16)

Lemma 6.1

Take any $h\in W_{2}^{\alpha }$, then $\|h\|_{1}\leq \sqrt {\tilde {M}_{\alpha }}\|h\|_{\alpha }$ holds, where $\tilde {M}_{\alpha }=\frac {1}{\alpha ^{2}{\Gamma }^{2}(\alpha )}$.

Proof

From the definition of $W_{2}^{\alpha }$, $h=J_{0}^{\alpha } h_{1}$ with $h_{1}\in W_{2,0}^{1}$. By Lemma 4.2, $\|h\|_{1}=\|J_{0}^{\alpha } h_{1}\|_{1}\leq \sqrt {\tilde {M}_{\alpha }}\|h_{1}\|_{1}=\sqrt {\tilde {M}_{\alpha }}\|h\|_{\alpha }$. □

Theorem 6.1

Suppose that F is defined by (15), then

$$ \begin{array}{@{}rcl@{}} F^{\prime}(u)h&=&D_{C}^{\alpha}h-\left[\frac{\partial}{\partial u}h+\frac{\partial}{\partial u^{\prime}}h^{\prime}+\frac{\partial}{\partial u(x-\tau)}h(x-\tau)\right.\\ && \left. +\frac{\partial}{\partial u^{\prime}(x-\tau)}h^{\prime}(x-\tau)]f[x,u(x),u^{\prime}(x),u(x - \tau),u^{\prime}(x - \tau)\right], \end{array} $$

(17)

where $F^{\prime }(u)$ refers to the Fréchet derivative [10].

Proof

Let $F(u)=D^{\alpha }_{C}u-g(x)-f[x,u(x),u^{\prime }(x),u(x-\tau ),u^{\prime }(x-\tau )]\triangleq F_{1}(u)-F_{2}(u)$, here $F_{1}(u)=D^{\alpha }_{C}u-g(x)$, $F_{2}(u)=f[x,u(x),u^{\prime }(x),u(x-\tau ),u^{\prime }(x-\tau )].$

According to the definition of F-derivative and property of Caputo derivatives, we have

$$ \underset{\left.\|h\|_{\alpha}\rightarrow 0\right.}{{\lim}}\frac{1}{\|h\|_{\alpha}}\left\| D^{\alpha}_{C}(u+h)-g(x)-[D^{\alpha}_{C}(u)-g(x)]-D^{\alpha}_{C}h\right\|_{1}=0. $$

So we can conclude that $F_{1}^{\prime }(u)h=D^{\alpha }_{C}h$, that is $F_{1}^{\prime }(u)=D^{\alpha }_{C}$. On the other hand,

$$ \begin{array}{@{}rcl@{}} f[x,y,z,p,q]& = & f[x,y_{0},z_{0},p_{0},q_{0}]+\left[\frac{\partial}{\partial y}(y - y_{0})+\frac{\partial}{\partial z}(z-z_{0})+\frac{\partial}{\partial p}(p-p_{0})\right.\\ && \left.+\frac{\partial}{\partial q}(q-q_{0})\right]f[x,y_{0},z_{0},p_{0},q_{0}]+O(h^{2}). \end{array} $$

Substituting $u(x)+h(x), u^{\prime }(x)+h^{\prime }(x), u(x-\tau )+h(x-\tau ), u^{\prime }(x-\tau )+h^{\prime }(x-\tau )$ for y, z, p, q and $u(x), u^{\prime }(x), u(x-\tau ), u^{\prime }(x-\tau )$ for y₀, z₀, p₀, q₀ in the above equation, we get

$$ \begin{array}{@{}rcl@{}} f[x,u(x)+h(x), u^{\prime}(x)+h^{\prime}(x), u(x-\tau)+h(x-\tau), u^{\prime}(x-\tau)+h^{\prime}(x-\tau)]\\= f[x,u(x),u^{\prime}(x),u(x-\tau),u^{\prime}(x-\tau)] \end{array} $$

$$ \begin{array}{@{}rcl@{}} &&+[\frac{\partial}{\partial u}h(x)+\frac{\partial}{\partial u^{\prime}}h^{\prime}(x)+\frac{\partial}{\partial u(x-\tau) }h(x-\tau)\\&&+\frac{\partial}{\partial u^{\prime}(x-\tau)}h^{\prime}(x-\tau)]f[x,u(x),u^{\prime}(x),u(x-\tau),u^{\prime}(x-\tau)]\\ +O(h^{2}). \end{array} $$

Therefore, ∃M > 0,

$$ \begin{array}{@{}rcl@{}} &&\frac{1}{\|h\|_{\alpha}}\|f[x,(u+h)(x), (u+h)^{\prime}(x), (u+h)(x-\tau), (u+h)^{\prime}(x-\tau)]\\&&-f[x,u(x),u^{\prime}(x),u(x-\tau),u^{\prime}(x-\tau)] \\ &&-[\frac{\partial}{\partial u}h(x)+\frac{\partial}{\partial u^{\prime}}h^{\prime}(x)+\frac{\partial}{\partial u(x-\tau) }h(x-\tau)\\&&+\frac{\partial}{\partial u^{\prime}(x-\tau)}h^{\prime}(x-\tau)]f[x,u(x),u^{\prime}(x),u(x-\tau),u^{\prime}(x-\tau)]\|_{1}\\ \end{array} $$

$\leq M \| h\|_{1}^{2}/\| h\|_{\alpha }\leq M\tilde {M}_{\alpha }{\| h\|_{\alpha }^{2}}/\| h\|_{\alpha }\leq M\tilde {M}_{\alpha }\|h\|_{\alpha }\rightarrow 0,~(\|h\|_{\alpha }\rightarrow 0),$ where Lemma 6.1 is used. Thus,

$$ \begin{array}{@{}rcl@{}} F_{2}^{\prime}(u)h&=&\left[\frac{\partial}{\partial u}h(x)+\frac{\partial}{\partial u^{\prime}}h^{\prime}(x)+\frac{\partial}{\partial u(x-\tau) }h(x-\tau)\right.\\ && \left. +\frac{\partial}{\partial u^{\prime}(x-\tau)}h^{\prime}(x-\tau)]f[x,u(x),u^{\prime}(x),u(x-\tau),u^{\prime}(x-\tau)\right]. \end{array} $$

Since $F^{\prime }(u)h=F_{1}^{\prime }(u)h+F_{2}^{\prime }(u)h$, then the conclusion holds. □

Remark 6.1

An inequality used here is $\|h^{2}\|_{1}\leq 2\sqrt {2}\|h\|_{1}^{2}$. In fact, according to the definition of the norm ∥⋅∥₁ of ${W^{1}_{2}}$ and Lemma 2.1, we can obtain

$$ \begin{array}{@{}rcl@{}} \|h^{2}\|_{1}^{2}&=&{{\int}_{0}^{1}}(2h\cdot h^{\prime})^{2}\mathrm{d}x=4{{\int}_{0}^{1}}h^{2}\cdot (h^{\prime})^{2}\mathrm{d}x\\ &\leq&4\|h\|_{C}^{2}{{\int}_{0}^{1}}(h^{\prime})^{2}\mathrm{d}x=4\|h\|_{C}^{2}\|h\|_{1}^{2}\\ &\leq&4(\sqrt{2}\|h\|_{1})^{2}\|h\|_{1}^{2}=8\|h\|_{1}^{4}. \end{array} $$

Squaring on both sides of the inequality, and the inequality $\|h^{2}\|_{1}\leq 2\sqrt {2}\|h\|_{1}^{2}$ holds.

The Newton’s iterative formula for solving F(u) = 0 defined by (16) is

$$ u_{k+1}=u_{k}-[F^{\prime}(u_{k})]^{-1}F(u_{k}),~~~k=0,1,2,\cdots, $$

(18)

with initial selection u₀ = 0, here $F^{\prime }(u)$ is defined by (17). Equation (18) can be transformed into

$$ F^{\prime}(u_{k})(u_{k+1}-u_{k})+F(u_{k})=0,~~~k=0,1,2,\cdots, $$

which are linear fractional delay differential (5), so we can solve them by the ε −approximate solution method constructed in Section 4.

Remark 6.2

One can refer to [9] about the method of selecting a initial value and the convergence of Newton’s iterative formula.

7 Algorithm implementation of Newton’s iterative formula

In this section, we will concretely show algorithm implementation of Newton’s iterative formula.

Assume

$$ u_{k+1}=\sum\limits_{i=0}^{n}c_{k+1,i}J_{0}^{\alpha}\psi_{i}(x), $$

$$ u_{k}=\sum\limits_{i=0}^{n}c_{k,i}J_{0}^{\alpha}\psi_{i}(x), $$

(19)

$$ u_{k+1}-u_{k}=\sum\limits_{i=0}^{n}d_{k,i}J_{0}^{\alpha}\psi_{i}(x), $$

(20)

where {c_{k, i}},{d_{k, i}} are unknown. It is not difficult to see that

$$ \begin{array}{@{}rcl@{}} c_{k+1,i}&=&c_{k,i}+d_{k,i}~~(i=0,1,2,\cdots,n), \end{array} $$

(21)

$$ \begin{array}{@{}rcl@{}} u_{k+1}&=&u_{k}+\sum\limits_{i=0}^{n}d_{k,i}J_{0}^{\alpha}\psi_{i}(x), \end{array} $$

(22)

$$ \begin{array}{@{}rcl@{}} F(u_{k})&=& \sum\limits_{i=0}^{n}c_{k,i}\psi_{i}(x) - f[x,u_{k}(x),u_{k}^{\prime}(x),u_{k}(x - \tau),u_{k}^{\prime}(x - \tau)] - g(x). \end{array} $$

(23)

Using (17) and (20), we have $F^{\prime }(u_{k})(u_{k+1}-u_{k})$

$$ \begin{array}{@{}rcl@{}} &=&D^{\alpha}_{C}(u_{k+1}-u_{k})-\left[\frac{\partial}{\partial u_{k}}(u_{k+1}-u_{k})+\frac{\partial}{\partial u^{\prime}_{k}}(u_{k+1}-u_{k})^{\prime}\right.\\ \!\!\!\!\!\!\!\!\!\!&& \left.+\frac{\partial}{\partial u_{k}(x-\tau) }(u_{k+1}-u_{k})(x-\tau)\right.\\ \!\!\!\!\!\!\!\!\!\!&&\left.+\frac{\partial}{\partial u^{\prime}_{k}(x-\tau)}(u_{k+1}-u_{k})^{\prime}(x-\tau)\right]f[x,u_{k},u_{k}^{\prime},u_{k}(x-\tau),u_{k}^{\prime}(x-\tau)]\\ \!\!\!\!\!\!\!\!\!\!&=&{\sum}_{i=0}^{n}d_{k,i}\psi_{i}(x)-\left[\frac{\partial}{\partial u_{k}}{\sum}_{i=0}^{n}d_{k,i}J_{0}^{\alpha}\psi_{i}(x) +\frac{\partial}{\partial u^{\prime}_{k}}{\sum}_{i=0}^{n}d_{k,i}J_{0}^{\alpha-1}\psi_{i}(x)\right.\\ \!\!\!\!\!\!\!\!\!\!&&\left. +\frac{\partial}{\partial u_{k}(x-\tau)}{\sum}_{i=0}^{n}d_{k,i}J_{0}^{\alpha}\psi_{i}(x-\tau)\right.\\ \!\!\!\!\!\!\!\!\!\!& &\left. +\frac{\partial}{\partial u^{\prime}_{k}(x - \tau)}{\sum}_{i=0}^{n}d_{k,i}J_{0}^{\alpha-1}\psi_{i}(x - \tau)\!\right]\!f[x,u_{k},u_{k}^{\prime},u_{k}(x - \tau),u_{k}^{\prime}(x - \tau)]. \end{array} $$

(24)

Denote

$$ R(x)\triangleq \big\|F^{\prime}(u_{k})(u_{k+1}-u_{k})+F(u_{k})\big\|_{1}^{2},~~~k=0,1,2,\cdots. $$

(25)

Substituting the above equations (19), (23), and (24) into the (25), we solve the following equations to obtain {d_{k, i}}:

$$ \frac{\partial R}{\partial d_{k,i}}=0,~~i=0,1,2,\cdots,n. $$

(26)

To sum up, the algorithm is as follows:

• Step 1 Homogenize the equation as (14).

• Step 2 Input {ψ_i(x)}, and compute $\{J_{0}^{\beta }\psi _{i}(x)\}$, for any β > 0.

• Step 3 Input α. Input the number of approximate items n. Set c_{0, i} = 0.

• Step 4 Begin the iterative procedure. From k = 0, do

  • (1) Compute u_k by (19).

  • (2) Compute the F(u_k), $F^{\prime }(u_{k})(u_{k+1}-u_{k})$ according to (23) and (24).

  • (3) Compute R(x) by (25), solve the equations (26), and obtain the {d_{k, i}}.

  • (4) Compute c_{k+ 1, i} = c_{k, i} + d_{k, i} (i = 0, 1, 2, ⋯ , n).

  • (5) If ∥u_k+ 1 − u_k∥_C ≥ ε, go to (1); or else go to Step 5.

• Step 5 Output the last approximate solution $u_{k+1}={\sum }_{i=0}^{n}c_{k+1,i}J_{0}^{\alpha }\psi _{i}(x)$.

Using the software Mathematica, we can get the approximate solution u_k+ 1(x). We don’t need too much iterations to reach desired approximate solutions because of high efficiency of Newton’s iterative method.

Remark 7.1

The algorithm can be extended to the case of m − 1 < α ≤ m (m ∈N₊) for the fractional delay differential (3).

8 Numerical examples

In this section, the algorithm presented above is applied to solve linear and nonlinear fractional delay differential equations. Three examples are considered to illustrate the efficiency of the suggested algorithm. The relative error here is defined as $R_{n}=\frac {u-u_{n}}{\|u\|_{C}}$ with the exact solution u and an approximate solution u_n obtained by Theorem 4.3. Basing on the numerical results, we adopt the formula $\log _{2}[R_{n}/R_{2n-1}]$ to estimate the convergence order.

Example 8.1

Consider the linear fractional differential equation with delay

$$ \left\{ \begin{array}{ll} D^{1.5}_{C}y(x)=xy(x)+\frac{x-1}{5}y^{\prime}(x)-y(x-0.2)+\frac{x}{5}y^{\prime}(x-0.2)+g(x), & x\in[0, 1],\\ y(x)=0, ~~-0.2\leq x\leq 0, \end{array} \right.\\ $$

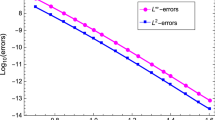
where g(x) is chosen such that the exact solution is x^2.3 or x^4.1. When the exact solution is x^2.3, we solve the equation with n = 65, 257, 513, respectively, and obtain the corresponding approximate solutions. The relative errors between the exact solution and the approximate solutions are displayed in Fig. 1. When the exact solution of this example is chosen to be x^4.1 which is of higher smoothness, the relative errors are displayed in Fig. 2. One can see that the relative errors are decreased with the increase of n. The results show that the error is decreased fast when the smoothness of solution is increased. In Table 1, we provide some numerical results illustrating the fact that the convergence order can be improved when smoothness of the solution is improved. Even if the solution of the equation is less smooth, the computing error is still acceptable for the engineering. Therefore, the algorithm is stable, reliable, and adaptive.

Fig. 1

The relative error curve with n = 65, 257, 513 when the exact solution is x^2.3 for Example 8.1

Fig. 2

The relative error curve with n = 65, 257, 513 when the exact solution is x^4.1 for Example 8.1

Table 1 The comparison of infinity-norm of the relative errors at discrete points and estimates of the convergence order on the interval [0, 1] between the exact solutions x^2.3 and x^4.1 for Example 8.1

Example 8.2

Let us consider the nonlinear fractional differential equation with delay

$$ \left\{ \begin{array}{ll} D^{1.5}_{C}y(x)=(x+1)y(x)+\frac{x-1}{2}y(x)y(x-0.1)+g(x), & x\in[0, 1],\\ y(x)=0, ~~-0.1\leq x\leq 0, \end{array} \right.\\ $$

where g(x) is chosen such that the exact solution of this example is x^2.3 or x^4.3. The relative errors between the exact solution and the approximate solutions with different times of iteration are displayed in Figs. 3 and 4 with n = 65, 129, 257 in both cases, respectively. The semi-log plots in error are displayed in Figs. 3 and 4. In Table 2, we compare the infinity-norm of relative errors at the discrete points and estimates of convergence order for both solution cases. The results show that our method is still valid, stable, and adaptive when solving nonlinear problems.

Fig. 3

The relative error curve with n = 65, 129, 257 after 1, 2, 3, and 4 iterations when the exact solution is x^2.3 for Example 8.2

Fig. 4

The relative error curve with n = 65, 129, 257 after 1, 2, 3, and 4 iterations when the exact solution is x^4.3 for Example 8.2

Table 2 The comparison of infinity-norm of the relative errors at discrete points and estimates of the convergence order on the interval [0, 1] between the exact solutions x^2.3 and x^4.3 for Example 8.2

Example 8.3

Consider the linear fractional differential equation with delay [15]

$$ \left\{ \begin{array}{ll} D^{0.5}_{C}y(x)=y(x-1)-y(x)+2x-1+\frac{\Gamma(3)}{\Gamma(5/2)}x^{3/2}, & x\in[0, 1],\\ y(x)=x^{2}, ~~-1\leq x\leq 0 {.} \end{array} \right.\\ $$

The exact solution of this example is x². The relative errors between the exact solution and the approximate solutions are displayed in Fig. 5 with n = 65, 257, 513, 1025, respectively. One can see that the relative errors are decreased with the increase of n . We compare the infinity-norm of absolute errors at the discrete points with that from Ref. [15] in Table 3. The numerical results show that our method has higher accuracy in this example and the computing errors may be acceptable for engineering.

Fig. 5

The relative error curve with n = 65,257,513,1025 for Example 8.3

Table 3 The comparison of infinity-norm of the absolute errors at discrete points with the backward difference method on the interval [0, 1] for Example 8.3

9 Conclusion

In this paper, we construct a new stable collocation method for solving a kind of nonlinear fractional delay differential equations. More suitable multiscale orthonormal bases of $W^{1}_{2,0}$ are constructed, error estimations of approximate solutions are given, and the highest convergence order can reach four in the sense of the norm of ${W_{2}^{1}}$. Newton’s iterative formula is used to linearize the nonlinear equation, and for the obtained linear equations we develop an ε-approximate solution method based on multiscale orthonormal bases to solve them. A concrete algorithm implementation is given. Numerical examples show that compared with [15], the presented method is more accurate in dealing with this kind of equations.