Stabilized index-2 co-simulation approach for solver coupling with algebraic constraints

Abstract

In the paper at hand, a co-simulation method on index-2 level is presented and analyzed. To explain the method, we consider two arbitrary mechanical subsystems, which are coupled by algebraic constraint equations, i.e., by means of ideal rigid joints. It is assumed that each subsystem has its own solver, integrating independently from the other subsystem solver. Both solvers are coupled by a weak coupling approach.

The initial point of the method investigated here is a formulation of the coupled problem on the basis of the stabilized index-2 formulation, which takes simultaneously into account the constraint equations on position level and—by introducing additional Lagrange multipliers—also the constraint equations on velocity level. The presented co-simulation method is based on a predictor/corrector approach. The Jacobian matrix for calculating corrected coupling variables can in a straightforward manner be calculated numerically and in parallel with the predictor step so that almost no additional computation time is required. For the corrector step, the macro-time step has to be repeated once. Therefore, the subsystem solvers have to be reinitialized at the previous macro-time point. This is the only elementary requirement on the subsystem solvers.

Appendices

Appendix A: Analytical approximation formulas for calculating the Jacobian matrix

As shown in Sects. 2 and 3, the partial derivatives of the state variables z _i ,z _j with respect to the coupling variables $\tilde{\boldsymbol{u}}_{j},\tilde{\boldsymbol{u}}_{i}$ may easily be calculated by finite differences. In this appendix, we briefly discuss an alternative possibility to calculate the partial derivatives. The key idea is to symbolically discretize the equations of motion for the coupling bodies i and j by an explicit time integration scheme and to carry out one integration step from T _N →T _N+1 (the initial conditions for this integration step are the corrected state variables z _i,N ,z _j,N at the macro-time point T _N ). This yields the discretized states z _i,N+1,z _j,N+1 at the macro-time point T _N+1. z _i,N+1,z _j,N+1 are then analytically differentiated with respect to the coupling variables $\tilde{\boldsymbol{u}}_{j},\tilde{\boldsymbol{u}}_{i}$. The result are analytical approximation formulas for the partial derivatives $\frac{\partial\boldsymbol{z}_{i,N+1}}{\partial \tilde{\boldsymbol{u}}_{j,N+1}} \big\vert_{\tilde{\boldsymbol{u}} _{c,N+1}^{p}}$ and $\frac{\partial\boldsymbol{z}_{j,N+1}}{\partial \tilde{\boldsymbol{u}}_{i,N+1}} \big\vert_{\tilde{\boldsymbol{u}} _{c,N+1}^{p}}$. In the following, the approach is explained for subsystem 1. For subsystem 2 the strategy is equivalent.

For the subsequent analysis, it is assumed that the reaction forces and reaction torques are zero (${}^{0} \boldsymbol{F}_{r_{i}} = \boldsymbol{0}, {}^{i} \boldsymbol{M}_{r_{i}} = \boldsymbol{0}$), i.e., we ride on the assumption that algebraic constraints do not exist between the coupling body i and the other bodies of subsystem 1. Under this assumption, the equations of motion for the coupling body i read as

Coupling body i (subsystem 1):

$$\begin{aligned} {}^{0} \dot{\boldsymbol{r}}_{S_i} =& {}^{0} \boldsymbol{v}_{S_i} + \boldsymbol{G}_{c_i} ( \boldsymbol{z}_{i}, \overline{\boldsymbol{u}}_{j} ) \boldsymbol{\mu}_{c}, \end{aligned}$$

(48a)

$$\begin{aligned} {}^{0} \dot{\boldsymbol{v}}_{S_i} =& \frac{1}{ m_{i}} \bigl[ {}^{0} \boldsymbol{F}_{a_i} ( \hat{ \boldsymbol{z}}_{1},t ) + \boldsymbol{G}_{c_i} ( \boldsymbol{z}_{i}, \overline{\boldsymbol{u}}_{j} ) \boldsymbol{ \lambda}_{c} \bigr], \end{aligned}$$

(48b)

$$\begin{aligned} \dot{\boldsymbol{\gamma}}_{i} =& \boldsymbol{B} ( \boldsymbol{\gamma}_{i} ) {}^{i} \boldsymbol{ \omega}_{i} + \boldsymbol{H}_{c_i} ( \boldsymbol{z}_{i}, \overline{\boldsymbol{u}}_{j} ) \boldsymbol{\mu}_{c}, \end{aligned}$$

(48c)

$$\begin{aligned} {}^{i} \dot{\boldsymbol{\omega}}_{i} =& {}^{i} \boldsymbol{J}_{i}^{-1} \bigl[ - {}^{i} \boldsymbol{\omega}_{i} \times{}^{i} \boldsymbol{J}_{i} {}^{i} \boldsymbol{\omega}_{i} + {}^{i} \boldsymbol{M}_{a_i} ( \hat{\boldsymbol{z}}_{1},t )+ \boldsymbol{H}_{c_i} ( \boldsymbol{z}_{i}, \overline{ \boldsymbol{u}}_{j} ) \boldsymbol{\lambda}_{c} \bigr]. \end{aligned}$$

(48d)

Compared to Eqs. (18a)–(18d), the notation has been slightly modified. The coupling variables $\tilde{\boldsymbol{u}}_{j}$ can be subdivided into the Lagrange multipliers λ _c ,μ _c and the additional coupling variables $\overline{\boldsymbol{u}}_{j}$ resulting from the co-simulation approach, i.e., $\overline{\boldsymbol{u}}_{j} = \tilde{\boldsymbol{u}}_{j} \setminus \{ \boldsymbol{\lambda}_{c}, \boldsymbol{\mu}_{c} \}$ (for the perpendicular joint, for instance, we have $\tilde{\boldsymbol{u}}_{j} = ( \lambda_{cp}\ \mu_{cp}\ \tilde{\boldsymbol{\gamma}}_{j} )^{T}$ and $\overline{\boldsymbol{u}}_{j} = \tilde{\boldsymbol{\gamma}}_{j}$, see Sect. 3.2.3). Based on the results of Sect. 3.2, it can easily be seen that the coupling force can be written as ${}^{0} \boldsymbol{F}_{c_{i}} = \boldsymbol{G}_{c_{i}} ( \boldsymbol{z}_{i}, \overline{\boldsymbol {u}}_{j} ) \boldsymbol{\lambda}_{c}$. Consequently, the projection term in the kinematical differential equation can be written as ${}^{0} \boldsymbol{V}_{c_{i}} = \boldsymbol{G}_{c_{i}} ( \boldsymbol{z}_{i}, \overline{\boldsymbol{u}}_{j} ) \boldsymbol{\mu}_{c}$. Accordingly, one gets ${}^{i} \boldsymbol{M}_{c_{i}} = \boldsymbol{H}_{c_{i}} ( \boldsymbol{z}_{i}, \overline{\boldsymbol{u}}_{j} ) \boldsymbol{\lambda}_{c}$ and ${}^{i} \boldsymbol{\Omega}_{c_{i}} = \boldsymbol{H}_{c_{i}} ( \boldsymbol{z}_{i}, \overline{\boldsymbol{u}}_{j} ) \boldsymbol{\mu}_{c}$. $\boldsymbol {G}_{c_{i}}$ and $\boldsymbol{H}_{c_{i}}$ depend on the constraint equations (for the perpendicular joint, for instance, we have $\boldsymbol{G}_{c_{i}}=\boldsymbol{0}$ and $\boldsymbol{H}_{c_{i}} = {}^{i} \boldsymbol{e}_{i} \times {}^{ij} \boldsymbol{T} ( \boldsymbol{\gamma}_{i}, \tilde{\boldsymbol{\gamma}}_{j} ) {}^{j} \boldsymbol{e}_{j}$, see Sect. 3.2.3).

To accomplish the single integration step from T _N to T _N+1, we assume that the state variables ${}^{0} \boldsymbol{r}_{S_{i},N}$, ${}^{0} \boldsymbol{v}_{S_{i},N}$, γ _i,N , ⁱ ω _i,N and the coupling variables $\tilde{\boldsymbol{u}}_{j,N}$ are known at the macro-time point T _N . Note again that the coupling variables are assumed to be constant during the macro-time step, i.e., $\tilde{\boldsymbol{u}}_{j}^{p} ( t ) = \tilde{\boldsymbol{u}}_{j,N+1}^{p} = \tilde{\boldsymbol{u}}_{j,N} =\mbox{const.}$ For the discretization of the ODE system (48a)–(48d), Heun’s method (explicit second-order Runge–Kutta method) is used. By performing one integration step from T _N to T _N+1=T _N +H and by calculating the partial derivatives with respect to λ _c,N+1, one eventually obtains the subsequent approximations for the partial derivatives of the state vector z _i with respect to the Lagrange multiplier λ _c

$$ \begin{aligned} \frac{\partial{}^{0} \boldsymbol{r}_{S_i,N+1}}{\partial \boldsymbol{\lambda}_{c,N+1}} \bigg\vert _{\tilde{\boldsymbol{u}} _{j,N+1}^{p}} &\approx\frac{H^{2}}{2 m_{i}} \boldsymbol{G}_{c_i} \bigl( \boldsymbol{z}_{i,N}, \overline{\boldsymbol{u}}_{j,N+1}^{p} \bigr), \\ \frac{\partial{}^{0} \boldsymbol{v}_{S_i,N+1}}{\partial \boldsymbol{\lambda}_{c,N+1}} \bigg\vert _{\tilde{\boldsymbol{u}} _{j,N+1}^{p}} &\approx\frac{H}{m_{i}} \boldsymbol{G}_{c_i} \bigl( \boldsymbol{z}_{i,N}, \overline{ \boldsymbol{u}}_{j,N+1}^{p} \bigr), \quad(* ) \\ \frac{\partial\boldsymbol{\gamma}_{i,N+1}}{\partial \boldsymbol{\lambda}_{c,N+1}} \bigg\vert _{\tilde{\boldsymbol{u}} _{j,N+1}^{p}} &\approx \frac{H^{2}}{2} \boldsymbol{B} ( \boldsymbol{\gamma}_{i,N} ) {}^i\boldsymbol{J}_i^{-1} \boldsymbol{H}_{c_i} \bigl( \boldsymbol{z}_{i,N}, \overline{\boldsymbol{u}}_{j,N+1}^{p} \bigr), \\ \frac{\partial{}^{i} \boldsymbol{\omega}_{i,N+1}}{\partial \boldsymbol{\lambda}_{c,N+1}} \bigg\vert _{\tilde{\boldsymbol{u}} _{j,N+1}^{p}} &\approx H {}^{i} \boldsymbol{J}_{i}^{-1} \boldsymbol{H}_{c_i} \bigl( \boldsymbol{z}_{i,N}, \overline{\boldsymbol{u}}_{j,N+1}^{p} \bigr). \quad(**) \end{aligned} $$

(49)

For the partial derivatives of the state vector z _i with respect to the coupling variables μ _c and $\overline{\boldsymbol{u}}_{j}$, equivalent formulas can be derived.

Please note that the Lagrange multiplier λ _c does not explicitly occur in the kinematical differential equations (48a) and (48c). To calculate the partial derivatives $\frac{\partial{}^{0} \boldsymbol{r}_{S_{i},N+1}}{\partial\boldsymbol{\lambda}_{c,N+1}}$ and $\frac{\partial\boldsymbol{\gamma}_{i,N+1}}{\partial \boldsymbol{\lambda}_{c,N+1}}$, it is therefore necessary to use a second-order integration scheme (alternatively, two integration steps with a first-order integration scheme could be applied). To compute the partial derivatives $\frac{\partial{}^{0} \boldsymbol{v}_{S_{i},N+1}}{\partial \boldsymbol{\lambda}_{c,N+1}}$ and $\frac{\partial{}^{i} \boldsymbol{\omega}_{i,N+1}}{\partial\boldsymbol{\lambda }_{c,N+1}}$, a first-order integration scheme would be sufficient. Integrating (48b) and (48d) with Euler explicit, for instance, directly yields the approximations (∗) and (∗∗) in Eq. (49).

The calculation of the partial derivatives on the basis of an explicit integration scheme can only be applied, if the reaction forces/torques are zero. If ${}^{0} \boldsymbol{F}_{r_{i}} \neq\boldsymbol{0}$ or ${}^{i} \boldsymbol{M}_{r_{i}} \neq\boldsymbol{0}$, subsystem 1 is described by a DAE system and the direct application of an explicit integration scheme is not possible. In this case, implicit integration schemes have to be applied. Alternatively, the underlying ODE of the DAE can be derived and discretized by an explicit integration scheme as described above. Please also note the discussion on this issue in [42].

Example

For the 1-DOF oscillator of Sect. 2, the following approximations for the partial derivatives are obtained

$$ \begin{aligned} \frac{\partial x_{1,N+1}}{\partial\lambda_{c,N+1}} \bigg\vert _{\lambda_{c,N+1}^{p}, \mu_{c,N+1}^{p}} &\approx\frac{H^{2}}{ 2m_{1}}, \qquad \frac{\partial v_{1,N+1}}{\partial\lambda_{c,N+1}} \bigg\vert _{\lambda_{c,N+1}^{p}, \mu_{c,N+1}^{p}} \approx\frac{H}{m_{1}}, \\ \frac{\partial x_{1,N+1}}{\partial\mu_{c,N+1}} \bigg\vert _{\lambda_{c,N+1}^{p}, \mu_{c,N+1}^{p}} &\approx H, \qquad \frac{\partial v_{1,N+1}}{\partial\mu_{c,N+1}} \bigg\vert _{\lambda_{c,N+1}^{p}, \mu_{c,N+1}^{p}} \approx- \frac{c_{1} H^{2}}{2m_{1}}, \\ \frac{\partial x_{2,N+1}}{\partial\lambda_{c,N+1}} \bigg\vert _{\lambda_{c,N+1}^{p}, \mu_{c,N+1}^{p}} &\approx- \frac{H^{2}}{2m_{2}}, \qquad \frac{\partial v_{2,N+1}}{\partial \lambda_{c,N+1}} \bigg\vert _{\lambda_{c,N+1}^{p}, \mu_{c,N+1}^{p}} \approx- \frac{H}{m_{2}}, \\ \frac{\partial x_{2,N+1}}{\partial\mu_{c,N+1}} \bigg\vert _{\lambda_{c,N+1}^{p}, \mu_{c,N+1}^{p}} &\approx-H, \qquad \frac{\partial v_{2,N+1}}{\partial \mu_{c,N+1}} \bigg\vert _{\lambda_{c,N+1}^{p}, \mu_{c,N+1}^{p}} \approx \frac{c_{2} H^{2}}{2m_{2}}. \end{aligned} $$

(50)

Appendix B: Simplified coupling formulation for the perpendicular joint

By connecting the coupling bodies i and j with a perpendicular joint, the additional coupling variables $\tilde{\boldsymbol{\gamma}}_{j}$ and $\tilde{\boldsymbol{\gamma}}_{i}$ have to be defined in order to calculate the coupling torques ${}^{i} \boldsymbol{M}_{c_{i}}$ and ${}^{j} \boldsymbol{M}_{c_{j}}$, see Sect. 3.2.3. Considering subsystem 1, λ _cp reflects the magnitude and ${}^{i} \boldsymbol{e}_{i} \times {}^{ij} \boldsymbol{T} ( \boldsymbol{\gamma}_{i}, \tilde{\boldsymbol{\gamma}}_{j} ) {}^{j} \boldsymbol{e}_{j}$ the direction of ${}^{i} \boldsymbol{M}_{c_{i}}$. The idea of the simplified formulation is to replace $\tilde{\boldsymbol{\gamma}}_{j}$ with the constant value γ _j,N during the macro-time step T _N →T _N+1. Then, the simplified coupling forces/torques, the projection terms for the kinematical differential equations and the coupling conditions read as

$$ \begin{aligned} &{}^{0} \boldsymbol{F}_{c_i} = \boldsymbol{0}, \qquad{}^{i} \boldsymbol{M}_{c_i} = {}^{i} \boldsymbol{e}_{i} \times {}^{ij} \boldsymbol{T} ( \boldsymbol{\gamma}_{i}, \boldsymbol{\gamma}_{j,N} ) {}^{j} \boldsymbol{e}_{j} \lambda_{cp}, \\ &{}^{0} \boldsymbol{V}_{c_i} = \boldsymbol{0}, \qquad {}^{i} \boldsymbol{\Omega}_{c_i} = {}^{i} \boldsymbol{e}_{i} \times {}^{ij} \boldsymbol{T} ( \boldsymbol{\gamma}_{i}, \boldsymbol{\gamma}_{j,N} ) {}^{j} \boldsymbol{e}_{j} \mu_{cp}, \\ &{}^{0} \boldsymbol{F}_{c_j} = \boldsymbol{0}, \qquad {}^{j} \boldsymbol{M}_{c_j} = {}^{j} \boldsymbol{e}_{j} \times {}^{ji} \boldsymbol{T} ( \boldsymbol{\gamma}_{i,N}, \boldsymbol{\gamma}_{j} ) {}^{i} \boldsymbol{e}_{i} \lambda_{cp}, \\ &{}^{0} \boldsymbol{V}_{c_j} = \boldsymbol{0}, \qquad {}^{j} \boldsymbol{\Omega}_{c_j} = {}^{j} \boldsymbol{e}_{j} \times {}^{ji} \boldsymbol{T} ( \boldsymbol{\gamma}_{i,N}, \boldsymbol{\gamma}_{j} ) {}^{i} \boldsymbol{e}_{i} \mu_{cp}, \\ &g_{cp\lambda} = 0, \qquad g_{cp\mu} = 0. \end{aligned} $$

(51)

Making use of the simplified formulation, the coupling conditions $\boldsymbol{g}_{c \gamma_{i}}$ and $\boldsymbol{g}_{c \gamma_{j}}$ are neglected. Equivalent simplified formulations can be used for other joints.

Appendix C: Formulation of the stabilized index-2 co-simulation approach using Euler parameters

In Sect. 3, the stabilized index-2 co-simulation method has been presented for the case that Euler angles are used to describe the rotation of the two coupling bodies. Using another parameterization for the spherical rotations, the formulas in Sect. 3 have to be modified slightly. In the following, we present the formulation of the co-simulation method for the case that Euler parameters are applied to describe 3D rotations [26]. Making use of Euler parameters, the orientation of an arbitrary body q is described by the four Euler parameters $\boldsymbol{q}_{q} = ( \begin{array}{cccc} q_{0_{q}}, & q_{1_{q}} & q_{2_{q}} & q_{3_{q}} \end{array} )^{T} \in\mathbb{R}^{4}$. The coordinates of the angular velocity with respect to the body fixed system K _Sq and the time derivative of the Euler parameters are related by the kinematical differential equation ${}^{q} \boldsymbol{\omega}_{q} = \boldsymbol{P} ( \boldsymbol {q}_{q} ) \dot{\boldsymbol{q}}_{q}$, where the matrix $\boldsymbol{P} ( \boldsymbol{q}_{q} ) \in\mathbb{R}^{3\times4}$ is given by

$$ \boldsymbol{P}= 2 \left( \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} - q_{1_q} & q_{0_q} & q_{3_q} & - q_{2_q} \\ - q_{2_q} & - q_{3_q} & q_{0_q} & q_{1_q} \\ -q_{3_q} & q_{2_q} & -q_{1_q} & q_{0_q} \end{array} \right). $$

(52)

The constraint equation for the four Euler parameters is given by $q_{0_{q}}^{2} + q_{1_{q}}^{2} + q_{2_{q}}^{2} + q_{3_{q}}^{2} -1= 0$. According to Sect. 3.1, we define the auxiliary vectors $\boldsymbol{y}_{i} = ( \begin{array}{cccc} y_{i1} & y_{i2} & \cdots& y_{i13} \end{array} )^{T} = ( \begin{array}{cccc} {}^{0} \boldsymbol{r}_{S_{i}} & \boldsymbol{q}_{i} & {}^{0} \boldsymbol{v}_{S_{i}} & {}^{i} \boldsymbol{\omega}_{i} \end{array} )^{T} \in\mathbb{R}^{13}$ and $\boldsymbol{y}_{j} = ( \begin{array}{cccc} y_{j1} & y_{j2} & \cdots& y_{j13} \end{array} )^{T} = ( \begin{array}{cccc} {}^{0} \boldsymbol{r}_{S_{j}} & \boldsymbol{q}_{j} & {}^{0} \boldsymbol{v}_{S_{j}} & {}^{j} \boldsymbol{\omega}_{j} \end{array} )^{T} \in\mathbb{R}^{13}$, which contain the position and velocity coordinates of the coupling bodies i and j. Both vectors are combined in the vector $\boldsymbol{y}_{c} = ( \boldsymbol{y}_{i}\ \boldsymbol{y}_{j} )^{T} \in\mathbb{R}^{26}$. The vectors $\hat{\boldsymbol{y}}_{1} \in\mathbb{R}^{13\cdot n_{1}}$ and $\hat{\boldsymbol{y}}_{2} \in\mathbb{R}^{13\cdot n_{2}}$ contain the position and velocity coordinates of all bodies of subsystem 1 and subsystem 2.

Applying Euler parameters and using the stabilized index-2 formulation, the equations of motion for the coupling bodies i and j read as

Coupling body i (subsystem 1):

$$ \begin{aligned} {}^{0} \dot{\boldsymbol{r}}_{S_i} &= {}^{0} \boldsymbol{v}_{S_i} + {}^{0} \boldsymbol{V}_{c_i}, \\ m_{i} {}^{0} \dot{\boldsymbol{v}}_{S_i} &= {}^{0} \boldsymbol{F}_{a_i} ( \hat{\boldsymbol{y}}_{1},t ) + {}^{0} \boldsymbol{F}_{r_i} + {}^{0} \boldsymbol{F}_{c_i}, \\ {}^{i} \boldsymbol{\omega}_{i} &= \boldsymbol{P} ( \boldsymbol{q}_{i} ) \dot{\boldsymbol{q}}_{i} + {}^{i} \boldsymbol{\Omega}_{c_i}, \\ 0 &= q_{0_i}^{2} + q_{1_i}^{2} + q_{2_i}^{2} + q_{3_i}^{2} -1, \\ {}^{i} \boldsymbol{J}_{i} {}^{i} \dot{ \boldsymbol{\omega}}_{i} + {}^{i} \boldsymbol{ \omega}_{i} \times{}^{i} \boldsymbol{J}_{i} {}^{i} \boldsymbol{\omega}_{i} &= {}^{i} \boldsymbol{M}_{a_i} ( \hat{\boldsymbol{y}}_{1},t )+ {}^{i} \boldsymbol{M}_{r_i} + {}^{i} \boldsymbol{M}_{c_i}; \end{aligned} $$

(53)

Coupling body j (subsystem 2):

$$ \begin{aligned} {}^{0} \dot{\boldsymbol{r}}_{S_j} &= {}^{0} \boldsymbol{v}_{S_j} + {}^{0} \boldsymbol{V}_{c_j}, \\ m_{j} {}^{0} \dot{\boldsymbol{v}}_{S_j} &= {}^{0} \boldsymbol{F}_{a_j} ( \hat{\boldsymbol{y}}_{2},t ) + {}^{0} \boldsymbol{F}_{r_j} + {}^{0} \boldsymbol{F}_{c_j}, \\ {}^{j} \boldsymbol{\omega}_{j} &= \boldsymbol{P} ( \boldsymbol{q}_{j} ) \dot{\boldsymbol{q}}_{j} + {}^{j} \boldsymbol{\Omega}_{c_j}, \\ 0 &= q_{0_j}^{2} + q_{1_j}^{2} + q_{2_j}^{2} + q_{3_j}^{2} -1, \\ {}^{j} \boldsymbol{J}_{j} {}^{j} \dot{ \boldsymbol{\omega}}_{j} + {}^{j} \boldsymbol{ \omega}_{j} \times{}^{j} \boldsymbol{J}_{j} {}^{j} \boldsymbol{\omega}_{j} &= {}^{j} \boldsymbol{M}_{a_j} ( \hat{\boldsymbol{y}}_{2},t ) + {}^{j} \boldsymbol{M}_{r_j} + {}^{j} \boldsymbol{M}_{c_j}. \end{aligned} $$

(54)

It should be stressed that the same notation has been used as in Sect. 3.1. The coupling relations are collected in the following subsections for the atpoint, the inplane and the perpendicular joint.

3.1 C.1 Atpoint joint (spherical joint)

By connecting the coupling points C _i und C _j with an atpoint joint, the coupling forces/torques, the projection terms for the kinematical differential equations and the 6 scalar coupling conditions are given by

$$ \begin{aligned} \bullet\ & \mbox{Reaction forces/torques (coupling body $i$):} \\ &{}^{0} \boldsymbol{F}_{c_i} = {}^{0} \boldsymbol{\lambda}_{ca}, \qquad{}^{i} \boldsymbol{M}_{c_i} = {}^{i} \boldsymbol{r}_{C_i} \times{}^{i0} \boldsymbol{T} ( \boldsymbol{q}_{i} ) {}^{0} \boldsymbol{\lambda}_{ca}, \\ \bullet\ & \mbox{Projection terms (coupling body $i$):} \\ &{}^{0} \boldsymbol{V}_{c_i} = {}^{0} \boldsymbol{\mu}_{ca}, \qquad{}^{i} \boldsymbol{ \Omega}_{c_i} = {}^{i} \boldsymbol{r}_{C_i} \times {}^{i0} \boldsymbol{T} ( \boldsymbol{q}_{i} ) {}^{0} \boldsymbol{\mu}_{ca}, \\ \bullet\ & \mbox{Reaction forces/torques (coupling body $j$):} \\ &{}^{0} \boldsymbol{F}_{c_j} =- {}^{0} \boldsymbol{\lambda}_{ca}, \qquad{}^{j} \boldsymbol{M}_{c_j} = - {}^{j} \boldsymbol{r}_{C_j} \times{}^{j0} \boldsymbol{T} ( \boldsymbol{q}_{j} ) {}^{0} \boldsymbol{\lambda}_{ca}, \\ \bullet\ & \mbox{Projection terms (coupling body $j$):} \\ &{}^{0} \boldsymbol{V}_{c_j} =- {}^{0} \boldsymbol{\mu}_{ca}, \qquad{}^{j} \boldsymbol{ \Omega}_{c_j} = - {}^{j} \boldsymbol{r}_{C_j} \times{}^{j0} \boldsymbol{T} ( \boldsymbol{q}_{j} ) {}^{0} \boldsymbol{\mu}_{ca}, \\ \bullet\ & \mbox{Coupling conditions:} \\ &\boldsymbol{g}_{ca\lambda} = \boldsymbol{0}, \qquad\boldsymbol {g}_{ca\mu} = \boldsymbol{0}. \end{aligned} $$

(55)

Compared with Eq. (24), the only difference is that the transformation matrices are parameterized with Euler parameters instead of Euler angles. Please note that the constraint equations for the Euler parameters q _i and q _j are considered in Eqs. (53) and (54).

3.2 C.2 Inplane joint

If the points C _i und C _j are coupled by an inplane joint, the coupling forces/torques, the projection terms for the kinematical differential equations and the altogether 13 scalar coupling conditions read as

$$ \begin{aligned}[b] \bullet\ & \mbox{Reaction forces/torques (coupling body $i$):} \\ &{}^{0} \boldsymbol{F}_{c_i} = {}^{0j} \boldsymbol{T} ( \tilde{\boldsymbol{q}}_{j} ) {}^{j} \boldsymbol{e}_{j} \lambda_{cd}, \qquad{}^{i} \boldsymbol{M}_{c_i} = {}^{i} \boldsymbol{r}_{C_i} \times{}^{ij} \boldsymbol{T} ( \boldsymbol{q}_{i}, \tilde{ \boldsymbol{q}}_{j} ) {}^{j} \boldsymbol{e}_{j} \lambda_{cd}, \\ \bullet\ & \mbox{Projection terms (coupling body $i$):} \\ &{}^{0} \boldsymbol{V}_{c_i} = {}^{0j} \boldsymbol{T} ( \tilde{\boldsymbol{q}}_{j} ) {}^{j} \boldsymbol{e}_{j} \mu_{cd}, \qquad{}^{i} \boldsymbol{\Omega}_{c_i} = {}^{i} \boldsymbol{r}_{C_i} \times{}^{ij} \boldsymbol{T} ( \boldsymbol{q}_{i}, \tilde{ \boldsymbol{q}}_{j} ) {}^{j} \boldsymbol{e}_{j} \mu_{cd}, \\ \bullet\ & \mbox{Reaction forces/torques (coupling body $j$):} \\ &\begin{aligned}[t] &{}^{0} \boldsymbol{F}_{c_j} =- {}^{0j} \boldsymbol{T} ( \boldsymbol{q}_{j} ) {}^{j} \boldsymbol{e}_{j} \lambda_{cd}, \\ &{}^{j} \boldsymbol{M}_{c_j} = {}^{j} \boldsymbol{e}_{j} \times {}^{j0} \boldsymbol{T} ( \boldsymbol{q}_{j} ) \bigl( {}^{0} \tilde{ \boldsymbol{r}}_{S_i} + {}^{0i} \boldsymbol{T} ( \tilde{ \boldsymbol{q}}_{i} ) {}^{i} \boldsymbol{r}_{C_i} - {}^{0} \boldsymbol{r}_{S_j} \bigr) \lambda_{cd}, \end{aligned} \end{aligned} $$

(56)

$$ \begin{aligned} \bullet\ & \mbox{Projection terms (coupling body $j$):} \\ &{}^{0} \boldsymbol{V}_{c_j} =- {}^{0j} \boldsymbol{T} ( \boldsymbol{q}_{j} ) {}^{j} \boldsymbol{e}_{j} \mu_{cd}, \qquad{}^{j} \boldsymbol{\Omega}_{c_j} = {}^{j} \boldsymbol{e}_{j} \times {}^{j0} \boldsymbol{T} ( \boldsymbol{q}_{j} ) \bigl( {}^{0} \tilde{\boldsymbol{r}}_{S_i} + {}^{0i} \boldsymbol{T} ( \tilde{\boldsymbol{q}}_{i} ) {}^{i} \boldsymbol{r}_{C_i} - {}^{0} \boldsymbol{r}_{S_j} \bigr) \mu_{cd}, \\ \bullet\ & \mbox{Coupling conditions:} \\ &g_{cd\lambda} =0, \qquad g_{cd\mu} =0, \qquad\boldsymbol{g}_{c r_i} := {}^{0} \tilde{\boldsymbol{r}}_{S_i} - {}^{0} \boldsymbol{r}_{S_i} = \boldsymbol{0}, \\ &\boldsymbol{g}_{c q_i} := \tilde{\boldsymbol{q}}_{i}^{*} - \boldsymbol{q}_{i}^{*} = \boldsymbol{0}, \qquad \boldsymbol{g}_{c q_j} := \tilde{\boldsymbol{q}}_{j}^{*} - \boldsymbol{q}_{j}^{*} = \boldsymbol{0}, \\ &g_{c \tilde{q}_i} := \tilde{q}_{0_i}^{2} + \tilde{q}_{1_i}^{2} + \tilde{q}_{2_i}^{2} + \tilde{q}_{3_i}^{2} -1=0, \qquad g_{c \tilde{q}_j} := \tilde{q}_{0_j}^{2} + \tilde{q}_{1_j}^{2} + \tilde{q}_{2_j}^{2} + \tilde{q}_{3_j}^{2} -1=0. \end{aligned} $$

As already outlined in Sect. 3.2.2, the state variables y _j are not available in subsystem 1 and the state variables y _i are not accessible in subsystem 2 during the subsystem integration from T _N to T _N+1. Therefore, the additional coupling variables $\tilde{\boldsymbol{q}}_{j}$ have to be defined in subsystem 1 and the additional coupling variables ${}^{0} \tilde{\boldsymbol{r}}_{S_{i}}$ and $\tilde{\boldsymbol{q}}_{i}$ in subsystem 2. The coupling variables $\tilde{\boldsymbol{q}}_{i} \in\mathbb{R}^{4}$ and $\tilde{\boldsymbol{q}}_{j} \in\mathbb{R}^{4}$ denote Euler parameters, for which the constraint equations $g_{c \tilde{q}_{i}}$ and $g_{c \tilde{q}_{j}}$ have to be considered. According to Sect. 3.2.2, the coupling conditions $\tilde{\boldsymbol{q}}_{j} = \boldsymbol {q}_{j}$ and $\tilde{\boldsymbol{q}}_{i} = \boldsymbol{q}_{i}$ have to be fulfilled. Due to the constraint equations $g_{c \tilde{q}_{i}}$ and $g_{c \tilde{q}_{j}}$ for $\tilde{\boldsymbol{q}}_{i}$ and $\tilde{\boldsymbol{q}}_{j}$ and due to the corresponding constraint equations for q _i and q _j in Eqs. (53) and (54), it is, however, sufficient to set equal three of the four Euler parameters. Therefore, we define the vectors $\boldsymbol{q}_{i}^{*} = ( \begin{array}{ccc} q_{0_{i}} & q_{1_{i}} & q_{2_{i}} \end{array} )^{T}$, $\boldsymbol{q}_{j}^{*} = ( \begin{array}{ccc} q_{0_{j}} & q_{1_{j}} & q_{2_{j}} \end{array} )^{T}$, $\tilde{\boldsymbol{q}}_{i}^{*} = ( \begin{array}{ccc} \tilde{q}_{0_{i}} & \tilde{q}_{1_{i}} & \tilde{q}_{2_{i}} \end{array} )^{T}$ and $\tilde{\boldsymbol{q}}_{j}^{*} = ( \begin{array}{ccc} \tilde{q}_{0_{j}} & \tilde{q}_{1_{j}} & \tilde{q}_{2_{j}} \end{array} )^{T}$, which contain the first three Euler parameters, in order to formulate the coupling equations $\boldsymbol{g}_{c q_{i}} := \tilde{\boldsymbol{q}}_{i}^{*} - \boldsymbol{q}_{i}^{*} = \boldsymbol{0}$ and $\boldsymbol{g}_{c q_{j}} := \tilde{\boldsymbol{q}}_{j}^{*} - \boldsymbol{q}_{j}^{*} = \boldsymbol{0}$.

3.3 C.3 Perpendicular joint

Using a perpendicular joint to connect C _i und C _j , the coupling forces/torques, the projection terms for the kinematical differential equations and the altogether 10 scalar coupling conditions are given by

$$ \begin{aligned} \bullet\ & \mbox{Reaction forces/torques (coupling body $i$):} \\ &{}^{0} \boldsymbol{F}_{c_i} = \boldsymbol{0}, \qquad {}^{i} \boldsymbol{M}_{c_i} = {}^{i} \boldsymbol{e}_{i} \times {}^{ij} \boldsymbol{T} ( \boldsymbol{q}_{i}, \tilde{\boldsymbol{q}}_{j} ) {}^{j} \boldsymbol{e}_{j} \lambda_{cp}, \\ \bullet\ & \mbox{Projection terms (coupling body $i$):} \\ &{}^{0} \boldsymbol{V}_{c_i} = \boldsymbol{0}, \qquad {}^{i} \boldsymbol{\Omega}_{c_i} = {}^{i} \boldsymbol{e}_{i} \times {}^{ij} \boldsymbol{T} ( \boldsymbol{q}_{i}, \tilde{\boldsymbol{q}}_{j} ) {}^{j} \boldsymbol{e}_{j} \mu_{cp}, \\ \bullet\ & \mbox{Reaction forces/torques (coupling body $j$):} \\ &{}^{0} \boldsymbol{F}_{c_j} = \boldsymbol{0}, \qquad {}^{j} \boldsymbol{M}_{c_j} = {}^{j} \boldsymbol{e}_{j} \times {}^{ji} \boldsymbol{T} ( \tilde{\boldsymbol{q}}_{i}, \boldsymbol{q}_{j} ) {}^{i} \boldsymbol{e}_{i} \lambda_{cp}, \\ \bullet\ & \mbox{Projection terms (coupling body $j$):} \\ &{}^{0} \boldsymbol{V}_{c_j} = \boldsymbol{0}, \qquad {}^{j} \boldsymbol{\Omega}_{c_j} = {}^{j} \boldsymbol{e}_{j} \times {}^{ji} \boldsymbol{T} ( \tilde{\boldsymbol{q}}_{i}, \boldsymbol{q}_{j} ) {}^{i} \boldsymbol{e}_{i} \mu_{cp}, \\ \bullet\ & \mbox{Coupling conditions:} \\ &g_{cp\lambda} = 0, \qquad g_{cp\mu} = 0, \qquad \boldsymbol{g}_{c q_i} := \tilde{\boldsymbol{q}}_{i}^{*} - \boldsymbol{q}_{i}^{*} = \boldsymbol{0}, \qquad \boldsymbol{g}_{c q_j} := \tilde{\boldsymbol{q}}_{j}^{*} - \boldsymbol{q}_{j}^{*} = \boldsymbol{0}, \\ &g_{c \tilde{q}_i} := \tilde{q}_{0_i}^{2} + \tilde{q}_{1_i}^{2} + \tilde{q}_{2_i}^{2} + \tilde{q}_{3_i}^{2} -1=0, \qquad g_{c \tilde{q}_j} := \tilde{q}_{0_j}^{2} + \tilde{q}_{1_j}^{2} + \tilde{q}_{2_j}^{2} + \tilde{q}_{3_j}^{2} -1=0. \end{aligned} $$

(57)

Appendix D: Stability analysis and test model for explicit and semi-implicit co-simulation approach

The definition of the stability of time integration methods is based on Dahlquist’s test equation $\dot{y} (t)=\lambda\cdot y (t)$, where y(t) is a scalar function of time and $\lambda= \lambda_{r} +i \lambda_{i} \mathbb{\in C}$ an arbitrary complex constant [24, 25]. From the mechanical point of view, this equation can be interpreted as the complex representation of the equation of motion for the homogenous linear single-mass oscillator. As well-known from literature, the stability behavior of a time integration method depends on two parameters, namely hλ _r and hλ _i , where h denotes the time-step size. Generally, 2D plots are used to illustrate the stability of time integration methods as a function of hλ _r and hλ _i .

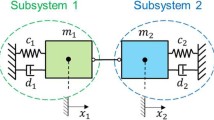
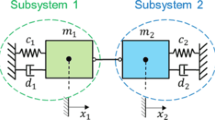
Following Dahlquist’s definition, it is straightforward to use the two-mass oscillator of Sect. 2 (see Fig. 1) as test model for co-simulation methods with algebraic constraints. The two-mass oscillator has five independent parameters, which can be shown by rewriting the equations of motion (4a)–(4c). Introducing the dimensionless time $\overline{t} = \frac{t}{H}$, the modified (dimensionless) velocities $\overline{v}_{1} =H\cdot v_{1}$ and $\overline{v}_{2} =H\cdot v_{2}$ as well as the five parameters

$$ \overline{c}_{1} = \frac{c_{1} \cdot H^{2}}{m_{1}}, \qquad \overline{d}_{1} = \frac{d_{1} \cdot H}{m_{1}}, \qquad \alpha_{m21} = \frac{m_{2}}{m_{1}}, \qquad\alpha_{c21} = \frac{c_{2}}{c_{1}}, \qquad \alpha_{d21} = \frac{d_{2}}{d_{1}}, $$

(58)

Eqs. (4a)–(4c) can be rewritten as

Subsystem 1:

$$ \begin{aligned} x_{1} ' &= \overline{v}_{1} + \overline{\mu}_{c}, \\ \overline{v}_{1} ' &=- \overline{c}_{1} \cdot x_{1} - \overline{d}_{1} \cdot \overline{v}_{1} + \overline{\lambda}_{c}; \end{aligned} $$

(59a)

Subsystem 2:

$$ \begin{aligned} x_{2} ' &= \overline{v}_{2} - \overline{\mu}_{c}, \\ \overline{v}_{2} ' &=- \frac{\alpha_{c21}}{\alpha_{m21}} \cdot \overline{c}_{1} \cdot x_{2} - \frac{\alpha_{d21}}{ \alpha_{m21}} \cdot \overline{d}_{1} \cdot \overline{v}_{2} - \frac{1}{\alpha_{m21}} \overline{ \lambda}_{c}; \end{aligned} $$

(59b)

Coupling conditions:

$$ \begin{aligned} g_{c\lambda} &:= x_{2} - x_{1} =0, \\ \overline{g}_{c\mu} &:= \overline{v}_{2} - \overline{v}_{1} =0. \end{aligned} $$

(59c)

Note that $(\cdot ) ' = \frac{d(\cdot )}{d \overline{t}}$ denotes the derivative with respect to the dimensionless time $\overline{t}$. Instead of using the five parameters defined in Eq. (58), it might be useful to define five other parameters for characterizing the stability behavior of co-simulation methods. According to the stability analysis for time integration schemes, where the two parameters hλ _r and hλ _i are used, choosing the following five parameters for investigating the stability of co-simulation schemes with algebraic constraints might be more convenient

$$ \begin{aligned} \overline{\lambda}_{r1} &=- \frac{\overline{d}_{1}}{2}, \qquad\overline{\lambda}_{i1} = \frac {1}{2} \sqrt{4 \cdot \overline{c}_{1} - \overline{d}_{1}^{2}}, \\ \alpha_{m21} &= \frac{m_{2}}{ m_{1}}, \qquad\alpha_{\lambda r21} = \frac{\overline{\lambda}_{r2}}{ \overline{\lambda}_{r1}} = \frac{\alpha_{d21}}{\alpha_{m21}}, \\ \alpha_{\lambda i21} &= \frac{\overline{\lambda}_{i2}}{ \overline{\lambda}_{i1}} = \frac{1}{\alpha_{m21}} \frac{\sqrt{4 \cdot \alpha_{m21} \cdot \alpha_{c21} \cdot \overline{c}_{1} - \alpha_{d21}^{2} \cdot \overline{d}_{1}^{2}}}{\sqrt{4 \cdot \overline {c}_{1} - \overline{d}_{1}^{2}}}. \end{aligned} $$

(60)

The physical meaning of these parameters is easily explained. $\overline{\lambda}_{r1}$ and $\overline{\lambda}_{i1}$, which characterize subsystem 1, denote the modified (dimensionless) real and imaginary part of the eigenvalue of subsystem 1. α _m21 terms the mass ratio. The parameters α _λr21 and α _λi21 describe the ratio of the real and imaginary part of the eigenvalue of subsystem 2 with respect to subsystem 1. To compare different co-simulation methods with 2D stability plots, it might be useful to fix the parameters α _m21, α _λr21 and α _λi21 and to determine the stability as a function of the two parameters $\overline{\lambda }_{r1}$ and $\overline{\lambda}_{i1}$.