1 Introduction

Chatter-free operation is critical for grinding as it  guarantees a good workpiece surface finish and prolongs life of a cutting tool. Chatter can be induced by various mechanism including thermomechanical, mode-coupling, frictional, or regenerative effects [40]. The regenerative chatter is one of the most common of dangerous phenomena and belongs to the class of self-excited vibration [1, 26, 27, 37]. Any fluctuation of cutting force induces a time-varying displacement of the cutting tool and consequently a non-constant depth of cut, which in turns yields a variation of the cutting force. As a result, chatter vibration is generated, and thus a wavy workpiece surface is produced.

Traditionally, the regenerative machining dynamics has been investigated by using the regenerative chatter theory, which is mathematically described by delayed differential equations (DDEs) [6, 7, 15, 17, 24]. After the regenerative effect was first reported by Arnold [2], it has been used to study various machining chatter in turning [36], milling [19], drilling [15] and grinding [11]. In 2001, Inasaki et al. [10] published a seminal paper in the Annals of the CIRP, which reported that the regenerative effect in the grinding is similar to self-excited vibration in the turning.

To describe the regenerative effect during grinding, the DDEs are employed, where the cutting force is modelled by the instantaneous grinding depth or in another word the chip thickness [2, 39]. A delay term represents the previous relative displacement between the tool and the workpiece in the previous turn, hence the DDEs can be naturally employed to model the regenerative dynamics. This idea was first introduced by Tobias [34], who investigated the regenerative turning chatter. Later on, the regenerative chatter theory was extensively adopted to different machining chatters including milling [19, 20] and grinding [7, 18].

In regard to the grinding chatter, Thompson in [29–33] carried out a series of studies on regenerative effects caused by the surfaces of both the workpiece and the grinding wheel. Kinematic models and time domain simulations were used in these investigations and other works, e.g. [5, 38]. Later on, dynamic models with time delays were established by Yuan et al. [44] and Liu and Payre [18] to examine grinding stability in a greater depth. Chung and Liu [7] studied theoretically the grinding chatter with the nonlinearity in the grinding force. They established that the nonlinear chatter can be induced by supercritical Hopf bifurcations [13, 22, 23]. Thereafter, Yan et al. [42] and Kim et al. [12] successively found Bautin (degenerated Hopf) bifurcation [13] in plunge and transverse grinding processes, respectively. That is to say, the grinding chatter can be triggered by either a supercritical or subcritical Hopf bifurcation [41]. Moreover, it was shown that the majority of grinding chatter is induced by the subcritical instability [43].

In comparison with the supercritical chatter, the subcritical one induces vibration with much larger amplitude by generating a negative grinding depth, which means a lost of contact between the grinding wheel and the workpiece. The vibration amplitude is limited not by the nonlinearity in the cutting force but by intermittent contacts, similar to impacts [28, 37, 41, 43]. For the stable grinding or small-amplitude chatter, the grinding wheel is in constant contact with the workpiece and the cutting process is continuous. For the large-amplitude chatter, however, the lost of contact between the workpiece and the tool occurs, and thus the cutting is intermittent or self-interrupted [25]. Specifically, during one revolution of the workpiece, some areas of its surface are cut, while some others are not.

When the DDEs are used to describe the regeneration effect, a time delay is a period between two passes of the tool through the same grinding position. Assuming a constant rotational speed of the workpiece, the time delay is equal to the workpiece period of rotation \(T_{\text{w}}\) (s). For the uncut area, the delay is changed into \(2 T_{\text{w}}\), as the upper chip surface was generated two revolutions ago. As the progress of the cutting continues, this delay can further increase to \(3 T_{\text{w}}, 4 T_{\text{w}}\) or even higher [16, 37]. Therefore, an alternative strategy must be constructed to keep tracking the uncut area in the workpiece surface and updating the delay accordingly, otherwise the DDEs approach becomes impractical.

Instead of using the DDEs and updating the delay, we can construct a function to record the profile of the workpiece [4], and then employ a partial differential equation (PDE) to update its profile. Hence, the original equations govern the displacements of the workpiece and the wheel, while the newly added PDE describes the profile of the workpiece [16, 37]. To solve the PDE, the Galerkin projection is used, and the original DDEs are expanded and transformed into ODEs [21, 35].

Using the ideas described above, this paper attempts to develop a new approach to study the self-interrupted grinding chatter. To begin with, Sect. 2 gives a general model of the grinding dynamics. Then, the DDEs are used in Sect. 3 to analyse the grinding stability using the continuation scheme and eigenvalue analysis [8, 22]. After that, the grinding chatter is analysed numerically by DDEBIFTOOL and the method of multiple scales (MMS) are performed to construct bifurcation diagrams. In Sect. 4, first the governing equations are formulated as PDEs. Then an additional function is introduced to record the workpiece profile and formulate the grinding depth. Next, the PDEs are transformed into the ODEs by using the Galerkin projection procedure. With these ODEs, the grinding dynamics is investigated by simulations and finite-difference method. The undertaken analysis confirms that the ODEs and the DDEs present similar results for the grinding without lost of contact. When the wheel loses contact with the workpiece, a discrepancy increases with time.

2 Dynamical model of plunge grinding

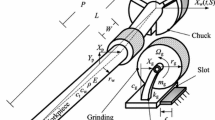
A plunge grinding process is illustrated in Fig. 1, where a workpiece is clamped and rotated by a chuck on its left end and is simply-supported by a tailstock on the right. In order to grind the workpiece, a rotating grinding wheel is fed into the workpiece. As material in the workpiece surface is removed during the wheel-workpiece interactions, a grinding force is generated, which is exerted on the wheel and the workpiece.

Fig. 1
figure 1

A schematic of the plunge grinding process. A workpiece has its right end simply supported by a tailstock, while it another end is clamped and rotated by a chuck. Meanwhile, a grinding wheel is rotated and plunged into the workpiece, grinding and regenerating the workpiece surface

Full size image

For a stable grinding process, displacements of the wheel and the workpiece are constant, and therefore the workpiece profile is round and flat. For an unstable grinding however, the profile becomes wavy and the grinding depth fluctuates. Consequently, a time-varying grinding force is generated, which promotes the grinding chatter. To theoretically study the grinding dynamics, the governing equations need to be developed.

The workpiece shown in Fig. 1 is represented as a beam of length L (m), radius \(r_{\text{w}}\) (m), mass density \(\rho\) (kg m\(^{-3}\)), Young’s modulus E (N m\(^{-2}\)) and damping \(c_{\text{w}}\) (N s m\(^{-2}\)). The cross-sectional area and the inertia moment of the workpiece are \(A=\pi r_{\text{w}}^2\) (m\(^2\)) and \(I=\pi r_{\text{w}}^4 /4\) (m\(^4\)) respectively. The grinding wheel is considered as a damped spring-mass system having mass \(m_{\text{g}}\) (kg), damping \(c_{\text{g}}\) (N s m\(^{-1}\)), and stiffness \(k_{\text{g}}\) (N m\(^{-1}\)). The workpiece rotates with a speed \(N_{\text{w}}\) (rpm), while the rotary speed of the wheel is \(N_{\text{g}}\) (rpm). At the position \(S=P\), the wheel is plunged into the workpiece with a feed speed f (m s\(^{-1}\)) causing the workpiece to be cut and generating the grinding force \(F_{\text{g}}\) (N).

As the workpiece is modelled as an Euler–Bernoulli beam and the grinding wheel as a spring-mass system; their displacements, \(X_{\text{w}}(t,S)\) (m) and \(X_{\text{g}}(t)\) (m), are governed by

$$\begin{aligned} &m_{\text{g}}{\frac{{\text{d}}^2 X_{\text{g}}(t)}{{\text{d}}t^2}}+c_{\text{g}}{\frac{{\text{d}}X_{\text{g}}(t)}{{\text{d}}t}}+k_{\text{g}}X_{\text{g}}(t)=F_{\text{g}},\\&\rho A {\frac{\partial ^2 X_{\text{w}}(t,S)}{\partial t^2}}+c_{\text{w}} {\frac{\partial X_{\text{w}}(t,S)}{\partial t}}+EI{\frac{\partial ^4 X_{\text{w}}(t,S)}{\partial S^4}}\\&\quad =-\delta \left( S-P\right) F_{\text{g}}, \end{aligned}$$
(1)

where \(\delta (S-P)\) is the Dirac delta function, representing the contact position. The boundary conditions of the workpiece displacement are

$$\begin{aligned}&X_{\text{w}}(t,0)={\frac{\partial X_{\text{w}}(t,0)}{\partial S}}=0\\&{\text{and}} \\&X_{\text{w}}(t,L)={\frac{\partial ^2 X_{\text{w}}(t,L)}{\partial S^2}}=0. \end{aligned}$$
(2)

The grinding force in Eq. (1), \(F_{\text{g}}\), is proportional to grinding depth \(D_{\text{g}}\). For a positive \(D_{\text{g}}\), the grinding force is given by Werner’s model [39]. \(F_{\text{g}}\) becomes zero if \(D_{\text{g}}\) is negative, which means the grinding force disappears when the workpiece and the wheel lose contact. Simply put, the grinding force \(F_{\text{g}}\) is given by

$$\begin{aligned} F_{\text{g}}= {\left\{ \begin{array}{ll} WKC^\nu \left( {\frac{r_{\text{w}} N_{\text{w}}}{r_{\text{g}} N_{\text{g}}}}\right) ^{2\mu -1}D_{\text{e}}^{1-\mu }D_{\text{g}}^\mu &{}{\text{if }} D_{\text{g}}>0,\\ 0 &{}{\text{if }}D_{\text{g}}\le 0, \end{array}\right. } \end{aligned}$$
(3)

where W (m) is the contact width, K (N m\(^{-2}\)) is the cutting stiffness, C represents the character of cutting edge distribution, \(D_{\text{e}}=2r_{\text{w}} r_{\text{g}}/(r_{\text{w}}+r_{\text{g}})\) is the equivalent diameter, \(\nu \in [0,1]\) and \(\mu \in [0.5,1]\) are nondimensional exponential parameters, and \(D_{\text{g}}\) is the instantaneous grinding depth [41]. In the following analysis, the grinding stiffness, \(K_{\text{g}}=WKC^\nu \left( {\frac{r_{\text{w}}}{r_{\text{g}}}}\right) ^{2\mu -1}\) (N m\(^{-1}\)) will be regarded as one parameter.

3 Analysis of grinding dynamics using DDEs

Based on the regenerative theory, the grinding depth \(D_{\text{g}}\) depends on the feed speed f and the surface regeneration [29]. When the rotating wheel interacts with the workpiece, a new workpiece surface is generated. After the workpiece makes one revolution, the wheel passes the same position for the second time; consequently, the instantaneous grinding depth equals to the radial distance between the old and the new surfaces.

3.1 Regeneration effect modelled by DDEs

As shown in Fig. 2, the regeneration effect can be represented by delayed terms [7, 18, 42]. Besides the feed in one revolution, \(fT_{\text{w}}\), the position of the new surface is influenced by the current workpiece and wheel displacements, \(X_{\text{w}}(t,P)\) and \(X_{\text{g}}(t)\). Meanwhile, the position of the old surfaces depends on the previous workpiece and wheel displacements, \(X_{\text{w}}(t-T_{\text{w}},P)\) and \(X_{\text{g}}(t-T_{\text{w}})\), where \(T_{\text{w}}=60/N_{\text{w}}\) is the rotational period of the workpiece. Moreover, if the wear in the wheel surface is considered, the regeneration at time \(t-T_{\text{g}}\) must be considered as well, where \(T_{\text{g}}=60/N_{\text{g}}\) is the rotational period of the wheel.

Fig. 2
figure 2

A schematic of regeneration effect between the workpiece and the wheel surfaces, described by DDEs. The workpiece surface is successively regenerated by the wheel, therefore the instantaneous grinding depth depends on the current and previous wheel-workpiece displacements

Full size image

For stable chatter-free grinding, the grinding depth is constant, \(D_{\text{g}}=f T_{\text{w}}\), and this is called nominal grinding depth [43]. In general, the instantaneous relative displacement between the workpiece and the wheel, \(X_{\text{w}}(t,P)\) and \(X_{\text{g}}(t)\), keeps varying. This variation perturbs the grinding depth to be \(D_{\text{g}}=fT_{\text{w}}+X_{\text{w}}(t,P)-X_{\text{g}}(t)\). Moreover, considering the regeneration effect of the workpiece, one can see that the instantaneous grinding depth is influenced by the position of the old workpiece surfaces as well. Therefore, the grinding depth can be described as \(D_{\text{g}}=fT_{\text{w}}+X_{\text{w}}(t,P)-X_{\text{g}}(t)-X_{\text{w}}(t-T_{\text{w}},P)\) \(+X_{\text{g}}(t-T_{\text{w}})\). In addition, when the regeneration effect of the wheel surface is considered, the grinding depth is described as

$$\begin{aligned} D_{\text{g}}& = fT_{\text{w}}+X_{\text{w}}(t,P)-X_{\text{g}}(t)\\& \quad -X_{\text{w}}(t-T_{\text{w}},P)+X_{\text{g}}(t-T_{\text{w}})\\& \quad -g\left( X_{\text{w}}(t-T_{\text{g}},P)-X_{\text{g}}(t-T_{\text{g}})\right) , \end{aligned}$$
(4)

where g is a dimensionless parameter related to the grinding ratio G.

The grinding ratio is given by

$$G={\frac{V_{\text{w}}}{V_{\text{g}}}},$$
(5)

where \(V_{\text{w}}\) is the volume of workpiece material removed, and \(V_{\text{g}}\) that of the grinding wheel. Due to the relative wheel-workpiece displacement at the time \(t-T_{\text{g}}\) (\([t-T_{\text{g}},t-T_{\text{g}}+\varDelta t]\) for example), the material removed volume \(V_{\text{w}}\) is increased by

$$\begin{aligned} \varDelta V_{\text{w}}=&W \left( X_{\text{w}}(t-T_{\text{g}},P)-X_{\text{g}}(t-T_{\text{g}})\right) \\&\times {\frac{N_{\text{w}} 2\pi r_{\text{w}}}{60}}\varDelta t. \end{aligned}$$
(6)

Simultaneously, the wheel is also being slowly regenerated with \(V_{\text{g}}\) increased by

$$\begin{aligned} \varDelta V_{\text{g}}=&W g\left( X_{\text{w}}(t-T_{\text{g}},P)-X_{\text{g}}(t-T_{\text{g}})\right) \\&\times {\frac{N_{\text{g}} 2\pi r_{\text{g}}}{60}}\varDelta t. \end{aligned}$$
(7)

Here, g indicates that the decrease of the wheel radius \(g(X_{\text{w}}(t-T_{\text{g}},P)-X_{\text{g}}(t-T_{\text{g}}))\) is smaller than that of the workpiece radius \((X_{\text{w}}(t-T_{\text{g}},P)-X_{\text{g}}(t-T_{\text{g}}))\). Combining these equations yields

$$G={\frac{\varDelta V_{\text{w}}}{\varDelta V_{\text{g}}}}={\frac{1}{g}\frac{N_{\text{w}}r_{\text{w}}}{N_{\text{g}}r_{\text{g}}}},$$
(8)

and

$$g={\frac{N_{\text{w}}r_{\text{w}}}{G N_{\text{g}}r_{\text{g}}}}.$$
(9)

As \(G\gg 1\) and \(N_{\text{g}}r_{\text{g}}>N_{\text{w}}r_{\text{w}}\), thus \(g\ll 1\) and the grinding depth can be simplified to

$$\begin{aligned} D_{\text{g}}=&fT_{\text{w}}+X_{\text{w}}(t,P)-X_{\text{g}}(t)\\&-X_{\text{w}}(t-T_{\text{w}},P)+X_{\text{g}}(t-T_{\text{w}}). \end{aligned}$$
(10)

3.2 DDE model

Given the boundary condition described by Eq. (2), the workpiece displacement can be expanded as [3]

$$\begin{aligned} X_{\text{w}}(t,S)=&\sum _{i=1}^nX_i(t)\bigg ({\frac{\sinh (k_i L)-\sin (k_i L)}{\cos (k_i L)-\cosh (k_i L)}}\\&\times \left( \cos (k_i S)-\cosh (k_i S)\right) \\&+\left( \sin (k_i S)-\sinh (k_i S)\right) \bigg ), \end{aligned}$$
(11)

where

$$k_i^4={\frac{\rho A}{E I}}\omega _i^2 \quad (i=1, 2, 3, \ldots ),$$
(12)

and \(\omega _i\) represents the natural frequency of the ith mode of the workpiece. Moreover, \(k_i\) is the solution of

$$\tanh (k_i L)=\tan (k_i L).$$
(13)

A numerical solution of Eq. (13) yields

$$k_1={\frac{3.9266}{L}},\quad k_2={\frac{7.0686}{L}},\quad k_3={\frac{10.2102}{L}},\ldots\,\, .$$
(14)

In practical applications, the first mode (\(i=1\)) of the beam is much often used than the other modes. Investigations carried out by Fu [9] and Altintas and Weck [1] show that the grinding chatter only involves the lowest modes of the workpiece. When the grinding wheel is located near the centre of the workpiece, the chatter frequency is dominated by the primary mode of the workpiece. Therefore, for the sake of simplicity, our analysis only considers \(n=1\),

$$X_{\text{w}}(t,S)=X_1(t)S_1(S)$$
(15)

where

$$\begin{aligned} S_1(S)=&{\frac{\sinh (k_1 L)-\sin (k_1 L)}{\cos (k_1 L)-\cosh (k_1 L)}}\\&\times \left( \cos (k_1 S)-\cosh (k_1 S)\right) \\&+\left( \sin (k_1 S)-\sinh (k_1 S)\right) . \end{aligned}$$
(16)

Next, by substituting Eqs. (3), (10), and (15) into Eq. (1), and using Galerkin projection, we obtain

$$\begin{aligned}&m_{\text{g}}{\frac{{\text{d}}^2 X_{\text{g}}(t)}{{\text{d}}t^2}}+c_{\text{g}}{\frac{{\text{d}}X_{\text{g}}(t)}{{\text{d}}t}}+k_{\text{g}}X_{\text{g}}(t)=K_{\text{g}}\\&\quad \times \left( {\frac{N_{\text{w}}}{N_{\text{g}}}}\right) ^{2\mu -1}D_{\text{e}}^{1-\mu }\big (fT_{\text{w}}+X_1(t)S_1(P)\\&\quad -X_{\text{g}}(t)-X_1(t-T_{\text{w}})S_1(P)+X_{\text{g}}(t-T_{\text{w}})\big )^\mu ,\\&\rho A {\frac{{\text{d}}^2 X_1(t)}{{\text{d}} t^2}}+c_{\text{w}} {\frac{{\text{d}} X_1(t)}{{\text{d}}t}}+EI k_1^4X_1(t)=-K_{\text{g}}\\&\quad \times \left( {\frac{N_{\text{w}}}{N_{\text{g}}}}\right) ^{2\mu -1} {\frac{S_1(P)}{\int _0^L{S_1(S)^2{\text{d}}S}}} D_{\text{e}}^{1-\mu }\bigg (fT_{\text{w}}\\&\quad +X_1(t)S_1(P)-X_{\text{g}}(t)\\&\quad -X_1(t-T_{\text{w}})S_1(P)+X_{\text{g}}(t-T_{\text{w}})\bigg )^\mu . \end{aligned}$$
(17)

When the grinding process is stable, the displacements of the workpiece and the wheel are constant. Mathematically, the corresponding displacements are called equilibria of Eq. (17), which are given by

$$\begin{aligned} X_{\text{g}}^{(0)}=&{\frac{K_{\text{g}}}{k_{\text{g}}}}\left( {\frac{N_{\text{w}}}{N_{\text{g}}}}\right) ^{2\mu -1}D_{\text{e}}^{1-\mu }\bigg (fT_{\text{w}}\bigg )^\mu ,\\ X_1^{(0)}=&-{\frac{S_1(P)}{E I k_1^4 \int _0^L{S_1(S)^2{\text{d}}S}}} K_{\text{g}}\left( {\frac{N_{\text{w}}}{N_{\text{g}}}}\right) ^{2\mu -1}\\&\times D_{\text{e}}^{1-\mu }\bigg (fT_{\text{w}}\bigg )^\mu . \end{aligned}$$
(18)

where \(X_{\text{g}}^{(0)}\) and \(X_{1}^{(0)}\) represent the equilibrium of \(X_{\text{g}}(t)\) and \(X_{\text{w}}(t)\) respectively.

Using Eq. (18), we can nondimensionalize Eq. (17) by introducing the following nondimensional parameters

$$\begin{aligned}&\tau =t{\sqrt{\frac{k_{\text{g}}}{m_{\text{g}}}}},\quad \tau _{\text{g}}=T_{\text{g}}{\sqrt{\frac{k_{\text{g}}}{m_{\text{g}}}}},\quad \tau _{\text{w}}=T_{\text{w}}{\sqrt{\frac{k_{\text{g}}}{m_{\text{g}}}}},\\&\kappa _{\text{w}}={\frac{E I k_1^4 m_{\text{g}}}{\rho A k_{\text{g}}}} \quad \gamma ={\frac{m_{\text{g}}S_1(P)^2}{\rho A \int _0^L{S_1(S)^2 {\text{d}}S}}},\\&\xi _{\text{g}}={\frac{c_{\text{g}}}{m_{\text{g}}}}{\sqrt{\frac{m_{\text{g}}}{k_{\text{g}}}}},\quad \xi _{\text{w}}={\frac{c_{\text{w}}}{\rho A}}{\sqrt{\frac{m_{\text{g}}}{k_{\text{g}}}}},\\&\kappa _{\text{c}}={\frac{K_{\text{g}}}{k_{\text{g}}}}\left( {\frac{D_{\text{e}}}{f}}{\sqrt{\frac{k_{\text{g}}}{m_{\text{g}}}}}\right) ^{1-\mu }\tau _{\text{g}}^{2\mu -1}. \end{aligned}$$
(19)

and variables

$$\begin{aligned} {\mathbf{y}}(\tau )=&\begin{pmatrix} y_1(\tau )\\ y_2(\tau )\\ y_3(\tau )\\ y_4(\tau ) \end{pmatrix}=\begin{pmatrix} {\frac{X_{\text{g}}(t)-X_{\text{g}}^{(0)}}{f}}{\sqrt{\frac{k_{\text{g}}}{m_{\text{g}}}}}\\ {\frac{X_1(t)-X_1^{(0)}}{f}}{\sqrt{\frac{k_{\text{g}}}{m_{\text{g}}}}} S_1(P)\\ {\frac{1}{f}}{\frac{{\text{d}}X_{\text{g}}(t)}{{\text{d}}t}}\\ {\frac{1}{f}}{\frac{{\text{d}}X_1(t)}{{\text{d}}t}} S_1(P) \end{pmatrix}, \\ \delta _{\text{d}}=&y_2(\tau )-y_1(\tau )+y_1(\tau -\tau _{\text{w}})-y_2(\tau -\tau _{\text{w}}),\\ d_{\text{g}}=&{\frac{D_{\text{g}}}{f}}{\sqrt{\frac{k_{\text{g}}}{m_{\text{g}}}}}=\delta _{\text{d}}+\tau _{\text{w}}. \end{aligned}$$
(20)

As a result, the nondimensional Eq. (17) is obtained as

$$\begin{aligned} {\frac{{\text{d}}{\mathbf{y}}(\tau)}{{\text{d}}\tau }}&={\mathbf{A}}{\mathbf{y}}(\tau )+{\mathbf{F_{dde}}}\\&\approx ({\mathbf{A}}-{\mathbf{D}}){\mathbf{y}}(\tau )+{\mathbf{D}}{\mathbf{y}}(\tau -\tau _{\text{w}})+{\mathbf{f}}, \end{aligned}$$
(21)

where

$$\begin{aligned} &{\mathbf{A}}=\begin{pmatrix} 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 1\\ -1 &{} 0 &{} -\xi _{\text{g}} &{} 0\\ 0 &{} -\kappa _{\text{w}} &{} 0 &{} -\xi _{\text{w}} \end{pmatrix},\\ &{\mathbf{D}}=\begin{pmatrix} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0\\ \tau _{\text{w}}^{-\mu }\mu \kappa _{\text{c}} &{} -\tau _{\text{w}}^{-\mu }\mu \kappa _{\text{c}} &{} 0 &{} 0\\ -\gamma \tau _{\text{w}}^{-\mu }\mu \kappa _{\text{c}} &{} \gamma \tau _{\text{w}}^{-\mu }\mu \kappa _{\text{c}} &{} 0 &{} 0 \end{pmatrix},\\ &{\mathbf{F_{dde}}}=\tau _{\text{w}}^{1-2\mu }\kappa _{\text{c}}\begin{pmatrix}{\begin{matrix} 0\\ 0\\ d_{\text{g}}^\mu -\tau _{\text{w}}^\mu \\ -\gamma d_{\text{g}}^\mu +\gamma \tau _{\text{w}}^\mu \end{matrix}} \end{pmatrix},\\ &{\mathbf{f}}={\frac{\mu (\mu -1)}{2\tau _{\text{w}}^{\mu +1}}}\kappa _{\text{c}}\begin{pmatrix} 0\\ 0\\ \delta _{\text{d}}^2(\tau )+\tau _{\text{w}}^{-1}{\frac{\mu -2}{3}}\delta _{\text{d}}^3(\tau )\\ -\gamma \delta _{\text{d}}^2(\tau )-\gamma \tau _{\text{w}}^{-1}{\frac{\mu -2}{3}} \delta _{\text{d}}^3(\tau ) \end{pmatrix}. \end{aligned}$$
(22)

3.3 Grinding stability

Equation (21) representing the nondimensional DDEs, governs the dynamics of the plunge grinding process, whose equilibria represent the stationary grinding. Thus, the stability of the equilibrium reflects the grinding stability. More specifically, when all the eigenvalues in terms of the equilibrium have negative real parts, the grinding is stable. On the contrary, grinding instability arises if the real part of any eigenvalue becomes positive. In case of a pair of pure imaginary eigenvalues, a Hopf bifurcation occurs and thus grinding chatter begins [42]. With increase of the real parts of the eigenvalues, the chatter amplitude grows. Simply put, Eq. (21) gives all the information required in the analysis of the grinding dynamics.

To examine the grinding stability, the eigenvalues are calculated [18, 42] and the characteristic equation of Eq. (21) is

$$\det \left( \lambda {\mathbf{I}}-{\mathbf{A}}-{\mathbf{D_{\text{w}}}}\exp (-\lambda \tau _{\text{w}})\right) =0,$$
(23)

where \(\lambda\) is the eigenvalue, and \(\det (\cdot )\) is the determinant of \(\cdot\). If \(\lambda =0\) is substituted into Eq. (23), one can obtain \(\det \left( \lambda {\mathbf{I}}-{\mathbf{A}}-{\mathbf{D_{\text{w}}}}\exp (-\lambda \tau _{\text{w}})\right) =\kappa _{\text{w}}\). Since \(\kappa _{\text{w}}>0, \lambda =0\) is not an eigenvalue of the grinding dynamics. Therefore, it can be concluded that the instability in the grinding can only be induced by pure imaginary eigenvalues, \(\lambda =\pm {\text{i}}\omega\). Correspondingly, we have

$$\begin{aligned} {\text{Re}}\left( \det \left( {\text{i}}\omega {\mathbf{I}}-{\mathbf{A}}-{\mathbf{D_{\text{w}}}}\exp (-{\text{i}}\omega \tau _{\text{w}})\right) \right) =0,\\ {\text{Im}}\left( \det \left( {\text{i}}\omega {\mathbf{I}}-{\mathbf{A}}-{\mathbf{D_{\text{w}}}}\exp (-{\text{i}}\omega \tau _{\text{w}})\right) \right) =0, \end{aligned}$$
(24)

where \({\text{Re}}(\cdot )\) and \({\text{Im}}(\cdot )\) represent the real and imaginary parts of \(\cdot\) respectively.

Equation (24) represents the critical case for the stable grinding, for which the stability boundary can be determined by solving it successively in the parameter space. To this end, the numerical continuation scheme [8, 43] described in “Appendix 1” is employed. Following the procedure illustrated in Fig. 14, we obtain the stability boundary of the grinding process, which is shown in Fig. 3.

Fig. 3
figure 3

Typical stability boundary of the plunge grinding process. The shaded region is the chatter-free, where no eigenvalue has positive real part. For further analysis of grinding dynamics, line A (\(\tau _{\text{w}}=10\) and \(\kappa _{\text{c}}\in [1.675, 2.1]\)) is marked to indicate the increase of \(\kappa _{\text{c}}\)

Full size image

In Fig. 3, the chatter-free region is shaded, while the chatter region is marked as white. In the chatter-free region, the grinding is linearly stable, whereas in the chatter region, the stability is lost and the chatter occurs. Moreover, Fig. 3 shows that the increase of \(\tau _{\text{w}}\) or the decrease of \(\kappa _{\text{c}}\) benefits the grinding stability. From Eq. (19) it can be concluded that a small rotational speed of the workpiece \(N_{\text{w}}\), a large rotational speed of the wheel \(N_{\text{g}}\), and a small grinding stiffness \(K_{\text{g}}\) should be chosen to obtain a stable grinding process. Here, the stiffness \(K_{\text{g}}=WKC^\nu \left( {\frac{r_{\text{w}}}{r_{\text{g}}}}\right) ^{2\mu -1}\) depends on many parameters and to realize the small \(K_{\text{g}}\), one should choose a small contact width W, a small cutting stiffness K (which can be realized by sharpening the grains of the wheel), a small characteristic parameter of cutting edge distribution \(C^\nu\) or a large wheel radius \(r_{\text{g}}\). Apparently, both small \(N_{\text{w}}\) and W, decrease the grinding efficiency. Thus, the best choice to avoid the grinding chatter is a large wheel speed \(N_{\text{g}}\).

3.4 Chatter predicted by DDEs

With the stability boundary obtained above, one can study the stable grinding in the chatter-free region and the grinding chatter in the chatter region. To this end, we use the method of multiple scales, simulation and DDEBIFTOOL to investigate the grinding dynamics near the boundary. Along Line A depicted in Fig. 3, a corresponding bifurcation diagram is constructed and shown in Fig. 4. As can be seen, a subcritical Hopf divides the parameter regions into three areas. The unconditionally chatter-free presents stable grinding, while the chatter vibration dominates the chatter region. In the conditionally chatter region, both stable and unstable grinding co-exist.

Fig. 4
figure 4

Bifurcation diagrams with parameter value selected on Line A marked in Fig. 3. It presents the relationship between \(d_{\text{g}}=\tau _{\text{w}}+\delta (\tau )\) and \(\kappa _{\text{c}}\). A subcritical Hopf bifurcation is generated near the stability boundary, which yields large-amplitude chatter. Stable chatter shows up only after the contact is lost (\(d_{\text{g}}<0\)). The subcritical instability divides the parameter region into three regions. In the conditionally chatter-free region, the grinding dynamics can be either stable or unstable. To illustrate, Points I and II are marked for further simulation

Full size image

With regards to Points I and II (\(\kappa _{\text{c}}=1.845\)), the time series of the grinding chatter and the stable grinding are plotted in Fig. 5. Point I represents the stable grinding, while Point II shows the grinding chatter. As shown in Fig. 5b, the grinding chatter is accompanied by the effect of losing contact, where the grinding force drops to zero for a negative grinding depth \(d_{\text{g}}\).

Fig. 5
figure 5

Time series of the nondimensional grinding depth \(d_{\text{g}}\), which corresponds to Points I and II marked in Fig. 4. a, b depict the stable grinding and the chatter vibration respectively

Full size image

For negative \(d_{\text{g}}\), no workpiece material is being removed by the grinding wheel and the workpiece profile in this area is unchanged. Mathematically, the corresponding time-delay is increased from \(\tau _{\text{w}}\) to \(2\tau _{\text{w}}\). For the next turn, such delay can further grow to \(3\tau _{\text{w}}, 4\tau _{\text{w}}\) and so on. Obviously, such multiple-delay effects cannot be adequately modelled and analysed by the DDEs, Eq. (21), therefore, in next section, we will adopt another model, which uses partial differential equations (PDEs) to conveniently record the evolution of the workpiece profile.

4 Analysis of grinding dynamics using PDEs

In the previous section, the regenerative grinding chatter was investigated by using the DDEs with fixed delays. If the workpiece profile is divided into several regions, then the corresponding time delays in different regions should be updated separately. As an example, Fig. 6 uses 16 regions and \(\tau _1, \ldots , \tau _{16}\) to track the multiple-delay effects of the workpiece regeneration. For an accurate simulation of the grinding dynamics, more regions and time delays are required, and then the analysis with the DDEs becomes a kinematic relationship similar to those studied by Thompson [29–33], Weck [38], and Li and Shin [14]. A similar investigation on a turning process was carried out by Liu et al. [16], who divided the workpiece profile into 600 segments for the simulation of the chatter with multiple-delay effects.

Fig. 6
figure 6

A schematic of multiple-delay effects along the circumference of the workpiece, which is due to the chatter accompanied with a loss of wheel-workpiece contact. In each regions of the workpiece profile, the time delays could be different and should be updated separately

Full size image

As the effect of losing contact cannot be fully captured by the DDEs with fixed delays, this section alternatively uses a PDE to describe the transformation of the workpiece profile. The profile is updated as soon as the grinding is started. Therefore, the regeneration effect on the workpiece is calculated, and thus the instantaneous grinding depth and the grinding force are computed.

4.1 Regeneration effect described by PDEs

A schematic of the regeneration caused by the workpiece is shown in Fig. 7, where sections of the workpiece and the grinding wheel are mapped onto a fixed plane. On the plane, the radius of the workpiece is recorded by \(R(t,\theta )\), where \(\theta (t)\in [0,2\pi ]\) is a coordinate fixed on the plane. Given the rotation direction of the workpiece, it is known that the workpiece enters the grinding area at \(\theta (t)=2\pi\), and then exits it at \(\theta (t)=0\). For \(\theta (t)\in (0,2\pi )\), by contrast, no cutting occurs.

Fig. 7
figure 7

A schematic of the regeneration effect caused by the workpiece, where the workpiece radius is monitored by \(R(t,\theta )\) instead of time delays

Full size image

At \(\theta (t)=2\pi\), the workpiece surface is cut and its radius is decreased from \(R(t,2\pi )\) to R(t, 0). Considering the feed and the instantaneous positions of the workpiece and the wheel, we can obtain the after-cutting radius:

$$R(t,0)=R_{\text{w}}(0)-ft-X_{\text{w}}(t,P)+X_{\text{g}}(t),$$
(25)

where \(R_{\text{w}}(0)\) is the initial radius of the workpiece.

After this cutting pass, next one will not occur until \(\theta\) is increased from 0 to \(2\pi\). Given the rotational speed of the workpiece, \(\varOmega _{\text{w}}={\frac{2\pi N_{\text{w}}}{60}}\), the angle can be written as \(\theta (t)=\varOmega _{\text{w}} t\). Therefore, the uncut surface has the relationship:

$$\begin{aligned} R(t,\theta )&=R(t-\varDelta t,\theta -\varDelta \theta )\\&=R(t-\varDelta t,\theta -\varOmega _{\text{w}}\varDelta t),\quad \theta \in (0,2\pi ], \end{aligned}$$
(26)

where \(\varDelta t\) and \(\varDelta \theta =\varOmega _{\text{w}}\varDelta t\) represent the increase of t and \(\theta\) respectively.

From Fig. 7, it is seen that the penetration of the wheel into the workpiece is the difference between \(R(t,2\pi )\) and R(t, 0). Namely, the workpiece radius is decreased from \(R(t,2\pi )\) to R(t, 0) by the cut of the wheel, with the grinding depth

$$D_{\text{g}}=R(t,2\pi )-R(t,0).$$
(27)

Given Eq. (26), the grinding depth, Eq. (27), can also be written as

$$\begin{aligned} D_{\text{g}} & =R(t,2\pi )-R(t,0)\\ =\,&R(t-\varDelta t,2\pi -\varOmega _{\text{w}} \varDelta t)-R(t,0)\\ & = R(t-T_{\text{w}},0)-R(t,0)\\ & =\,fT_{\text{w}}+X_{\text{w}}(t,P)-X_{\text{g}}(t)\\& \quad -X_{\text{w}}(t-T_{\text{w}},P)+X_{\text{g}}(t-T_{\text{w}}). \end{aligned}$$
(28)

Obviously, Eq. (28) gives the same grinding depth as that presented in Eq. (10). This ensures that the regeneration effects in these different forms (DDEs or PDEs) are identical.

When a loss of contact occurs, \(D_{\text{g}}\le 0\), the workpiece-wheel interactions are on hold and therefore the workpiece radius at \(\theta =0\) is unchanged. In this case, we have \(R(t,0)=R(t,2\pi )\). In combination with Eq. (25), the after-cutting workpiece radius (\(\theta =0\)) can be written as

$$\begin{aligned} R(t,0)={\left\{ \begin{array}{ll} R_{\text{w}}(0)-ft-X_{\text{w}}(t,P)+X_{\text{g}}(t),&{}{\text{if }} D_{\text{g}}>0,\\ R(t,2\pi ), &{}{\text{if }} D_{\text{g}} \le 0, \end{array}\right. } \end{aligned}$$
(29)

or

$$R(t,0)=\min \left( R_{\text{w}}(0)-ft-X_{\text{w}}(t,P)+X_{\text{g}}(t),R(t,2\pi )\right).$$
(30)

In the uncut zone (\(\theta \in (0,2\pi ]\)), it is obtained from Eq. (26) that

$$\begin{aligned} {\frac{\partial R(t,\theta )}{\partial t}}&=\lim \limits _{\varDelta t \rightarrow 0}{\frac{R(t+\varDelta t,\theta )-R(t,\theta )}{\varDelta t}}\\&=\varOmega _{\text{w}}\lim \limits _{\varDelta t \rightarrow 0}{\frac{R(t+\varDelta t,\theta )-R(t+\varDelta t,\theta +\varDelta \theta )}{\varDelta \theta }}\\&=-\varOmega _{\text{w}}{\frac{\partial R(t,\theta )}{\partial \theta }}. \end{aligned}$$
(31)

Next, introducing \({\tilde{R}}(t,\theta )=R(t,\theta )+ft-{\frac{f}{\varOmega _{\text{w}}}}\theta -R_{\text{w}}(0)\) into Eqs. (31) and (30) yields the governing equation of the workpiece profile

$${\frac{\partial {\tilde{R}}(t,\theta )}{\partial t}}+\varOmega _{\text{w}}{\frac{\partial {\tilde{R}}(t,\theta )}{\partial \theta }}=0,\quad \theta \in (0,2\pi ],$$
(32)

and its boundary condition

$${\tilde{R}}(t,0)=\min \left( -X_{\text{w}}(t,P)+X_{\text{g}}(t),{\tilde{R}}(t,2\pi )+fT_{\text{w}}\right).$$
(33)

Correspondingly, the grinding depth is

$$\begin{aligned} D_{\text{g}}&={\tilde{R}}(t,2\pi )-{\tilde{R}}(t,0)+fT_{\text{w}}\\&=\max \left( fT_{\text{w}}+{\tilde{R}}(t,2\pi )+X_{\text{w}}(t,P)-X_{\text{g}}(t),0\right). \end{aligned}$$
(34)

Now, all the governing equations of the grinding dynamics are obtained, where Eqs. (32) and (33) determine the workpiece profile, while Eqs. (1), (3) and (34) govern the evolution of the workpiece and the wheel displacements.

4.2 Model simplification

Before analysing the grinding dynamics, Eqs. (1), (34), (32) and (33) are to be simplified. Repeating the procedure used in Sect. 3.2, one can obtain the corresponding nondimensional equations:

$${\frac{{\text{d}}{\mathbf{y}}(\tau)}{{\text{d}}\tau }}= {\mathbf{A}}{\mathbf{y}}(\tau )+{\mathbf{F_{pde}}},$$
(35)
$${\frac{\partial {\tilde{r}}(\tau ,\theta )}{\partial \tau }}+{\frac{2\pi }{\tau _{\text{w}}}}{\frac{\partial {\tilde{r}}(\tau ,\theta )}{\partial \theta }}=0,$$
(36)
$${\tilde{r}}(\tau ,0)= \min \left( -y_2(\tau )+y_1(\tau ),{\tilde{r}}(\tau ,2\pi )+\tau _{\text{w}}\right).$$
(37)

and

$$d_{\text{g}}=\max \left( \tau _{\text{w}}+{\tilde{r}}(\tau ,2\pi )+y_2(\tau )-y_1(\tau ),0\right),$$
(38)

where

$$\begin{aligned} {\mathbf{F_{pde}}}&=\begin{pmatrix} 0\\ 0\\ \tau _{\text{w}}^{1-2\mu }\kappa _{\text{c}} d_{\text{g}}^\mu -\tau _{\text{w}}^{1-2\mu }\kappa _{\text{c}} \tau _{\text{w}}^\mu \\ -\gamma \tau _{\text{w}}^{1-2\mu }\kappa _{\text{c}} d_{\text{g}}^\mu +\gamma \tau _{\text{w}}^{1-2\mu }\kappa _{\text{c}} \tau _{\text{w}}^\mu \end{pmatrix},\\ {\tilde{r}}(\tau ,\theta )&={\frac{{\tilde{R}}(\tau ,\theta )}{f}}{\sqrt{\frac{k_{\text{g}}}{m_{\text{g}}}}}. \end{aligned}$$
(39)

As a counterpart of Eq. (21), Eq. (35) governs the grinding dynamics as well, that is, the delay terms (\(y_1(\tau -\tau _{\text{w}})-y_2(\tau -\tau _{\text{w}})\)) in \({\mathbf{F_{dde}}}\) is substituted by \({\tilde{r}}(\tau ,2\pi )\) in \({\mathbf{F_{pde}}}\), where \({\tilde{r}}(\tau ,\theta )\) is described by Eq. (36).

As Eq. (36) is a PDE, Galerkin projection can be used to map \({\tilde{r}}(\tau ,\theta )\) onto its shape functions. Since Eq. (36) is very similar to that used by Wahi and Chatterjee [37], we can use the same shape functions:

$$\begin{aligned} {\tilde{r}}(\tau ,\theta )& =\,a_0(\tau )\left( 1-{\frac{\theta }{2\pi }}\right) +a_1(\tau ){\frac{\theta }{2\pi }}\\& \quad +\sum _{j=1}^{M-1}a_{j+1}(\tau )\sin \left( {\frac{j\theta }{2}}\right) . \end{aligned}$$
(40)

From Eq. (40), it is obtained that \({\tilde{r}}(\tau ,0)=a_0(\tau )\) and \({\tilde{r}}(\tau ,2\pi )=a_1(\tau )\). Thus Eq. (37) can be written as

$$a_0(\tau )=\min \left( -y_2(\tau )+y_1(\tau ),a_1(\tau )+\tau _{\text{w}}\right).$$
(41)

Moreover, one can use

$$\begin{aligned} {\frac{{\text{d}}a_0(\tau )}{{\text{d}}\tau }}={\left\{ \begin{array}{ll} {\frac{{\text{d}}y_1(\tau )}{{\text{d}}\tau }}-{\frac{{\text{d}}y_2(\tau )}{{\text{d}}\tau }},&{}{\text{if }} y_1(\tau )-y_2(\tau )<a_1(\tau )+\tau _{\text{w}},\\ {\frac{{\text{d}}a_1(\tau )}{{\text{d}}\tau }}, &{}{\text{if }} y_1(\tau )-y_2(\tau ) \ge a_1(\tau )+\tau _{\text{w}}. \end{array}\right. } \end{aligned}$$
(42)

Substituting Eq. (40) into Eq. (36) yields

$$\begin{aligned}&{\frac{{\text{d}}a_0(\tau )}{{\text{d}}\tau }}\left( 1-{\frac{\theta }{2\pi }}\right) +{\frac{{\text{d}}a_1(\tau )}{{\text{d}}\tau }}{\frac{\theta }{2\pi }}\\&\quad +\sum _{j=1}^{M-1}{\frac{{\text{d}}a_{j+1}(\tau )}{{\text{d}}\tau }}\sin \left( {\frac{j\theta }{2}}\right) -{\frac{1}{\tau _{\text{w}}}}a_0(\tau )\\&\quad +{\frac{1}{\tau _{\text{w}}}}a_1(\tau )+{\frac{2\pi }{\tau _{\text{w}}}}\sum _{j=1}^{M-1}{\frac{j}{2}}\cos \left( {\frac{j\theta }{2}}\right) a_{j+1}(\tau )=0. \end{aligned}$$
(43)

Then, applying the Galerkin projection and making the left hand side of Eq. (43) be orthogonal to the shaped functions given by Eq. (40), one has

$$\begin{aligned}&\int _0^{2\pi }\bigg ({\frac{{\text{d}}a_0(\tau )}{{\text{d}}\tau }}\left( 1-{\frac{\theta }{2\pi }}\right) +{\frac{{\text{d}}a_1(\tau )}{{\text{d}}\tau }}{\frac{\theta }{2\pi }}\\&\quad +\sum _{j=1}^{M-1}{\frac{{\text{d}}a_{j+1}(\tau )}{{\text{d}}\tau }}\sin \left( {\frac{j\theta }{2}}\right) -{\frac{1}{\tau _{\text{w}}}}a_0(\tau )+{\frac{1}{\tau _{\text{w}}}}a_1(\tau )\\&\quad +{\frac{2\pi }{\tau _{\text{w}}}}\sum _{j=1}^{M-1}{\frac{j}{2}}\cos \left( {\frac{j\theta }{2}}\right) a_{j+1}(\tau )\bigg )\times {\frac{\theta }{2\pi }}{\text{d}}\theta =0, \end{aligned}$$
(44)

and

$$\begin{aligned}&\int _0^{2\pi }\bigg ({\frac{{\text{d}}a_0(\tau )}{{\text{d}}\tau }}\left( 1-{\frac{\theta }{2\pi }}\right) +{\frac{{\text{d}}a_1(\tau )}{{\text{d}}\tau }}{\frac{\theta }{2\pi }}\\&+\sum _{j=1}^{M-1}{\frac{{\text{d}}a_{j+1}(\tau )}{{\text{d}}\tau }}\sin \left( {\frac{j\theta }{2}}\right) -{\frac{1}{\tau _{\text{w}}}}a_0(\tau )+{\frac{1}{\tau _{\text{w}}}}a_1(\tau )\\&+{\frac{2\pi }{\tau _{\text{w}}}}\sum _{j=1}^{M-1}{\frac{j}{2}}\cos \left( {\frac{j\theta }{2}}\right) a_{j+1}(\tau )\bigg )\sin \left( {\frac{k\theta }{2}}\right) {\text{d}}\theta =0, \end{aligned}$$
(45)

where \(k=1,2,3,\ldots ,M-1\). Therefore, the grinding dynamics is governed by the ordinary differential equations (ODEs): Eqs. (35), (44) and (45).

Substituting \(a_0(\tau )\) and \({\frac{{\text{d}}a_0(\tau )}{{\text{d}}\tau }}\) in these equations by using Eqs. (41) and (42), and letting

$${\mathbf{a}}(\tau )=(y_1(\tau ),\ldots ,y_4(\tau ),a_1(\tau ),\ldots ,a_{M}(\tau ))^{\text{T}},$$
(46)

one can combine Eqs. (35), (44) and (45) to obtain

$${\frac{{\text{d}}{\mathbf{a}}(\tau )}{{\text{d}}\tau }}={\mathbf{B}}^{-1}{\mathbf{C}}{\mathbf{a}}(\tau )+{\mathbf{B}}^{-1}{\mathbf{F}},$$
(47)

where

$$\begin{aligned} {\mathbf{B}}=&\begin{pmatrix} {\mathbf{I}}_{4\times 4} &{} {\mathbf{0}}_{4\times M}\\ ({\mathbf{B}}_3)_{M\times 4} &{} ({\mathbf{B}}_4)_{M\times M} \end{pmatrix}_{(M+4)\times (M+4)},\\ {\mathbf{C}}=&\begin{pmatrix} ({\mathbf{C}}_1)_{4\times 4} &{} {\mathbf{0}}_{4\times M}\\ ({\mathbf{C}}_3)_{M\times 4} &{} ({\mathbf{C}}_4)_{M\times M} \end{pmatrix}_{(M+4)\times (M+4)}, \\ {\mathbf{F}}=&\begin{pmatrix} 0\\ 0\\ H\tau _{\text{w}}^{1-2\mu }\kappa _{\text{c}} d_{\text{g}}^\mu -\tau _{\text{w}}^{1-2\mu }\kappa _{\text{c}} \tau _{\text{w}}^\mu \\ -H\gamma \tau _{\text{w}}^{1-2\mu }\kappa _{\text{c}} d_{\text{g}}^\mu +\gamma \tau _{\text{w}}^{1-2\mu }\kappa _{\text{c}} \tau _{\text{w}}^\mu \\ (1-H)\int _0^{2\pi }{\frac{\theta }{2\pi }}{\text{d}}\theta \\ (1-H)\int _0^{2\pi }\sin \left( {\frac{1\theta }{2}}\right) {\text{d}}\theta \\ \vdots \\ (1-H)\int _0^{2\pi }\sin \left( {\frac{(M-1)\theta }{2}}\right) {\text{d}}\theta \end{pmatrix}_{(M+4)\times 1}, \end{aligned}$$
(48)

where \({\mathbf{I}}\) is an identity matrix, \({\mathbf{0}}\) a zero matrix, and H a Heaviside function defined as

$$\begin{aligned} H={\left\{ \begin{array}{ll} 1, &{}{\text{if }} y_1(\tau )-y_2(\tau )<a_1(\tau )+\tau _{\text{w}}{\text{ (cuting)}},\\ 0, &{}{\text{if }} y_1(\tau )-y_2(\tau )\ge a_1(\tau )+\tau _{\text{w}}{\text{ (lost of contact)}}. \end{array}\right. } \end{aligned}$$
(49)

To represent the elements in Eq. (48), one introduces some coefficients as

$$\begin{aligned} (c_0)_0=&\int _0^{2\pi }\left( 1-{\frac{\theta }{2\pi }}\right) {\frac{\theta }{2\pi }}{\text{d}}\theta ,\\ (c_0)_i=&\int _0^{2\pi }\left( 1-{\frac{\theta }{2\pi }}\right) \sin \left( {\frac{i\theta }{2}}\right) {\text{d}}\theta ,\\ (c_1)_0=&\int _0^{2\pi }\left( {\frac{\theta }{2\pi }}\right) ^2{\text{d}}\theta ,\\ (c_1)_i=&\int _0^{2\pi }{\frac{\theta }{2\pi }}\sin \left( {\frac{i\theta }{2}}\right) {\text{d}}\theta ,\\ (c_s)_i=&\int _0^{2\pi }\sin \left( {\frac{i\theta }{2}}\right) ^2{\text{d}}\theta ,\\ (c_c)_{0j}=&-{\frac{\pi }{\tau _{\text{w}}}}\int _0^{2\pi }j{\frac{\theta }{2\pi }}\cos \left( {\frac{j\theta }{2}}\right) {\text{d}}\theta ,\\ (c_c)_{ij}=&-{\frac{\pi }{\tau _{\text{w}}}}\int _0^{2\pi }j\sin \left( {\frac{i\theta }{2}}\right) \cos \left( {\frac{j\theta }{2}}\right) {\text{d}}\theta , \end{aligned}$$
(50)

where \(i, j=1, 2, \ldots , M-1\). Then these sub-matrices can be written as

$$\begin{aligned}&({\mathbf{B}}_3)_{M\times 4}=\begin{pmatrix} H (c_0)_0&{} -H (c_0)_0&{} 0&{} 0\\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ H (c_0)_{M-1}&{} -H (c_0)_{M-1}&{} 0&{} 0 \end{pmatrix},\\&({\mathbf{B}}_4)_{M\times M}\\&\quad =\begin{pmatrix} (c_1)_0+(1-H)(c_0)_0&{} (c_1)_1&{} \cdots &{} \cdots &{} (c_1)_{M-1}\\ \vdots &{}(c_s)_1&{} 0&{} \cdots &{} 0 \\ \vdots &{}0&{} {\ddots }&{} {\ddots }&{} \vdots \\ \vdots &{}\vdots &{} {\ddots }&{} {\ddots }&{} 0\\ (c_1)_{M-1}+(1-H)(c_0)_{M-1}&{}0&{} \cdots &{} 0&{} (c_s)_{M-1}\\ \end{pmatrix}, \end{aligned}$$
(51)

and

$$\begin{aligned}&({\mathbf{C}}_1)_{4\times 4}=\begin{pmatrix} {\begin{matrix} 0&{} 0&{} 1&{} 0\\ 0&{} 0&{} 0&{} 1\\ -1&{} 0&{} -\xi _{\text{g}}&{} 0\\ 0&{} -\kappa _{\text{w}}&{} 0&{} -\xi _{\text{w}}\\ \end{matrix}} \end{pmatrix},\\&({\mathbf{C}}_3)_{M\times 4}=\begin{pmatrix} H_0 &{} -H_0 &{} 0 &{} 0\\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ H_{M-1} &{} -H_{M-1} &{} 0 &{} 0 \end{pmatrix}\\&({\mathbf{C}}_4)_{M\times M}\\&\quad =\begin{pmatrix} -H_0 &{} (c_c)_{01} &{} \cdots &{} (c_c)_{0(M-1)}\\ \vdots &{} \vdots &{} {\ddots } &{} \vdots \\ -H_{M-1} &{} (c_c)_{(M-1)1} &{} \cdots &{} (c_c)_{(M-1)(M-1)} \end{pmatrix}. \end{aligned}$$
(52)

where \(H_i\) (\(i=0,1,2,\ldots ,M-1\)) is given by \(H_i={\frac{H}{\tau _{\text{w}}}}\left( (c_0)_i+(c_1)_i\right)\). After all the coefficients of Eq. (47) are obtained from Eqs. (48), (51) and (52), a numerical simulation is carried out to investigate the grinding dynamics.

4.3 Grinding dynamics

As expressed in Eq. (40), \({\tilde{r}}(\tau , \theta )\) is approximated by the shape functions and a larger M can reduce the approximation error. In [37], Wahi and Chatterjee obtained the convergence of the Galerkin approximation for \(M>25\). In this analysis, several values of M were tested and no apparent improvement of the approximation accuracy can be observed when \(M>50\). Thus, \(M=100\) was selected in the following simulations. In accordance with Point I marked in Fig. 4 and the time series plotted in Fig. 5a, the grinding dynamics described by the PDEs is obtained and shown in Fig. 8. As seen, the time series from PDEs is marked by dots, which are in a good agreement with the results obtained from DDEs (solid line).

Fig. 8
figure 8

a Time series of the stable grinding with respect to Point I in Fig. 4. Solutions of the DDEs and the PDEs are plotted in solid and dots respectively. To illustrate the similarity of the two solutions, b part of the solutions is replotted in a magnified window

Full size image

In contrast, the discrepancy between the DDEs and the PDEs can be significant when the contact is lost. To illustrate, the time series with respect to Point II are plotted in Fig. 9, where the grinding chatter given by both the DDEs and the PDEs are depicted. Moreover, two regions of Fig. 9a are blown up to show more details. Figure 9b shows the onset of losing contact, where the DDEs and the PDEs still show the same behaviour. In Fig. 9c, slightly different results are observed. Comparing these two predictions, the chatter computed by the DDEs has slightly larger amplitude and lower frequency than that from the ODEs.

Fig. 9
figure 9

a Time series of the chatter motion with respect to Point II in Fig. 4. Solid lines represent the solutions from the DDEs, while dots stand for the solutions of the PDEs. More details are replotted in the zoomed views, where b shows the occurrence of lost of contact, and c illustrates the two solutions separate from each other when the grinding is influenced by losing contact

Full size image

It is seen that the chatter obtained by the DDEs has a larger amplitude than that of the PDEs. This because the current grinding depth is overestimated by the DDEs when the cutting is absent. This is represented in Fig. 10. It is assumed that a loss of wheel-workpiece contact occurred at \(\tau -\tau _{\text{w}}\), which introduced a negative grinding depth, \(d_{\text{g}}(\tau -\tau _{\text{w}})<0\), and a free fly of the wheel leaving an uncut surface on the workpiece. Then, the time delay should be doubled and the real current grinding depth should be \(d_{\text{real}}=2\tau _{\text{w}}+y_2(\tau )-y_1(\tau )+y_1(\tau -2\tau _{\text{w}})-y_2(\tau -2\tau _{\text{w}})\). However, as seen in Fig. 10, the DDEs overestimates the current grinding depth to be \(d_{\text{g}}=d_{\text{real}}+d_{\text{over}}=d_{\text{real}}-d_{\text{g}}(\tau -\tau _{\text{w}})>d_{\text{real}}\). Therefore, the DDEs predicts a larger depth and thus a larger grinding force. Since the regenerative grinding force is the source of the chatter, one can understand that the chatter amplitude is overestimated by the DDEs.

Fig. 10
figure 10

A schematic showing a mechanism of overestimating grinding depth by the DDEs when a loss of contact occurs. An overestimated grinding depth \(d_{\text{over}}\) (the green part) is added to the real grinding depth \(d_{\text{real}}\) (the grey part)

Full size image

A further comparison between the results obtained from the DDEs and the PDEs is given in bifurcation diagrams depicted in Fig. 11, which were constructed from numerical simulations of the stable grinding processes. The filled circles stand for the stable solutions of the DDEs, and the filled rectangles represent the stable solutions of the PDEs. The unfilled circles represent the unstable periodical solutions of the DDEs, which is obtained by DDEBIFTOOL [8]. By contrast, the unstable periodic solutions of the PDEs are marked by unfilled rectangles, which are obtained by finite-difference method [22]. A detailed description of the finite-difference method is given in “Appendix 2”.

Fig. 11
figure 11

Bifurcation diagrams obtained by using the DDEs and the PDEs. The solutions of the DDEs are marked by circles, where the filled ones stand for the stable solutions and the unfilled ones are unstable. Rectangles represent the solutions of the PDEs, where the filled are stable and the unfilled are unstable

Full size image

To illustrate behaviour of the unstable periodic solution obtained by the finite-difference method, phase portrait with respect to Point III marked in Fig. 11 is plotted in Fig. 12. The unfilled circles represent the periodic solution of the DDEs obtained by DDEBIFTOOL. The orbit calculated by the finite-difference method is marked with the unfilled rectangles. As seen, the two results are consistent with each other.

Fig. 12
figure 12

Phase portraits of the unstable periodic solutions obtained by using the DDEs (unfilled circles) and the PDEs (unfilled rectangles)

Full size image

4.4 Workpiece profile

When the PDEs are used for the chatter analysis, the workpiece profile is recorded by \({\tilde{r}}(\tau ,\theta )\). Therefore, unlike the DDEs, the workpiece profile can be reconstructed by using Eq. (40). With regards to the time series depicted in Figs. 8 and 9, the profiles are plotted in Fig. 13.

Fig. 13
figure 13

Workpiece profiles of the stable and the unstable grinding, which varies with respect to time \(\tau\). a The workpiece profile is gradually flatted, which corresponds with the stable grinding illustrated in Fig. 8. b The chatter, which is seen in Fig. 9, leaves wavy profile in the workpiece surface

Full size image

Figure 13a illustrates the workpiece profile when the grinding is stable, where at the beginning, the profile \({\tilde{r}}(\tau ,\theta )\) fluctuates with respect to \(\theta\) (\(\theta \in [0,2\pi )\)). With the increase of time \(\tau\) however, \({\tilde{r}}(\tau ,\theta )\) become linear and consequently the wavy workpiece profile becomes flat. By contrast, the grinding chatter presents a wavy profile in Fig. 13.

It should be remarked here that the workpiece profile is a by-product of the chatter analysis, which is a straightforward result of Eq. (40) and no extra effort is required. If the DDEs were employed, an illustration of the workpiece profile is possible as well, but more efforts should be put into the simulation and the result is indirect. A similar problem was investigated by Liu et al. [16] in a study of a turning chatter. Besides the DDEs, they also introduced a PDE, \(U(\theta ,t)\), to record the workpiece profile. Then, the profile was divided into 600 segments and the surfaces in each segments were updated separately according to the condition of contact. This approach can predict the profile, but extra efforts are required since both the DDEs and the PDEs are employed and the profile and the delays in each segments should be updated simultaneously during the simulation.

5 Conclusions

In this paper for the first time, the self-interrupted grinding chatter for which a loss of contact between the workpiece and the grinding wheel occurs, was investigated by using the DDEs and the PDEs. Eigenvalues and continuation calculations were used to investigate the grinding stability. Thereafter, bifurcation analysis based on the MMS, DDEBIFTOOL, the numerical simulations and the finite-difference method were performed to predict the grinding chatter in the unstable regions.

Near the stability boundary, bifurcation analysis has been performed by using the MMS, DDEBIFTOOL and the numerical simulations. It has been found that the grinding chatter is mainly generated by subcritical Hopf bifurcation, which presents large-amplitude chatter. As a result, the grinding chatter is accompanied with the effect of losing contact. Correspondingly, the time delay used in the DDEs is transformed from \(\tau _{\text{w}}\) to \(2\tau _{\text{w}}, 3\tau _{\text{w}}\), or even larger. A such multiple delay effect cannot be accurately described by the DDEs.

To analyse the grinding chatter with the multiple-delay effect, the PDEs have been introduced to monitor the workpiece profile. Simulations and finite-difference method have been used to obtain the stable and the unstable solutions of the PDEs respectively. The time histories, the bifurcation diagrams and the phase portraits obtained from the DDEs and the PDEs have been compared. It has been seen that the DDEs and the PDEs give the same results when the wheel grinds being in contact with the workpiece. When the wheel loses contact with the workpiece, their discrepancy increases with respect to time due to the multiple-delay effect. More specifically, the grinding chatter obtained from the PDEs has smaller amplitude than that from the DDEs.

It has been proven that the regeneration effect in the grinding can be accurately captured by both the DDEs or the PDEs when the wheel grinds the workpiece continuously. The DDEs is very useful for the analysis of the grinding dynamics when the wheel-workpiece interactions are on hold, either in the case of the stable grinding or the chatter with small fluctuation. When the large-amplitude chatter occurs, the grinding is self-interrupted and then the DDEs with fixed delays are impractical. In contrast, the PDEs are not affected by the multiple-delay effect and can be an effective alternative for the analysis of the self-interrupted grinding chatter.