1 Introduction

The Rayleigh equation determines a typical non-linear system with one degree of freedom which admits auto-oscillations. This equation was named after Lord Rayleigh who investigated equations of this type related to problems in acoustics [1]. The special case of the Rayleigh equation for is the Vander Pol equation [2]. In general, the Duffing equation [3] does not admit an exact symbolic solution. However, it is resolved many approximate methods [4, 5].

The differential transform method (DTM) is a numerical as well as analytical method for solving integral equations, ordinary, partial differential equations and differential equation systems. The method provides the solution in terms of convergent series with easily computable components. The concept of the differential transform was first proposed by Zhou [6] and its main application concern with both linear and nonlinear initial value problems in electrical circuit analysis. The DTM gives exact values of the nth derivative of an analytic function at a point in terms of known and unknown boundary conditions in a fast manner. This method constructs, for differential equations, an analytical solution in the form of a polynomial. It is different from the traditional high order Taylor series method, which requires symbolic computations of the necessary derivatives of the data functions. The Taylor series method is computationally taken long time for large orders. The DTM is an iterative procedure for obtaining analytic Taylor series solutions of differential equations. Different applications of DTM can be found in [7–29].

However, DTM has some drawbacks. By using the DTM, we obtain a series solution, actually a truncated series solution. This series solution does not exhibit the real behaviors of the problem but gives a good approximation to the true solution in a very small region. To overcome the shortcoming, MsDTM was presented in [30, 31]. On the other hand, MsDTM has also some drawbacks. By using the DTM, the interval [0, T] is divided into M sub-interval and the series solutions is obtained in t∈[t i ,t i+1], i=0,1,…,M−1. In some problems, interval [0,T] can be required a very small sub-division of intervals. In this case, both the solution time lengthens and series solutions are obtained for a great number of sub-intervals.

The main aim of this paper is to extend the application of the multi-step differential transform method [30, 31] to solve a fractional order non-linear oscillator and vibration equation.

This paper is organized as follows:

In Sects. 2 and 3, we describe fractional DTM and multi-step DTM briefly. To show in efficiency of this method, we give some examples and numerical results in Sect. 4. The conclusions are then given in the final Sect. 5.

2 Fractional differential transform method

Consider a general system of fractional differential equations:

$$ D^{m}x(t)+f(x)D_{*}^{\alpha}x(t)+h\bigl(t,x,x ' ,x'' ,\dots\bigr)=0, $$
(1)

where \(D_{*}^{\alpha}\) is the derivative of x of order α in the sense of Caputo and m−1<α≤m, subject to the initial conditions

$$ x^{ (i )}(0)=c_{i},\quad i=0,1,\dots,m-1. $$
(2)

In this paper, we introduce the multi-step fractional differential transform method used in this paper to obtain approximate analytical solutions for the fractional differential equations (1). This method has been developed in [32] as follows:

(3)

for m−1≤q<m,m∈Z +, x>x 0. Let us expand the analytical and continuous function f(x) in terms of fractional power series as follows:

(4)

where α is the order of fraction and F(k) is the fractional differential transform of f(x).

In order to avoid fractional initial and boundary conditions, we define the fractional derivative in the Caputo sense. The relation between the Riemann-Liouville operator and Caputo operator is given by

(5)

Setting \(f(x)-\sum_{k=0}^{m-1}\frac{1}{k!}(x-x_{0})^{k}f^{ (k )}(x_{0})\) in Eq. (3) and using Eq. (5), we obtain fractional derivative in the Caputo sense [32–34] as follows:

(6)

since the initial conditions are implemented are implemented to the integer order derivatives, the transform of the initial conditions are defined as follows:

(7)

where, q is the order of fractional differential equation considered. The following theorems that can be deduced from Eqs. (4) and (5) are given below, for proofs and detailed see [34–36].

Theorem 1

If z(t)=x(t)±y(t), then Z(k)=X(k)±Y(k).

Theorem 2

If z(t)=cy(t), then Z(k)=cY(k).

Theorem 3

If z(t)=x(t)y(t) and u(t)=f(t)g(t)h(t), then

$$Z(k)= \sum_{k_{1}=0}^{k}X(k_{1})Y(k-k_{1}) $$

and

$$U(k)= \sum_{k_{2}=0}^{k} \sum_{k_{1}=0}^{k_2} F(k_{1})G(k_2-k_{1}) H(k-k_2). $$

Theorem 4

If z(t)=(t−t 0)n, then Z(k)=δ(k−αp) where

Theorem 5

If \(z(t)=D_{t_{0}}^{q}[g(t)]\) then \(Z(k)= \frac{\varGamma(q+1+\frac{k}{\alpha} )}{\varGamma(1+\frac {k}{\alpha} )}G(k+\alpha q)\).

According to fractional DTM, by taking differential transformed both sides of the equations given Eqs. (1) and (2) is transformed as follows:

(8)
(9)

where, \(\alpha=\frac{p}{q}\) is the order of fractional differential equation considered. Therefore, according to DTM the N-term approximations for (1) can be expressed as

$$ x(t)=\sum_{k=1}^{N}X(k)t^{\alpha k}. $$
(10)

3 Solutions by MsDTM

Let [0,T] be the interval over which we want to find the solution of the initial value problem (1). In actual applications of the DTM, the approximate solution of the initial value problem (1)–(2) can be expressed by the finite series,

$$ x(t)=\sum_{i=0}^{N}b_{i}t^{\alpha i}, \quad t\in[0,T]. $$
(11)

Assume that the interval [0,T] is divided into N subintervals [t n−1,t n ], n=1,2,…,N of equal step size h=T/N by using the nodes t n =nh. The main ideas of the multi-step DTM are as follows [30, 31]. First, we apply the DTM to Eq. (1) over the interval [0,t 1], we will obtain the following approximate solution,

$$ x_{1}(t)=\sum_{i=0}^{N}b_{1i}t^{\alpha i}, \quad t\in[0,t_{1}] $$
(12)

using the initial conditions \(x_{1}^{ (k )}(0)=d_{k}\). For n≥2 and at each subinterval [t n−1,t n ] we will use the initial conditions \(x_{n}^{ (k )}(t_{n-1})=x(t_{n-1})\) and apply the DTM to Eq. (1) over the interval [t n−1,t n ], where t i in Eq. (12) is replaced by t n−1. The process is repeated and generates a sequence of approximate solutions x n (t), n=1,2,…,N for the solution x(t),

$$ x_{n}(t)=\sum_{i=0}^{N}b_{ni}(t-t_{n-1})^{\alpha i}, \quad t\in[t_{n},t_{n+1}] $$
(13)

In fact, the multi-step DTM assumes the following solution,

(14)

4 Applications

Example 1

(The Duffing equation)

The Duffing equation is a non-linear second-order differential equation as follows:

$$ \everymath{\displaystyle }\begin{array}{@{}lll} \frac{d^{\alpha}x}{dt^{\alpha}}+x+\varepsilon x^{3}=0 \cr\noalign{\vspace{3pt}} x(0)=0,\quad x ' (0)=1. \end{array} $$
(15)

We will apply classic DTM and the multi-step DTM to nonlinear ordinary differential equation (15). Applying classic DTM for Eq. (15)

(16)

where X i (n), for n=1,…,M, satisfy the following recurrence relations,

(17)

By applying the multi-step DTM to Eq. (15) is obtained Eq. (18) as following:

(18)

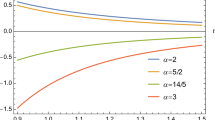
The solutions of Eq. (15) corresponding to ε=0.1,0.5,1,3 and \(\alpha=\frac{3}{2}\), respectively, are shown in Fig. 1. The results show that in the interval 0<ε≤3 the frequency increases with increases ε.

Fig. 1
figure 1

Plots of displacement x versus time t for \(\alpha =\frac{3}{2}\) and different value of ε

Full size image

The solutions of Eq. (15) corresponding to ε=0.1,0.5,1,3 and \(\alpha=\frac{5}{3}\), respectively, are shown in Fig. 2. The results show that in the interval 0<ε≤3 the frequency increases with increases ε. The results obtained from in Figs. 1 and 2 show that in the interval 1<α<2 the frequency decreases with increases.

Fig. 2
figure 2

Plots of displacement x versus time t for \(\alpha =\frac{5}{3}\) and different value of ε

Full size image

Table 1 shows the approximate solutions for Eq. (15) obtained for different values of a using MsDTM with the Runge Kutta method. From the numerical results in Table 1, it is clear that the approximate solutions are in high agreement with the RKM solutions, when α=2.

Table 1 Approximate solutions for Duffing equation (15), when ε=0.1, obtained using multi-step DTM and RK4 method
Full size table

Example 2

(The Vander Pol equation)

Consider the following Vander Pol equation.

$$ \everymath{\displaystyle }\begin{array}{@{}lll} \frac{d^{2}x}{dt^{2}}+\mu\bigl(x^{2}-1\bigr)\frac{d^{\alpha }x}{dt^{\alpha}}+x= a \sin(wt), \cr\noalign{\vspace{3pt}} y(0)=0 ,\qquad y'(0)=0. \end{array} $$
(19)

Taking classic-DTM of both sides Eq. (19), we obtain the following recurrence relation:

$$ \everymath{\displaystyle }\begin{array}[b]{@{}lll} \frac{\varGamma(\frac{k+q+rq}{q})}{\varGamma(\frac{k+q}{q})}X(k+rq) -\mu\frac{\varGamma(\frac{k+q+p}{q})}{\varGamma(\frac{k+q}{q})}X(k+p) \cr\noalign{\vspace{3pt}} \qquad{} +\mu\sum_{k_{2}=0}^{k}\sum_{k_{1}=0}^{k_{2}}\frac{\varGamma (\frac{k-k_{2}+q+p}{q})}{\varGamma(\frac{k-k_{2}+q}{q})} \end{array} $$
(20)

where A(k) is the fractional differential transform of sin(wt) that can be obtained using Eq. (4) [34] as

$$A(K)= \sum^{\infty}_{i=0} \frac{(-1)^{i}w^{2i+1}\delta(k-(2i+1)q)}{(2i+1)!}, $$

According to the multi-step DTM, the series solution for Vander Pol equation (19) is given by,

(21)

where X i (n), for n=1,…,M, satisfy the following recurrence relations,

$$ \everymath{\displaystyle }\begin{array}{@{}lll} \frac{\varGamma(\frac{k+q+rq}{q})}{\varGamma(\frac {k+q}{q})}X_{i}(k+rq)-\mu\frac{\varGamma(\frac {k+q+p}{q})}{\varGamma(\frac{k+q}{q})}X_{i}(k+p) \cr\noalign{\vspace{2pt}} \qquad{} +\mu\sum_{k_{2}=0}^{k}\sum_{k_{1}=0}^{k_{2}}\frac{\varGamma(\frac {k-k_{2}+q+p}{q})}{\varGamma(\frac{k-k_{2}+q}{q})} X_{i}(k_{1})X_{i}(k_{2}-k_{1}) \cr\noalign{\vspace{2pt}} \qquad{} \times X_{i}(k-k_{2}+p)+X_{i}(k) \cr\noalign{\vspace{2pt}} \quad{} =\frac{a\sum_{i=0}^{\infty}(-1)^{i}w^{2i+1}\delta(k-(2i+1)q)}{(2i+1)!}, \cr\noalign{\vspace{2pt}} X_{0}(0)=0,\qquad X_{0}(q)=0 \cr\noalign{\vspace{2pt}} X_{i+1}(0)=X_{i}\bigl(t^{*}\bigr),\qquad X_{i+1}(q)=X_{i}\bigl(t^{*}\bigr) \cr\noalign{\vspace{2pt}} t\in[t_{i},t_{i+1}],\qquad t^{*}=t_{i},\quad i=0,\dots,M-1 \end{array} $$
(22)

Figure 3 shows the approximate solutions for \(\alpha=\frac{1}{2}\), a=1.31, w=0.5 and μ=0.1,0.5,1,2. The solutions of Eq. (19) corresponding to μ=0.1,0.5,1,2 and \(\alpha=\frac{2}{3}\), respectively, are shown in Fig. 4. The results indicate that in the interval 0<μ≤2 the frequency increases with increases μ. The results obtained from in Figs. 3 and 4 show that in the interval 0<α<1 the frequency decreases with increases.

Fig. 3
figure 3

Plots of displacement x versus time t for \(\alpha =\frac{1}{2}\) and different value of μ

Full size image
Fig. 4
figure 4

Plots of displacement x versus time t for \(\alpha =\frac{2}{3}\) and different value of μ

Full size image

Table 2 shows the approximate solutions for Eq. (19) obtained for different values of a using MsDTM with the Runge Kutta Method. From the numerical results in Table 2, it is clear that the approximate solutions are in high agreement with the RKM solutions, when α=1.

Table 2 Approximate solutions for Vander Pol equation (19), when μ=0.1, obtained using multi-step DTM and RK4 method
Full size table

Example 3

(Fractional Rayleigh differential equation)

Consider the following fractional Rayleigh differential equation.

$$ \everymath{\displaystyle }\begin{array}{@{}lll} \frac{d^{2}x}{dt^{2}}=-x-\varphi \biggl(1-\frac{1}{3}\biggl(\frac{d^{\alpha}x}{dt^{\alpha }}\biggr)^{2}\biggr)\frac{dx}{dt}, \end{array} $$
(23)
$$ x(0)=1 ,\qquad x'(0)=0. $$

Taking classic-DTM of both sides Eq. (23), we obtain the following recurrence relation:

$$ \everymath{\displaystyle }\begin{array}{@{}lll} \frac{\varGamma(\frac{k+q+rq}{q})}{\varGamma(\frac {k+q}{q})}X(k+rq)\cr\noalign{\vspace{5pt}} \qquad {} =-X(k)-\varphi(k+1)X(k+1) \cr\noalign{\vspace{5pt}} \quad{}+\frac{\varphi}{3}\sum_{k_{2}=0}^{k}\sum_{k_{1}=0}^{k_{2}} \frac{\varGamma(\frac{k_{2}-k_{1}+q+p}{q})}{\varGamma(\frac {k_{2}-k_{1}+q}{q})} \frac{\varGamma(\frac{k-k_{2}+q+p}{q})}{\varGamma(\frac{k-k_{2}+q}{q})} \cr\noalign{\vspace{5pt}} \quad{} \times X(k_{1}) X(k_{2}-k_{1}+p)X(k-k_{2}+p), \cr\noalign{\vspace{5pt}} X(0)=1,\qquad X(q)=0. \end{array} $$
(24)

According to the multi-step DTM, the series solution for Rayleigh equation (23) is given by,

(25)

where X i (n), for n=1,…,M, satisfy the following recurrence relations,

(26)

Figure 5 shows the approximate solutions for \(\alpha=\frac {1}{2}\) and φ=0.1,0.5,1,2. The solutions of Eq. (23) corresponding to φ=0.1,0.5,1,2 and \(\alpha=\frac{1}{4}\), respectively, are shown in Fig. 6. The results indicate that in the interval 0<φ≤2 the frequency decreases with increases φ. The results obtained from in Figs. 5 and 6 show that in the interval 0<α<1 the frequency decreases with increases.

Fig. 5
figure 5

Plots of displacement x versus time t for \(\alpha =\frac{1}{2}\) and different value of φ

Full size image
Fig. 6
figure 6

Plots of displacement x versus time t for \(\alpha =\frac{1}{2}\) and different value of φ

Full size image

Table 3 shows the approximate solutions for Eq. (23) obtained for different values of a using MsDTM with the Runge Kutta Method. From the numerical results in Table 3, it is clear that the approximate solutions are in high agreement with the RKM solutions, when α=1.

Table 3 Approximate solutions for Rayleigh differential equation (23), when φ=0.1, obtained using multi-step DTM and RK4 method
Full size table

Example 4

(Vibration differential equation)

Consider the following vibration equation with fractional damping, with one degree of freedom [37]:

$$ \everymath{\displaystyle }\begin{array}{@{}lll} D^{2}x(t)+\frac{c}{m}D^{\alpha}x(t)+\frac{k}{m}x(t)=f_{0}\sin(w_{e}t), \cr\noalign{\vspace{3pt}} x(0)=\frac{1}{4},\qquad x ' (0)=0, \end{array} $$
(27)

where \(D=\frac{d}{dt}\) is the differential operator. Another common form of Eq. (27) is

(28)

with

Taking classic-DTM of both sides Eq. (28), we obtain the following recurrence relation:

(29)

According to the multi-step DTM, the series solution for vibration equation (28) is given by,

(30)

where X i (n), for n=1…M, satisfy the following recurrence relations,

$$ \everymath{\displaystyle }\begin{array}{@{}lll} \frac{\varGamma(\frac{k+q+rq}{q})}{\varGamma(\frac{k+q}{q})}X_{i}(k+rq) \cr\noalign{\vspace{3pt}} \qquad{} +2\mu w_{n}^{2-\frac{p}{q}}\frac{\varGamma(\frac {k+q+p}{q})}{\varGamma(\frac{k+q}{q})}X_{i}(k+p)+w_{n}^{2}X_{i}(k) \cr\noalign{\vspace{3pt}} \quad{} =\frac{f_{0}\sum_{i=0}^{\infty}(-1)^{i}w_{e}^{2i+1}\delta (k-(2i+1)q)}{(2i+1)!} \cr\noalign{\vspace{3pt}} X_{0}(0)=\frac{1}{4},\qquad X_{0}(q)=0, \end{array} $$
(31)

The results in Fig. 7 compatible with those obtained in [37] using the Adomian decomposition method.

Fig. 7
figure 7

(a1), (b1), (c1), (d1), (e1) and (f1) solution curves for problems (a), (b), (c), (d), (e) and (f) in Table 4, respectively

Full size image

For the solution of Eq. (28), the parameter values of Table 4 were used. Table 5 shows the approximate solutions for Eq. (27) obtained for different values of a using MsDTM with the Runge Kutta Method. From the numerical results in Table 5, it is clear that the approximate solutions are in high agreement with the RKM solutions, when α=1.

Table 4 Numerical parameters of the examples [37]
Full size table
Table 5 Approximate solutions for vibration differential equation (27), when c=1,m=1,k=100,f=1,w θ =0, obtained using multi-step DTM and RK4 method
Full size table

5 Conclusions

In this work, we carefully applied the multi-step DTM, a reliable modification of the DTM that improves the convergence of the series solution. The method provides immediate and visible symbolic terms of analytic solutions, as well as numerical solutions for wide classes of linear and nonlinear fractional differential equations. The validity of the proposed method has been successful by applying it for Duffing, The Vander Pol, Rayleigh and vibration equations. The method was used in a direct way without using linearization, perturbation or restrictive assumptions. It provides the solutions in terms of convergent series with easily computable components and the results have shown remarkable performance. Therefore, the proposed method is very efficient and accurate method that can be used to provide analytical solutions for nonlinear fractional-order differential equations.