1 Introduction

The thermodynamic properties of the high-temperature superconducting state in cuprates can be described quantitatively on the basis of the three postulates [1].

  1. The first postulate states:

    In the superconductivity domain of cuprates, the fundamental role is played by the electrons on the C u O 2 planes.

From the mathematical point of view, the above assumption means that the electron-hopping integral in the direction perpendicular to the copper-oxygen plane can be ignored in the considerations.

It should be noted that the quasi-two-dimensionality of the electron system in cuprates significantly affects only some thermodynamic parameters of the superconducting state. In particular, due to the high electron density of states at the Fermi level (the van Hove singularity), it causes a very significant increase in the critical temperature ([T C]max ≃ 200 K) and an equally strong decline in the value of the isotope coefficient [2–6].

On the other hand, taking into account only the geometrical reduction of the electron system cannot explain the high values of the ratio of the zero-temperature energy gap amplitude (G(0)) to the critical temperature (R G ≡ G(0)/k B T C), which are commonly observed in cuprates (especially for the low value of the hole concentration) [7–11].

The second postulate has the following content: In cuprates exists the conventional electron-phonon interaction, which does not have to be strong.

This finding indicates that the pairing mechanism in cuprates is not the result of the purely electronic correlation of the Hubbard-type. However, the classical electron-phonon interaction alone is not able to wholly explain all the anomalous properties of the high-temperature superconducting state. In particular, a special attention should be paid to the weak dependence of the energy gap amplitude on the temperature in the range from 0 to T C, which is often observed in the underdoped cuprates [12].

The last postulate states: In cuprates exist strong electronic correlations, but the electron-electron scattering in the superconductivity domain is inseparably connected with the absorption or emission of vibrational quanta.

The cited postulate assumes that the classical electron-phonon interaction must coexist with the strong electron correlations, which are renormalized by the phonons.

It is really obvious that complement of the first two postulates by the third postulate makes it possible to quantitatively describe the dependence of the energy gap on the hole concentration and temperature. At the same time, the determined values of the parameter R G fairly agree with the experimental results [1, 13, 14].

In the presented paper, we have calculated the values of the energy gap for Bi2Sr2−x La x CuO6+δ (BSLCO) superconductor. The selected values of the hole concentration and the temperature have been taken into consideration. The obtained results have been compared to the existing experimental data.

2 The Model and the Results

The average value of the energy gap amplitude \((G(T)~\equiv ~2\left (V+\frac {U}{6}\left |{\Delta }(T)\right |^{2}\right )\left |{\Delta }\left (T\right )\right |\)) should be calculated with the help of the equation below [1]:

$$ 1=\left(V+\frac{U}{6}|{\Delta}\left(T\right)|^{2}\right)\frac{1}{N_{0}}\sum\limits_{\mathbf{k}}^{\omega_{0}} \frac{\eta^{2}(\mathbf{k})}{2E_{\mathbf{k}}}\text{tgh}\frac{\beta E_{\mathbf{k}}}{2}, $$
(1)

where V and U denote the effective pairing potential for the electron-phonon interaction and the electron-electron-phonon interaction, respectively. The symbol |Δ(T)| is the amplitude of the anisotropic order parameter of the d wave symmetry type: η(k) ≡ 2[cos(k x) − cos(k y)]. The function E k is given by the following expression:

$$ E_{\mathbf{k}}\equiv\sqrt{\varepsilon_{\mathbf{k}}^{2}+\left(V+ \frac{U}{6}|{\Delta}(T)|^{2}\right)^{2}\left(|{\Delta}\left(T\right)|\eta\left(\mathbf{k}\right)\right)^{2}}, $$
(2)

where ε k denotes the band energy for the square lattice: ε k = − t γ(k), while t is the hopping integral and γ(k) ≡ 2[cos(k x)+ cos(k y)]. The quantity β has the following form: β≡1/k B T, where k B is the Boltzmann constant.

During the numerical calculations, it has been assumed: \({\sum }_{\mathbf {k}}^{\omega _{0}}\simeq {\int }_{-\pi }^{\pi }{\int }_{-\pi }^{\pi }dk_{\mathrm {x}}dk_{\mathrm {y}}\theta \left (\omega _{0}-\left |\varepsilon _{\left (k_{\mathrm {x}},k_{\mathrm {y}}\right )} \right |\right )\), where 𝜃 is the Heaviside function. The normalization constant should be determined with the help of the formula \(N_{0}\equiv 1/{\sum }_{\mathrm {k}}^{\omega _{0}}\); the symbol ω 0 represents the Debye frequency.

The input parameters for (1) are: the hopping integral, the Debye frequency, the V and U potentials. The values of the first two quantities are equal to: t = 350 meV [15–17] and ω 0 = 80 meV [18–22].

The parameters V and U should be calculated on the basis of the experimental dependencies of the critical temperature (T C) and the pseudogap temperature (T ⋆) on the hole concentration (p). The corresponding courses have been presented in Fig. 1. One should remember that the potential V is the unique function of the critical temperature, while the value of U depends on both T C and T ⋆. Of course, the presented approach explicitly assumes that the dependence of the thermodynamic parameters of the superconducting state on p is fully taken into account by the appropriate selection of V and U potentials.

Fig. 1
figure 1

The dependence of T C and T ⋆ on the hole concentration for BSLCO [23]

Full size image

The results obtained for V and U have been collected in Table 1. It is easy to notice that the value of the potential V is small when compared to the value of U. This is mainly due to the fact that the parameter U is divided by 6 and at the same time further multiplied by a relatively small value |Δ(T)|2. Interpreting the quantity \(\overline {U}\equiv {\frac {U}{6}\left |{\Delta }(T)\right |^{2}}\) as the effective pairing potential for the electron-electron-phonon interaction, it can be relatively simply shown that the value of \(\overline {U}\) is comparable to V.

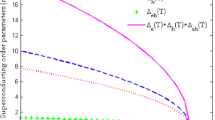
Table 1 The parameters V and U for BSLCO calculated by using the experimental values of T C and T ⋆
Full size table

Figure 2 presents the dependence of the average value of the energy gap amplitude on temperature for the selected values of the hole concentration.

Fig. 2
figure 2

The dependence of the average amplitude of the energy gap on temperature.The red dashed line determines the position of the critical temperature

Full size image

It can be seen that even for the temperature much higher than T C, the function G(T) takes values very weakly dependent on T. A significant decrease in G(T) has been observed only in the vicinity of the pseudogap temperature. At the same time, the averaged amplitude of the energy gap disappears abruptly in T ⋆, which is associated with too large approximations applied during deriving the (1). In particular, these include a failure in taking account of the chemical potential in the present formalism and excluding the strong-coupling and retardation effects, which are normally taken into account, for example in the Eliashberg formalism [24–26].

On the other hand, the impact of the hole concentration on G is significant, with the particularly high values of the energy gap amplitude taken in the underdoped region. It is worth noting that with the increase of the hole concentration, G strongly decreases—yielding the lowest values in the overdoped region.

When analysing the obtained results, it is also easy to notice that the value of the amplitude of the energy gap is very strongly correlated with the value of the pseudogap temperature. Whereas, the energy gap is not simply related to the critical temperature.

The easiest way to quantitatively explore the correlations between the amplitude of the energy gap and the critical temperature or the pseudogap temperature is to determine the values of the dimensionless ratios:

$$ R_{\mathrm{G}}\equiv \frac{G(0)}{k_{\mathrm{B}}T_{\mathrm{C}}}, \qquad \text{and} \qquad R_{\mathrm{G}}^{\star}\equiv \frac{G(0)}{k_{\mathrm{B}}T^{\star}}. $$
(3)

The obtained results have been presented in Fig. 3. In particular, Fig. 3a shows the plot of the dependence of R G on p. In contrast, Fig. 3b presents the form of the function \(R_{\mathrm {G}}^{\star }(p)\).

Fig. 3
figure 3

The influence of the hole concentration on the value of the ratio R G and \(R^{\star }_{\mathrm {G}}\)

Full size image

It has been found that with the increasing p, the parameter R G greatly decreases from the value 32.98 to 7.98. Note that the obtained result is entirely contrary to the predictions of the classical Bardeen-Cooper-Schrieffer (BCS) theory, which assumes the universal relationship between the amplitude of the energy gap and the critical temperature: G(0)=3.53 k B T C [27, 28].

On the other hand, from Fig. 3b, it is clear that the amplitude of the zero-temperature energy gap scales with the pseudogap temperature. However, the proportionality factor is lower than in the BCS theory and is approximately equal to 2.9.

The explicit dependence of the energy gap on the momentum should be calculated using the following [29]:

$$\begin{array}{@{}rcl@{}} \phi_{\mathbf{k}}&=& \left(\frac{1}{N_{0}}{\sum}_{\mathbf{k}_{1}}^{\omega_{0}}\eta\left(\mathbf{k_{1}}\right)\phi_{\mathbf{k}_{1}}\right) \\ &&\times\left[\!v\,+\,u\!\left(\frac{1}{N_{0}}\sum\limits_{\mathbf{k}_{2}}^{\omega_{0}}\eta\left(\mathbf{k_{2}}\right)\phi_{\mathbf{k}_{2}}\right)\!\left(\!\frac{1}{N_{0}}\!\sum\limits_{\mathbf{k}_{3}}^{\omega_{0}}\eta\left(\mathbf{k_{3}}\right)\phi_{\mathbf{k}_{3}}^{\star}\right)\!\right]\\ &&\times \eta(\mathbf{k})\chi_{\mathbf{k}}, \end{array} $$
(4)

where the anomalous thermal average is given by the expression: ϕ k ≡ < c −k ↓ c k ↑ >. The symbol c k σ is the annihilation operator for the electron state of the wave vector k and spin σ. Additionally:

$$ \chi_{\mathbf{k}}\equiv\frac{\text{tg}\left[\frac{i\beta}{2}\sqrt{\varepsilon_{\mathbf{k}}^{2}+M_{\mathbf{k}}^{2}}\right]} {2i\sqrt{\varepsilon_{\mathbf{k}}^{2}+M_{\mathbf{k}}^{2}}}, $$
(5)

and

$$\begin{array}{@{}rcl@{}} M_{\mathbf{k}}^{2}&\equiv& \eta^{2}(\mathbf{k})\left(\frac{1}{N_{0}}\sum\limits_{\mathbf{k}_{1}}^{\omega_{0}}\eta_{\mathbf{k}_{1}}\phi_{\mathbf{k}_{1}}^{\star}\right) \left(\frac{1}{N_{0}}\sum\limits_{\mathbf{k}_{2}}^{\omega_{0}}\eta_{\mathbf{k}_{2}}\phi_{\mathbf{k}_{2}}\right)\\ &&\times\left[v+u\left(\frac{1}{N_{0}}\sum\limits_{\mathbf{k}_{3}}^{\omega_{0}}\eta_{\mathbf{k}_{3}}\phi_{\mathbf{k}_{3}}\right)\! \left(\frac{1}{N_{0}}\sum\limits_{\mathbf{k}_{4}}^{\omega_{0}}\eta_{\mathbf{k}_{4}}\phi_{\mathbf{k}_{4}}^{\star}\right)\!\right]^{2} \end{array} $$
(6)

The star in (6) represents the complex coupling.

The energy gap within the framework of the presented formalism is defined by the following formula: G k ≡ 2η(k)|ϕ k | [v + u|η(k)||ϕ k |2].

The values of the function G k have been calculated in the presented work for the lowest hole concentration (p = 0.127), where the maximum is reached by the pseudogap temperature and for p = 0.162 (the optimal doping), where the highest value is taken by the critical temperature.

For ease of comparison of the theoretical results with the experimental data, the values of the energy gap have been plotted as the function of the angle: α ≡ arctan(k y/k x).

Figure 4 presents the results obtained for the extremely low value of the hole concentration (p = 0.127).

Fig. 4
figure 4

The circles represent the values of the energy gap for the angle α and the selected temperatures. The red line determines the average values of the energy gap. It has been assumed that p = 0.127

Full size image

It can be seen that in the anti-nodal region (α = 0), the values of the energy gap for T = 0 K are included within the range from about 26 to 66 meV. Additionally, it should be emphasized that the mean value of the energy gap is equal to 46 meV, which corresponds well with the results obtained from (1).

Then, the attention has been drawn to the fact that with the increase of temperature, the values of the energy gap in the anti-nodal region virtually do not change. However, the function G(α) in the nodal area clearly decreases with the increasing temperature, which at the temperatures comparable to T ⋆, results in the closure of the energy gap in the surrounding of α = 45 °.

The results for optimal doping have been presented in Fig. 5.

Fig. 5
figure 5

The circles represent the values of the energy gap for the angle α and the selected temperatures. The red line determines the average values of the energy gap. The yellow squares are the experimental values of the energy gap presented in the paper [30]. It has been assumed that p = 0.162

Full size image

In the considered case in the anti-nodal region, the energy gap for T = 0 K takes the values from about 16 to 45 meV. Thus, the average value of G(0) equals to 30.5 meV. It should be noted that the above result agrees fairly well with the predictions based on the (1).

The theoretical results obtained for the optimal doping in this paper have been also compared with the experimental data obtained by using the angle-resolved photoemission spectroscopy (ARPES) method [30]. On the basis of Fig. 5, it is easy to conclude that the presented model correctly reproduces the results of the experiments.

3 Summary

The presented paper determines the values of the energy gap for the Bi2Sr2−x La x CuO6+δ (BSLCO) superconductor. A wide range of the hole concentration has been taken into consideration. The numerical calculations have been conducted in the framework of the theory, which assumes that strong electronic correlations are renormalized by the phonons.

In the first step, it has been shown that the average value of the energy gap amplitude is particularly high in the underdoped region—due to the strong correlation between G(0) and the pseudogap temperature. However, no correlation between G(0) and the value of the critical temperature has been noted, which stands in the sharp contrast with the predictions of the classical BCS theory.

These observations have been quantitatively characterized by estimating the values of the ratios R G and \(R_{\mathrm {G}}^{\star }\). It has been shown that with the increasing hole concentration (p ∈ 〈0.127, 0.198 〉), the value of the parameter R G very significantly decreases from 32.98 to 7.98. On the other hand, \(R_{\mathrm {G}}^{\star }\) poorly responds to the change of the doping: \(R_{\mathrm {G}}^{\star }\sim 2.9\).

The undertaken analysis also allowed us to designate the dependence of the values of the energy gap on the wave vector. It has been found that the energy gap in the anti-nodal region is very weakly dependent on the temperature, even above the critical temperature. From the physical point of view, the obtained result means the existence of the pseudogap in the electronic density of states. It is worth noting that the positive effect of the temperature on the values of the energy gap can be observed in the nodal region, especially for the temperatures comparable to T ⋆.

The numerical results obtained for the optimal doping have been compared with the ARPES experimental data. The conducted analysis has proved that the experimental results can be reproduced with a satisfactory accuracy in the framework of the presented formalism.