A PCA approach to population analysis: with application to a Phase II depression trial

Abstract

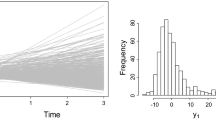
For psychiatric diseases, established mechanistic models are lacking and alternative empirical mathematical structures are usually explored by a trial-and-error procedure. To address this problem, one of the most promising approaches is an automated model-free technique that extracts the model structure directly from the statistical properties of the data. In this paper, a linear-in-parameter modelling approach is developed based on principal component analysis (PCA). The model complexity, i.e. the number of components entering the PCA-based model, is selected by either cross-validation or Mallows’ Cp criterion. This new approach has been validated on both simulated and clinical data taken from a Phase II depression trial. Simulated datasets are generated through three parametric models: Weibull, Inverse Bateman and Weibull-and-Linear. In particular, concerning simulated datasets, it is found that the PCA approach compares very favourably with some of the popular parametric models used for analyzing data collected during psychiatric trials. Furthermore, the proposed method performs well on the experimental data. This approach can be useful whenever a mechanistic modelling procedure cannot be pursued. Moreover, it could support subsequent semi-mechanistic model building.

Appendix

How to obtain the covariance matrix of the unobservable response

The following preposition shows that the SVD of the covariance matrix $\Sigma_{Y}$ provides also the principal vectors of the covariance matrix $\Sigma_{X}$ of the unobservable true response $X_i, i = 1, \ldots, M.$

Proposition

Let U _X  = U _Y and D _X  = D _Y  − σ ² I. Then, the SVD of $\Sigma_X$ is $\Sigma_X = U_X D_X U_X^T$.

Proof

In view of (16),

$$ \begin{aligned} U_X \Sigma_X U_X^T &= U_Y (\Sigma_Y - \sigma^2 {\bf I}) U_Y^T \\ &= D_Y - \sigma^2 U_Y U_Y^T \\ &= D_Y - \sigma^2 {\bf I} = D_X \end{aligned} $$

(27)

□

Hyperparameter estimation

If the variance matrix $\Sigma_{\overline{X}}$ of the fixed effect parameters $\overline{X}$ were finite, the marginal likelihood would be given by

$$ p({\bf Y}|\varvec{\lambda}) = N(0, \varvec{\overline{\Phi}} \Upsigma_{\overline{X}} {\varvec{\overline{\Phi}}}^T + {\varvec{\widetilde{\Phi}}} \Omega {\varvec{\widetilde{\Phi}}}^T + \sigma^2 {\bf I}) $$

(28)

Hence, the ML estimate $\varvec{\lambda}^{ML}$ would be

$$ \varvec{\lambda}^{ML} = \arg \max_{\varvec{\lambda}} p({\bf Y}|\varvec{\lambda}) $$

(29)

In order to obtain the ML estimate of $\varvec{\lambda}$, the fixed effect parameter vector $\overline{X}$ must be integrated out of the joint density $p({\bf Y},\overline{X})$. Indeed,

$$ p({\bf Y}|\varvec{\lambda}) = \int p({\bf Y}|\overline{X}, \varvec{\lambda}) p(\overline{X}|\varvec{\lambda}) d\overline{X} $$

(30)

where $p(\overline{X}|\varvec{\lambda})$ is the prior density for the fixed-effect vector $\overline{X}$.

In the proposed model, an improper prior for $\overline{X}$ is assumed, that is $\Sigma_{ \overline{X}}$ is infinite. Fortunately, the improper, flat nature of $p(\overline{X}|\varvec{\lambda})$ does not hinder the closed-form calculation of a function $G(\varvec{\lambda})$ proportional to the marginal likelihood:

$$ p({\bf Y}|\varvec{\lambda}) \propto G(\varvec{\lambda}) = \int{p({\bf Y} | \overline{X}, \varvec{\lambda})} d\overline{X} $$

(31)

By rearranging the integral (31) as explained in [22], the result is

$$ G(\varvec{\lambda}) = \int{p({\bf Y} | \overline{X}, \varvec{\lambda}) d\overline{X}} = \frac{\sqrt{(2\pi)^r|\widetilde{\Upsigma}|}}{\sqrt{(2\pi)^n |\Upsigma|}}e^{-\frac{1}{2} \gamma^T \gamma} $$

(32)

where $\Sigma = {\varvec{\widetilde{\Phi}}} {\varvec{\Omega}} {\varvec{\widetilde{\Phi}}}^T + \sigma^2 {\bf I}_{Mn}, \overline{\Sigma} = ({\varvec{\overline{\Phi}}}^T \Sigma^{-1} {\varvec{\overline{\Phi}}})^{-1}$ and $\gamma^T \gamma = {\bf Y}^T \Sigma^{-1} {\bf Y} - {\bf Y}^T \Sigma^{-1} \varvec{\overline{\Phi}} \widetilde{\Sigma} \varvec{\overline{\Phi}}^T \Sigma^{-1} {\bf Y}$.

Hence, the ML estimation problem is reformulated as

$$ \varvec{\lambda}^{ML} = \arg \max_{\varvec{\lambda}} G(\varvec{\lambda}) $$

(33)

Estimation of fixed and random effects

Once the hyperparameter vector has been estimated, as specified in the previous subsection, then the fixed and random effects, $\overline{X}$ and $\varvec{\eta}$, are easily estimated applying the standard conditional posterior formula for the model (21):

$$ \begin{aligned} \hat{\varvec{\beta}} =& [\hat{\overline{X}}^T \quad \hat{\varvec{\eta}}^T]^T \\ =& (\varvec{\Phi}^T \varvec{\Phi} + \sigma^2 \Upsigma_{\varvec{\beta}}^{-1})^{-1} \varvec{\Phi}^T {\bf Y} \\ =& (\varvec{\Phi}^T \varvec{\Phi} + \sigma^2 \varvec{\Uplambda})^{-1} \varvec{\Phi}^T {\bf Y} \end{aligned} $$

(34)

$$ \varvec{\Uplambda} = \left( \begin{array}{cc} 0 & 0 \\ 0 & \varvec{\Omega}^{-1} \end{array}\right) $$

$$ Var[\varvec{\beta}|{\bf Y}, \varvec{\lambda}^{ML}] = \sigma^2 (\varvec{\Phi}^T \varvec{\Phi} + \sigma^2 \varvec{\Uplambda})^{-1} $$

(35)

Connection with Restricted Maximum Likelihood approach

In this work, parameters are estimated according to an established approach. As shown by Harville [32] in a frequentist framework, the same point estimates of λ, $\overline{X}$ and η would be obtained by resorting to Restricted Maximum Likelihood estimation.