Generating a smallest binary tree by proper selection of the longest edges to bisect in a unit simplex refinement

Abstract

In several areas like global optimization using branch-and-bound methods for mixture design, the unit n-simplex is refined by longest edge bisection (LEB). This process provides a binary search tree. For $n>2$, simplices appearing during the refinement process can have more than one longest edge (LE). The size of the resulting binary tree depends on the specific sequence of bisected longest edges. The questions are how to calculate the size of one of the smallest binary trees generated by LEB and how to find the corresponding sequence of LEs to bisect, which can be represented by a set of LE indices. Algorithms answering these questions are presented here. We focus on sets of LE indices that are repeated at a level of the binary tree. A set of LEs was presented in Aparicio et al. (Informatica 26(1):17–32, 2015), for $n=3$. An additional question is whether this set is the best one under the so-called $m_k$-valid condition.

1 Introduction

Global Optimization deals with finding the minimum or maximum value of an objective function f on a closed set with a non-empty interior. We focus here on the standard n-simplex defined in the ($n+1$)-dimensional space

$$\begin{aligned} S=\left\{ x \in {\mathbb {R}}^{n+1} \mid \sum _{j=1}^{n+1} x_j = 1; \ x_j \ge 0 \right\} . \end{aligned}$$

(1)

We study the binary tree (BT) implicitly generated by the refinement of the n-simplex where the simplex division is defined by the Longest Edge Bisection rule (LEB) (Adler 1983; Hendrix et al. 2012; Horst 1997). We investigate how the choice of the next longest edge (LE) to be bisected affects the total number of generated simplices in the BT. One of the questions is how to determine the sequence of LEs to be bisected which generates the smallest number of simplices in the complete BT. Several heuristics have been presented (Aparicio et al. 2014) and have been applied to Global Optimization algorithms in Herrera et al. (2014). Determination of the set of indices of bisected LEs (one per simplex) to generate one of the smallest BT requires a complete enumeration of all possible LEB combinations.

Calculation of distances between vertices to determine the longest edges is a computationally intensive operation in the partition process. This computation can be avoided by precomputing a set of LE indices to be bisected. Each LE is stored as a pair of vertex indices for a simplex in the BT. It is desirable to find sets with an appropriate repetition of LE indices, because their computational management is more efficient than distance calculation. We look for sets of LEs with a high repetition of longest edge indices per level of any of the smallest BTs.

A set of LE indices generating the minimum number of classes of simplices (Aparicio et al. 2013), was presented in Aparicio et al. (2015). Another research question in this study is whether that set also provides one of the smallest trees, given a value of the stopping criterion on the size of the subsimplices. Additionally, we investigate whether such set is the best under the $m_k$-valid condition presented in Sect. 4.

The paper is organized as follows. Section 2 introduces the simplex refinement by LEB. An algorithm to determine the smallest possible size of the binary tree is studied in Sect. 3. Section 4 introduces the concept of $m_k$-validity. Section 5 shows an algorithm to generate a tree containing all possible smallest binary trees. Section 7 develops an algorithm to search $m_k$-valid sequences in the output of the algorithm of Section 5. Section 8 shows the results of the developed algorithms applied to a 3-simplex. Finally, conclusions and future research are discussed in Sect. 9.

2 Simplex refinement using longest edge bisection

We consider a regular n-simplex called $S_1$ scaled to have edge length 1, where the Euclidean distance norm is used. $S_1$ is considered the set to be refined, i.e.

$$\begin{aligned} S_1 = \left\{ x \in {\mathbb {R}}^{n+1} \ \ \sum _{j=1}^{n+1} x_j = \frac{\sqrt{2}}{2}; \ x_j \ge 0 \right\} . \end{aligned}$$

(2)

An n-simplex S is defined by the convex hull $S=conv(V)$ of its vertex set $V=\{v_1,\ldots ,\ v_{n+1}\},\ v_j \in {\mathbb {R}}^{n+1}$. Let $\omega (S)$ denote the size (width) of a simplex S given by the length of its longest edge. Having a set of indices for the vertices of a simplex, we can also derive the idea of identifying the set of edges of a simplex as pairs of vertex indices $E_h=\{j,k\} : j=2,\ \ldots ,\ n+1;\ k=1,\ \ldots ,\ j-1;\ j\ne k$. The edge index is given by $h=\frac{(j-1)(j-2)}{2}+ k$, $h=1, \ldots ,n(n+1)/2$. Figure 1 shows a 2-simplex of size 1.

Fig. 1

A regular 2-simplex with edge length 1

Longest edge bisection (LEB) is a popular way of iteratively refining a simplex in the context of the finite element method, since it is very simple and can easily be applied in higher dimensions (Hannukainen et al. 2014). It is based on splitting a simplex using the hyperplane that connects the mid point of the longest edge of a simplex with the opposite vertices, as illustrated in Fig. 2.

Fig. 2

Example of the first Longest Edge Bisection (LEB) on a regular 3-simplex

Algorithm 1 shows the Simplex Refinement (SR) process which bisects the initial simplex iteratively. In principle, the refinement can continue infinitely. We study the process with a stopping criterion, i.e., the branching process continues until the size of the simplex is smaller than or equal to the desired accuracy $\epsilon$. The set $\Lambda$ contains the leaves of the tree, i.e., the simplices that have not been refined yet. Figure 3 illustrates the result of the SR algorithm on a 2-simplex with termination criterion $\omega (S)\le \epsilon =0.5$. The number of levels in the BT is 4 and the number of generated simplices from $S_1$ is 10.

Fig. 3

Binary tree generated by the SR algorithm on a 2-simplex with $\epsilon =0.5$

Bisecting a 2-simplex does not require any selection among the longest edges in SelectLE(), as the longest edge is either unique or the choice does not alter the size of the resulting BT. We follow a rule described in Mitchell (1989), where one can avoid edge length calculations in a 2-simplex by always bisecting the edge with vertices $\{1,2\}$ and numbering the new vertex as the last one of the set of vertices in the generated new sub-simplices. The bisection in Algorithm 2 follows a similar numbering for the new vertex in the general case ($n>2$).

Figure 2 shows the bisection of a regular 3-simplex. It does not matter which edge is selected first, because all generated sub-simplices differ only in orientation. Notice that after the first subdivision, the generated sub-simplices are irregular and have three (out of six) edges with the longest length. Therefore, we need to make a decision on which longest edge should be bisected.

The number of simplices in the finite BT generated by Algorithm 1 depends on how fast the simplex size decreases when we go deeper into the tree. We are interested in the combinatorial optimization problem of choosing vertices j, k in SelectLE() to obtain one of the smallest size binary trees.

3 An algorithm to determine the size of a smallest tree

This section describes an algorithm for determining the size of the smallest binary tree generated using Longest Edge Bisection as the rule for subdividing simplices. We apply a full enumeration of simplices to check every division option, i.e. one for each longest edge, and count the number of sub-simplices in each sub-tree generated from that option. Algorithm 3 performs this task recursively. The algorithm only considers the size of the smallest sub-trees. It has the initial simplex and the required precision as input parameters and returns the number of simplices of the smallest trees.

Algorithm 3 determines the size of the smallest sub-tree from a sub-simplex when it is bisected by one of its longest edges $E_h$, with vertices $\{j,k\}$ (see line 4). It recursively calls itself to get the smallest sub-tree size for the two generated sub-simplices (see lines 5, 6). When the recursive algorithm is back at the initial simplex, the size of the smallest trees is known and the algorithm ends. The algorithm does not provide information about which longest edges have been bisected to generate one of the smallest trees.

Figure 3 illustrates running Algorithm 3 on a 2-simplex for $\epsilon =0.5$. The BT has 10 sub-simplices. Although the 2-simplex is not a very interesting case because irregular simplices have just one longest edge, the illustration facilitates discussing several details not included in Algorithm 3 for the sake of simplicity:

Remark 1

In Algorithm 3, if $S_l$ and $S_r$ are symmetric, only one of them is processed and the algorithm returns twice the size of the evaluated sub-tree. In the example of Fig. 3, siblings $S_2$ and $S_3$ and also $S_{10}$, $S_{11}$ and $S_{12},S_{13}$ are symmetric.

Remark 2

Algorithm 3 only has to process one of the longest edges for a regular simplex, because any edge division will return the same sub-tree size. Simplices $S_1$, $S_4$ and $S_7$ are regular in Fig. 3.

Remark 3

For an irregular simplex with several longest edges, it is of interest to determine those edges producing similar pairs of siblings. Therefore, Algorithm 3 only has to process one of the pairs. This will be studied in a future work.

4 The $m_k$-valid condition

For $n>2$, many different Smallest Binary Trees (SBTs) can be generated by iteratively applying LEB. Given a SBT, a vector or sequence of longest edges, SQ-LE, can be determined beforehand in order to be used in Algorithm 1. The element SQ-LE$_i$ specifies one of the longest edges of $S_i$. The number of elements of the SQ-LE vector is the same as the number of (non-leaf) nodes of the corresponding SBT. This number increases as the dimension n increases and the value of $\epsilon$ decreases. So, it can be very large.

Given the numbering of simplices in Algorithm 1, the level where the simplex $S_i$ is located in a BT is determined by $\ell =\lceil 1+\log _2 i \rceil$. We focus on the idea that the longest edge index to be bisected is the same in various simplices at the same level of the tree. We derive several conditions that the set of longest edge indices must fulfil.

Definition 1

Two simplices have a longest edge index h in common when the edge $E_h = \{j,k\}=\{k,j\}$ is a longest edge in both simplices. The longest edges in both simplices sharing an index may be the same or different.

Definition 2

Let $m\in {\mathbb {N}}^+$. Simplex i at level $\ell$ is in subset $M_j$, $j=0,\ \ldots ,\ m-1$, if $j=i\!\!\mod m$.

Definition 3

Subset $M_j$ at level $\ell$ (see Definition 2) is called valid if there exists an edge index h such that $E_h$ is a longest edge for all simplices in $M_j$.

Notice that $M_j$ can be valid due to several LE indices.

Definition 4

Level $\ell$ in a BT is called m-valid if all subsets $M_j,\ j=0,\ldots ,m-1$ at level $\ell$ are valid (see Definition 3).

Notice that an edge index h validating subset $M_j$ can be different from edge index g validating subset $M_k,\ j\ne k$.

Remark 4

An m-valid level may have less than m simplices.

Definition 5

A binary tree with $L+1$ levels is m-valid when all its first L levels are m-valid (see Definition 4).

Notice that the set of LE indices validating a level of the BT can be different to the set of LE indices validating another level of the BT.

Definition 6

Given a m-valid SBT with $L+1$ levels, let $L\times m$ matrix A be defined by elements $a_{\ell ,j}$ that denote an index h of a LE validating subset $M_j$ at level $\ell$.

Notice that not all elements of matrix A may have a number due to the absence of the corresponding nodes in the binary tree.

Property 1

A BT generated by LEB, with $L+1$ levels and maximum $2^{L-1}$ elements at level L, is always m-valid for $m=2^{L-1}$.

Property 2

Given $k\in {\mathbb {N}}$, a $2^k$-valid binary tree is also $2^{k+1}$-valid.

Property 2 and the number of nodes ($2^{\ell -1}$) at level $\ell$ of a BT suggest to use $m=2^k$.

An SQ-LE vector has less memory requirements than a matrix A$_{(L\times m)}$ with $m=2^{L-1}$. Therefore, we are interested in values of $k < L-1$.

Definition 7

A binary tree is $m_k$-valid if it is m-valid (see Definition 5) with $m=2^k$, $k\in {\mathbb {N}},\ k<L-1$.

For instance in Table 1, levels 1 to 3 are 1-valid and level 4 is 2-valid.

Table 1 3-simplex instance. Indices of longest edges bisected for each simplex in each level of the BT with the minimum number of classes of simplices (see Algorithm 1) (Aparicio et al. 2015)

Definition 8

A binary tree which is not $m_k$-valid is called $m_k$-invalid.

Property 3

Any binary tree generated from an $m_k$-invalid binary tree by increasing its number of levels, is $m_k$-invalid.

The existence of an $m_k$-valid SBT depends on the combinations of longest edge indices making a level of the SBT $m_k$-valid, which also depends on the selected combinations at previous levels.

In the worst case, the number of combinations of longest edge indices causing a level to be $m_k$-valid level is given by the sum of possible combinations making the level 1-valid, 2-valid, $\ldots ,$ and $2^k$-valid:

$$\begin{aligned} \sum _{i=0}^{k} \left( \begin{array}{c} ne\\ 2^k \end{array} \right) \end{aligned}$$

(3)

with $ne=\frac{n(n+1)}{2}$ the number of edges of an n-simplex.

To find all $m_k$-valid SBTs, we need an algorithm generating all possible SBTs and an algorithm to discard those trees that are $m_k$-invalid. The following sections describe these algorithms.

5 ASBT algorithm (all smallest binary trees)

The ASBT algorithm stores all SBTs in a single general tree (GT). In this way, only longest edges providing SBTs will remain in the GT. Each node N of the GT contains the following information:

• $S=conv(V)$: The current simplex.

• The set of longest edges of S, with the following information for each longest edge $E_h=\{j,k\}$:

  • $R_h$: the total size of the two generated sub-trees.

  • $N_{lh}$: left node.

  • $N_{rh}$: right node.

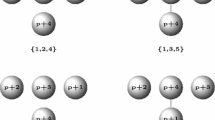
A pseudocode of Algorithm ASBT is given in Algorithm 4. It is an extension of the recursive algorithm presented in Sect. 3, where only those LE options generating a SBT are stored in the GT. The input parameters are the initial regular simplex $S_1$ and the desired precision $\epsilon$. Figure 4 shows the first levels of the GT for a 3-simplex.

Fig. 4

General Tree for a 3-simplex. Only one edge of $S_1$ is evaluated because it is regular. $S_2$ is generated but not evaluated because $S_2$ is symmetric with respect to $S_3$. The same happens with one of the instances of $S_6$ and $S_7$

The results of Algorithm 4 are the SBT size generated by LEB and the root node of the GT, i.e., N containing $S_1$. Following the simplex enumeration of Algorithm 1, where a LEB of simplex $S_i$ generates sub-simplices $S_{2i}$ and $S_{2i+1}$, there exist many instances of $S_i$ in the GT. Each instance depends on the longest edges bisected at higher levels in the GT tree. In Algorithm 4, line 12, those longest edges, and sub-trees generated from them, that do not result in a SBT are removed from the GT.

6 NSBT-GT algorithm (number of SBTs in GT)

Algorithm 5 counts the number of SBTs in the GT. It does not count all possible SBTs because symmetries are avoided (see Fig. 4). It is a recursive algorithm counting the binary trees from leafs to root node. The number of SBTs in each node of the GT depends on the number of binary trees in each of the descendants, $N_{lh}$ and $N_{lh}$ of the current simplex split over longest edge $E_h$ and the combination of them. For example, if we have a node with two children, one generating two binary trees (it has at least two LE) and the other generating three binary trees (it has at least three LE), the number of binary trees generated from the current node is six by combination of them. The NSBT-GT algorithm starts with the root node of the GT, as result of Algorithm 4.

Table 3 in Sect. 8 shows the number of SBTs in the GT for different values of $\epsilon$.

7 M$_K$-SBT algorithm ($m_k$-valid smallest binary trees)

Algorithm 6 finds the $m_k$-valid SBTs in the GT. The algorithm generates partial matrices during the search, according to Definition 6. Each partial matrix A$_{\ell \times m}$ determines a different smallest binary sub-tree (SBST), indicating how to divide its simplices up to level $\ell$. A$_{(\ell +1)\times m}$ matrices are generated from a A$_{\ell \times m}$ (see Eq. (3) for the worst case number of combinations) by visiting nodes at level $\ell$+1 in the GT, following the bisection of the longest edges previously determined by partial matrix A$_{\ell \times m}$. A partial matrix A$_{\ell \times m}$ which is not able to generate a $m_k$-valid SBST at level $\ell +1$ is discarded from the search. The search continues until there is no matrix generating a $m_k$-valid SBST at the next level, or there is no next level to visit.

Algorithm 6 follows the general structure of a B&B algorithm, iterating over partial matrices stored in $\Lambda$. The first partial matrix A$_{\ell \times m}$ stores the index of the first longest edge, but it can be any of the edges of the initial regular simplex. In line 10, new $m_k$-valid partial matrices at $\ell +1$ level are produced from the selected A$_{\ell \times m}$ partial matrix (see Definition 7). For instance, for a 3-simplex and $k=0$, Algorithm 6 generates in line 10 partial matrices ${1\atopwithdelims ()1}$, ${1\atopwithdelims ()2}$, and ${1\atopwithdelims ()4}$ from the initial partial matrix A$_{1\times 1}$=(1) (see Fig. 4). Those partial matrices that are not rejected and can not progress on GT are stored in $\Omega$ (see line 8).

8 Results for a 3-simplex

Algorithms have been coded in C/C++ and they have been executed in a BullX-UAL node, under Ubuntu 12.04.3 LTS. A node consists of two processors Intel^® Xeon^® E5-2650 with 8 cores at 2,00 GHz and 64GB of RAM.

Table 1 shows the indices $\{i,j\}$ of the longest edges bisected at every level of the binary tree for a 3-simplex. This set of indices generates binary trees with the minimum number of eight classes of simplices (Aparicio et al. 2015). Two simplices belong to the same class if one can be obtained by scaling, translation and rotation/flip of the other, see Aparicio et al. (2015). The set in Table 1 can be used in Algorithm 1, line 6, to generate such trees. For different $\epsilon$ values the algorithm obtains different trees.

A matrix generating the smallest number of simplex classes for a 3-simplex, denoted by A-3SNC, can be derived from Table 1. The set of LEs in A-3SNC is 2-valid. Levels 1-3,5 and 6 are 1-valid and levels 4 and 7 are 2-valid. A-3SNC can be applied to generate a BT with more than 7 levels because levels 8-10 use the same longest edge indices as at levels 5-7, and those repeat for all further levels.

Column MinTree in Table 2 shows the guaranteed smallest size of binary trees for a regular 3-simplex (see Eq. (2)) obtained by Algorithm 3 and several values of $\epsilon$. Column A-3SNC_in_SR() shows the size of the binary tree generated by the SR Algorithm (Algorithm 1) when the longest edge indices in Table 1 are used for the same instances of the problem. Comparing both columns in Table 2, the SR Algorithm generates smallest binary trees for $\epsilon =1/2^j$, using A-3SNC. The use of A-3SNC also returns the best result for other values of $\epsilon$, but there exist values of $\epsilon$ that do not provide a SBT. Table 2 shows some of them in boldface. The reason of such suboptimal results is that longest edges with a size different than $1/2^j$ appear in the refinement process. In Fig. 3, $S_5$ and $S_6$ are examples for the 2-simplex case.

Table 2 Size of a smallest binary tree (MinTree()) and the size of the binary tree generated by SR() with the A-3SNC matrix for a 3-simplex varying the accuracy $\epsilon$

Table 3 shows the size |GT| of the general tree, the number of smallest binary trees in GT counted by Algorithm 5 (SBTs), the number of partial matrices (npm) and the number of final matrices (nfm) evaluated by Algorithm 6, for the same instances of the problem shown in Table 2. The input value k is set to 2 (see Definition 7). The size of the GT tree is much smaller than the size of one of the corresponding SBTs because only one of the symmetric simplices is processed (see Remark 1, Fig. 4). Nevertheless, results for values smaller than $\epsilon < 1/2^6$ could not be calculated due to the high computational requirements of the algorithms.

Table 3 Results of Algorithms 4, 5 and 6 for a 3-simplex and $k=2$

Algorithm 6 returns only one possible 4-valid matrix for the check marked instances in Table 3 equal to A-3SNC. Those instances without a check mark do not present a 4-valid matrix. A-3SNC matrix is actually 2-valid but it is also $2^k$-valid for a 3-simplex and $k\ge 1$ (see Property 2).

The smallest possible matrix is 1-valid with the same longest edge index for every level. As A-3SNC is the only 2-valid set, such a matrix does not exist with the reordering of vertices in Algorithm 2. Therefore, A-3SNC is the $m_k$-valid matrix with the smallest k value.

The use of A-3SNC needs the same method of reindexing of vertices at each simplex, according to Algorithm 2. The computational cost of this reindexing is much lower than the calculation of distances between vertices. The computation cost difference increases with n.

The analogous problem to the one tackled here is to find the smallest number of reindexes of vertices at simplices such that the same longest edge index is bisected for any simplex in a SBT. This approach seems to be as difficult as the one tackled here. In the worst case, it is necessary to provide a reindexing for each simplex. Nevertheless, it could be an interesting approach to address in a future work.

The investigation and application of the algorithms for the 4-simplex requires the use of parallel computing due to the memory and computational requirements to generate a 4-valid matrix for a small accuracy $\epsilon$ to allow every initial edge be bisected several times.

9 Conclusions and future research

This work studies how to obtain matrices showing the indices of the longest edges to bisect a regular n-simplex generating a smallest binary tree in its iterative refinement. We focus on matrices with high occurrence of the longest edge indices to divide per level of the binary tree. We conclude that the sequence presented in Aparicio et al. (2015) is the unique 2-valid and 4-valid (see Definition 7 and Property 2) for some termination criteria. The combinatorial complexity of the problem allows us to show results only for $n=3$ and $\epsilon$ $\ge$ $1/2^6$. Higher n and smaller $\epsilon$ values will require the improvement of the sequential algorithms and to develop parallel versions of them.