1 Introduction

The study of Bianchi type-IX cosmological models are interesting because these models allow not only expansion but also rotation and shear and in general are anisotropic. Many of the authors have been taken keen interest in studying Bianchi type-IX universes because we have a familiar solution like Robertson-Walker universe with positive curvature, the de-sitter universe, the Taub-NUT solution etc. Raj Bali et al. [1] have obtained Bianchi type-IX cosmological model with viscous fluid in general relativity. The phenomena of expanding universe, primordial nucleo-synthesis, the observed isotropy of the cosmic background radiations were supposed to be successfully explained by big-bang cosmology based on Einstein field equation. However, the big-bang model is known to have the short coming in the following aspects:

  1. i)

    The model has singularity in the past and possible one in future,

  2. ii)

    The conservation of energy is violated,

  3. iii)

    It leads to a very small particle horizon,

  4. iv)

    No consistent scenario exists that explained the origin, evolution and characteristic of structures in the universe at small scale,

  5. v)

    It has flatness problems.

Therefore, to overcome the singularities of big-bang cosmology, the alternative theories were proposed from time to time; the best well known theory was steady state theory of Bondi and Gold [2]. In this theory, the steady state model does not have any singular beginning or an end on the cosmic time scale and the statistical properties of the large scale features of the universe do not change. Further, the constancy of the mass density has been accounted by continuous creation of matter going on in contrast to the one time infinite and explosive creation of matter at t = 0 as in the earlier standard model, the principle of conservation of matter was violated in this formalism. To overcome this difficulty, Hoyle and Narlikar [3] adopted a field theoretical approach by introducing a massless and charge less scalar field C in the Einstein-Hilbert action to account for matter creation. According to Hoyle and Narlikar [3], in the C-field theory there is no big-bang type of singularity as in the steady state theory of Bondi and Gold [2, 16]. Narlikar et al. [4] pointed out that the matter creation is accomplished at the expense of negative energy C-field. A solution of Einstein field equation admitting radiation with negative energy massless scalar creation matter was obtained by Narlikar and Padmanabhan [5]. This solution is free from singularity and provides a natural explanation to the particle horizon and flatness problem. The study of Hoyle and Narlikar theory for the higher dimensional space-time of was carried out by Chaterjee and Banerjee [6]. Bali and Tikekar [7], Bali et al. [8, 13–15] have investigatedC-field cosmological models for dust distribution with variable gravitational constant in FRW space-time. The solution of Einstein’s field equation in the presence of creation field has been obtained for Bianchi type space-time by Singh and Chaubey [9]. Recently, Adhav et al. [10, 11] has been studied LRS Bianchi type-I, V universe in C-field cosmology. Bali and Saraf [1] have also examined Bianchi type-I dust universe with decaying vacuum energy in C-field.

In the present paper, we have considered a Bianchi type-IX space-time for ideal fluid dust distribution in Hoyle and Narlikar C-field cosmology. We have assumed that the creation field is a function of time t only i.e. C(x, t) = C(t) and investigate Bianchi type-IX dust filled universe and also study the physical and geometrical parameters of the model in detailed.

2 The Metric and Field Equation

We have consider Bianchi type-IX metric,

$$ ds^{2}=-dt^{2}+a^{2}dx^{2}+b^{2}dy^{2}+\left({b^{2}\sin^{2} y+a^{2}\cos^{2}y} \right)dz^{2}-2a^{2}\cos y\,dxdz, $$
(1)

in which, a and b are the function of t alone.

Hoyle and Narlikar [4, 12] modifies the Einstein’s field equation by introducing C-field as,

$$ {R_{i}^{j}} -\frac{1}{2}R{g_{i}^{j}} =-8\pi G\left[ {T_{i\left(m \right)}^{j} +T_{i\left(c \right)}^{j} } \right]. $$
(2)

The energy momentum tensor \(T_{i\left (m \right )}^{j} \) for ideal fluid and \(T_{i\left (c \right )}^{j} \) for creation field is,

$$ T_{i\left(m \right)}^{j} =\left({p+\rho } \right)u_{i} u^{j}+p{g_{i}^{j}} , $$
(3)
$$ T_{i\left(c \right)}^{j} =-f\left({C_{i} C^{j}-\frac{1}{2}{g_{i}^{j}} C^{a}C_{a} } \right), $$
(4)

where, f >0 is a coupling constant between matter and creation field and \(C_{i} =\frac {dC}{dx^{i}}\).

The field (2) and the energy momentum tensors (3), (4) for the metric (1) lead to,

$$ 2\frac{\dot{a} \dot{b} }{ab}+\frac{{\dot{b}^{2}} }{b^{2}}+\frac{1}{b^{2}}-\frac{1}{4}\frac{a^{2}}{b^{4}}=8\pi G\left({\rho -\frac{1}{2}f\dot{C}^{2}} \right), $$
(5)
$$ 2\frac{{\ddot{b}}}{b}+\frac{{\dot{b}^{2}} }{b^{2}}+\frac{1}{b^{2}}-\frac{3}{4}\frac{a^{2}}{b^{4}}=8\pi G\left({-p+\frac{1}{2}f\dot{C}^{2}} \right), $$
(6)
$$ \frac{\ddot{a}}{a}+\frac{\ddot{b}}{b}+\frac{\dot{a} \dot{b}}{ab}+\frac{1}{4}\frac{a^{2}}{b^{4}}=8\pi G\left({-p+\frac{1}{2}f\dot{C}^{2}} \right). $$
(7)

3 Solution of Field Equation

According to Hoyle and Narlikar [3], we have taken zero pressure matter field. From Bianchi identity, we have

$$ \left({G{T_{i}^{j}} } \right);j=0 $$
(8)

Further solving (8) we obtain,

$$ \left({\dot{G} \rho +\dot{\rho} G-\frac{1}{2}f\dot{G} \dot{C}^{2}} \right)+G\rho \left({\frac{\dot{a} }{a}+2\frac{\dot{b}}{b}} \right)=Gf\dot{C} \left\{ {\ddot{C} +\dot{C} \left({\frac{\dot{a}}{a}+2\frac{\dot{b}}{b}} \right)} \right\}, $$
(9)

which yields \(\dot {C} =1\), using source equation, \(C_{;i}^{i} =\frac {n}{f}\).

For zero pressure matter i.e. \(p=0,\,\dot {C} =1\), the field (5), (6) and (7) leads to,

$$ 2\frac{\dot{a} \dot{b} }{ab}+\frac{\dot{b}^{2}}{b^{2}}+\frac{1}{b^{2}}-\frac{1}{4}\frac{a^{2}}{b^{4}}=8\pi G\rho -4\pi Gf, $$
(10)
$$ 2\frac{\ddot{b}}{b}+\frac{\dot{b}^{2}}{b^{2}}+\frac{1}{b^{2}}-\frac{3}{4}\frac{a^{2}}{b^{4}}=4\pi Gf, $$
(11)
$$ \frac{\ddot{a}}{b}+\frac{\ddot{b}}{b}+\frac{\dot{a} \dot{b}}{ab}+\frac{1}{4}\frac{a^{2}}{b^{4}}=4\pi Gf. $$
(12)

From (11) and (12) we have,

$$ \frac{\ddot{a}}{a}-\frac{\ddot{b}}{b}+\frac{\dot{a} \dot{b}}{ab}-\frac{\dot{b}^{2}}{b^{2}}-\frac{1}{b^{2}}+\frac{a^{2}}{b^{4}}=0. $$
(13)

From (10) and (12) we obtain,

$$ \frac{\ddot{a}}{a}+\frac{\ddot{b}}{b}+3\frac{\dot{a} \dot{b}}{ab}+\frac{\dot{b}^{2}}{b^{2}}+\frac{1}{b^{2}}=8\pi G\rho $$
(14)

To get the deterministic solution of the (12), (13) and (14), we assume a condition between metric potentials a and b as,

$$ a=b^{n} $$
(15)

Using condition (15) in (13) we obtain,

$$ 2\ddot{b} +2\left({n+1} \right)\frac{\dot{b}^{2}}{b^{2}}=\frac{2}{b\left({n-1} \right)}-\frac{2b^{2n-3}}{n-1} $$
(16)

We assume that,

$$ \dot{b} =f\left(b \right) $$
(17)
$$ \dot{b} =ff^{I} $$
(18)

in which \(f^{I}=\frac {df}{db}\)

Therefore, (16), (17) and (18) yields,

$$ \frac{df^{2}}{db}+2\left({n+1} \right)\frac{f^{2}}{b}=\frac{2}{b\left({n-1} \right)}-\frac{2b^{2n-3}}{n-1} $$
(19)

(19) implies that,

$$ f^{2}=\frac{1}{n^{2}-1}-\frac{b^{2\left({n-1} \right)}}{2n\left({n-1} \right)}+Db^{-2\left({n+1} \right)}, $$
(20)

where D is integration constant.

From (17) and (18), we obtain,

$$ \dot{b} =\left\{ {\frac{1}{n^{2}-1}-\frac{b^{2\left({n-1} \right)}}{2n\left({n-1} \right)}+Db^{-2\left({n+1} \right)}} \right\}^{\frac{1}{2}},\quad \quad \left({n\ne 1} \right) $$
(21)

(21) leads to,

$$ \int {\left\{ {\frac{1}{n^{2}-1}-\frac{b^{2\left({n-1} \right)}}{2n\left({n-1} \right)}+Db^{-2\left({n+1} \right)}} \right\}^{-\frac{1}{2}}db=\pm \left({t-t_{0} } \right),} $$
(22)

where t 0 is constant of integration.

Using condition (15) in (14), yields,

$$ \frac{n+1}{n-1}\frac{1}{b^{2}}-\frac{n+1}{n-1}b^{2\left({n-2} \right)}+\frac{1}{b^{2}}=8\pi G\rho $$
(23)

The space-time (1) reduce the form

$$ \begin{array}{l} ds^{2}=-\left\{ {\frac{1}{n^{2}-1}-\frac{T^{2\left({n-1} \right)}}{2n\left({n-1} \right)}+DT^{-2\left({n+1} \right)}} \right\}^{-1}dT^{2}+T^{2n}dX^{2}+T^{2}dY^{2}+ \\ \quad \quad \quad \quad \quad \left({T^{2}\sin^{2}Y+T^{2n}\cos^{2}Y} \right)dZ^{2}-2T^{2n}\cos Y\,dXdZ \\ \end{array} $$
(24)

in which, b = T, x = X, y = Y, z = Z.

4 Physical and Geometrical Features

The energy density of matter is obtained as,

$$ \rho =\frac{1}{8\pi G}\left\{ {\frac{n+1}{n-1}\frac{1}{T^{2}}-\frac{n+1}{n-1}T^{2\left({n-2} \right)}+\frac{1}{T^{2}}} \right\} $$
(25)

and the spatial volume is given by,

$$ V=\sqrt {-g} =ab^{2}\sin y=T^{2(n+1)}\sin Y $$
(26)

For the flow vector u i, the scalar of expansion (𝜃) obtained as,

$$ \theta =\left( {n+2} \right)\left\{ {\frac{1}{T^{2}\left( {n^{2}-1} \right)}-\frac{T^{2\left( {n-2} \right)}}{2n\left( {n-1} \right)}+DT^{-2\left( {n+2} \right)}} \right\}^{\frac{1}{2}} $$
(27)

The non-vanishing component of shear σ i j are obtained as,

$$ \sigma_{11} =-\frac{1}{3}\left( {n+2} \right)T^{2n}\left\{ {\frac{1}{T^{2}\left( {n^{2}-1} \right)}-\frac{T^{2\left( {n-2} \right)}}{2n\left( {n-1} \right)}+DT^{-2\left( {n+2} \right)}} \right\}^{\frac{1}{2}} $$
(28)
$$ \sigma_{22} =-\frac{1}{3}\left( {n+2} \right)T^{2}\left\{ {\frac{1}{T^{2}\left( {n^{2}-1} \right)}-\frac{T^{2\left( {n-2} \right)}}{2n\left( {n-1} \right)}+DT^{-2\left( {n+2} \right)}} \right\}^{\frac{1}{2}} $$
(29)
$$\begin{array}{@{}rcl@{}} \sigma_{33} =-\frac{1}{3}\left({n+2} \right)\left({T^{2} \sin^{2}Y+T^{2n}\cos^{2}Y} \right)\left\{ {\frac{1}{T^{2}\left({n^{2}-1} \right)}-\frac{T^{2\left({n-2}\right)}}{2n\left({n-1} \right)}+DT^{-2\left({n+2} \right)}} \right\}^{\frac{1}{2}} \end{array} $$
(30)
$$ \sigma_{44} =\frac{2}{3}\left({n+2} \right)\left\{ {\frac{1}{T^{2}\left({n^{2}-1} \right)}-\frac{T^{2\left({n-2} \right)}}{2n\left({n-1} \right)}+DT^{-2\left({n+2} \right)}} \right\}^{\frac{1}{2}} $$
(31)
$$ \sigma_{13} =\frac{2}{3}\left({n+2} \right)T^{2n}\cos Y\left\{ {\frac{1}{T^{2}\left({n^{2}-1} \right)}-\frac{T^{2\left({n-2} \right)}}{2n\left({n-1} \right)}+DT^{-2\left({n+2} \right)}} \right\}^{\frac{1}{2}} $$
(32)

Hence,

$$ \sigma^{2}=\frac{1}{2}\left({n+2} \right)^{2}\left\{ {\frac{1}{T^{2}\left({n^{2}-1} \right)}-\frac{T^{2\left({n-2} \right)}}{2n\left({n-1} \right)}+DT^{-2\left({n+2} \right)}} \right\} $$
(33)

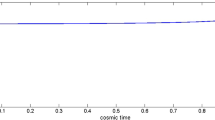
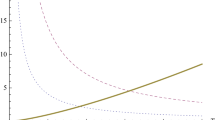
From (25) and (33), it is observed that initially when T→0then ρ→∞,σ→∞and V=0.Also for large values of T,ρ,σ and Vare infinite .It implies that the inverse expanding.

5 Conclusion

From (27), it is clear that the scalar expansion (𝜃) decreases as time increases and its stop at T = ∞ and n = −2. Also, we have observed that the ratio \(\lim _{T\to \infty } \left ({\frac {\sigma }{\theta }} \right )^{2}=\frac {1}{2}\ne 0\), it implies that the model does not approach isotropy for large value of T. However, for n = −2 the cosmological model (24) is not isotropized. The expansion in the model starts with big-bang at T = 0 and n = 1, for n=0, 1 the expansion in the model start with big-bang. Also for n=-2 scalar expansion (𝜃) decreases as time increases and vice-versa. The model (24) is expanding, the expansion in the model starts with big-bang T = 0 and n=1.The spatial volume increases with time. The creation field increases with time which supports the result obtained by Hoyle and Narlikar [4, 16].