Scalar–tensor theories with an external scalar

Abstract

Scalar–tensor (ST) gravity is considered in the case where the scalar is an external field. We show that general relativity (GR) and usual ST gravity are particular cases of the external scalar–tensor (EST) gravity. It is shown with a particular cosmological example that it is possible to join a part of a GR solution to a part of a ST one such that the complete solution neither belongs to GR nor to ST, but fully satisfies the EST field equations. We argue that external fields may effectively work as a type of screening mechanism for ST theories.

Appendices

Appendix 1: From diffeomorphism invariance to the stress tensor conservation

Consider the diffeomorphism

$$\begin{aligned} x^{\prime a}=x^{a}+\xi ^{a}\left( x^{c}\right) . \end{aligned}$$

(31)

If the metric’s components are considered as functions of the coordinates (rather than as functions of the point), the difference $\delta g_{ab}\equiv g_{ab}^{\prime }\left( x\right) -g_{ab}\left( x\right)$ (that is not the components’ variation at a given point) induced by (31) reads, at first order in $\xi$ [32]

$$\begin{aligned} \delta g_{ab}=-g_{ac}\partial _{b}\xi ^{c}-g_{bc}\partial _{a}\xi ^{c}-\xi ^{c}\partial _{c}g_{ab}. \end{aligned}$$

(32)

Following the same lines, any scalar field $\phi$, while its numerical value at any point is a gauge invariant, is varied as $\delta \phi \equiv \phi ^{\prime }\left( x\right) -\phi \left( x\right) =-\xi ^{c}\partial _{c}\phi$ by (31) if $\phi$ is regarded as a function of the coordinates. The diffeomorphism results in the following matter sector of (1) variation

$$\begin{aligned} \delta S_{m}=\int \left( \frac{\delta \left( \sqrt{-g}L_{m}\right) }{\delta \Psi }\delta \Psi +\frac{\delta \left( \sqrt{-g}L_{m}\right) }{\delta g_{ab}} \delta g_{ab}\right) d^{4}x \end{aligned}$$

(33)

where the matter Lagrangian $L_{m}$ is defined by $S_{m}=\int d^{4}x\sqrt{-g }L_{m}$, and where the symbol $\frac{\delta l}{\delta F}$ represents the usual functional derivative of l w.r.t. the field F. If the part $L_{m}$ of the Lagrangian is a scalar, $\int d^{4}x\sqrt{-g}L_{m}$ is an invariant integral and $\delta S_{m}$ is then necessarily zero whatever $\xi$. If none of the matter fields $\Psi$ is external, each $\Psi$ generates a Lagrange equation, and since all the $\Psi$ occurrences in the total action (1) enters the matter sector, this Lagrange equation just reads $\frac{\delta \left( \sqrt{-g}L_{m}\right) }{\delta \Psi }=0$. Thence, one gets, using the stress tensor definition $T^{ab}=\frac{2}{\sqrt{-g}}\frac{ \delta \left( \sqrt{-g}L_{m}\right) }{\delta g_{ab}}$ and (32)

$$\begin{aligned} \int \sqrt{-g}T^{ab}\left( g_{ac}\partial _{b}\xi ^{c}+g_{bc}\partial _{a}\xi ^{c}+\xi ^{c}\partial _{c}g_{ab}\right) d^{4}x=0. \end{aligned}$$

(34)

Since this occurs whatever $\xi$, one gets, after some usual algebra, the conservation equation (3).

Let us remark that (3) is not recovered if the scalar field $\Phi$ enters $S_{m}$, for two reasons. The first one, relevant in the context of the present paper, is that $\Phi$ is an external field, and then does not generate a Lagrange equation. Second, even in the case were $\Phi$ would be non external, the resulting Lagrange equation $\frac{\delta \left( \sqrt{-g}L\right) }{\delta \Phi }=0$ would not reduce to $\frac{\delta \left( \sqrt{-g}L_{m}\right) }{\delta \Phi }=0$, since the matter sector does not contain all the scalar contributions to the action.

Appendix 2: On the continuity of $\left( \Phi a^{2}\right) ^{\prime \prime }$

At $t=t_{m}$, one can easily compute the left and right limits of the second derivatives, using (13) with $t_{0}=0$, (14), (27), (28), (29) and the continuity relations (22), (23), (24), (25). For the scale factor, one gets

$$\begin{aligned} a^{\prime \prime }\left( t_{m}^{-}\right)= & {} a_{ GR }^{\prime \prime }\left( t_{m}\right) =-\frac{2A}{9t_{m}^{4/3}}, \nonumber \\ a^{\prime \prime }\left( t_{m}^{+}\right)= & {} a_{ BD }^{\prime \prime }\left( t_{m}\right) =-\frac{4\left( 3+\omega \right) A}{9\left( 3+2\omega \right) t_{m}^{4/3}}, \end{aligned}$$

(35)

and they are different, meaning that $a^{\prime \prime }$ is discontinuous at $t_{m}$ (thence that $a^{\prime \prime }\left( t_{m}\right)$ does not exist). The same occurs for the scalar field

$$\begin{aligned} \Phi ^{\prime \prime }\left( t_{m}^{-}\right)= & {} \Phi _{ GR }^{\prime \prime }\left( t_{m}\right) =0, \nonumber \\ \Phi ^{\prime \prime }\left( t_{m}^{+}\right)= & {} \Phi _{ BD }^{\prime \prime }\left( t_{m}\right) =\frac{4C}{3\left( 3+2\omega \right) t_{m}^{2}}. \end{aligned}$$

(36)

Now, consider the quantity $\left( \Phi a^{2}\right) ^{\prime \prime }$. In the GR phase

$$\begin{aligned} \left( \Phi a^{2}\right) _{ GR }= CA ^{2}t^{4/3}. \end{aligned}$$

(37)

Thence

$$\begin{aligned} \left( \Phi a^{2}\right) ^{\prime \prime }\left( t_{m}^{-}\right) =\left( \Phi a^{2}\right) _{ GR }^{\prime \prime }\left( t_{m}\right) =\frac{4 CA ^{2}}{ 9t_{m}^{2/3}}. \end{aligned}$$

(38)

In the BD phase

$$\begin{aligned} \left( \Phi a^{2}\right) _{ BD }=\Phi _{0}B^{2}\left( t-t_{+}\right) ^{2q_{+}+p_{+}}\left( t-t_{-}\right) ^{2q_{-}+p_{-}}. \end{aligned}$$

(39)

Thence, using (25),

$$\begin{aligned} \left( \frac{\left( \Phi a^{2}\right) _{ BD }^{\prime \prime }}{\left( \Phi a^{2}\right) _{ BD }}\right) \left( t_{m}\right) =\frac{16}{9t_{m}^{2}}-\frac{ 2q_{+}+p_{+}}{\left( t_{m}-t_{+}\right) ^{2}}-\frac{2q_{-}+p_{-}}{\left( t_{m}-t_{-}\right) ^{2}} \end{aligned}$$

(40)

and one gets

$$\begin{aligned} \left( \Phi a^{2}\right) ^{\prime \prime }\left( t_{m}^{+}\right) =\left( \Phi a^{2}\right) _{ BD }^{\prime \prime }\left( t_{m}\right) =\frac{4 CA ^{2}}{ 9t_{m}^{2/3}}=\left( \Phi a^{2}\right) ^{\prime \prime }\left( t_{m}^{-}\right) . \end{aligned}$$

(41)

Since $\left( \Phi a^{2}\right) ^{\prime }\left( t_{m}\right)$ is well-defined, $\left( \Phi a^{2}\right) ^{\prime \prime }$ is then continuous at $t_{m}$, with the value just calculated.

Appendix 3: The general linear barotropic case

In Sect. 3.2 it is presented a cosmological model whose matter content is a simple dust fluid. This simple kind of matter was used since the main purpose was to show the existence of nontrivial EST solutions. In this appendix we show that the existence of nontrivial EST solutions can also be found in systems with non negligible pressure, in particular we consider a barotropic fluid. It turns out that the case of a perfect fluid with a barotropic equation of state having the form $P=n\epsilon$ is also tractable, leading to similar computations. Indeed, the BD solution reads in this case [28] (just considering theories with $\omega >-3/2$)

$$\begin{aligned}&a_{ BD }\left( t\right) =\widetilde{B}^{\frac{1}{1-n}}\left( \widetilde{t}- \widetilde{t}_{+}\right) ^{Q_{+}}\left( \widetilde{t}-\widetilde{t} _{-}\right) ^{Q_{-}} , \end{aligned}$$

(42)

$$\begin{aligned}&\Phi _{ BD }\left( t\right) =\widetilde{\Phi }_{0}\left( \widetilde{t}- \widetilde{t}_{+}\right) ^{P_{+}}\left( \widetilde{t}-\widetilde{t} _{-}\right) ^{P_{-}}, \end{aligned}$$

(43)

$$\begin{aligned}&\epsilon _{ BD }\left( t\right) a_{ BD }\left( t\right) ^{3+3n} =\widetilde{M} \end{aligned}$$

(44)

with

$$\begin{aligned} Q_{\pm }= & {} \frac{1+\left( 1-n\right) \omega \pm \sqrt{1+\frac{2}{3}\omega } }{4-6n+3\left( 1-n\right) ^{2}\omega }, \end{aligned}$$

(45)

$$\begin{aligned} P_{\pm }= & {} \frac{1-3n\mp 3\left( 1-n\right) \sqrt{1+\frac{2}{3}\omega }}{ 4-6n+3\left( 1-n\right) ^{2}\omega }, \end{aligned}$$

(46)

where $\widetilde{t}$ is a conformal time defined by

$$\begin{aligned} dt=a^{3n}d\widetilde{t}. \end{aligned}$$

(47)

The constants $\widetilde{B}, \widetilde{\Phi }_{0}, \widetilde{t}_{-}, \widetilde{t} _{+}$ and $\widetilde{M}$ are the five integration constants. The GR solution $a_{ GR }\left( t\right) \propto \left( t-t_{0}\right) ^{2/\left( 3+3n\right) }$ can be written, using the same conformal time, and choosing the origin of time such that $t_{0}=0$,

$$\begin{aligned}&a_{ GR }\left( t\right) =\widetilde{A}\widetilde{t}^{2/\left( 3-3n\right) }, \end{aligned}$$

(48)

$$\begin{aligned}&\Phi _{ GR }\left( t\right) =\widetilde{C}, \end{aligned}$$

(49)

$$\begin{aligned}&\epsilon _{ GR }\left( t\right) a_{ GR }\left( t\right) ^{3+3n} =\widetilde{M}. \end{aligned}$$

(50)

The continuity of the scale factor and the scalar and of their derivatives with respect to t result in the continuity of their derivatives with respect to the conformal time $\widetilde{t}$, since $\frac{d}{d\widetilde{t} }=\frac{dt}{d\widetilde{t}}\frac{d}{dt}=a^{3n}\frac{d}{dt}$. These continuities at $\widetilde{t}_{m}$ lead to a system that can be put on a form very close to (22)–(25),

$$\begin{aligned}&\widetilde{\Phi }_{0}\left( \widetilde{t}_{m}-\widetilde{t}_{+}\right) ^{P_{+}}\left( \widetilde{t}_{m}-\widetilde{t}_{-}\right) ^{P_{-}}= \widetilde{C}, \end{aligned}$$

(51)

$$\begin{aligned}&\frac{P_{+}}{\widetilde{t}_{m}-\widetilde{t}_{+}}+\frac{P_{-}}{\widetilde{t} _{m}-\widetilde{t}_{-}}=0, \end{aligned}$$

(52)

$$\begin{aligned}&\widetilde{B}\left( \widetilde{t}_{m}-\widetilde{t}_{+}\right) ^{\left( 1-n\right) Q_{+}}\left( \widetilde{t}_{m}-\widetilde{t}_{-}\right) ^{\left( 1-n\right) Q_{-}}=\widetilde{A}\widetilde{t}_{m}^{2/3}, \end{aligned}$$

(53)

$$\begin{aligned}&\frac{\left( 1-n\right) Q_{+}}{\widetilde{t}_{m}-\widetilde{t}_{+}}+\frac{ \left( 1-n\right) Q_{-}}{\widetilde{t}_{m}-\widetilde{t}_{-}}=\frac{2}{3 \widetilde{t}_{m}}. \end{aligned}$$

(54)

The solution for the BD constants is then the same as for the dust case, just replacing the exponents $p_{\pm }$ and $q_{\pm }$ by $P_{\pm }$ and $\left( 1-n\right) Q_{\pm }$ respectively.

Appendix 4: A mechanical example with an external coordinate

This appendix aims to clarify the physical meaning of external fields by providing an additional example within a very simple context, that of a planar double pendulum.

Before considering the case with external coordinates, consider the usual Lagrangian for the double pendulum subject to a uniform gravitational acceleration whose norm is denoted by g [37],

$$\begin{aligned} L(\theta _i,\dot{\theta }_i)=\frac{1}{2} \dot{\theta }_1^2 l_1^2 \left( m_1+m_2\right) +\frac{1}{2} \dot{\theta }_2^2 l_2^2 m_2+\dot{\theta }_1 \dot{\theta }_2 l_1 l_2 m_2 \cos \left( \theta _1-\theta _2\right) - V(\theta _i), \end{aligned}$$

(55)

with

$$\begin{aligned} V(\theta _i) = - g l_2 m_2 \cos \left( \theta _2\right) -g l_1 \left( m_1+m_2\right) \cos \left( \theta _1\right) , \end{aligned}$$

(56)

where $\theta _i$ is used as a shorthand notation for $\theta _1, \theta _2$, the particle masses are denoted by $m_1$ and $m_2, m_1$ is supported by a wire of negligible mass of length $l_1, m_1$ and $m_2$ are connected by another wire of length $l_2, \theta _1$ and $\theta _2$ are the position angles of each of the particles in regard to a straight line parallel to the gravitational acceleration vector $\varvec{g}$.

The equations of motion read

$$\begin{aligned}&\left( 1 + \frac{m_2}{m_1} \right) \frac{l_1}{l_2} \ddot{\theta }_1 + \frac{m_2}{m_1} \ddot{\theta }_2 \cos \left( \theta _1-\theta _2\right) + \frac{m_2}{m_1}\dot{\theta }_2^2 \sin \left( \theta _1-\theta _2\right) \nonumber \\&\quad + \,\frac{g}{l_2} \left( 1 + \frac{m_2}{m_1}\right) \sin \left( \theta _1\right) = 0, \end{aligned}$$

(57)

$$\begin{aligned}&\ddot{\theta }_2 \frac{l_2}{l_1}+ \ddot{\theta }_1 \cos \left( \theta _1-\theta _2\right) - \dot{\theta }_1^2 \sin \left( \theta _1-\theta _2\right) +\frac{g}{l_1} \sin \left( \theta _2\right) = 0. \end{aligned}$$

(58)

Considering that $m_1$ is sufficiently large, the above equations can be written as

$$\begin{aligned}&l_1\ddot{\theta }_1=-g \sin \left( \theta _1\right) , \end{aligned}$$

(59)

$$\begin{aligned}&\frac{l_2}{l_1}\ddot{\theta }_2 = -\frac{g \sin \left( \theta _2\right) }{l_1} - \ddot{\theta }_1 \cos \left( \theta _1-\theta _2\right) + \dot{\theta }_1^2 \sin (\theta _1-\theta _2). \end{aligned}$$

(60)

In this limit, the second pendulum has no effect on the first one. Alternatively, one can also consider the regime $m_1 \gg m_2$ right in the Lagrangian (or the action), and the resulting Lagrangian reads

$$\begin{aligned} L (\theta _i, \dot{\theta }_i)= & {} m_2 \left\{ \frac{1}{2} \dot{\theta }_2^2 l_2^2+\dot{\theta }_1 \dot{\theta }_2 l_1l_2 \cos \left( \theta _1-\theta _2\right) + g l_2 \cos (\theta _2)\right\} \nonumber \\&+\,\left( m_1+m_2\right) \left( g l_1 \cos \left( \theta _1\right) +\frac{1}{2} \dot{\theta }_1^2 l_1^2\right) \nonumber \\= & {} m_2 L_2(\theta _i,\dot{\theta }_i) + (m_1 + m_2) L_1(\theta _1,\dot{\theta }_1) \nonumber \\\approx & {} m_2 L_2(\theta _2,\dot{\theta }_2, t) + m_1 L_1(\theta _1,\dot{\theta }_1). \end{aligned}$$

(61)

The last approximation is constituted by two parts, the first is a trivial one in which it was used that $m_1 + m_2 \approx m_1$. The second part refers to the replacement $L_2(\theta _i, \dot{\theta }_i) \rightarrow L_2(\theta _2, \dot{\theta }_2, t)$, in which $L_2$ becomes a function of the second particle only, and the occurrence of $\theta _1$ inside $L_2$ is seen just as function of the time variable t, not a generalised coordinate with the same status of $\theta _2$. This type of decoupling on the dynamics of the particles 1 and 2 is expected since, by requiring that $m_1$ is sufficiently large, the extremum of the total action $\int L dt$ should be achieved only when both $m_2 \int L_2 dt$ and $m_1\int L_1 dt$ are independently extremized. Hence, a consistent approach is the following: from the Euler–Lagrange equations of $L_1$ one derives $\theta _1(t)$; and with this result, the $\theta _1$ solution is inserted into $L_2$, which is then used to derive the $\theta _2$ solution.

Another way of justifying why it is correct and necessary to use $L_2(\theta _i, \dot{\theta }_i) \rightarrow L_2(\theta _2, \dot{\theta }_2, t)$, when the regime $m_1 \gg m_2$ is considered, comes from the fact that the Euler–Lagrange equations of $L_1(\theta _1, \dot{\theta }_1)$ leads to the Eq. (59), while the Euler–Lagrange equation of $L_2(\theta _2,\dot{\theta }_2, t)$ leads to Eq. (60). Moreover, if one considers $L_2$ as a function of $\theta _1$ and derive its corresponding Euler–Lagrange equation, the derived equation is not compatible with Eq. (60). Hence it is wrong to deal with $\theta _1$ in $L_2$ as if it were a standard coordinate: $\theta _1$ is an external coordinate in $L_2(\theta _2, \dot{\theta }_2,t)$.

In the following a generalisation of the picture above presented will be considered. Eventually, the dynamics of the external coordinate may not be well known, that is, the Lagrangian $L_1$ may be more complex. Since Eq. (60) does not depend on $L_1$, one can use $L_2$ in a more general situation in which $L_1$ is unknown. In this setting, it will not be possible in general to derive the full solution of both $\theta _1$ and $\theta _2$, unless additional information is provided. Nonetheless we stress that it is correct to use Eq. (60) even though $L_1$, and consequently $\theta _1(t)$, is unknown.

Consider the Lagrangian

$$\begin{aligned} \tilde{L}(\theta _i, \dot{\theta }_i) = L(\theta _i, \dot{\theta }_i) + k L_3( \theta _1, \dot{\theta }_1, \ddot{\theta }_1, \ldots ), \end{aligned}$$

(62)

where L is given by Eq. (55), k is a dimensionless quantity, and $L_3$ is any function that depends only on $\theta _1$ and its derivatives (it may or may not depend on higher derivatives). Here it is not assumed that $m_1 \gg m_2$. Nonetheless, for k sufficiently large the same argument used in the case in which $m_1$ is sufficiently large can be used. Therefore the extremum of the action $\int \tilde{L} dt$ will be achieved only when both $\int L dt$ and $\int L_3 dt$ are extremized, thus, in the regime $k \gg 1$, one can write

$$\begin{aligned} \tilde{L}(\theta _i, \dot{\theta }_i) \approx L(\theta _2, \dot{\theta }_2, t) + k L_3( \theta _1, \dot{\theta }_1, \ddot{\theta }_1, \ldots ), \end{aligned}$$

(63)

where the explicit time dependence of L comes from the solution of $\theta _1(t)$, which in turn can be directly derived from the equations of motion of $\int L_3 dt$. It should be noted that even if the Lagrangian $L_3$ is unknown, one can use the equation of motion of $L_2$ with respect to $\theta _2$, while $\theta _1$ is seen as an external coordinate. In this case, $\theta _1(t)$ will be an arbitrary function.

Appendix 5: A first test of an EST model with SN data

The main intention of the present paper is to show the existence of nontrivial solutions within the EST approach. It has been shown in other sections that the matching between GR and BD solutions, in the context of the EST approach, is possible. Although, for the moment, the resulting cosmological model is too simplified to constitute a realistic scenario, it is already possible to test the configuration here obtained with SN data. This is done here both to show that it is possible and as a first step towards testing EST models. To this end, we use the binned JLA sample [38]. The advantage of such sample is related to the binned process which lead to less important effects due to different calibration methods.

Fig. 2

The $1\sigma$ and $2 \sigma$ confidence regions in the $(\omega , t_m)$ space. The SN fit was done with three free parameters, the latter two and the Hubble parameter (h). For the result above, h was marginalised

We match the flat CDM model of GR with the flat BD solutions used above. Of course, the observational test disfavour strongly the CDM with respect to the $\Lambda$CDM model. We use the expressions derived above, and consider three free parameters, the matching time $t_m$, the parameter $\omega$ and the Hubble parameter h. As usual, the fit is done looking for the values of these parameters that lead to the global minimum of $\chi ^2$.

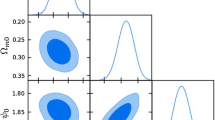
The results indicate that the global maximum of probability (or global minimum of $\chi ^2$) occurs for $t_m = t_0$, where $t_0$ is the present time, implying that the data favours no phase transition and the universe is still in the GR phase. The derived value of the minimum $\chi ^2$ is not small in comparison to the standard cosmological model $\Lambda$CDM, but this is expected since this model includes no dark energy. The resulting fit is just as good as that of a pure CDM model. Likewise pure CDM, the minimum $\chi ^2$, for this set of data, is $\chi ^2 \approx 350$. There is a local maximum for $t_m = 0$ corresponding to a pure BD phase, for the latter, the corresponding value is $\chi ^2 \approx 353$. For comparison purposes, the minimum $\chi ^2$ for $\Lambda$CDM is 29. The $1 \sigma$ and $2 \sigma$ confidence regions are displayed in Fig. 2. As expected, the higher is $\omega$, more similar the dynamics of the BD and the GR phases become, and hence it becomes more probable for the transition to happen in an instant before $t_0$.

A complete statistical study would imply to consider other tests and to introduce a mechanism to accelerate the expansion of the universe. This has in part been done in Ref. [39] in the context of the usual BD theory by including the possibility of $\omega < - 4/3$, what has been excluded in our analysis. In that reference, it has been found, comparing the pure BD flat matter dominated phase with the $\Lambda$CDM, that the BD model is slightly favoured for $\omega \lesssim - 4/3$.