Electrostatics in a simple wormhole revisited

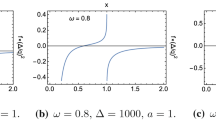
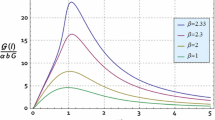
Abstract

The electrostatic potential generated by a point charge at rest in a simple static, spherically symmetric wormhole is given in the form of series of multipoles and in closed form. The general potential which is physically acceptable depends on a constant due to the fact that the monopole solution is arbitrary. When the wormhole has $Z_2$-symmetry, the potential is completely determined. The calculation of the electrostatic self-energy and of the self-force is performed in all cases considered.

Appendices

Appendix A: The Green function of the radial differential equations

Let the self-adjoint differential equation with a source term

$$\begin{aligned} \frac{d}{dx}\left( p(x)\frac{dA}{dx}\right) +q(x)A=c\delta (x-a) , \end{aligned}$$

(60)

and the corresponding homogeneous equation

$$\begin{aligned} \frac{d}{dx}\left( p(x)\frac{dA}{dx}\right) +q(x)A=0 , \end{aligned}$$

(61)

where the functions $p,\,dp/dx$ and $q$ are continuous and moreover $p$ is strictly positive on $(-\infty , \infty )$.

In the context of our present work, we assume that the homogeneous equation (61), admits two regular solutions $A^{(i)}$ and $A^{(e)}$, linearly independent, having respectively the following boundary conditions:

$$\begin{aligned} \lim _{x\rightarrow -\infty } A^{(i)}(x) =0 , \quad \lim _{x\rightarrow \infty }A^{(e)}(x) =0. \end{aligned}$$

(62)

The solutions $A^{(i)}$ and $A^{(e)}$ are fixed up to a multiplicative constant. The nonvanishing Wronskian $\mathcal{W}(A^{(i)},A^{(e)})$ can be easily expressed in the form

$$\begin{aligned} \mathcal{W}( A^{(i)},A^{(e)}) (x)=\frac{k}{p(x)} , \end{aligned}$$

(63)

where $k$ is a constant.

The Green function $A(x,a)$ of the differential equation (60), which verifies the boundary conditions

$$\begin{aligned} \lim _{x\rightarrow -\infty } A(x,a)=0 , \quad \lim _{x\rightarrow \infty } A(x,a)=0 , \end{aligned}$$

(64)

is defined by the other following properties:

• a. $A(x,a)$ satisfies the homogeneous equation (61) except at $x=a$.

• b. $A(x,a)$ is continuous at $x=a$.

• c. The derivative of $A(x,a)$ with respect to $x$ has a jump discontinuity of magnitude $c/p(a)$ at $x=a$.

These conditions ensure that $A(x,a)$ satisfies the differential equation (60) in the sense of distributions with the boundary conditions (64).

It is now possible to determine this Green function $A(x,a)$ with the help of the functions $A^{(i)}$ and $A^{(e)}$. Consider the function $H$ defined by

$$\begin{aligned} H(x,a)=\frac{c}{k}\left\{ \begin{array}{ll} A^{(i)}(x)A^{(e)}(a) \quad \mathrm{if} \quad x\le a , \\ A^{(i)}(a)A^{(e)}(x) \quad \mathrm{if} \quad x\ge a \end{array} \right.. \end{aligned}$$

(65)

It is obvious that $H(x,a)$ verifies all the properties of a Green function. For simplicity, it is possible to take $k=c$ by a judicious choice of functions $A^{(i)}$ and $A^{(e)}$ defined up to a multiplicative constant. Thus, the Green function of the differential equation (60) has expression (65) with $k=c$ that one can rewrite in the form

$$\begin{aligned} A(x,a)=\theta (a-x)A^{(i)}(x)A^{(e)}(a)+\theta (x-a)A^{(i)}(a)A^{(e)}(x) , \end{aligned}$$

(66)

where $\theta$ is the Heaviside step function.

Appendix B: Explicit electrostatic potential in higher dimensions

Metric (1) can be easily generalised to describe the spacetime representing a wormhole in $n+1$ dimensions, $n\ge 3$. We take

$$\begin{aligned} ds^2=-dt^2+dl^2+( l^2+w^2) d\Omega _{n-1}^{2} , \end{aligned}$$

(67)

with $-\infty <l<\infty$, and where $d\Omega _{n-1}^{2}$ is the metric of the sphere $S^{n-1}$ described in the coordinates $(\vartheta _1,\dots ,\vartheta _{n-2},\varphi )$. The change of radial coordinates (33) expresses metric (67) in isotropic coordinates

$$\begin{aligned} ds^2=-dt^2+\left( 1+\frac{w^2}{4r^2}\right)^2 \left( dr^2+r^2d\Omega _{n-1}^{2}\right) \end{aligned}$$

(68)

with $r>0$. We set the associated Cartesian coordinates $(x^i),\,i=1,\dots ,n$. Metric (68) can be written thereby

$$\begin{aligned} ds^2=-dt^2+\left( 1+\frac{w^2}{4r^2}\right)^2\left( ( dx^1)^2+\cdots +( dx^n)^2\right) , \end{aligned}$$

(69)

where $r=\sqrt{( x^1)^2+\cdots +( x^n)^2}$.

We consider the usual Maxwell equations in a spacetime of $n+1$ dimensions. The charge density $\rho$ for a point charge $e$ located at $x^i=x_{0}^{i}$ has the expression

$$\begin{aligned} \rho (x^i)=\frac{e}{\sqrt{-g}}\delta ^{(n)}( x^i-x_{0}^{i}) , \end{aligned}$$

(70)

where $g$ is the determinant of metric (69) given by

$$\begin{aligned} \sqrt{-g}=\left(1+\frac{w^2}{4r^2}\right)^n. \end{aligned}$$

(71)

The electrostatic equation in metric (69) takes the form

$$\begin{aligned} \triangle V+h(r)\frac{x^i}{r}\partial _iV=-2(n-2)\frac{\pi ^{n/2}}{\Gamma (n/2)}\frac{e}{\displaystyle \left( 1+\frac{w^2}{4r^2}\right)^{n-2}} \delta ^{(n)}(x^i-x_{0}^{i}) , \end{aligned}$$

(72)

where $\triangle$ is the usual Laplacian operator, and in which the function $h$ has the expression

$$\begin{aligned} h(r)=\frac{1}{\displaystyle \left( 1+\frac{w^2}{4r^2}\right)^{n-2}}\frac{d}{dr}\left( 1+\frac{w^2}{4r^2}\right)^{n-2} =-\frac{(n-2)w^2}{2r(r^2+w^2/4)}. \end{aligned}$$

(73)

In a previous work [17] , it was shown that exact solutions to the electrostatic equation (72) exist in the form

$$\begin{aligned} V(x)=g(r)g(r_0)F\left( \frac{\Gamma (x,x_0)}{k(r)k(r_0)}\right) , \end{aligned}$$

(74)

with

$$\begin{aligned} \Gamma (x,x_0)=(x^1-x_{0}^{1})^2+\cdots +(x^n-x_{0}^{n})^2, \end{aligned}$$

(75)

if the function $h$ satisfies a certain differential equation. It may be only the type II with $a=w/2$ in the classification of this work. Consequently, the function $h$ must satisfy the differential equation

$$\begin{aligned} \frac{d}{dr}h+\frac{1}{2}h^2+\frac{n-1}{r}h-\frac{2[ -n(n-2)w^2/4-Ab^2]}{(r^2+w^2/4)^2}=0 \end{aligned}$$

(76)

in which the two constants $b$ et $A$ are to be fixed.

From (73), we calculate

$$\begin{aligned} \frac{d}{dr}h+\frac{1}{2}h^2+\frac{n-1}{r}h=-\frac{(n^2-6n+8)w ^2}{2(r^2+w^2/4)^2}. \end{aligned}$$

(77)

By comparing (76) and (77), we find the value of the constants: $b=w/2$ and $A=-4n+8$.

We are thus in the case where the electrostatic equation (72) has solutions in the form (74). According to the results of the work [17], the functions $k$ and $g$ are expressed as

$$\begin{aligned} k(r)=\frac{r^2+w^2/4}{w/2} , \quad g(r)=\frac{r^{n-2}}{(r^2+w^2/4)^{n-2}} , \end{aligned}$$

(78)

and the function $F$ is determined by the differential equation

$$\begin{aligned} 4(-s^2+s)F^{\prime \prime }+(-4ns+n)F^{\prime }+(-4n+8)F=0. \end{aligned}$$

(79)

As variable $s$ we have set

$$\begin{aligned} s=\frac{\Gamma (x,x_0)}{k(r)k(r_0)}. \end{aligned}$$

(80)

The value $s=0$ corresponds to the position of the point charge. We emphasize that

$$\begin{aligned} 0\le s\le 1. \end{aligned}$$

(81)

This comes from that fact that we can always take the particular case where the point charge is located at $\vartheta _1=0$ without lost of generality, due to the spherical symmetry. Inequality (81) is then written

$$\begin{aligned} w^2(r^2-2rr_0\cos \vartheta _1 +r_{0}^{2})\le 4(r^2+w^2/4)(r_{0}^{2}+w^2/4) , \end{aligned}$$

which is equivalent to the recognized inequality

$$\begin{aligned} 4r^2r_{0}^{2}+2rr_0w^2\cos \vartheta _1+w^4/4 \ge 0. \end{aligned}$$

We firstly find a particular solution to (79)

$$\begin{aligned} F_e(s)=\frac{1}{[s(1-s)]^{n/2-1}}. \end{aligned}$$

(82)

A classical method shows that the general solution to (79) is given by

$$\begin{aligned} F(s)=\frac{1}{[s(1-s)]^{n/2-1}}\left\{ f_1+f_2\int \limits _{0}^{s}[u(1-u)]^{n/2-2}du \right\} \end{aligned}$$

(83)

where $f_1$ and $f_2$ are two arbitrary constants. The integral in (83) can be explicitly performed for all values of $n$.

We will choose the constants $f_1$ and $f_2$ first of all so that solution (74) is regular everywhere, except at $x=x_0$. This occurs if the function $F$, given by (83), has only a singularity at $s=0$. Now we have

$$\begin{aligned} \int \limits _{0}^{s}[u(1-u)]^{n/2-2}du -\int \limits _{0}^{1}[u(1-u)]^{n/2-2}du \sim (1-s)^{n/2-1} \quad \mathrm{as}\quad s\rightarrow 1 , \end{aligned}$$

therefore we take the relation

$$\begin{aligned} f_1+f_2\int \limits _{0}^{1}[u(1-u)]^{n/2-2}du=0. \end{aligned}$$

(84)

The important point is that solution (74) satisfies the electrostatic equation (72) in the sense of distributions. By noticing from (83) that

$$\begin{aligned} F(s) \sim \frac{f_1}{s^{n/2-1}} \quad \mathrm{as} \quad s \rightarrow 0 , \end{aligned}$$

we can deduce the most divergent part of $V$ as $x\rightarrow x_0$

$$\begin{aligned} V(x) \sim f_1\left( \frac{2}{w}\right)^{n-2}\frac{1}{(1+w^2/4r_{0}^{2})^{n/2-1}(1+w^2/4r^{2})^{n/2-1}}\frac{1}{[\Gamma (x,x_0)]^{n/2-1}}.\qquad \quad \end{aligned}$$

(85)

By considering the source term of Eq. (72), we take

$$\begin{aligned} f_1=e\left( \frac{w}{2}\right)^{n-2} , \end{aligned}$$

(86)

since

$$\begin{aligned} \triangle \frac{1}{[\Gamma (x,x_0)]^{n/2-1}} =-2(n-2)\frac{\pi ^{n/2}}{\Gamma (n/2)}\delta ^{(n)}(x,x_0). \end{aligned}$$

So ,we obtain

$$\begin{aligned} F(s)\!=\!e\left(\! \frac{w}{2}\!\right)^{n-2}\frac{1}{[s(1-s)]^{n/2-1}}\left\{ 1-\frac{1}{\int _{0}^{1}[u(1-u)]^{n/2-2}du}\int \limits _{0}^{s}[u(1-u)]^{n/2-2}du \right\} .\qquad \end{aligned}$$

(87)

Now with (78), (80) and (87), we are in position to write from (74) the potential $V(x)$ generated by a point charge at $x=x_0$.