Skip to main content

Advertisement

SpringerLink
Log in

Review of Methodologies for Offshore Wind Resource Assessment in European Seas

  • Original Paper
  • Published:
Surveys in Geophysics Aims and scope Submit manuscript

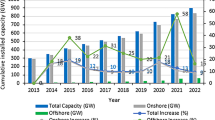
Abstract

The wind resource offshore is generally larger than at geographically nearby onshore sites, which can offset the higher installation, operation and maintenance costs associated with offshore wind parks. Successful offshore wind energy development relies to some extent on accurate prediction of wind resources, but since installing and operating a meteorological mast in situ is expensive, prospective sites must be carefully evaluated. Accordingly, one can conceptualize the wind resource assessment process as a two-phase activity: (i) an evaluation of wind resources at the regional scale to locate promising wind farm sites and (ii) a site specific evaluation of wind climatology and vertical profiles of wind and atmospheric turbulence, in addition to an assessment of historical and possibly future changes due to climate non-stationarity. Phase (i) of the process can involve use of in situ observations of opportunity derived from ships, lighthouses and buoys in conjunction with model tools and remote sensing products. The reliability of such data sources has been extensively investigated in different national and European projects especially in Northern Europe, and the results are summarized herein. Phase (ii) of the project often still requires in situ observations (which may or may not be supplemented with ground-based remote sensing technologies) and application of tools to provide a climatological context for the resulting measurements. Current methodologies for undertaking these aspects of the resource assessment are reviewed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  • Accadia C, Zecchetto S, Lavagnini A, Speranza A (2007) Comparison of 10-m wind forecasts from a regional area model and QuikSCAT Scatterometer wind observations over the Mediterranean Sea. Mon Weather Rev 135:1945–1960. doi:10.1175/MWR3370.1

    Article  Google Scholar 

  • Adrian G, Fiedler F (1991) Simulation of unstationary wind and temperature fields over complex terrain and comparison with observations. Beitr Phys Atmos 64:27–48

    Google Scholar 

  • Akhmatov V, Knudsen H (2007) Large penetration of wind and dispersed generation into Danish power grid. Electric Power Syst Res 77:1228–1238. doi:10.1016/j.epsr.2006.08.009

    Article  Google Scholar 

  • Akhmatov V, Rasmussen C, Eriksen PB, Pedersen J (2007) Technical aspects of status and expected future trends for wind power in Denmark. Wind Energy 10:31–49. doi:10.1002/we.206

    Article  Google Scholar 

  • Antoniou I, Joergensen HE, Mikkelsen T, Frandsen S, Barthelmie R, Perstrup C, Hurtig M (2006) Offshore wind profile measurements from remote sensing instruments. In: European Wind Energy Association Conference, Athens, Greece, February 2006, 10 pp

  • Badger J, Barthelmie RJ, Frandsen S, Christiansen MB (2006) Mesoscale modelling for an offshore wind farm. In: Proceedings (online) European Wind Energy Conference and Exhibition, Athens (GR), 27 Feb–2 Mar 2006, European Wind Energy Association, 6 pp

  • Barthelmie RJ (1999) The effects of atmospheric stability on coastal wind climates. Meteorol Appl 6:39–47. doi:10.1017/S1350482799000961

    Article  Google Scholar 

  • Barthelmie RJ (2001a) Evaluating the impact of wind induced roughness change and tidal range on extrapolation of offshore vertical wind speed profiles. Wind Energy 4:99–105. doi:10.1002/we.45

    Article  Google Scholar 

  • Barthelmie RJ (2001b) Modelling and measurements of coastal wind speeds. In: Majumdar SK, Miller EW, Panah AI (eds) Renewable energy: trends and prospects. Pennsylvania Academy of Science, Easton, PA, pp 961–975

    Google Scholar 

  • Barthelmie RJ (2007) Wind energy. Status Trends Geogr Compass 1(3):275–301. doi:10.1111/j.1749-8198.2007.00030.x

    Article  Google Scholar 

  • Barthelmie RJ, Pryor SC (2003) Can satellite sampling of offshore wind speeds realistically represent wind speed distributions? J Appl Meteorol 42:83–94. doi:10.1175/1520-0450(2003)042<0083:CSSOOW>2.0.CO;2

    Article  Google Scholar 

  • Barthelmie RJ, Pryor SC (2006) Challenges in predicting power output from offshore wind farms. J Energy Eng 132:91–103. doi:10.1061/(ASCE)0733-9402(2006)132:3(91)

    Article  Google Scholar 

  • Barthelmie RJ, Grisogono B, Pryor SC (1996) Observations and simulations of diurnal cycles of near-surface wind speeds over land and sea. J Geophys Res Atmos 101:21, 327–321, 337

    Google Scholar 

  • Barthelmie RJ, Courtney M, Lange B, Nielsen M, Sempreviva AM, Svenson J, Olsen F, Christensen T (1999) Offshore wind resources at Danish measurement sites. In: Proceedings of the 1999 European wind energy conference and exhibition. James and James Scientific Publishers Ltd, Nice, pp 1101–1104

  • Barthelmie RJ, Folkerts L, Ormel F, Sanderhoff P, Eecen P, Stobbe O, Nielsen NM (2003) Offshore wind turbine wakes measured by SODAR. J Atmos Ocean Technol 30:466–477. doi:10.1175/1520-0426(2003)20<466:OWTWMB>2.0.CO;2

    Article  Google Scholar 

  • Barthelmie RJ, Larsen GC, Pryor SC, Jørgensen HE, Bergström H, Schlez W, Rados K, Lange B, Vølund P, Neckelmann S, Mogensen S, Schepers G, Hegberg T, Folkerts L, Magnusson M (2004) Efficient development of offshore windfarms (ENDOW): modelling wake and boundary layer interactions. Wind Energy 7:225–245. doi:10.1002/we.121

    Article  Google Scholar 

  • Barthelmie R, Hansen O, Enevoldsen K, Hoejstrup J, Larsen SE, Frandsen S, Pryor S, Motta M, Sanderhoff P (2005) Ten years of meteorological measurements for offshore wind farms. J Sol Energy Eng 127(2):170–176. doi:10.1115/1.1850489

    Article  Google Scholar 

  • Barthelmie RJ, Folkerts L, Rados K, Larsen GC, Pryor SC, Frandsen S, Lange B, Schepers G, Ormel F (2006) Comparison of wake model simulations with offshore wind turbine wake profiles measured by SODAR. J Atmos Ocean Technol 23:888–901. doi:10.1175/JTECH1886.1

    Article  Google Scholar 

  • Barthelmie RJ, Frandsen ST, Nielsen NM, Pryor SC, Rethore PE, Joergensen HE (2007a) Modelling and measurements of power losses and turbulence intensity in wind turbine wakes at Middelgrunden offshore wind farm. Wind Energy 10:217–228

    Google Scholar 

  • Barthelmie RJ, Badger J, Pryor SC, Hasager CB, Christiansen MB, Jørgensen HE (2007b) Offshore coastal wind speed gradients: issues for the design and development of large offshore windfarms. Wind Eng 31(6):369–382. doi:10.1260/030952407784079762

    Article  Google Scholar 

  • Barthelmie RJ, Pryor SC, Frandsen ST (2008) Climatological and meteorological aspects of predicting offshore wind energy. In: Twidell J, Gaudiosi G (eds) Offshore wind energy (in press)

  • Benjamin SG, Miller PA (1990) An alternative sea level pressure reduction and a statistical comparison of geostrophic wind estimated with observed surface winds. Mon Weather Rev 118:2099–2116. doi:10.1175/1520-0493(1990)118<2099:AASLPR>2.0.CO;2

    Article  Google Scholar 

  • Bergstroem H (2001) Boundary-layer modelling for wind climate estimates. Wind Eng 25(5):289–299. doi:10.1260/030952401760177864

    Article  Google Scholar 

  • Bergstroem H, Barthelmie RJ (2002) Offshore boundary-layer modelling. Global Windpower, EWEA, Paris

    Google Scholar 

  • Bingöl F, Mann J, Foussekis D (2008a) LiDAR error estimation with WAsP Engineering. In: Fourteenth international symposium for the advancement of boundary layer remote sensing, Risø (DK), 23–25 June 2008. IOP Conference Series: Earth Environment Science (2008) 1, 012058 (9 pp)

  • Bingöl F, Trujillo JJ, Mann J, Larsen GC (2008b) Fast wake measurements with LiDAR at Risø test field. In: Fourteenth international symposium for the advancement of boundary layer remote sensing, Risø (DK), 23–25 Jun 2008. IOP Conference Series: Earth Environment Science (2008) 1, 012022 (9 pp)

  • Boerreson JA (1987) Wind Atlas for the North Sea and the Norwegian Sea. Norwegian University Press, Oslo, p 346

    Google Scholar 

  • Bourassa AM, Legler DM, O’Brien JJ, Smith SR (2003) SeaWinds validation with research vessels. J Geophys Res 108. doi:10.1029/2001JC001028

  • Bumke K, Hasse L (1989) An analysis scheme for determination of true surface winds at sea from ship synoptic wind and pressure observations. Boundary-Layer Meteorol 47:295–308. doi:10.1007/BF00122335

    Article  Google Scholar 

  • Bunn JC, Watson SJ (1996) A new matrix method of predicting long-term wind roses with MCP. In: Zervos A, Ehmann H, Helm P (eds) Proceedings of the European Wind Energy Conference (EWEC), HS Stephens and Associates, Göteborg, Sweden, 20–24 May 1996, Bedford, UK, pp 588–591

  • Buzzi A, Fantini M, Malguzzi P, Nerozzi F (1994) Validation of a limited area model in cases of Mediterranean cyclogenesis: surface fields and precipitation scores. Meteorol Atmos Phys 53:53–67. doi:10.1007/BF01029609

    Article  Google Scholar 

  • Cassola F, Burlando M, Villa L, Latona P, Ratto C (2006) Evaluation of the offshore wind potential along the Italian coasts. In: Proceedings of the offshore wind energy in Mediterranean and Other European Seas, OWEMES, conference, Civitavecchia, Italy, 19–21 April 2006. Available on CD ROM

  • Cavaleri L (2005) The wind and wave atlas of the Mediterranean Sea – the calibration phase. Adv Geosci 2:255–257

    Article  Google Scholar 

  • Charnock H (1955) Wind stress on a water surface. Q J R Meteorol Soc 81:639–640. doi:10.1002/qj.49708135027

    Article  Google Scholar 

  • Christiansen MB, Koch W, Horstmann J, Hasager CB, Nielsen M (2006) Wind resource assessment from C-band SAR. Remote Sens Environ 105:68–81. doi:10.1016/j.rse.2006.06.005

    Article  Google Scholar 

  • Coelingh JP, van Wijk AJM, Holtslag AAM (1998) Analysis of wind speed observations over the North Sea coast. J Wind Eng Ind Aerodyn 73:125–144. doi:10.1016/S0167-6105(97)00285-7

    Article  Google Scholar 

  • Coelingh J, Folkerts L, van Zuylen E (2003) Offshore sodar measurements – 1 year experience. In: Proceedings of the offshore wind energy in Mediterranean and other European Seas OWEMES conference, Naples, April 2003, ATENA/ENEA, pp 51–64

  • Coindreau O, Hourdin F, Haeffelin M, Mathieu A, Rio C (2007) Assessment of physical parameterizations using a global climate model with stretchable grid and nudging. Mon Weather Rev 135:1474–1489. doi:10.1175/MWR3338.1

    Article  Google Scholar 

  • Dorman CE, Winant CD (1995) Buoy observations of the atmosphere along the west coast of the United States, 1981–1990. J Geophys Res 100:16029–16044. doi:10.1029/95JC00964

    Article  Google Scholar 

  • EWEA (2007) Delivering offshore wind power in Europe. Published by European Wind Energy Association, December 2007. http://www.ewea.org/fileadmin/ewea_documents/images/publications/offshore_report/ewea-offshore_report.pdf

  • EWEA (2008) European Wind Energy Association Annual report 2007. Available at www.ewea.org

  • Firestone J, Kempton W (2007) Public opinion about large offshore wind power: underlying factors. Energy Policy 35:1584–1598. doi:10.1016/j.enpol.2006.04.010

    Article  Google Scholar 

  • Frandsen S, Chacon L, Crespo A, Enevoldsen P, Gomez-Elvira R, Hernandez J, Hoejstrup J, Manuel F, Thomsen K, Sørensen P (1996) Measurements on and modelling of offshore wind farms. Risø-R-903(EN), Risø National Laboratory, Denmark, p 101

    Google Scholar 

  • Frank HP, Rathman O, Mortensen NG, Landberg L (2001a) The numerical wind atlas – the KAMM/WasP method. ISBN 87-550-2909-4, Risø-R-1252(EN), Risø National Laboratory, Roskilde, Denmark, 60 pp. http://www.risoe.dk/rispubl/VEA/ris-r-1252.htm

  • French R, Bonnett D, Sandon J (2005) Wind power: a major opportunity for the UK. Proc Inst Civ Eng 158:20–27. doi:10.1680/cien.2005.158.6.20

    Article  Google Scholar 

  • Furevik BR, Espedal HA, Hamre T, Hasager CB, Johannessen OM, Jørgensen BH, Rathmann O (2003) Satellite-based wind maps as guidance for siting offshore wind farms. Wind Eng 27(5):327–338(12). doi:10.1260/030952403322770931

    Article  Google Scholar 

  • Ganader H, Dahlman S, Ronsten G, Bergstroem H (2001) Medium term evaluation of meteorological conditions, power performance and loads on the first Swedish offshore wind farm at Bockstigen European Wind Energy Association Offshore Wind Energy Conference, Brussels, p 4

  • Garrad AD, Adams BM, Matthies H, Scherweit M (1993) An assessment of the offshore wind potential in the EC. In: Proceedings of 15th British Wind Energy Conference, pp 401–406

  • Gibson JK, Kållberg P, Uppala S, Hernandez A, Nomura A, Serrano E (1997) ERA description. ERA-15 Project Report Series No. 1, ECMWF, July 1997

  • Gilhousen DB (1987) A field evaluation of NBDC moored buoy winds. J Atmos Ocean Technol 4:94–104. doi:10.1175/1520-0426(1987)004<0094:AFEONM>2.0.CO;2

    Article  Google Scholar 

  • Graham AE (1982) Winds estimated by the voluntary observing fleet compared with instrumental measurements at fixed positions. Meteorol Mag 1325:312–326

    Google Scholar 

  • Gryning SE, Batchvarova E, Brümmer B, Jørgensen HE, Larsen SE (2007) On the extension of the wind profile over homogeneous terrain beyond the surface boundary layer. Boundary-Layer Meteorol 124:251–268. doi:10.1007/s10546-007-9166-9

    Article  Google Scholar 

  • Hasager CB, Dellwik E, Nielsen M, Furevik BR (2004) Validation of ERS-2 SAR offshore wind-speed maps in the North Sea. Int J Remote Sens 25:3817–3841. doi:10.1080/01431160410001688286

    Article  Google Scholar 

  • Hasager CB, Nielsen M, Astrup P, Barthelmie R, Dellwik E, Jensen NO, Joergensen EH, Pryor S, Rathmann O, Furevik BR (2005) Offshore wind resource assessed from satellite SAR wind field maps. Wind Energy 8:403–419. doi:10.1002/we.150

    Article  Google Scholar 

  • Hasager CB, Barthelmie R, Christiansen MB, Nielsen M, Pryor SC (2006) Quantifying offshore wind resources from satellite maps: study area the North Sea. Wind Energy 9:63–74. doi:10.1002/we.190

    Article  Google Scholar 

  • Hasager CB, Astrup P, Nielsen M, Christiansen MB, Badger J, Nielsen P, Sørensen PB, Barthelmie RJ, Pryor SC, Bergstroem H (2007) SAT-WIND project. Final report. Risø-R-1586(EN). Risø National Laboratory, Technical University of Denmark, Roskilde, Denmark, 131 pp. http://www.risoe.dk/rispubl/reports/ris-r-1586.pdf

  • Hersbach H, Stoffelen A, de Haan S (2007) An improved C-band scatterometer ocean geophysical model function: CMOD5. J Geophys Res 112:C03006. doi:10.1029/2006JC003743

    Article  Google Scholar 

  • Hsu SA (1988) Coastal meteorology. Academic Press Inc., London, 260 pp

  • Hunter E, Chant R, Bowers L, Glenn S, Kohut J (2007) Spatial and temporal variability of diurnal wind forcing in the coastal ocean. 34, L03607. doi:10.1029/2006GL028945

  • IEA (2005) Offshore wind experiences. Available from http://www.iea.org/

  • IEA (2008) IEA wind energy annual report 2008. Kendall Printing Company, USA

    Google Scholar 

  • Jimenez B, Durante F, Lange B, Kreutzer T, Tambke J (2007) Offshore wind resource assessment with WAsP and MM5: comparative study for the German Bight. Wind Energy 10:121–134. doi:10.1002/we.212

    Article  Google Scholar 

  • Joergensen BH, Hasager CB, Astrup P Rathmann O, Barthelmie RJ, Pryor S (2001) Off-shore wind fields obtained from mesoscale modeling and satellite SAR images offshore wind energy (CD-ROM). EWEA Offshore Wind Energy special topic conference, 10–12 Dec 2001. European Wind Energy Association, Brussels, p 4

  • Kalnay E, Kanamitsu M, Kistler R, Collins W, Deaven D, Gandin L, Iredell M, Saha S, White G, Woollen J, Chelliah M, Zhu Y, Chelliah M, Ebisuzaki W, Higgins W, Janowiak J, Mo KC, Ropelweski C, Wang J, Leetmaa A, Reynolds R, Jenne R, Joseph D (1996) The NCEP/NCAR 40 reanalysis project. Bull Am Meteorol Soc 77:437–471. doi:10.1175/1520-0477(1996)077<0437:TNYRP>2.0.CO;2

    Article  Google Scholar 

  • Kara AB, Wallcraft AJ, Hurlburt HE (2007) A correction for land contamination of atmospheric variables near land-sea boundaries. J Phys Oceanogr 37:803–818. doi:10.1175/JPO2984.1

    Article  Google Scholar 

  • Kerbaol V, Chapron B, Vachon PW (1998) Analysis of ERS-1/2 synthetic aperture radar wave mode imagettes. J Geophys Res 103:7833–7846. doi:10.1029/97JC01579

    Article  Google Scholar 

  • Koch W, Feser F (2006) Relationship between SAR-derived wind vectors and wind at 10-m height represented by a mesoscale model. Mon Weather Rev 134:1505–1517. doi:10.1175/MWR3134.1

    Article  Google Scholar 

  • Korevaar CG (1990) North Sea climate based on observations from ships and lightvessels. Kluwer Academic Publishers, London, p 152

    Google Scholar 

  • Koutiva XT, Vrionis TD, Vovos NA, Giannakopols GB (2006) Optimal integration of an offshore wind farm to a weak AC grid. IEEE Trans Power Deliv 21:987–994. doi:10.1109/TPWRD.2005.859275

    Article  Google Scholar 

  • Lange B, Hoejstrup J (2001) Evaluation of the wind-resource estimation program WAsP for offshore applications. J Wind Eng Ind Aerodyn 89:271–291. doi:10.1016/S0167-6105(00)00082-9

    Article  Google Scholar 

  • Lange B, Larsen SE, Hoejstrup J, Barthelmie R (2004) The influence of thermal effects on the wind speed profile of the coastal marine boundary layer. Boundary-Layer Meteorol 112:587–617. doi:10.1023/B:BOUN.0000030652.20894.83

    Article  Google Scholar 

  • Larsen GC, Hansen K (2001) Database on wind characteristics; contents of database bank. Report No. Risø-R-1301(EN), Risø National Laboratory, Roskilde, Denmark

  • Lavagnini A, Sempreviva AM, Barthelmie RJ (2003) Estimating wind energy potential offshore in Mediterranean areas. Wind Energy 6:23–34. doi:10.1002/we.81

    Article  Google Scholar 

  • Lavagnini A, Sempreviva AM, Transerici C, Accadia C, Casaioli M, Mariani S, Speranza A (2006) Offshore wind climatology over the Mediterranean basin. Wind Energy 9:251–266. doi:10.1002/we.169

    Article  Google Scholar 

  • Lehner S, Horstmann J, Koch W, Rosenthal W (1998) Mesoscale wind measurements using recalibrated ERS SAR images. J Geophys Res 103:7847–7856. doi:10.1029/97JC02726

    Article  Google Scholar 

  • Manwell JF, McGowan JG, Rogers AL (2002) Wind energy explained: theory, design and application. Wiley, New York, p 590

    Book  Google Scholar 

  • McQueen D, Watson S (2006) Validation of wind speed prediction methods at offshore sites. Wind Energy 9:75–85. doi:10.1002/we.181

    Article  Google Scholar 

  • Mechali M, Jensen L, Barthelmie R, Frandsen S, Rethore PE (2006) Wake effects at Horns Rev and their influence on energy production. In: Proceedings of the European wind energy conference and exhibition, Athens, Greece, p 10

  • Mesinger F, DiMego G, Kalnay E, Mitchell K, Shafran PC, Ebisuzaki W, Jovic D, Woollen J, Rogers E, Berbery EH, Ek MB, Fan Y, Grumbine R, Higgins W, Li H, Lin Y, Manikin G, Parrish D, Shi W (2006) North American regional reanalysis. Bull Am Meteorol Soc 87:343–360. doi:10.1175/BAMS-87-3-343

    Article  Google Scholar 

  • Monaldo F, Thomson D, Pichel W, Clemente-Colon P (2004) A systematic comparison of QuikSCAT and SAR ocean surface wind speeds. IEEE Trans Geosci Rem Sens 42:283–291. doi:10.1109/TGRS.2003.817213

    Article  Google Scholar 

  • Mortensen NG, Heathfield DN, Myllerup L, Landberg L, Rathmann O (2005) Wind Atlas Analysis and Application Program: WAsP 8 Help Facility. 335 Topics. Risø National Laboratory, Roskilde, Denmark. ISBN 87-550-3457-8

  • Motta M, Barthelmie RJ, Vølund P (2003) Stability effects on predicted wind speed profiles and power output at the Vindeby offshore wind farm. e-WindEng (001), pp 1–5, ISSN 1901-9181

  • Motta M, Barthelmie RJ, Vølund P (2005) The influence of non-logarithmic wind speed profiles on potential power output at Danish offshore sites. Wind Energy 8:219–236. doi:10.1002/we.146

    Article  Google Scholar 

  • Neckelmann S, Petersen J (2000) Evaluation of the stand alone wind and wave measurement systems for the Horns Rev 150 MW offshore wind farm in Denmark. OWEMES 2000, Sicily, Italy, ATENA/ENEA, pp 17–27

  • Negra NB, Todorovic J, Ackermann T (2006) Loss evaluation of HVAC and HVDC transmission solutions for large offshore wind farms. Electric Power Syst Res 76:916–927. doi:10.1016/j.epsr.2005.11.004

    Article  Google Scholar 

  • Neumann T, Nolopp K, Herklotz K (2004) First operating experience with the Fino1 research platform in the North Sea. DEWI Magazin 24:27–32

    Google Scholar 

  • Niklasson G (1997) Bockstigen-Valar 2.5 MW offshore wind farm. In: Proceedings of Offshore Wind Energy in Mediterranean and other European Seas OWEMES 97 conference, La Maddalena, Italy, 10–11 April 1997

  • Onogi K, Koide H, Sakamoto M, Kobayashi S, Tsutsui J, Hatsushika H, Matsumoto T, Yamazaki N, Kamahori H, Takahashi K, Kato K, Oyama R, Ose T, Kadokura S, Wada K (2005) JRA-25: Japanese 25-year reanalysis project – progress and status. Q J R Meteorol Soc 131:3259–3268. doi:10.1256/qj.05.88

    Article  Google Scholar 

  • Petersen EL (1992) Wind resources of Europe (the offshore and coastal resources). EWEA special topic conference ’92, 8–11 September 1992, Herning, Denmark

  • Pryor SC, Barthelmie RJ (2001) Comparison of potential power production at on- and off-shore sites. Wind Energy 4:173–181. doi:10.1002/we.54

    Article  Google Scholar 

  • Pryor SC, Barthelmie RJ (2003) Long term trends in near surface flow over the Baltic. Int J Climatol 23:271–289. doi:10.1002/joc.878

    Article  Google Scholar 

  • Pryor SC, Nielsen M, Barthelmie RJ, Mann J (2004) Can satellite sampling of offshore wind speeds realistically represent wind speed distributions? Part II: quantifying uncertainties associated with sampling strategy and distribution fitting methods. J Appl Meteorol 43:739–750. doi:10.1175/2096.1

    Article  Google Scholar 

  • Pryor SC, Barthelmie RJ, Kjellström E (2005a) Analyses of the potential climate change impact on wind energy resources in northern Europe using output from a Regional Climate Model. Clim Dyn 25:815–835. doi:10.1007/s00382-005-0072-x

    Article  Google Scholar 

  • Pryor SC, Barthelmie RJ, Schoof JT (2005b) The impact of non-stationarities in the climate system on the definition of ‘a normal wind year’: a case study from the Baltic. Int J Climatol 25:735–752. doi:10.1002/joc.1151

    Article  Google Scholar 

  • Pryor SC, Schoof JT, Barthelmie RJ (2005c) Climate change impacts on wind speeds and wind energy density in northern Europe: results from empirical downscaling of multiple AOGCMs. Clim Res 29:183–198. doi:10.3354/cr029183

    Article  Google Scholar 

  • Pryor SC, Schoof JT, Barthelmie RJ (2005d) Empirical downscaling of wind speed probability distributions. J Geophys Res 110. doi:10.1029/2005JD005899

  • Pryor SC, Barthelmie RJ, Schoof JT (2006) Inter-annual variability of wind indices over Europe. Wind Energy 9:27–38. doi:10.1002/we.178

    Article  Google Scholar 

  • Pryor SC, Barthelmie RJ, Young DT, Takle ES, Arritt RW, Flory D, Gutowski WJ Jr, Nunes A, Road J (2008) Wind speed trends over the contiguous USA. J Geophys Res (in review)

  • Quayle RG (1980) Climatic comparisons of estimated and measured winds from ships. J Appl Meteorol 19:142–156. doi:10.1175/1520-0450(1980)019<0142:CCOEAM>2.0.CO;2

    Article  Google Scholar 

  • Ratto CF, Festa R, Romeo C, Frumento OA, Galluzzi M (1994) Mass-consistent models for wind fields over complex terrain: the state of the art. Environ Softw 9:247–268. doi:10.1016/0266-9838(94)90023-X

    Article  Google Scholar 

  • Rogers A, Rogers J, Manwell JF (2005) Comparison of the performance of four measure-correlate-predict algorithms. J Wind Eng Ind Aerodyn 93:243–264. doi:10.1016/j.jweia.2004.12.002

    Article  Google Scholar 

  • Schmidt H, Puttker J (1991) Wind and wave conditions in 55 European coastal sea areas, determined from weather and wave observations of voluntary commercial ships. Deutscher Wetterdienst Seewetteramt, Hamburg, Germany

    Google Scholar 

  • Sempreviva AM, Furevik B, Barthelmie R (2004) Offshore wind resource in the Mediterranean. In: Proceeding of the European wind energy conference EWEC, London, November 2004. Available on CDROM

  • Sempreviva AM, Furevik BR, Barthelmie RJ, Cheruy F, Jimenes B, Transerici C (2006) Offshore wind energy potential in the Mediterranean basin. In: Proceedings of the conference, offshore wind energy in Mediterranean and other European Seas, OWEMES, Civitavecchia, Italy, 19–21 April 2006, http://192.107.92.31/test/owemes/8.pdf

  • Sempreviva AM, Furevik BR, Cheruy F, Transerici C, Barthelmie R (2007) Comparison of the offshore wind climatology from quikSCAT and the GCM LMDZOR in the Mediterranean Sea basin. In: Proceedings of the European Offshore Wind Energy conference, Berlin, 1–4 December 2007. Available on CDROM

  • Sjöholm M, Mikkelsen T, Mann J, Enevoldsen K, Courtney M (2008) Time series analysis of continuous-wave coherent Doppler LIDAR wind measurements. 14. International symposium for the advancement of boundary layer remote sensing, Risø (DK), 23–25 Jun 2008. IOP Conf. Ser: Earth Environ. Sci.1, 012051 6p

  • Smith DA, Harris M, Coffey AS, Mikkelsen T, Joergensen HE, Mann J, Danielian R (2006) Wind LIDAR evaluation at the Danish wind test site in Høvsøre. Wind Energy 9:87–93. doi:10.1002/we.193

    Article  Google Scholar 

  • Soukissian TH, Chronis GT, Nittis K (1999) POSEIDON: operational marine monitoring system for Greek Seas. Sea Technol 40:31–37

    Google Scholar 

  • Soukissian TH, Prospathopoulos A, Diamanti C (2002) Wave and wind data analysis of the Aegean Sea. Preliminary results. Glob Atmos Ocean Syst 8(2–3):163–189. doi:10.1080/1023673029000003525

    Article  Google Scholar 

  • Stoffelen A, Anderson DLT (1997) Scatterometer data interpretation: estimation and validation of the transfer function CMOD4. J Geophys Res 102:5767–5780. doi:10.1029/96JC02860

    Article  Google Scholar 

  • Stull RB (1988) Introduction to the boundary-layer meteorology. Kluwer Academic Publishers, Dordrecht, 666 pp

  • Suzuki N, Donelan MA, Plant WJ (2007) On the sub-grid-scale variability of oceanic winds and the accuracy of numerical weather prediction models as deduced from QuikSCAT backscatter distributions. J Geophys Res 112. doi:10.1029/2005JC003437

  • Tambke J, Lange M, Focken U, Wolff J, Bye J (2005) Forecasting offshore wind speeds above the North Sea. Wind Energy 8:3–16. doi:10.1002/we.140

    Article  Google Scholar 

  • Troen I, Petersen EL (1989) European Wind Atlas. Risø National Laboratory, Roskilde, Denmark, ISBN 87-550-1482-8, 656 pp

  • Uppala SM, Kållberg PW, Simmons AJ, Andrae U, da Costa Bechtold V, Fiorino M, Gibson JK, Haseler J, Hernandez A, Kelly GA, Li X, Onogi K, Saarinen S, Sokka N, Allan RP, Andersson E, Arpe K, Balmaseda MA, Beljaars ACM, van de Berg L, Bidlot J, Bormann N, Caires S, Chevallier F, Dethof A, Dragosavac M, Fisher M, Fuentes M, Hagemann S, Hólm E, Hoskins BJ, Isaksen L, Janssen PAEM, Jenne R, McNally AP, Mahfouf J-F, Morcrette J-J, Rayner NA, Saunders RW, Simon P, Sterl A, Trenberth KE, Untch A, Vasiljevic D, Viterbo P, Woollen J (2005) The ERA-40 reanalysis. Q J R Meteorol Soc 131:2961–3012. doi:10.1256/qj.04.176

    Article  Google Scholar 

  • Van Wijk AJM, Niuewenhout FDJ, Turkenburg WC (1986) Development of a diabatic procedure for wind speed extrapolation in a coastal region. In: Proceedings of the European wind energy conference, EWEC 1986, October 1986, Rome, Italy

  • Vermeulen PEJ, Oemraw B, Wieringa J (1985) Wind tunnel measurements of the flow distortion near the anemometer positions on Penzoil k-13A platform. Report No. TNO 85-01246, Apeldoorn, The Netherlands

  • Watson G, Halliday J, Palutikof J, Holt T, Barthelmie R, Coelingh J, Folkerts L, Wiegerinck G, van Zuylen E, Cleijne J, Hommel G (2000) POWER – a methodology for the prediction of offshore wind energy resources. In: Proceedings of the offshore wind energy in Mediterranean and Other European Seas OWEMES conference. ATENA/ENEA, Sicily, pp 111–122

  • Wilhelmsson D, Malm T, Ohman MC (2006) The influence of offshore wind power on demersal fish. ICES J Mar Sci 63:775–784. doi:10.1016/j.icesjms.2006.02.001

    Article  Google Scholar 

  • Young GS, Sikora TD, Winstead NS (2007) Manual and semi automated wind direction editing for use in the generation of synthetic aperture radar wind speed imagery. J Appl Meteorol Climatol 46:776–790. doi:10.1175/JAM2507.1

    Article  Google Scholar 

Download references

Acknowledgements

This work was partially funded by the European Commission project “Prediction Of Waves, Wakes and Offshore Wind” (POW’WOW) (019898(SES6)). Rebecca Barthelmie acknowledges support from the Scottish Funding Council and the Edinburgh Research Partnership. Sara Pryor acknowledges funding support from the National Science Foundation (grant # 0618364). The authors wish to thank ESA—European Space Agency—for supplying Fig. 10.

Author information

Authors and Affiliations

  1. Institute of Atmospheric Sciences and Climate, ISAC-CNR c/o CRATI, Zona Industriale Lamezia Terme, 88046, Lamezia Terme, Italy

    A. M. Sempreviva

  2. Wind Energy Division, Risø National Laboratory for Sustainable Energy, Technical University of Denmark, P.O. Box 49, 4000, Roskilde, Denmark

    A. M. Sempreviva

  3. Atmospheric Science Program, Department of Geography, Indiana University, Bloomington, IN, 47405, USA

    R. J. Barthelmie & S. C. Pryor

  4. Institute for Energy Systems, School of Engineering and Electronics, The University of Edinburgh, Edinburgh, Scotland, UK

    R. J. Barthelmie

Authors
  1. A. M. Sempreviva
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. J. Barthelmie
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. C. Pryor
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. M. Sempreviva.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Sempreviva, A.M., Barthelmie, R.J. & Pryor, S.C. Review of Methodologies for Offshore Wind Resource Assessment in European Seas. Surv Geophys 29, 471–497 (2008). https://doi.org/10.1007/s10712-008-9050-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10712-008-9050-2

Keywords

Search

Navigation