1 Introduction

Despite ongoing advocacy for moving mathematics teaching in more student-centred directions, research indicates that achieving this poses considerable challenges. The struggle to break away from rule-based, rote-oriented practices towards more conceptually oriented exploratory engagement is, we argue, most acute in contexts where teaching takes place in a language that is different from the teachers’ and their students’ home language (L1), as is the case for most South African classrooms. The significance of this paper does, however, extend beyond a South African context. Worldwide, issues relating to multilingualism are an increasing focus of attention. Globalisation and mass migration have led to “rapidly changing demographics [that] challenge education systems everywhere” (Heugh, Prinsloo, Makgamatha, Diedericks, & Winnaar, 2017, p. 197).

The guiding dyad for this paper is ‘right answerism’ as against ‘exploratory talk’. Barnes (2010) describes ‘exploratory talk’ as the antithesis of ‘right answerism’. ‘Right answerism’, most common where a culture of asking closed questions prevails, limits students’ opportunities “to think aloud ... to talk their way into understanding”. ‘Exploratory talk’, by contrast, constitutes “a ready tool for trying out different ways of thinking and understanding” (Barnes, 2010, pp. 7–9). This paper is concerned with the predicament facing students who are expected to learn mathematics in and through a second language (L2) before they have become adequately proficient in that language. ‘Right answerism’ in such non-ideal circumstances may constitute a short-term survival mechanism. In the longer term, however, it undermines genuine opportunities for using language as a tool for the kind of mathematical thinking that conduces to development of “deep and interconnected understandings of mathematical concepts, procedures, and principles, not simply an ability to memorize formulas and apply procedures” (Stein, Grover, & Henningsen, 1996, p. 456).

For this paper, we analyse classroom talk excerpts from a South African grade 4 mathematics lesson. The lesson was taught in English, an L2 to both the teacher (Ms. M) and her students (we use pseudonyms throughout in referring to individual children). isiXhosa is the L1 for both Ms. M and her students, but, while Ms. M is a competent bilingual, her students clearly struggled to articulate their thinking in English.

The focus of Ms. M’s lesson was the relative sizes of different unit fractions. Helping students grasp the inverse order relationship in unit fractions is “not easy to attain” (Cortina, Visnovska, & Zuniga, 2014, p. 81). In the case of Ms. M’s lesson, she wanted students to demonstrate that they understood that ¼ > 1/8, even though, in whole number terms, 4 < 8. Her struggle in getting this across to the children was, we believe, compounded because discussion had to take place through an L2. Our question then for this paper is: “What is the nature of the talk in the observed lesson and how does it appear to enable or constrain mathematical meaning-making?”

Our work is broadly guided by a socio-cultural perspective (Vygotsky, 1930). Of particular relevance to this paper is the assumption that learning mathematics involves mediation as students move from ‘everyday’ and ‘spontaneous’ concepts towards the increasingly ‘abstract’ and ‘scientific’ mathematical concepts they will encounter as they move up through the grades. Embedded in such ‘scientific’ concepts is significantly more information requiring processing than would be the case in a simple ‘everyday’ exchange. Such processing becomes infinitely greater where students are operating through an, as yet, incompletely-mastered L2. Our analysis draws on aspects of the work of two educational linguists: Cummins and Gibbons.

2 Sociolinguistic insights

2.1 Mastery of academic language in and through an L2

Cummins developed and refined a number of conceptual frameworks which in our view have both theoretical and pragmatic cogency. A core concern throughout his work has been enhancement of educational prospects for language-minority students. His work highlights links between students’ L1 proficiency and their developing proficiency in an L2; principally mastery of academic language in and through the L2.

Cummins (1979) made the important distinction between students’ interpersonal communication skills (BICS), which he also refers to as ‘conversational fluency’, and their cognitive academic language proficiency (CALP). CALP refers to a student’s ability to engage in more academically oriented classroom discourse around ideas and concepts. Cummins has been instrumental in alerting educators to risks associated with a conflation of L2 students’ everyday conversational and academic language proficiencies. While noting the importance of viewing BICS and CALP as operating along a continuum, not dichotomously (Cummins, 1984), he provided research evidence indicating that whereas conversational fluency in an L2 develops quite quickly (within 6 months to 2 years, depending on how much exposure students have to the L2), developing native-like proficiency in the more formal, academic registers associated with curriculum content takes considerably longer (5 to 7, or even 10 years) (Cummins, 1994). Such findings draw attention to difficulties students face when required to transition to an L2 as the language of learning and teaching (LoLT) before they are adequately proficient in it beyond the “fluent ... peer-appropriate face-to-face communicative skill” level (Cummins, 1984, p. 6).

For many students, school constitutes their main exposure to the L2, and, unless schools are sensitive to differences between “the surface or conversational aspects of children’s language and the deeper [cognitively demanding] aspects of proficiency ... more closely related to conceptual and academic development” (Cummins, 1994, p. 37), the danger exists that basic conversational fluency is taken as evidence of L2 students’ overall linguistic proficiency. This may lead to premature withdrawal of support for ongoing development of their CALP in the L2, making it that much more difficult for L2 students to realise their academic potential.

Cummins considers monolingual approaches in multilingual contexts as exclusionary and devaluing of the identities of marginalised students (2015). Writing of underachievement in South African rural and township schools, he advocated for expansion of “the instructional space to include students’ and teachers’ multilingual repertoires” (2015, p. 278). Acknowledgement of students’ L1 as an important parallel resource underpins Cummins’s linguistic interdependence hypothesis. Through cross-lingual transfer, he argued, “conceptual knowledge developed in one language helps to make input in the other language comprehensible” (2000, p. 39). Using the image of a ‘dual-iceberg’ (see Fig. 1, below), he explained that while surface features of students’ L1 and L2 may differ (in terms of grammar; phonology etc.), any number of common underlying proficiencies transcend such surface differences. This would include students’ literacy skills; numeracy skills; existing conceptual understandings; and the cognitive skills required in using language to think, to reason, and to explore ideas.

Fig. 1
figure 1

Cummins’s representation of cross-lingual transfer (2005, p. 7, adapted)

Full size image

The implication from Fig. 1 is that if bilingual students have in their L1 the conceptual grasp, for example, that ‘the greater the number of equal pieces a whole is divided into, the smaller each piece will be’; there would be no need to learn this general principle afresh in the L2. All that would be needed would be new linguistic ‘labels’ for revisiting this concept in L2. This notwithstanding, Cummins cautions that ease of transfer of proficiencies across languages is to an extent influenced by whether or not the languages involved are cognate (2005). Whereas English and German, for example, are cognate languages (they come from the same language family), English and isiXhosa (Ms. M’s and her students’ L1) are non-cognate languages.

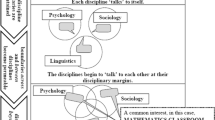
To assist teachers in pitching tasks appropriately Cummins (1994) used two intersecting continua to indicate that a task’s linguistic and conceptual challenge is a function of (a) the extent to which it is embedded in more concrete and familiar territory, where contextual clues aid comprehension, and (b) the level of cognitive demand.

In relation to Barnes’s idea of helping (L2) students “talk their way into understanding” (2010, p. 7), the route through Cummins’s quadrants (Fig. 2, above) would be to move from cognitively undemanding and context-embedded talk (quadrant A); through talk that is more cognitively demanding but still context-embedded (quadrant B); and on towards more cognitively demanding discussion involving progressively more specialised, formal, and abstract discipline-based academic registers (quadrant D). Time spent in quadrant C (context-reduced/cognitively undemanding) would generally be seen as having negligible pedagogical merit. Some iterative movement along both continuum axes as the teacher monitors and responds to students’ developing linguistic and conceptual proficiencies would, however, be necessary.

Fig. 2
figure 2

Cummins’s cognitive and contextual demands framework (1994, p. 41, adapted)

Full size image

What makes specialised registers more cognitively challenging is their ‘semantic density’ (Maton, 2011). More meaning becomes condensed within a word or phrase. So, for example, ‘one whole cut into two equal parts’ is less semantically dense and thus easier to conceptualise than ‘½’ or ‘1 is the numerator and 2 is the denominator’. Discussion in quadrant A (about, for example, dividing a cake into two equal parts) prepares students for the transition to specialised, discipline-based talk. So, in relation to teaching unit fractions, a teacher might start (as did Ms. M) in the everyday by establishing whether or not, for example, students liked cake (quadrant A). Desirable though it may be to start younger students off here, remaining in Quadrant A for any extended period would be counterproductive, so next would be to get students to imagine dividing a cake into equal parts (for example, eighths or quarters), and to think about which fraction portion of the cake would be the bigger (quadrant B), and why (an open question which would begin the move towards quadrant D). Conceptualising mathematically which unit fraction (written in symbolic form) is bigger: ¼ or 1/8? would mark entry into quadrant D where the general principle that the smaller the denominator, the bigger the unit fraction could then be established. Once a student has grasped a particular general principle, while semantic density would remain an intrinsic feature of the text involved, the cognitive demand relating to ‘making meaning’ of the general principle would diminish. This is because automaticity (“rapid”, “precise” and “unconscious processing” (Silberstein, 1994, p. 7)) at both the semantic and the conceptual level would have kicked in.

Criticisms have been levelled at aspects of Cummins’s theoretical constructs, in particular that his distinction between BICS and CALP is insufficiently nuanced and contributes to deficit views of L2 students (Edelsky, 1990; MacSwan, 2000). A more detailed and holistic reading of his work, however, coupled with recognition of the positive impact his ideas continue to have in the multilingual education field, serves, we believe, to offset such criticism. Cummins himself writes that his theoretical constructs should not be viewed as “valid or invalid, true or false” but assessed rather in terms of their “adequacy and usefulness” (2016, p. 941). (See Cummins (2017) for further explication of his BICS/CALP distinction, plus his response to critiques of his work, including implications around deficit.)

2.2 The ‘mode continuum’

Gibbons, working in the area of academic language and literacy development, notes that successful teaching, particularly in L2 contexts, requires “mediation across orders of discourse” as students “learn to use language for a range of purposes” (2003, p. 250). Guidance in navigating the ‘mode continuum’ from common-sense “more spoken-like” expression of ideas towards the more specialist, cognitively demanding, and “written-like” subject-specific articulation required within different curriculum areas is very important (Gibbons, 2006, p. 34 [italics in the original]). Equally important is a “high-challenge, high-support” classroom ethos (Gibbons, 2015, p. 18). Table 1 outlines key differences between these modes.

Table 1 Comparison of different modes of discourse
Full size table

The stylistic features of more spoken-like language (face-to-face interaction, spontaneity, lexical simplicity) echo Barnes’s characterisation of the kind of ‘exploratory talk’ that affords students opportunities to “relate new ways of thinking to … existing preconceptions” (2010, p. 8), thus providing a ‘bridge’ into the more formal, specialised written-like language generally associated with more precise subject-specific meaning. Teachers’ ‘meshing’ of “everyday and subject specific ways of meaning ... building on [students’] prior knowledge and current language as a way of introducing them to new language” (Gibbons, 2009, p. 62) is especially helpful when students face the dual challenge of acquiring an L2 while simultaneously using it to ‘make meaning’ of classroom encounters with mathematics.

2.3 Models for bilingual education

The degree to which L2 students can draw on some measure of common underlying proficiency from their L1 depends on what opportunities they have had to develop literacy and numeracy proficiencies in their L1. This is largely a function of what model of bilingual education they experience. In Fig. 3, below, we summarise from the literature five key models of bilingual education. We represent these graphically relative to the concepts of ‘additive’ and ‘subtractive’ bilingualism: additive bilingualism being where students learn and use an L2 “at no cost to their first language”; subtractive being where students’ opportunities to use their L1 are “taken away”, risking its “being replaced by the second language” (Baker, 2011, p. 4).

Fig. 3
figure 3

Some models of bilingual education

Full size image

Many countries, South Africa included, advocate additive multilingualism, whereby students’ L1s remain a resource to draw on throughout their schooling (models D and E of Fig. 3). In practice, however, most students across sub-Saharan Africa (see Heugh, 2005) experience model B of Fig. 3. They start their schooling in L1 and then move to a dominant (often, former colonial) language in their fourth year of schooling (see, for example, Essien, 2018). This ‘early exit’ model’ “shows an inherent design flaw”; namely, “it is almost impossible for learners to learn enough of the second language in three years to switch to a second-language medium of instruction in grade 4” (Heugh, 2005, pp. 6; 7).

We have explored the notion of ‘conversational’ as compared with ‘academic’ language and the importance of balancing cognitive demand with contextual support as students encounter increasingly generalised (and generalizable) forms of mathematical knowledge and reasoning. We have noted also the importance, particularly in L2 circumstances, of mediating students’ movement along the mode continuum from more spoken-like to more written-like linguistic proficiencies. We have identified a range of models of bilingual education and argued that additive forms facilitate students’ opportunities for building upon their common underlying proficiency. We now embed our discussion within the South African context. We use these sociolinguistic perspectives to analyse the classroom talk in one of Ms. M’s grade 4 lessons to illuminate some aspects of the challenge she faced in attempting to move away from ‘right answerism’ and towards more ‘exploratory talk’.

3 Contextual background

South Africa’s Language in Education Policy (Department of Education DoE, 1997) advocates additive bilingualism. Despite English being the home language for less than 10% of the population, it dominates the education landscape, so conducing instead to subtractive linguistic circumstances. Drawing on Department of Basic Education (DBE) data, Robertson and Graven (2015) noted that roughly 20% of Grade 1 students begin their schooling through English, but by grade 4 this increases sharply to 80%. Overwhelmingly, Black parents choose English believing it to be their children’s route to accessing ‘social goods’ (Setati, 2008). Macdonald, however, used the metaphor ‘swimming up the waterfall’ to “convey the nearly impossible demands put upon African children in their pursuit of genuine learning through the medium of English in primary school” (2002, p. 112); a demand further compounded by an expanding and progressively more abstract mathematics curriculum as students move up the grades.

South African state schools are classified into five quintiles (Qs) based on catchment area (designated according to the income, unemployment rate, and level of education in the community a school serves). Q1 represents the ‘poorest’; Q5 the ‘least poor’ schools (DoE, 1998). Despite the State’s ‘pro-poor’ ideology whereby more state funding is allocated to the poorest schools, the educational performance of students attending Q1–4 schools is “increasingly below the required level” (Adler & Pillay, 2017, p. 13). In specific relation to mathematics, a majority of students attending such schools lag by as many as 3 years behind grade standard (Schollar, 2008).

The impact of poverty on students’ opportunities to achieve is well-documented. Equally well-documented are links between proficiency in the LoLT and achievement. In a report on South African grades 5 and 6 students’ participation in the Third International Mathematics and Science Study (TIMSS) (1995), for example, Howie (1997) identified language as a key contributory factor to students’ low mathematics achievement compared with students from other participating countries. She noted that differences between home and instructional language, “often lead to communication problems, particularly where unfamiliar new concepts … are involved” (Howie, 1997, p. 54). Similarly, in their review of research at the language/mathematics interface, Setati, Chitera, and Essien (2009) noted that “all research in this area of study identifies language as a major determinant of success in mathematics learning” (p. 66). They further noted that little consensus existed regarding how best to mediate at this interface. While larger-scale studies advocated stronger efforts at improving students’ proficiency in the LoLT (English, predominantly); smaller-scale studies recommended greater commitment to use of students’ home languages as resources for mathematical meaning-making. The Report on South Africa’s participation in the most recent Trends in International Mathematics and Science Study (TIMSS) (2015) too noted the significant advantage enjoyed by students “across the TIMSS 2015 cohort” who “always or almost always spoke the language of learning and teaching at home” (Reddy et al., 2016, p. 8).

4 Empirical component

We demonstrate in the following sections what our sociolinguistic tools allow us to see relative to one teacher’s challenge of eliciting exploratory talk around unit fractions in and through an L2. We begin by briefly outlining our decisions as regards the selection of site, participant teacher, and lesson.

4.1 Site/ participant/ lesson selection

Ms. M was included in the broader case study of which this paper is a part because, for the period 2011–2015, she participated in a project run by Rhodes University’s South African Numeracy Chair (SANC). This Chair is held by the second author. The project was a professional development (PD) programme focussing on the needs of primary school mathematics teachers. The importance of student-centred interactional styles, including high levels of verbal participation, was foregrounded throughout the running of this programme.

Motivated by a desire to identify and explore synergistic opportunities at the literacy/numeracy interface when students are learning mathematics in and through an L2, the first author actively participated alongside teachers in SANC’s PD project from 2013.

The broader study looked at grade 4 mathematics teachers’ use of classroom talk and how such talk appeared to enable and/or constrain mathematical meaning-making. Data, based on classroom observation and interviews for two grade 4 teachers in two schools, were collected over 4 weeks of teaching. Thirty-one mathematics lessons were observed. Audio-/video-recordings of all lessons and interviews were transcribed verbatim for subsequent analysis. Data from the broader study for both sites revealed low levels of student verbal participation in the observed lessons, and little exploratory-type talk (Robertson, 2017).

Grade 4 was selected because it is a critical transitional year. Many students, particularly those from disadvantaged backgrounds, are vulnerable to falling into what is termed the ‘fourth grade slump’ (Chall & Jacobs, 2003) as the carefully-scaffolded literacy and numeracy texts and tasks of earlier grades give way to an expanded curriculum and the expectation of more self-directed learning. For the majority of South African children this is also the year English becomes the LoLT.

For this paper, we had a choice of two L2 learning contexts from the broader study. While both teachers in the study taught through L2, different models of bilingual education were practised. Ms. M’s school (a Q4 school) had a ‘straight for English’ policy. From grade 1 all teaching at the school, apart from isiXhosa lessons, was conducted in English, representing the most subtractive model of bilingual education (model A of Fig. 3). At Ms. P’s school (a Q3 school), model B of Fig. 3 was practised. Its grade 4s were thus in their first year of an L2 LoLT.

We chose Ms. M’s classroom for this paper because, despite 4 years of exposure to an English LoLT, significant challenges remained in trying to elicit exploratory-type talk during mathematics lessons. We suggest part of these challenges could be put down to a policy anomaly. When schools opt for the ‘straight for English’ route, they must gear their English language teaching towards the English Home Language curriculum (DoE, 2002). Consequently, although English was Ms. M’s students’ L2, paradoxically—in curricular terms—it was designated their L1; and, despite Ms. M and her grade 4 s all being native speakers of isiXhosa, isiXhosa was taught as an L2. Accepting Cummins’s 5–7 year time frame for developing CALP in an L2, this meant that Ms. M’s students, as artificially designated ‘English Home Language’ students, would not have had the benefit of English Second language instruction explicitly geared towards developing communicative and academic competence in English (a situation likely compounded by English and isiXhosa being non-cognate languages).

Fourteen of Ms. M’s observed grade 4 mathematics lessons were included in the broader study. Six involved teaching fractions. In this paper, we focus on the talk observed in the first fraction lesson. We regard this choice as ‘convenient’ in the sense that we do not then have to elaborate on any of the preceding lessons. Similar arguments could be made for choosing a subsequent lesson since the broader study’s findings did establish that the patterns of discourse we illuminate in this paper are not atypical (see Robertson, 2017).

Results from Ms. M’s students’ grade 4 Mathematics Annual National Assessments (ANAs) indicate that many struggled with the assessment tasks. Most students (75%) scored below 50%. The class average was 37.9%; 3.1% above provincial average; 0.9% above national average (DBE, 2014, pp. 9; 52). The following interview comment from Ms. M regarding how she saw the relationship between her grade 4s’ L2 proficiencies and the linguistic demands of the mathematics classroom reverberates with the ‘swimming up the waterfall’ metaphor cited earlier (Macdonald, 2002). Through these words we see Ms. M placing language, particularly use of English, at the heart of her students’ struggle with mathematical meaning-making:

Language is very important, because maths isn’t only about numbers: ‘add this’, ‘subtract this’. There’s lots of language involved. There’s English language first of all: that is a challenge to these learners. And also the maths language itself. So, if one doesn’t have English as a language and also the maths language, then […] there’s no learning and teaching that is taking place. And what frustrates ~ I’m in the Grade 4 class ~ it’s as though I am teaching to the Grade 2s. [...] I think I’m going nowhere. I’m doing nothing. Because I think, “How can I move on when they don’t understand?” Sometimes I think it’s easy. But to them, it’s not easy. (Interview 2, Lines 56–66)

4.2 Students’ observed language behaviours

During the first author’s periods of observation, when arriving at Ms. M’s school just before school or during mid-morning break-times, she overheard the noisy playground exuberance of the students’ L1 social communications. Once inside the classroom, such exuberance abated: time now for more academically-oriented talk. In terms of Cummins’s distinction between conversational and academic forms of communication, what was overheard outside the classroom was the student’s primary discourse (L1 BICS). It was grade-appropriate competence in a secondary discourse (mathematical CALP in and through an L2) that was required in the classroom. As Ms. M remarked, however, “all these learners here at school are Xhosa-speaking learners, and maths is done in English. [...] I think that is a main problem” (Interview 1, Lines 73–75).

4.3 Analysis of observed classroom talk

The 50 -in lesson comprised 372 turns. In the following analysis of lesson talk, we focus on turns 1–158. Table 2’s structuring (below) derives from a combination of Cummins’s distinction between BICS and CALP and Gibbons’s articulation of the need for explicit mediation of students’ movement across different orders of classroom discourse from more spoken-like to more written-like expressions of (mathematical) thinking. Our initial fine-grained analysis of turns 1–158 included an attempt to add to the above combination some of the features identified by mathematics education researchers as characteristic of cognitively demanding mathematical tasks (tasks that require, inter alia, that students respond to questions/input in multiple ways, and/or justify their reasoning). We quickly found, however, that there was no straight-forward alignment between this sort of task-oriented framework and our desired talk-oriented framework. We therefore decided to keep within the Cummins/Gibbons amalgam. Based on this amalgam, we have classified the lesson talk for turns 1–158 into the three categories below. (Talk related to discipline and classroom management was omitted.)

  1. (1)

    Talk that is embedded within students’ lived-experience, and reflective of an ‘everyday’ BICS−/spoken-like register;

  2. (2)

    Talk that more closely aligns with an ‘academic’ CALP−/written-like classroom register;

  3. (3)

    Talk that contains both BICS- and CALP-like features, and which invites discussion to move in more ‘exploratory’ directions.

Table 2 Analysis of movement across a BICS-/CALP-like continuum (lesson turns 1–158)
Full size table

Both authors independently coded the transcript into these three categories. There was a high degree of inter-rater agreement. For the few utterances where there was disagreement, consensus was reached following discussion.

Table 3 below provides a summary of our analysis of the nature of the talk reflected in Table 2.

Table 3 Overall analysis of observed talk
Full size table

Linking our categorisation of the classroom talk back to Cummins’s quadrant framework (Fig. 2), we notice Ms. M’s efforts to move discussion from quadrant A (context-embedded, cognitively undemanding) through quadrant B (still context-embedded, but more cognitively demanding) and across into quadrant D where talk becomes more semantically-dense, mathematically-precise, context-reduced, and geared towards establishing the general principle that the bigger the denominator, the smaller the unit fraction. We see that Ms. M’s attempts at a stronger ‘bridging’ or ‘meshing’ across and between conversational (BICS-type) and formal, academic (CALP-type) talk in exploring the ‘which is bigger/smaller’ questions and her ‘why?’, ‘why not?, ‘which?’ questions produce only brief responses, more reflective of ‘right answerism’ than of exploratory engagement. Essentially, the more CALP-like, context-reduced ‘classroom’ talk we have assigned to Table 2’s right-hand column would seem to be more characteristic of Cummins’s Quadrant C. Almost all utterances in this column can be categorised as single, unambiguous ‘right’ (or ‘wrong’) answers, based on students’ attempts at recalling, re-capping, and/or reiterating previously-established mathematical ‘facts’ and/or attempting to remember previously-covered mathematical terminology. Once known (automatised), this CALP-like talk on unit fractions (including using the appropriate terminology) would become no more challenging than BICS-like talk. Of note, while developing new specialised language is likely to be challenging because of the semantic density of terms such as ‘numerator,’ few other characteristics of more cognitively demanding mathematical talk (such as talk that, in Stein et al.’s (1996) terms, involved answering questions in multiple ways, drawing on multiple representations, or justifying one’s answers) were evident. Almost all the CALP-like talk shown in Table 2 is at the most basic level. There is little evidence of students taking up Ms. M’s challenge to explain or explore in general terms why ¼ > 1/8; or to explain or justify their responses to her various promptings.

Although we cannot make a definitive claim, it is possible that Ms. M’s use of the cake example and the initial fractions ¼ and 1/8 were a strategic choice based on her awareness that the example of dividing a cake is commonly used in the context of the fraction problems included in the Mathematics ANA papers. So, while this lesson failed to establish the general principle that the bigger the denominator the smaller the unit fraction, it is possible that knowing a set of specific facts about the relative sizes of halves, quarters and eighths in the context of cakes would enable her students to answer correctly were such questions to be included in an external assessment task; this despite their not knowing the underlying principle.

Table 4, below, lists the students’ verbal contributions throughout the course of the whole lesson (turns 1–372), arranged according to which end of Gibbons’s ‘mode continuum’ the utterances most closely reflect. As Table 4 shows, marked features of Ms. M’s students’ talk were its briefness (most of it of a one- or two-word order), its often being given in chorus, and none of it being self-initiated. This pattern is not dissimilar to that noted by other South African researchers (for example, Hoadley, 2012), a difference being, however, the prominence given to the importance of ‘maths talk’ during Ms. M’s 5 years’ of participation in SANC activities.

Table 4 Ms M’s students’ verbal contributions for the full lesson (turns 1–372)
Full size table

The ratio of ‘chorused’ to ‘individualised’ responses in Table 4 (58 to 42%) was not out of character with the patterns of verbal behaviour observed in Ms. M’s other mathematics lessons. In terms of Cummins’s ‘conversational’ versus ‘academic’ language distinction, several of the student answers listed in Table 4 would classify as coming from BICS-type language usage (e.g., ‘number’; ‘a little bit hard’; ‘fish’; ‘yes’) and others might be regarded as being of a more CALP-type (e.g., ‘seventh’; ‘because the quarter is bigger than the eighth’; ‘denominator’; ‘numerator’). Relative also to Gibbons’s mode continuum (2006), the utterances listed in Table 4 represent a mix of more spoken-like (e.g. ‘number at the bottom’) and more written-like (e.g., ‘Because the quarter is bigger than the eighth’; ‘denominator’ (×4); ‘nominator’ [sic]).

Linking our discussion to our Barnes ‘right answerism’/ ‘exploratory talk’ dyad, we note the absence of the latter. Just three answers began with ‘Because ~’ (a word that potentially marks the start of a reasoning chain). When looked at in context (see Table 2), we note, however, that the students’ use of ‘because’ was instead simply echoing their teacher’s earlier phrasing. They do not repond “in terms of the logic of the text” but “rather ... in terms of prior knowledge” (Cummins, 1984, p. 12). Ms. M’s more open questions asking ‘why?’ (turns 43; 45; 47; 49; 60; 85 and 136), and ‘reason?’ (turn 91) created possibilities for more exploratory talk. This, however, was not realised. For example, turn 85 (‘because it is bigger’) and turn 92 (‘because the quarter is bigger than the eighth’) essentially repeated what was established by previous students who answered ‘a quarter’ to the question ‘which is bigger?’ Answering ‘because it is bigger’ is simply adding the question into the phrasing of the answer. It is not talk indicative of students’ reasoning - based on their having grasped the inverse order relationship - as to why 1/4 is the bigger unit fraction. We thus argue that, while Ms. M’s more open, probing questions as to ‘why’ a quarter is bigger than an eighth (turns 60 and 84) had the potential to elicit student utterances that ‘meshed’ CALP- and BICS-type talk in Quadrant B, such utterances were not forthcoming. Students simply reiterated what had been observed previously coming from classmates: ‘It’s bigger’ (turn 61); ‘Because it is bigger’ (turn 85) and ‘Because the quarter is bigger than the eighth’ (turn 92). Similarly, when she got students to look at a chart to physically see that ¼ is bigger than 1/8 (turns 70–80), a student then had to recite the context-reduced (though example specific) mathematical fact that ‘the quarter is bigger than the eighth’ (turn 92). Furthermore, the predominance of short responses, often chorused, too is suggestive of ‘right answerism’, as is the high frequency of ‘yes’ (21, and mostly in chorus) and ‘no’ (4, 3 being again in chorus). The inclusion of other unit fractions (1/2, 1/5, and 1/7) was used not to draw attention to the general principle guiding comparison of all unit fractions, but to the common numerator (1) and the opportunity to remind students, of mathematical terminology (‘numerator’, ‘denominator’) by getting them to chant these terms out loud (turns 110–115).

While we see in Table 4, some balance between specialised CALP-type and everyday BICS-type responses, we see little of the blended ‘exploratory talk’ needed to move students along the mode continuum towards more specialised articulations of proportional reasoning. For Barnes (2010) ‘right answerism’ involves giving back to the teacher what has been given or previously established. While one would need the full lesson transcript to contextualise each response, most student responses can in this sense be categorised as ‘right answerism’ rather than exploratory talk. Modelling appropriate L2 language (of both a BICS- and a CALP- sort) constitutes a powerful means of simultaneously supporting students’ ongoing L2 acquisition plus exemplifying for them how they themselves might set about generating their own chains of mathematical reasoning. In generating such reasoning chains, we hold the view that, were it not for her school’s straight-for-English policy, Ms. M might have felt freer in terms of using her and her students’ shared L1 (IsiXhosa), as an important additional linguistic and conceptualising resource. This may then well have strengthened her students’ capacity for mathematical meaning-making. We note, given the 5–7 year time-span research indicates is needed for development of L2 CALP (Cummins, 1979), that moving along the ‘mode continuum’ required that Ms. M’s students communicate in English at a level that appeared beyond them.

An additive (as opposed to subtractive) form of bilingualism, in which students were genuinely afforded access to their L1 meaning-making resources would, in Cummins’s terms, have likely promoted “more cognitively engaged learning” (2005, p. 13). In terms of Cummins’s conceptually-persuasive common underlying proficiency hypothesis (2005), use of isiXhosa may have enabled Ms. M’s students to then transfer some of their L1 mathematical meanings across into the L2. We make this suggestion on the basis of observations from the broader study (Robertson, 2017). As is reported here, the second grade 4 mathematics teacher in the study (Ms. P) made extensive use of her and her students’ native isiXhosa. This appeared to impact positively on aspects of the children’s conceptual understanding, strategic competence and adaptive reasoning (after Kilpatrick et al., National Research Council, 2001, p. 116). While we are not claiming that teachers who teach in isiXhosa (or other first languages of learners) are more likely to engage in explorative talk as against ‘right answerism’, the broader study showed that for the two teachers who participated in PD that foregrounded promoting explorative talk in the classroom, and aimed to develop this, the challenge for Ms. M who taught solely in English appeared greater than for Ms. P who drew extensively on isiXhosa.

5 Concluding discussion

Our unpacking of turns 1–158 of Ms. M’s lesson on unit fractions has shown that time spent at the everyday BICS-type level of engagement, and attempts at moving to more formal, CALP-type reasoning are being frustrated by the students’ linguistic under-preparedness to follow their teacher into quadrant B territory. In quadrant B students could have had more opportunity to ‘mesh’ everyday and academic meaning-making talk. They could have conceptually engaged in exploratory talk around everyday notions of how big a slice of cake they might get relative to how many slices the cake is to be divided into. They could have connected the everyday principle that the more people you share the cake with, the smaller the piece of cake (which students seemed to know well) with the more abstract generalised mathematical principle that the greater the denominator of a unit fraction, the smaller the fraction. We note that, having spent most of the lesson time in quadrant A (context-embedded, cognitively undemanding), relatively little time was spent in quadrant B (still context-embedded, but more cognitively demanding). Instead, the students’ unresponsiveness seemed to repeatedly drive Ms. M into the context-reduced and cognitively undemanding space of Quadrant C. What was notably absent was students’ generalised (albeit emergent) mathematical talk of the inverse order relationship in unit fractions which might have been encouraged and engaged within a more context-reduced and cognitively demanding quadrant D-type space.

Because few South African teachers have received support around ways of mediating students’ L2 acquisition in tandem with their mathematics learning, the struggle to move from ‘right answerism’ to more exploratory patterns of classroom talk is seldom explicitly noted or deliberately addressed. Drawing on socio-linguistic theory, we have illuminated the extent and nature of Ms. M’s linguistic and pedagogic challenge relative to helping her students ‘make mathematical meaning’ in a context of subtractive bilingualism. As Table 4 data showed, when called upon to display their mathematical reasoning in L2, predominantly one- to two-word responses were forthcoming, with little evidence of students entering into more exploratory mathematical discourse.

Ms. M’s students’ ‘right’ or ‘wrong’ responses (often chorused) and the relative absence of exploratory discourse, might well invoke a deficit judgement. In trying to explain these findings in non-deficit terms, we have drawn on research around the development of proficiency in ‘academic’ (as opposed to ‘social’) language. Ms. M’s students were neither operating in an immersion situation where they would be mixing with native English-speaking peers and teachers, nor benefitting from the more explicit L2 instruction built into the English Second Language curriculum. We therefore argue that the development of BICS-type discourse in an L2 (let alone CALP-type discourse) would require a great deal more time, attention, practice, and repetition than would be the case were Ms. M’s students learning mathematics in their L1. We argue that the school’s imperative to use L2 as the only medium of instruction results in a ‘subtractive’ form of bilingualism which constrains students’ opportunities to engage in more exploratory forms of mathematics classroom talk.

The discussion and data presented in this paper indicate a need to further assist mathematics teachers like Ms. M towards strategies which replace the short-circuit of ‘right answerism’ with a more sustainable capacity for ‘exploratory’ forms of mathematical talk. This would involve finding ways to support both the L1 and the L2 proficiencies of their students as they move beyond everyday ways of meaning-making towards more mathematically rich ways of articulating mathematical reasoning. Without such support, many students in mathematics classrooms across South Africa risk not simply remaining trapped at the bottom of Macdonald’s metaphorical waterfall but being swept aside by the force of the water. Such a scenario is not unique to South Africa. As noted in our Introduction, multilingualism is increasingly a feature of classrooms across the globe.