Convergence rate for a Radau hp collocation method applied to constrained optimal control

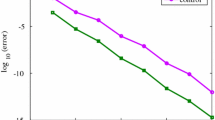
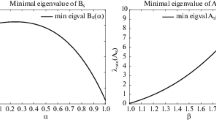
Abstract

For control problems with control constraints, a local convergence rate is established for an hp-method based on collocation at the Radau quadrature points in each mesh interval of the discretization. If the continuous problem has a sufficiently smooth solution and the Hamiltonian satisfies a strong convexity condition, then the discrete problem possesses a local minimizer in a neighborhood of the continuous solution, and as either the number of collocation points or the number of mesh intervals increase, the discrete solution convergences to the continuous solution in the sup-norm. The convergence is exponentially fast with respect to the degree of the polynomials on each mesh interval, while the error is bounded by a polynomial in the mesh spacing. An advantage of the hp-scheme over global polynomials is that there is a convergence guarantee when the mesh is sufficiently small, while the convergence result for global polynomials requires that a norm of the linearized dynamics is sufficiently small. Numerical examples explore the convergence theory.

Appendix: Proof of (P1) and (P2)

We analyze (P1) and (P2) when $\tau _i$, $1 \le i \le N$, are either the Radau quadrature points analyzed in this paper, or the Gauss quadrature points studied in [36].

Lemma 10.1

For either the Gauss or Radau quadrature points, the rows of the matrix $[\mathbf{{W}}^{1/2}\mathbf{{D}}_{1:N}]^{-1}$ have Euclidean length bounded by $\sqrt{2}$. For the Gauss quadrature points, $\Vert \mathbf{{D}}_{1:N}^{-1}\Vert _\infty \le 2$, and $\Vert \mathbf{{D}}_{1:N}^{-1}\Vert _\infty$ approaches 2 as N tends to infinity, while for the Radau quadrature points, $\Vert \mathbf{{D}}_{1:N}^{-1}\Vert _\infty = 2$.

Proof

Given $\mathbf{{p}} \in \mathbb {R}^N$, let $p \in \mathcal{{P}}_N$ denote the polynomial that satisfies $p(-1) = 0$ and $p(\tau _i) = p_i$, $1 \le i \le N$. Let $\dot{\mathbf{{p}}} \in \mathbb {R}^N$ denote the vector with components $\dot{p}_i = \dot{p}(\tau _i)$, and let $\ell _j$ be the Lagrange polynomial defined by

$$\begin{aligned} \ell _j(\tau ) = \prod ^{N}_{\begin{array}{c} i=1\\ i\ne j \end{array}} \frac{\tau -\tau _i}{\tau _j-\tau _i}, \quad 1 \le j \le N. \end{aligned}$$

The identity

$$\begin{aligned} \dot{p}(\tau ) = \sum _{j=1}^N \ell _j(\tau ) \dot{p}_j \end{aligned}$$

(10.1)

holds since $\dot{p} \in \mathcal{{P}}_{N-1}$ and the polynomials on each side of (10.1) are equal at the N quadrature points. Integrate (10.1) to obtain

$$\begin{aligned} p_i = \int _{-1}^{\tau _i} \dot{p}(\tau )\; d\tau = \sum _{j=1}^N \left( \int _{-1}^{\tau _i} \ell _j(\tau ) \; d\tau \right) \dot{p}_j . \end{aligned}$$

(10.2)

Since $\mathbf{{D}}$ is a differentiation matrix and $p(-1) = 0$, it follows that $\mathbf{{D}}_{1:N}\mathbf{{p}} = \dot{\mathbf{{p}}}$. If the vector $\dot{\mathbf{{p}}} = \mathbf{{0}}$, then the polynomial $\dot{p} = 0$ since $\dot{p}$ has degree $N-1$ and vanishes at N points. Since $p(-1) = 0$, it follows that polynomial $p = 0$, which implies that the vector $\mathbf{{p}} = \mathbf{{0}}$. Hence, $\mathbf{{D}}_{1:N}$ is invertible, and $\mathbf{{p}} = \mathbf{{D}}^{-1}\dot{\mathbf{{p}}}$. Comparing the equality $\mathbf{{p}} = \mathbf{{D}}^{-1}\dot{\mathbf{{p}}}$ to (10.2), we deduce that

$$\begin{aligned} (\mathbf{{D}}^{-1})_{ij} = \int _{-1}^{\tau _i} \ell _j(\tau )\; d\tau . \end{aligned}$$

(10.3)

Choose any $s \in [-1, 1]$ and define

$$\begin{aligned} d_j(s) = \int _{-1}^s \ell _j(\tau ) \; d\tau \quad \text{ and } \quad R(s) = \sum _{j=1}^N \frac{d_j(s)^2}{\omega _j}. \end{aligned}$$

Observe that $(\mathbf{{D}}^{-1})_{ij} = d_j(\tau _i)$ and $R(\tau _i)$ is the square of the Euclidean length of row i in $(\mathbf{{W}}^{1/2}\mathbf{{D}})^{-1}$. Let $q \in \mathcal{{P}}_{N-1}$ be the polynomial defined by

$$\begin{aligned} q(\tau ) = \sum _{j=1}^N \frac{d_j(s) \ell _j(\tau )}{\omega _j}. \end{aligned}$$

Hence, by the triangle and Schwarz inequalities,

$$\begin{aligned} R(s) = \int _{-1}^s q(\tau ) \; d\tau \le \int _{-1}^1 |q(\tau )| \;d \tau \le \sqrt{2} \left( \int _{-1}^1 q(\tau )^2 \; d \tau \right) ^{1/2}. \end{aligned}$$

(10.4)

Since $q^2 \in \mathcal{{P}}_{2N-2}$, both Radau and Gauss quadrature are exact, and

$$\begin{aligned} \int _{-1}^1 q(\tau )^2 \; d\tau = \sum _{i=1}^N \omega _i q(\tau _i)^2, \end{aligned}$$

(10.5)

where the $\tau _j$ are either the Radau or Gauss quadrature points and the $\omega _j$ are the associated weights. Since $\ell _j(\tau _i) = 1$ for $i = j$ and $\ell _j(\tau _i) = 0$ otherwise, it follows from the definition of q that $q(\tau _i) = d_i(s)/\omega _i$. This substitution in (10.5) yields

$$\begin{aligned} \int _{-1}^1 q(\tau )^2 \; d\tau = \sum _{i=1}^N \frac{ d_i (s)^2}{\omega _j} = R(s) . \end{aligned}$$

(10.6)

Equating the expressions (10.4) and (10.6) implies that

$$\begin{aligned} \left( \int _{-1}^1 q(\tau )^2 \; d \tau \right) ^{1/2} \le \sqrt{2}. \end{aligned}$$

By (10.6), $R(s) \le 2$ for any $s \in [-1, 1]$. In particular, $R(\tau _i) \le 2$ for $1 \le i \le N$. Since $R(\tau _i)$ is the square of the Euclidean length of row i in $(\mathbf{{W}}^{1/2}\mathbf{{D}})^{-1}$, the rows of $(\mathbf{{W}}^{1/2}\mathbf{{D}})^{-1}$ have Euclidean length bounded by $\sqrt{2}$. This result holds for both the Radau and Gauss quadrature points since since $q^2 \in \mathcal{{P}}_{2N-2}$, and both Radau and Gauss quadrature are exact for polynomials of this degree.

If $\mathbf{{r}}$ is a row of $\mathbf{{D}}_{1:N}^{-1}$, then by the Schwarz inequality and the fact that the quadrature weights sum to 2 and the rows of the matrix $[\mathbf{{W}}^{1/2}\mathbf{{D}}_{1:N}]^{-1}$ have Euclidean length bounded by $\sqrt{2}$, we have

$$\begin{aligned} \sum _{i=1}^N |r_i| = \sum _{i=1}^N \sqrt{\omega _i} \left( |r_i|/\sqrt{\omega _i}\right) \le \left( \sum _{i=1}^N \omega _i \right) ^{1/2} \left( \sum _{i=1}^N r_i^2/\omega _i \right) ^{1/2} \le 2. \end{aligned}$$

(10.7)

Consequently, the absolute row sums for $\mathbf{{D}}_{1:N}^{-1}$ are all bounded by 2, or equivalently, $\Vert \mathbf{{D}}_{1:N}^{-1}\Vert _\infty \le 2$. Given any polynomial $p \in \mathcal{{P}}_N$ with $p(-1) = 0$ and $|\dot{p}(\tau _i)| \le 1$ for $1 \le i \le N$, it is observed in Section 9 of [36] that $\Vert \mathbf{{D}}_{1:N}^{-1}\Vert _\infty \ge$$\max \{p(\tau _i) : 1 \le i \le N\}$. Take $p(\tau ) = 1 + \tau$ to deduce that $\Vert \mathbf{{D}}_{1:N}^{-1}\Vert _\infty \ge 1 + \tau _N$. Hence, $1 + \tau _N \le \Vert \mathbf{{D}}_{1:N}^{-1}\Vert _\infty \le 2$. Since $\tau _N = 1$ for the Radau points, it follows that $\Vert \mathbf{{D}}_{1:N}^{-1}\Vert _\infty = 2$. For the Gauss points, $\tau _N$ approaches 1 as N tends to infinity; consequently, $\Vert \mathbf{{D}}_{1:N}^{-1}\Vert _\infty$ approaches 2 as N tends to infinity for the Gauss points. $\square$