Convergence Rate for a Gauss Collocation Method Applied to Unconstrained Optimal Control

Abstract

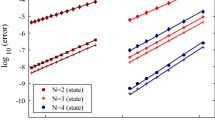
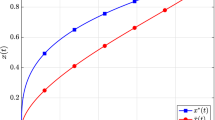
A local convergence rate is established for an orthogonal collocation method based on Gauss quadrature applied to an unconstrained optimal control problem. If the continuous problem has a smooth solution and the Hamiltonian satisfies a strong convexity condition, then the discrete problem possesses a local minimizer in a neighborhood of the continuous solution, and as the number of collocation points increases, the discrete solution converges to the continuous solution at the collocation points, exponentially fast in the sup-norm. Numerical examples illustrating the convergence theory are provided.

Appendix

In (15), we define a new matrix $\mathbf{{D}}^\dagger$ in terms of the differentiation matrix $\mathbf{{D}}$. The following proposition shows that the elements of $\mathbf{{D}}^\dagger$ can be gotten by rearranging the elements of $\mathbf{{D}}$.

Proposition 10.1

The entries of the matrices $\mathbf{{D}}$ and $\mathbf{{D}}^\dagger$ satisfy

$$\begin{aligned} D_{ij} = -D_{N+1-i, N+1-j}^\dagger , \quad 1 \le i \le N, \quad 1 \le j \le N. \end{aligned}$$

(60)

In other words, $\mathbf{{D}}_{1:N} = -\mathbf{{J}} \mathbf{{D}}_{1:N}^\dagger \mathbf{{J}}$ where $\mathbf{{J}}$ is the exchange matrix with ones on its counterdiagonal and zeros elsewhere. Equivalently, $\mathbf{{D}}_{1:N}^\dagger = -\mathbf{{J}} \mathbf{{D}}_{1:N} \mathbf{{J}}$.

Proof

By (9) the elements of $\mathbf{{D}}$ can be expressed in terms of the derivatives of a set of Lagrange basis functions evaluated at the collocation points:

$$\begin{aligned} D_{ij} = \dot{L}_j(\tau _i) \quad \text{ where } L_j \in \mathcal{{P}}_N, \quad L_j (\tau _k) = \left\{ \begin{array}{ll} 1 &{} \text{ if } k = j, \\ 0 &{} \text{ if } 0 \le k \le N, \; k \ne j. \end{array} \right. \end{aligned}$$

In (9) we give an explicit formula for the Lagrange basis functions, while here we express the basis function in terms of polynomials $L_j$ that equal one at $\tau _j$ and vanish at $\tau _k$ where $0 \le k \le N$, $k \ne j$. These $N +1$ conditions uniquely define $L_j \in \mathcal{{P}}_N$. Similarly, by Garg et al. [2, Thm. 1], the entries of $\mathbf{{D}}_{1:N}^\dagger$ are given by

$$\begin{aligned} D_{ij}^\dagger = \dot{M}_j(\tau _i) \quad \text{ where } M_j \in \mathcal{{P}}_N, \quad M_j (\tau _k) = \left\{ \begin{array}{ll} 1 &{} \text{ if } k = j, \\ 0 &{} \text{ if } 1 \le k \le N+1, \; k \ne j . \end{array} \right. \end{aligned}$$

Observe that $M_{N+1-j}(t) = L_j (-t)$ due to the symmetry of the quadrature points around $t = 0$:

• (a) Since $-\tau _{N+1-j} = \tau _j$, we have $L_j (-\tau _{N+1-j}) = L_j (\tau _j) = 1$.

• (b) Since $\tau _{N+1} = 1$ and $\tau _0 = -1$, we have $L_j (-\tau _{N+1}) = L_j (\tau _0) = 0$.

• (c) Since $-\tau _i = \tau _{N+1-i}$, we have $L_j (-\tau _{i}) = L_j (\tau _{N+1-i}) = 0$ if $i \ne N+1-j$.

Since $M_{N+1-j}(t)$ is equal to $L_j (-t)$ at $N+1$ distinct points, the two polynomials are equal everywhere. Replacing $M_{N+1-j}(t)$ by $L_j (-t)$, we have

$$\begin{aligned} D_{N+1-i, N+1-j}^\dagger = -\dot{L}_j (-\tau _{N+1-i}) = - \dot{L}_j (\tau _i) =-D_{ij}. \end{aligned}$$

$\square$

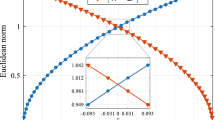
Tables 1 and 2 illustrate properties (P1) and (P2) for the differentiation matrix $\mathbf{{D}}$. In Table 1, we observe that $\Vert \mathbf{{D}}_{1:N}^{-1}\Vert _\infty$ monotonically approaches the upper limit 2. More precisely, it is found that $\Vert \mathbf{{D}}_{1:N}^{-1}\Vert _\infty = 1 + \tau _N$, where the final collocation point $\tau _N$ approaches one as N tends to infinity. In Table 2, we give the maximum 2-norm of the rows of $[\mathbf{{W}}^{1/2} \mathbf{{D}}_{1:N}]^{-1}$. It is found that the maximum is attained by the last row of $[\mathbf{{W}}^{1/2} \mathbf{{D}}_{1:N}]^{-1}$, and the maximum monotonically approaches $\sqrt{2}$.

Table 1 $\Vert \mathbf{D}_{1:N}^{-1}\Vert _\infty$

Table 2 Maximum Euclidean norm for the rows of $[\mathbf{{W}}^{1/2}{} \mathbf{D}_{1:N}]^{-1}$