AIC for the non-concave penalized likelihood method

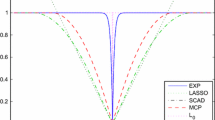
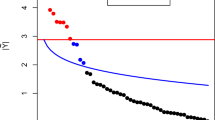
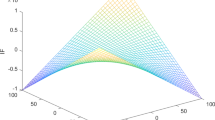
Abstract

Non-concave penalized maximum likelihood methods are widely used because they are more efficient than the Lasso. They include a tuning parameter which controls a penalty level, and several information criteria have been developed for selecting it. While these criteria assure the model selection consistency, they have a problem in that there are no appropriate rules for choosing one from the class of information criteria satisfying such a preferred asymptotic property. In this paper, we derive an information criterion based on the original definition of the AIC by considering minimization of the prediction error rather than model selection consistency. Concretely speaking, we derive a function of the score statistic that is asymptotically equivalent to the non-concave penalized maximum likelihood estimator and then provide an estimator of the Kullback–Leibler divergence between the true distribution and the estimated distribution based on the function, whose bias converges in mean to zero.

Proofs

1.1 Proof of Lemma 2

From (R1), the first term in the right-hand side of (3) converges in probability to $h(\varvec{\beta })$ for each $\varvec{\beta }$. In addition, from the convexity of $g_i(\varvec{\beta })$ with respect to $\varvec{\beta }$, we have

$$\begin{aligned} \sup _{\varvec{\beta }\in K}\bigg |\frac{1}{n}\sum _{i=1}^{n}\{g_{i}(\varvec{\beta }^{*})-g_{i}(\varvec{\beta })\}-h(\varvec{\beta })\bigg |{\mathop {\rightarrow }\limits ^{\mathrm{p}}} 0 \end{aligned}$$

for any compact set K (Andersen and Gill 1982; Pollard 1991). Accordingly, we have

$$\begin{aligned} \sup _{\varvec{\beta }\in K}|\mu _{n}(\varvec{\beta })-h(\varvec{\beta })|{\mathop {\rightarrow }\limits ^{\mathrm{p}}}0. \end{aligned}$$

(37)

Note that in the following inequality,

$$\begin{aligned} \mu _{n}(\varvec{\beta })\ge \frac{1}{n}\sum _{i=1}^{n}\{g_{i}(\varvec{\beta }^{*})-g_{i}(\varvec{\beta })\}-\frac{1}{n^{1/2}}\sum _{j=1}^pp_{\lambda }(\beta _j^*) \equiv \mu _{n}^{(0)}(\varvec{\beta }), \end{aligned}$$

the argmin of the right-hand side is the maximum likelihood estimator and is $\mathrm{O}_{\mathrm{p}}(1)$. Also, note that for some $M\ (>0)$,

$$\begin{aligned} \mathrm{P}(|\hat{\varvec{\beta }}_{\lambda }|>M) \le \mathrm{P}\bigg (\inf _{|\varvec{\beta }|>M}\mu _{n}(\varvec{\beta })\le \mu _{n}(\varvec{0})\bigg ) \le \mathrm{P}\bigg (\inf _{|\varvec{\beta }|>M}\mu _{n}^{(0)}(\varvec{\beta })\le \mu _{n}^{(0)}(\varvec{0})\bigg ) \end{aligned}$$

because $p_{\lambda }(0)=0$ from (C5). Therefore, we have

$$\begin{aligned} \hat{\varvec{\beta }}_{\lambda }=\underset{\varvec{\beta }\in \mathcal{B}}{\mathrm{agmin}}\;\mu _{n}(\varvec{\beta })=\mathrm{O}_{\mathrm{p}}(1). \end{aligned}$$

(38)

From (37) and (38), we obtain

$$\begin{aligned} \hat{\varvec{\beta }}_{\lambda } =\underset{\varvec{\beta }\in \mathcal{B}}{\mathrm{argmin}}\;\mu _{n}(\varvec{\beta }) {\mathop {\rightarrow }\limits ^{\mathrm{p}}}\underset{\varvec{\beta }\in \mathcal{B}}{\mathrm{argmin}}\;h(\varvec{\beta }) =\varvec{\beta }^{*}. \end{aligned}$$

The last equality holds from (1). $\square$

1.2 Proof of (8)

Let $\varvec{u}=\tilde{\varvec{u}}_{n}+l\varvec{w}$, where $\varvec{w}$ is a unit vector, and let $l\in (\delta ,\xi )$. The strong convexity of $\eta _{n}(\varvec{u})$ implies

$$\begin{aligned} (1-\delta /l)\eta _{n}(\tilde{\varvec{u}}_{n})+(\delta /l)\eta _{n}(\varvec{u}) > \eta _{n}(\tilde{\varvec{u}}_{n}+\delta \varvec{w}), \end{aligned}$$

and we thus have

$$\begin{aligned} (\delta /l)\left\{ \nu _{n}(\varvec{u})-\nu _{n}(\tilde{\varvec{u}}_{n})\right\}&> \nu _{n}(\tilde{\varvec{u}}_{n}+\delta \varvec{w})-\nu _{n}(\tilde{\varvec{u}}_{n}) \\&\quad +\,(1-\delta /l)\phi _{n}(\tilde{\varvec{u}}_{n})+(\delta /l)\phi _{n}(\varvec{u})-\phi _{n}(\tilde{\varvec{u}}_{n}+\delta \varvec{w}) \\&\quad +\,(1-\delta /l)\psi _{n}(\tilde{\varvec{u}}_{n}^{\dagger })+(\delta /l)\psi _{n}(\varvec{u}^{\dagger })-\psi _{n}(\tilde{\varvec{u}}_{n}^{\dagger }+\delta \varvec{w}^{\dagger }). \end{aligned}$$

Since it follows that

$$\begin{aligned}&\nu _{n}(\tilde{\varvec{u}}_{n}+\delta \varvec{w})-\nu _{n}(\tilde{\varvec{u}}_{n}) \\&\quad =\big \{\nu _{n}(\tilde{\varvec{u}}_{n}+\delta \varvec{w})-\tilde{\nu }_{n}(\tilde{\varvec{u}}_{n}+\delta \varvec{w})\big \}+\big \{\tilde{\nu }_{n}(\tilde{\varvec{u}}_{n}+\delta \varvec{w})-\tilde{\nu }_{n}(\tilde{\varvec{u}}_{n})\big \}+\big \{\tilde{\nu }_{n}(\tilde{\varvec{u}}_{n})-\nu _{n}(\tilde{\varvec{u}}_{n})\big \} \\&\quad \ge \varUpsilon _{n}(\delta )-2\varDelta _{n}(\delta ), \end{aligned}$$

we obtain from (6) and (7) that, for any $\varepsilon \;(>0)$,

$$\begin{aligned} (\delta /l)\{\nu _{n}(\varvec{u})-\nu _{n}(\tilde{\varvec{u}}_{n})\} > \varUpsilon _{n}(\delta )-2\varDelta _{n}(\delta )-\varepsilon \end{aligned}$$

for sufficiently large n and sufficiently small $\gamma$. If $2\varDelta _{n}(\delta )+\varepsilon <\varUpsilon _{n}(\delta )$, then $\nu _{n}(\varvec{u})\ge \nu _{n}(\tilde{\varvec{u}}_{n})$ for any $\varvec{u}$ such that $|\varvec{u}^{\dagger }|\le \gamma$ and $\delta \le |\varvec{u}-\tilde{\varvec{u}}_{n}|\le \xi$. This means $\varvec{u}_{n}$ must satisfy $|\varvec{u}_{n}^{\dagger }|> \gamma$ or $|\varvec{u}_{n}-\tilde{\varvec{u}}_{n}|\not \in [\delta ,\xi ]$ in order for $\varvec{u}_{n}$ to be the argmin of $\nu _{n}(\varvec{u})$. Hence, we obtain (8). $\square$

1.3 Proof of (17)

Let us consider a random function $\mu _{n}(\varvec{\beta })$ in (3). Since $p_{\lambda }(0)=0$ from (C5), we have

$$\begin{aligned} \mu _{n}(\hat{\varvec{\beta }}_{\lambda }) =&-n^{-1/2}\varvec{s}_{n}^{\mathrm{T}}(\hat{\varvec{\beta }}_{\lambda }-\varvec{\beta }^{*})+(\hat{\varvec{\beta }}_{\lambda }-\varvec{\beta }^{*})^{\mathrm{T}}\varvec{J}_{n}(\tilde{\varvec{\beta }})(\hat{\varvec{\beta }}_{\lambda }-\varvec{\beta }^{*})/2 \\&+n^{-1/2}\sum _{j\in \mathcal{J}^{(1)}}p_{\lambda }(\hat{\beta }_{\lambda ,j})+n^{-1/2}\sum _{j\in \mathcal{J}^{(2)}}p'_{\lambda }(\beta _{j}^{*})(\hat{\beta }_{\lambda ,j}-\beta _{j}^{*})\{1+\mathrm{o}_{\mathrm{p}}(1)\}, \end{aligned}$$

where $\tilde{\varvec{\beta }}$ is a vector on the segment from $\hat{\varvec{\beta }}_{\lambda }$ to $\varvec{\beta }^{*}$. Then, we have

$$\begin{aligned} 0 \ge \mu _{n}(\hat{\varvec{\beta }}_{\lambda })-\mu _{n}(\varvec{\beta }^{*}) \ne \mathrm{O}_{\mathrm{p}}(n^{-1/2}|\hat{\varvec{\beta }}_{\lambda }-\varvec{\beta }^{*}|)+(\hat{\varvec{\beta }}_{\lambda }-\varvec{\beta }^{*})^{\mathrm{T}}\varvec{J}_{n}(\tilde{\varvec{\beta }})(\hat{\varvec{\beta }}_{\lambda }-\varvec{\beta }^{*})/2 \end{aligned}$$

because $\varvec{s}_{n}=\mathrm{O}_{\mathrm{p}}(1)$. From (C2) and (C3), $\varvec{J}_{n}(\tilde{\varvec{\beta }})$ is positive definite for sufficiently large n, and therefore, it follows that

$$\begin{aligned} \hat{\varvec{\beta }}_{\lambda }-\varvec{\beta }^{*}=\mathrm{O}_{\mathrm{p}}(n^{-1/2}). \end{aligned}$$

(39)

Let us express $\mu _{n}(\varvec{\beta })$ by $\mu _{n}(\varvec{\beta }^{(1)},\varvec{\beta }^{(2)})$. Because $0\ge \mu _{n}(\hat{\varvec{\beta }}_{\lambda }^{(1)},\hat{\varvec{\beta }}_{\lambda }^{(2)})-\mu _{n}(\varvec{0},\hat{\varvec{\beta }}_{\lambda }^{(2)})$, we see that

$$\begin{aligned}&-n^{-1/2}\varvec{s}_{n}^{(1)\mathrm{T}}\hat{\varvec{\beta }}_{\lambda }^{(1)} +\hat{\varvec{\beta }}_{\lambda }^{(1)\mathrm{T}}\varvec{J}^{(11)}_{n}(\tilde{\varvec{\beta }})\hat{\varvec{\beta }}_{\lambda }^{(1)}/2 \\&+\hat{\varvec{\beta }}_{\lambda }^{(1)\mathrm{T}}\varvec{J}^{(11)}_{n}(\tilde{\varvec{\beta }})(\hat{\varvec{\beta }}_{\lambda }^{(2)}-\varvec{\beta }^{*(2)}) +n^{-1/2}\sum _{j\in \mathcal{J}^{(1)}}p_{\lambda }(\hat{\beta }_{\lambda ,j}) \end{aligned}$$

is non-positive. Here, we use the fact that $\sum _{j\in \mathcal{J}^{(1)}}p_{\lambda }(\hat{\beta }_{\lambda ,j})$ reduces to $\lambda \Vert \hat{\varvec{\beta }}_{\lambda }^{(1)}\Vert _{q}^{q}\{1+\mathrm{o}_{\mathrm{p}}(1)\}$ from (C5) and (39) and that $\varvec{J}_{n}(\tilde{\varvec{\beta }})$ is positive definite for sufficiently large n. Accordingly, we have

$$\begin{aligned} |\hat{\varvec{\beta }}_{\lambda }^{(1)}|^{2}+n^{-1/2}\Vert \hat{\varvec{\beta }}_{\lambda }^{(1)}\Vert _{q}^{q}\{1+\mathrm{o}_{\mathrm{p}}(1)\}=\mathrm{O}_{\mathrm{p}}(n^{-1/2}|\hat{\varvec{\beta }}_{\lambda }^{(1)}|) \end{aligned}$$

and thus $\Vert \hat{\varvec{\beta }}_{\lambda }^{(1)}\Vert _{q}^{q}=\mathrm{O}_{\mathrm{p}}(|\hat{\varvec{\beta }}_{\lambda }^{(1)}|)$ since the first term on the left-hand side is nonnegative. Hence, we have

$$\begin{aligned} \mathrm{P}(\hat{\varvec{\beta }}_{\lambda }^{(1)}=\varvec{0})\rightarrow 1 \end{aligned}$$

(40)

because $0<q<1$ and $\hat{\varvec{\beta }}_{\lambda }^{(1)}=\mathrm{o}_{\mathrm{p}}(1)$. This implies the former in (17). Since $\tilde{\varvec{u}}_{n}^{(2)}$ is trivially $\mathrm{O}_{\mathrm{p}}(1)$, we obtain the latter of (17) from (39) and (40). $\square$

1.4 Proof of (19) and (20)

Let $\eta _{n}(\varvec{u}^{(1)},\varvec{u}^{(2)})$ be the one with $q=1$ in (9), and let $\tilde{\eta }_{n}(\varvec{u}^{(1)},\varvec{u}^{(2)})=-\varvec{u}^{\mathrm{T}}\varvec{s}_{n}+\varvec{u}^{\mathrm{T}}\varvec{J}\varvec{u}/2$ in place of (10). Then, we can obtain $\eta _{n}(\varvec{u}^{(1)},\varvec{u}^{(2)})=\tilde{\eta }_{n}(\varvec{u}^{(1)},\varvec{u}^{(2)})+\mathrm{o}_{\mathrm{p}}(1)$ by taking a Taylor expansion around $(\varvec{u}^{(1)},\varvec{u}^{(2)})=(\varvec{0},\varvec{0})$. In addition, let $\phi _{n}(\varvec{u})$ and $\phi (\varvec{u})$ be $\phi _{n}(\varvec{u})+\psi _{n}(\varvec{u}^{\dagger })$ and $\phi (\varvec{u})+\psi (\varvec{u}^{\dagger })$ with $q=1$ in (11), (12), and (13), let $\varvec{u}^{\dagger }$ be empty vector and $\psi _{n}(\varvec{u}^{\dagger })=\psi (\varvec{u}^{\dagger })=0$, and define $\nu _{n}(\varvec{u}^{(1)},\varvec{u}^{(2)})=\eta _{n}(\varvec{u}^{(1)},\varvec{u}^{(2)})+\phi _{n}(\varvec{u})+\psi _{n}(\varvec{u}^{\dagger })$ and $\tilde{\nu }_{n}(\varvec{u}^{(1)},\varvec{u}^{(2)})=\tilde{\eta }_{n}(\varvec{u}^{(1)},\varvec{u}^{(2)})+\phi (\varvec{u})+\psi (\varvec{u}^{\dagger })$ again. Here, note that

$$\begin{aligned} (\varvec{u}_{n}^{(1)},\varvec{u}_{n}^{(2)}) =\underset{(\varvec{u}^{(1)},\varvec{u}^{(2)})}{\mathrm{argmin}}\nu _{n}(\varvec{u}^{(1)},\varvec{u}^{(2)}) =(n^{1/2}\hat{\varvec{\beta }}^{(1)}_{\lambda },n^{1/2}(\hat{\varvec{\beta }}^{(2)}_{\lambda }-\varvec{\beta }^{*(2)})). \end{aligned}$$

Next, because

$$\begin{aligned} \tilde{\nu }_{n}(\varvec{u}^{(1)},\varvec{u}^{(2)})&=\Vert \varvec{u}^{(2)}-\varvec{J}^{(22)-1}\{-\varvec{J}^{(21)}\varvec{u}^{(1)} +(\varvec{s}_{n}^{(2)}-\varvec{p}'^{(2)}_{\lambda })\}\Vert _{\varvec{J}^{(22)}}^{2}/2 \\&\quad +\varvec{u}^{(1)\mathrm{T}}\varvec{J}^{(1|2)}\varvec{u}^{(1)}/2 -\varvec{u}^{(1)\mathrm{T}}\varvec{\tau }_{\lambda }(\varvec{s}_{n}) +\lambda \Vert \varvec{u}^{(1)}\Vert _{1} -\Vert \varvec{s}_{n}^{(2)}\\&\quad -\varvec{p}'^{(2)}_{\lambda }\Vert _{\varvec{J}^{(22)-1}}^{2}/2, \end{aligned}$$

we see by using $\hat{\varvec{u}}_{n}^{(1)}$ in (18) that

$$\begin{aligned} (\tilde{\varvec{u}}_{n}^{(1)},\tilde{\varvec{u}}_{n}^{(2)})&=\underset{(\varvec{u}^{(1)},\varvec{u}^{(2)})}{\mathrm{argmin}}\tilde{\nu }_{n}(\varvec{u}^{(1)},\varvec{u}^{(2)}) \\&=(\hat{\varvec{u}}_{n}^{(1)},-\varvec{J}^{(22)-1}\varvec{J}^{(21)}\hat{\varvec{u}}_{n}^{(1)}+\varvec{J}^{(22)-1}(\varvec{s}_{n}^{(2)}-\varvec{p}'^{(2)}_{\lambda })), \end{aligned}$$

where we have denoted $\varvec{x}^{\mathrm{T}}A\varvec{x}$ by $\Vert \varvec{x}\Vert _{A}^{2}$ for an appropriate size of matrix A and vector $\varvec{x}$. Now, we apply Lemma 3 and evaluate the right-hand side in (4). In the same way as in (15), it follows that $\varDelta _{n}(\delta )$ converges in probability to 0. Next, the definition of $\tilde{\varvec{u}}_{n}^{(1)}$ ensures that

$$\begin{aligned} \varvec{J}^{(1|2)}\tilde{\varvec{u}}_{n}^{(1)}-\varvec{\tau }_{\lambda }(\varvec{s}_{n})+\lambda \varvec{\gamma }=\varvec{0}, \end{aligned}$$

where $\varvec{\gamma }$ is a $|\mathcal{J}^{(1)}|$-dimensional vector such that $\gamma _{j}=1$ when $\hat{u}_{n,j}^{(1)}>0$, $\gamma _{j}=-1$ when $\hat{u}_{n,j}^{(1)}<0$, and $\gamma _{j}\in [-1,1]$ when $\hat{u}_{n,j}^{(1)}=0$. Thus, noting that $\tilde{\varvec{u}}_{n}^{(1)\mathrm{T}}\varvec{\gamma }=\Vert \tilde{\varvec{u}}_{n}^{(1)}\Vert _{1}$, we can write $\tilde{\nu }_{n}(\varvec{u}^{(1)},\varvec{u}^{(2)})-\tilde{\nu }_{n}(\tilde{\varvec{u}}_{n}^{(1)},\tilde{\varvec{u}}_{n}^{(2)})$ as

$$\begin{aligned}&\Vert \varvec{u}^{(1)}-\tilde{\varvec{u}}_{n}^{(1)}\Vert _{\varvec{J}^{(1|2)}}^{2}/2 +\lambda \sum _{j\in \mathcal{J}^{(1)}}\left( |u_{j}|-\gamma _{j}u_{j}\right) \nonumber \\&+\Vert \varvec{u}^{(2)}-\varvec{J}^{(22)-1}\{-\varvec{J}^{(21)}\varvec{u}^{(1)} +(\varvec{s}_{n}^{(2)}-\varvec{p}'^{(2)}_{\lambda })\}\Vert _{\varvec{J}^{(22)}}^{2}/2 \end{aligned}$$

(41)

after a simple calculation. Let $\varvec{w}_{1}$ and $\varvec{w}_{2}$ be unit vectors such that $\varvec{u}^{(1)}=\tilde{\varvec{u}}_{n}^{(1)}+\zeta \varvec{w}_{1}$ and $\varvec{u}^{(2)}=\tilde{\varvec{u}}_{n}^{(2)}+(\delta ^{2}-\zeta ^{2})^{1/2}\varvec{w}_{2}$, where $0\le \zeta \le \delta$. Then, letting $\rho ^{(22)}$ and $\rho ^{(1|2)}\;(>0)$ be half the smallest eigenvalues of $\varvec{J}^{(22)}$ and $\varvec{J}^{(1|2)}$, respectively, it follows that

$$\begin{aligned} \varUpsilon _{n}(\delta ) \ge \min _{0\le \zeta \le \delta }\left\{ \rho ^{(1|2)}\zeta ^{2}+\rho ^{(22)}|(\delta ^{2}-\zeta ^{2})^{1/2}\varvec{w}_{2}+\zeta \varvec{J}^{(22)-1}\varvec{J}^{(21)}\varvec{w}_{1}|^{2}\right\} >0 \end{aligned}$$

because the second term in (41) is nonnegative. Hence, the first term on the right-hand side in (4) converges to 0. In addition, because $(\varvec{u}_{n}^{(1)},\varvec{u}_{n}^{(2)})$ is $\mathrm{O}_{\mathrm{p}}(1)$ from (39) and $(\tilde{\varvec{u}}_{n}^{(1)},\tilde{\varvec{u}}_{n}^{(2)})$ is also $\mathrm{O}_{\mathrm{p}}(1)$, the second term on the right-hand side in (4) can be made arbitrarily small by considering a sufficiently large $\xi$. Thus, we have $|\varvec{u}-\tilde{\varvec{u}}_{n}|=\mathrm{o}_{\mathrm{p}}(1)$, and as a consequence, we obtain (19) and (20). $\square$

1.5 Proof of (26)

Because $n^{1/2}\hat{\varvec{\beta }}_{\lambda }^{(1)}=\hat{\varvec{u}}_{n}^{(1)}+\mathrm{o}_{\mathrm{p}}(1)$ from Theorem 1, the terms including $\hat{\varvec{\beta }}_{\lambda }^{(1)}$ do not reduce to $\mathrm{o}_{\mathrm{p}}(1)$ in this case. Therefore, (24) is expressed as

$$\begin{aligned}&\hat{\varvec{u}}_{n}^{ (1)\mathrm{T}}\left( \varvec{s}_{n}^{(1)}-\varvec{J}^{(12)}\varvec{J}^{(22)-1}\varvec{s}_{n}^{(2)}\right) +\left( \varvec{s}_{n}^{(2)}-\varvec{p}'^{(2)}_{\lambda }\right) ^{\mathrm{T}}\varvec{J}^{(22)-1}\varvec{s}_{n}^{(2)} \\&-\hat{\varvec{u}}_{n}^{ (1)\mathrm{T}}\varvec{J}^{(1|2)}\hat{\varvec{u}}_{n}/2-\left( \varvec{s}_{n}^{(2)}-\varvec{p}'^{(2)}_{\lambda }\right) ^\mathrm{T}\varvec{J}^{(22)}\left( \varvec{s}_{n}^{(2)}-\varvec{p}'^{(2)}_{\lambda }\right) /2+\mathrm{o}_{\mathrm{p}}(1), \end{aligned}$$

and this converges in distribution to

$$\begin{aligned}&\hat{\varvec{u}}^{ (1)\mathrm{T}}\varvec{s}^{(1|2)}+\left( \varvec{s}^{(2)}-\varvec{p}'^{(2)}_{\lambda }\right) ^{\mathrm{T}}\varvec{J}^{(22)-1}\varvec{s}^{(2)} \\&-\hat{\varvec{u}}^{ (1)\mathrm{T}}\varvec{J}^{(1|2)}\hat{\varvec{u}}/2-\left( \varvec{s}^{(2)}-\varvec{p}'^{(2)}_{\lambda }\right) ^\mathrm{T}\varvec{J}^{(22)}\left( \varvec{s}^{(2)}-\varvec{p}'^{(2)}_{\lambda }\right) /2. \end{aligned}$$

In the same way, (25) is expressed as

$$\begin{aligned}&\hat{\varvec{u}}_{n}^{ (1)\mathrm{T}}\left( \tilde{\varvec{s}}_{n}^{(1)}-\varvec{J}^{(12)}\varvec{J}^{(22)-1}\tilde{\varvec{s}}_{n}^{(2)}\right) +\left( \varvec{s}_{n}^{(2)}-\varvec{p}'^{(2)}_{\lambda }\right) ^{\mathrm{T}}\varvec{J}^{(22)-1}\tilde{\varvec{s}}_{n}^{(2)} \\&-\hat{\varvec{u}}_{n}^{ (1)\mathrm{T}}\varvec{J}^{(1|2)}\hat{\varvec{u}}_{n}/2-\left( \varvec{s}_{n}^{(2)}-\varvec{p}'^{(2)}_{\lambda }\right) ^\mathrm{T}\varvec{J}^{(22)}\left( \varvec{s}_{n}^{(2)}-\varvec{p}'^{(2)}_{\lambda }\right) /2+\mathrm{o}_{\mathrm{p}}(1), \end{aligned}$$

and this converges in distribution to

$$\begin{aligned}&\hat{\varvec{u}}^{ (1)\mathrm{T}}\tilde{\varvec{s}}^{(1|2)}+\left( \varvec{s}^{(2)}-\varvec{p}'^{(2)}_{\lambda }\right) ^{\mathrm{T}}\varvec{J}^{(22)-1}\tilde{\varvec{s}}^{(2)} \\&-\hat{\varvec{u}}^{ (1)\mathrm{T}}\varvec{J}^{(1|2)}\hat{\varvec{u}}/2-\left( \varvec{s}^{(2)}-\varvec{p}'^{(2)}_{\lambda }\right) ^\mathrm{T}\varvec{J}^{(22)}\left( \varvec{s}^{(2)}-\varvec{p}'^{(2)}_{\lambda }\right) /2, \end{aligned}$$

where $\tilde{\varvec{s}}_{n}^{(1)},\;\tilde{\varvec{s}}^{(2)},\;\tilde{\varvec{s}}^{(1|2)}$, and $\tilde{\varvec{s}}^{(2)}$ are copies of $\varvec{s}_{n}^{(1)},\;\varvec{s}^{(2)},\;\varvec{s}^{(1|2)}$, and $\varvec{s}^{(2)}$, respectively. Thus, we see that

$$\begin{aligned} z^{\mathrm{limit}} =&\hat{\varvec{u}}^{ (1)\mathrm{T}}\varvec{s}^{(1|2)}+\left( \varvec{s}^{(2)}-\varvec{p}'^{(2)}_{\lambda }\right) ^{\mathrm{T}}\varvec{J}^{(22)-1}\varvec{s}^{(2)}\nonumber \\&-\hat{\varvec{u}}^{ (1)\mathrm{T}}\tilde{\varvec{s}}^{(1|2)}-\left( \varvec{s}^{(2)}-\varvec{p}'^{(2)}_{\lambda }\right) ^{\mathrm{T}}\varvec{J}^{(22)-1}\tilde{\varvec{s}}^{(2)}. \end{aligned}$$

Since $\tilde{\varvec{s}}$ and $\varvec{s}$ are independently distributed according to $\mathrm{N}(\varvec{0},\varvec{J}^{(22)})$, the asymptotic bias reduces to

$$\begin{aligned} \mathrm{E}\left[ z^{\mathrm{limit}}\right] =\mathrm{E}\left[ \hat{\varvec{u}}^{ (1)\mathrm{T}}\varvec{s}^{(1|2)}\right] +\mathrm{E}\left[ (\varvec{s}^{(2)}-\varvec{p}'^{(2)}_{\lambda })^{\mathrm{T}}\varvec{J}^{(22)-1}\varvec{s}^{(2)}\right] . \end{aligned}$$

As a result, we obtain (26).$\square$