1 Introduction

Bonthuis et al. (2009) have been explored mechanism for flow generation in fluid-filled nanochannels employing coupling between translational and rotational (angular) momentum. High-frequency electric field giving source of momentum dipoles leads to effect of pumping and hydraulic power plants on the nanoscale. They have shown that for rotating electric fields, nonvanishing flow is obtained through an appropriate boundary condition for the molecular spin (angular velocity). De Luca et al. (2013a, b) have been developed electropumping of water for rotating electric fields using nonequilibrium molecular dynamics (NEMD). They have assumed that linear and angular momentum of molecular structure of fluids can couple effectively allowing mechanism for the exchange of streaming and angular velocity. In this approach, the boundary conditions play a significant role, both in hydrophilic/hydrophobic effect and in electric field coupling. De Luca et al. (2013a) have proposed that slip boundary conditions for molecular spin (angular velocity) and translational velocity play a main role and leads to the pumping effect. Owing to this inconvenient boundary condition, one can observe confinement the angular momentum and it conversion into linear streaming flow. Having this motivation in mind, in our report we develop a more general statement for the molecular slip boundary condition. We are starting from a general form of boundary condition within a thin shell-like slip layer (Zhang et al. 2012; Eremeyev and Zubov 2009; Tabeling 2011). We present results of a correct formulation of angular momentum boundary condition which allows a general action similar to the rotating electric dipoles Grekova and Zhilin (2001).

Discussing in Section 196–205 of “Classical Field Theories,” some generalization of the first and second Euler laws, Truesdell and Toupin (1960) have made a proposition that among of assigned torques the most important one is a couple stress vector \({\mathbf m} _{(\mathbf n)}\). This couple stress vector, by extending the Cauchy stress principle, is a manifestation of couple stress tensor at the boundary \(\partial V\) of continuum oriented by a normal \(\mathbf n\), i.e., \({\mathbf m} _{(\mathbf n)}={\mathbf{m\,n }}=m_{ij}n_j{\mathbf e} _i\). Since \({\mathbf m}_{(\mathbf n)}\) is to be treated as a contact torque and since on the second side of boundary surface there is designed contact boundary torque \({\mathbf q}_{\partial V}\), then still adopting Cauchy’s argumentation, Truesdell and Toupin propose the following boundary conditions [eq. 203.6]

$$\begin{aligned} {\mathbf q}_{\partial V}={\mathbf m} \,{\mathbf n} ={\mathbf m}_{(\mathbf n)}. \end{aligned}$$
(1)

An existence of internal couple stress tensor \(\mathbf m\) was postulated on the fluid continuum ground and commented in the papers by Aero et al. (1965), Condiff and Dahler (1964), Eringen (1964), Łukasiewicz (1999), Eringen (1996), Kucaba-Piętal (2004), Hoffmann et al. (2007). This tensor is fundamentally nonsymmetric and its presence leads to the appearance of a nonsymmetric part of the Cauchy stress tensor \({\mathbf t} \ne {\mathbf t} ^{\mathrm{T}}\). Both tensors \(\mathbf t\), \(\mathbf m\) are the measures related to the Euler description and therefore we can say that these are Cauchy’s type tensors. Yet, in fluid mechanics, for balancing linear and angular momentum we prefer more adequate names for these tensors, i.e., “the momentum flux tensor” and “the angular momentum flux tensor”.

Quite similarly to the Navier slip condition, the expression (1) can be treated as a simplest model of the angular velocity slip condition, if we define the angular friction torque \({\mathbf q}_{\partial V}\) as a linear function of a total angular velocity calculated at the boundary and a surface angular friction coefficient \(c:{\mathbf{q }}_{\partial V}=c\left( \frac{1}{2}{\mathrm{rot}}{\mathbf{v }}+{\varvec{\omega }}\right) .\)

In fluid mechanics, a rotor of the velocity field is called a vorticity \({\mathbf w} =\frac{1}{2}{\mathrm{rot}}{\mathbf v}\) and \(\varvec{\omega }\) is a spin (angular velocity) vector postulated as an independent function of continuum particle. Within asymmetric hydrodynamics (which is a branch of the Cosserat continuum), the couple stress tensor in (1) can consist of elastic and viscous components. It is a main difference with the Cauchy stress tensor, where an elastic part is a spherical one \({\mathbf t} ^{\left( e\right) }=-p{\mathbf I}\) and depends only on the thermodynamical pressure. Restricting, for the moment, to the simplest definition of viscous couple stress \({\mathbf m} =\eta _2{\mathbf k}\) by Listov (1967), where rate of curvature deformation is defined as a spatial gradient of the angular velocity only \({\mathbf k} ={\mathrm{grad}}\varvec{\omega }=\omega _{i,j}{\mathbf e}_i\otimes {\mathbf e}_j\), we can express the simplest boundary condition (1) in Navier’s-like form:

$$\begin{aligned} c\left( \frac{1}{2}{\mathrm{rot}}{\mathbf v} +{\varvec{\omega }}\right) = \eta _2\,{\mathrm{grad}}{\varvec{\omega }}\,{\mathbf n} \quad {\mathrm{on}}\quad \partial V. \end{aligned}$$
(2)

We will call it “the angular velocity slip condition.” Coefficient of the angular friction \(c\) plays a role of an external viscosity coefficient, which differs for different contacting continua. The ratio \(l_{\mathrm{ang}}=\eta _2/c\) has a dimension of a length and, in the analogy to the Navier–Stokes layer, would be named “the angular slip length.” The angular slip velocity concept and the surface angular slip Eq. (2) were introduced in the literature by Aero et al. (1965). In the present paper, we are going to extend the angular velocity slip Eq. (2) to a more complete form.

2 Mathematical modeling of the slip layer

The details of mathematical derivations for momentum transport in the moving slip layer in a fluid continuum one can find in the previous author’s paper Badur et al. (2011b). Here only the most useful relations for angular momentum derivations are brought.

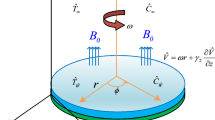
Let assume that two three-dimensional continua under consideration, i.e., bulk fluid \({\mathcal {A}}\) (fluid that form a slip layer) and continuum \({\mathcal {B}}\) (contacting solid or fluid) are separated by a very thin slip layer, as shown in Fig. 1. This layer can be treated as a shell-like two-dimensional material body \({\mathcal {M}}\) represented mathematically by a middle surface \(S\) and upper and lower surfaces \(S^{+}\) and \(S^{-}\), respectively. Let the body orientation \({\mathcal {A}}\) be the same as an orientation of the surface layer \({\mathbf n}_{A}={\mathbf n}_{S}={\mathbf n}_{S^{+}}={\mathbf n}\). If both \({\mathcal {A}}\) and \({\mathcal {B}}\) are fluids, then the Navier–Stokes boundary layer represents the moving interfacial region where physical properties change abruptly. Therefore in the layer, we observe different so-called apparent material properties. These are quite different from that in the contacting bulk continuum \({\mathcal {A}}\) and \({\mathcal {B}}\). Thus, we define an excess of layer density \(\rho _s\), the layer angular inertia tensor \({\mathbf J}_s\), the layer particle velocity \({\mathbf v}_s\) and an excess of layer momentum density \({\mathbf s}_s=\rho _s{\mathbf v}_s\). Due to experimental data that indicate a possible mechanism of particle rolling, we additionally postulate an internal particle spin or a angular velocity \({\varvec{\omega }}_s\) and corresponding excess of angular momentum density \({{\varvec{l}}}_s={\mathbf J}_s{\varvec{\omega }}_s\). Finally, let us postulate a surface excess of momentum flux \({\mathbf t}_s\) and a surface excess of angular momentum flux \({\mathbf m}_s\).

Fig. 1
figure 1

Outline of the Navier–Stokes boundary layer and the pill-box balance domain

Full size image

We assume that generally the considered layer moves in a space with a geometrical, migration velocity \(\mathbf u\), which differs from material velocity \({\mathbf v}_{A}\) in \({\mathcal {A}}\), velocity \({\mathbf v}_{B}\) in \({\mathcal {B}}\) and velocity \({\mathbf v}_{s}\) in \({\mathcal {M}}\). In particular case, the velocity \({\mathbf u}\) means the rate of changing a phase transition surface within the fluid at rest. Usually, the component \(u_n\) normal to moving middle surface \({\mathcal {M}}\) differs from normal components of \({\mathbf v}_{A}\), \({\mathbf v}_{B}\) and \({\mathbf v}_{s}\). It practically means that there is also some mass transport through the layer. The geometrical velocity is usually determined from a special evolution equation. If \({\mathbf u} = {\mathbf v}\), then the moving layer is material, and when \({\mathbf u} ={\mathbf v} _s{\mathbf I} _s+u_n{\mathbf n}\), then the surface is semi-coherent. In the derivations by Navier and Stokes, the surface layer density was assumed as equal to zero. However in the present approach, we determine the slip velocity \({\mathbf v} _s\) from an independent balance of the layer momentum as proposed by Badur et al. (2011b). Similar method is applied for the determination of angular velocity slip.

Recall that within the Navier–Stokes layer, we have introduced the concept of an “excess of momentum flux” which is described by the surface nonsymmetric dyade, \({\mathbf t} _s\) in the following form:

$$\begin{aligned} {\mathbf t} _{s}\left( \xi ^{}\right) = t^{\alpha \beta }{\mathbf a} _\alpha \otimes {\mathbf a} _\beta + t^{n \alpha }{\mathbf n} \otimes {\mathbf a} _\alpha + t^{\alpha n}{\mathbf a} _\alpha \otimes {\mathbf n} + t^{nn}{\mathbf n} \otimes {\mathbf n}, \end{aligned}$$
(3)

where \(\xi ^\alpha\), \(\alpha =1,2\) are local surface curvilinear coordinates on \({\mathcal {M}}\), and \({\mathbf a} _\alpha\), \(\mathbf n\) are the base vectors on the middle surface of the layer \({\mathcal {M}}\). A dyade \({\mathbf t} _s\) governs the momentum transport within the layer, and therefore, it has tangential and normal components. It should be noted that the physical properties of the layer are unknown a priori since they depend on the resulting apparent properties in both continua \({\mathcal {A}}\) and \({\mathcal {B}}\).

The balances of the layer mass and momentum can be established using postulated notions, i.e., \(\rho _s\), \({\mathbf v}_{s}\), \({\mathbf t}_{s}\), \({\mathbf m}_s\), \(\varvec{\omega }_s\) and employing some mathematical relations. Let introduce the Weatherburn surface fundamental dyades in Pietraszkiewicz (1977):

$$\begin{aligned} {\mathbf I}_{s}&= {\mathbf I} -{\mathbf n} \otimes {\mathbf n} ={\mathrm{grad}}_{s}{\mathbf x} _{s}=a^{\alpha \beta }{\mathbf a} _\alpha \otimes {\mathbf a} _\beta ,\end{aligned}$$
(4)
$$\begin{aligned} {\mathbf{II }}_{s}&= -{\mathrm{grad}}_{s}{\mathbf n} =b^{\alpha \beta }{\mathbf a} _\alpha \otimes {\mathbf a} _\beta. \end{aligned}$$
(5)

These diades are called the first and second fundamental form of the surface \({\mathcal {M}}\). Surface gradient acts also on the coordinate dependent base \({\mathbf a} _{\alpha }\), \(\mathbf n\). Thus, the surface gradient of velocity is calculated to be:

$$\begin{aligned} {\mathrm{grad}}_{s}{\mathbf v} _{s}&= \left( v^{\alpha }{\mathbf a} _\alpha +v_n{\mathbf n} \right) \otimes \nabla _\beta {\mathbf a} ^\beta \nonumber \\&= \left( v_{\alpha \mid \beta }-v_n b_{\alpha \beta }\right) {\mathbf a} ^\alpha \otimes {\mathbf a} ^\beta + \left( v^\alpha b_{\alpha \beta }+v_{n,\beta }\right) {\mathbf n} \otimes {\mathbf a} ^{\beta }. \end{aligned}$$
(6)

The surface divergence of this vector needs the contraction operation made on the surface gradient in the following form:

$$\begin{aligned} {\mathrm{div}}_{s}{\mathbf v} _{s}&= \mathsf C _{1,2}{\mathrm{grad}}_{s}{\mathbf v} _{s}= \left( v_{\alpha \mid \beta }-v_n b_{\alpha \beta }\right) a^{\alpha \beta }\nonumber \\&= {v^{\alpha }}_{\mid \alpha }-v_n {b^{\alpha }}_{\alpha }={\mathrm{div}}_{s}\left( {\mathbf v} _{s\parallel }\right) -v_n {\mathrm{I}}_b. \end{aligned}$$
(7)

The invariants of the second fundamental form of the curvature diade are \({\mathrm{I}}_b={\mathrm{tr}}{\mathbf{II }}_{s}={b^{\alpha }}_{\alpha }={b^{1}}_{1}+{b^{2}}_{2}=\left( \frac{1}{r_1}+\frac{1}{r_2}\right)\), \({\mathrm{II}}_b = {\mathrm{det}}{\mathbf{II }}_{s}={\mathrm{det}} \left( b_{\alpha \beta }\right)\). In analogy to the three-dimensional case, rate of the surface deformation can be defined as a symmetric part of the surface gradient of velocity by Truesdell and Toupin (1960):

$$\begin{aligned} {\mathbf d}_s&= \frac{1}{2}\left( {\mathrm{grad}}_{s}{\mathbf v}_{s}+{\mathrm{grad}}_{s}^{\mathrm{T}}{\mathbf v}_{s}\right) \nonumber \\&= \left[ \frac{1}{2}\left( v_{\alpha \mid \beta }+v_{\beta \mid \alpha }\right) -v_n b_{\alpha \beta }\right] {\mathbf a} ^{\alpha }\otimes {\mathbf a} ^{\beta }+\frac{1}{2}\left( v^\alpha b_{\alpha \beta }+ v_{n,\beta }\right) \left( {\mathbf n} \otimes {\mathbf a} ^\beta +{\mathbf a} ^\beta \otimes {\mathbf n} \right) . \end{aligned}$$
(8)

Then the first invariant of \({\mathbf d} _s\) is:

$$\begin{aligned} {\mathrm{I}}_{{\mathbf{d}}_s}={\mathrm{tr}}{\mathbf d} _s={\mathsf{C }}_{1,2}{\mathbf d} _s= {v^{\alpha }}_{\mid \alpha }-v_n{\mathrm{I}}_b. \end{aligned}$$
(9)

The surface gradient of a surface tensor, for instance the flux of angular momentum, can be written as:

$$\begin{aligned} {\mathrm{grad}}_{s}{\mathbf m} _{s}&= {\mathbf m} _{s}\otimes \left( \nabla _\gamma {\mathbf a} ^\gamma \right) = {m^{\alpha \beta }}_{\mid \gamma }{\mathbf a} _\alpha \otimes {\mathbf a} _\beta \otimes {\mathbf a} ^\gamma + m^{\alpha \beta }b_{\alpha \gamma }{\mathbf n} \otimes {\mathbf a} _\beta \otimes {\mathbf a} ^\gamma \nonumber \\&\quad +m^{\alpha \beta }b_{\beta \gamma }{\mathbf a} _\alpha \otimes {\mathbf n} \otimes {\mathbf a} ^\gamma + {m^{n\alpha }}_{\mid \gamma }\left( {\mathbf n} \otimes {\mathbf a} _\alpha \otimes {\mathbf a} ^\gamma +{\mathbf a} _\alpha \otimes {\mathbf n} \otimes {\mathbf a} ^\gamma \right) \nonumber \\&\quad +\left( 2m^{n\alpha }b_{\alpha \gamma }+{m^{nn}}_{\mid \gamma }\right) {\mathbf n} \otimes {\mathbf n} \otimes {\mathbf a} ^\gamma \nonumber \\&\quad -m^{n\alpha }{b^\varepsilon }_{\gamma }\left( {\mathbf a} _\varepsilon \otimes {\mathbf a} _\alpha \otimes {\mathbf a} ^\gamma + {\mathbf a} _\alpha \otimes {\mathbf a} _\varepsilon \otimes {\mathbf a} ^\gamma \right) \nonumber \\&\quad -m^{nn}{b^\varepsilon }_{\gamma }\left( {\mathbf a} _\varepsilon \otimes {\mathbf n} \otimes {\mathbf a} ^\gamma + {\mathbf n} \otimes {\mathbf a} _\varepsilon \otimes {\mathbf a} ^\gamma \right) , \end{aligned}$$
(10)

and its divergence:

$$\begin{aligned} {\mathrm{div}}_{s}{\mathbf m} _{s}&= \mathsf{C }_{2,3}{\mathrm{grad}}_{s}{\mathbf m} _{s}= \left( {m^{\alpha \beta }}_{\mid \beta }-m^{n\beta }{b^\alpha }_\beta -{\mathrm{I}}_b m^{\alpha n}\right) {\mathbf a} _\alpha \nonumber \\&\quad +\left( m^{\alpha \beta }b_{\alpha \beta }+{m^{n\alpha }}_{\mid \alpha }-{\mathrm{I}}_b m^{nn}\right) {\mathbf n}. \end{aligned}$$
(11)

After employing an useful identities as \(\left( d_t={\mathrm{d}}/{\mathrm{d}}t;\,\partial _t=\partial /\partial t\right)\), we can write the following theorems:

  • the Reynolds transport theorem for angular momentum in continuum \({\mathcal {A}}\) with the moving subsurface \(S^{+}\):

    $$\begin{aligned} d_{t} \int \!\!\int \!\!\int _A {{\varvec{l}}}_A {\mathrm{d}}v&= \int \!\!\int \!\!\int _A \partial _t \left( {{\varvec{l}}}_A\right) {\mathrm{d}}v + \iint _{\partial A} {{\varvec{l}}}_A \otimes {\mathbf v} _A{\mathbf n} _A {\mathrm{d}}s + \int _{S^{+}}{{\varvec{l}}}_A \otimes {\mathbf w} {\mathbf n} ^{+}{\mathrm{d}}s \nonumber \\&= \int \!\!\int \!\!\int _A \partial _t \left[ {{\varvec{l}}}_A + {\mathrm{div}}\left( {{\varvec{l}}}_A \otimes {\mathbf v} _A\right) \right] {\mathrm{d}}v+ \iint _{S^{+}}{{\varvec{l}}}_A \otimes \left( {\mathbf w} -{\mathbf v} _A\right) {\mathbf n} ^{+}{\mathrm{d}}s;\end{aligned}$$
    (12)

  • the Slattery transport theorem for the surface angular momentum by Povstenko and Podstigach (1983):

    $$\begin{aligned} d_{t} \iint _{S(t)}{{\varvec{l}}}_s {\mathrm{d}}s&= \iint _{S}\left[ \partial _t\left( {{\varvec{l}}}_s\right) +{\mathrm{div}}_s \left( {{\varvec{l}}}_s\otimes {\mathbf v} _{s\parallel }\right) -{{\varvec{l}}}_s w_n {\mathrm{I}}_b\right] {\mathrm{d}}s\nonumber \\&\quad +\int _{{\mathcal {L}}} {{\varvec{l}}}_s\otimes \left( {\mathbf w} _{\parallel }-{\mathbf v} _{s\parallel }\right) {\mathbf n} _l{\mathrm{d}}l \end{aligned}$$
    (13)

  • the Stokes–Weatherburn surface identity by Weatherburn (1930):

    $$\begin{aligned} \int _{{\mathcal {L}}} {\mathbf m} _s {\mathbf v} {\mathrm{d}}l = \iint _{S}\left[ {\mathrm{div}}_s{\mathbf m} _s+\left( {\mathrm{tr}}{\mathbf{II }}_s\right) {\mathbf m} _s{\mathbf n} \right] {\mathrm{d}}s, \end{aligned}$$
    (14)

3 Angular momentum balance in the slip layer

A motion of the slip layer particle is governed by its slip velocity \({\mathbf v} _s={\mathbf v} _{s\parallel }+v_n{\mathbf n}\) and the angular slip velocity \({\varvec{\omega }}_s={\varvec{\omega }}_{s\parallel }+\omega _n{\mathbf n}\). Inertia properties of the layer particle are described by the layer density \(\rho _s\) and the layer symmetric inertia tensor \({\mathbf J} _s=J_{ij}{\mathbf e} _i\otimes {\mathbf e} _j={\mathbf J} _s^{\mathrm{T}}\). The layer momentum, according to Galileo’s postulate, is given as a linear relation between density and velocity: \({\mathbf s} _s=\rho _s{\mathbf v} _s\). Similarly, the layer angular momentum \({{\varvec{l}}}_s\) is defined by a Galilean-like constitutive equation \({{\varvec{l}}}_s={\mathbf J} _s{\varvec{\omega }}_s\).

According to the laws of classical mechanics, the second Euler law of motion is determined completely by two vector measures (eq. 196.3 in Truesdell and Toupin 1960) described by a Newton-like equation of motion:

$$\begin{aligned} \frac{\mathrm{d}}{{\mathrm{d}}t}{\mathbf{L }}={\mathbf M}. \end{aligned}$$
(15)

The vector \(\mathbf L\) represents a total angular momentum taken with respect to the common origin, and the vector \(\mathbf M\) is an absolute vector defining the torque acting on the bodies. Let us propose that both resultant vectors \(\mathbf L\) and \(\mathbf M\) have a contribution coming from the moment of momentum and from the internal couples:

$$\begin{aligned} {\mathbf L}&= \int \!\!\int \!\!\int _{A\cup B}\left( {{\varvec{l}}}+{\mathbf x} \times {\mathbf s} \right) {\mathrm{d}}v+\iint _S \left( {{\varvec{l}}}_s+{\mathbf x} _s\times {\mathbf s} _s\right) {\mathrm{d}}s,\end{aligned}$$
(16)
$$\begin{aligned} {\mathbf M}&= \int \!\!\int \!\!\int _{A\cup B}\rho \left( {\mathbf c} +{\mathbf x} \times {\mathbf b} \right) {\mathrm{d}}v+ \iint _{\partial {A}\cup \partial {B}} \left( {\mathbf m} _{\mathbf{n }}+{\mathbf x} _s\times {\mathbf t} _{\left( {\mathbf n} \right) }\right) {\mathrm{d}}s\nonumber \\&\quad +\iint _{S}\rho \left( {\mathbf c} _s+{\mathbf x} _s\times {\mathbf b} _s\right) {\mathrm{d}}s+ \int _{\partial {S}} \left( {\mathbf m} _{\left( {\varvec{\nu }}\right) }+{\mathbf x} _s\times {\mathbf t} _{\left( {\varvec{\nu }}\right) }\right) {\mathrm{d}}l. \end{aligned}$$
(17)

Some quantities, which are well known in three-dimensional bulk Cosserat continua, appear here (Eringen 1964; Kafadar and Eringen 1971), i.e., \({{\varvec{l}}}\), \(\mathbf s\) are the bulk angular and linear momentum; \(\mathbf c\), \(\mathbf b\) are the body couple and body force densities. According to extended Cauchy postulate by Truesdell and Toupin (1960), the boundary traction and torque are \({\mathbf t} _{\left( {\mathbf n} \right) }={\mathbf t} {\mathbf n}\) and \({\mathbf m} _{\left( \mathbf n \right) }=\mathbf m \mathbf n\), respectively. Considered diades \({\mathbf t} =t_{ij}{\mathbf e} _{i}\otimes {\mathbf e} _{j}\ne {\mathbf t} ^{\mathrm{T}}\) and \({\mathbf m} =m_{ij}{\mathbf e} _{i}\otimes {\mathbf e} _{j}\ne {\mathbf m} ^{\mathrm{T}}\) represent Cauchy-type nonsymmetric diades called the momentum flux tensor and the angular momentum flux tensor, respectively (Neff and Jeong 2009).

In analogy to the early postulated layer body force \({\mathbf b} _s\) by Badur et al. (2011b), the body couple or body torque density \({\mathbf c} _s\), which arise from internal interactions between both bulk continua, can appear in the moving layer. Also in analogy to the postulated layer stress tensor \({\mathbf t} _s\) by Badur et al. (2011b), we postulate an existence of the couple layer stress:Footnote 1

$$\begin{aligned} {\mathbf m} _{s}= m_{\alpha \beta }{\mathbf a} ^\alpha \otimes {\mathbf a} ^\beta + m_{n \alpha }{\mathbf n} \otimes {\mathbf a} ^\alpha + m_{\alpha n}{\mathbf a} ^\alpha \otimes {\mathbf n} + m_{nn}{\mathbf n} \otimes {\mathbf n}, \end{aligned}$$
(18)

which arises in such the same way that the tensor \(\mathbf t _s\) does. The traction on a linear boundary of surface \(S\) is a prolongation of \(\mathbf t _s\), \(\mathbf m _s\) onto the boundary oriented by a unit vector \({\varvec{\nu }}=\nu _\alpha \mathbf a ^\alpha\) tangent to \(S\) and normal to the boundary curve \({\mathcal {L}}\):

$$\begin{aligned} \mathbf t _{\left( {\varvec{\nu }}\right) }=\mathbf t _s{\varvec{\nu }}; \quad \mathbf m _{\left( {\varvec{\nu }}\right) }=\mathbf m _s{\varvec{\nu }}. \end{aligned}$$
(19)

From definition (11), it practically means that only \(3\times 2\) components undergo the surface divergence operation. Nevertheless, according to Stokes-Weatherburn theorem (14), all the components of surface tensors are indeed to be angular momentum, and therefore, during formulation of the constitutive equations, one should take tensors of not only \(3\times 2\) components but also those of \(2\times 3\) components.

Traditionally, in rational mechanics we are looking for a local statement of the second Euler law (15) by employing Reynolds’ transport theorem and the Gauss–Ostrogradskii theorem to divergence. Additionally, the Reynolds–Slattery (12), (13) and Stokes–Weatherburn [see (14)] theorems should be simultaneously used. Yet one additional, not classical operation, that come from the vector multiplication between the position vector and the traction vector, should be also defined here in details.Footnote 2 Adopting Mindlin and Tiersten (1962) denotations, one obtains by calculation:

$$\begin{aligned} \iint _{\partial {A}}\mathbf x \times \mathbf t _{\left( \mathbf n \right) }{\mathrm{d}}s&= \iint _{\partial {A}}\mathbf x \times \left( \mathbf t \mathbf n \right) {\mathrm{d}}s= \int \!\!\int \!\!\int _{V}{\mathrm{div}}\left( \mathbf x \times \mathbf t \right) {\mathrm{d}}v\nonumber \\&= \iint _{\partial {A}}\left( \mathbf x \times \mathbf t \right) \mathbf n {\mathrm{d}}s=\int \!\!\int \!\!\int _{V}[\mathbf x \times \left( {\mathrm{div}}\mathbf t \right) +\mathbf I \left( \times \cdot \right) \mathbf t ]{\mathrm{d}}v\nonumber \\&= \int \!\!\int \!\!\int _{V}[\mathbf x \times \left( {\mathrm{div}}\mathbf t \right) -\mathbf t _\times ]{\mathrm{d}}v . \end{aligned}$$
(20)

Looking on the shell-like layer shown in Fig. 1, we conclude that the traction forces \(\mathbf t _{\left( \mathbf n \right) }\) and traction couples \(\mathbf m _{\left( \mathbf n \right) }\) are given at the contact surfaces \(S^{+}\), \(S^{-}\), respectively. Those quantities shifted to a basic surface \(S\) by an internal equilibrium should be replaced by the system of traction forces \(\mathbf t _{\left( \mathbf n \right) A}\), \(\mathbf t _{\left( \mathbf n \right) B}\) and couples \(\mathbf m _{\left( \mathbf n \right) A}\), \(\mathbf m _{\left( \mathbf n \right) B}\) coming from the continua \({\mathcal {A}}\), \({\mathcal {B}}\), and friction forces \(\mathbf f _A\), \(\mathbf f _B\) and couples \(\mathbf q _A\), \(\mathbf q _B\) coming from the layer reaction:

$$\begin{aligned}&\mathbf t _{\left( \mathbf n \right) +}= \mathbf t _{\left( \mathbf n \right) A}-\mathbf f _A;\quad \mathbf t _{\left( \mathbf n \right) -}= \mathbf t _{\left( \mathbf n \right) B}-\mathbf f _B;\nonumber \\&\mathbf m _{\left( \mathbf n \right) +}= \mathbf m _{\left( \mathbf n \right) A}-\mathbf q _A;\quad \mathbf m _{\left( \mathbf n \right) -}= \mathbf m _{\left( \mathbf n \right) B}-\mathbf q _B. \end{aligned}$$
(21)

Now, taking into account the Reynolds and Slattery transport theorems and employing the Gauss–Ostrogradzki and Stokes–Weatherburn identities, after step-by-step calculations, we transform (15) into:

$$\begin{aligned}&\int \!\!\int \!\!\int _V \langle \mathbf x \times [\partial _t\mathbf s +{\mathrm{div}}\left( \mathbf s \otimes \mathbf v \right) -{\mathrm{div}}\mathbf t -\rho \mathbf b ]\nonumber \\&\quad +[\partial _t {{\varvec{l}}}+{\mathrm{div}}\left( {{\varvec{l}}}\otimes \mathbf v \right) -{\mathrm{div}}\mathbf m +\mathbf t _{\times }-\rho \mathbf c ] \rangle {\mathrm{d}}v\nonumber \\&\quad +\iint _S \langle \mathbf x _s\times [\partial _t\mathbf s _s+{\mathrm{div}}_s\left( \mathbf s _s\otimes \mathbf v _{s\parallel }\right) - \mathbf s u_n {\mathrm{I}}_b -{\mathrm{div}}_s\mathbf t _s-{\mathrm{I}}_b\mathbf t \mathbf n \nonumber \\&\quad -\left( \mathbf t _{\left( \mathbf n \right) A}+\mathbf t _{\left( \mathbf n \right) B}-\mathbf f _A-\mathbf f _B\right) -\rho _s\mathbf b _s]\rangle {\mathrm{d}}s\nonumber \\&\quad +\iint _S \langle \partial _t {{\varvec{l}}}_s+{\mathrm{div}}_s\left( {{\varvec{l}}}_s\otimes \mathbf v _{s\parallel }\right) -{{\varvec{l}}}_s u_n {\mathrm{I}}_b-{\mathrm{div}}_s\mathbf m _s+{\mathrm{I}}_b\mathbf m _s\mathbf n +\left( \mathbf t _s\right) _\times \nonumber \\&\quad -\left( \mathbf m _{\left( \mathbf n \right) A}+\mathbf m _{\left( \mathbf n \right) B}-\mathbf q _A-\mathbf q _B\right) -\rho _s\mathbf c \rangle {\mathrm{d}}s\nonumber \\&\quad +\int _l\langle \mathbf x _l\times [\mathbf s \otimes \left( \mathbf u _\parallel - \mathbf v _{s\parallel }\right) {\varvec{\nu }}]+ \mathbf I _s\otimes \left( \mathbf u _\parallel - \mathbf v _{s\parallel }\right) {\varvec{\nu }} \rangle {\mathrm{d}}l=0. \end{aligned}$$
(22)

Finally, taking into account a local form of the balance of momentum for the bulk and slip layer by Badur et al. (2011b):

$$\begin{aligned}&\partial _t\left( \rho \mathbf v \right) +{\mathrm{div}}\left( \rho \mathbf v \otimes \mathbf v \right) = {\mathrm{div}}\mathbf t +\rho \mathbf b ,\quad {\mathrm{for}}\,{\mathcal {A}}\cup {\mathcal {B}}\end{aligned}$$
(23)
$$\begin{aligned}&\partial _t\left( \mathbf s _s\right) +{\mathrm{div}}_s\left( \mathbf s _s\otimes \mathbf v _\parallel \right) -u_n {\mathrm{I}}_b \mathbf s _s= {\mathrm{div}}_s\mathbf t _s+{\mathrm{I}}_b\mathbf t _s\mathbf n \nonumber \\&\quad +[\mathbf t _A\mathbf n _A+\mathbf t _B\mathbf n _B-\mathbf f _A-\mathbf f _B]+\rho _s\mathbf b _s,\quad {\mathrm{on}}\,{\mathcal {M}} \end{aligned}$$
(24)

we obtain the local form of the angular momentum equations:

$$\begin{aligned}&\partial _t\left( {{\varvec{l}}}\,\right) +{\mathrm{div}}\left( {{\varvec{l}}}\otimes \mathbf v \right) = {\mathrm{div}}\,\mathbf m -\mathbf t _{\times }+\rho \mathbf c ,\quad {\mathrm{for}}\,{\mathcal {A}}\cup {\mathcal {B}}\end{aligned}$$
(25)
$$\begin{aligned}&\partial _t\left( {{\varvec{l}}}_s\right) +{\mathrm{div}}_s\left( {{\varvec{l}}}_s\otimes \mathbf v _\parallel \right) -u_n {\mathrm{I}}_b {{\varvec{l}}}_s= {\mathrm{div}}_s\mathbf m _s+{\mathrm{I}}_b\mathbf m _s\mathbf n +\left( {\mathrm{grad}}_s\mathbf x _s\right) ^{\mathrm{T}}\left( \times \cdot \right) \mathbf t _s\nonumber \\&\quad +[\mathbf m _{\left( \mathbf n \right) A}+\mathbf m _{\left( \mathbf n \right) B}-\mathbf q _A-\mathbf q _B]+\rho _s\mathbf c _s,\quad {\mathrm{on}}\,{\mathcal {M}} \end{aligned}$$
(26)

The last equation is a generalization of “ABK” Eq. (2).Footnote 3 If layer particle cannot be able to induce the internal inertia tensor \(\mathbf J _s\), then the angular momentum leads to a static relation between layer couples, the axial of layer stress, the bulk couples and the friction torque. If layer stress is symmetric, then it appears as a condition, quite similar to the Poisson boundary condition:

$$\begin{aligned} \mathbf f _{\partial V}=\mathbf t \mathbf n +{\mathrm{div}}_s\left( \gamma \mathbf I _s\right) , \end{aligned}$$
(27)

where \(\gamma\) is the Young–Laplace surface tension. Assuming now that the layer couple consists of only the Gibbs surface bending \(C\): \(\mathbf m _s=C\mathbf I _s\) and \(\mathbf t _s=\mathbf t ^{\mathrm{T}}_s\), \(\mathbf c _s=0\) , we are able to extend some previous Gibbs writings to a Poisson-like boundary condition:

$$\begin{aligned} \mathbf q _{\partial V}=\mathbf m \mathbf n +{\mathrm{div}}_s\left( C\mathbf I _s\right) , \end{aligned}$$
(28)

Note that in contrast to Young–Laplace and Gibbs, the Poisson version of capillarity condition consists of parameters that depend on the position \(\gamma =\gamma \left( \mathbf x _s\right)\), \(C=C\left( \mathbf x _s\right)\).

4 Constitutive equations for a boundary friction resistance

According to the classical d’Alembert–du Buat hypothesis, the total resistance of fluid depends on both resistance induced in the bulk and within the boundary layer, see: Ziółkowski and Badur (2014). Therefore, the boundary friction force \(\mathbf f _{\partial V}=\mathbf f _A\) and the boundary friction moment \(\mathbf q _{\partial V}=\mathbf q _A\) should be correctly stated. Let us introduce an auxiliary unit versors:

$$\begin{aligned} \mathbf{e }_\mathbf{v }=\frac{\mathbf{v }_s}{|\mathbf{v }_s|},\quad \mathbf{e }_{{\varvec{\omega }}}=\frac{{\varvec{\omega }}_s+\mathbf{w }_s}{|{\varvec{\omega }}_s+\mathbf{w }_s|}, \end{aligned}$$
(29)

which represent the slip velocity direction and the total angular slip velocity direction, respectively. Assuming a possible form of friction mathematical models and restricting ourselves only to isotropic friction by Zmitrowicz (2006), we postulate, as in the classical Coulomb hypothesis of resistance, that the layer resistance contains three different contributions, i.e.: adherence, laminar and turbulent (skin eddies):

$$\begin{aligned} \mathbf f _{\partial V}&= \nu _0\varpi \mathbf e _\mathbf{v }+\nu \mathbf v _s+ \nu _2\left( \mathbf v _s\cdot \mathbf v _s\right) {\mathbf e} _{\mathbf{v }},\end{aligned}$$
(30)
$$\begin{aligned} {\mathbf q} _{\partial V}&= c_0 k {\mathbf e} _{{\varvec{\omega }}}+ c\left( {\varvec{\omega }}_s+{\mathbf w} _s\right) + c_2\left( {\varvec{\omega }}_s+{\mathbf w} _s\right) ^2{\mathbf e} _{{\varvec{\omega }}}. \end{aligned}$$
(31)

Three force friction coefficients \(\nu _0\), \(\nu\), \(\nu _2\) and three torque friction coefficients \(c_0\), \(c\), \(c_2\) are to be determined from appropriate experiments in nano-flows. Note that they depend not only on the fluid material but also on a kind of contacting body. Coefficients \(\nu _2\) and \(c_2\) are responsible for conversion of a layer kinetic energy into the skin eddies, which are responsible for an inception and development of a bulk turbulence in Karcz and Badur (2003). In above equations, \(\varpi\) \([{\mathrm{N}}/{\mathrm{m}}^2]\) represents a postulated adherence force normal to a surface by Stokes (1845), and \(k\) \([{\mathrm{Nm}}/{\mathrm{m}}^2]\) is a normal torque pressure. Generally, the adherence part is assumed to be similar to Coulomb’s dry friction normal force.Footnote 4

Note that four from six of friction coefficients have already been proposed and used in the literature. The linear friction \(\nu\) was introduced by Navier on the base of the variational arguments in Navier (1827) [p. 415]. The eddy friction force coefficient \(\nu _2\) was proposed in Boussinesq (1877) [p. 42, eq. 22], and nowadays it is used in some untypical models of turbulence [see, for example, Karcz and Badur (2003), Ziółkowski and Badur (2014), Straughan and Harfash (2013)]. Duhem proposed and tested the adherence coefficient \(\nu _0\) Duhem (1903) [p. 216]. Finally, the coefficient \(c\) was postulated by Aero et al. (1965) [eq. 6.4].

5 Constitutive equations for the layer momentum and angular momentum fluxes

Fluid contained in the Navier–Stokes slip layer still possesses typical feature of fluidity, i.e., viscosity; therefore, the elastic stresses are limited only to the tangential surface pressures \({\mathbf t} ^{\left( rec\right) }_s=-p_s{\mathbf I} _s\) and the surface torque \({\mathbf m} ^{\left( rec\right) }_s=-k_s{\mathbf I} _s\). Both state parameters need a thermodynamical constitutive equations and should be differentiated from the normal Stokes pressure \(\varpi\) and torque \(k\), which appears in Eqs. (30) and (31).

Viscous parts of \({\mathbf t} _s\), \({\mathbf m} _s\) as in the normal Cauchy-like mechanics, would be expressed by appropriate “rates of deformation.” In general, these rates are defined in the same manner, independently of continua dimension. The procedure starts from the Lagrangian deformation measures which, after material time differentiation, are “pushed forward” to the Eulerian “picture”. Adopting here three-dimensional operations of “pull back” and the “push forward” discovered by Kafadar and Eringen (1971), to a two-dimensional shell-like layer, we find the following surface rate of deformation introduced by Rey (2006), Stumpf and Badur (1993):

$$\begin{aligned} {\mathbf e} _s&= {\mathrm{grad}}_s{\mathbf v} _s-\in {\varvec{\omega }}_s={\mathbf R} ^{\mathrm{T}}\frac{d}{dt}\left( {\mathbf U} \right) {\mathbf F} ^{-1}_s,\end{aligned}$$
(32)
$$\begin{aligned} {\mathbf k} _s&= {\mathrm{grad}}_s{\varvec{\omega }}_s={\mathbf R} ^{\mathrm{T}}\frac{d}{dt}\left( {\mathbf G} \right) {\mathbf F} ^{-1}_s. \end{aligned}$$
(33)

In an analogy to 3D case \({\mathbf e} _s\), \({\mathbf k} _s\) should be called “the positional deformation rate” and “the curvature rate.” In Eq. (32), above \(\in =-{\mathbf I} \times {\mathbf I}\) is the Ricci alternator, \({\mathbf F} _s={\mathrm{Grad}}_s{\mathbf x} _s\) is the surface deformation gradient, and \(\mathbf R\) is rotation tensor such as \({\mathbf R} ^{\mathrm{T}}={\mathbf R} ^{-1}\). Lagrangian measure of position and curvature \(\mathbf U\), \(\mathbf G\) are one-point tensors of Jaumann–Trefftz type, proposed by Kafadar and Eringen (1971). These are the following functions of the referential gradient of position \({\mathbf F} _s\), rotation tensor \(\mathbf R\) and the gradient of rotation tensorFootnote 5 \({\mathrm{Grad}}_s{\mathbf R}\) proposed in analogy to Kafadar and Eringen (1971):

$$\begin{aligned} {\mathbf U} ={\mathbf R} ^{\mathrm{T}}{\mathrm{Grad}}_s{\mathbf x},\quad {\mathbf G} =-\frac{1}{2}\in \left( {\mathbf R} ^{\mathrm{T}}{\mathrm{Grad}}_s{\mathbf R} \right) . \end{aligned}$$
(34)

According to Mindlin and Tiersten (1962) concept of body with constrained rotation and independently from a contribution of the free rotational measures, there is also a contribution form constrained rotation, that is, expressed by a second gradient of slip velocity \({\mathbf k} ^{\left( 2\right) }_s={\mathrm{grad}}_s\left( {\mathrm{grad}}_s{\mathbf v} _s\right)\). This measure can contributes only to the symmetric part of \({\mathbf t} _s\) by surface divergence.

Now the viscous stresses and couples can be expressed by linear combination of \({\mathbf e} _s\), \({\mathbf k} _s\), \({\mathbf k} ^{\left( 2\right) }_s\):

$$\begin{aligned} {\mathbf t} ^{({\mathrm{vis}})}_s&= \alpha _1{\mathrm{tr}}\left( {\mathbf e} _s\right) {\mathbf I} _s+ \alpha _2{\mathbf e} _s+\alpha _3{\mathbf e} ^{\mathrm{T}}_s-{\mathrm{div}}_s\left( {\mathbf m} ^{\left( 2\right) }_s\right) ,\end{aligned}$$
(35)
$$\begin{aligned} {\mathbf m} ^{\left( {\mathrm{vis}}\right) }_s&= \alpha _4{\mathrm{tr}}\left( {\mathbf e} _s\right) {\mathbf I} _s+\alpha _5 {\mathbf k} _s+\alpha _6 {\mathbf k} ^{\mathrm{T}}_s, \end{aligned}$$
(36)

where \(\alpha _1\), \(\alpha _2\) and \(\alpha _3\), \(\alpha _4\), \(\alpha _5\), \(\alpha _6\) are the bulk and shear coefficients of viscosity, respectively. The third-order symmetric couple tensor \({\mathbf m} ^{\left( 2\right) }_s\) describes symmetric contribution to the surface Cauchy tensor from the second gradient of slip velocity \({\mathbf k} ^{\left( 2\right) }_s\). A simplest expression for \({\mathbf m} ^{\left( 2\right) }_s\) is as follows:

$$\begin{aligned} -{\mathbf m} ^{\left( 2\right) }_s=\lambda _1{\mathbf I} _s\otimes {\mathrm{lap}}_s{\mathbf v} _s+\lambda _2{\mathrm{grad}}_s{\mathbf d} _s. \end{aligned}$$
(37)

Taking into account that \({\mathrm{div}}_s\left( {\mathrm{grad}}_s\left( \cdot \right) \right) ={\mathrm{lap}}_s\left( \cdot \right)\) is a surface laplacian, after substitution of (37) to (35) we obtain:

$$\begin{aligned} {\mathbf t} ^{( {\mathrm{vis}}) }_s=\alpha _1{\mathrm{tr}}\left( {\mathbf e} _s\right) {\mathbf I} _s+ \alpha _2{\mathbf e} _s+\alpha _3{\mathbf e} ^{\mathrm{T}}_s+ \lambda _1{\mathrm{lap}}_s\left( {\mathrm{div}}_s{\mathbf v} _s\right) +\lambda _2{\mathrm{grad}}_s{\mathbf d} _s, \end{aligned}$$
(38)

Further, a dimensional argument yields two constants \(\lambda _1\), \(\lambda _2\) and constants \(\alpha _1\), \(\alpha _2\), which are related by a material length of type \(l^2_s=\lambda _2/\alpha _2\) by Fried and Gurtin (2005), that is, appropriate to the modeling of fluid in the nanoscale.

6 An example: a stationary flow of the Cosserat fluid through a pipe

Let us consider a flow of fluid in a straight pipe of circular cross section of radius \(R\) and z-axis of cylindrical coordinate system \((r,\phi ,z)\). In analogy to the Hagen–Poiseuille simplified flow, let the vectors of the translational velocity and the spin to be in the form \({\mathbf {v}}=v (r){\mathbf {e}}_{z}\), \({\varvec{\omega }}=\omega (r){\mathbf {e}}_{\varphi }\). For the only two components \(v\), \(\omega\), the system of momentum and moment of momentum equations Eqs. (24), (26) is reduced to:

$$\begin{aligned} \left. \begin{array}{c} \rho v,_{t}=\rho b+(\lambda +2\mu )(rv,_{r}),_{r}+(\mu -\gamma )(rv,_{r}),_{r}-\gamma (r\omega ),_{r}+rp,_{z}\\ \rho I\omega ,_{t}=\rho \Gamma +(\eta +\tau +\theta )(\omega ,_{r}+\omega /r),_{r}-\gamma (v,_{r}+2\omega ) \end{array} \right\} \end{aligned}$$
(39)

where \(\lambda\), \(\mu\) are two translational viscosity coefficients and \(\gamma\), \(\eta\), \(\tau\), \(\theta\) are four rotational viscosity coefficients by Rey (2006), Stumpf and Badur (1993). Boundary conditions are \(r=R\)

$$\begin{aligned} v-\theta \mu ^{-1}\omega ,_{r}=0 \quad \hbox {(translational no-slip)},\quad c\omega =2(\eta +\tau +\theta )\omega ,_{r} \quad \hbox {(spin-slip)}. \end{aligned}$$
(40)

Further putting \(p,_{z}=const\), \(b\), \(\Gamma =0\). We have a solution:

$$\begin{aligned} v=B+ \frac{1}{4\mu }p,_{z}r^{2}-\frac{\theta }{\mu }CI_{0},\quad \omega =Ck_{2}I_{2}-\frac{1}{4\mu }p,_{z}r, \end{aligned}$$
(41)

where \(I_{0}\), \(I_{2}\) are the Bessel functions of zeroth and second order with argument \(I_{0}(r/k_{2})\) and \(I_{2}(r/k_{2})\), \(k_{2}^{2}=0,5\theta (\mu -\gamma )\mu ^{-1}\gamma {-1}\). From the boundary conditions, we have the constant \(B\), \(C\) and a parameter Ae expressed by:

$$\begin{aligned} B&= -\frac{1}{4\mu }p,_{z}R^{2}+\frac{\theta }{\mu }CI_{0}(k),\quad k=R/k_{2}\end{aligned}$$
(42)
$$\begin{aligned} C&= \frac{1}{4\mu }p,_{z}C_{R},\quad C_{R}^{-1}=k^{-1}I_{1}(k)+{\mathrm{Ae}}I_{2}(k),\end{aligned}$$
(43)
$$\begin{aligned} {\mathrm{Ae}}&= 1-\frac{\tau }{\theta }-\frac{cR}{\theta }. \end{aligned}$$
(44)

Substituting further \(\xi =r/R\), \(a=(2\mu )^{0,5}R\dot{\theta }^{-0,5}\) and constants \(B\), \(C\), we have the axial velocity field given by:

$$\begin{aligned} v(r)=-\frac{1}{4\mu }p,_{z}R^{2}\left[ 1-\xi ^{2}+\frac{2}{a^{2}}\frac{I_{0}(k\xi )-I_{0}(\xi )}{k^{-1}I_{1}(k)+{\mathrm{Ae}}I_{2}(k)}\right] \end{aligned}$$
(45)

If by \(Q_{H-P}=-\frac{\pi }{8\mu }p,_{z}R^{4}\), we denote known Hagen–Poiseuille volume flux (the volume discharge Kucaba-Piętal 2004) than taking \(Q_{spin}=\iint v(r)dA\) one can obtain:

$$\begin{aligned} Q_{spin}=Q_{H-P}\left[ 1-\frac{4}{a^{2}}\left( {\mathrm{Ae}}+\frac{I_{1}(k)}{kI_{2}(k)}\right) ^{-1}\right] . \end{aligned}$$
(46)

It is obvious that solution depends on value of the dimensionless parameter that physically should be interpreted as dimensionless spin friction coefficient. Flow enhancement, observed in nanotubes, can be realized when is less than zero or \(cR/\theta \ge 1\)

7 Conclusions

A numerous experimental discoveries of enhancement transport phenomena in nano-flows turned our attention to more accurate modeling of the boundary condition by Capritz and Podio-Guidugli (2004). Researches agree that the nano-fluidics flows are characterized mainly by a one fundamental distinctive property, which is a huge surface to volume ratio. The classical Navier–Stokes model of bulk flow is not satisfactory for the very small characteristic length scale; therefore, models with molecular spin by Hansen et al. (2009) or those employed a higher-order velocity gradients by Fried and Gurtin (2005) should be applied. But in some cases, a successful description of nano-flows can be find also with the classical Navier–Stokes model in the bulk and a nonclassical Navier slip layer.

In the present paper, we have introduced the angular slip velocity variable into consideration, under assumption that the molecule rolling on a surface can be a proper mechanism for further enhancement of nano-flows properties. The appropriate balance of angular momentum, that base on our previously elaborated algorithm in Badur et al. (2011b), has been proposed. The angular momentum equation in the slip layer imposes relation between the surface stress tensor, surface couple tensor and frictional couples.

Similar to Gurtin and Murdoch (1975), this formulation assumes that both surface tensors \({\mathbf t} _s\) and \({\mathbf m} _s\) consist of the capillarity contribution independently of another recoverable stress state. The modeling formalism adopted here leads to a direct incorporation of all slipping and rolling effects and fulfills basic principles of rational mechanics.