Abstract
We present a model for stress-fiber reorganization and the associated contractility that includes both the kinetics of stress-fiber formation and dissociation as well as the kinetics of stress-fiber remodeling. These kinetics are motivated by considering the enthalpies of the actin/myosin functional units that constitute the stress fibers. The stress, strain and strain rate dependence of the stress-fiber dynamics are natural outcomes of the approach. The model is presented in a general 3D framework and includes the transport of the unbound stress-fiber proteins. Predictions of the model for a range of cyclic loadings are illustrated to rationalize hitherto apparently contrasting observations. These observations include: (1) For strain amplitudes around 10 % and cyclic frequencies of about 1 Hz, stress fibers align perpendicular to the straining direction in cells subjected to cyclic straining on a 2D substrate while the stress fibers align parallel with the straining direction in cells constrained in a 3D tissue. (2) At lower applied cyclic frequencies, stress fibers in cells on 2D substrates display no sensitivity to symmetric applied strain versus time waveforms but realign in response to applied loadings with a fast lengthening rate and slow shortening. (3) At very low applied cyclic frequencies (on the order of mHz) with symmetric strain versus time waveforms, cells on 2D substrates orient perpendicular to the direction of cyclic straining above a critical strain amplitude.


















Similar content being viewed by others
Notes
ATP hydrolysis driving the growth of actin filaments (F-actin) from the polymerization of G-actin monomers is widely accepted; see for example Howard (2001). The reaction (2.10) is motivated from these understanding.
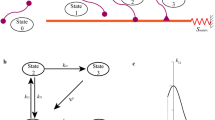
Fig. 4 The energy landscape of the stress-fiber proteins \((n^{R}=1)\). The sketch shows the standard enthalpies of the unclustered unbound proteins, one packet of clustered (intermediate stage) unbound proteins that comprises aggregates to form three functional units and the stress-fiber comprising \(n=3\) functional units that forms from this one packet. The activation barrier between the clustered unbound proteins and the bound proteins within the stress-fiber is also indicated
See Obbink-Huizer et al. (2014) for a detailed discussion on the effect of the gel/matrix stiffness.
A mildly anisotropic distribution of \(\xi \) with alignment perpendicular to the imposed loading for the fast lengthening and square waveform cases.
Fig. 15 Predictions of the response of cells (slow stress-fiber remodeling) on substrates (type I experiments) subjected to cyclic loading with a symmetric triangular, b fast lengthening, c square and d fast shortening waveforms and \(E_{\mathrm{max}}=0.1\) and \(f=0.1\,\hbox {Hz}\). Results are shown for (1) circular histograms of \(\xi \) at steady state after cyclic loading; (2) the variation of \({\tilde{\varepsilon }}_{n}^{0}\) and \({\tilde{\varepsilon }}_{n}^{90}\) with time over five cycles during the steady-state phase and (3) the corresponding variations of \(\hat{n}_{0}\) and \(\hat{n}_{90}\)
References
Aref A, Horvath R, Ramsden JJ (2010) Spreading kinetics for quantifying cell state during stem cell differentiation. J Biol Phys Chem 10:145–151
Buck RC (1980) Reorientation response of cells to repeated stretch and recoil of the substratum. Exp Cell Res 127(2):470–474
Burridge K, Chrzanowska-Wodnicka M (1996) Focal adhesions, contractility and signaling. Annu Rev Cell Dev Biol 12:463–469
Byers HR, Fujiwara K (1982) Stress fibers in cells in situ: immunofluorescence visualization with antiactin, antimyosin and anti-alpha-actinin. J Cell Biol 93:804–811
Chen CS, Alonso JL, Ostuni E, Whitesides GM, Ingber DE (2003) Cell shape provides global control of focal adhesion assembly. Biochem Biophys Res Commun 307:355–361
De Bruyn PPH, Cho Y (1974) Contractile structures in endothelial cells of splenic sinusoids. J Ultrastruct Res 49:24–33
Deshpande VS, McMeeking RM, Evans AG (2006) A bio-chemo-mechanical model for cell contractility. Proc Natl Acad Sci USA 103:14015–14020
Discher DE, Janmey P, Wang YL (2005) Tissue cells feel and respond to the stiffness of their substrate. Science 310:1139–1143
Eisenberg E, Hill TL, Yi-Der Chen (1980) Cross-bridge model for muscle contraction. Biophys J 29:195–227
Evans E, Ritchie K (1997) Dynamic strength of molecular adhesion bonds. Biophys J 72:1541–1555
Faust U, Hampe N, Rubner W, Kirchgessner N, Safran S, Hoffmann B, Merkel R (2011) Cyclic stress at mHz frequencies aligns fibroblasts in direction of zero strain. PLoS One 6(12):e28963
Foolen J, Deshpande VS, Kanters FMW, Baaijens FPT (2012) The influence of matrix integrity on stress-fiber remodeling in 3D. Biomaterials 33:7508–7518
Gauvin R, Parenteau-Bareil R, Larouche D, Marcoux H, Bisson F, Bonnet A, Auger FA, Bolduc S, Germain L (2011) Dynamic mechanical stimulations induce anisotropy and improve the tensile properties of engineered tissues produced without exogenous scaffolding. Acta Biomater 7(9):3294–3301
Gordon SR, Essner E, Rothstein H (1982) In situ demonstration of actin in normal and injured ocular tissues using 7-nitrobenz-2-oxa-1,3-diazole phallacidin. Cell Motil Cytoskelet 4:343–354
Guterl KA, Haggart CR, Janssen PM, Holmes JW (2007) Isometric contraction induces rapid myocyte remodeling in rat right ventricular papillary muscles. Am J Heart Circ Physiol 293:H3706–H3712
Hill AV (1938) The heat of shortening and the dynamic constants of muscle. Proc R Soc B 126:136–195
Howard J (2001) Mechanics of motor proteins and the cytoskeleton. Sinauer Associated Inc., Sunderland
Hunter P (1995) Myocardial constitutive laws for continuum mechanics models of the heart. In: Sideman S, Beyar R (eds) Molecular and subcellular cardiology. Springer, New York, pp 303–318
Jungbauer S, Gao H, Spatz JP, Kemkemer R (2008) Two characteristic regimes in frequency-dependent dynamic reorientation of fibroblasts on cyclically stretched substrates. Biophys J 95(7):3470–3478
Kaunas R, Nguyen P, Usami S, Chien S (2005) Cooperative effects of Rho and mechanical stretch on stress-fiber organization. Proc Natl Acad Sci USA 102(44):15895–15900
Kolega J (1986) Effects of mechanical tension on protrusive activity and microfilament and intermediate filament organization in an epidermal epithelium moving in culture. J Cell Biol 102:1400–1411
Langanger G, Moeremans M, Daneels G, Sobieszek A, De Brabander M, De Mey J (1986) The molecular organisation of myosin in stress-fiber of cultured cells. J Cell Biol 102:200–209
Lucas SM, Ruff RL, Binder MD (1995) Specific tension measurements in single soleus and medial gastrocnemius muscle fibers of the cat. Exp Neurol 95:142–154
McGarry JP, Fu J, Yang MT, Chen CS, McMeeking RM, Evans AG, Deshpande VS (2009) Simulation of the contractile response of cells on an array of micro-posts. Philos Trans R Soc A 367(1902):3477–3497
McGrath JL, Tardy Y, Dewey CF, Meister JJ, Hartwig JH (1998) Simultaneous measurements of actin filament turnover, filament fraction and monomer diffusion in endothelial cells. Biophys J 75:2070–2078
McMahon TA (1984) Muscles, reflexes and locomotion. Princeton University Press, Princeton
Mochitate K, Pawelek P, Grinnell F (1991) Stress relaxation of contracted collagen gels: disruption of actin filament bundles, release of cell surface fibronectin, and down-regulation of DNA and protein synthesis. Exp Cell Res 193:198–207
Neidlinger-Wilke C, Grood ES, Wang JH-C, Brand RA, Claes L (2001) Cell alignment is induced by cyclic changes in cell length: studies of cells grown in cyclically stretched substrates. J Orthop Res 19(2):286–293
Nieponice A, Maul TM, Cumer JM, Soletti L, Vorp DA (2007) Mechanical stimulation induces morphological and phenotypic changes in bone marrow-derived progenitor cells within a three-dimensional fibrin matrix. J Biomed Mater Res A 81(3):523–530
Obbink-Huizer C, Oomens CWJ, Loerakker S, Foolen J, Bouten CVC, Baaijens FPT (2014) Computational model predicts cell orientation in response to a range of mechanical stimuli. Biomech Model Mechanobiol 13:227–236
Parker KK, Brock AL, Brangwynne C, Mannix RJ, Wang N, Ostuni E, Geisse NA, Adams JC, Whitesides GM, Ingber DE (2002) Directional control of lamellipodia extension by constraining cell shape and orienting cell tractional forces. FASEB J 16:1195–1204
Pathak A, McMeeking RM, Evans AG, Deshpande VS (2011) An analysis of the co-operative mechano-sensitive feedback between intracellular signaling, focal adhesion developed and stress-fiber contractility. ASME J Appl Mech 78:041001-1
Ronan W, Deshpande VS, McMeeking RM, McGarry JP (2012) Numerical investigation of the active role of the actin cytoskeleton in the compression resistance of cells. J Mech Behav Biomed Mater 14:143–157
Tan JL, Tien J, Pirone DM, Gray DS, Bhadriraju K, Chen CS (2003) Cells lying on a bed of microneedles: an approach to isolate mechanical force. Proc Natl Acad Sci USA 100:1484–1489
Thavandiran N, Dubois N, Mikryukov A, Massé S, Beca B, Simmons CB, Deshpande VS, McGarry JP, Chen CS, Nanthakumar K, Keller K, Radisic M, Zandstra PW (2013) Design criteria-guided formulation of pluripotent stem cell-derived cardiac microtissues. Proc Natl Acad Sci USA 110:E4698–E4707
Thomopoulos S, Fomovsky GM, Holmes JW (2005) The development of structural and mechanical anisotropy in fibroblast populated collagen gels. J Biomech Eng ASME 127:742–750
Tondon A, Hui-Ju H, Kaunas R (2012) Dependence of cyclic stretch-induced stress-fiber reorientation on stretch waveform. J Biomech 45:728–735
Vernerey FJ, Farsad M (2011) A constrained mixture approach to mechano-sensing and force generation in contractile cells. J Mech Behav Biomed Mater 4(8):1683–1699
Vigliotti A, McMeeking RM, Deshpande VS (2015) Simulation of the cytoskeletal response of cells on grooved or patterned substrates. J R Soc Interface 12:20141320
Wang JH, Thampatty BP (2006) An introductory review of cell mechanobiology. Biomech Model Mechanobiol 5:1–16
Wei Z, Deshpande VS, McMeeking RM, Evans AG (2008) Analysis and interpretation of stress-fiber organization in cells subject to cyclic stretch. J Biomech Eng ASME 130:031009-1
Acknowledgments
A.V. and V.S.D. acknowledge the Royal Society for supporting A.V. through a Newton International Fellowship. Insightful discussions with Prof. R. M. McMeeking (UCSB) are gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Appendix: Chemical potentials of the stress-fiber proteins
Appendix: Chemical potentials of the stress-fiber proteins
Here, we derive expressions for the chemical potential \(\chi _{u}\) of the aggregate of unbound molecules that form a single functional unit and the chemical potential \(\chi _{b}\) of a functional unit within a stress-fiber comprising n units. These chemical potentials are derived using the enthalpies and the constraints imposed on the formation of stress fibers in deriving the kinetic Eq. (2.16). We shall employ classical statistical mechanics using the assumption of non-interacting particles, i.e., an ideal system.
Consider a segment subtending a unit solid angle within the RVE. Within this segment, there are \(\eta \) stress fibers each comprising n functional units and aggregates of unbound molecules that form \(N_{u}/(2\pi )\) functional units. For notational simplicity, we denote \(\bar{N}_{u} \equiv N_{u}/(2\pi )\), \(\bar{N}_{b}\equiv \eta n\) and \(\bar{N}_{T}\equiv \bar{N}_{u}+\bar{N}_{b}\). First consider the mixing between the \(\bar{N}_{L}\) lattice sites and the \(\bar{N}_{u}\) unbound aggregates of molecules. The \(\bar{N}_{u}\) identical aggregates of molecules and the \((\bar{N}_{L}-\bar{N}_{u})\) identical empty lattice sites in the mixture can be arranged in
ways and Boltzmann’s entropy formula then gives the entropy of mixing as
Using Stirling’s approximation (\(\ln M!\approx M\ln M-M\) for large M) we have
Upon assuming that the entropy of the unbound molecules prior to mixing with the lattice is zero, the chemical potential of the unbound molecules is given by
where \({\hat{N}}_L \equiv \bar{N}_{L}/N_{0}\). Since \(\bar{N}_{u} \ll \bar{N}_L \) (i.e., dilute assumption), \(\chi _{u} \) simplifies to
Now consider the stress fibers. In deriving the kinetic Eq. (2.16), we have assumed that there exists an intermediate stage where the unbound molecules first cluster into packets comprising unbound molecules that can form n functional units and some of these packets react to form stress fibers also comprising n functional units. To calculate the chemical potentials of the bound molecules within stress fibers and the unbound molecules in the intermediate stage, consider the following two mixing processes. First consider the mixing between \(\bar{N}_{u} /n\) identical packets of unbound proteins and \(\bar{N}_{b} /n\) identical packets bound proteins where \(\bar{N}_T \equiv \bar{N}_{u} +\bar{N}_{b} \). Using Boltzmann’s entropy formula, the entropy of mixing in this process is
which simplifies using Stirling’s approximation to
The chemical potentials of the bound proteins and unbound proteins after this first step are
and
respectively, where \(\partial \bar{N}_{u} /\partial \bar{N}_{b} =-1\) as the mixing process occurs at constant \(\bar{N}_T \). Second, recall that the unbound aggregate of proteins occupy lattice sites and thus we mix the \(\bar{N}_{u} \) unbound protein aggregates with the \(\bar{N}_L \) lattice sites lattice while not mixing the \(\bar{N}_{u} /n\) and \(\bar{N}_{b} /n\) packets. The entropy of mixing of this process is given by Eqs. (8.1) and (8.2). Again using the dilute assumption \((\bar{N}_{u} \ll \bar{N}_L)\), the chemical potentials of the bound and unbound molecules in their intermediate stage follow as
and
respectively. In deriving Eqs. (8.10) and (8.11), we have used the fact that now \(\partial \bar{N}_{u} /\partial \bar{N}_{b} =1\) as in this step we do not change the number of bound and unbound molecules with respect to each but rather calculate the variation in the entropy while changing the number of stress-fiber protein molecules with respect to the fixed number of lattice sites.
Comparing the chemical potentials \(\chi _I\) and \(\chi _{u}\), we see that the clustering reaction is endergonic and the unclustering reaction is exergonic when \({\hat{N}}_{u}/({2\pi {\hat{\eta }} \hat{n}})>1\) and vice-versa when \({\hat{N}}_{u}/(2\pi {\hat{\eta }}\hat{n})<1\). This is rationalized by the fact that when the stress-fiber concentration is small compared to the unbound protein concentration, the geometrical constraints imposed by the stress fibers are small and clustering requires an entropy reduction but the situation is reversed at high stress-fiber concentrations. We emphasize that the unbound proteins in their intermediate clustered state are unstable (due to their low entropy compared to their unclustered counterparts) and not physically present in the system at any given time. Rather this intermediate state is a transient state in the reaction for the formation/dissociation of the stress fibers.
Equilibrium between the bound and unbound proteins occurs when their chemical potentials equalize, i.e., \(\chi _{u}=\chi _{b}\). Setting \({\dot{\hat{\eta }}}=0\) in Eq. (2.16) and simplifying reduces Eq. (2.16) to the condition \(\chi _{u} =\chi _{b}\) consistent with the chemical potentials derived here from statistical mechanics considerations.
Finally, we note that the free energy of the stress-fiber proteins within a RVE is given as
and this expression can be integrated over the entire cell volume \(V_{0}\) to give the free energy of the stress-fiber proteins in the cell as
Rights and permissions
About this article
Cite this article
Vigliotti, A., Ronan, W., Baaijens, F.P.T. et al. A thermodynamically motivated model for stress-fiber reorganization. Biomech Model Mechanobiol 15, 761–789 (2016). https://doi.org/10.1007/s10237-015-0722-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10237-015-0722-9