Staged financing: a trade-off theory of holdup and option value

Abstract

This paper investigates financial contract design in venture capital investments and shows that staged financing is the implementation of optimal contracts. In designing contracts, venture capitalists consider the value of real options and the costs of holdup. This consideration boils down to contract rigidity and flexibility: rigid contracts mitigate the holdup problem of entrepreneurs, but have little option values, whereas flexible contracts create real options for venture capitalists in corporate decision-making, but yield weak bargaining power when ventures appear promising. In optimal contracts, venture capitalists choose flexibility by separating capital into stages and then strategically allocating control rights at each stage. This strategy creates option value in corporate governance, and can protect sunk investments in distress while capturing the potential benefits of good outcomes.

Appendices

Glossary of symbols

c :

Marginal cost of effort.

d :

Disagreement point in Nash bargaining.

E :

The entrepreneur.

e :

Effort exerted by the entrepreneur.

h :

Precision of prior distributions.

k :

Capital investment by the venture capitalist.

p :

The probability of a successful exit, i.e., an IPO.

$p_{T}$, $p_{E}$, $p_{M}$ :

The probabilities of some quality being above a given threshold.

${\hat{p}}_{T}$, ${\hat{p}}_{E}$ :

The posterior probabilities of some quality being above that threshold.

s :

The severance payment to E.

u :

The expected payoff.

V :

The venture capitalist.

w :

The pecuniary transfer between the venture capitalist and the resident manager.

x :

A signal of the technology’s quality.

y :

A signal of the entrepreneur’s managerial ability.

$\alpha$ :

Share of the company’s ownership, $0\le \alpha \le 1$.

$\delta _{C}$ :

The quality of the venture, $\delta _{C}=\min \{\delta _{T},\delta _{E}\}$ or $\min \{\delta _{T},\delta _{M}\}$.

$\delta _{E}$, $\delta _{M}$ :

The entrepreneur or outside manager’s abilities.

$\delta _{T}$ :

The quality of the technology.

${\tilde{\delta }}$ :

The posterior beliefs about that quality.

Proofs

Proof of Lemma 1

Note that

$$\begin{aligned} {\hat{p}}_{T}&~=~ \text {Pr}(\delta _{T}^{\prime } > \delta ^{*}) \\&~=~ \sqrt{\frac{{\hat{h}}_{T}}{2\pi }} \int _{\delta ^{*}}^{\infty } e^{ - \frac{{\hat{h}}_{T}}{2} (t-{\hat{\delta }}_{T})^{2} } dt \\&~=~ \sqrt{\frac{h_{T}+h_{x}}{2\pi }} \int _{\delta ^{*}}^{\infty } \exp \Big [ - \frac{h_{T}+h_{x}}{2} \big ( t - \frac{xh_{x}}{h_{T}+h_{x}} \big )^{2} \Big ] dt \\&~=~ 1 - \Phi \Big ( \sqrt{h_{T}+h_{x}} \big ( \delta ^{*} - \frac{xh_{x}}{h_{T}+h_{x}} \big ) \Big ). \end{aligned}$$

Hence, ${\hat{p}}_{T}$ is a smooth, strictly increasing function of signal x. Denote this function as ${\hat{p}}_{T}=f(x)$. The prior probability density function for x is $\phi (\sqrt{h_{T}h_{x}/(h_{T}+h_{x})}x)$ by assumption. Thus the prior probability density function for ${\hat{p}}_{T}$ is given by

$$\begin{aligned} \rho _{T}({\hat{p}}_{T})~=~ \frac{\phi (\sqrt{h_{T}h_{x}/(h_{T}+h_{x})}f^{-1}({\hat{p}}_{T}))}{f^{\prime }(f^{-1}({\hat{p}}_{T}))}, \end{aligned}$$

by the change in variables formula for the density functions of random variables. The proof is the same for signal y and probability ${\hat{p}}_{E}$. $\square$

Proof of Lemma 2

Because the expected gain of V, E, or M is $\alpha Q(k) (1+\mu (e)) \text {Pr}(IPO)$, which is separable, where $\alpha$ is the fraction of ownership, the question boils down to comparing different ${\hat{p}}$’s under the management of E or M. Because ${\hat{p}}_{T}$ is the same in each situation, I only need to compare ${\hat{p}}_{E}=$Pr$({\tilde{\delta }}_{E}>\delta ^{*})$ and ${\hat{p}}_{M}=$Pr$(\delta _{M}>\delta ^{*})$.

By the calculation in Sect. 2.3,

$$\begin{aligned} \text {Pr}({\tilde{\delta }}_{E} > \delta ^{*})= & {} \sqrt{\frac{{\hat{h}}_{E}}{2\pi }} \int _{\delta ^{*}}^{\infty } e^{ - \frac{{\hat{h}}_{E}}{2} (t-{\hat{\delta }}_{E})^{2} } dt\\= & {} \sqrt{\frac{h_{E}+h_{y}}{2\pi }} \int _{\delta ^{*}}^{\infty } \exp \Big [ - \frac{h_{E}+h_{y}}{2} \big ( t - \frac{yh_{y}}{h_{E}+h_{y}} \big )^{2} \Big ] dt, \end{aligned}$$

and

$$\begin{aligned} \text {Pr}(\delta _{M} > \delta ^{*}) ~=~ \sqrt{\frac{h_{M}}{2\pi }} \int _{\delta ^{*}}^{\infty } e^{ - \frac{h_{M}}{2} t^{2} } dt. \end{aligned}$$

Pr$({\tilde{\delta }}_{E}>\delta ^{*})$ is a continuous, strictly increasing function of y, whereas Pr$(\delta _{M}>\delta ^{*})$ is a constant function with respect to y. We set the two probabilities $\text {Pr}({\tilde{\delta }}_{E}> \delta ^{*})=\text {Pr}(\delta _{M} > \delta ^{*})$ to find $y^{*}$.

We have

$$\begin{aligned} \lim _{y\rightarrow +\infty } \text {Pr} ({\tilde{\delta }}_{E}>\delta ^{*}) = 1>\text {Pr} (\delta _{M}>\delta ^{*}) >0 \end{aligned}$$

and

$$\begin{aligned} \lim _{y\rightarrow -\infty } \text {Pr} ({\tilde{\delta }}_{E}>\delta ^{*}) = 0. \end{aligned}$$

The existence of $y^{*}$ follows from the intermediate value theorem. The value of $y^{*}$ is unique for each given k, e, x, and ownership structure. It can be numerically calculated from the implicit function theorem by equating Pr$({\tilde{\delta }}_{E}>\delta ^{*})$ and Pr$(\delta _{M}>\delta ^{*})$. $yh_{y}/(h_{E}+h_{y})\le \delta ^{*}$ and then $y^{*}>(h_{E}+h_{y})\delta ^{*}/h_{y}$ holds because $h_{E}=h_{M}$, $h_{y}>0$ implies ${\hat{h}}_{E}>h_{M}$, and $y^{*}$ is the intersection of two reverse cumulative normal distribution functions. $\square$

Proof of Proposition 1

Suppose that after stage 3, E’s existing ownership stake is $\alpha _{E}^{0}$. If V decides to remove E, it is a costly decision because E is now an owner-manager. In this case, V offers E a severance payment s sufficient to render her indifferent to staying or leaving, and E leaves.

Let V’s offer comprise a new proportion of ownership stake $\alpha _{E}^{1}$ and a pecuniary payment of $s_{E}$. For E to be willing to give up her management position, the severance payment must satisfy the following condition.

$$\begin{aligned}&s_{E} + \alpha _{E}^{1} Q(k_{0}+\Delta k) (1+\mu (e_{0}+\Delta e_{M})) {\hat{p}}_{T} p_{M}\\&\quad = \max _{\Delta e_{E} \ge 0} \alpha _{E}^{0} Q(k_{0}) (1+\mu (e_{0}+\Delta e_{E})) {\hat{p}}_{T} {\hat{p}}_{E} -c\Delta e_{E}, \end{aligned}$$

where $\Delta k \ge 0$ and $\Delta e_{M}\ge 0$ are V and M’s further inputs under M’s management. The severance payment is nonnegative because E has limited liability, and her participation constraint would be violated if the expected continuation payoff were negative. In that case, she would be willing to leave the company without a severance payment from V.

Let $e_{E}^{*}$ be the optimal solution of the right-hand side, a solution that exists on interval $[0,\infty )$ by Assumption 2. Then, the condition can be rewritten as

$$\begin{aligned}&s_{E} + \alpha _{E}^{1} Q(k_{0}+\Delta k) (1+\mu (e_{0}+\Delta e_{M})) {\hat{p}}_{T} p_{M}\nonumber \\&\quad = \alpha _{E}^{0} Q(k_{0}) (1+\mu (e_{0}+e_{E}^{*})) {\hat{p}}_{T} {\hat{p}}_{E} -c e_{E}^{*}. \end{aligned}$$

(7)

Because M has no bargaining power, V can make her a take-it-or-leave-it offer at stage 5M, solving the following optimization problem.

$$\begin{aligned}&\max _{s_{E},\alpha _{E}^{1},w_{M},\alpha _{M}, \Delta k,\Delta e_{M}} (1-\alpha _{E}^{1}-\alpha _{M}) Q(k_{0}+\Delta k) (1+\mu (e_{0}+\Delta e_{M})) {\hat{p}}_{T} p_{M}\nonumber \\&\qquad -R\Delta k - s_{E} - w_{M}, \end{aligned}$$

(8)

subject to constraints that include M’s incentive compatibility (IC) constraint

$$\begin{aligned} \max _{\Delta e_{M} \ge 0} w_{M} + \alpha _{M} Q(k_{0}+\Delta k) (1+\mu (e_{0}+\Delta e_{M})) {\hat{p}}_{T} p_{M} -c\Delta e_{M}. \end{aligned}$$

(9)

Let

$$\begin{aligned} e_{M}^{*} \in \mathop {\hbox {argmax}}\limits _{\Delta e_{M} \ge 0} w_{M} + \alpha _{M} Q(k_{0}+\Delta k) (1+\mu (e_{0}+\Delta e_{M})) {\hat{p}}_{T} p_{M} -c\Delta e_{M}. \end{aligned}$$

The optimization problem is also subject to M’s individual rationality (IR) constraint

$$\begin{aligned} w_{M} + \alpha _{M} Q(k_{0}+\Delta k) (1+\mu (e_{0}+e_{M}^{*})) {\hat{p}}_{T} p_{M} - c e_{M}^{*} = 0, \end{aligned}$$

(10)

and to condition (7).

Suppose that ${\hat{p}}={\hat{p}}_{T} p_{M}$ is high enough to make it optimal for V to continue investing. M’s IC constraint (9) can be replaced by the first-order condition as

$$\begin{aligned} \alpha _{M} Q(k_{0}+\Delta k) \mu ^{\prime } (e_{0}+\Delta e_{M}) {\hat{p}}_{T} p_{M} - c = 0. \end{aligned}$$

(11)

Hence, V solves problem (8) subject to constraints (11), (10), and (7). Substituting $s_{E}$, $w_{M}$ in (8) from constraints (10) and (7), V solves

$$\begin{aligned}&\max _{\alpha _{E}^{1},\alpha _{M}, \Delta k,\Delta e_{M}} Q(k_{0}+\Delta k) (1+\mu (e_{0}+\Delta e_{M})) {\hat{p}}_{T} p_{M} -R\Delta k \nonumber \\&\quad -c\Delta e_{M} - ( \alpha _{E}^{0} Q(k_{0}) (1+\mu (e_{0}+e_{E}^{*})) {\hat{p}}_{T} {\hat{p}}_{E} -c e_{E}^{*} ) \end{aligned}$$

(12)

subject to constraint (11) and $\alpha _{M}\in [0,1-\alpha _{E}^{1}]$.

It is easy to see that when $\alpha _{M}=1$, M’s effort input $\Delta e_{M}$ and V’s investment $\Delta k$ both increase the overall effort and investment levels to the first best, conditioned on all available information. Thus, in E’s severance payment, $\alpha _{E}^{1}=0$ and $s_{E}\ge 0$ because

$$\begin{aligned} s_{E}= & {} \max _{\Delta e_{E} \ge 0} \alpha _{E}^{0} Q(k_{0}) (1+\mu (e_{0}+\Delta e_{E})) {\hat{p}}_{T} {\hat{p}}_{E} -c\Delta e_{E}\\\ge & {} \alpha _{E}^{0} Q(k_{0}) (1+\mu (e_{0})) {\hat{p}}_{T} {\hat{p}}_{E} \ge 0. \end{aligned}$$

$\square$

Proof of Lemma 3

Denote $p={\hat{p}}_{T}{\hat{p}}_{E}$ or $p={\hat{p}}_{T}p_{M}$. Note that ${\mathcal {U}}(k_{0},e_{0};p)>Q(k_{0})(1+\mu (e_{0}))p-Rk_{0}-ce_{0}$ almost surely, with the exception that $(k_{0},e_{0})$ is on the first best investment frontier corresponding to p. Now, $e_{0}=0$. V’s expected payoff is

$$\begin{aligned} {\mathcal {U}}(k_{0},0;{\hat{p}}_{T}p_{M}), \text {or}~ Q(k_{0}){\hat{p}}_{T}p_{M}-Rk_{0}, \end{aligned}$$

if M is the manager and

$$\begin{aligned} \frac{1}{2} \Big [ {\mathcal {U}}(k_{0},0;{\hat{p}}_{T}{\hat{p}}_{E}) + Q(k_{0}){\hat{p}}_{T}{\hat{p}}_{E}-Rk_{0}\Big ], ~\text {or}~ Q(k_{0}){\hat{p}}_{T}{\hat{p}}_{E}-Rk_{0}, \end{aligned}$$

if E is the manager.

If staying private leads to a higher interim expected payoff for V, then it is optimal for him to keep E as the manager as long as ${\hat{p}}_{E}\ge p_{M}$ because $Q(k_{0})>0$ by Assumption 1.

As ${\hat{p}}_{T}$ increases, V requires E to have stronger ability if retaining her as manager is desirable. To see that this is the case, suppose that $p_{M}={\hat{p}}_{E}$; then, either

$$\begin{aligned} {\mathcal {U}}(k_{0},0;{\hat{p}}_{T}p_{M}) > Q(k_{0}){\hat{p}}_{T}p_{M}-Rk_{0} = Q(k_{0}){\hat{p}}_{T}{\hat{p}}_{E}-Rk_{0} \end{aligned}$$

for a sufficiently high value of ${\hat{p}}_{T}$ or

$$\begin{aligned} {\mathcal {U}}(k_{0},0;{\hat{p}}_{T}p_{M}) = {\mathcal {U}}(k_{0},0;{\hat{p}}_{T}{\hat{p}}_{E}) > \frac{1}{2} {\mathcal {U}}(k_{0},0;{\hat{p}}_{T}{\hat{p}}_{E}) + \frac{1}{2} Q(k_{0}){\hat{p}}_{T}{\hat{p}}_{E}-\frac{1}{2}Rk_{0} \end{aligned}$$

by inequality ${\mathcal {U}}(k_{0},e_{0};p)>Q(k_{0})(1+\mu (e_{0}))p-Rk_{0}$ given at the beginning of the proof, with $e_{0}=0$. Hence, V prefers E to be a manager only when ${\hat{p}}_{E}>p_{M}$.

V’s expected payoff when E is the manager (the right-hand side of the inequalities) is strictly increasing in ${\hat{p}}_{E}$ by the envelope theorem. Consider two equations:

$$\begin{aligned} {\mathcal {U}}(k_{0},0;{\hat{p}}_{T}p_{M}) = Q(k_{0}){\hat{p}}_{T}{\hat{p}}_{E}-Rk_{0} \end{aligned}$$

and

$$\begin{aligned} {\mathcal {U}}(k_{0},0;{\hat{p}}_{T}p_{M}) = \frac{1}{2} {\mathcal {U}}(k_{0},0;{\hat{p}}_{T}{\hat{p}}_{E}) + \frac{1}{2} Q(k_{0}){\hat{p}}_{T}{\hat{p}}_{E}-\frac{1}{2}Rk_{0}. \end{aligned}$$

Solve for ${\hat{p}}_{E}$ as a function of ${\hat{p}}_{T}$, and then for a function of x with $k_{0}$ as one of the parameters. The solution exists by the implicit function theorem. Denote that solution as ${\tilde{p}}_{E,s}(k_{0},x)$. ${\tilde{p}}_{E,s}(k_{0},x)\ge p_{M}$. We cannot guarantee that the solution is less than or equal to 1. When it is, it gives the threshold ${\tilde{y}}_{E,s}(k_{0},x)$ by a function similar to function $f^{-1}$ in the proof of Lemma 1; otherwise, set ${\tilde{y}}_{E,s}(k_{0},x)$ equal to $+\infty$. From the proof of Lemma 2, we have ${\tilde{y}}_{E,s}(k_{0},x)\ge y^{*}$ for any $k_{0}$, and x. $\square$

Proof of Lemma 4

Given $\alpha _{V}^{0}=1$ and $e_{0}=0$ after stage 3, V chooses between continuing with the venture and quitting. If V decides to continue, $\alpha _{E}^{1}(x)=1$ and ${\bar{w}}_{E}(x)=0$. Accordingly, V’s interim expected payoff from an IPO is ${\mathcal {U}}(k_{0},0;p)$. If V decides to quit, his interim expected payoff is $Q(k_{0})p-Rk_{0}$.

Hence, V’s interim expected payoff is essentially

$$\begin{aligned} \max \Big \{~ {\mathcal {U}} (k_{0},0;p), ~Q(k_{0})p-Rk_{0}~ \Big \}. \end{aligned}$$

(13)

Take the difference between these two payoffs with p as a parameter:

$$\begin{aligned} {\mathcal {U}} (k_{0},0;p) - Q(k_{0})p + Rk_{0} ~=~ {\mathcal {S}} (k_{0},0;p). \end{aligned}$$

(14)

By the envelope theorem, ${\mathcal {S}} (k_{0},0;p)$ is strictly increasing in p and goes from 0 to a positive constant as p goes from 0 to 1. Then, by the intermediate value theorem, there exists a ${\tilde{p}}_{l}(k_{0})$ and thus a corresponding ${\tilde{x}}_{l}(k_{0})=f^{-1}({\tilde{p}}_{l}(k_{0}))$, such that V chooses liquidation if $x\le {\tilde{x}}_{l}(k_{0})$ and further investment if $x>{\tilde{x}}_{l}(k_{0})$ after stage 3.

Probability ${\tilde{p}}_{l}(k_{0})$ gives the threshold for ${\hat{p}}_{T}p_{M}$ in the choice of quitting or investing with M as the manager.

The second case is similar. Given $\alpha _{V}^{0}=1$, $e_{0}=0$ after stage 3, V chooses between continuing the venture and quitting. If V decides to continue investing, $\alpha _{E}^{1}=1$, and ${\bar{w}}_{E}$ is chosen such that his interim expected payoff is

$$\begin{aligned} d_{V} + \frac{1}{2} {\mathcal {S}}(k_{0},0;p)= & {} \frac{1}{2} \Big [ \max _{\Delta k\ge 0,\Delta e\ge 0} Q(k_{0}+\Delta k)(1+\mu (\Delta e))p\\&-R(k_{0}+\Delta k) -c\Delta e + Q(k_{0})p \Big ], \end{aligned}$$

where $d_{V}=Q(k_{0})p-Rk_{0}$ because $\alpha _{V}^{0}=1$, $e_{0}=0$. If V decides to quit, his interim expected payoff is $Q(k_{0})p-Rk_{0}$.

Accordingly, V’s interim expected payoff from either outcome, IPO or failure, is

$$\begin{aligned} \max \Big \{~ \frac{1}{2} \Big [ {\mathcal {U}} (k_{0},0;p) + Q(k_{0})p-Rk_{0} \Big ], ~Q(k_{0})p-Rk_{0}~ \Big \}. \end{aligned}$$

(15)

Take the difference between these two payoffs with p as a parameter:

$$\begin{aligned} \frac{1}{2} \Big [ {\mathcal {U}} (k_{0},0;p) + Q(k_{0})p-Rk_{0} \Big ] - Q(k_{0})p+Rk_{0} = \frac{1}{2} {\mathcal {S}} (k_{0},0;p). \end{aligned}$$

(16)

By the envelope theorem, ${\mathcal {S}} (k_{0},0;p)/2$ is strictly increasing in p and goes from 0 to a positive constant as p goes from 0 to 1. Then, by the intermediate value theorem, there exists a ${\tilde{p}}_{s}(k_{0})$ and thus a corresponding ${\tilde{x}}_{s}(k_{0})=f^{-1}({\tilde{p}}_{s}(k_{0}))$, such that V chooses to quit if $x\le {\tilde{x}}_{s}(k_{0})$ and to invest if $x>{\tilde{x}}_{s}(k_{0})$ after stage 3.

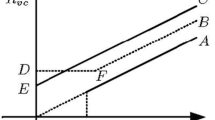
Probability ${\tilde{p}}_{s}(k_{0})$ gives the threshold for ${\hat{p}}_{T}{\hat{p}}_{E}$ in the choice of quitting or investing with E as the manager, and ${\tilde{p}}_{E,s}(k_{0},x)$ in the proof of Lemma 3 gives the threshold for ${\hat{p}}_{E}$ in the choice of manager E or M. Combining all of these boundary conditions, we have Fig. 2. $\square$

Proof of Proposition 2

The timeline of the game is stages 1, 2, 3, and 4; 5E, 6E, and 7E; or 5M, 6M, and 7M. Negotiations and contracting take place at stages 1, 5E, or 5M. Investments are made simultaneously by V and E at stages 2 and 6E, or by V and M at stage 6M. Signals x and y are realized at stage 3. All uncertainties concerning the technology, managerial ability, and an IPO are resolved at stage 7E or 7M.

The posterior probability of an IPO, as perceived by V, E, and M, from stage 3 onwards is $p={\hat{p}}_{T}{\hat{p}}_{E}$ $(p={\hat{p}}_{T}p_{M})$, and the stage 1 prior probability distribution of p is given by $\rho =\rho _{T}\rho _{E}$ ($\rho =\rho _{T}$, no signal to be observed for M).

Because the contracts are non-contingent, let $\alpha _{V}^{0}$, $\alpha _{E}^{0}$ be the ownership structure after investments $k_{0}$, $e_{0}$ and signals x and y. If V decides to continue investing at stage 4 with E as the manager, and if V and E’s contracting and investing behavior are optimal at stages 5E and 6E, then V’s interim expected payoff is

$$\begin{aligned} u_{V}&~=~ d_{V} + \frac{1}{2} {\mathcal {S}} \\&~=~ \alpha _{V}^{0}Q(k_{0})(1+\mu (e_{0})){\hat{p}}_{T}{\hat{p}}_{E}-Rk_{0} + \frac{1}{2} {\mathcal {S}} (k_{0},e_{0};{\hat{p}}_{T}{\hat{p}}_{E}) \\&~=~ \frac{1}{2} {\mathcal {U}} (k_{0},e_{0};{\hat{p}}_{T}{\hat{p}}_{E}) + (\alpha _{V}^{0} - \frac{1}{2}) Q(k_{0})(1+\mu (e_{0})){\hat{p}}_{T}{\hat{p}}_{E}. \end{aligned}$$

Then, V would choose an $\alpha _{V}^{0}$, that is as high as possible at stage 1. If V decides to continue investing at stage 4 with M as the manager, then his maximal interim expectation of a final payoff is

$$\begin{aligned} {\mathcal {U}} (k_{0},e_{0};{\hat{p}}_{T}p_{M}) - \Big [ \max _{\Delta e_{E} \ge 0} \alpha _{E}^{0} Q(k_{0}) (1+\mu (e_{0}+\Delta e_{E})) {\hat{p}}_{T} {\hat{p}}_{E}-Rk_{0} -c\Delta e_{E} \Big ], \end{aligned}$$

which would be maximized when $\alpha _{V}^{0}=1$ such that $\alpha _{E}^{0}=0$. Additionally, V will have full control if $\alpha _{V}^{0}=1$. Thus, $\alpha _{V}^{0}=1$ is optimal at stage 1 with a short-term contract.

We claim that E will not exert effort, $e_{0}=0$, at stage 2 in this scenario. $\alpha _{E}^{0}=0$, which implies $d_{E}=0$. Let $k^{*}$ and $e^{*}$ denote V and E’s optimal incremental investments at stage 6E. Then,

$$\begin{aligned} Q(k_{0}+k^{*})\mu ^{\prime }(e_{0}+e^{*})p = 1 \end{aligned}$$

if $e^{*}>0$ and

$$\begin{aligned} Q(k_{0}+k^{*})\mu ^{\prime }(e_{0}+e^{*})p \le 1 \end{aligned}$$

if $e^{*}=0$, because it is optimal for E to exert a positive amount of effort when the left-hand side is strictly greater than 1.

E’s expected payoff at stage 1 is

$$\begin{aligned}&\frac{1}{2} \int _{p\in I} \Big [ Q(k_{0}+k^{*})(1+\mu (e_{0}+e^{*}))p - Rk^{*} \\&\quad - ce^{*} - Q(k_{0})(1+\mu (e_{0}))p \Big ] \rho (p) dp - ce_{0}, \end{aligned}$$

where I is a region for p in the signal space ${\mathcal {X}} \times {\mathcal {Y}}$, where V decides to continue investing, and $p={\hat{p}}_{T}{\hat{p}}_{E}$, $\rho =\rho _{T}\rho _{E}$.

Take the first-order derivative with respect to $e_{0}$ using the envelope theorem. Because both $k^{*}$ and $e^{*}$ are functions of $e_{0}$,

$$\begin{aligned} \frac{1}{2} \int _{p\in I} \Big [ Q(k_{0}+k^{*})\mu ^{\prime }(e_{0}+e^{*})p - Q(k_{0})\mu ^{\prime }(e_{0})p \Big ] \rho (p) dp - c. \end{aligned}$$

Note that the first term of the integrand is less than or equal to 1 and its second term of is positive. Hence, the integral is strictly less than 1 regardless of the interval I, which means that E’s optimal initial effort investment is $e_{0}=0$.

Given $\alpha _{V}^{0}=1$ and $e_{0}=0$ after stage 3, we can apply the results of Lemma 4. V makes decisions according to the allocations of the signal realizations to regions $\Pi _{L,E}$, $\Pi _{L,M}$, $\Pi _{I,E}$, and $\Pi _{I,M}$. Because $\alpha _{E}^{0}=0$, replacing E with M is costless. If V decides to continue investing, he will transfer his entire ownership stake to the manager. If V decides instead to quit, he will retain all of that stake, allowing him to recoup part of the investment.

By backward induction, V then solves the optimal initial investment level $k_{0s}$, which is the solution of

$$\begin{aligned}&\max _{k_{0}} \Big \{~ \int _{\Pi _{L,E}} Q(k_{0}){\hat{p}}_{T}{\hat{p}}_{E} \rho (p) dp + \int _{\Pi _{L,M}} Q(k_{0}){\hat{p}}_{T}p_{M} \rho (p) dp \nonumber \\&\quad + \int _{\Pi _{I,E}} \frac{1}{2} \Big [ {\mathcal {U}} (k_{0},0;{\hat{p}}_{T}{\hat{p}}_{E}) + Q(k_{0}){\hat{p}}_{T}{\hat{p}}_{E} \Big ] \rho (p) dp\nonumber \\&\quad + \int _{\Pi _{I,M}} {\mathcal {U}} (k_{0},0;{\hat{p}}_{T}p_{M}) \rho (p) dp - Rk_{0} \Big \}. \end{aligned}$$

(17)

The solution always exists because $k_{0}$ lies in a closed interval bounded by 0 and the maximal investment level of the first best investment frontier, which is compact. Then, $y_{E,s}^{*}(x)={\tilde{y}}_{E,s}(k_{0s},x)$ for the optimal $k_{0s}$. $\square$

Proof of Proposition 3

The renegotiation of existing rigid contracts can occur only at stage 5E. Given any contingent contract, any pair of initial investment $k_{0}$, $e_{0}$, and any signal realizations x, y, E’s interim expected payoff at stage 5E can be either nonnegative or strictly negative. In the first case, E actually takes all of the expected surplus, and she will not accept any new contract proposed by V. In the latter, E is protected by limited liability, meaning that she can resign from the manager’s position and have an outside reservation utility of at least 0 by assumption. By resigning, E can ensure a payoff that is at least as good as that she would receive if she accepted V’s take-it-or-leave-it offer. However, V will renegotiate the contract only if E is perceived to be a better manager than M, ${\hat{p}}_{E}>p_{M}$. V has to recruit M as the manager if E rejects his offer, but doing so leads to a lower expected payoff for V because E is supported by her higher perceived ability. Hence, if V and E have equal opportunities for proposing a new contract, we conclude that they will share the surplus equally, as predicted by Rubinstein’s bargaining model. $\square$

Proof of Proposition 4

Using backward induction, given initial investments $k_{0}$, $e_{0}$ at stage 2 and signal realizations x, y at stage 3, suppose that the initial contract is contingent on signal x with components $\alpha _{V}^{0}(x)$, $\alpha _{E}^{0}(x)$, and $w_{E}(x)$.

$w_{E}(x)$ determines the share of surplus ${\mathcal {U}}(k_{0},e_{0};{\hat{p}}_{T}{\hat{p}}_{E})$, which also depends on the realization of signal y. If $w_{E}(x)$ grants V the exact surplus corresponding to signal ${\bar{y}}$, then V loses all of the extra surplus when $y>{\bar{y}}$ because there is no alternative contract, which Pareto-improves both V and E’s payoffs. By Proposition 3, V and E renegotiate the existing contract when $y\le {\bar{y}}$ if V plans to retain E. Thus, $w_{E}(x)$ is chosen to allocate ${\mathcal {U}}(k_{0},e_{0};{\hat{p}}_{T})$ to V as if ${\hat{p}}_{E}=1$.

Next, we find the optimal $\alpha _{V}^{0}(x)$ and $\alpha _{E}^{0}(x)$. When x is low, it is optimal for V to retain full ownership, and then $\alpha _{V}^{0}(x)=1$ for such an x. As x increases, V considers whether to transfer ownership to E. However, y is random and uncorrelated to x. When y is low enough that choosing M as the manager is optimal, V needs to repurchase the shares from E at cost

$$\begin{aligned} \max _{\Delta e_{E}} \alpha _{E}^{0}(x)Q(k_{0})(1+\mu (e_{0}+\Delta e_{E})) {\hat{p}}_{T}{\hat{p}}_{E} -c(e_{0}+\Delta e_{E}) \end{aligned}$$

by Proposition 1. To minimize that cost, V can either reduce $k_{0}$ or reduce $\alpha _{E}^{0}(x)$. Because $\lim _{k\rightarrow 0+}Q^{\prime }(k)=+\infty$ and renegotiation is inevitable, $k_{0}>0$. Thus, $\alpha _{E}^{0}(x)=0$ for any x. Then, $w_{E}(x)=0$ to satisfy E’s initial IR constraint. The rigid contingent contract is degenerated and cannot be renegotiation-proof. $\square$

Proof of Proposition 6

To show that $k_{0s}>0$, it is sufficient to show that the area of $\Pi _{I,E}$ has a strictly positive lower bound. We do not need to consider the region of $\Pi _{L,E}$ because it will no longer exist if $k_{0}=0$, where ${\tilde{p}}_{s}(0)={\tilde{p}}_{l}(0)=0$. This condition is sufficient because V’s interim expected payoff in this region is

$$\begin{aligned} \frac{1}{2} \Big [ {\mathcal {U}}(k_{0},0;p) + Q(k_{0})p-Rk_{0} \Big ], \end{aligned}$$

and $\lim _{k\rightarrow 0+}Q^{\prime }(k)=+\infty$.

Suppose that $p_{M}<{\tilde{p}}_{M}$; then, there exists a constant $\varepsilon >0$ such that $p_{M}\le {\tilde{p}}_{M}-\varepsilon$. The requirement that $p_{M}<1/2$ is not a strong assumption; it is true only as long as IPO threshold $\delta ^{*}>0$, which is reasonable.

Now consider the segment of function ${\tilde{p}}_{E,s}(k_{0},x)$ that separates regions $\Pi _{I,E}$ and $\Pi _{I,M}$. It is the solution of ${\hat{p}}_{E}$ as an implicit function of ${\hat{p}}_{T}$ given by the equation

$$\begin{aligned} {\mathcal {U}}(k_{0},0;{\hat{p}}_{T}p_{M}) = \frac{1}{2} {\mathcal {U}}(k_{0},0;{\hat{p}}_{T}{\hat{p}}_{E}) + \frac{1}{2} Q(k_{0}){\hat{p}}_{T}{\hat{p}}_{E}-\frac{1}{2}Rk_{0}. \end{aligned}$$

For any $k_{0}$ and x (which corresponds to ${\hat{p}}_{T}>0$), set $p_{M}\rightarrow 0$ on the left-hand side of the equation. The left-hand side goes to 0, while the right-hand side remains strictly positive. Also ${\mathcal {U}}(k_{0},0;{\hat{p}}_{T}p_{M})$ is increasing in $p_{M}$, which ensures that the set ${\mathcal {M}}(k_{0},x)$ is nonempty. Because $p_{M}<{\tilde{p}}_{M}$ by assumption, we can apply the implicit function theorem for any $k_{0}$ and x.

Define

$$\begin{aligned} {\mathcal {F}} := 2~{\mathcal {U}}(k_{0},0;{\hat{p}}_{T}p_{M}) - {\mathcal {U}}(k_{0},0;{\hat{p}}_{T}{\hat{p}}_{E}) - Q(k_{0}){\hat{p}}_{T}{\hat{p}}_{E}+Rk_{0}. \end{aligned}$$

Let $k_{M}$, $e_{M}$ be the solutions for ${\mathcal {U}}(k_{0},0;{\hat{p}}_{T}p_{M})$; that is,

$$\begin{aligned} {\mathcal {U}}(k_{0},0;{\hat{p}}_{T}p_{M}) = Q(k_{0}+k_{M})(1+\mu (e_{M})){\hat{p}}_{T}p_{M} -R(k_{0}+ k_{M}) -c e_{M}. \end{aligned}$$

Similarly, let $k_{E}$, $e_{E}$ be the solutions for ${\mathcal {U}}(k_{0},0;{\hat{p}}_{T}{\hat{p}}_{E})$. Using the envelope theorem, we have

$$\begin{aligned} \frac{\partial {\mathcal {F}}}{\partial {\hat{p}}_{T}}= & {} 2 Q(k_{0}+k_{M})(1+\mu (e_{M})) p_{M} - Q(k_{0}+k_{E})(1+\mu (e_{E})){\hat{p}}_{E} - Q(k_{0}) {\hat{p}}_{E};\\ \frac{\partial {\mathcal {F}}}{\partial {\hat{p}}_{E}}= & {} - Q(k_{0}+k_{E})(1+\mu (e_{E})){\hat{p}}_{T} - Q(k_{0}) {\hat{p}}_{T}. \end{aligned}$$

Hence, the sign of $d{\hat{p}}_{E}/d{\hat{p}}_{T}$ is the same as the sign of $\partial {\mathcal {F}}/\partial {\hat{p}}_{T}$.

If ${\hat{p}}_{E}>2p_{M}$, then $k_{E}\ge k_{M}$ and $e_{E}\ge e_{M}$, meaning $\partial {\mathcal {F}}/\partial {\hat{p}}_{T}<0$, and thus $d{\hat{p}}_{E}/d{\hat{p}}_{T}<0$. If ${\hat{p}}_{E}\le 2p_{M}$ is true at the initial point of segment ${\tilde{p}}_{E,s}(k_{0},x)$, which separates regions $\Pi _{I,E}$ and $\Pi _{I,M}$, then ${\tilde{p}}_{E,s}(k_{0},x)\le 1-2\varepsilon$ because $p_{M}\le {\tilde{p}}_{M}-\varepsilon \le 1/2-\varepsilon$, and $d{\hat{p}}_{E}/d{\hat{p}}_{T}<0$ once ${\hat{p}}_{E}\ge 2p_{M}-\tau$ for some $\tau >0$ that is sufficiently small.

At the initial point, ${\hat{p}}_{T}$ and ${\hat{p}}_{E}$ satisfy

$$\begin{aligned}&Q(k_{0}+k_{M})(1+\mu (e_{M})){\hat{p}}_{T}p_{M} - Rk_{M} -c e_{M} \\&\quad = ~\frac{1}{2} \Big [ Q(k_{0}+k_{E})(1+\mu (e_{E})){\hat{p}}_{T}{\hat{p}}_{E} - Rk_{E} -c e_{E} + Q(k_{0}){\hat{p}}_{T}{\hat{p}}_{E} \Big ] \\&\quad = ~Q(k_{0}){\hat{p}}_{T}{\hat{p}}_{E}. \end{aligned}$$

Then subtract $Q(k_{0}){\hat{p}}_{T}{\hat{p}}_{E}$ from each equation above:

$$\begin{aligned}&Q(k_{0}+k_{M})(1+\mu (e_{M})){\hat{p}}_{T}p_{M} - Rk_{M} -c e_{M} - Q(k_{0}){\hat{p}}_{T}{\hat{p}}_{E} \\&\quad = ~0\\&\quad = ~\frac{1}{2} \Big [ Q(k_{0}+k_{E})(1+\mu (e_{E})){\hat{p}}_{T}{\hat{p}}_{E} - Rk_{E} -c e_{E} - Q(k_{0}){\hat{p}}_{T}{\hat{p}}_{E} \Big ]. \end{aligned}$$

Note that ${\tilde{p}}_{l}(k_{0})$ is the solution for p from the first equality if we replace $Q(k_{0}){\hat{p}}_{T}{\hat{p}}_{E}$ with $Q(k_{0}){\hat{p}}_{T}p_{M}$, and ${\tilde{p}}_{s}(k_{0})$ is the solution for p from the second equality. If ${\tilde{p}}_{s}(k_{0})\le 2{\tilde{p}}_{l}(k_{0})$, then ${\hat{p}}_{T}{\hat{p}}_{E}\le 2{\hat{p}}_{T}p_{M}$, and finally ${\hat{p}}_{E}\le 2p_{M}$ because ${\hat{p}}_{T}{\hat{p}}_{E}={\tilde{p}}_{s}(k_{0})$ and ${\hat{p}}_{T}p_{M}\ge {\tilde{p}}_{l}(k_{0})$. The latter inequality results from ${\hat{p}}_{E}={\tilde{p}}_{E,s}(k_{0},x)\ge p_{M}$ at that point, and ${\hat{p}}_{T}p_{M}$ has to be greater than or equal to ${\tilde{p}}_{l}(k_{0})$ for the equality to hold.

We now show that ${\tilde{p}}_{s}(k_{0})\le 2{\tilde{p}}_{l}(k_{0})$ (a geometric proof). Suppose that $k_{0}\ne 0$. By definition, ${\tilde{p}}_{l}(k_{0})$ is the solution of

$$\begin{aligned} {\mathcal {S}}(k_{0},0;p)~=~0, \end{aligned}$$

and ${\tilde{p}}_{s}(k_{0})$ is the solution of

$$\begin{aligned} \frac{1}{2} {\mathcal {S}}(k_{0},0;p)~=~0. \end{aligned}$$

By the envelope theorem, simply taking the second-order derivative is sufficient to show that ${\mathcal {S}}(k_{0},0;p)$ is a convex function in p. Let ${\mathcal {L}}_{l,1}$ be the straight line tangent to ${\mathcal {S}}(k_{0},0;p)$ at point ${\tilde{p}}_{l}(k_{0})$, and ${\mathcal {L}}_{s,1}$ be the straight line tangent to ${\mathcal {S}}(k_{0},0;p)$ at point ${\tilde{p}}_{s}(k_{0})$. We know that ${\tilde{p}}_{s}(k_{0})>{\tilde{p}}_{l}(k_{0})$ and that function ${\mathcal {S}}(k_{0},0;p)$ is convex, and thus the intersection of ${\mathcal {L}}_{l,1}$ and ${\mathcal {L}}_{s,1}$ falls strictly between ${\tilde{p}}_{l}(k_{0})$ and ${\tilde{p}}_{s}(k_{0})$. Let ${\mathcal {L}}_{l,1/2}$ and ${\mathcal {L}}_{s,1/2}$ be the straight lines scaled down from ${\mathcal {L}}_{l,1}$ and ${\mathcal {L}}_{s,1}$ by 1 / 2. ${\mathcal {L}}_{s,1/2}$ is in fact tangent to ${\mathcal {S}}(k_{0},0;p)/2$ at the point ${\tilde{p}}_{s}(k_{0})$. The intersection of ${\mathcal {L}}_{l,1/2}$ and ${\mathcal {L}}_{s,1/2}$ has the same p value as that of ${\mathcal {L}}_{l,1}$ and ${\mathcal {L}}_{s,1}$, which is strictly less than ${\tilde{p}}_{s}(k_{0})$. However, ${\mathcal {L}}_{l,1/2}$ has a smaller slope than ${\mathcal {L}}_{s,1/2}$ because ${\mathcal {S}}(k_{0},0;p)/2$ is a convex function in p. Denote the crossing point by ${\tilde{p}}_{l,1/2}$. Then, ${\tilde{p}}_{l,1/2}>{\tilde{p}}_{s}(k_{0})$ because line ${\mathcal {L}}_{l,1/2}$ is below ${\mathcal {S}}(k_{0},0;p)/2$.

Simple algebra shows that $2{\tilde{p}}_{l}(k_{0})>{\tilde{p}}_{l,1/2}$. This finishes the proof of this claim.

The next step is to show that ${\tilde{p}}_{s}(k_{0})$ has an upper bound that is strictly less than 1. By the definition of ${\tilde{p}}_{s}(k_{0})$, it is the solution of equation

$$\begin{aligned} Q(k_{0})p ~=~\frac{1}{2} \Big [ Q(k_{0}+k_{E})(1+\mu (e_{E}))p - Rk_{E} -c e_{E} + Q(k_{0})p \Big ]. \end{aligned}$$

Let ${\overline{k}}$ be the maximal investment level on the first best investment frontier, and then ${\tilde{p}}_{s}(k_{0})$ is bounded above by

$$\begin{aligned} Q({\overline{k}})p ~=~\frac{1}{2} \Big [ Q({\overline{k}})(1+\mu (e_{E}))p -c e_{E} + Q({\overline{k}})p \Big ], \end{aligned}$$

or simplified as $Q({\overline{k}})\mu (e_{E})p -c e_{E}=0$. So ${\tilde{p}}_{s}(k_{0})\le {\tilde{p}}_{s}({\overline{k}})$. Because $\mu (\cdot )$ is sufficiently productive such that the first best investment frontier is nonempty, $e_{E}>0$ for $k_{0}={\overline{k}}$, which corresponds to $p=1$. However, the left-hand side is 0 when $p=1$, and so ${\tilde{p}}_{s}({\overline{k}})<1$. This finishes the proof showing that ${\tilde{p}}_{s}(k_{0})$ has an upper bound strictly less than 1.

Accordingly, the area of region $\Pi _{I,E}$ has a lower bound $2\varepsilon (1-{\tilde{p}}_{s}({\overline{k}}))$, and, by the argument at the beginning of this section, $k_{0s}>0$. $\square$

Proof of Lemma 5

Consider a general moral hazard problem faced by V:

$$\begin{aligned} \max _{k\ge 0,e\ge 0,0\le \alpha _{V}\le 1,w_{E}} \alpha _{V}Q(k)(1+\mu (e))p-Rk-w_{E}, \end{aligned}$$

(18)

subject to E’s IC constraint

$$\begin{aligned} e \in \mathop {\hbox {argmax}}\limits _{e^{\prime }\ge 0} ~w_{E}+\alpha _{E}Q(k)(1+\mu (e^{\prime }))p-ce^{\prime } \end{aligned}$$

(19)

and IR constraint

$$\begin{aligned} w_{E}+\alpha _{E}Q(k)(1+\mu (e))p-ce\ge {\bar{w}}_{E}. \end{aligned}$$

(20)

By Assumption 2, $\mu (\cdot )$ is strictly concave and $\mu ^{\prime }(\cdot )$ is strictly decreasing and goes to 0 as e goes to infinity. The question of whether we can replace E’s IC constraint with the first-order condition depends on the marginal productivity of both V and E and the probability of an IPO. In general, E’s IC constraint is equivalent to either $e=0$ or first-order condition

$$\begin{aligned} e \big [ \alpha _{E}Q(k) \mu ^{\prime }(e) p-c \big ] = 0. \end{aligned}$$

(21)

Because the solution varies with parameter p, and E’s optimal effort level is nondecreasing in p and bounded below by 0, there exists a $p_{0}\in [0,1]$ such that the IC constraint is $e=0$ when $p\le p_{0}$ and the first-order condition when $p>p_{0}$. $p_{0}$ depends on the marginal productivity of both V and E. If $p_{0}=1$, then ${\underline{p}}={\overline{p}}=p_{0}=1$ because V has no incentive to transfer ownership to E. If $p_{0}<1$, then it is obvious that ${\underline{p}}\ge p_{0}$ for the same reason. It is thus valid to replace E’s IC constraint with the first-order condition of (19).

Fig. 4

Investment curves

It is easy to see that when $\alpha _{E}=1$, V and E’s investment levels are the solutions of (6). This is the first best investment frontier, the upper left investment curve in Fig. 4. Then, $w_{E}$ is chosen such that E’s IR constraint is binding.

Given V and E’s sunk capital investments and effort $(k_{0},e_{0})$ at stage 2, we can suppose that they are both rational in the sense that they will not invest beyond the maximum capital investment level for $p=1$ and the first best investment frontier. Define ${\overline{p}}$ as the solution of the following pair of equations.

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}Q^{\prime }(k_{0})(1+\mu (e))p-1=0, \\ &{}Q(k_{0})\mu ^{\prime }(e)p-1=0, \end{array}\right. } \end{aligned}$$

(22)

with p, e being unknown variables. Define ${\underline{p}}$ as the solution of the following pair of equations.

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}Q^{\prime }(k)(1+\mu (e_{0}))p-1=0, \\ &{}Q(k)\mu ^{\prime }(e_{0})p-1=0, \end{array}\right. } \end{aligned}$$

(23)

with p, k being unknown variables. The solutions for p for Eqs. (22) and (23) exist and are nonnegative. Taking Eq. (23) for example,

$$\begin{aligned} p = \frac{1}{Q^{\prime }(k)(1+\mu (e_{0}))} \end{aligned}$$

is increasing from 0 to positive infinity as k goes from 0 to infinity, and

$$\begin{aligned} p = \frac{1}{Q(k)\mu ^{\prime }(e_{0})} \end{aligned}$$

is decreasing from positive infinity to a constant as k goes from 0 to infinity. ${\underline{p}}$, ${\overline{p}}\le 1$ because we assume that both V and E are rational and will not invest $(k_{0},e_{0})$ beyond the first best. We also assume that $p_{0}<1$. ${\underline{p}}\le {\overline{p}}$ because E will not exert effort beyond the first best investment frontier given V’s capital investment $k_{0}$.

Fig. 5

Incremental investments

In Fig. 5, as $p>{\overline{p}}$, both V and E increase their investment levels to the first best. When ${\underline{p}}<p\le {\overline{p}}$, V invests $k_{0}$, which is over-investing, but he cannot disinvest, so the optimal incremental investment is $\Delta k=0$. E will make an incremental investment that exceeds the first best, because

$$\begin{aligned} \mu ^{\prime }(e)=\frac{1}{Q(k_{0})p}, \end{aligned}$$

V is over-investing, and V and E’s investments are strictly complements outside boundary $k=0$ and $e=0$ globally. When $p\le {\underline{p}}$, both V and E have overinvested, so $\Delta k=0$ and $\Delta e=0$, and the allocation of ownership is no longer important with regard to the investment per se. $\square$

Proof of Proposition 7

The timeline of the game is stages 1, 2, 3, 5E, 6E, and 7E. Negotiations and contracting are conducted at stages 1 and 5E. Investments are made simultaneously by V and E at stages 2 and 6E. Signal x is realized at stage 3. All uncertainties concerning the technology, the two managers’ abilities, and IPO likelihood are resolved at stage 7E.

The posterior probability of IPO perceived by V and E from stage 3 onwards is $p={\hat{p}}_{T}{\hat{p}}_{E}$, and the stage 1 prior probability distribution of p is given by $\rho =\rho _{T}\rho _{E}$. In this section, E’s ability is certain and is above the threshold $\delta ^{*}$, and so ${\hat{p}}_{E}=1$, $p={\hat{p}}_{T}$, and $\rho =\rho _{T}$ (Fig. 2).

Because the contracts are short-term, we let $\alpha _{V}^{0}$, $\alpha _{E}^{0}$ be the ownership structure after investments $k_{0}$, $e_{0}$ and signal x. If V and E’s contracting and investing behavior are optimal at stages 5E and 6E, then V’s interim expected payoff from an IPO is

$$\begin{aligned} u_{V}&~=~ d_{V} + \frac{1}{2} {\mathcal {S}} \\&~=~ \alpha _{V}^{0}Q(k_{0})(1+\mu (e_{0}))p-Rk_{0} + \frac{1}{2} {\mathcal {S}} (k_{0},e_{0};p) \\&~=~ \frac{1}{2} {\mathcal {U}} (k_{0},e_{0};p) + (\alpha _{V}^{0} - \frac{1}{2}) Q(k_{0})(1+\mu (e_{0}))p. \end{aligned}$$

Then, V will choose $\alpha _{V}^{0}$ as high as possible at stage 1. Hence, $\alpha _{V}^{0}=1$ is optimal at stage 1 with a short-term contract.

Then, $\alpha _{E}^{0}=0$, which implies $d_{E}=0$. Let $k^{*}$ and $e^{*}$ denote V and E’s optimal incremental investments at stage 6E. Then,

$$\begin{aligned} Q(k_{0}+k^{*})\mu ^{\prime }(e_{0}+e^{*})p = 1 \end{aligned}$$

if $e^{*}>0$ and

$$\begin{aligned} Q(k_{0}+k^{*})\mu ^{\prime }(e_{0}+e^{*})p \le 1 \end{aligned}$$

if $e^{*}=0$ because it is optimal for E to exert a positive amount of effort when the left-hand side is strictly greater than 1.

E’s expected payoff at stage 1 is

$$\begin{aligned}&\frac{1}{2} \int _{p\in I} \Big [ Q(k_{0}+k^{*})(1+\mu (e_{0}+e^{*}))p - Rk^{*}\\&\quad -c e^{*} - Q(k_{0})(1+\mu (e_{0}))p \Big ] \rho (p) dp -c e_{0}, \end{aligned}$$

where I is the interval for p in which V decides to continue investing.

Take the first-order derivative with respect to $e_{0}$ using the envelope theorem because both $k^{*}$ and $e^{*}$ are functions of $e_{0}$:

$$\begin{aligned} \frac{1}{2} \int _{p\in I} \Big [ Q(k_{0}+k^{*})\mu ^{\prime }(e_{0}+e^{*})p - Q(k_{0})\mu ^{\prime }(e_{0})p \Big ] \rho (p) dp - c. \end{aligned}$$

Note that the first term of the integrand is less than or equal to 1 and that the second term of the integrand is positive. Hence, the integral is strictly less than 1 regardless of interval I, which means that E’s optimal initial effort investment is $e_{0}=0$.

We have solved ${\tilde{p}}_{s}(k_{0})$, and thus a corresponding ${\tilde{x}}_{s}(k_{0})=f^{-1}({\tilde{p}}_{s}(k_{0}))$ in Lemma 4, such that V chooses to quit if $x\le {\tilde{x}}_{s}(k_{0})$ and to invest if $x>{\tilde{x}}_{s}(k_{0})$ after stage 3.

V’s optimal initial investment level $k_{0s}$ is the solution of

$$\begin{aligned} \max _{k_{0}} \int _{0}^{1} \max \Big \{~ \frac{1}{2} \Big [ {\mathcal {U}} (k_{0},0;p) + Q(k_{0})p \Big ], ~Q(k_{0})p~ \Big \} \rho (p) dp - Rk_{0}. \end{aligned}$$

(24)

The solution always exists because $k_{0}$ lies in a closed interval bounded by 0 and the maximal investment level of the first best investment frontier, which is compact. Then, $x_{s}^{*}={\tilde{x}}_{s}(k_{0s})$ for the optimal $k_{0s}$. $\square$

Proof of Proposition 8

We start from the same setting as that in the proof of Proposition 7. The timeline of the game is stages 1, 2, 3, 5E, 6E, and 7E. Contracting occurs at stage 1. Investments are made simultaneously by V and E at stages 2 and 6E. Signal x is realized at stage 3. All uncertainties concerning the technology, the two managers’ abilities, and IPO likelihood are resolved at stage 7E. Suppose that E’s ability is certain and above threshold $\delta ^{*}$, and so ${\hat{p}}_{E}=1$, $p={\hat{p}}_{T}$, and $\rho =\rho _{T}$.

Suppose that the contract is rigid and then apply backward induction. The state space of signal x is perfectly foreseeable, and x is contractible, meaning that V will (weakly) prefer a contract contingent on signal x because any contract unrelated to x would be an extreme form of a contingent contract. Then, after the realization of signal x at stage 3, the contract is the solution of the following.

$$\begin{aligned} \max _{\Delta k\ge 0,\Delta e\ge 0,0\le \alpha _{V}\le 1, w_{E}} \alpha _{V}Q(k_{0}+\Delta k)(1+\mu (e_{0}+\Delta e))p -R(k_{0}+\Delta k)-w_{E},\nonumber \\ \end{aligned}$$

(25)

subject to E’s IC constraint,

$$\begin{aligned} e \in \mathop {\hbox {argmax}}\limits _{e'\ge 0} ~w_{E}+\alpha _{E}Q(k_{0}+\Delta k) (1+\mu (e_{0}+ e'))p-c(e_{0}+ e'), \end{aligned}$$

(26)

and IR constraint,

$$\begin{aligned} w_{E}+\alpha _{E}Q(k_{0}+\Delta k) (1+\mu (e_{0}+e))p-c(e_{0}+ e)\ge {\bar{w}}_{E}, \end{aligned}$$

(27)

where $\alpha _{E}$, $w_{E}$, and ${\bar{w}}_{E}$ are functions of x, which is suppressed for notation simplification. If V chooses to continue investing, it is easy to see that the optimal solution involves $\alpha _{E}(x)=1$.

Because V enjoys sole bargaining power at stage 1, V chooses ${\bar{w}}_{E}(x)=0$. Given V’s proposal of ${\bar{w}}_{E}(x)=0$, E exerts zero effort at stage 2: $e_{0}=0$. Then it is optimal for V to be the sole owner of the company until stage 3: $\alpha _{V}=1$. The next step is to search for the range of x in which V keeps investing.

We have solved for ${\tilde{p}}_{l}(k_{0})$, and thus a corresponding ${\tilde{x}}_{l}(k_{0})=f^{-1}({\tilde{p}}_{l}(k_{0}))$ in Lemma 4, such that V chooses to quit if $x\le {\tilde{x}}_{l}(k_{0})$ and to invest if $x>{\tilde{x}}_{l}(k_{0})$ after stage 3.

V’s optimal initial investment level $k_{0l}$ is the solution of

$$\begin{aligned} \max _{k_{0}} \int _{0}^{1} \max \Big \{~ {\mathcal {U}} (k_{0},0;p), ~Q(k_{0})p~ \Big \} \rho (p) dp - Rk_{0}. \end{aligned}$$

(28)

The solution always exists because $k_{0}$ lies in a closed interval bounded by 0 and the maximal investment level of the first best investment frontier, which is compact. Then, $x_{l}^{*}={\tilde{x}}_{l}(k_{0l})$ for the optimal $k_{0l}$. $\square$

Proof of Proposition 9

This proof will show that $k_{0s}>k_{0l}\ge 0$, and ultimately $x_{s}^{*}>x_{l}^{*}$. Then, for some realization in the signal space of x, V will not choose to continue investing under a flexible short-term contract, but will choose to do so under a rigid relatively long-term contract, which establishes the inefficiencies in both capital investments and the choice of technology.

To show that $x_{s}^{*}>x_{l}^{*}$, we first need to show that ${\tilde{p}}_{s}(k_{0})>{\tilde{p}}_{l}(k_{0})$ for each $k_{0}>0$; then for the V’s optimal initial investment levels, $k_{0s}>k_{0l}\ge 0$; and, finally, that ${\tilde{p}}_{l}(k_{0})$ is (weakly) increasing in $k_{0}$ for $k_{0}\ge k_{0l}$. Combining these three gives us

$$\begin{aligned} {\tilde{p}}_{s}(k_{0s}) > {\tilde{p}}_{l}(k_{0s}) \ge {\tilde{p}}_{l}(k_{0l}). \end{aligned}$$

Finally, by Lemma 1, $f^{-1}(\cdot )$ is a strictly increasing function of p, and so $x_{s}^{*}>x_{l}^{*}$ from the definition of $x_{s}^{*}$ and $x_{l}^{*}$.

Next, we prove the claim that $k_{0s}>k_{0l}\ge 0$. Let $k^{*}$ and $e^{*}$ denote V and E’s optimal incremental investments at stage 6E, as in the proof of Proposition 7. From Eqs. (24) and (28), we know that $k_{0s}$ solves

$$\begin{aligned} \max _{k_{0}} \int _{0}^{{\tilde{p}}_{s}(k_{0})} Q(k_{0})p \rho (p) dp +\int _{{\tilde{p}}_{s}(k_{0})}^{1} \frac{1}{2} \Big [ {\mathcal {U}} (k_{0},0;p) + Q(k_{0})p \Big ] \rho (p) dp - Rk_{0}\nonumber \\ \end{aligned}$$

(29)

and that $k_{0l}$ solves

$$\begin{aligned} \max _{k_{0}} \int _{0}^{{\tilde{p}}_{l}(k_{0})} Q(k_{0})p\rho (p) dp +\int _{{\tilde{p}}_{l}(k_{0})}^{1} {\mathcal {U}} (k_{0},0;p) \rho (p) dp - Rk_{0}. \end{aligned}$$

(30)

By the definition of ${\mathcal {U}}$ and $k^{*}$, $e^{*}$,

$$\begin{aligned} {\mathcal {U}} (k_{0},0;p) ~=~ Q(k_{0}+k^{*})(1 + \mu (e^{*}))p - R(k_{0}+k^{*}) -c e^{*}. \end{aligned}$$

Taking derivative with respect to $k^{*}$ gives us

$$\begin{aligned} Q^{\prime }(k_{0}+k^{*})(1 + \mu (e^{*}))p ~=~ R \end{aligned}$$

if $k^{*}>0$ and

$$\begin{aligned} Q^{\prime }(k_{0}+k^{*})(1 + \mu (e^{*}))p ~\le ~ R \end{aligned}$$

if $k^{*}=0$. Because both $k^{*}$ and $e^{*}$ are functions of $k_{0}$ and p, using the envelope theorem and the two (in)equalities above, we can see that

$$\begin{aligned} Q^{\prime }(k_{0}+k^{*})(1 + \mu (e^{*}))p ~\le ~ R \end{aligned}$$

holds for all $k_{0}$ when the derivative is taken with respect to $k_{0}$.

Because $e_{0}=0$ and ${\underline{p}}$ is the minimum probability of an IPO such that E has an incentive to exert incremental effort, ${\tilde{p}}_{s}(k_{0})\ge {\underline{p}}$, where ${\underline{p}}$ is defined as in Lemma 5. Because ${\tilde{p}}_{s}(k_{0})$ satisfies

$$\begin{aligned} \frac{1}{2} {\mathcal {S}} (k_{0},0;p)~=~0, \end{aligned}$$

it is a differentiable function of $k_{0}$ by the implicit function theorem.

The solution of (29) exists, because $k_{0}$ lies in a compact set. If the first-order derivative of the objective function in (29) has a positive right limit at $k_{0}=0$ and the first-order condition has a unique solution, then $k_{0s}$ is the unique interior solution of (29) and the first-order condition is sufficient and necessary. Taking the first order derivative of the objective function in (29), and setting it equal to 0, we have

$$\begin{aligned}&\int _{0}^{{\tilde{p}}_{s}(k_{0})} Q^{\prime }(k_{0})p\rho (p) dp + \int _{{\tilde{p}}_{s}(k_{0})}^{1} \frac{1}{2} \Big [ Q^{\prime }(k_{0}+k^{*})(1 + \mu (e^{*}))p \nonumber \\&\quad + Q^{\prime }(k_{0})p \Big ] \rho (p) dp ~=~ R. \end{aligned}$$

(31)

The term involving the derivative of ${\tilde{p}}_{s}(k_{0})$ is 0 by the choice of ${\tilde{p}}_{s}(k_{0})$. All terms in the integrands are nonnegative, and so

$$\begin{aligned}&\int _{0}^{{\tilde{p}}_{s}(k_{0})} Q^{\prime }(k_{0})p\rho (p) dp + \int _{{\tilde{p}}_{s}(k_{0})}^{1} \frac{1}{2} \Big [ Q^{\prime }(k_{0}+k^{*})(1 + \mu (e^{*}))p \\&\qquad + Q^{\prime }(k_{0})p \Big ] \rho (p) dp \ge \frac{1}{2} Q^{\prime }(k_{0}) \int _{0}^{1}p\rho (p)dp. \end{aligned}$$

By assumption, $\lim _{k\rightarrow 0+}Q^{\prime }(k)=+\infty$. Hence, the first-order derivative of the objective function in (29) has a positive right limit at $k_{0}=0$. Now, $Q^{\prime }(\cdot )$ is strictly monotonically decreasing, and $\lim _{k\rightarrow +\infty }Q^{\prime }(k)=0$, and thus the first-order condition has a unique solution by the intermediate value theorem. This finishes the proof of the claim that $k_{0s}>0$.

If $k_{0l}=0$, there is nothing to prove. So assuming that $k_{0l}>0$, for ${\tilde{p}}_{l}(k_{0})$,

$$\begin{aligned} \int _{0}^{{\tilde{p}}_{l}(k_{0})} Q^{\prime }(k_{0})p\rho (p) dp + \int _{{\tilde{p}}_{l}(k_{0})}^{1} Q^{\prime }(k_{0}+k^{*})(1 + \mu (e^{*}))p \rho (p) dp ~=~ R \end{aligned}$$

(32)

because it is possible that ${\underline{p}}>0$. Then $k_{0l}>0$ because ${\tilde{p}}_{l}(k_{0})\ge {\underline{p}}$.

If

$$\begin{aligned}&\int _{0}^{{\tilde{p}}_{s}(k_{0l})} Q^{\prime }(k_{0l})p\rho (p) dp + \int _{{\tilde{p}}_{s}(k_{0l})}^{1} \frac{1}{2} \Big [ Q^{\prime }(k_{0l}+k^{*})(1 + \mu (e^{*}))p\nonumber \\&\quad + Q^{\prime }(k_{0l})p \Big ] \rho (p) dp ~>~ R, \end{aligned}$$

(33)

then the implication is that $k_{0s}>k_{0l}$, because all of the terms in the integrands are less than or equal to 1 except for the $Q^{\prime }(\cdot )p$ terms, and $Q^{\prime }(\cdot )$ is a decreasing function.

Taking the difference between the left-hand side of (33) and the left-hand side of (32), with $k_{0}=k_{0l}$, we have

$$\begin{aligned}&\int _{0}^{{\tilde{p}}_{s}(k_{0l})} Q^{\prime }(k_{0l})p\rho (p) dp + \int _{{\tilde{p}}_{s}(k_{0l})}^{1} \frac{1}{2} \Big [ Q^{\prime }(k_{0l}+k^{*})(1 + \mu (e^{*}))p\\&\qquad +Q^{\prime }(k_{0l})p \Big ] \rho (p) dp \\&\qquad - \int _{0}^{{\tilde{p}}_{l}(k_{0l})} Q^{\prime }(k_{0l})p \rho (p) dp - \int _{{\tilde{p}}_{l}(k_{0l})}^{1} Q^{\prime }(k_{0l}+k^{*})(1 + \mu (e^{*}))p \rho (p) dp \\&\quad = \int _{{\tilde{p}}_{l}(k_{0l})}^{{\tilde{p}}_{s}(k_{0l})} \Big [ Q^{\prime }(k_{0l})p - Q^{\prime }(k_{0l}+k^{*})(1 + \mu (e^{*}))p \Big ] \rho (p) dp \\&\qquad + \int _{{\tilde{p}}_{s}(k_{0l})}^{1} \frac{1}{2} \Big [ Q^{\prime }(k_{0l})p - Q^{\prime }(k_{0l}+k^{*})(1 + \mu (e^{*}))p \Big ] \rho (p) dp. \end{aligned}$$

Note that $Q^{\prime }(k_{0l}+k^{*})(1 + \mu (e^{*}))p\le 1$ and $Q^{\prime }(k_{0l})p>1$ as long as $~p\ge {\tilde{p}}_{l}(k_{0l})$ because $Q^{\prime }(k_{0l})p$ is an increasing function in p, and Eq. (32) holds if $k_{0l}>0$. By assumption, $Q^{\prime }(k_{0l})p>1$ as long as $p\ge {\tilde{p}}_{s}(k_{0l})$. Then, this difference is strictly greater than 0. This finishes the proof of the claim that $k_{0s}>k_{0l}$.

For the third claim, we need to show that ${\tilde{p}}_{l}(k_{0})$ is increasing in $k_{0}$ for $k_{0}\ge k_{0l}$. Denote

$$\begin{aligned} {\mathcal {F}}~:=~{\mathcal {S}}(k_{0},0;p) ~=~Q(k_{0}+k^{*})(1+\mu (e^{*}))p-Rk^{*}-ce^{*} -Q(k_{0})p. \end{aligned}$$

Then,

$$\begin{aligned} \frac{\partial {\mathcal {F}}}{\partial p} ~=~Q(k_{0}+k^{*})(1+\mu (e^{*}))-Q(k_{0}) ~>~0, \end{aligned}$$

and

$$\begin{aligned} \frac{\partial {\mathcal {F}}}{\partial k_{0}} ~=~Q^{\prime }(k_{0}+k^{*})(1+\mu (e^{*}))p -Q^{\prime }(k_{0})p. \end{aligned}$$

Hence, the sign of $d{\tilde{p}}_{l}(k_{0})/dk_{0}$ is the opposite of the sign of $\partial {\mathcal {F}}/\partial k_{0}$. However, we know that $\partial {\mathcal {F}}/\partial k_{0}$ is negative at $k_{0}=k_{0l}$ by the condition (32). By Assumption 1,

$$\begin{aligned} \lim _{k_{0} \rightarrow \infty } \frac{\partial {\mathcal {F}}}{\partial k_{0}}~<~0, \end{aligned}$$

and for a $k_{0}\ge k_{0l}$ that is sufficiently large, $k^{*}=0$. Then,

$$\begin{aligned} \frac{\partial ^{2} {\mathcal {F}}}{\partial k_{0}^{2}} ~\approx ~Q^{\prime \prime }(k_{0})\mu (e^{*})p~<~0, \end{aligned}$$

which implies that $\partial {\mathcal {F}}/\partial k_{0}<0$ for $k_{0}\ge k_{0l}$. Thus, ${\tilde{p}}_{l}(k_{0})$ is increasing for $k_{0}\ge k_{0l}$.

Finally,

$$\begin{aligned}&\int _{0}^{{\tilde{p}}_{s}(k_{0s})} Q(k_{0s})p \rho (p) dp + \int _{{\tilde{p}}_{s}(k_{0s})}^{1} \frac{1}{2} \Big [ {\mathcal {U}} (k_{0s},0;p) + Q(k_{0s})p \Big ] \rho (p) dp - Rk_{0s} \\&\quad \le \int _{0}^{{\tilde{p}}_{s}(k_{0s})} Q(k_{0s})p \rho (p) dp + \int _{{\tilde{p}}_{s}(k_{0s})}^{1} {\mathcal {U}} (k_{0s},0;p) \rho (p) dp - Rk_{0s} \\&\quad < \int _{0}^{{\tilde{p}}_{l}(k_{0s})} Q(k_{0s})p \rho (p) dp + \int _{{\tilde{p}}_{l}(k_{0s})}^{1} {\mathcal {U}} (k_{0s},0;p) \rho (p) dp - Rk_{0s} \\&\quad \le \int _{0}^{{\tilde{p}}_{l}(k_{0l})} Q(k_{0l})p \rho (p) dp + \int _{{\tilde{p}}_{l}(k_{0l})}^{1} {\mathcal {U}} (k_{0l},0;p) \rho (p) dp - Rk_{0l}. \end{aligned}$$

The first inequality arises because

$$\begin{aligned} {\mathcal {U}} (k_{0s},0;p) ~=~ Q(k_{0s} + k^{*})(1 + \mu (e^{*}))p - R(k_{0}+k^{*}) -c e^{*} ~\ge ~ Q(k_{0s})p-Rk_{0}. \end{aligned}$$

The second is because ${\tilde{p}}_{l}(k_{0s})<{\tilde{p}}_{s}(k_{0s})$, and ${\tilde{p}}_{l}(k_{0s})$ is the solution for a rigid long-term contract when the initial investment is $k_{0s}$. Hence ${\mathcal {S}} (k_{0s},0;p)>0$ on the interval of $({\tilde{p}}_{l}(k_{0s}),{\tilde{p}}_{s}(k_{0s}))$. The inequality is strict because ${\mathcal {S}} (k_{0},0;p)$ is increasing in p. The last inequality follows from the definition of $k_{0l}$. Hence, the flexible short-term contract is inferior. $\square$

Proof of Proposition 10

Finally, suppose that the quality of the technology is uncertain, but E’s ability is certain and greater than threshold $\delta ^{*}$. A feasible sequence of flexible short-term contracts comprises an initial contract that coordinates V and E’s investment actions up to stage 3 and a continuing contract that governs the rest of the investment process. Using a sequence of short-term contracts incurs costs in two ways: $k_{0s}>k_{0l}\ge 0$, and the first best investment levels may not be feasible if ${\hat{p}}_{T}$ is very low, and $qk_{0}<k_{0}$ in the case of quitting. E will share a positive amount of surplus ${\mathcal {S}}(k_{0},0;p)/2$ if V decides to continue investing with E as the manager. At the same time, given any initial contract, the state space of x, V and E’s investments at stage 2, and an ownership structure based on the realization of signal x are all perfectly predictable. Then, for V, a rigid contract contingent on x at stage 1 that coordinates the entire investment process would perform no worse than a sequence of flexible contracts for each given x. $\square$