A hybrid ‘FE-Meshfree’ QUAD4 element with nonlocal features

Abstract

A new element is developed by introducing a nonlocal-integrated displacement interpolation into the ‘FE-Meshfree’ QUAD4 element recently published. Both nodal displacement and elemental strain are constructed using the nonlocal concept so that the elemental stiffness matrix and the resulting deformation fields are naturally nonlocal, leading to a significant difference when compared with nonlocal simulations using existing finite elements where local fields are output firstly in each incremental step and their nonlocal counterparts are obtained by averaging. The proposed element has the capability of predicting the nonlocal characteristics of localized deformations, with the intrinsic material length included into the nonlocal averaging. Several examples are employed to demonstrate the advantage of the proposed element in capturing highly localized deformations.

Appendices

Appendix A: Approximation of influence region

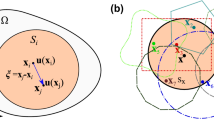
In Eq. 18, an approximation has been made. As shown in Fig. 2, when we calculate the displacement at point $\left( x,y\right)$ via the integration in Eq. 18, the integration region is made up of all elements falling into the red circle centered by the center of the element that the point $\left( x,y\right)$ lies in. When the contribution of the integration point $\left( \xi ,\eta \right)$ is considered, in principle the displacement vector $\underset{L\,\times \,1}{\varvec{u}}\left( \xi ,\eta \right)$ is composed of the displacement of each node falling into the blue circle corresponding to the element that the point $\left( \xi ,\eta \right)$ lies in, as shown in Eq. 14. Since the blue circle and the red circle generally do not overlap, displacements of nodes within the blue circle but outside the red also have influence. However, we argue that nodal displacements outside the red circle are neglect-able when calculating the elemental displacement field of the element at the center of the red circle, as long as the radius of the red circle is chosen to be large enough compared with the the characteristic length. This is easy to understand because of the fast decay of the exponential function in Eq. 18.

Under this approximation, we explain the construction of $\underset{1\,\times \, L}{\varvec{\hat{\varPsi }}}$ in Eq. 18. Still take Fig. 2 as an example. In the influence region for point $\left( x,y\right)$, denoted as $\varOmega \left( x,y\right)$, there are 52 nodes which are numbered in the figure, say $\alpha =1,2,\ldots ,52$. In the influence region for point $\left( \xi ,\eta \right)$, say $\varOmega \left( \xi ,\eta \right)$, some nodes fall into $\varOmega \left( x,y\right)$, while others do not. Only nodes lying in the common part of $\varOmega \left( x,y\right)$ and $\varOmega \left( \xi ,\eta \right)$ are accounted in Eq. 18. Therefore, each of those common nodes is numbered differently in two regions, and we define a number mapping for common nodes as follows

$$\begin{aligned} \alpha \rightarrow f\left( \alpha \right) ,\quad \big (\alpha \in \varOmega \left( x,y\big ),\; f\left( \alpha \right) \in \varOmega \left( \xi ,\eta \right) \right) \end{aligned}$$

(52)

Then $\underset{1\,\times \, L}{\varvec{\hat{\varPsi }}}\left( \xi ,\eta \right)$ in Eq. 18 can be expressed in the form

$$\begin{aligned} \underset{1\,\times \, L}{\varvec{\hat{\varPsi }}}\left( \xi ,\eta \right) = \left[ \begin{array}{ccccc} \hat{\varPsi }_{1}&\hat{\varPsi }_{2}&\hat{\varPsi }_{3}&\ldots&\hat{\varPsi }_{52}\end{array}\right] \end{aligned}$$

(53)

where,

$$\begin{aligned} \hat{\varPsi }_{\alpha }={\left\{ \begin{array}{ll} 0 &{} \alpha \notin \varOmega \left( \xi ,\eta \right) \\ \varPsi _{f\left( \alpha \right) } &{} \alpha \in \varOmega \left( \xi ,\eta \right) \end{array}\right. } \end{aligned}$$

(54)

Analogously, $\underset{1\,\times \, L}{\varvec{\hat{\varPsi }_{,x}}}$ in Eq. 21 and $\underset{1\,\times \, L}{\varvec{\hat{\varPsi }_{,y}}}$ in Eq. 22 are obtained as

$$\begin{aligned}&\underset{1\,\times \, L}{\varvec{\hat{\varPsi }_{,x}}}\left( \xi ,\eta \right) =\left[ \begin{array}{ccccc} \hat{\varPsi }_{1,x}&\hat{\varPsi }_{2,x}&\hat{\varPsi }_{3,x}&\ldots&\hat{\varPsi }_{52,x}\end{array}\right] \end{aligned}$$

(55)

$$\begin{aligned}&\underset{1\,\times \,u L}{\varvec{\hat{\varPsi }_{,y}}}\left( \xi ,\eta \right) =\left[ \begin{array}{ccccc} \hat{\varPsi }_{1,y}&\hat{\varPsi }_{2,y}&\hat{\varPsi }_{3,y}&\ldots&\hat{\varPsi }_{52,y}\end{array}\right] \end{aligned}$$

(56)

where,

$$\begin{aligned} \hat{\varPsi }_{\alpha ,x}= & {} {\left\{ \begin{array}{ll} 0 &{}\quad \alpha \notin \varOmega \left( \xi ,\eta \right) \\ \varPsi _{f\left( \alpha \right) ,x} &{}\quad \alpha \in \varOmega \left( \xi ,\eta \right) \end{array}\right. } \end{aligned}$$

(57)

$$\begin{aligned} \hat{\varPsi }_{\alpha ,y}= & {} {\left\{ \begin{array}{ll} 0 &{}\quad \alpha \notin \varOmega \left( \xi ,\eta \right) \\ \varPsi _{f\left( \alpha \right) ,y} &{}\quad \alpha \in \varOmega \left( \xi ,\eta \right) \end{array}\right. } \end{aligned}$$

(58)

Appendix B: Challenge in calculating derivatives of Eq. 18

To obtain the stains, one may be curious why we do not directly calculate derivatives of Eq. 18 instead of using Eqs. 20–25. This is explained as follows.

Operation $\frac{\partial }{\partial x}$ on both sides of Eq. 18 gives

$$\begin{aligned} \frac{\partial u\left( x,y\right) }{\partial x}=\left[ \frac{1}{V_{r}\left( x,y\right) }\frac{\partial I}{\partial x}-\frac{I}{V_{r}^{2}\left( x,y\right) }\frac{\partial V_{r}\left( x,y\right) }{\partial x}\right] \underset{L\times 1}{\varvec{u}}\nonumber \\ \end{aligned}$$

(59)

where,

$$\begin{aligned}&I=\int _{\varOmega _{e}}e^{-\frac{\pi \left[ \left( \xi -x\right) ^{2} +\left( \eta -y\right) ^{2}\right] }{l^{2}}}\underset{1\times L}{\varvec{\hat{\varPsi }}}\left( \xi ,\eta \right) d\xi d\eta \end{aligned}$$

(60)

$$\begin{aligned}&\frac{\partial I}{\partial x}=-\frac{2\pi }{l^{2}}\int _{\varOmega _{e}} \left( \xi -x\right) e^{-\frac{\pi \left[ \left( \xi -x\right) ^{2} +\left( \eta -y\right) ^{2}\right] }{l^{2}}}\underset{1\times L}{\varvec{\hat{\varPsi }}}\left( \xi ,\eta \right) d\xi d\eta \nonumber \\ \end{aligned}$$

(61)

$$\begin{aligned}&\frac{\partial V_{r}\left( x,y\right) }{\partial x}=-\frac{2\pi }{l^{2}}\int _{\varOmega _{e}} \left( \xi -x\right) e^{-\frac{\pi \left[ \left( \xi -x\right) ^{2} +\left( \eta -y\right) ^{2}\right] }{l^{2}}}d\xi d\eta \nonumber \\ \end{aligned}$$

(62)

From Eqs. 61 and 62, the contributions from integration points with $\xi =x$ are zero. But this is unrealistic. As an example, according to Eq. 59, the point $\left( x,y\right)$ itself has no contribution to the derivative at the same point, which is unreasonable.