An On-line Competitive Algorithm for Coloring Bipartite Graphs Without Long Induced Paths

Abstract

The existence of an on-line competitive algorithm for coloring bipartite graphs is a tantalizing open problem. So far there are only partial positive results for bipartite graphs with certain small forbidden graphs as induced subgraphs. We propose an on-line competitive coloring algorithm for $P_9$-free bipartite graphs.

1 Introduction

A proper coloring of a graph is an assignment of colors to its vertices such that adjacent vertices receive distinct colors. It is easy to devise a (linear time) algorithm for 2-coloring bipartite graphs. Now, imagine that an algorithm receives vertices of a graph one by one knowing only the adjacency status of the vertex to vertices presented so far. The color of the current vertex must be fixed by the algorithm before the next vertex is revealed and it cannot be changed afterwards. This kind of algorithm is called an on-line coloring algorithm.

Formally, an on-line graph $(G,\pi )$ is a graph G with a permutation $\pi$ of its vertices. An on-line coloring algorithm A takes an on-line graph $(G,\pi )$, say $\pi =(v_1,\ldots ,v_n)$, as an input. It produces a proper coloring of the vertices of G where the color of a vertex $v_i$, for $i=1,\ldots ,n$, depends only on the subgraph of G induced by $v_1,\ldots ,v_i$. It is convenient to imagine that consecutive vertices along $\pi$ are revealed by some adaptive (malicious) adversary and the coloring process is a game between that adversary and the on-line algorithm.

Still, it is an easy exercise to show that if an adversary presents a bipartite graph and all the time the graph presented so far is connected then there is an on-line algorithm 2-coloring these graphs. But if an adversary can present a bipartite graph without any additional constraints then it can trick out any on-line algorithm to use an arbitrary number of colors!

Indeed, there is a strategy for the adversary forcing any on-line algorithm to use at least $\lfloor \log n\rfloor +1$ colors on a forest of size n. On the other hand, the First-Fit algorithm (that is an on-line algorithm coloring each incoming vertex with the least admissible natural number) uses at most $\lfloor \log n\rfloor +1$ colors on forests of size n. When the game is played on bipartite graphs, an adversary can easily force First-Fit to use $\lceil \frac{n}{2}\rceil$ colors on a bipartite graph of size n. Lovász, Saks and Trotter [12] proposed a simple on-line algorithm (in fact as an exercise; see also [8]) using at most $2\log n+1$ colors on bipartite graphs of size n. This is best possible up to an additive constant as Gutowski et al. [4] showed that there is a strategy for the adversary forcing any on-line algorithm to use at least $2\log n -10$ colors on a bipartite graph of size n.

For an on-line algorithm A by $A(G,\pi )$ we mean the number of colors that A uses against an adversary presenting graph G with presentation order $\pi$.

An on-line coloring algorithm A is competitive on a class of graphs $\mathcal {G}$ if there is a function f such that for every $G\in \mathcal {G}$ and permutation $\pi$ of vertices of G we have $A(G,\pi )\leqslant f(\chi (G))$. As we have discussed, there is no competitive coloring algorithm for forests. But there are reasonable classes of graphs admitting competitive algorithms, e.g., interval graphs can be colored on-line with at most $3\chi -2$ colors (where $\chi$ is the chromatic number of the presented graph; see [11]) and cocomparability graphs can be colored on-line with a number of colors bounded by a tower function in terms of $\chi$ (see [9]). Also classes of graphs defined in terms of forbidden induced subgraphs were investigated in this context. For example, $P_4$-free graphs (also known as cographs) are colored by First-Fit optimally, i.e. with $\chi$ colors, since any maximal independent set meets all maximal cliques in a $P_4$-free graph. Also $P_5$-free graphs can be colored on-line with $O(4^\chi )$ colors (see [10]). And to complete the picture there is no competitive algorithm for $P_6$-free graphs as Gyárfás and Lehel [6] showed a strategy for the adversary forcing any on-line algorithm to use an arbitrary number of colors on bipartite $P_6$-free graphs.

Confronted with so many negative results, it is not surprising that Gyárfás, Király and Lehel [5] introduced a relaxed version of competitiveness for on-line algorithms. The idea is to measure the efficiency of an on-line algorithm by comparing it to the best on-line algorithm for a given input. Hence, the on-line chromatic number of a graph G is defined as

$$\begin{aligned} \chi _*(G) = \inf _A \max _{\pi } A(G,\pi ), \end{aligned}$$

where the infimum is taken over all on-line algorithms A and the maximum is taken over all permutations $\pi$ of vertices of G. An on-line algorithm A is on-line competitive for a class of graphs $\mathcal {G}$, if there is a function f such that for every $G\in \mathcal {G}$ and permutation $\pi$ of vertices of G we have $A(G,\pi ) \leqslant f(\chi _*(G))$.

Why are on-line competitive algorithms interesting? Imagine that you design an algorithm and the input graph is not known in advance. If your algorithm is on-line competitive then you have an insurance that whenever your algorithm uses many colors on some graph G with presentation order $\pi$ then any other on-line algorithm may also be forced to use many colors on the same graph G with some presentation order $\pi '$. This means that our algorithm is competing here also with those algorithms designed only for the single graph G. (More precisely, algorithm may be designed for a single graph G, thus knows in advance the graph that eventually will come on-line, but for each arriving vertex v, it may not be able to guess where in the graph v belongs.) The idea of comparing the outputs of two on-line algorithms directly (not via the optimal off-line result) is present in the literature. We refer the reader to [1], where a number of measures are discussed in the context of on-line bin packing problems. In particular, the relative worst order ratio, introduced there, is closely related to our setting for on-line colorings.

It may be true that there is an on-line competitive algorithm for all graphs. This is open, even for the class of all bipartite graphs. To the best of the authors’ knowledge, there is no promising approach for the negative answer for these questions. However, there are some partial positive results. Gyárfás and Lehel [7] have shown that First-Fit is on-line competitive for forests and it is even optimal in the sense that if First-Fit uses k colors on G then the on-line chromatic number of G is k as well. They also have shown [5] that First-Fit is competitive (with an exponential bounding function) for graphs of girth at least 5. Finally, Broersma, Capponi and Paulusma [3] proposed an on-line coloring algorithm for $P_7$-free bipartite graphs using at most $8\chi _*+8$ colors on graphs with on-line chromatic number $\chi _*$.

The contribution of this paper is the following theorem.

Theorem 1

There is an on-line competitive algorithm coloring $P_9$-free bipartite graphs and using at most $6(\chi _*+1)^2$ colors, where $\chi _*$ is the on-line chromatic number of the presented graph.

Note that this is a full version of [13] published in the proceedings of ISAAC 2014. In [13], we discuss how our techniques simplify results for $P_7$-free bipartite graphs. Already in [13], we presented Algorithm 1 with a proof that it is on-line competitive for $P_8$-free bipartite graphs. (This may be a good warmup or source of extra intuition behind the arguments in this paper.)

2 Forcing Structure

In this section we introduce a family of bipartite graphs without long induced paths ($P_6$-free) and with arbitrarily large on-line chromatic number. Our on-line algorithm, Algorithm 1, has the property that whenever it uses many colors on a graph G then G has a large graph from our family as an induced subgraph and therefore G has a large on-line chromatic number, as desired.

A connected bipartite graph G has a unique partition of vertices into two independent sets. We call these partition sets the sides of G. A vertex v in a bipartite graph G is universal to a subgraph C of G if v is adjacent to all vertices of C in one of the sides of G.

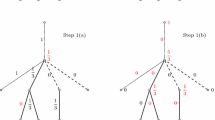
Consider a family of connected bipartite graphs $\left\{ X_k\right\} _{k\geqslant 1}$ defined recursively as follows. Each $X_k$ has a distinguished vertex called the root. The side of $X_k$ containing the root of $X_k$, we call the root side of $X_k$, while the other side we call the non-root side. $X_1$ is a single vertex being the root. $X_2$ is a single edge with one of its vertices being the root. $X_k$, for $k\geqslant 3$, is a graph formed by two disjoint copies of $X_{k-1}$, say $X^1_{k-1}$ and $X^2_{k-1}$, with no edge between the copies, and one extra vertex v adjacent to all vertices on the root side of $X^1_{k-1}$ and all vertices on the non-root side of $X^2_{k-1}$. The vertex v is the root of $X_k$. Note that for each k, the root of $X_k$ is adjacent to the whole non-root side of $X_k$, i.e., the root of $X_k$ is universal in $X_k$. See Fig. 1 for a schematic illustration of $X_k$ for various k.

Fig. 1

Family of bipartite graphs

A family of $P_6$-free bipartite graphs with arbitrarily large on-line chromatic number was first presented in [6]. The family $\left\{ X_k\right\} _{k\geqslant 1}$ was already studied in [2], in particular Claim 3 is proved there. Since we use this claim in the proof of our main theorem and for the sake of completeness, we give a proof for it below. One can easily verify, by induction, that $X_k$ is $P_6$-free for $k\geqslant 1$.

Claim 2

Let $k\geqslant 2$. Then, for every binary sequence $\alpha _1,\ldots ,\alpha _{k-1}$, there are copies $Y_1,\ldots ,Y_{k-1}$ of $X_1,\ldots ,X_{k-1}$ contained as induced subgraphs in $X_k$ satisfying the following two properties. First, they are pairwise disjoint with no edges between them. And second, for every $i\in \{1,\ldots ,k-1\}$ the root of $Y_i$ is on the root side of $X_k$ if and only if $\alpha _i=1$.

Proof

We prove the lemma by induction on k. For the base case $k=2$, fix $\alpha _1\in \left\{ 0,1\right\}$. Now, $X_2$ is an edge and one can put $Y_1$ as a single vertex being the root of $X_2$ if $\alpha _1=1$, and being the other vertex if $\alpha _1=0$. So suppose $k\geqslant 3$. By definition, $X_k$ consists of two independent copies $X_{k-1}^1$ and $X_{k-1}^2$ of $X_{k-1}$ and a root vertex that is universal to the root side of $X_{k-1}^1$ and to the non-root side of $X_{k-1}^2$. Let us first consider the case $\alpha _{k-1}=0$. Then $X_{k-1}^1$ is a copy of $X_{k-1}$ with its root on the non-root side of $X_k$, as required. On $X_{k-1}^2$ we apply induction for the sequence $\alpha _1,\ldots ,\alpha _{k-2}$. Hence there are copies $Y_1,\ldots ,Y_{k-2}$ of $X_1,\ldots ,X_{k-2}$ as induced subgraphs of $X_{k-1}^2$ satisying the following properties. They are pairwise disjoint with no edges between them and clearly with no edges to $X_{k-1}^1$ as well. And for all $i\in \{1,\ldots ,k-2\}$, the root of $Y_i$ is on the root side of $X_{k-1}^2$ if and only if $\alpha _i=1$. Since the root of $X_{k-1}^2$ is contained in the rood side of $X_k$, the result follows.

The case $\alpha _{k-1}=1$ is similar with the difference that we use $X_{k-1}^2$ as a copy of $X_{k-1}$ and that we apply induction on $X_{k-1}^1$ for the sequence $\overline{\alpha _1},\ldots ,\overline{\alpha _{k-2}}$.$\square$

Claim 3

If G contains $X_k$ as an induced subgraph, then $\chi _*(G)\geqslant k$.

Proof

Let A be any on-line coloring algorithm. We prove by induction on k that the adversary can present the vertices of G such that A uses at least k colors. It is clear that any coloring algorithm has to use one color for $X_1$ and two colors for $X_2$. So suppose that $k\geqslant 3$. The adversary starts with presenting disjoint copies $Y_1,\ldots ,Y_{k-1}$ of $X_1,\ldots ,X_{k-1}$ one after another, with no edges between the copies, and by induction he can do this in such a way that A uses i colors on $Y_i$, for $i\in \left\{ 1,\ldots ,k-1\right\}$. Therefore there are distinct colors $c_1,\ldots ,c_{k-1}$ such that $c_i$ is used on $Y_i$ for every i. Let $v_i\in Y_i$ be a vertex colored with $c_i$ and set $\alpha _i=1$ if $v_i$ is on the non-root side of $Y_i$, and $\alpha _i=0$ otherwise.

Now we explain how to embed $Y_1,\ldots ,Y_{k-1}$ into G. Let v be the root of the induced copy of $X_k$ contained in G. By Claim 2 there are pairwise disjoint copies $Y_1,\ldots ,Y_{k-1}$ of $X_1,\ldots ,X_{k-1}$ in $X_k$ with no edges between the copies, and such that for all $i\in \{1,\ldots ,k-1\}$ the root of $Y_i$ is on the same side as v if and only if $\alpha _i=1$. By the choice of $\alpha _i$ it follows that $v_i$ is on the non-root side of $X_k$, for all $i\in \left\{ 1,\ldots ,k-1\right\}$. Since v is universal in $X_k$, it is adjacent to $v_i$ for all i.

After presenting all $Y_1,\ldots ,Y_{k-1}$ the adversary introduces vertex v being the root of $X_k$ in G, and forces A to use a color different from $c_1,\ldots ,c_{k-1}$.$\square$

3 The Algorithm

We present a new on-line algorithm for bipartite graphs, Algorithm 1, and we prove that this algorithm is on-line competitive for $P_9$-free bipartite graphs. It builds on the algorithm BicolorMax from [3], where it is shown that BicolorMax is on-line competitive on $P_7$-free graphs (see also [13] for a simple proof of this fact). BicolorMax aims to force the existence of a large member of the family $\left\{ X_k\right\} _{k\geqslant 1}$ in a $P_7$-free graph G whenever it uses many colors on G. Algorithm 1 generalizes this behaviour to $P_9$-free graphs.

Algorithm 1 uses three disjoint palettes of colors, $\left\{ a_n\right\} _{n\geqslant 1}$, $\left\{ b_n\right\} _{n\geqslant 1}$ and $\left\{ c_n\right\} _{n\geqslant 1}$. In the following whenever the algorithm fixes a color of a vertex v we are going to refer to it by $\mathrm{color}(v)$. Also for any set of vertices X we denote $\mathrm{color}(X)=\left\{ \mathrm{color}(x)\mid x\in X\right\}$. We say that v has color index i if $\mathrm{color}(v)\in \left\{ a_i,b_i,c_i\right\}$.

Suppose an adversary presents a new vertex v of a bipartite graph G. Then let $G_i[v]$ be the subgraph spanned by the vertices presented so far and colored with a color from $\left\{ a_1,\ldots ,a_i,b_1,\ldots ,b_i,c_1,\ldots ,c_i\right\}$, together with vertex v, which is uncolored yet. With $C_i[v]$ we denote the connected component of $G_i[v]$ containing v. For convenience put $C_0[v]=\left\{ v\right\}$. Furthermore, let $C_i(v)$ be the graph $C_i[v]$ without vertex v. Note that by these definitions it already follows that if $w\in C_i(v)$ then $C_j[w]\subseteq C_i(v)$ for all $j\leqslant i$. We will use this fact throughout the rest of the paper. For a vertex x in $C_i(v)$ it will be convenient to denote by $C_i^x(v)$ the connected component of $C_i(v)$ that contains x. We say that a color c is mixed in a connected subgraph C of G if c is used on vertices on both sides of C.

Now we are ready for a description of our algorithm. After Claim 5 we give some intuition about it.

Claim 4

Algorithm 1 gives a proper coloring of on-line bipartite graphs.

Proof

Suppose an adversary introduces a vertex v of a bipartite graph G. We have to show that Algorithm 1 colors v properly, i.e., no vertex presented before v and adjacent to v has the same color as v. Let $k\geqslant 1$ be the color index of v and $(I_1,I_2)$ be the bipartition of $C_{k}[v]$ such that $v\in I_1$.

If v is colored with $a_k$, then there is no vertex in $I_2$ colored with $a_k$ because of the first if-condition. In particular, no neighbor of v is colored with $a_k$.

If v is colored with $b_k$, then there is a vertex $u\in I_2$ with $\mathrm{color}(u)=a_k$. Suppose v is not colored properly, which means that there is a vertex $w\in I_2$ with color $b_k$. When w was introduced, there must have been a vertex $u'$ on the other side of w in $C_{k}[w]$ with $\mathrm{color}(w)=a_k$. Since $C_k[w]\subseteq C_k[v]$ it follows that $u'\in I_1$. But then u and $u'$ certify that color $a_k$ is mixed in $C_k[v]$, which contradicts the fact that the color index of v is k.

We are left with the case that v is colored with $c_k$. Because of the second if-condition in the algorithm, a vertex can only get color $c_k$ if there is no vertex in $I_2$ colored with $c_k$, so in particular no neighbor of v is colored with $c_k$.$\square$

The following claim captures an idea behind maintaining the first two palettes of colors (the $a_i$’s and $b_i$’s). Namely, to force a single $a_i$-color to be mixed we need to introduce a vertex merging two components. This idea is already present in previous works [2, 3].

Claim 5

Suppose an adversary presents a bipartite graph G to Algorithm 1. Let $v\in V(G)$ and let x, y be two vertices from opposite sides of $C_{i}[v]$ both colored with $a_i$ for some $i\geqslant 1$. Then x and y lie in different connected components of $C_{i}(v)$.

Proof

Let v, x and y be like in the statement of the claim. We are going to prove that at any moment after the introduction of x and y, both x and y lie in different connected components of the subgraph spanned by vertices colored with $a_1,b_1,c_1,\ldots ,a_i,b_i,c_i$.

Say x is presented before y. We claim that $x\not \in C_i[y]$. If not, then x and y are on opposite sides in $C_i[y]$ (because, by assumption, they are on opposite sides in $C_i[v]$). Therefore, when Algorithm 1 is processing vertex y then the first if-condition is satisfied because of $\mathrm{color}(x)=a_i$, and hence y would have received color $b_i$. This is a contradiction to our assumptions and shows $x\not \in C_i[y]$.

Now consider any vertex w presented after y and suppose the statement is true before w is introduced. If $x\not \in C_i[w]$ or $y\not \in C_i[w]$ then whatever color is used for w this vertex does not merge the components of x and y in the subgraph spanned by vertices presented so far and colored with $a_1,b_1,c_1,\ldots ,a_i,b_i,c_i$. Otherwise $x,y\in C_i[w]$. This means that color $a_{i}$ is mixed in $C_i[w]$ and therefore w receives a color with an index at least $i+1$. Thus, the subgraph spanned by the vertices of the colors $a_1,b_1,c_1,\ldots ,a_i,b_i,c_i$ stays the same and x and y remain in different connected components of this graph.

Since all vertices in $C_i(v)$ are colored with $a_1,b_1,c_1,\ldots ,a_i,b_i,c_i$, we conclude that x and y lie in different components of $C_i(v)$.$\square$

We proceed with some useful definitions. Figure 2 provides an illustration of them and is also helpful to understand upcoming proofs.

Fig. 2

The top and the bottom sides are the two color classes of G. Suppose that vertex v has color index k and the figure depicts the structure of $C_{k-1}[v]$. Vertices $v_1$ and $v_2$ are the children of v and hence they lie on different sides and are colored with $a_{k-1}$. Note that removing v from $C_{k-1}[v]$ disconnects $C_{k-1}^{v_1}(v)$ and $C_{k-1}^{v_2}(v)$

Consider a vertex v with a color index $k\geqslant 2$. Let $v_1,v_2$ be the earliest introduced vertices from the opposite sides of $C_{k-1}(v)$ colored with $a_{k-1}$ (so witnessing that $a_{k-1}$ is mixed). We call $v_1$ and $v_2$ the children of v. By Claim 5 it follows that $C_{k-1}^{v_1}(v)$ and $C_{k-1}^{v_2}(v)$ are distinct, and hence they are disjoint and no edge is connecting them. In other words, v is merging the components $C_{k-1}^{v_1}(v)$ and $C_{k-1}^{v_2}(v)$.

Somehow, an intermediate goal on our way to find a large forcing structure is to find a vertex that is universal to two large and well-structured components. E.g., under the assumption that the graph is $P_6$-free, it would be straightforward to verify that v is universal to both $C_{k-1}^{v_1}(v)$ and $C_{k-1}^{v_2}(v)$. In the case of $P_9$-free graphs we have to elaborate a bit more to see vertices that are universal to appropriate large components. For each $i\geqslant 1$ and vertex x in $C_i(v)$, let $C_i^x[v]=C_i^x(v)\cup \left\{ v\right\}$ denote the component of $C_i(v)$ that contains x together with vertex v.

Suppose that an adversary presents a graph G which is $P_9$-free. Consider $v\in V(G)$ with color index $k\geqslant 3$, and let $v_1$ and $v_2$ be children of v. Note that at least one of $C_{k-1}^{v_1}[v]$ and $C_{k-1}^{v_2}[v]$ does not contain an induced $P_5$ with one endpoint in v. Indeed, the join of two such paths at v would end up in an induced $P_9$, which is forbidden in G. Choose (arbitrarily) $i\in \left\{ 1,2\right\}$ such that the component $C_{k-1}^{v_i}[v]$ has no induced $P_5$ ending at v, and let $v_{i,1},v_{i,2}$ be the children of $v_i$. We call $v_{i,1}$ and $v_{i,2}$ the grandchildren of v.

The next claim describes a property of a component containing grandchildren of a given vertex, namely, that under certain conditions we win a universal vertex to a subcomponent. The way our algorithm uses the third palette of colors, the $c_i$’s, is inspired by this property.

Claim 6

Suppose an adversary presents a bipartite graph G to Algorithm 1. Let x be a vertex with color index $i\geqslant 2$. Suppose that vertex $y\in C_{i-1}(x)$, with color index j, lies on the other side of x in G and y is not adjacent to x. If there is no induced path on 5 vertices in $C^y_{i-1}[x]$ with one endpoint in x, then x has a neighbor in $C^y_{i-1}(x)$ that is universal to $C_{j-1}[y]$.

Fig. 3

Claim 6: situation in which x has a neighbor z in $C_{j-1}[y]$

Proof

We can assume that y has color index $j\geqslant 2$, as otherwise $C_{j-1}[y]=C_0[y]=\left\{ y\right\}$ and vacuously any neighbor w of x is universal to $C_{j-1}[y]$, since w and y are on the same side and hence the side of $C_{j-1}[y]$ that w should be adjacent to is empty.

Suppose for contradiction that x has a neighbor z in $C_{j-1}[y]\subseteq C_{i-1}^y(x)$ (see Fig. 3). Since x and y are not adjacent we have $y\ne z$. As $C^z_{j-1}[y]$ is connected, there is an induced path P connecting x and y that has only vertices of $C^z_{j-1}(y)$ as inner vertices. Clearly, P is a path on at least 4 vertices. Now the color index of y, namely $j\geqslant 2$, assures from Algorithm 1 the existence of a mixed pair colored with $a_{j-1}$ in $C_{j-1}[y]$ and with Claim 5 it follows that $C_{j-1}(y)$ has at least two connected components. In particular, there is a component $C'$ of $C_{j-1}(y)$ other than $C^z_{j-1}(y)$. Clearly, y has a neighbor $z'$ in $C'$, which we use to extend P at y. Since there is no edge between $C^z_{j-1}(y)$ and $C'$, vertex $z'$ is not adjacent to the inner vertices of P. And as G is bipartite $z'$ cannot be adjacent to x. We conclude the existence of an induced path on at least 5 vertices in $C^y_{i-1}[x]$ with x and $z'$ being its endpoints, a contradiction.

So it may be assumed that x has no neighbor in $C_{j-1}[y]$. Together with our assumptions a shortest path connecting x and y in $C_{i-1}^y[x]$ contains exactly 4 vertices. Let $P=(x,r,s,y)$ be such a path. We claim that vertex r is universal to $C_{j-1}[y]$. Suppose to the contrary that there is a vertex $s'$ in $C_{j-1}[y]$ which is on the other side of y and which is not adjacent to r. Let $Q=(y,s_1,r_1,\ldots ,s_{\ell -1},r_{\ell -1},s_{\ell }=s')$ be a shortest path connecting y and $s'$ in $C_{j-1}[y]$. For convenience put $s_0=s$. Now we choose the minimal $m\geqslant 0$ such that r is adjacent to $s_m$ but not to $s_{m+1}$. Such an m exists since r is adjacent to $s_0=s$ but not to $s_{\ell }$. If $m=0$ then the path $(x,r,s,y,s_1)$ is an induced path on 5 vertices, and if $m>0$ then the path $(x,r,s_m,r_m,s_{m+1})$ contains 5 vertices and is induced unless x and $r_m$ are adjacent. But the latter is not possible since x has no neighbor in $C_{j-1}[y]$. Thus, in both cases we get a contradiction and we conclude that r is universal to $C_{j-1}[y]$. $\square$

In the following we write $v\rightarrow _i w$ for $v,w\in V(G)$, if there is a sequence $v=x_1,\ldots ,x_j=w$ with $j\leqslant i$, such that $x_{\ell +1}$ is a grandchild of $x_{\ell }$ for all $\ell \in \left\{ 1,\ldots ,j-1\right\}$. Moreover, we define $S_i(v)=\left\{ w\in V(G)\mid v\rightarrow _i w\right\}$. Thus, $S_1(v)=\left\{ v\right\}$ for every $v\in V(G)$.

We make some immediate observations concerning this definition. Let $v\in V(G)$ be a vertex with color index $k\geqslant 3$. Then each $w\in S_i(v)$ has color index at least $k-2i+2$ (this can be proved by induction on i) and the graph $C_{k-1}^w[v]$ does not contain an induced $P_5$ with one endpoint in v (this follows by definition). Furthermore, each vertex in $S_i(v)$ is connected to v by a path in G and all vertices in the path, except v, have color index at most $k-1$. This proves that $S_i(v) \subseteq C_{k-1}[v]$, for all $i\geqslant 1$. Note also that if $v_1$ and $v_2$ are the grandchildren of v then we have $S_i(v)=\left\{ v\right\} \cup S_{i-1}(v_1) \cup S_{i-1}(v_2)$. By definition $v_1$ and $v_2$ are the children of a child $v'$ of v. It follows that $S_{i-1}(v_1)\subseteq C_{k-2}^{v_1}(v')$ and $S_{i-1}(v_2)\subseteq C_{k-2}^{v_2}(v')$. By Claim 5, we get that $C_{k-2}^{v_1}(v')$ and $C_{k-2}^{v_2}(v')$ are distinct. In particular, $S_{i-1}(v_1)$ and $S_{i-1}(v_2)$ are disjoint and there is no edge between them.

For a vertex $v\in V(G)$, $S_{i}(v)$ is complete in G if for every $u,w\in S_i(v)$ such that $u\rightarrow _i w$ and u, w lying on opposite sides of G, we have u and w being adjacent in G. Note that v is a universal vertex in $S_i(v)$, provided $S_i(v)$ is complete.$\square$

Claim 7

Suppose an adversary presents a bipartite graph G to Algorithm 1. Let $v\in V(G)$ be a vertex with color index k and let $k\geqslant 2i \geqslant 2$. If $S_{i}(v)$ is complete then $S_{i}(v)$ contains an induced copy of $X_{i}$ in G with v being the root of the copy.

Proof

We prove the claim by induction on i. For $i=1$ we work with $S_1(v)$ and $X_1$ being graphs with one vertex only, so the statement is trivial. For $i\geqslant 2$, let $v_1$ and $v_2$ be the grandchildren of v. Recall that $S_i(v)=\{v\}\cup S_{i-1}(v_1)\cup S_{i-1}(v_2)$. Since $S_i(v)$ is complete it also follows that $S_{i-1}(v_1)$ and $S_{i-1}(v_2)$ are complete. So by the induction hypothesis there are induced copies $X_{i-1}^1$, $X_{i-1}^2$ of $X_{i-1}$ in $S_{i-1}(v_1)$ and $S_{i-1}(v_2)$, respectively, and rooted in $v_1$ and $v_2$, respectively. Recall that $S_{i-1}(v_1)$ and $S_{i-1}(v_2)$ are disjoint and there is no edge between them. Thus, the copies $X_{i-1}^1$ and $X_{i-1}^2$ of $X_{i-1}$ are disjoint and there is no edge between them, as well. Since $S_i(v)$ is complete v is universal to both of the copies, and since by definition $v_1$ and $v_2$ lie on opposite sides in G we get that the vertices of $X_{i-1}^1 \cup X_{i-1}^2 \cup \left\{ v\right\}$ induce a copy of $X_i$ in G.$\square$

Claim 8

Suppose an adversary presents a $P_9$-free bipartite graph G to Algorithm 1 and suppose vertex v is colored with $a_{k}$ for some $k\geqslant 2$. Then $C_{k}[v]$ contains an induced copy of $X_{\lfloor \sqrt{k/2}\rfloor }$ such that its root lies on the same side as v in G.

Proof

We prove the claim by induction on k. For $k=2$ the statement is trivial. So suppose that $k\geqslant 3$. If $S_{\lfloor \sqrt{k/2}\rfloor }(v)$ is complete then by Claim 7 we get an induced copy of $X_{\lfloor \sqrt{k/2}\rfloor }$ with a root mapped to v, as required.

From now on we assume that $S_{\lfloor \sqrt{k/2}\rfloor }(v)$ is not complete. Let $(I_1,I_2)$ be the bipartition of $C_{k}[v]$ such that $v\in I_1$. First, we will prove that there are vertices $z,z'\in C_{k}[v]$ such that $z'\in I_1$, z has color index $\ell \geqslant k-\sqrt{2k}+2$, and $z'$ is universal to $C_{\ell -1}[z]$. To do so we consider the reason why Algorithm 1 colors v with $a_{k}$.

The first possibility is that the second if-condition of the algorithm is satisfied, that is, there is a vertex $u\in I_2$ colored with $c_{k}$. Now from the third if-condition u can only receive color $c_{k}$ if there are vertices $w, w'\in C_{k}[u]$ such that $w'$ is on the other side of u in $C_{k}[u]$, w has color index $j\geqslant k-\sqrt{2k}+2$, and $w'$ is universal to $C_{j-1}[w]$. Since $C_{k}(u)\subseteq C_{k}(v)$ and $u\in I_2$ we have $w'\in I_1$. Therefore, $z=w$ and $z'=w'$ are the vertices we are looking for.

The second reason for coloring v with $a_{k}$ could be that Algorithm 1 reaches its last line. In particular this means, that there is no vertex of color $a_{k}$ or $c_{k}$ in $I_2$. Now we are going to make use of the fact that $S_{\lfloor \sqrt{k/2}\rfloor }(v)$ is not complete. There are vertices $x,y\in S_{\lfloor \sqrt{k/2}\rfloor }(v)\subseteq C_{k}[v]$ such that $x\rightarrow _{\lfloor \sqrt{k/2}\rfloor } y$, the vertices x and y lie on different sides of $C_{k}[v]$ and are not adjacent. Let i and j be the color indices of x and y, respectively. Note that $k\geqslant i > j\geqslant k-2\lfloor \sqrt{k/2}\rfloor +2$. By the definition of a grandchild it follows that $C_{i-1}^y[x]$ does not contain an induced $P_5$ with one endpoint in x. Hence we can apply Claim 6 and it follows that x has a neighbor $r\in C_{i-1}^y(x)$ that is universal to $C_{j-1}[y]$. We set $z'=r$ and $z=y$. Then, we have that $z'$ is universal to $C_{j-1}[z]$ with

$$\begin{aligned} j \geqslant k-2\lfloor \sqrt{k/2}\rfloor +2\geqslant k-\sqrt{2k}+2. \end{aligned}$$

Since $z'\in C_k[v]$ we have $z'\in I_1$ or $z'\in I_2$. However, the latter is not possible as then z and $z'$ would fulfill the conditions of the third if-statement in Algorithm 1, which contradicts the fact that Algorithm 1 reached the last line while processing v. We conclude that $z'\in I_1$, which completes the proof of our subclaim.

Now fix $z,z'$ witnessing our subclaim. Let $z_1$ and $z_2$ be the children of z. Both vertices received color $a_{\ell -1}$ and they are on different sides of G. By the induction hypothesis $C_{\ell -1}[z_1]$ and $C_{\ell -1}[z_2]$ each contain a copy of $X_{\lfloor \sqrt{(\ell -1)/2}\rfloor }$ such that the roots are on the same side as $z_1$ and $z_2$, respectively. Since there is no edge between $C_{\ell -1}[z_1]$ and $C_{\ell -1}[z_2]$ (this is a consequence of Claim 5) and both are contained in $C_{\ell -1}[z]$, it follows that $z'$ together with the copies of $X_{\lfloor \sqrt{(\ell -1)/2}\rfloor }$ induce a copy of $X_{\lfloor \sqrt{(\ell -1)/2}\rfloor +1}$ that has $z'$ as its root (see Fig. 4). Since $C_{\ell -1}[z]$ is contained in $C_{k}[v]$ and $z'$ is on the same side as v and since

$$\begin{aligned} \lfloor \sqrt{(\ell -1)/2}\rfloor +1\geqslant \left\lfloor \sqrt{(k-\sqrt{2k}+1)/2}\right\rfloor +1\geqslant \left\lfloor \sqrt{k/2-\sqrt{k/2}}\right\rfloor +1\geqslant \left\lfloor \sqrt{k/2}\right\rfloor , \end{aligned}$$

for all $k\geqslant 0$, the proof is complete.$\square$

Fig. 4

Final step in Claim 8. The value m stands for $\lfloor \sqrt{(\ell -1)/2}\rfloor$

Now we are able to prove our main theorem.

Proof

(of Theorem 1) Let k be the largest color index used by Algorithm 1 while coloring vertices of G. In particular, Algorithm 1 uses at most 3k colors for G. If $k=1$ then the statement is obvious. Suppose $k\geqslant 2$. There must be a vertex in G colored with $a_k$. By Claim 8 it follows that G contains $X_{\lfloor \sqrt{k/2}\rfloor }$ and by Claim 3, $\chi _*(G)\geqslant \lfloor \sqrt{k/2}\rfloor \geqslant \sqrt{k/2} -1$. This together with $3k= 6(\sqrt{k/2}-1+1)^2\leqslant 6(\chi _*(G)+1)^2$ completes the proof.$\square$