Advertisement

Archive of Applied Mechanics

, Volume 87, Issue 5, pp 881–892 | Cite as

Transverse vibrations of a beam under an axial load: minimal model of a triangular frame

  • Paweł FritzkowskiEmail author
Open Access
Special
First Online:

Abstract

The paper is devoted to transverse in-plane vibrations of a beam which is a part of a symmetrical triangular frame. A mathematical model based on the Hamilton principle, formulated for large deflections of the beam subjected to dynamic axial excitation, is presented. An approximate nonlinear ordinary differential equation for the vibration amplitude is derived by means of the Galerkin method. Dynamics of the system is studied numerically for the two cases: harmonic and pulsating load. Various values of the model parameters, including the excitation amplitude and frequency, are considered. The amplitude is taken to be below or above the static critical load. The regions of stable and unstable solutions are determined in parameter planes by evaluation of the maximal Lyapunov exponent. The results are compared to the case of the abbreviated (linear) dynamical system. The stable and unstable beam responses are analysed and classified.

Keywords

Triangular frame Nonlinear vibrations Dynamic stability Time-periodic systems 

1 Introduction

Behaviour of elastic structures like beams/columns under axial loads is a classical problem, studied mainly in the context of static or dynamic stability. Timoshenko and Gere [21] discussed elastic buckling of a wide variety of structural elements, including bars and frames. An extensive review of stability problems was presented by Bažant and Cedolin [2]. Virgin [23] focused attention on the interplay between vibrations and stability in axially loaded structures. Parametrically excited systems of this type, described by linear or nonlinear time-periodic models, were considered by McLachlan [17], Gutowski and Swietlicki [8], and Łuczko [13]. The general theory of dynamic stability of elastic structures and its applications were presented by Bolotin [4].

This paper is devoted to nonlinear vibrations of a beam which is a part of a symmetrical triangular frame. Recently, Magnucki and Milecki [14] studied static buckling of such a system. However, closed planar frames, including the triangular ones, are rarely analysed in the literature related to the field of dynamics. Moreover, vibrational problems for frame structures are usually solved by using the finite element approach (e.g. see [22, 24]). In what follows, the cross-beam of the triangular frame is appropriately isolated from the system, which simplifies both the model and analysis.

The work is an extension of the conference paper [7]. In Sect. 2, a minimal mathematical model for vibration of the triangular frame is formulated. Section 3 begins with a short discussion of a parametric and nonlinear character of the system in terms of analytical methods. Then, the results of numerical studies for harmonic and pulsating loads are presented. Finally, conclusions and remarks are given in Sect. 4.

2 Mathematical model

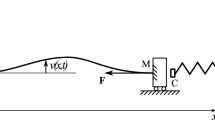
Consider a symmetrical triangular frame (see Fig. 1a) whose arms (1) of length \(L_1\) are connected via a cross-beam (2) of length \(L_2\). The arms have a rectangular cross section (\(b \times c\)). The cross section of the beam, in turn, has the shape of a circular ring: its outer and inner diameters are denoted by \(d_1\) and \(d_0\), respectively. The vertex C of the frame is fixed while the others, A and B, are simply supported out-of-plane and subjected to in-plane load.
Fig. 1

Mechanical system to be considered: a the full triangular frame, b the cross-beam isolated from the system

Such a system can be regarded as a simple representation of a brake triangle that has been produced on a large scale for the railway industry. It is an important component of bogie brake systems suitable for various types of wagons. The triangle transmits the braking force from a brake cylinder to brake pads that, in turn, mate with rail wheels [15].

In paper by Magnucki and Milecki [14], one can find, among others, the relations between the internal forces in the cross-beam, i.e. the axial force \(N_2\) and the bending moment \(M_{b2}\), and the load F. Now, in-plane vibrations of the system are considered, i.e. the load is assumed to be a function of time, \(F = F(t)\). To simplify dynamic analysis, the beam is isolated from the structure as can be seen in Fig. 1b. The beam is treated as simply supported but subjected to the axial force \(N_2(t)\) and opposite end moments \(M_{2}(t)\). For simplicity energy dissipation is neglected.

Behaviour of the beam is described by the transverse deflection \(w(x,\, t)\). The axial displacement of a given point is \(u(x,\, z,\, t)\), where z denotes the distance from the neutral surface. A small element of the beam is illustrated in Fig. 2. In order to describe vibrations of the system, we take an approximate energy approach.

In case of large deflections, the normal strain can be written as
$$\begin{aligned} \varepsilon _{x} = \frac{\partial u}{\partial x} + \frac{1}{2}\left( \frac{\partial w}{\partial x} \right) ^2 \qquad \text {with}\quad u= -z \frac{\partial w}{\partial x}\,. \end{aligned}$$
(1)
For a linearly elastic material, the strain energy of the system is given by
$$\begin{aligned} U = \frac{1}{2} E \int \limits _{0}^{L_2} \int \limits _{A_2} \varepsilon _{x}^2\, \text {d}A_2\, \text {d}x = \frac{1}{2} E \int \limits _{0}^{L_2} \left[ J_{y2} \left( \frac{\partial ^2 w}{\partial x^2} \right) ^2 + \frac{1}{4} A_2 \left( \frac{\partial w}{\partial x} \right) ^4 \right] \, \text {d}x\,, \end{aligned}$$
(2)
in which E is Young’s modulus and
$$\begin{aligned} A_2 = \frac{\pi }{4} (d_1^2 - d_0^2),\qquad J_{y2} = \frac{\pi }{64} (d_1^4 - d_0^4) \end{aligned}$$
(3)
are the area of the cross section and its moment of inertia about the neutral axis. It is assumed that the rotary inertia of the beam can be neglected, thus the kinetic energy has the form
$$\begin{aligned} T = \frac{1}{2} \rho A_2 \int \limits _{0}^{L_2} \left( \frac{\partial w}{\partial t} \right) ^2 \, \text {d}x\,, \end{aligned}$$
(4)
where \(\rho \) denotes the material density. Finally, the work done by the load is expressed as
$$\begin{aligned} W = N_2(t) \int \limits _{0}^{L_2/2} \left( \frac{\partial w}{\partial x} \right) ^2 \, \text {d}x \end{aligned}$$
(5)
Note that the effect of the moments \(M_{2}\) are not included at this stage. The application of Hamilton’s principle
$$\begin{aligned} \delta \int \limits _{t_1}^{t_2} (T - U + W)\, \text {d}t = 0 \end{aligned}$$
(6)
leads to the following partial differential equation of the transverse beam motion:
$$\begin{aligned} \rho A_2 \frac{\partial ^2 w}{\partial t^2} + EJ_{y2} \frac{\partial ^{4} w}{\partial x^{4}} + N_2(t) \frac{\partial ^2 w}{\partial x^2} - \frac{3}{2} EA_2 \left( \frac{\partial w}{\partial x} \right) ^2 \frac{\partial ^2 w}{\partial x^2} = 0 \end{aligned}$$
(7)
The first three terms of this equation are the same as in case of the linear model based on the Euler–Bernoulli beam theory (see [2, 12, 20, 23]), while the last term results from the geometric nonlinearity included in Eq. (1).
We restrict our attention to the first mode of vibration, hence the deflection is approximated by
$$\begin{aligned} w(x,\, t)= w_a(t)\,\varphi (x) \end{aligned}$$
(8)
where \(w_a(t)\) is the modal amplitude, and \(\varphi (x)\) is the mode shape function assumed to have the form
$$\begin{aligned} \varphi (x) = \frac{1}{1+\alpha _0} \left[ \sin \left( \pi \frac{x}{L_2} \right) - \alpha _0\sin \left( 3\pi \frac{x}{L_2} \right) \right] . \end{aligned}$$
(9)
Such a mode shape allows to incorporate (indirectly) into the model the effect of the end moments \(M_{2}\). The parameter \(\alpha _0\) will be further specified as a function of other characteristics of the system. For the triangular frame member \(\alpha _0 > 0\), while the special case \(\alpha _0 = 0\) corresponds to a simply supported beam (see Fig. 3).
Fig. 2

Beam under planar deflection

Using the classical Galerkin method, we obtain the approximate equation of motion for the modal amplitude:
$$\begin{aligned} \ddot{q} + c_1 \left[ 1 - \widetilde{N}_2(t) \right] q+ c_3 q^3 = 0\,, \end{aligned}$$
(10)
where \(q= w_a/d_1\) and \(\widetilde{N}_2\) is the relative (dimensionless) axial force. The coefficients \(c_1\) and \(c_3\) are dependent on the beam parameters, and can be determined by considering the static case (\(\ddot{q} = 0\)) and the relationships given in [14]:
$$\begin{aligned} c_1= \frac{1+9\alpha _0^2}{1+\alpha _0^2}\, \frac{\pi ^2}{\rho A_2 L_2^2} N_{2\text {cr}}\,, \qquad c_3= \frac{3}{8}\, \frac{1-4\alpha _0+ 36\alpha _0^2 + 81\alpha _0^4}{(1+\alpha _0)^2(1+\alpha _0^2)}\, \frac{\pi ^4 E d_1^2}{\rho L_2^4}\,, \end{aligned}$$
(11)
where
$$\begin{aligned} \alpha _0= \frac{1}{3} \sqrt{\frac{\kappa -1}{9-\kappa }}\,,\qquad \kappa = \frac{N_{2\text {cr}}}{N_{2\text {cr}}^{\text {E}}}\,,\qquad N_{2\text {cr}}^{\text {E}}= \frac{\pi ^2 E J_{y2}}{L_2^2}\,. \end{aligned}$$
(12)
Note that \(N_{2\text {cr}}^{\text {E}}\) is the Euler critical axial load for a beam/column, while \(N_{2\text {cr}}\) is the critical force that corresponds to the static critical load \(F_{\text {cr}}\) calculated for the triangular frame. The quantity \(\widetilde{N}_2\) in Eq. (10) is normalized just by \(N_{2\text {cr}}\), that is, \(\widetilde{N}_2(t) = N_2(t)/N_{2\text {cr}}\).
Fig. 3

Mode shape function for various values of \(\alpha _0\)

In the examples below, we suppose that \(\widetilde{N}_2(t)\) is a periodic function:
$$\begin{aligned} \widetilde{N}_2(t) = \widetilde{N}_2(t+T^{*}) \end{aligned}$$
(13)
where \(T^{*}= 2\pi /\omega \). It is convenient to introduce the dimensionless quantities:
$$\begin{aligned} \tau = \omega _1 t\,,\qquad \varOmega = \omega /\omega _1\,,\qquad \gamma = c_3/c_1\,, \end{aligned}$$
(14)
where \(\omega _1 = \sqrt{c_1}\) is the first natural frequency of a load-free beam. Finally, Eq. (10) can be rewritten as
$$\begin{aligned} \ddot{q} + \left[ 1 - \widetilde{N}_2(\tau ) \right] q+ \gamma q^3 = 0 \end{aligned}$$
(15)
Now \(q= q(\tau )\), an overdot denotes differentiation with respect to \(\tau \), and \(\widetilde{N}_2(\tau )\) is periodic with a period \(T = \omega _1 T^{*}= 2\pi /\varOmega \). Thus, the fully nondimensionalized ordinary differential equation (15) takes a form of the well-known Hill’s equation enriched with a nonlinear term of the Duffing type. This discrete system can be treated as a minimal model for vibrations of the triangular frame, focused on its neuralgic member, i.e. the cross-beam.

3 Numerical studies of the nonlinear system

3.1 Remarks on analytical treatment of nonlinear time-periodic ODEs

The single approximate governing equation (15) seems to have a quite simple form. However, it combines two fundamental features that considerably complicate solving the problem analytically. Firstly, the model is an ODE with a time-periodic coefficient, i.e. a parametrically excited system. Secondly, it includes a strong nonlinearity.

For the last decades, especially since 1950s, extensive efforts have been undertaken in the area of linear parametric systems, where the Floquet theory plays the central role. In particular, due to its usefullness in many physical problems, the Mathieu equation
$$\begin{aligned} \ddot{q} + \left( \omega _0^2 + \varepsilon \cos {t} \right) q = 0 \end{aligned}$$
(16)
has been studied thoroughly and elucidated. Various methods have been employed to investigate stability of steady-state solutions. The stability boundaries can be approximated by using, among others, i) infinite Hill’s determinant, the harmonic balance method, or ii) perturbation methods (e.g. the Lindstedt–Poincaré technique, the method of multiple scales) [2, 3, 4, 5, 8, 17, 18]. The second approach requires the assumption that the time-varying coefficient is relatively small (\(\varepsilon \ll 1\)). In the context of beams under axial excitation, the Mathieu-Hill type equations are analysed, for instance, in [9, 10, 23].
Today there exist a number of approximate analytical solution procedures applicable to nonlinear dynamical systems (see [1, 6, 18]). Nevertheless, the vast majority of them take their roots from the classical perturbation approach (e.g. the averaging methods, the Krylov-Bogolubov-Mitropolskij method, the method of multiple scales, the homotopy perturbation method, etc.). Thus, the techniques work well in case of weakly nonlinear oscillators
$$\begin{aligned} \ddot{q} + \omega _0^2 q = \varepsilon Q(t,\, q,\, \dot{q}), \end{aligned}$$
(17)
when the so-called small parameter \(\varepsilon \ll 1\) can be associated with the nonlinear part Q of the governing equation. In recent years, some analytical methods for strongly nonlinear systems have been developed, too (e.g. the modified/adopted Lindstedt–Poincaré method or homotopy method). Usually, they are suited to certain type of nonlinearity only and are not generally applicable [6, 16].

As will be seen further, from practical viewpoint Eq. (15) cannot be considered to contain the small perturbation parameter. In other words, the influence of both the cubic and time-periodic terms is rather strong. Due to limitations of the most of analytical methods and for convenience reasons, character of our studies is almost purely numerical.

3.2 Vibrations under harmonic load

We focus attention on a symmetrical triangular frame with the parameter values given in Table 1. This particular set of values is used in the railway industry. The area of the arms’ cross section, \(A_1\), is constant, while the dimension b (and \(c = A_1/b\)) will be altered.
Table 1

Basic values of parameters used in numerical simulations

Parameter

Value

Unit

Beam length, \(L_2\)

1352

mm

Inner diameter, \(d_0\)

50

mm

Outer diameter, \(d_1\)

60

mm

Area of the cross section of the arms, \(A_1\)

1000

mm\(^2\)

Angle between the arms and cross-beam, \(\alpha \)

\(\pi /9\)

rad

Young’s modulus, E

\(2\times 10^5\)

MPa

Density, \(\rho \)

7850

\(\hbox {kg/m}^3\)

In engineering practice, the width of the arms is one of the most important parameters. In the static case, for example, flat buckling of the triangular frame can occur for small values of b (at the given data: \(b \le 18\) mm); otherwise, the system undergoes lateral buckling [14]. As presented in Fig. 4, the static critical load of the beam, \(N_{2\text {cr}}\), increases with increasing b. At the same time, such a strengthening of the arms in respect of in-plane bending decreases the coefficient of the cubic term, \(\gamma \). The question is how it affects the dynamics of the beam.
Fig. 4

Effect of the dimension b on: a the critical axial load, b the coefficient \(\gamma \)

First, we assume that the structure is subjected to harmonic load and the relative axial force on the cross-beam is \(\widetilde{N}_2(t) = a\sin (\omega t)\) with \(\omega = 2\pi f\). Consequently, the initial value problem under consideration is
$$\begin{aligned}&\ddot{q} + \left[ 1 - a\sin (\varOmega t) \right] q+ \gamma q^3 = 0 \end{aligned}$$
(18)
$$\begin{aligned}&q(0)= \varepsilon _{0}\,,\qquad \dot{q}(0) = 0 \,. \end{aligned}$$
(19)
The quantity \(\varepsilon _{0}\) can be regarded as the relative amplitude of the beam imperfection.
Fig. 5

Results for \(b = 20\) mm: a stable (white) and unstable (shaded) regions for the beam, b maximal value of the quantity \(X_{\text {rel}}\); black lines depict stability boundaries of the linear system

Initially, the results obtained for \(b = 20\) mm are presented (\(\gamma \approx 1.69\)); suppose that the imperfection amplitude \(\varepsilon _{0}= 10^{-3}\). Figure 5a shows the parameter plane \((\varOmega ,\, a)\) with regions of stable and unstable motion of the system. More precisely, the areas filled with grey relate to positive values of the maximal Lyapunov exponent (MLE), \(\lambda _{1}\). The map has been computed with steps \(\Delta f = 1\) Hz and \(\Delta a = 0.1\). The Lyapunov exponents have been evaluated using the Gram-Schmidt orthogonalization procedure and renormalization [13, 19]. Taking into account relatively slow convergence of the numerical computations in the analysed undamped case, vibrations are classified as chaotic if \(\lambda _{1}\ge \varepsilon _{1}\), where \(\varepsilon _{1}\) is a small positive value (here \(\varepsilon _{1}= 0.02\)).

For comparison purposes, stability boundaries for the abbreviated system (\(\gamma = 0\)) are shown. The transition curves correspond to 1T-periodic (solid line) and 2T-periodic solutions (dashed line) [4, 8, 17]. Here, the dependencies \(a(\varOmega )\) have been determined by means of the Rayleigh method that, in fact, is a variant of the harmonic balance method. The steady-state solutions are assumed to have the forms [8]:
$$\begin{aligned} q_{1}(\tau ) = B_0 + C_2 \sin (\varOmega \tau ) + D_2 \cos (\varOmega \tau ) + C_4 \sin (2\varOmega \tau ) + D_4 \cos (2\varOmega \tau ) \end{aligned}$$
(20)
and
$$\begin{aligned} q_{2}(\tau ) = C_1 \sin \left( \frac{\varOmega }{2} \tau \right) + D_1 \cos \left( \frac{\varOmega }{2} \tau \right) + C_3 \sin \left( \frac{3\varOmega }{2} \tau \right) + D_3 \cos \left( \frac{3\varOmega }{2} \tau \right) \end{aligned}$$
(21)
As can be seen, the numerical results based on the nonlinear model fit well into the instability tongues for the linear system. However, these two cases are not fully comparable. Unstable solutions of the Hill equation (or the Mathieu equation) increase unboundedly with time, while the nonlinear term \(\gamma q^3\) causes amplitude limitation [17]. Thus, deflections of the beam may become very large but remain bounded.
Fig. 6

Stable (white) and unstable (shaded) regions for the beam (\(b = 50\) mm) and stability boundaries of the linear system

Fig. 7

Results for \(b = 20\) mm: a stable (white) and unstable (shaded) regions for the beam, b values of the maximal Lyapunov exponent

Fig. 8

Location of selected points in \((\varOmega ,\, a)\) plane for the cases shown in Fig. 9: \(A = (1.6;\, 0.3), B = (1.6;\, 1), C = (1.6;\, 2), D = (1.6;\, 3)\)

Fig. 9

Phase portraits for \(\varOmega = 1.6: \mathbf{a}~a=0.3, \mathbf{b}~a=1, \mathbf{c}~a=2, \mathbf{d}~a=3\)

This type of behaviour can be detected by analysis of the displacement and velocity amplitudes. Let \(\mathbf {X} = [q,\, \dot{q}]^\text {T}\) be the state vector of the system. Character of the system evolution can be assessed, for example, by the measure
$$\begin{aligned} X_{\text {rel}}(\tau ) = \frac{\Vert \mathbf {X}(\tau ) \Vert }{\Vert \mathbf {X}(0) \Vert }\,, \end{aligned}$$
(22)
where \(\Vert \cdot \Vert \) denotes the Euclidean norm. The maximal values of \(X_{\text {rel}}(\tau )\) found in the range \(0 \le \tau \le 5\times 10^4\) are plotted in Fig. 5b. The contour line corresponding to \(X_{\text {rel}}= 100\) coincides largely with the curves \(a(\varOmega )\), especially for lower a. As the load amplitude increases, \(X_{\text {rel}}\) grows significantly but does not exceed \(4\times 10^4\).
As results from Fig. 5a, there are scattered subregions of regular motion for \(a > 1\), above the curves corresponding to the linear system. In fact, quasi-periodic and almost periodic vibrations can be easily found there.
Fig. 10

Frequency spectra for \(\varOmega = 1.6: \mathbf{a}~a=0.3, \mathbf{b}~a=1, \mathbf{c}~a=2, \mathbf{d}~a=3\)

Fig. 11

System response for \(\varOmega = 1.6\): a stable vibrations (\(a=0.3\)), b unstable vibrations (\(a=1\))

By analogy to Fig. 5, a stability diagram for \(b = 50\) mm (\(\gamma \approx 1.14\)) is shown in Fig. 6. As in the previous case, the critical value of \(\lambda _{1}\) has been set to 0.02. Again the lower contour of the unstable region is quite well approximated by the curves determined analytically for the linear system. Nevertheless, it seems that an increase in b gradually enlarges the scattered regions indicating regular dynamics and shifts them towards lower values of both the load amplitude and frequency.

More detailed analysis of numerical solutions is presented in the next subsection.

3.3 Vibrations under pulsating load

The example of harmonic load is convenient for confrontation of the results with the classical linear case. Nevertheless, the minimal model based on the relationships given in Ref. [14] is dedicated to a cross-beam being in compression rather than in tension. Therefore, let us assume now that the beam is subjected to a periodic compressive axial load, and the following initial value problem is considered:
$$\begin{aligned}&\ddot{q} + \left[ 1 - a\sin ^2\left( \frac{\varOmega }{2} t \right) \right] q+ \gamma q^3 = 0 \end{aligned}$$
(23)
$$\begin{aligned}&q(0)= \varepsilon _{0}\,,\qquad \dot{q}(0) = 0 \,, \end{aligned}$$
(24)
so that the period of the load is still \(T = 2\pi /\varOmega \).

In Fig. 7a, the stable and unstable regions for the beam are presented for \(b = 20\) mm (\(\lambda _{1}= 0.02, \varepsilon _{0}= 10^{-3}\)). The transition curves resulting from the simple approximation of type (20) do not occur in pairs and therefore do not form the typical tongues. However, the stability boundary with a tip at \(\varOmega = 2\) is sufficiently accurately predicted by the linear case. Unlike in the previous numerical experiment, there are no scattered subregions of stable solutions for high values of a.

To give a deeper insight into the approximate values of the maximal Lyapunov exponent, a more detailed filled contour plot is given in Fig. 7b. Each cell is a rectangle of dimensions \(\Delta \varOmega \times \Delta a\). As can be seen, there are only several single points representing \(\lambda _{1}< 0\). The stable region relates mostly to the range \(0 \le \lambda _{1}< 0.01\). The unstable region, in turn, is mainly occupied by the cells connected with evidently chaotic dynamics (\(\lambda _{1}\ge 1\)). Thus, the maps should be treated as a rather rough evaluation tool for determination of the vibration type. Naturally, this approximate character is a matter of a balance between the three factors: resolution of the map (\(\Delta \varOmega , \Delta a\)), length of the analysed time range of the system evolution, and computation time.

Selected steady-state responses of the system for \(\varOmega = 1.6\) (see Fig. 8) are illustrated in Fig. 9 in the form of phase portraits. Similar to the linear case, the stable region is dominated by aperiodic vibrations. Below and above the instability tongue (\(a = 0.3\) and \(a = 1\)) quasi-periodic motion occurs (Fig. 9a, c). In the first case, the plane phase \((q,\, \dot{q})\) is occupied by the trajectory projection so densely that the diagram constitutes an annulus. More disordered vibrations with much higher amplitudes of both the displacement and velocity can be observed within the unstable regions. The solution corresponding to \(a = 2\) is depicted in Fig. 9b, while apparently chaotic behaviour for \(a = 3\) is shown in Fig. 9d. Note that \(q > 1\) means \(w_a > d_1\), i.e. large deflections of the beam, which definitely goes beyond the classical (linear) beam theory.

The vibrations can be more precisely classified by means of the Poincaré maps and frequency spectra. The results of the application of the fast Fourier transform (FFT) are presented in Fig. 10. Here, \(\varOmega _k\) is a discrete dimensionless frequency (\(k = 0,1,2,\ldots \)), i.e. related to \(\omega _1\), whereas \(|\overline{q}_k|\) denotes the spectral magnitude. The spectra of a discrete nature with two dominating frequencies correspond to the quasi-periodic solutions (Fig. 10a, c). Presumably, these frequencies are incommensurable. The chaotic solution typically has a continuous Fourier spectrum (Fig. 10d). A similar effect occurs for the other unstable case; however, the spectral lines are concentrated over a narrower frequency range (Fig. 10b).

Instability of the latter type may require more attention. As mentioned before, the beam is excited to high amplitudes which nevertheless do not increase exponentially like in the linear system. Differences between such behaviour and the stable one are shown in Fig. 11. In the standard quasi-periodic case, the peak amplitude varies approximately sinusoidally. The unstable response undergoes another kind of modulation: the amplitude changes sharply from very low to very high values (small vs. large deflections). This beating-like phenomenon was analysed by Kidachi and Onogi [11] who studied the Mathieu equation modified by cubic nonlinearity. The researchers used the term ’pseudo-unstable state’. More precisely, such a solution is unstable in the sense that it exhibits exponential growth and decay by turns. For the same reason, the response does not escape to infinity, and the system cyclically returns to the neighbourhood of the initial state.

Comparison of the discussed results and the ones for \(b = 50\) mm indicated very slight differences in the stability diagrams and the maps of the MLE values. Also, a more detailed analysis of the MLE computed at selected levels of the amplitude a in the frequency range \(0 < \varOmega \le 2.5\), for \(10 \le b \le 90\) mm (\(\Delta b = 1\) mm) has been conducted. The effect of b on \(\lambda _{1}\) seems to be negligible; all in all, the stable and unstable ranges (at certain a) remain the same. Moreover, the results turned out to be almost insensitive to changes in the initial value, \(\varepsilon _{0}\). However, it should be noted that only relatively small imperfection amplitudes were examined (e.g. \(\varepsilon _{0}= 2\times 10^{-3},\, 5\times 10^{-3},\, 10^{-2}\)).

4 Conclusions

The problem of dynamics of the symmetrical triangular frame has been reduced to the problem of transverse parametric vibration of the cross-beam. The minimal mathematical model of the system has been formulated by means of the Hamilton principle and the Galerkin method. The time-periodic and nonlinear character of the system has been briefly discussed in terms of approximate analytical methods. The regions of stable and unstable solutions have been determined in the ’load frequency–amplitude’ plane. For harmonic axial load, the lower boundaries of the parametric instability zones are well approximated by the transition curves specified for the abbreviated system. Moreover, some scattered subregions of regular motion occur and become larger as the width of the frame arms increases. This effect is not present in the case of pulsating load. The stable regions are dominated by quasi-periodic dynamics of the nonlinear system. Within the unstable regions, in turn, the vibration amplitude of the beam increases significantly but remains bounded. The behaviour is not necessarily strictly chaotic, the pseudo-unstable states can be observed too.

This kind of analysis, focused on both the vibration type and amplitude growth, is crucial in the formulation of safety conditions for the structure, i.e. certain criteria for the so-called technical stability. However, from a practical viewpoint, the dynamic stability issue is associated mainly with behaviour of a system under suddenly applied loads (e.g. an impulse or step load). Since the problem is of great importance in the particular case of brake triangles, it merits special attention in further studies of the mechanical system.

Notes

Acknowledgments

The research has been supported by 02/21/DSMK/3457 Grant and 02/21/DSPB/3477 Grant.

References

  1. 1.
    Awrejcewicz, J., Manevitch, L.I., Andrianov, I.V.: Asymptotic Approaches in Nonlinear Dynamics: New Trends and Applications. Springer, Berlin (1998)CrossRefzbMATHGoogle Scholar
  2. 2.
    Bažant, Z.P., Cedolin, L.: Stability of Structures: Elastic, Inelastic, Fracture and Damage Theories. World Scientific, London (2010)zbMATHGoogle Scholar
  3. 3.
    Bogoliubov, N., Mitropolsky, Y.A.: Asymptotic Methods in the Theory of Non-Linear Oscillations. Gordon & Breach, New York (1961)Google Scholar
  4. 4.
    Bolotin, V.V.: The Dynamic Stability of Elastic Systems. Holden-Day, San Francisco (1964)zbMATHGoogle Scholar
  5. 5.
    Cunningham, W.J.: Introduction to Nonlinear Analysis. McGraw-Hill, New York (1958)zbMATHGoogle Scholar
  6. 6.
    Cveticanin, L.: Strongly Nonlinear Oscillators: Analytical Solutions. Springer, Cham (2014)CrossRefzbMATHGoogle Scholar
  7. 7.
    Fritzkowski, P., Magnucki, K., Milecki, S.: Nonlinear transverse vibrations of a beam under an axial load. In: Awrejcewicz, J., Kaźmierczak, M., Mrozowski, J., Olejnik, P. (eds.) Dynamical Systems: Mechatronics and Life Sciences, pp. 175–184. Łódź, Poland (2015). 13th Conference on Dynamical Systems—Theory and Applications DSTA 2015Google Scholar
  8. 8.
    Gutowski, R., Swietlicki, W.A.: Dynamics and Vibrations of Mechanical Systems. PWN, Warsaw (1986). (in Polish)Google Scholar
  9. 9.
    Huang, Y.Q., Lu, H.W., Fu, J.Y., Liu, A.R., Gu, M.: Dynamic stability of Euler beams under axial unsteady wind force. Math. Probl. Eng. 2014(4), 434,868 (2014)MathSciNetGoogle Scholar
  10. 10.
    Jing, L., Shang-Chun, F., Yan, L., Zhan-She, G.: Dynamic stability of parametrically-excited linear resonant beams under periodic axial force. Chin. Phys. B 21(11), 110,401 (2012)CrossRefGoogle Scholar
  11. 11.
    Kidachi, H., Onogi, H.: Note on the stability of the nonlinear Mathieu equation. Prog. Theor. Phys. 98(4), 755–773 (1997)MathSciNetCrossRefGoogle Scholar
  12. 12.
    Kovacic, I., Brennan, M.J. (eds.): The Duffing Equation: Nonlinear Oscillators and Their Behaviour. Wiley, New York (2011)zbMATHGoogle Scholar
  13. 13.
    Łuczko, J.: Regular and Chaotic Vibrations in Nonlinear Mechanical Systems. Publishing House of the Cracow University of Technology, Cracow (2008). (in Polish)Google Scholar
  14. 14.
    Magnucki, K., Milecki, S.: Elastic buckling of a triangular frame subject to in-plane tension. J. Theor. Appl. Mech. 53(3), 581–591 (2015)CrossRefGoogle Scholar
  15. 15.
    Magnucki, K., Stawecki, W. (eds.): Strength and Stability of a Brake Triangle. The Rail Vehicles Institute TABOR, Poznan (2015). (in Polish)Google Scholar
  16. 16.
    Marinca, V., Herisanu, N.: Nonlinear Dynamical Systems in Engineering: Some Approximate Approaches. Springer, Heidelberg (2011)CrossRefzbMATHGoogle Scholar
  17. 17.
    McLachlan, N.W.: Ordinary Non-linear Differential Equations in Engineering and Physical Sciences. Oxford University Press, London (1950)zbMATHGoogle Scholar
  18. 18.
    Nayfeh, A.H., Mook, D.T.: Nonlinear Oscillations. Wiley, New York (1995)CrossRefzbMATHGoogle Scholar
  19. 19.
    Ott, E.: Chaos in Dynamical Systems. Cambridge University Press, Cambridge (2002)CrossRefzbMATHGoogle Scholar
  20. 20.
    Rao, S.S.: Vibration of Continuous Systems. Wiley, Hoboken (2007)Google Scholar
  21. 21.
    Timoshenko, S.P., Gere, J.M.: Theory of Elastic Stability. McGraw-Hill, New York (1963)Google Scholar
  22. 22.
    Triantafyllou, S., Koumousis, V.: Small and large displacement dynamic analysis of frame structures based on hysteretic beam elements. J. Eng. Mech. 138(1), 36–49 (2012)CrossRefGoogle Scholar
  23. 23.
    Virgin, L.N.: Vibration of Axially Loaded Structures. Cambridge University Press, New York (2007)CrossRefzbMATHGoogle Scholar
  24. 24.
    Xue, Q., Meek, J.L.: Dynamic response and instability of frame structures. Comput. Methods Appl. Mech. Eng. 190, 5233–5242 (2001)CrossRefzbMATHGoogle Scholar

Copyright information

© The Author(s) 2016

Open AccessThis article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Authors and Affiliations

  1. 1.Institute of Applied MechanicsPoznan University of TechnologyPoznanPoland

Personalised recommendations