Modeling and numerical results for the argumental transverse vibration of a beam excited through permanent or intermittent elastic contact by a harmonic axial motion

Abstract

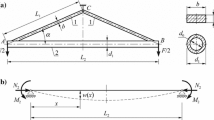
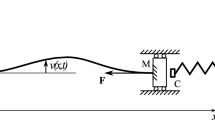
The argumental transverse vibration of a beam excited axially by an harmonic motion transmitted through intermittent or permanent elastic contact is studied. It is shown that this vibration is governed by a nonlinear argumental equation, namely that a vibration in the fundamental transverse mode of the beam can occur when the frequency of the excitation is many times the frequency of the fundamental transverse mode. Two cases are considered: the hinged–(hinged–guided) case and the clamped–(clamped–guided) case. A “natural” model is given and an approached smooth model is derived. The averaging method yields a standard system of differential equations for the smooth model. The stationary condition is represented and studied in the (excitation amplitude, oscillator amplitude)-plane. Stability is studied under symbolic form, and a simple criterion, applicable in said plane, is brought out. The possibility of a stationary condition with permanent contact is discussed. With the help of the Van der Pol representation, numeric simulations allow a comparison between the natural model and the smooth model, leading to clues about the natural model obtained from symbolic relations obtained from the smoothed model.

Appendices

Appendix A: Approximation to a truncated parabola

In this appendix, an approximation to a $C^0$-class function J is studied.

Single-parabola case Define function J(x) as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} J(x)=\alpha +\beta \, x^2 &{} \mathrm {if} \; \alpha +\beta \, x^2 \le 0 \\ J(x)=0 &{} \mathrm {otherwise} \end{array}\right. } \end{aligned}$$

with $\alpha < 0$ and $\beta > 0$. This is a $C^0$-class function. Consider (Fig. 33) that function

$$\begin{aligned} J_\mathrm{approx}(x)=\frac{\alpha }{1+\lambda \; \beta / \alpha \, x^2}, \end{aligned}$$

with $-\,8 \le \lambda \le -\,2$, is a fair approximation to J(x). $J_\mathrm{approx}$ is of class $C^\infty$.

Fig. 33

Exact truncated parabola J(x) (solid line) and approaching function $J_\mathrm{approx}(x)$ (dotted line) J, with $\alpha =J(0)=-5 \; 10^{-4}$, $\beta =10$, and $\lambda =-2.5$. (Color figure online)

By construction, the exact and the approached curves coincide at $(x=0, J(0)=\alpha )$.

Parameter $\lambda$ can be determined by choosing a coincidence point common to the exact and the approached curves. If the desired coincidence point is determined by its abscissa $x_1$, then take: $\lambda =\frac{-\alpha }{\alpha +\beta \, x_1^2}$, so that

$J_\mathrm{approx}(x)=\frac{\alpha }{1-\frac{\beta }{\alpha +\beta \, x_1^2} x^2}$.

Now, if the coincidence point is determined by its ordinate $J_{co}=J(x_1)$, take $\lambda =-\frac{J(0)}{J_{co}}$, so that

$J_\mathrm{approx}(x)=\frac{\alpha }{1-\frac{J(0)}{J_{co}}\frac{\beta }{\alpha } \, x^2}$.

Fig. 34

Exact truncated parabola J (solid line) and approaching function $J_\mathrm{approx}$ (dotted line), with $\alpha =-5 \; 10^{-4}$, $\beta =5$, $\lambda =-2$, and a plateau at ordinate $-4 \; 10^{-4}$. (Color figure online)

Fig. 35

J function consisting of two parabola arcs (solid lines), one at left of point I with vertex $V_1$ at $\alpha _1$, and one at right of point I with vertex $V_2$ at $\alpha _2/2$. Construction lines for the rest of the parabolas are in dotted lines. The “mean” parabola representing $J_\mathrm{approx}$ is the dash-dotted line. Parameters: $\alpha _1=-5 \; 10^{-4}$, $\alpha _2=-8 \; 10^{-4}$, and $\beta =10$. For clarity’s sake, only the positive abscissae are represented. (Color figure online)

Plateau case In case the vertex of parabola $J(x)=\alpha +\beta \, x^2$ is truncated, the function J to be approximated shows a plateau, as shown in Fig. 34. Let $J_{pl}$ be the plateau’s ordinate, and $J_{co}$ the coincidence point’s ordinate. Then, as previously, $\lambda =-\frac{J_{pl}}{J_{co}}$. Searching an approximating function under the form $J_\mathrm{approx}(x)=\frac{J_{pl}}{1+\zeta \, x^2}$, search for the expression of $\zeta$ by writing that functions J (truncated parabola) and $J_\mathrm{approx}$ coincide at ordinate $J_{pl}/(-\,\lambda )$. Obtain $\zeta =\beta \frac{1+\lambda }{\alpha +\frac{J_{pl}}{\lambda }}$, and therefore

$$\begin{aligned} J_\mathrm{approx}(x)=\frac{J_{pl}}{1+\beta \frac{1+\lambda }{\alpha +\frac{J_{pl}}{\lambda }} x^2}. \end{aligned}$$

(56)

Composite-parabola case In this case, function J(x) consists of two connected parabola arcs, intersecting at point I, as shown in Fig. 35. First parabola (left of point I) is $J(x)=\alpha _1+\beta \, x^2$, with vertex at $V_1$, while second one (right of point I) is $J(x)=(\alpha _2+\beta \, x^2)/2$, with vertex at $V_2$. The idea is to use the mean parabola to approximate the two parabola arcs. Let P and Q be the respective points of the higher and lower parabolae located at ordinate zero. Let T be the geometric mean of points P and Q, and let the vertical-axis parabola passing through T and having vertex $V_1$ be called “mean parabola,” with equation $J(x)=\alpha _1+\xi \, x^2$, with $\xi$ being a parameter to be determined. It holds $x_Q=\sqrt{-\alpha _1/\beta }$, $x_P=\sqrt{-\alpha _2/\beta }$, and $x_T^2=x_P \, x_Q=\sqrt{\alpha _1 \alpha _2}/\beta$. Obtain $\xi =\beta \sqrt{\frac{\alpha _1}{\alpha _2}}$. Now to approximate the mean parabola representing equation $J(x)=\alpha _1+\xi \, x^2$, use function $J_\mathrm{approx}(x)=\frac{\alpha _1}{1+\lambda \frac{\beta _\mathrm{app}}{\alpha _1}}$, where $\beta _\mathrm{app}$ is a coefficient to be determined. Obtain

$$\begin{aligned} J_\mathrm{approx}(x)=\frac{\alpha _1}{1-\frac{\lambda \beta }{\sqrt{\alpha _1 \alpha _2}} x^2}. \end{aligned}$$

(57)

Appendix B: A stability criterion

In this appendix, it is brought out a stability criterion of a differential equation system which is encountered in a number of argumental physical setups after applying the averaging method. This is an extension to the stability criterion given in [5].

Consider a differential system as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{a}=A f(a) \sin (n \, \varphi )+g(a)=F(a, \varphi ) \\ \dot{\varphi }=A j(a) \cos (n \, \varphi )+h(a)+A k(a)=G(a, \varphi ), \end{array}\right. } \end{aligned}$$

(58)

where A is a constant representative of the excitation’s amplitude, and the dot notation represents the differentiation w.r.t. (with respect to) reduced time $\tau$. This kind of system is obtained when a solution of the form $a(\tau ) sin(\rho \tau +\varphi (\tau ))$ is tested, where a and $\varphi$ are slowly varying quantities (slowly is meant with reference to the excitation source) and $\rho$ is a parameter to be determined.

To bring out a stability criterion, use the same process than in [5], using the same notations.

From condition $F'_a+G'_\varphi <0$, a first inequality is obtained, which is the same as in [5], as follows:

$$\begin{aligned} f \frac{\mathrm {d}}{\mathrm {d}a} \left( \frac{g}{f} \right) + n j \frac{g}{f} < 0, \end{aligned}$$

where a quote applied to a lowercase letter denotes the differentiation w.r.t. a, while the quote applied to an uppercase letter denotes the differentiation w.r.t. the index of said letter.

Then, recalling that the second inequality characterizing a stable stationary condition writes

$$\begin{aligned} F'_a G'_\varphi -F'_\varphi G'_a>0, \end{aligned}$$

(59)

obtain

$$\begin{aligned}&\frac{F'_a G'_\varphi -F'_\varphi G'_a}{n} \nonumber \\&\quad =-f' j \frac{g^2}{f^2}+g' j \frac{g}{f}-j' f \frac{(h+Ak)^2}{j^2}\nonumber \\&\qquad +\frac{f}{j} (h+A k)(h'+A k'). \end{aligned}$$

(60)

In system (58), make $\dot{a}=0$ and $\dot{\varphi }=0$, and then eliminate $\varphi$, to obtain a system which represents the locus of the stationary condition expressed in the coordinates $(A, a_S)$:

$$\begin{aligned} A^2=\frac{g^2}{f^2}+\frac{(h+A k)^2}{j^2}. \end{aligned}$$

(61)

Then, along said locus, consider A as a function of $a_S$ and differentiate Eq. (61) w.r.t. $a_S$ to obtain:

$$\begin{aligned} A'=\frac{\frac{g g'}{f^2}-\frac{g^2 f'}{f^3}+\frac{(h+A k) (h'+A k')}{j^2}-\frac{(h+A k)^2 j'}{j^3}}{A-\frac{h+A k}{j} \frac{k}{j}}. \end{aligned}$$

Compare with Eq. (60) to deduce, after a few transformations, a relation along the locus of the stationary condition:

$$\begin{aligned} F'_a G'_\varphi -F'_\varphi G'_a=\frac{1}{2} j f \frac{\mathrm {d} A^2}{\mathrm {d}a} \left( A-\frac{h+A k}{j} \frac{k}{j} \right) \frac{n}{A}. \end{aligned}$$

(62)

Use Eq. (59) and substitute $2 A A'$ for $\frac{\mathrm {d} A^2}{\mathrm {d}a}$ in Eq. (62) to obtain the second inequality characterizing the stable stationary condition:

$$\begin{aligned} j f A' \left( A-\frac{h+A k}{j} \frac{k}{j}\right) >0. \end{aligned}$$

(63)

Horizontal tangent Notice that this inequality vanishes when $A'=0$, i.e., when the locus of the stationary condition has a horizontal tangent. Now differentiate Eq. (61) w.r.t. A and a, to obtain

$$\begin{aligned}&2 \left( \frac{(h+A k) k}{j^2} - A \right) \mathrm {d}A\\&\quad +\,\frac{\partial }{\partial a}\left( \frac{g^2}{f^2}+\frac{(h+A k)^2}{j^2} \right) \mathrm {d}a=0, \end{aligned}$$

which shows that expression

$$\begin{aligned} \frac{(h+A k) k}{j^2} - A \end{aligned}$$

(64)

vanishes at points where the locus of the stationary condition defined by Eq. (61) has a vertical tangent. It follows that inequality (63) vanishes at points where the tangent to said locus has a horizontal or a vertical tangent. And when both $A'$ and (64) change sign at the same point, the validity of the stability criterion (63) remains when going through said point. This situation occurs when the vertical tangent is at a point where the locus curve is convex. Conversely, if the vertical tangent is an inflexion point, only (64) changes sign, and consequently the stability criterion toggles.

The rules regarding tangents also hold in the $(a_A, a_S)$-plane defined in this paper, because $A(a_A)$ is a monotonic increasing function of $a_A$.

Appendix C: Approximation to the amplitude and mean value of function $\mathbf {y_\mathrm{approx}}$

1.1 Amplitude

Define $a_\mathrm{Acrit}=\left| \frac{F_0}{k \, L} \right| =-\frac{F_0}{k \, L}$ and form the expression of $\hat{y}_\mathrm{approx}=(H_l-L_l)/2$:

$$\begin{aligned} {\left\{ \begin{array}{ll} \hat{y}_\mathrm{approx} = a_A &{} \mathrm {if} \; \frac{\pi ^2}{4} q_1^2 \le a_\mathrm{Acrit}-a_A \\ \hat{y}_\mathrm{approx} =0 &{} \mathrm {if} \; a_\mathrm{Acrit}+a_A < \frac{\pi ^2}{4} q_1^2 \\ \hat{y}_\mathrm{approx} = K_1 &{} \mathrm {otherwise} \end{array}\right. } \end{aligned}$$

(65)

with $K_1=-\frac{1}{2} \left( \frac{F_0}{k \, L}-a_A+\frac{\pi ^2}{4} q_1^2 \right)$.

From the piecewise definition of $\hat{y}_\mathrm{approx}$ in Eq. (65), search a $C^\infty$ approximation to $\hat{y}_\mathrm{approx}$. Two cases must be distinguished, depending on the position of $a_A$ versus $a_\mathrm{Acrit}$.

Case $a_A>a_\mathrm{Acrit}$ In this case, the first case of Eqs. (65) cannot exist. It follows that this is a “single-parabola case” as per “Appendix A.”

The parabola’s vertex is at ordinate $\frac{1}{2} \left( -\frac{F_0}{k \, L}+a_A \right)$. With the notations of “Appendix A,” $\alpha =\frac{1}{2} \left( -\frac{F_0}{k \, L}+a_A \right)$, $\beta =-\frac{\pi ^2}{8}$, and $x=q_1$. Hence, the function $J_\mathrm{approx}$ approaching $\hat{y}_\mathrm{approx}$ writes

$$\begin{aligned} J_\mathrm{approx}(q_1)=\frac{\frac{1}{2} \left( -\frac{F_0}{k \, L}+a_A \right) }{1-\frac{\pi ^2}{4}\frac{\lambda }{\left( -\frac{F_0}{k \, L}+a_A \right) } \; q_1^2}. \end{aligned}$$

(66)

At this point, it would be nice to have a value of $\lambda$ such that the denominator in expression (66) be independent of $a_A$. Knowing that $\lambda$ must be comprised between $-2$ and $-8$ (see “Appendix A”), this is possible if $\lambda =-\frac{\frac{F_0}{k \, L}-a_A}{\frac{F_0}{k \, L}}$ and $a_A<7 a_\mathrm{Acrit}$, which is physically within reason. With this expression for $\lambda$, it holds

$$\begin{aligned} J_\mathrm{approx}(q_1)=\frac{\frac{1}{2} \left( -\frac{F_0}{k \, L}+a_A \right) }{1+B \, q_1^2}, \end{aligned}$$

(67)

with $B=-\frac{\pi ^2 k \, L}{4 F_0}=\frac{\pi ^2}{4 \; a_\mathrm{Acrit}}$.

Case $a_A \le a_\mathrm{Acrit}$ In this case, all three cases of Eq. (65) are valid. It follows that this is a “plateau case” as per “Appendix A.” The plateau is at ordinate $a_A$. Using Eq. (56) of “Appendix A” with $J_{pl}=a_A$, $\alpha =\frac{1}{2} \left( -\frac{F_0}{k \, L}+a_A \right)$, $\beta =-\frac{\pi ^2}{8}$, and $x=q_1$, this can be approximated by:

$$\begin{aligned} J_\mathrm{approx}=\frac{a_A}{1+E q_1^2}, \end{aligned}$$

with

$$\begin{aligned} E=-\frac{\pi ^2}{4} \frac{1+\lambda }{\left( \frac{2}{\lambda }+1 \right) a_A-\frac{F_0}{k \, L}}. \end{aligned}$$

Notice that if $\lambda =-2$, expression E is independent of $a_A$. Therefore, in this case, this value of $\lambda$ is chosen, and it follows that $E=-\frac{\pi ^2 k \, L}{4 F_0}$, which is the same value as B in the case $a_A>a_\mathrm{Acrit}$.

Conclusion for the expression of $\hat{y}_\mathrm{approx}$ Finally:

$$\begin{aligned} {\left\{ \begin{array}{ll} \hat{y}_\mathrm{approx} \approx \frac{a_A}{1+B \, q_1^2} &{} \mathrm {if} \; a_A < a_\mathrm{Acrit} \\ \hat{y}_\mathrm{approx} \approx \frac{1}{2} \; \frac{\frac{-F_0}{k \, L}+a_A}{1+B \, q_1^2} &{} \mathrm {otherwise} \end{array}\right. } \end{aligned}$$

with $B=-\frac{\pi ^2 k \, L}{4 F_0}=\frac{\pi ^2}{4 \; a_\mathrm{Acrit}}$.

1.2 Mean value

Form the expression of $\overline{y}_\mathrm{approx}=(H_l+L_l)/2$:

$$\begin{aligned} {\left\{ \begin{array}{ll} \overline{y}_\mathrm{approx} = \frac{F_0}{k \, L}+\frac{\pi ^2}{4} q_1^2 &{} \mathrm {if} \; \frac{\pi ^2}{4} q_1^2 \le a_\mathrm{Acrit}-a_A \\ \overline{y}_\mathrm{approx} =0 &{} \mathrm {if} \; a_\mathrm{Acrit}+a_A < \frac{\pi ^2}{4} q_1^2 \\ \overline{y}_\mathrm{approx} = K_2 &{} \mathrm {otherwise} \end{array}\right. } \end{aligned}$$

(68)

with $K_2=\frac{1}{2} \left( \frac{F_0}{k \, L}-a_A+\frac{\pi ^2}{4} q_1^2 \right)$.

Notice that $K_2=-K_1$.

From the piecewise definition of $\overline{y}_\mathrm{approx}$ in Eq. (68), search a $C^\infty$ approximation to $\overline{y}_\mathrm{approx}$. Two cases must be distinguished, depending on the position of $a_A$ versus $a_\mathrm{Acrit}$.

Case $a_A>a_\mathrm{Acrit}$ In this case, the first case of Eq. (68) cannot exist. It follows that this is a single-parabola case as per “Appendix A.” The parabola’s equation is $J(q_1)=K_2$, and the vertex is at ordinate $\frac{1}{2} \left( \frac{F_0}{k \, L} - a_A \right)$, which is negative. Noticing that, excepted for the sign, these parameters are the same as for the approximation of $\hat{y}_\mathrm{approx}$ for $a_A>a_\mathrm{Acrit}$, and using the same method as for obtaining Eq. (67), put

$$\begin{aligned} \lambda =-\kappa \frac{\frac{F_0}{k \, L}-a_A}{\frac{F_0}{k \, L}}=-\kappa \frac{a_\mathrm{Acrit}+a_A}{a_\mathrm{Acrit}}, \end{aligned}$$

with $\kappa =2$ to ensure continuity of expression C (defined below) with case $a_A<a_\mathrm{Acrit}$, and obtain

$$\begin{aligned} J_\mathrm{approx}(q_1)&=\frac{\frac{1}{2} \left( \frac{F_0}{k \, L}-a_A \right) }{1+C \, q_1^2} \\&=\frac{1}{2} \left( \frac{F_0}{k \, L}-a_A \right) \left( 1-\frac{C \, q_1^2}{1+C \, q_1^2} \right) , \end{aligned}$$

with $C=-\frac{\pi ^2 k \, L}{2 F_0}=\frac{\pi ^2}{2 \; a_\mathrm{Acrit}}$. It can be seen that the model is limited to $a_A<3 a_\mathrm{Acrit}$ to ensure that $-\,8< \lambda < -\,2$.

Case $a_A<a_\mathrm{Acrit}$ In this case, all three cases of Eq. (68) are valid. This is a composite-parabola case as per “Appendix A.” Here, $\alpha _1=F_0/(k \, L)$, $\beta =\pi ^2/4$, and $\alpha _2=F_0/((k \, L)-a_A$. Using Eq. (57) of “Appendix A,” $\overline{y}_\mathrm{approx}$ can be approximated by: $\frac{F_0}{k \, L} \; \frac{1}{1+C \, q_1^2}$, with

$$\begin{aligned} C=-\lambda \frac{\pi ^2}{4} \frac{1}{\sqrt{\left( -\frac{F_0}{k \, L}\right) \left( -\frac{F_0}{k \, L}+a_A\right) }}. \end{aligned}$$

However, this expression depends on $a_A$, while, in the other cases, it does not. The idea is to choose $\lambda$ so as to have C independent of $a_A$, after noticing that $\lambda$ needs not be a constant, but only needs to be between $-\,8$ and $-\,2$ (see “Appendix A”).

Put

$$\begin{aligned} \lambda =\kappa \frac{\sqrt{\left( -\frac{F_0}{k \, L}\right) \left( -\frac{F_0}{k \, L}+a_A\right) }}{\frac{F_0}{k \, L}}, \end{aligned}$$

where $\kappa$ is a coefficient to be determined. After a few calculus, condition $-\,4 \le \lambda \le -\,2$ leads to

$$\begin{aligned} \frac{4}{\kappa ^2}-1 \le \frac{a_A}{|\frac{F_0}{k \, L}|} \le \frac{16}{\kappa ^2}-1. \end{aligned}$$

(69)

Since here $a_A<a_\mathrm{Acrit}=\left| \frac{F_0}{k \, L} \right|$, it holds $0< \frac{a_A}{|\frac{F_0}{k \, L}|} < 1$. It follows that the value $\kappa =2$ satisfies (69). Finally, C writes:

$$\begin{aligned} C=-\frac{\pi ^2}{2} \frac{k \, L}{F_0}=\frac{\pi ^2}{2 \; a_\mathrm{Acrit}}. \end{aligned}$$

(70)

Then,

$$\begin{aligned} \overline{y}_\mathrm{approx} \approx \frac{F_0}{k \, L} \; \frac{1}{1+C \, q_1^2}=\frac{F_0}{k \, L} \; \left( 1-\frac{C \, q_1^2}{1+C \, q_1^2} \right) . \end{aligned}$$

Conclusion for the expression of $\overline{y}_\mathrm{approx}$ Finally, the mean value of function $y_\mathrm{approx}$ writes:

$$\begin{aligned} {\left\{ \begin{array}{ll} \overline{y}_\mathrm{approx} \approx \frac{F_0}{k \, L} \; \left( 1-\frac{C \, q_1^2}{1+C \, q_1^2} \right) &{} \mathrm {if} \; a_A < a_\mathrm{Acrit} \\ \overline{y}_\mathrm{approx} \approx \frac{1}{2} \left( \frac{F_0}{k \, L}-a_A \right) \left( 1-\frac{C \, q_1^2}{1+C \, q_1^2} \right) &{} \mathrm {otherwise,} \end{array}\right. } \end{aligned}$$

with $C=-\frac{\pi ^2 k \, L}{2 F_0}=\frac{\pi ^2}{2 \; a_\mathrm{Acrit}}$ and $a_A<3 a_\mathrm{Acrit}$.