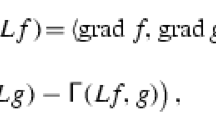Curvature-dimension inequalities on sub-Riemannian manifolds obtained from Riemannian foliations: part II

Abstract

Using the curvature-dimension inequality proved in Part I, we look at consequences of this inequality in terms of the interaction between the sub-Riemannian geometry and the heat semigroup $P_t$ corresponding to the sub-Laplacian. We give bounds for the gradient, entropy, a Poincaré inequality and a Li-Yau type inequality. These results require that the gradient of $P_t f$ remains uniformly bounded whenever the gradient of f is bounded and we give several sufficient conditions for this to hold.

Appendix

1.1 Graded analysis on forms

Let $(M, \mathcal {H}, \mathbf {h})$ be a sub-Riemannian manifold with an integrable complement $\mathcal {V}$, and let $\mathbf {v}$ be a chosen positive definite metric tensor on $\mathcal {V}$. Let ${{\mathrm{\mathbf {g}}}}= {{\mathrm{pr}}}_{\mathcal {H}}^* \mathbf {h}+ {{\mathrm{pr}}}_{\mathcal {V}}^* \mathbf {v}$ be the corresponding Riemannian metric. The subbundle $\mathcal {V}$ gives us a foliation of M, and corresponding to this foliation we have a grading on forms, see e.g. [1, 2]. Let $\varOmega (M)$ be the algebra of differential forms on M. Let ${{\mathrm{Ann}}}(\mathcal {H})$ and ${{\mathrm{Ann}}}(\mathcal {V})$ be the subbundles of $T^*M$ of elements vanishing on respectively $\mathcal {H}$ and $\mathcal {V}$. If either a or b is a negative integer, then $\eta \in \varOmega (M)$ is a homogeneous element of degree (a, b) if and only if $\eta = 0$. Otherwise, for nonnegative integers a and b, $\eta$ is a homogeneous element of degree (a, b), if it is a sum of elements which can be written as

$$\begin{aligned} \alpha \wedge \beta , \quad \textstyle \alpha \in \varGamma (\bigwedge ^a {{\mathrm{Ann}}}(\mathcal {V})),\ \beta \in \varGamma (\bigwedge ^b {{\mathrm{Ann}}}(\mathcal {H})). \end{aligned}$$

Relative to this grading, we can split the exterior differential d into graded components

$$\begin{aligned} d = d^{1,0} + d^{0,1} + d^{2,-1} . \end{aligned}$$

The same is true for its formal dual

$$\begin{aligned} \delta = \delta ^{-1,0} + \delta ^{0,-1} + \delta ^{-2,1} , \end{aligned}$$

i.e. the dual with respect to the inner product on forms of compact support $\alpha , \beta$, defined by

$$\begin{aligned} \langle \alpha , \beta \rangle = \int _M \alpha \wedge \star \beta , \qquad \alpha ,\beta \text { of compact support}, \end{aligned}$$

(6.1)

where $\star$ is the Hodge star operator defined relative to ${{\mathrm{\mathbf {g}}}}$. Note that $\delta ^{-a,-b}$ is the formal dual of $d^{a,b}$ from our assumptions that $\mathcal {H}$ and $\mathcal {V}$ are orthogonal. We will give formulas for each graded component.

1.2 Metric-preserving complement and local representation

We will use $\flat :TM \rightarrow T^*M$ for the map with inverse $\sharp$. Let $\mathring{\nabla }$ be defined as in (2.1) relative to ${{\mathrm{\mathbf {g}}}}$ and the splitting $TM = \mathcal {H}\oplus \mathcal {V}$. If $\alpha$ is a one-form and $A_1, \ldots , A_n$ and $V_1, \ldots , V_\nu$ are respective local orthonormal bases of $\mathcal {H}$ and $\mathcal {V}$, then locally

$$\begin{aligned} d\alpha =&\sum _{i=1}^n \flat A_i \wedge \mathring{\nabla }_{A_i} \alpha + \sum _{s=1}^\nu \flat V_s \wedge \mathring{\nabla }_{V_s} \alpha - \alpha \circ \mathcal {R}, \end{aligned}$$

and hence each of the three terms are local representations of respectively $d^{1,0} \alpha ,$ $d^{0,1} \alpha$ and $d^{2,-1} \alpha$. Local representations on forms of all orders follow.

Assume now that $\mathring{\nabla }{{\mathrm{\mathbf {g}}}}= 0$, i.e. $\mathcal {V}$ is a metric-preserving compliment of $(\mathcal {H}, \mathbf {h})$ with a metric tensor $\mathbf {v}$ satisfying $\mathring{\nabla }\mathbf {v}^* = 0$. From the formula of $d^{1,0} \eta = \sum _{i=1}^n \flat A_i \wedge \mathring{\nabla }_{A_i} \eta$, we obtain $\delta ^{-1,0}\eta = - \sum _{i=1}^n \iota _{A_i} \mathring{\nabla }_{A_i} \eta$ for any form $\eta$. Let $\varDelta _{\mathbf {h}}$ be the sub-Laplacian of $\mathcal {V}$ or equivalently ${{\mathrm{vol}}}$. Let $\varDelta$ be the Laplacian of ${{\mathrm{\mathbf {g}}}}$. Then it is clear that for any $f \in C^\infty (M)$, we have

$$\begin{aligned} \varDelta f = -\delta df, \qquad \varDelta _{\mathbf {h}}f = -\delta ^{-1,0} d^{1,0} f. \end{aligned}$$

Lemma 6.1

For any form $\eta \in \varOmega (M)$, we have

$$\begin{aligned} \delta ^{-1,0} d^{0,1} \alpha = - d^{0,1} \delta ^{-1,0} \alpha , \quad \delta ^{0,-1} d^{1,0} \alpha = - d^{1,0} \delta ^{0,-1} \alpha . \end{aligned}$$

(6.2)

As a consequence, for any $f \in C^\infty (M)$ we have $\varDelta _{\mathbf {h}}\varDelta f= \varDelta \varDelta _{\mathbf {h}}f.$

The following result is helpful for our computation in Part I, Lemma 3.3 (b) and Corollary 3.11.

Lemma 6.2

• (a) For any horizontal $A \in \varGamma (\mathcal {H})$, a vertical $V \in \varGamma (\mathcal {V})$ and arbitrary vector filed $Z \in \varGamma (TM)$, we have

  $$\begin{aligned} {{\mathrm{\mathbf {g}}}}(R^{\mathring{\nabla }}(A,V) Z, A) = 0. \end{aligned}$$

• (b) If $\mathring{\nabla }{{\mathrm{\mathbf {g}}}}= 0$, then for every point $x_0$, there exist local orthonormal bases $A_1, \ldots , A_n$ and $V_1, \ldots V_\nu$, defined in a neighborhood of $x_0$, such that for any $Y \in \varGamma (TM)$,

  

Proof of Lemma 6.1

It is sufficient to show one of the identities in (6.2), since $\delta ^{-1,0}d^{0,1}$ is the formal dual of $\delta ^{0,-1} d^{1,0}$. From Lemma 6.2 (a), any $A \in \varGamma (\mathcal {H})$ and $V \in \varGamma (\mathcal {V})$ satisfy

$$\begin{aligned} \iota _A \mathring{\nabla }_V \mathring{\nabla }_A \alpha = \iota _A \mathring{\nabla }_A \mathring{\nabla }_V \alpha + \iota _A \mathring{\nabla }_{[V,A]} \alpha . \end{aligned}$$

From the definition of $\mathring{\nabla }$, it follows that $T^{\mathring{\nabla }}(A,V) = 0$, where $T^{\mathring{\nabla }}$ is the torsion of $\mathring{\nabla }$. For a given point $x_0 \in M$, let $A_1, \ldots , A_n$ and $V_1, \ldots , V_\nu$ be as in Lemma 6.2 (b). All terms below are evaluated at the point $x_0$, giving us

$$\begin{aligned} d^{0,1} \delta ^{-1,0} \alpha&= -\sum _{s=1}^\nu \sum _{i=1}^n \flat V_s \wedge \mathring{\nabla }_{V_s} \iota _{A_i} \mathring{\nabla }_{A_i} \alpha \\&= -\sum _{s=1}^\nu \sum _{i=1}^n \flat V_s \wedge \iota _{\mathring{\nabla }_{V_s} A_i} \mathring{\nabla }_{A_i} \alpha -\sum _{s=1}^\nu \sum _{i=1}^n \flat V_s \wedge \iota _{A_i} \mathring{\nabla }_{V_s} \mathring{\nabla }_{A_i} \alpha \\&= -\frac{1}{2} \sum _{s=1}^\nu \sum _{i,j=1}^n {{\mathrm{\mathbf {g}}}}(V_s, \mathcal {R}(A_i, A_j)) \flat V_s \wedge \iota _{A_j} \mathring{\nabla }_{A_i} \alpha \\&\quad -\,\sum _{s=1}^\nu \sum _{i=1}^n \flat V_s \wedge \iota _{A_i} \mathring{\nabla }_{A_i} \mathring{\nabla }_{V_s} \alpha -\sum _{s=1}^\nu \sum _{i=1}^n \flat V_s \wedge \iota _{A_i} \mathring{\nabla }_{\mathring{\nabla }_{V_s} A_i - \mathring{\nabla }_{A_i} V_s} \alpha \\&=\sum _{s=1}^\nu \sum _{i,j=1}^n \iota _{A_i} \left( \flat V_s \wedge \mathring{\nabla }_{A_i} \mathring{\nabla }_{V_s} \right) \alpha \\&= \sum _{s=1}^\nu \sum _{i,j=1}^n \iota _{A_i} \mathring{\nabla }_{A_i} \left( \flat V_s \wedge \mathring{\nabla }_{V_s} \right) \alpha = -\delta ^{-1,0} d^{1,0} \alpha . \end{aligned}$$

Next, we prove the identity $[\varDelta _{\mathbf {h}}, \varDelta ] f = 0$. If we consider the degree (1, 1)-part of $d^2 = 0$, we get

$$\begin{aligned} d^{0,1} d^{1,0} + d^{1,0} d^{0,1} = 0. \end{aligned}$$

The same relation will then hold for their formal duals. Since $\varDelta f = \varDelta _{\mathbf {h}}f - \delta ^{0,1} d^{0,1} f,$ it is sufficient to show that $\varDelta _{\mathbf {h}}\delta ^{0,-1} d^{0,1} f = \delta ^{0,-1} d^{0,1} \varDelta _{\mathbf {h}}f.$ This gives us the result

$$\begin{aligned}&\varDelta _{\mathbf {h}}\delta ^{0,-1} d^{0,1} f = -\delta ^{-1,0} d^{1,0} \delta ^{0,-1} d^{0,1} f = - \delta ^{0,-1} d^{0,1} \delta ^{-1,0} d^{1,0} f = \delta ^{0,-1} d^{0,1} \varDelta _{\mathbf {h}}f, \end{aligned}$$

since we have to do an even number of permutations. $\square$

1.3 Spectral theory of the sub-Laplacian

Let L be a self-adjoint operator on $L^2(M,{{\mathrm{vol}}})$ with domain ${{\mathrm{Dom}}}(L)$. Define $\Vert f\Vert _{{{\mathrm{Dom}}}(L)}^2 = \Vert f\Vert ^2_{L^2} +\Vert Lf\Vert _{L^2}^2$. Write the spectral decomposition of L as $L = \int _{-\infty }^\infty \lambda dE_\lambda$ with respect to the corresponding projector valued spectral measure $E_\lambda$. For any Borel measurable function $\varphi :{{\mathrm{\mathbb {R}}}}\rightarrow {{\mathrm{\mathbb {R}}}}$, we write $\varphi (L)$ for the operator $\varphi (L) := \int _{-\infty }^\infty \varphi (\lambda ) dE_{\lambda }$ which is self adjoint on its domain

$$\begin{aligned} {{\mathrm{Dom}}}(\varphi (L)) = \left\{ f \in L^2(M, {{\mathrm{vol}}}) \, :\, \int _{-\infty }^\infty \varphi (\lambda )^2 d\langle E_\lambda f, f \rangle \right\} . \end{aligned}$$

In particular, if $\varphi$ is bounded, $\varphi (L)$ is defined on the entire of $L^2(M,{{\mathrm{vol}}})$. See [15, Ch VIII.3] for details.

Let $(M, \mathcal {H}, \mathbf {h})$ be a sub-Riemannian manifold with sub-Laplacian $\varDelta _{\mathbf {h}}$ defined relative to a volume form ${{\mathrm{vol}}}$. Assume that $\mathcal {H}$ is bracket-generating and that $(M, \mathsf {d}_{cc})$ is complete metric space, where $\mathsf {d}_{cc}$ is the Carnot-Carathéodory metric of $(\mathcal {H}, \mathbf {h})$. Then

$$\begin{aligned} \int _M f \varDelta _{\mathbf {h}}gd\hbox {vol}= \int _M g \varDelta _{\mathbf {h}}f d\hbox {vol}\quad \text {and}\quad \int f \varDelta _{\mathbf {h}}fd\hbox {vol}\le 0. \end{aligned}$$

From [17, Section 12], we have that $\varDelta _{\mathbf {h}}$ is a an essentially self adjoint operator on $C_c^\infty (M)$. We denote its unique self-adjoint extension by $\varDelta _{\mathbf {h}}$ as well with domain ${{\mathrm{Dom}}}(\varDelta _{\mathbf {h}}) \subseteq L^2(M, {{\mathrm{vol}}}).$

Since $\varDelta _{\mathbf {h}}$ is non-positive and the maps $\lambda \mapsto e^{t\lambda /2}$ and $\lambda \mapsto \lambda ^j e^{t\lambda /2}$ are bounded on $(- \infty , 0]$ for $t > 0$, $j > 0$, we have that $f \mapsto e^{t/2 \varDelta _{\mathbf {h}}} f$ is a map from $L^2(M, {{\mathrm{vol}}})$ into $\cap _{j=1}^\infty {{\mathrm{Dom}}}(\varDelta _{\mathbf {h}}^j)$. Define $P_tf$ as in Sect. 3.1 with respect to $\frac{1}{2}\varDelta _{\mathbf {h}}$-diffusions for bounded measurable functions f. Then clearly $\Vert P_t f\Vert _{L^\infty } \le \Vert f\Vert _{L^\infty }$. Since $\varDelta _{\mathbf {h}}$ is symmetric with respect to ${{\mathrm{vol}}}$ and $P_t 1 \le 1$, we obtain $\Vert P_t f\Vert _{L^1} \le \Vert f\Vert _{L^1}$ as well. The Riesz–Thorin theorem then ensures that $\Vert P_t f\Vert _{L^p} \le \Vert f\Vert _{L^p}$ for any $1 \le p \le \infty .$ In particular, $P_t f$ is in $L^2(M, {{\mathrm{vol}}})$ whenever f is in $L^2(M, {{\mathrm{vol}}})$. This implies that $P_t f = e^{t/2\varDelta _{\mathbf {h}}} f$ for any bounded $f \in L^2(M, {{\mathrm{vol}}})$ by the following result.

Lemma 6.3

([14, Prop], [8, Prop 4.1]) Let L be equal to the Laplacian $\varDelta$ or sub-Laplacian $\varDelta _{\mathbf {h}}$ defined relative to a complete Riemannian or sub-Riemannian metric, respectively. Let $u_t(x)$ be a solution in $L^2(M,{{\mathrm{vol}}})$ of the heat equation

$$\begin{aligned} (\partial _t - L) u_t = 0, \quad u_0 = f, \end{aligned}$$

for a function $f \in L^2(M,{{\mathrm{vol}}})$. Then $u_t(x)$ is the unique solution of this equation in $L^2(M,{{\mathrm{vol}}})$.

Hence, we will from now on just write $P_t = e^{t/2 \varDelta _{\mathbf {h}}}$ without much abuse of notation.

1.3.1 Global bounds using spectral theory

We now introduce some additional assumptions. Assume that ${{\mathrm{\mathbf {g}}}}$ is a complete Riemannian metric with volume form ${{\mathrm{vol}}}$, such that ${{\mathrm{\mathbf {g}}}}|_{\mathcal {H}} = \mathbf {h}, \mathcal {H}^\perp = \mathcal {V}$ and ${{\mathrm{\mathbf {g}}}}|_{\mathcal {V}} = \mathbf {v}.$ Let $\varDelta$ be the Laplace-Beltrami operator of ${{\mathrm{\mathbf {g}}}}$ and write $\varDelta f = \varDelta _{\mathbf {h}}f + \varDelta _{\mathbf {v}}f$ where $\varDelta _{\mathbf {v}}f = {{\mathrm{div}}}\,\sharp ^{{\mathbf v}^*}df$. Since ${{\mathrm{\mathbf {g}}}}$ is complete, $\varDelta$ is also essentially self-adjoint on $C_c^\infty (M)$ by [16] and we will also denote its unique self-adjoint extension by the same symbol.

Assume that $\mathring{\nabla }{{\mathrm{\mathbf {g}}}}= 0$ where $\mathring{\nabla }$ is defined as in (2.1). Recall that $\varDelta _{\mathbf {h}}$ and $\varDelta$ commute on $C_c^\infty (M)$ by Lemma 6.1.

Lemma 6.4

• (a) The operators $\varDelta _{\mathbf {h}}$ and $\varDelta$ spectrally commute, i.e. for any bounded Borel function $\varphi : {{\mathrm{\mathbb {R}}}}\rightarrow {{\mathrm{\mathbb {R}}}}$ and $f \in L^2(M,{{\mathrm{vol}}})$,

  $$\begin{aligned} \varphi (\varDelta _{\mathbf {h}}) \varphi (\varDelta )f = \varphi (\varDelta ) \varphi (\varDelta _{\mathbf {h}})f. \end{aligned}$$

  Also ${{\mathrm{Dom}}}(\varDelta ) \subseteq {{\mathrm{Dom}}}(\varDelta _{\mathbf {h}}).$

• (b) Assume that $\varDelta _{\mathbf {h}}$ satisfies the assumptions of Theorem 2.2 with $m_{\mathcal {R}}>0$. Then there exist a constant $C = C(\rho _1, \rho _2)$ such that for any $f\in C^\infty (M) \cap {{\mathrm{Dom}}}(\varDelta _{\mathbf {h}}^2)$,

  $$\begin{aligned} C\Vert f\Vert _{{{\mathrm{Dom}}}(\varDelta _{\mathbf {h}}^2)}^2 = C\left( \Vert f\Vert ^2_{L^2} + \Vert \varDelta _{\mathbf {h}}^2 f\Vert _{L^2}^2 \right) , \end{aligned}$$

  is an upper bound for

  $$\begin{aligned} \int _M \mathsf {\Gamma }^{\mathbf {h}^*}(f)\,d\hbox {vol}, \quad \int _M \mathsf {\Gamma }^{\mathbf {h}^*}_2(f),d\hbox {vol}, \quad \int _M \mathsf {\Gamma }^{\mathbf {v}^*}(f)\,d\hbox {vol}\quad \text {and} \quad \int _M \mathsf {\Gamma }^{\mathbf {v}^*}_2(f)\,d\hbox {vol}. \end{aligned}$$

Proof

• (a) Note first that for any $f \in C_c^\infty (M)$, using Lemma 6.1 and the inner product (6.1)

  $$\begin{aligned} \int _M \varDelta _{\mathbf {v}}f \varDelta _{\mathbf {h}}f\,d\hbox {vol}&= \langle \delta ^{0,-1} d^{0,1} f, \delta ^{-1,0} d^{1,0} f\rangle = \langle d^{0,1} f, d^{0,1} \delta ^{-1,0} d^{1,0}f \rangle \\&= - \langle d^{0,1} f, \delta ^{-1,0} d^{0,1} d^{1,0}f \rangle = \langle d^{1,0} d^{0,1} f, d^{1,0} d^{0,1} f \rangle \ge 0. \end{aligned}$$

  Hence

  $$\begin{aligned} \int _M (\varDelta _{\mathbf {h}}f)^2\,d\hbox {vol}\le \int _M ((\varDelta _{\mathbf {h}}+ \varDelta _{\mathbf {v}}) f)^2\,d\hbox {vol}= \int _M (\varDelta f)^2\,d\hbox {vol}, \end{aligned}$$

  and hence $\Vert \varDelta _{\mathbf {h}}f\Vert _{L^2} \le \Vert \varDelta f\Vert _{L^2}$ is true for any $f \in {{\mathrm{Dom}}}(\varDelta )$. We conclude that ${{\mathrm{Dom}}}(\varDelta ) \subseteq {{\mathrm{Dom}}}(\varDelta _{\mathbf {h}})$. Define $Q_t = e^{t/2 \varDelta }$. It follows that, for any $f \in {{\mathrm{Dom}}}(\varDelta _{\mathbf {h}})$, $u_t = \varDelta _{\mathbf {h}}Q_t f$ is an $L^2(M,{{\mathrm{vol}}})$ solution of

  $$\begin{aligned} \left( \frac{\partial }{\partial t} - \frac{1}{2} \varDelta \right) u_t = 0, \quad u_0 = \varDelta _{\mathbf {h}}f. \end{aligned}$$

  In conclusion, by Lemma 6.3 we obtain $\varDelta _{\mathbf {h}}Q_t f = Q_t \varDelta _{\mathbf {h}}f$. For any $s >0$ and $f \in L^2(M, {{\mathrm{vol}}})$, we know that $Q_sf \in {{\mathrm{Dom}}}(\varDelta ) \subseteq {{\mathrm{Dom}}}(\varDelta _{\mathbf {h}})$, and since

  $$\begin{aligned} (\partial _t - \frac{1}{2} \varDelta _{\mathbf {h}}) Q_s P_t f = 0, \end{aligned}$$

  it again follows from Lemma 6.3 that $P_t Q_s f = Q_s P_t f$ for any $s,t \ge 0$ and $f \in L^2(M, {{\mathrm{vol}}})$. It follows that the operators spectrally commute, see [15, Chapter VIII.5].

• (b) From Theorem 2.2, we know that $\varDelta _{\mathbf {h}}$ satisfies (CD) with $\rho _2 >0$ and an appropriately chosen value of c. The proof is otherwise identical to [8, Lemma 3.4 & Prop 3.6] and is therefore omitted. $\square$

1.3.2 Proof of Theorem 3.4

We are going to prove that (A) holds without using stochastic analysis. We therefore need the following lemma.

Lemma 6.5

([8, Prop 4.2]) Assume that $(M, {{\mathrm{\mathbf {g}}}})$ is a complete Riemannian manifold. For any $T> 0$, let $u, v\in C^\infty (M \times [0,T])$, $(x,t) \mapsto u_t(x)$, $(x,t) \mapsto v_t(x)$ be smooth functions satisfying the following conditions:

• (i) For any $t \in [0,T]$, $u_t \in L^2(M,{{\mathrm{vol}}})$ and $\int _0^T \Vert u_t\Vert _{L^2} dt < \infty .$

• (ii) For some $1\le p \le \infty ,$ $\int _0^T \Vert \mathsf {\Gamma }^{\mathbf {h}^*}(u_t)^{1/2} \Vert _{L^p}\,d\hbox {vol}< \infty .$

• (iii) For any $t \in [0,T]$, $v_t \in L^q(M,{{\mathrm{vol}}})$ and $\int _0^T \Vert v_t\Vert _{L^q} dt < \infty$ for some $1 \le q \le \infty$.

Then, if $(L + \frac{\partial }{\partial t} ) u \ge v$ holds on $M\times [0,T]$, we have

$$\begin{aligned} P_T u_T \ge u_0 + \int _0^t P_t v_t dt. \end{aligned}$$

Let $P_t = e^{t/2 \varDelta _{\mathbf {h}}}$. For given compactly supported $f\in C_c^\infty (M)$ and $T>0$, define function

$$\begin{aligned} z_{t,\varepsilon } = \left( \mathsf {\Gamma }^{\mathbf {v}^*}(P_{T-t} f) + \varepsilon ^2 \right) ^{1/2} - \varepsilon , \end{aligned}$$

(6.3)

with $\varepsilon > 0, t\in [0,T]$. Since $P_t f \in {{\mathrm{Dom}}}(\varDelta _{\mathbf {h}}^2)$, Lemma 6.4 (b) tells us that,

$$\begin{aligned} \Vert z_{t,\varepsilon }\Vert _{L^2} \le \int _M \mathsf {\Gamma }^{\mathbf {v}^*}(P_{T-t}),{{\mathrm{vol}}}\le C \Vert P_{T-t} f\Vert _{{{\mathrm{Dom}}}(\varDelta _{\mathbf {h}}^2)} < \infty , \end{aligned}$$

so that $z_{t,\varepsilon } \in L^2(M, {{\mathrm{vol}}})$. By Proposition 2.3,

$$\begin{aligned} \mathsf {\Gamma }^{\mathbf {h}^*}(z_{t,\varepsilon }) \le \frac{\mathsf {\Gamma }^{\mathbf {h}^*}(\mathsf {\Gamma }^{\mathbf {v}^*}(P_{T-t} f))}{4 z_{t,\varepsilon } + \varepsilon } \le \mathsf {\Gamma }_2^{\mathbf {v}^*}(P_{T-t} f). \end{aligned}$$

(6.4)

From Lemma 6.4 (b) it follows that both (i) and (ii) of Lemma 6.5 is satisfied. Hence, using that from Proposition 2.3

$$\begin{aligned}&\left( \partial _t -\frac{1}{2} \varDelta _{\mathbf {h}}\right) z_{t,\varepsilon } \nonumber \\&\quad = \frac{1}{2 (z_{t,\varepsilon } + \varepsilon )^3} \left( \mathsf {\Gamma }^{\mathbf {v}^*}(P_{T-t} f) \mathsf {\Gamma }^{\mathbf {v}^*}_2(P_{T-t} f) - \frac{1}{4} \mathsf {\Gamma }^{\mathbf {h}^*}(\mathsf {\Gamma }^{\mathbf {v}^*}(P_{T-t} f)) \right) \ge 0, \end{aligned}$$

(6.5)

we get $P_T z_{T,\varepsilon } = P_T (\mathsf {\Gamma }^{\mathbf {v}^*}(f) + \varepsilon ^2 )^{1/2} - P_T \varepsilon \ge z_{0,\varepsilon } = (\mathsf {\Gamma }^{\mathbf {v}^*}(P_Tf) + \varepsilon ^2)^{1/2} - \varepsilon$. By letting $\varepsilon$ tend to 0, we obtain

$$\begin{aligned} \sqrt{\mathsf {\Gamma }^{\mathbf {v}^*}(P_Tf)} \le P_T \sqrt{\mathsf {\Gamma }^{\mathbf {v}^*}(f)}. \end{aligned}$$

(6.6)

Next, let $y_{t,\varepsilon } = \left( \mathsf {\Gamma }^{\mathbf {h}^*}(P_{T-t} f) + \varepsilon ^2 \right) ^{1/2} - \varepsilon$, choose any $\alpha > \max \{ -\rho _{\mathcal {H}}, \mathscr {M}_{\mathcal {HV}}^2 \} \ge 0$ and define

$$\begin{aligned} u_{t,\varepsilon } = e^{-\alpha /2(T-t)} \big (y_{t,\varepsilon } + \ell \mathsf {\Gamma }^{\mathbf {v}^*}(P_{T-t}(f)) \big ). \end{aligned}$$

Note first that

$$\begin{aligned}&\left( \frac{\partial }{\partial t} + \frac{1}{2} \varDelta _{\mathbf {h}}\right) u_{t,\varepsilon }\\&\quad = \frac{e^{-\alpha /2(T-t)}}{2 y_{t,\varepsilon } + 2 \varepsilon } \left( \mathsf {\Gamma }^{\mathbf {h}^*}_2(P_{T-t} f) + \ell y_{t,\varepsilon } \mathsf {\Gamma }^{\mathbf {v}^*}_2(P_{T-t} f) - \frac{1}{4y_{t,\varepsilon }^2} \mathsf {\Gamma }^{\mathbf {h}^*}(\mathsf {\Gamma }^{\mathbf {h}^*}(P_{T-t}f)) \right) \\&\qquad +\, \frac{\alpha e^{-\alpha /2(T-t)}}{2 y_{t,\varepsilon } + 2 \varepsilon } \left( \mathsf {\Gamma }^{\mathbf {h}^*}(P_{T-t} f) + \varepsilon + \ell y_{t,s} \mathsf {\Gamma }^{\mathbf {v}^*}(P_{T-t}f) \right) . \end{aligned}$$

We use Proposition 2.3 with $\ell$ replaced by $\ell y_{t,\varepsilon }$ to get

$$\begin{aligned} \frac{1}{4 y_{t,\varepsilon }^2} \mathsf {\Gamma }^{\mathbf {h}^*}(\mathsf {\Gamma }^{\mathbf {h}^*}(P_{T-t}f))&\le \mathsf {\Gamma }^{\mathbf {h}^*}_2(f) - (\rho _{\mathcal {H}}- c^{-1} - \ell ^{-1} y_{t,\varepsilon }^{-1}) \mathsf {\Gamma }^{\mathbf {h}^*}(f)\\&\quad +\, \ell y_{t,\varepsilon } \mathsf {\Gamma }^{\mathbf {v}^*}_2(f) - c \mathscr {M}_{\mathcal {HV}}^2 \mathsf {\Gamma }^{\mathbf {v}^*}(f). \end{aligned}$$

As a result, for any $c > 0$, $\left( \frac{\partial }{\partial t} + \frac{1}{2} \varDelta _{\mathbf {h}}\right) u_{t,\varepsilon }$ has lower bound

$$\begin{aligned}&\frac{e^{-\alpha /2(T-t)}}{2 y_{t,\varepsilon } + 2\varepsilon } \left( (\rho _{\mathcal {H}}- c^{-1} - \ell ^{-1} y_{t,\varepsilon }^{-1} ) \mathsf {\Gamma }^{\mathbf {h}^*}(P_{T-t} f) - c \mathscr {M}_{\mathcal {HV}}^2 \mathsf {\Gamma }^{\mathbf {v}^*}(P_{T-t} f) \right) \\&\quad + \frac{\alpha e^{-\alpha /2(T-t)}}{2 y_{t,\varepsilon } + 2\varepsilon } \left( \mathsf {\Gamma }^{\mathbf {h}^*}(P_{T-t} f) + \ell y_{t,\varepsilon } \mathsf {\Gamma }^{\mathbf {v}^*}(P_{T-t}f) \right) . \end{aligned}$$

Since it is true for any value of $c >0$, it remains true for $c = \ell y_{t,\varepsilon }$, and hence

$$\begin{aligned} \left( \frac{\partial }{\partial t} + \frac{1}{2} \varDelta _{\mathbf {h}}\right) u_{t,\varepsilon } \ge&- \frac{e^{-\alpha /2(T-t)}}{\ell }. \end{aligned}$$

In a similar way as before, we can verify that the conditions of Lemma 6.5 hold by using Lemma 6.4. We can hence conclude that

$$\begin{aligned} u_{0,\varepsilon }&= e^{-\alpha T/2} (y_{0,\varepsilon } + \ell \mathsf {\Gamma }^{\mathbf {v}^*}(P_Tf)) \\&\le P_T u_{T,\varepsilon } + \int _0^T P_t \frac{e^{-\alpha (T-t)/2}}{\ell } \, dt \\&\le P_T \left( y_{T,\varepsilon } + \ell \mathsf {\Gamma }^{\mathbf {v}^*}(f) \right) + \frac{2}{\alpha \ell } \left( 1- e^{- \alpha T/2} \right) . \end{aligned}$$

Multiplying with $e^{\alpha T/2}$ on both sides, letting $\varepsilon \rightarrow 0$ and $\alpha \rightarrow k := \max \{ - \rho _{\mathcal {H}}, {\mathscr {M}}_{\mathcal {R}}\}$, we finally get that for any $\ell > 0$,

$$\begin{aligned} \sqrt{\mathsf {\Gamma }^{\mathbf {h}^*}(P_Tf)} + \ell \mathsf {\Gamma }^{\mathbf {v}^*}(P_T f) \le e^{k T/2} P_T\left( \sqrt{\mathsf {\Gamma }^{\mathbf {h}^*}(f)} + \ell \mathsf {\Gamma }^{\mathbf {v}^*}(f) \right) + \ell ^{-1} F_k(T), \end{aligned}$$

(6.7)

where

$$\begin{aligned} F_k(t) = {\left\{ \begin{array}{ll} \frac{2}{k} ( e^{k t/2} - 1) &{} \text {if } k >0, \\ t &{} \text {if } k =0. \end{array}\right. } \end{aligned}$$

Since this estimate holds pointwise, it holds for $\ell = \big (P_T\mathsf {\Gamma }^{\mathbf {v}^*}(f)- \mathsf {\Gamma }^{\mathbf {v}^*}(P_Tf)\big )^{-1/2}$ or $\ell = \infty$ at points where $P_T \mathsf {\Gamma }^{\mathbf {v}^*}(f)- \mathsf {\Gamma }^{\mathbf {v}^*}(P_Tf) = 0$. The resulting inequality is

$$\begin{aligned} \sqrt{\mathsf {\Gamma }^{\mathbf {h}^*}(P_Tf)} \le e^{k T/2} P_T \sqrt{\mathsf {\Gamma }^{\mathbf {h}^*}(f)} + (e^{k T/2} +F_k(T)) \sqrt{P_T\mathsf {\Gamma }^{\mathbf {v}^*}(f)- \mathsf {\Gamma }^{\mathbf {v}^*}(P_tf)}. \end{aligned}$$

(6.8)

We will now show how this inequality implies (A). Since ${{\mathrm{\mathbf {g}}}}$ is complete, there exist a sequence of compactly supported functions $g_n \in C^\infty (M)$ satisfying $g_n \uparrow 1$ pointwise and $\Vert \mathsf {\Gamma }^{\mathbf {h}^* + \mathbf {v}^*}(g_n)\Vert _{L^\infty } \rightarrow 0.$ It follows from Eqs. (6.6) and (6.8) that

$$\begin{aligned} \lim _{n \rightarrow \infty } \Vert \mathsf {\Gamma }^{\mathbf {h}^* + \mathbf {v}^*}(P_t g_n)\Vert _{L^\infty } \rightarrow 0 \end{aligned}$$

as well. Hence, since $P_t g_n \rightarrow P_t 1$ and $\Vert dP_t g_n\Vert _{{{\mathrm{\mathbf {g}}}}^*}$ approach 0 uniformly, we have that $\mathsf {\Gamma }^{{{\mathrm{\mathbf {g}}}}^*}(P_t1) = 0$. It follows that $P_t1 = 1$.

To finish the proof, consider a smooth function $f \in C^\infty (M)$ with $\Vert f\Vert _{L^\infty } < \infty$ and $\Vert \mathsf {\Gamma }^{\mathbf {h}^* + \mathbf {v}^*}(f)\Vert _{L^\infty } < \infty .$ Define $f_n = g_n f \in C^\infty (M)$. Then $P_Tf_n \rightarrow P_T f$ pointwise. It follows that

$$\begin{aligned} \int _a^b dP_T f(\dot{\gamma }(t)) \, dt = \lim _{n\rightarrow \infty } \int _a^b dP_T f_n \left( \dot{\gamma }(t)\right) \, dt \end{aligned}$$

(6.9)

for any smooth curve $\gamma :[a,b] \rightarrow M$. We want to use the dominated convergence theorem to show that the integral sign and limit on the right side of (6.9) can be interchanged.

Without loss of generality, we may assume that $\Vert \mathsf {\Gamma }^{\mathbf {h}^*}(g_n)\Vert _{L^\infty } < 1$ for any n. We then note that

$$\begin{aligned} \left\| \sqrt{\mathsf {\Gamma }^{\mathbf {h}^* + \mathbf {v}^*}(f_n)} \right\| _{L^\infty } \le \Vert f\Vert _{L^\infty } + \left\| \sqrt{\mathsf {\Gamma }^{\mathbf {h}^*}(f)} \right\| _{L^\infty }=:K < \infty . \end{aligned}$$

This relation, combined with (6.6) and (6.8), gives us

$$\begin{aligned} \left\| \sqrt{ \mathsf {\Gamma }^{\mathbf {h}^*+ \mathbf {v}^*} (P_Tf_n) }\right\| _{L^\infty } \le \left( 2e^{kT/2} + F_k(T) +1 \right) K. \end{aligned}$$

Furthermore, the dominated convergence theorem tells us that both $P_T \mathsf {\Gamma }^{\mathbf {v}^*}(f_m-f_n)$ and $\lim _{n \rightarrow \infty } P_T \mathsf {\Gamma }^{\mathbf {h}^*}(f_n - f_m)$ approach 0 pointwise as $n,m \rightarrow \infty$. By inserting $f_n-f_m$ into (6.6) and (6.8), we see that $\mathsf {\Gamma }^{\mathbf {h}^* + \mathbf {v}^*}(P_T f_n)$ at any fixed point is a Cauchy sequence and hence convergent. We conclude that

$$\begin{aligned} \int _a^b dP_T f (\dot{\gamma }(t)) dt = \int _a^b \left( \lim _{n \rightarrow \infty } dP_T f_n\right) (\dot{\gamma }(t)) dt. \end{aligned}$$

It follows that $dP_t f - \lim _{n \rightarrow \infty } dP_t f$ vanishes outside a set of measure zero along any curve, so

$$\begin{aligned} \Vert \mathsf {\Gamma }^{\mathbf {h}^* + \mathbf {v}^*}(P_T f) \Vert _{L^\infty } = \lim _{n \rightarrow \infty } \Vert \mathsf {\Gamma }^{\mathbf {h}^* + \mathbf {v}^*}(P_T f_n ) \Vert _{L^\infty } < \infty . \end{aligned}$$

In conclusion, we have proven that condition (A) holds. Without any loss of generality we can put $\ell = 1$, since we can obtain all the other inequalities by replacing f with $\ell f$. $\square$

Remark 6.6

If we know that any $\frac{1}{2} \varDelta _{\mathbf {h}}$-diffusion starting at a point has infinite lifetime then using Lemma 6.4, we can actually make a probabilistic proof. We outline the proof here. We will only prove the inequality (6.6) as the proof of (6.7) is similar.

We will again use $z_{t,\varepsilon }$ as in (6.3). Let $X = X(x)$ be an $\frac{1}{2} \varDelta _{\mathbf {h}}$-diffusion with $X_0(x) = x \in M$. We define $Z^{\varepsilon }$ by $Z^{\varepsilon }_t = z_{t,\varepsilon } \circ X_t$. Then $Z^{\varepsilon }$ is a local submartingale by (6.5). By using the Burkholder-Davis-Gundy inequality, there exist a constant B such that

$$\begin{aligned} \mathbb {E}\left[ \sup _{0 \le s \le t} Z_s^{\varepsilon } \right] \le B \mathbb {E}\left[ \sqrt{ \langle Z^{\varepsilon } \rangle _{t } } \right] + z_{0,\varepsilon }(x) + \mathbb {E}\left[ \int _0^{t} \left( \partial _s - \frac{1}{2} \varDelta _{\mathbf {h}}\right) z_{s,\varepsilon } \circ X_s \,ds \right] \end{aligned}$$

where $\langle Z^{\varepsilon } \rangle _t = \int _0^t \mathsf {\Gamma }^{\mathbf {h}^*}(z_{s,\varepsilon }) \circ X_s\, ds$ is the quadratic variation of $Z^{\varepsilon }$. By the Cauchy–Schwartz inequality and the bound (6.4), we get the conclusion

$$\begin{aligned} \mathbb {E}\left[ \sqrt{ \langle Z^{\varepsilon } \rangle _t } \right] \le p_{2t}(x,x)\, \sqrt{ \int _0^t \Vert \mathsf {\Gamma }^{\mathbf {v}^*}_2(P_{T-s} f) \Vert _{L^1} \,dt} < \infty \end{aligned}$$

which means that $\mathbb {E}\left[ \sup _{0 \le s \le t \wedge \tau } Z_s^{\varepsilon } \right] <\infty$. Hence, $Z^{\varepsilon }$ is a true submartingale, giving us (6.6).

1.4 Interpretation of ${{\mathrm{Ric}}}_{\mathcal {HV}}$

Let $\mathcal {V}$ be any integrable subbundle. Choose a subbundle $\mathcal {H}$ such that $TM = \mathcal {H}\oplus \mathcal {V}$. Any such choice of $\mathcal {H}$ correspond uniquely to a constant rank endomorphism ${{\mathrm{pr}}}= {{\mathrm{pr}}}_{\mathcal {V}}: TM \rightarrow \mathcal {V}\subseteq TM$. This can be considered as a splitting of the short exact sequence $\mathcal {V}\rightarrow TM \mathop {\rightarrow }\limits ^{F} TM/\mathcal {V}.$

Let $\varOmega (M)$ be the the exterior algebra of M with ${{\mathrm{\mathbb {Z}}}}\times {{\mathrm{\mathbb {Z}}}}$-grading of Sect. 6.1. Choose nondegenerate metric tensors

on $\mathcal {V}$ and $TM/\mathcal {V}$. Since $\bigwedge ^\nu \mathcal {V}^* \oplus \bigwedge ^n (TM/\mathcal {V})^*$ is canonically isomorphic to $\bigwedge ^{n+\nu } T^*M$, the choices of $\mathbf {v}$ and gives us a volume form ${{\mathrm{vol}}}$ on M.

We also have an energy functional defined on projections to $\mathcal {V}$. Relative to ${{\mathrm{pr}}}$, define a Riemannian metric . We introduce a functional E on the space of projections ${{\mathrm{pr}}}$ by

$$\begin{aligned} E({{\mathrm{pr}}}) = \int _M \Vert \mathcal {R}_{{{\mathrm{pr}}}}\Vert ^2_{\wedge ^2 {{\mathrm{\mathbf {g}}}}_{{{\mathrm{pr}}}}^* \otimes {{\mathrm{\mathbf {g}}}}_{{{\mathrm{pr}}}}}\,d\hbox {vol}\end{aligned}$$

where $\mathcal {R}_{{{\mathrm{pr}}}}$ is the curvature of $\mathcal {H}= \ker {{\mathrm{pr}}}$. We can only be sure that the integral is finite if M is compact, so we will assume this, and consider our calculations as purely formal when this is not the case.

Let $\nabla = \nabla ^{{{\mathrm{pr}}}}$ be the restriction of the Levi-Civita connection of ${{\mathrm{\mathbf {g}}}}_{{{\mathrm{pr}}}}$ to $\mathcal {V}$. Introduce a exterior covariant derivative of $d_{\nabla }$ on $\mathcal {V}$-valued forms in the usual way, i.e. for any section $V \in \varGamma (\mathcal {V})$, we have and if $\alpha$ is a $\mathcal {V}$-valued k-form, while $\mu$ is a form in the usual sense, then

$$\begin{aligned} d_\nabla (\alpha \wedge \mu ) = (d_\nabla \alpha ) \wedge \mu + (-1)^k \alpha \wedge d\mu . \end{aligned}$$

We can split this operator into graded components $d_{\nabla } = d^{1,0}_{\nabla } + d^{0,1}_{\nabla } + d^{2,-1}_{\nabla }$ and do the same with its formal dual $\delta _{\nabla } = \delta ^{-1,0}_\nabla + \delta ^{0,-1}_{\nabla } + \delta _{\nabla }^{2,-1}$.

Proposition 6.7

The endomorphism ${{\mathrm{pr}}}$ is a critical value of E if and only if $\delta ^{-1,0}_{\nabla } \mathcal {R}= 0$. In particular, if ${{\mathrm{\mathbf {g}}}}$ satisfies

$$\begin{aligned} {{\mathrm{tr}}}_{\mathcal {V}} (\mathcal {L}_{A} {{\mathrm{\mathbf {g}}}})(\times , \times ) = 0, \quad \text {for any } A \in \varGamma (\mathcal {H}), \end{aligned}$$

(6.10)

then ${{\mathrm{pr}}}$ is a critical value if and only if ${{\mathrm{Ric}}}_{\mathcal {HV}}= 0.$

Recall from Part I, Sect. 2.4 that condition (6.10) is equivalent to the leafs of the foliation of $\mathcal {F}$ being minimal submanifolds. If $\mathcal {V}$ is the vertical bundle of a submersion $\pi :M \rightarrow B$, then we can identify $TM/\mathcal {V}$ with $\pi ^* TB$. In this case, a critical value of E can be considered as an optimal way of choosing an Ehresmann connection on $\pi$.

Proof

We write ${{\mathrm{id}}}:= {{\mathrm{id}}}_{TM}$ for the identity on TM. Let ${{\mathrm{pr}}}$ be a projection to $\mathcal {V}$ and $\alpha : TM \rightarrow \mathcal {V}$ be any $\mathcal {V}$-values one-from with $\mathcal {V}\subseteq \ker \alpha$. Define a curve in the space projections ${{\mathrm{pr}}}_t = {{\mathrm{pr}}}+ t\alpha$. Then

$$\begin{aligned} {{\mathrm{\mathbf {g}}}}_t(v,v) := {{\mathrm{\mathbf {g}}}}_{{{\mathrm{pr}}}_t}(v,v) = {{\mathrm{\mathbf {g}}}}_{{{\mathrm{pr}}}}(v,v) +2t \mathbf {v}(\alpha v, {{\mathrm{pr}}}v) + t^2 \mathbf {v}(\alpha v, \alpha v). \end{aligned}$$

Let $\mathcal {R}_t$ be the curvature of ${{\mathrm{pr}}}_t$. Then

$$\begin{aligned} \mathcal {R}_t(A,Z)&= \mathcal {R}(A,Z) + t \alpha [({{\mathrm{id}}}-{{\mathrm{pr}}}) A, ({{\mathrm{id}}}- {{\mathrm{pr}}})Z] \\&\quad - t \left( {{\mathrm{pr}}}[\alpha A, ({{\mathrm{id}}}-{{\mathrm{pr}}}) Z ] + {{\mathrm{pr}}}[ ({{\mathrm{id}}}-{{\mathrm{pr}}}) A, \alpha Z ]\right) + O(t^2). \end{aligned}$$

If $\nabla ^t = \nabla ^{{{\mathrm{pr}}}_t}$, then

where $(d_\nabla \alpha )_{1,1}$ is the (1,1)-graded component of $d_\nabla \alpha$ and

$$\begin{aligned} \mathbf {v}((d_{\nabla }\alpha )^\top _{1,1}(A,V_1),V_2) = \mathbf {v}((d_\nabla \alpha )_{1,1}(A,V_1),V_2). \end{aligned}$$

Since $\mathcal {R}_t = -d_{\nabla }^{2,-1} {{\mathrm{pr}}}_t$, we get

$$\begin{aligned} \left. \frac{d}{dt} E({{\mathrm{pr}}}_t) \right| _{t=0}&= \int _M (\wedge ^2 {{\mathrm{\mathbf {g}}}}_{{{\mathrm{pr}}}}^* \otimes {{\mathrm{\mathbf {g}}}}_{{{\mathrm{pr}}}})( d_{\nabla }^{2,-1} {{\mathrm{pr}}}, d_\nabla ^{1,0} \alpha )\,d\hbox {vol}\\&= - \int _M (\mathbf {h}^* \otimes \mathbf {v})(\delta _{\nabla }^{-1,0} \mathcal {R}, \alpha )\,d\hbox {vol}. \end{aligned}$$

Hence, ${{\mathrm{pr}}}$ is a critical value if and only if $\delta ^{-1,0}_\nabla \mathcal {R}=0$.

We give a local expression for this identity. Let $A_1, \ldots , A_n$ be a local orthonormal basis of $\mathcal {H}$. Then

where N is defined by ${{\mathrm{\mathbf {g}}}}_{{{\mathrm{pr}}}}(A,N) = - \frac{1}{2} {{\mathrm{tr}}}_{\mathcal {V}} (\mathcal {L}_{{{\mathrm{pr}}}_{\mathcal {H}} A} {{\mathrm{\mathbf {g}}}})(\times , \times )$ and is the (0,0)-degree component of the Levi-Civita connection, i.e.

This coincides with ${{\mathrm{Ric}}}_{\mathcal {HV}}$ when (6.10) holds. $\square$

1.5 If $\mathcal {V}$ is not integrable

Let $(M, {{\mathrm{\mathbf {g}}}})$ be a complete Riemannian manifold and let $\mathcal {H}$ be a bracket-generating subbundle of TM with orthogonal complement $\mathcal {V}$. Define $\mathring{\nabla }$ as in (2.1) with respect to ${{\mathrm{\mathbf {g}}}}$ and the splitting $TM = \mathcal {H}\oplus \mathcal {V}$ and assume that $\mathring{\nabla }{{\mathrm{\mathbf {g}}}}= 0$. Let $\varDelta _{\mathbf {h}}$ be the sub-Laplacian defined relative to $\mathcal {V}$ or equivalently to the volume form of ${{\mathrm{\mathbf {g}}}}$. Then it may happen that (CD) holds for $\varDelta _{\mathbf {h}}$ even without assuming that $\mathcal {V}$ is integrable. More precisely, we will need the condition

(6.11)

We refer to $\mathcal {R}$ and $\overline{\mathcal {R}}$ as respectively the curvature and the co-curvature of $\mathcal {H}$.

In Part I, Section 3.8, we showed that Theorem 2.2 and Proposition 2.3 hold with the same definitions and with $\mathcal {V}$ not integrable, as long as (6.11) also holds. The same is true for Theorem 3.4. We give some brief details regarding this.

First of all, in Sect. 6.1, the exterior derivative d now also has a part of degree $(-1,2)$, determined by

$$\begin{aligned} d^{-1,2} f =0, \quad d^{-1,2} \alpha = - \alpha \circ \overline{\mathcal {R}}, \qquad f \in C^\infty (M),\ \alpha \in \varGamma (T^*M), \end{aligned}$$

and hence, the co-differential has a degree $(1,-2)$-part. However, these do not have any significance for our calculations. More troubling is the fact that both Lemma 6.2 (a) and the formula for $\mathring{\nabla }_Z V_s|_{x_0}$ in Lemma 6.2 (b) are false when $\mathcal {V}$ is not integrable. However, (6.11) ensures that

$$\begin{aligned} \sum _{i=1}^n {{\mathrm{\mathbf {g}}}}(R^{\mathring{\nabla }}(A_i, V) Z, A_i)=0 \end{aligned}$$

for any orthonormal basis $A_1, \ldots , A_n$ of $\mathcal {H}$ and vertical vector field V, which is all we need for the proof of Lemma 6.1. Furthermore the same proof is still holds even if now in Lemma 6.2 (b), as the extra terms cancel out.

Once Lemma 6.1 holds, there is no problem with the rest of the proof of Theorem 3.4. See Part I, Section 4.6 for an example where this theorem holds.