Releasing information in private-value second-price auctions

Abstract

I investigate the incentives to release information in markets in which auctioneers running second-price auctions compete for buyers by releasing information about their products before buyers decide in which auction they wish to participate. I provide sufficient conditions for the existence of an equilibrium in which both sellers release information even if there are only two buyers in the market. This result is in contrast to previous findings reported in the literature showing that the optimal decision for a monopolist facing a fixed set of two buyers is to not release any information. Thus, the results of the paper suggest that competition between auctioneers strengthens the incentives to release information in markets in which selling mechanisms are second-price auctions.

Appendix: proofs

This appendix presents the proofs of all the results reported in the main text of the paper.

Proof

(Proposition 1) This proposition is proven as a special case of the more general result in which sellers choose between granting full access, partial access, or no access to information.

Proposition 5

Consider the two-stage game in which sellers grant full access, partial access, or no access to information in the first stage and buyers decide on which auction to participate in the second stage. There is a symmetric equilibrium of the buyers’ participation game in which the participation strategies of the two buyers are as follows:

• 1. In any subgame in which no seller grants access to information, each buyer visits seller A’s auction with a probability equal to .

• 2. In subgames in which one seller grants either full access or partial access to information and the other seller grants no access to information, there is a value $\omega ^{*}\in (\overline{\omega },\underline{\omega })$ such that buyers visit the seller who releases information with probability one if and only if their valuations of this seller’s object are greater than or equal to $\omega ^{*}$ and visit the other seller if and only if their valuations are lower than $\omega ^{*}$. The value $\omega ^{*}$ is given by the unique solution to:

  $$\begin{aligned} \omega ^{*}[G(\omega ^{*};p)]^{n-1}-\mu [(1-G(\omega ^{*};p)]^{n-1}=0 \end{aligned}$$

  (5)

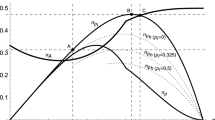
• 3. In subgames in which each seller grants either partial or full access to information, there exists a continuous and non-decreasing function $\rho :[0,1]\longrightarrow [0,1]$ such that a buyer with valuations $(\omega _{A},\omega _{B})$ visits the seller A with probability one if and only if $\omega _{B}\le \rho (\omega _{A})$ and visits seller B with probability one if and only if $\omega _{B}>\rho (\omega _{A})$. Moreover, if both sellers grant either partial access or full access to information, then the function $\rho$ is unique and equal to the identity function.

Proof

The proof of part (1) is straightforward and hence omitted. The proofs of parts (2) and (3) make use of the following lemma, which allows for focus on equilibria in which buyers use cutoff strategies.

Lemma 1

Let $\hat{\pi }$ be buyer i’s best response to the strategy profile $\pi$.

• (i) In any subgame in which only one seller (say seller A) grants some access to information, there exists a $\omega ^{*}\in [\underline{\omega },\overline{\omega }]$ such that the strategy $\pi ^{*}$ defined by

  $$\begin{aligned} \pi ^{*}(\omega _{A},\mu )={\left\{ \begin{array}{ll} 1 &{} \text { if }\ \omega _{A}\ge \omega ^{*}\\ 0 &{} \text { if }\ \omega _{A}<\omega ^{*} \end{array}\right. } \end{aligned}$$

  is also a best response to $\pi$.

• (ii) In any subgame in which both sellers grant either partial or full information, there exists a non-decreasing and continuous function $\rho$ such that the participation strategy $\pi ^{*}$ defined by

  $$\begin{aligned} \pi ^{*}(\omega _{A},\omega _{B})={\left\{ \begin{array}{ll} 1 &{} \text { if }\ \omega _{B}\le \rho (\omega _{A})\\ 0 &{} \text { if }\ \omega _{B}>\rho (\omega _{A}) \end{array}\right. } \end{aligned}$$

  is also a best response to $\hat{\pi }$.

Proof

Based on truthful bidding, i.i.d. valuations across both buyers and across sellers and standard incentive compatibility arguments, buyer i’s expected payoff if participating in seller j’s auction with a valuation $\omega _j$ given the other buyers’ participation strategy $\pi$ can be written as:

$$\begin{aligned} \mathscr {U}_{j}(\omega _{j};\pi )&=\int _{\underline{\omega }}^{\omega _{j}}Q_{j}(t;\pi )\text {d}t \end{aligned}$$

(6)

where $Q_{j}(\omega _{j};\pi )$, $j=A,B$, is the reduced-form probability of winning seller j’s object when buyer i has a valuation equal to $\omega _{j}$ and buyers other than buyer i use the participation strategy $\pi$. It is immediately clear that this payoff function is continuous (because its derivative is Lebesgue integrable), bounded above by one and below by zero, and strictly increasing over the interval $(\underline{\omega },\overline{\omega })$.

Consider case (i), i.e., the case in which only seller A grants some access to information. Buyer i’s expected payoff if participating in seller A’s auction can be written in the form of Eq. (6), whereas buyer i’s expected payoff if participating in seller B’s auction can be written as:

$$\begin{aligned} \mathscr {U}_B(\mu ;\pi )= \mu \left( \int _{0}^{1} \pi (t)\text {d}G(t;p) \right) ^{n-1} \end{aligned}$$

because every participant in seller B’s auction submits the same bid equal to $\mu$ and buyer i pockets a positive payoff if, and only if, he or she is alone in the auction. It is immediately clear that either $\mathscr {U}_A(\omega _A;\pi )\ge \mathscr {U}_B(\mu ;\pi )$ for all $\omega _A$ or $\mathscr {U}_A(\omega _A;\pi )< \mathscr {U}_B(\mu ;\pi )$ for $\omega _A$ less than some $\omega ^*$, and $\mathscr {U}_A(\omega _A;\pi )\ge \mathscr {U}_B(\mu ;\pi )$ for all $\omega _A$ greater than $\omega ^*$. It follows that buyer i’s best response $\hat{\pi }$ to the strategy profile $\pi$ must take the form of a cutoff strategy in any subgame in which only one seller releases information.

Next, consider case (ii), i.e., the subgame in which both sellers release some information. Suppose that $\mathscr {U}_{A}(\overline{\omega };\pi )=0$ and $\mathscr {U}_{B}(\overline{\omega };\pi )>0$. Let $\rho (\omega _{A})\equiv \underline{\omega }$. Therefore, the participation strategy

$$\begin{aligned} \pi ^{*}(\omega _{A},\omega _{B})={\left\{ \begin{array}{ll} 1 &{} \text { if }\omega _{B}\le \rho (\omega _{A})\\ 0 &{} \text { if }\omega _{B}>\rho (\omega _{A})\ \end{array}\right. } \end{aligned}$$

must be buyer i’s best response to $\pi$ because the payoff functions are not decreasing with respect to their own valuations, and hence, $\mathscr {U}_{A}(\omega _{A};\pi )\le \mathscr {U}_{A}(1;\pi )=0$ for all $\omega _{A}$, and $\mathscr {U}_{B}(\omega _{B};\pi )>0$ if $\omega _{B}>\underline{\omega }$. Similar reasoning applies to the cases in which $\mathscr {U}_{B}(1;\pi )=0$, where $\rho$ is defined as the constant function equal to $\overline{\omega }$. In all other cases, the intermediate value theorem allows, for each number $\omega _{A}\in [\underline{\omega },\overline{\omega }]$, the assignment of another number $\omega _{B}^{*}(\omega _{A})$ such that $\mathscr {U}_{A}(\omega _{A};\pi )=\mathscr {U}_{B}(\omega _{B}^{*}(\omega _{A});\pi )$ and $\rho (\omega _{A})\equiv \omega _{B}^{*}(\omega _{A})$. Moreover, because $\mathscr {U}_{A}(\cdot ;\pi )$ is non-decreasing, $\rho$ must also be non-decreasing. Continuity follows from continuity of the buyer’s payoff functions. $\square$

The proof of part (2) follows from (i) in Lemma 1 and what has been outlined in the main text of Sect. 4.1. To prove part (3), suppose that every buyer other than buyer i uses a symmetric participation strategy $\pi$ characterized by the continuous and non-decreasing function $\rho$. To simplify notation, let p and $p'$ denote the choices of information structures made by seller A and seller B, respectively, with the proviso that a value of p less than one denotes a seller A who has granted partial access to information, whereas a value of p equal to one denotes a seller A who has granted full access to information (and similarly for seller B). Finally, let $G(\omega _{A})=F\left( \frac{\omega _{A}-(1-p)\mu }{p}\right)$, $\omega _A \in [\underline{\omega },\overline{\omega }]=[(1-p)\mu ,p+(1-p)\mu ]$, and $H(\omega _{B})=F\left( \frac{\omega _{B}-(1-p')\mu }{p'}\right)$, $\omega _B\in [\underline{\omega }',\overline{\omega }']=[(1-p')\mu ,p'+(1-p')\mu ]$.

Buyer 1’s expected payoffs when valuations are $(\omega _{A},\omega _{B})$, and the other buyers use the symmetric participation strategy $\pi$ are

$$\begin{aligned} \mathscr {U}_{A}(\omega _{A};\rho )= & {} \max \left\{ 0;\int _{\underline{\omega }}^{\omega _{A}}\left[ 1-\int _{t}^{1}H(\rho (\tau ))\text {d}G(\tau )\right] ^{n-1}\text {d}t\right\} \end{aligned}$$

(7)

$$\begin{aligned} \mathscr {U}_{B}(\omega _{B};\rho )= & {} \max \left\{ 0;\int _{\underline{\omega }'}^{\omega _{B}}\left[ H(t)G(\rho ^{-1}(t))+\int _{\rho ^{-1}(t)}^{1}H(\rho (\tau ))\text {d}G(\tau )\right] ^{n-1}\text {d}t\right\} \nonumber \\ \end{aligned}$$

(8)

where $\rho ^{-1}(t)$ is defined as

$$\begin{aligned} \rho ^{-1}(t)={\left\{ \begin{array}{ll} 0 &{} \text {if }t<\rho (0)\\ \max \{s\in [0,1]:t\ge \rho (s)\} &{} \text {if }t\ge \rho (0) \end{array}\right. } \end{aligned}$$

The terms inside the integral in Eqs. (7) and (8) correspond to the probability of winning the seller’s object, which is equal to the probability that the other buyer either does not participate in the auction or he or she does so with a valuation lower than that of the buyer.

Let T be buyer 1’s best response, which is an operator mapping continuous and non-decreasing functions:

$$\begin{aligned} (T\rho )(\omega _{A})=\max _{t\in [0,1]}\left\{ t\,:\,\mathscr {U}_{B}(t;\rho )\le \mathscr {U}_{A}(\omega _{A};\rho )\right\} \end{aligned}$$

The following lemma establishes the existence of a non-empty interval within which the indifference condition

$$\begin{aligned} \mathscr {U}_{B}(T\rho (\omega _A);\rho )=\mathscr {U}_{A}(\omega _{A};\rho ) \end{aligned}$$

(9)

holds.

Lemma 2

There exists a value $\bar{v} \in (0,1]$ such that condition (9) holds for all $\omega _A \in [0,\bar{v}]$.

Proof

Let $\bar{v}_{A}=\max \{t\in [0,1]:\mathscr {U}_{A}(t;\pi ')\le \mathscr {U}_{B}(1;\pi ')\}$, where the payoff functions are given by Eqs. (7) and (8). Clearly, $\bar{v}_{A}>0$ because $\bar{v}_{A}=0$ requires $\mathscr {U}_{B}(\cdot ;\rho ')=0$, which cannot happen because $\rho '$ is continuous and non-decreasing and $\rho '(\cdot )\equiv 0$ is not a fixed point of T. Therefore, the intermediate value theorem implies the existence of a number $v_{B}^{*}(v_{A})$ such that $\mathscr {U}_{A}(v_{A};\rho ')=\mathscr {U}_{B}(v_{B}^{*}(v_{A});\rho ')$ for every $v_{A}\in [0,\bar{v}_{A}]$. Furthermore, this number must be unique because $\mathscr {U}_{B}(\cdot ;\rho ')$ is strictly increasing in $v_{B}$. $\square$

Lemma 2 guarantees that

$$\begin{aligned} \frac{\text {d}\rho '(v_{A})}{\text {d}v_{A}}=\left( \frac{1-\int _{v_{A}}^{1}F(\rho '(t))f(t)\text {d}t}{F(\rho '(v_{A}))F(\rho ^{'-1}(\rho '(v_{A}))+\int _{\rho ^{'-1}(\rho '(v_{A}))}^{1}F(\rho '(t))f(t)\text {d}t}\right) ^{n-1} \end{aligned}$$

(10)

holds $\forall v_{A}\in (0,\bar{v}_{A})$, because $\mathscr {U}_{A}(v_{A};\rho ')=\mathscr {U}_{B}(\rho '(v_{A});\rho ')$ holds for every $v_{A}$ within this interval. Therefore, the existence of a fixed point of T can be found by showing existence of a solution to the IVP problem formed by the integro-differential equation (10), and the initial condition $T\rho (\omega _A)=\underline{\omega }$.

Lemma 3

There exists a continuous and increasing function $z:[\underline{\omega },\overline{\omega }]\rightarrow \mathbb {R}$ satisfying

$$\begin{aligned} \frac{\text {d}z(t)}{\text {d}t}&=\left( \frac{1-\int _{t}^{1}H(z(s))\text {d}G(s)}{H(z(t))G(t)+\int _{t}^{1}H(z(t))\text {d}G(t)}\right) ^{n-1}\\ z(\underline{\omega })&=\underline{\omega }' \end{aligned}$$

(IVP)

such that the function $\rho ^{*}(\omega _{A}):=\min \{z(\omega _{A});\overline{\omega }'\}$ is a fixed point of T.

Proof

To avoid the potential problem of a denominator equal to zero in the above integro-differential equation, the existence of a solution to this IVP is shown indirectly. First, it is shown that a pair of continuous functions that solves the following auxiliary problem exists:

$$\begin{aligned} \frac{\text {d}\phi (t)}{\text {d}t}&=\left( \frac{1-\phi _{2}(t)}{H(\phi _{1}(t))G(t)+\phi _{2}(t)}\right) ^{n-1}\\ \frac{\text {d}\phi _{2}(t)}{\text {d}t}&=-H(\phi _{1}(t))\text {d}G(t)\\ \phi _{1}(\underline{\omega })&=\underline{\omega }'\\ \phi _{2}(\underline{\omega })&=\theta \end{aligned}$$

(IVP′)

where $\theta \in (0,1)$ is a constant parameter. Second, the family of solutions $\left\{ (\phi _{1}^{\theta };\phi _{2}^{\theta })\right\} _{\theta \in (0,1)}$ is used to show existence of a root $\theta ^{*}$ to the equation

$$\begin{aligned} \phi _{2}^{\theta }(\overline{\omega })=0 \end{aligned}$$

(11)

which is then used to express the function $\phi _{2}^{\theta ^{*}}$ in terms of $\phi _{1}^{\theta ^{*}}$ as follows:

$$\begin{aligned} \phi _{2}^{\theta ^{*}}(\omega )&=\phi _{2}^{\theta ^{*}}(\overline{\omega })+\int _{\omega }^{\overline{\omega }}H(\phi _{1}^{\theta ^{*}}(t))\text {d}G(t)\\&=\int _{\omega }^{\overline{\omega }}H(\phi _{1}^{\theta ^{*}}(t))\text {d}G(t)\,\text {d}dt \end{aligned}$$

Finally, substituting $\phi _{2}^{\theta ^{*}}$ into the auxiliary IVP problem yields a continuous and increasing function $\phi _{1}^{\theta ^{*}}$ that by construction satisfies:

$$\begin{aligned} \frac{\text {d}z(t)}{\text {d}t}&=\left( \frac{1-\int _{t}^{1}H(z(s))\text {d}G(s)}{H(z(t))G(t)+\int _{t}^{1}H(z(t))\text {d}G(t)}\right) ^{n-1}\\ z(\underline{\omega })&=\underline{\omega }' \end{aligned}$$

(IVP)

which is the desired result.

Consider the problem IVP$^{\prime }$. Let $\theta \in (0,1)$ be a constant parameter and define the domain:

$$\begin{aligned} D=\left\{ (t,y_{1},y_{2})\in \mathbb {R}^{3}:\underline{\omega }\le t\le \overline{\omega };\,\underline{\omega }'\le y_{1}<\overline{\omega }';\,\theta \le y_{2}\le 1\right\} \end{aligned}$$

and the mapping $\Gamma :D\rightarrow \mathbb {R}^{2}$ by $\Gamma (t,\mathbf {y})=\left[ \gamma _{1}(t,\mathbf {y});\gamma _{2}(t,\mathbf {y})\right]$, $\mathbf {y}=(y_{1},y_{2})\in \mathbb {R}^{2}$, where

$$\begin{aligned} \gamma _{1}(t,\mathbf {y})= & {} \left( \frac{1-y_{2}}{H(y_{1})G(t)+y_{2}}\right) ^{n-1}\\ \gamma _{2}(t,\mathbf {y})= & {} -H(y_{1})\text {d}G(t) \end{aligned}$$

Clearly $\gamma _{1}(t,\mathbf {y})$ and $\gamma _{2}(t,\mathbf {y})$ are uniformly continuous functions of t because (i) $y_{2}\ge \theta >0$ and $H(y_{1})G(t)\ge 0$; (ii) $H(\cdot )$ and $G(\cdot )$ are continuously differentiable functions, bounded below by zero and above by one, and (iii) t belongs to a compact interval. Furthermore, the denominator of $\gamma _{1}$ is bounded below by $\theta$, and hence, $\Gamma (t,\mathbf {y})$ is Lipschitz continuous with respect to its second argument. Finally, $|\gamma _{1}(t,\mathbf {y})|\le \frac{1-\theta }{\theta }$ and $|\gamma _{2}(t,\mathbf {y})|\le \bar{f}$, where $\bar{f}$ is a bound for the density function f and $\Gamma (t,\mathbf {y})$ is a bounded function.

Consider the space $\mathscr {C}$ of continuous vector-valued functions $\phi =(\phi _{1},\phi _{2})$, defined on $[\underline{\omega },\overline{\omega }]$ equipped with the $\sup$ norm, and let $\mathscr {D}=\{\phi \in \mathscr {C}:\,\Vert \phi _{1}(t)-\underline{\omega }\ \Vert \le \frac{1-\theta }{\theta };\Vert \phi _{2}(t)-\theta \Vert \le \bar{f}\}$ be a subset of $\mathscr {C}$ whose graph belongs to D. The set $\mathscr {D}$ is a convex, closed, and bounded subset of Banach space. Let K be the operator defined on $\mathscr {D}$ by:

$$\begin{aligned} (K\phi )(t)&=\phi _{0}+\int _{\underline{\omega }}^{\omega }\Gamma (\tau ,\phi (\tau ))\text {d}\tau \\ \phi _{0}&=(\underline{\omega }';\theta ) \end{aligned}$$

where the integral term should be understood as a tuple of integrals. It is immediately clear that $(K\phi )$ is a continuous vector-valued function whose graph belongs to $\mathscr {D}$. Hence, K maps $\mathscr {D}$ onto itself. Moreover, K is a continuous operator because $\Gamma (t,\cdot )$ is Lipschitz continuous with respect to its second argument. Therefore, based on the Schauder fixed-point theorem, K admits a fixed point.

Let $\phi ^{\theta }=(\phi _{1}^{\theta },\phi _{2}^{\theta })$ be a solution to (IVP’). Integrate $\phi _{2}^{\theta }$ from $\underline{\omega }$ to $\omega$, and let $\psi (\theta )\equiv \phi _{2}^{\theta }(\overline{\omega })$:

$$\begin{aligned} \psi (\theta )=\theta -\int _{\underline{\omega }}^{\overline{\omega }}H(\phi _{1}^{\theta }(\tau ))dG(\tau )\text {d}\tau \end{aligned}$$

(12)

The function $\psi (\theta )$ is continuous with respect to $\theta$ because standard considerations in the theory of differential equations (e.g., Kreider et al. 1968, Theorems 9–12) ensure that $\phi ^{\theta }=(\phi _{1}^{\theta },\phi _{2}^{\theta })$ is continuously differentiable with respect to $\theta \in (0,1)$. Furthermore, because $H(\omega )$ is bounded above by one and below by zero, $\theta -1<\psi (\theta )<\theta$. Therefore, $\psi (\theta )<0$ for sufficiently small values of $\theta$, and $\psi (\theta )>0$ for values of $\theta$ sufficiently close to one, from which it follows that there is at least one $\theta ^{*}\in (0,1)$ such that $\psi (\theta ^{*})=0$. Take any such $\theta ^{*}$ and let $\phi ^{\theta ^{*}}=(\phi _{1}^{\theta ^{*}},\phi _{2}^{\theta ^{*}})$ be a solution to the problem (IVP$^{\prime }$) when $\theta =\theta ^{*}$. Integrating $\frac{\text {d}\phi _{2}^{\theta ^{*}}(t)}{\text {d}t}$ from $\omega$ to $\overline{\omega }$ yields

$$\begin{aligned} \phi _{2}^{\theta ^{*}}(\omega )= & {} \phi _{2}^{\theta ^{*}}(\overline{\omega })+\int _{\omega }^{\overline{\omega }}H(\phi _{1}^{\theta ^{*}}(t))\text {d}G(t)\\= & {} \int _{\omega }^{\overline{\omega }}H(\phi _{1}^{\theta ^{*}}(t))\text {d}G(t) \end{aligned}$$

because $\phi _{2}^{\theta ^{*}}(\overline{\omega })\equiv \psi (\theta ^{*})=0$. $\phi _{2}^{\theta ^{*}}(\underline{\omega })=\theta ^{*}<1$, and $\phi _{2}^{\theta ^{*}}(t)<\phi _{2}^{\theta ^{*}}(\underline{\omega })$ because $\frac{\text {d}\phi _{2}^{\theta ^{*}}(t)}{\text {d}t}<0$, $1-\phi _{2}^{\theta ^{*}}(t)>0$. Therefore, $\phi _{1}^{\theta ^{*}}$ is increasing and continuous. Moreover, replacing $\phi _{2}^{\theta ^{*}}$ in the first and third equations of (IVP$^{\prime }$) yields

$$\begin{aligned} \frac{\text {d}\phi _{1}^{\theta ^{*}}(t)}{\text {d}t}&=\left( \frac{1-\int _{\omega }^{\overline{\omega }}H(\phi _{1}^{\theta ^{*}}(t))\text {d}G(t)}{H(\phi _{1}^{\theta ^{*}}(t))G(t)+\int _{t}^{1}H(\phi _{1}^{\theta ^{*}}(t))\text {d}G(t)}\right) ^{n-1}\\ \phi _{1}^{\theta ^{*}}(\underline{\omega })&=\underline{\omega }' \end{aligned}$$

and $\phi _{1}^{\theta ^{*}}$ solves the problem (IVP). $\square$

Lemma 3 ensures the existence of a continuous and increasing function $\rho ^{*}$ such that the participation strategy $\pi ^{*}$,

$$\begin{aligned} \pi ^{*}(\omega _{A},\omega _{B})={\left\{ \begin{array}{ll} 1 &{} \text {if }\omega _{B}\le \rho ^{*}(\omega _{A})\\ 0 &{} \text {if }\omega _{B}>\rho ^{*}(\omega _{A}) \end{array}\right. } \end{aligned}$$

(13)

describes a symmetric equilibrium of a subgame in which both sellers release some information. Next, it is proven that $\rho ^{*}(v_{A})=v_{A}$ in any subgame in which either both sellers grant either partial or full access to information. For simplicity, suppose that both sellers grant full access to information and that buyers other than buyer i use the cutoff $\rho ^{*}(v_{A})=v_{A}$. Based on Eqs. (7) and (8), buyer i’s expected payoffs when valuations are $(v_{A},v_{B})$ and other buyers use the participation strategy $\pi ^{*}$ with cutoff $\rho ^{*}(v_{A})=v_{A}$ become:

$$\begin{aligned} \mathscr {U}_{A}(v_{A};\pi ^{*})&:=\int _{0}^{v_{A}}\left( \frac{1}{2}+\frac{F^{2}(t)}{2}\right) ^{n-1}\text {d}t\\ \mathscr {U}_{2}(v_{B};\pi ^{*})&=\int _{0}^{v_{B}}\left( \frac{1}{2}+\frac{F^{2}(t)}{2}\right) ^{n-1}\text {d}t \end{aligned}$$

It is immediately clear that $\mathscr {U}_{A}(v_{A};\rho ^{*})\ge \mathscr {U}_{B}(v_{B};\rho ^{*})$ if and only if $v_{A}\ge v_{B}$, from which it follows that using the participation strategy $\pi ^{*}$ with cutoff $\rho ^{*}$ must be buyer 1’s best response to $\pi ^{*}$. The uniqueness of this cutoff function is shown by contradiction. Suppose that T admits another fixed point $\rho '$ such that the participation strategy $\pi '$,

$$\begin{aligned} \pi '(\omega _{A},\omega _{B})={\left\{ \begin{array}{ll} 1 &{} \text {if }\omega _{B}\le \rho '(\omega _{A})\\ 0 &{} \text {if }\omega _{B}>\rho '(\omega _{A}) \end{array}\right. } \end{aligned}$$

also is a symmetric equilibrium participation strategy of the subgame. The function $\rho '$ must differ from $\rho ^{*}$ within the whole (0, 1) interval, or it must cross $\rho ^{*}$ at least once within $(0,\bar{v}_{A})$. If $\rho '(v_{A})>\rho ^{*}(v_{A})$, then $\frac{\text {d}\rho '(v_{A})}{\text {d}v_{A}}<1$ based on Eq. (10), and hence,

$$\begin{aligned} \rho '(v_{A})&=\rho '(0)+\int _{0}^{v_{A}}\frac{\text {d}\rho '(t)}{\text {d}t}\text {d}t\\&<\rho ^{*}(0)+\int _{0}^{v_{A}}\frac{\text {d}\rho ^{*}(t)}{\text {d}t}\text {d}t\\&=\rho ^{*}(v_{A}) \end{aligned}$$

which is a contradiction. If $\rho '$ crosses $\rho ^{*}$ at some point $\hat{v}_{A}\in (0,1)$ such that $\rho '(v_{A})>\rho ^{*}(v_{A})$ for all $v_{A}>\hat{v}_{A}$, then the slope of $\rho '$ evaluated at $v_{A}=\hat{v}_{A}$ must be less than one because $\rho '(\hat{v}_{A})=\rho ^{*}(\hat{v}_{A})$ and $\rho '(\hat{v}_{A})>\rho ^{*}(\hat{v}_{A})$ imply that $\rho '^{-1}(\rho '(\hat{v}_{A}))=\rho ^{*-1}(\rho ^{*}(\hat{v}_{A}))$, and $\left. \frac{\text {d}\rho '(v_{A})}{\text {d}v_{A}}\right| _{v_{A}=\hat{v}_{A}}<1$. However, a slope less than one implies that $\rho '$ must cut $\rho ^{*}$ from above, and hence, there must exist a $\varepsilon >0$ such that $\rho '(v_{A})<\rho ^{*}(v_{A})$ for $v_{A}\in (\hat{v}_{A},\hat{v}_{A}+\varepsilon )$, which contradicts the fact that $\rho '(v_{A})>\rho ^{*}(v_{A})$ for all $v_{A}>\hat{v}_{A}$. A similar argument shows that $\rho '(v_{A})>\rho ^{*}(v_{A})$ for all $v_{A}>\hat{v}_{A}$ cannot hold either. Therefore, $\rho '$ and $\rho ^{*}$ must coincide, and T must admit a unique fixed point $\rho ^{*}(v_{A})=v_{A}$ in any subgame in which both sellers grant either partial or full access to information. $\square$

Proof

(Proposition 2) The following lemma is instrumental in proving this proposition.

Lemma 4

Let $v^{*}$ be the cutoff used by buyers to decide which auction to participate in when only one seller releases information. If $\mu \le m$, then $\mu \le v^{*}\le m$ with strict inequality if $\mu <m$. Similarly, if $\mu > m$, then $m< v^{*} < \mu$.

Proof

Define $\xi :[0,1]\rightarrow [0,1]$ as follows:

$$\begin{aligned} \xi (t):=tF(t)^{n-1}-\mu (1-F(t))^{n-1} \end{aligned}$$

It is immediately clear that $\xi$ is continuous and strictly increasing and that $\xi (v^{*})=0$ because $v^{*}$ satisfies Eq. (1) in Proposition 1. If $\mu =m$, then $\xi (m)=\xi (\mu )=0$, and $v^{*}=\mu =m$. If $\mu <m$, then $F(\mu )<F(m)=\frac{1}{2}$ and hence $\xi (\mu )=\mu \left( F(\mu )^{n-1}-(1-F(\mu ))^{n-1}\right) <\xi (v^{*})=0$ and $\xi (m)=(m-\mu )\left( \frac{1}{2}\right) ^{n-1}>\xi (v^{*})=0$ because $\xi$ is a strictly increasing function and $\mu <m$. Furthermore, $\xi$ has a unique strictly increasing inverse, and hence, $\psi (\mu )<\xi (v^{*})<\xi (m)$ implies $\mu<v^{*}<m$. A similar argument shows that $m< v^{*} < \mu$ if $m < \mu$. $\square$

Consider the case in which a seller expects a rival to not release information. Based on Proposition 1, not releasing information will induce a visiting probability equal to and an expected price equal to $\mu$, whereas releasing information will induce a visiting probability equal to $(1-F(v^{*}))$ and an expected price equal to the expected value of the second-highest valuation conditional on valuations being greater than the cutoff value $v^{*}$. From Lemma 4, condition (I) implies $\mu \le v^* \le m$, and hence, (i) $1-F(v^{*})\ge \frac{1}{2}$ and (ii) bids are never lower than $v^{*}$, and hence, higher than $\mu$. Therefore, if condition (I) holds, then releasing information yields a higher expected traffic and a higher expected price, and hence, a higher payoff than not releasing information when the seller’s rival does not release information.

Next, consider the case in which a seller expects a rival to release information. By not releasing information, the seller induces a visiting probability equal to $F(v^{*})$ and an expected price equal to $\mu$. Alternatively, by releasing information the seller induces a visiting probability equal to $\int _{0}^{1}F(v_{A})\text {d}F(v_{A})=\frac{1}{2}$ and an expected price equal to the expected value of the second-highest valuation conditional on valuations of the seller’s object being greater than their valuations of the rival’s. If condition (I) holds, then Lemma 4 ensures $F(v^{*})\le \frac{1}{2}$. If condition (II) holds, the expected value of the second-highest valuation conditional on participation is always greater than $\mu$. Therefore, releasing information yields a higher payoff than not releasing information when the seller’s rival releases information, and releasing information must be a dominant strategy for the sellers. $\square$

Proof

(Theorem 1) As outlined in the main text, the proof consists in showing that either condition in the Theorem is sufficient for conditions (I) and (II) in Proposition 2 to hold.

Condition 1 in the theorem implies a mean weakly lower than the median of $F(\cdot )$ because this c.d.f. is a strictly increasing and convex function with an increasing inverse. Condition 2 also implies a mean weakly lower than the median because this condition ensures that $F^{-1}(t)+F^{-1}(1-t)$ is non-decreasing for , and because , $F^{-1}(t)+F^{-1}(1-t) \le 2m$ for $0< t< 1$, and

(for details, see Van Zwet (1979)). Therefore, either condition in the theorem ensures that condition (I) in proposition 2 holds true.

Next, we show that each condition in the theorem is sufficient for the expected value of the second-highest valuation conditional on participation when both sellers release information to be higher than $\mu$. Let $\mu _{k}$ be the expected value of the second-highest valuation in any seller’s auction conditional on both sellers releasing information and the seller being matched with exactly k buyers, $k\ge 2$. To prove the claim, it is sufficient to show that $\mu _{2}\ge \mu$ because the distribution of the second-highest valuation when $k+1$ buyers are matched with the seller dominates, in the first-order stochastic sense, the distribution of this order statistic when the seller is matched with only k buyers, and hence $\mu _{k+1}\ge \mu _{k}$, $k\ge 2$.

Because buyers visit the seller’s auction with probability one whenever their valuation of this seller’s object is greater than their valuation of the rival’s, the distribution of valuations conditional on participation must be equal to $F^{2}(v)$. This c.d.f. induces a distribution of the second-highest valuation when the seller is matched with two buyers equal to $Z(t)=\left[ F^{2}(v)\right] ^{2}+2\left[ F^{2}(v)\right] \left[ 1-F^{2}(v)\right]$. Therefore, integration by parts yields:

$$\begin{aligned} \mu _{2}&=\int _{0}^{1}t\,\text {d}Z(t)\\&=1-\int _{0}^{1}\left\{ 2F^{2}(v)-F^{4}(v)\right\} \text {d}v \end{aligned}$$

and

$$\begin{aligned} \mu _{2}-\mu =\int _{0}^{1}I(u)\omega (u)du \end{aligned}$$

where $u:=F(v)$, $I(u)=u-2u^{2}+u^{4}$, and $\omega (u)=\frac{1}{f(F^{-1}(u))}$. Suppose that condition 1 in the theorem holds true. Therefore, $\omega '(u)=-\frac{f'(F^{-1}(u))}{f^{2}(F^{-1}(u))}\le 0$ because $f'(\cdot )\ge 0$, and

$$\begin{aligned} \mu _{2}-\mu&=\omega (1)\left( \int _{0}^{1}I(u)du\right) -\int _{0}^{1}\left( \int _{0}^{u}I(t)dt\right) \omega '(u)\text {d}u\\&>0 \end{aligned}$$

after integration by parts because $\omega (1)=\frac{1}{f(1)}>0$, and $\int _{0}^{u}I(t)\text {d}t\ge 0$, for all $u\in [0,1]$, with strict inequality if $u\in (0,1)$. Next, suppose that condition 2 holds true. Because the polynomial I(u) is equal to zero when $u=0$, $u=1$, and $u=\bar{u}\approx 0.618$, strictly positive for $0<u<\bar{u}$ and strictly negative for $\bar{u}<u<1$,

$$\begin{aligned} \int _{0}^{1/2}I(u)\omega (u)\text {d}u&=\int _{0}^{\bar{t}}I(u)\omega (u)\text {d}u+\int _{\bar{t}}^{1/2}I(u)\omega (u)\text {d}u\\&>\int _{\bar{t}}^{1/2}I(u)\omega (u)\text {d}u \end{aligned}$$

$\bar{t}=1-\bar{u}$, and

$$\begin{aligned} \int _{0}^{1/2}I(1-t)\omega (1-t)\text {d}t&=\int _{0}^{\bar{t}}I(1-t)\omega (1-t)\text {d}t+\int _{\bar{t}}^{1/2}I(1-t)\omega (1-t)\text {d}t\\&<\int _{\bar{t}}^{1/2}I(1-t)\omega (1-t)\text {d}t \end{aligned}$$

because $\omega (u)\ge \omega (1-u)$ for all as $f(F^{-1}(t))\le f(F^{-1}(1-t))$ for all $0<t<\frac{1}{2}$. Therefore,

$$\begin{aligned} \mu _{2}-\mu&=\int _{0}^{1/2}I(u)\omega (u)\text {d}u-\int _{0}^{1/2}I(1-t)\omega (1-t)\text {d}t\\&>\int _{\bar{t}}^{1/2}I(u)\omega (u)\text {d}u-\int _{\bar{t}}^{1/2}I(1-t)\omega (1-t)\text {d}t\\&\ge 0 \end{aligned}$$

where the last inequality holds because $I(t)-I(1-t)\ge 0$ for $t\in [\bar{t},1/2]$. Therefore, $\mu _{2}>\mu$, and hence, $\mu _{k}\ge \mu$ for all $k=2,\ldots ,n$.

It follows that either condition in the theorem is sufficient for conditions (I) and (II) in Proposition 2 to hold, and hence, for the game to have a unique equilibrium in which both sellers release information. $\square$

Proof

(Proposition 3) The proof consists in showing the existence of some $n^*$ such that if $n>n^*$ then not releasing information is never a best response. Without loss of generality, consider seller A, and suppose that seller B does not release information. By not releasing information, seller A expects a payoff equal to

$$\begin{aligned} V(0,0)&=(1-Z(m))\mu \end{aligned}$$

where $Z(t):=F^n(t)+nF^{n-1}(t)(1-F(t))$. Alternatively, by releasing information, seller A expects a payoff equal to

$$\begin{aligned} V(1,0)&=n(n-1)\int _{v^*}^1 t(1-F(t))F^{n-2}(t)f(t)\text {d}t\\&= 1 - v^*Z(v^*)-\int _{v^*}^1 Z(t)\text {d}t \end{aligned}$$

where the second line follows from integration by parts. If $\mu \le m$, then $\mu \le v^* \le m$ based on part 1 of Lemma 4, and hence,

$$\begin{aligned} V(1,0)&= 1 - v^*Z(v^*)-\int _{v^*}^1 Z(t)\text {d}t\\&>(1-Z(v^*))v^*\\&\ge (1-Z(m))\mu \\&=V(0,0) \end{aligned}$$

because $v^*\ge \mu$, and $v^* \le m$ implies $Z(v^*)\le Z(m)$. If $\mu >m$, then $m<v^* <\mu$ based on the same arguments used to prove part 1 of Lemma 4. Hence,

$$\begin{aligned} V(1,0)&>1-\mu Z(\mu ) - \int _{\mu }^1 Z(t)\text {d}t\\&>(1-Z(\mu ))\mu \end{aligned}$$

for all n. Because Z(t) is increasing in t and $\mu >m$, $Z(\mu )>Z(m)$ and $Z(\mu )$ tends to zero at a much faster rate than Z(m). Therefore, there must exist some $n_1$ such that $V(1,0)-V(0,0)>0$ for all $n>n_1$.

Next, suppose that seller B releases information. Let $\tilde{Z}(t)=Q^n(t)+nQ^{n-1}(t)(1-Q(t)$, where $Q(t)=\left( \frac{1}{2} + \frac{F^2(t)}{2}\right)$ is the probability that a buyer with valuation equal to t wins seller A’s object. Use integration by parts to write seller A’s payoff when releasing information as follows:

$$\begin{aligned} V(1,1)&=n(n-1)\int _0^1 t(1-Q(t))Q^{n-2}(t)\text {d}Q(t)\\&=1- \int _{0}^{1}\tilde{Z}(t)\text {d}t \end{aligned}$$

Define the mapping $\eta (n)$ by

$$\begin{aligned} \eta (n):= \int _0^1 \left\{ \tilde{Z}(t) - F(t) \right\} \text {d}t \end{aligned}$$

Clearly, $\eta (n)$ decreases with n, $\eta (2)>0$, and $\eta (n)< 0$ for sufficiently large n. Let $n_2$ be the lowest value of n such that $\eta (n)<0$ for all $n>n_2$. Therefore, for all $n>n_2$,

$$\begin{aligned} V(1,1) - \mu&= \int _0^1 \left\{ F(t) - \tilde{Z}(t) \right\} \text {d}t\\&>0 \end{aligned}$$

and seller A must be better off releasing information in response to a seller B who also releases information because seller A’s expected payoff if not releasing information is at most equal to $\mu$. Consequently, if $n>n^{*}:=\max \{n_{1},n_2\}$, then not releasing information is never a best response for the sellers and the probability with which any seller does not release information in equilibrium must be nil. $\square$

Proof

(Proposition 4) The proof of part (1) consists in showing that under conditions (I$^{\prime }$), (II$^{\prime }$), and (III$^{\prime }$), not releasing information and releasing information are best responses to each other.

Suppose that seller B does release information. By not releasing information, seller A induces a visiting probability equal to $F(v^*)$ and an expected price equal to $\mu$. Alternatively, by releasing information, the seller induces a visiting probability equal to and an expected price equal to the expected value of the second-highest valuation conditional on participation. Based on condition (I$^{\prime }$), $m<\mu$ and hence, $m<v^* <\mu$ from Lemma 4. Therefore, , and each buyer visits seller A more often when this seller does not release information. Furthermore, from condition (II$^{\prime }$), the expected value of the second-highest valuation conditional on both sellers releasing information and the seller being matched with exactly n buyers, $\mu _n$, must be lower than $\mu$:

$$\begin{aligned} \mu _n {-} \mu&= \left( 1- \int _0^1 \left\{ [F^2(t)]^n+n[F^2(t)]^{n-1}(1-F^2(t))\right\} \text {d}t\right) - \left( 1-\int _0^1 F(t)\text {d}t \right) \\&=\left( \int _0^1 \left\{ F(t) - [F^2(t)]^n-n[F^2(t)]^{n-1}(1-F^2(t))\right\} \text {d}t \right) \\&\le 0 \end{aligned}$$

Therefore, the price expected by a seller who is matched with k buyers, $k\le n$, must be lower than $\mu$ because the distribution of the second-highest valuation when the seller is matched with $k+1$ buyers dominates, in the first-order stochastic sense, the distribution of this order statistic when the seller is matched with only k buyers. Overall, this finding implies that under conditions (I$^{\prime }$) and (II$^{\prime }$) seller A is better off not releasing information in response to a seller B who releases information.

Now consider a seller B who does not release information. From the proof of Proposition 3, seller A’s expected payoff if not releasing information is:

$$\begin{aligned} V(0,0)=\left( 1-\left( \frac{1}{2}\right) ^n - n\left( \frac{1}{2}\right) ^n\right) \mu \end{aligned}$$

and seller A’s expected payoff if releasing information is:

$$\begin{aligned} V(1,0) = n(n-1)\int _{v^*}^1 t(1-F(t))F^{n-2}(t)f(t)\text {d}t \end{aligned}$$

which, after integration by parts, can be written as:

$$\begin{aligned} V(1,0) = n\int _{v^*}^1 \phi (t)F^{n-1}(t)f(t)\text {d}t - n\mu (1-F(v^*))^n \end{aligned}$$

where $\phi (t)=\left( t-\frac{1-F(t)}{f(t)}\right)$. Because $m<v^*<\mu$ from condition 1, . Hence,

$$\begin{aligned} V(1,0)&> \int _{\mu }^1 \left( t-\frac{1-F(t)}{f(t)}\right) \text {d}F^{n}(t) - n\mu \left( \frac{1}{2}\right) ^n\\ \end{aligned}$$

Thus, under condition (III$^{\prime }$),

$$\begin{aligned} V(1,0) - V(0,0)&> \int _{\mu }^1 \phi (t)\text {d}F^{n} -\left( 1-\left( \frac{1}{2}\right) ^n\right) \mu \\&\ge 0 \end{aligned}$$

and the seller A is better off releasing information against a seller B who does not do so.

The proof of part (2) consists in showing that under conditions (I$^{\prime }$) and (IV$^{\prime }$) not releasing information is a best response to itself. Under condition (I$^{\prime }$), $m<v^*<\mu$, and hence,

$$\begin{aligned} V(1,0) - V(0,0)&< \int _{m}^1 \phi (t)\text {d}F^{n} -\left( 1-\left( \frac{1}{2}\right) ^n\right) \mu \\&\le 0 \end{aligned}$$

where the last inequality follows from condition (IV$^{\prime }$). Therefore, not releasing information must be seller A’s best response to seller B’s decision of not releasing information, and the game must yield an equilibrium in which no seller releases information. $\square$

Proof

(Theorem 2) Existence of an equilibrium in which buyers use the symmetric participation strategy given by Proposition 5 is guaranteed because the seller’s action space is finite. The rest of the proof consists in showing that not releasing information is never a best response.

In what follows, take the perspective of seller A and consider any $p \in (0,1)$. Because the conditions of Theorem 1 hold true, giving full access to information is seller A’s best response whenever seller B either denies access to information or grants full access to it. Thus, suppose that seller B grants partial access to information. By mimicking seller B’s choice (i.e., by giving partial access to information), seller A expects a payoff equal to

$$\begin{aligned} V(p,p){=}n(n-1)\int _{\underline{\omega }}^{\overline{\omega }}\omega \left( \frac{1}{2}+\frac{G^{2}(\omega ;p)}{2}\right) ^{n-2}\left( \frac{1}{2}-\frac{G^{2}(\omega ;p)}{2}\right) G(\omega ;p)\text {d}G(\omega ;p) \end{aligned}$$

where $\underline{\omega }=(1-p)\mu$ and $\overline{\omega }=p+(1-p)\mu$. By a change of variables, V(p, p) can be written as follows:

$$\begin{aligned} V(p,p)=n(n-1)\int _{0}^{1}(pt+(1-p)\mu )H(t)^{n-2}(1-H(t))\text {d}H(t) \end{aligned}$$

where $H(t)=\left( \frac{1}{2}+\frac{F^{2}(t)}{2}\right)$. By integrating by parts, this payoff becomes

$$\begin{aligned} V(p,p)=p\int _{0}^{1}t\text {d}Z(t)+\left( 1-p\right) \mu (1-Z(0)) \end{aligned}$$

where $Z(t)=H^{n}(t)+nH^{n-1}(t)(1-H(t))$. Alternatively, by denying access to information, seller A induces a continuation equilibrium in which buyers whose estimates of seller B’s object are below the cutoff value $\omega ^{*}$ that solves Eq. (5) visit the auction with probability one. Therefore, seller A’s payoff if not releasing information is:

$$\begin{aligned} V(0,p)= & {} \left( 1-(1-G(\omega ^{*};p))^{n}-nG(\omega ^{*};p)(1-G(\omega ^{*};p))^{n-1}\right) \mu \end{aligned}$$

where $G(\cdot ;p)=F\left( \frac{\omega -(1-p)\mu }{p}\right)$. Under the conditions outlined in Theorem 1, $\mu \le \omega ^{*}\le m$ irrespective of p by the exact same arguments used in Lemma 4. Therefore, $G(\omega ^{*};p)\le \frac{1}{2}$, and thus,

$$\begin{aligned} V(0,p)&=\left( 1-(1-G(\omega ^{*};p))^{n}-nG(\omega ^{*};p)(1-G(\omega ^{*};p))^{n-1}\right) \mu \\&\le \left( 1-\left( \frac{1}{2}\right) ^{n}-n\left( \frac{1}{2}\right) ^{n}\right) \mu \\&=V(0,0) \end{aligned}$$

Because conditions (1) and (2) in Theorem 1 hold, , and $\mu _2 \ge \mu$, $k=2,\ldots ,n$, where $\mu _k$ is the expected value of the second-highest valuation conditional on both sellers releasing information and the seller being matched with exactly k buyers, $k\ge 2$. Write the seller’s expected payoff when both sellers release information as follows:

$$\begin{aligned} V(1,1)&= \sum _{k=2}^n \left( {\begin{array}{c}n\\ k\end{array}}\right) \left( \frac{1}{2} \right) ^n \mu _k\\&> \left( 1-\left( \frac{1}{2}\right) ^n - n\left( \frac{1}{2}\right) ^n \right) \mu _2\\&\ge \left( 1-\left( \frac{1}{2}\right) ^n - n\left( \frac{1}{2}\right) ^n \right) \mu \\&= (1-Z(0))\mu \\&= V(0,0) \end{aligned}$$

where the second line follows because the distribution of the second-highest valuation when $k+1$ buyers are matched with the seller dominates in the first-order stochastic sense, the distribution of this order statistics when the seller is matched with only k buyers. Therefore,

$$\begin{aligned} V(p,p)&= p\int _{0}^{1}t\,\text {d}Z(t)+\left( 1-p\right) \mu (1-Z(0))\\&= p\left( \int _{0}^{1}t\,\text {d}Z(t) - \mu (1-Z(0))\right) + (1-Z(0))\mu \\&= p(V(1,1)-V(0,0)) + V(0,0)\\&>V(0,0)\\&\ge V(0,p) \end{aligned}$$

and seller A is better off mimicking seller B’s choice when the probability with which signals reveal the truth about valuations is equal to p. It follows that not releasing information is never a best response for the sellers, which completes the proof. $\square$