Abstract
The upper tail of the firm size distribution is often assumed to follow a Power Law. Several recent papers, using different estimators and different data sets, conclude that the Zipf Law, in particular, provides a good fit, implying that the fraction of firms with size above a given value is inversely proportional to the value itself. In this article we compare the asymptotic and small sample properties of different methods through which this conclusion has been reached. We find that the family of estimators most widely adopted, based on an OLS regression, is in fact unreliable and basically useless for appropriate inference. This finding raises doubts about previously identified Zipf behavior. Based on extensive numerical analysis, we recommend the adoption of the Hill estimator over any other method when individual observations are available.


Similar content being viewed by others
Notes
Notice however that the common practice is to not report explicitly the t-test. An exception is in di Giovanni and Levchenko (2010).
In principle, there exist alternative ways to test the validity of the Zipf Law. For instance, one can compare goodness-of-fit measures in the upper tail of the estimated distribution or rely upon information criteria based on likelihood ratios for nested models.
A huge literature studies the asymptotic and small sample behavior of the original Hill statistic under departures from the assumption of Power Law distributed data. The common approach is to focus on the case where the underlying distribution obeys conditions defining max-stable laws. Along these lines, weak consistency was proved in Mason (1982) under the condition that, as N → ∞, k → ∞ and k/N → 0; Hall (1982) established asymptotic normality; bias and asymptotic variance are studied in Pictet et al. (1998); Resnick and Starica (1998) provide an extension to dependent observations. Relatedly, another line of research compares the performance of the Hill statistic against other tail index estimators, when confronted with data artificially generated from a number of different distributions with different tail behaviors. See Pictet et al. (1998), De Haan and Peng (1998), and Weron (2001), and the references therein.
It is reported that this cut-off roughly corresponds to an institutional threshold on annual sales (750,000 Euro) that defines different accounting standards in place in France for firms above or below the threshold.
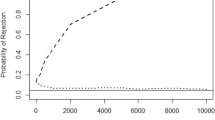
Convergence is already reached with this sample size, so results are informative also for even larger sample sizes encountered in the literature, such as in di Giovanni et al. (2011).
We report CDF and PDF estimates with 15 bins, given the smaller bias found above as compared to the 40 bins case.
As in previous section, CDF and PDF estimates are computed with 15 bins, given the superior performance as compared to the 40-bins version.
Gibrat’s Law of proportionate effects prescribes β = 1 and i.i.d. shocks. Deviations with β < 1 are usually observed form smaller firms, together with a negative relationship between variance of growth shocks and initial size, which also contradicts the Law. The Laplacian or nearly Laplacian of the shocks has been found to be robust and invariant across countries and also across sectors, even at different level of sectoral aggregation. See Amaral et al. (1997), Bottazzi and Secchi (2006), Bottazzi et al. (2011), and Bottazzi et al. (2014).
We also experimented with different values of σ and Gaussian growth shocks. Results are basically identical and available upon request.
Binned estimators employ 15 bins.
References
Amaral L, Buldyrev S, Havlin S, Maass P, Salinger M, Stanley H, Stanley M (1997) Scaling behavior in economics: The problem of quantifying company growth. Physica A 244:1–24
Axtell RL (2001) Zipf Distribution of U.S. Firm Sizes. Sci 293:1818–1820
Beirlant J, Dierckx G, Goegebeur Y, Matthys G (1999) Tail Index Estimation and an Exponential Regression Model. Extremes 2:177–200
Beirlant J, Vynckier P, Teugels J (1996) Tail Index Estimation, Pareto Quantile Plots, and Regression Diagnostics. J Am Stat Assoc 91:1659–1667
Bottazzi G, Coad A, Jacoby N, Secchi A (2011) Corporate Growth and Industrial Dynamics: Evidence from French Manufacturing. Appl Econ:43
Bottazzi G, Secchi A (2006) Explaining the Distribution of Firms Growth Rates. The RAND J Econ 37:235–256
Bottazzi G, Secchi A, Tamagni F (2014) Financial constraints and firm dynamics. Small Bus Econ 42:99–116
Danielsonn J, Haan LD, Peng L, Vries CGD (2001) Using a Bootstrap Method to Choose the Sample Fraction in Tail Index Estimation. J Multivar Anal 76:226–248
De Haan L, Peng L (1998) Comparison of tail index estimators. Statistica Neerlandica 52:60–70
de Wit G (2005) Firm size distributions: An overview of steady-state distributions resulting from firm dynamics models. Int J Ind Organ 23:423–450
di Giovanni J, Levchenko AA (2010) Firm Entry, Trade, and Welfare in Zipf’s World, NBER Working Papers 16313, National Bureau of Economic Research
di Giovanni J, Levchenko AA, Ranciére R (2011) Power laws in firm size and openness to trade: Measurement and implications. J Int Econ 85:42–52
DuMouchel WH (1983) Estimating the Stable Index α in Order to Measure Tail Thickness: A Critique. The Ann Stat 11:1019–1031
Fujiwara Y, Guilmi CD, Aoyama H, Gallegati M, Souma W (2003) Do Pareto-Zipf and Gibrat laws hold true? An analysis with European Firms, Quantitative Finance Papers. arXiv:cond-mat/0310061
Gabaix X (2009) Power Laws in Economics and Finance. Ann Rev Econ 1:255–293. also available as NBER Working Paper n. 14299
Gabaix X, Ibragimov R (2011) Rank-1/2: A Simple Way to Improve the OLS Estimation of Tail Exponents. J Bus Econ Stat 29:24–39
Gabaix X, Landier A (2008) Why Has CEO Pay Increased So Much?. The Q J Econ 123:49–100
Hall P (1982) On Some Simple Estimates of an Exponent of Regular Variation. J Royal Stat Soc. Series B (Methodological) 44:37–42
Hall P, Welsh A (1985) Adaptive Estimates of Regular Variation. The Ann Stat 13:331–341
Hill B (1975) A Simple General Approach to Inference About the Tail of a Distribution. The Ann Stat 3:1163–1174
Johnson NL, Kotz S, Balakrishnan N (1994) Continuous univariate distributions. Wiley, New York
Kleiber C, Kotz S (2003) Statistical Size Distributions in Economics and Actuarial Sciences. Wiley, New York
Luttmer EGJ (2007) Selection, growth and the size distribution of firms. The Q J Econ 122:1103–1144
Mason DM (1982) Laws of Large Numbers for Sums of Extreme Values. The Ann Probab 10:754–764
Newman M (2005) Power Laws, Pareto Distributions and Zipf’s Law. Contemp Phys 46:323–351
Okuyama K, Takayasu M, Takayasu H (1999) Zipf’s law in income distribution of companies. Physica A 269:125–131
Pareto V (1886) Sur la courbe de la répartition de la richesse, Université de Lousanne English translation:. Rivista di Politica Economica 87(1997):645–700
Pictet OV, Dacorogna MM, Muller UA (1998) Hill, Bootstrap and Jacknife Estimator for Heavy Tails in. In: Feldman ARJRE, Taqqu MS (eds) A Practical Guide to Heavy Tails. Birkhauser, Boston, pp 283–310
Podobnik B, Horvatic D, Petersen AM, Urosevic B, Stanley EH (2010) Bankruptcy risk model and empirical tests. Proc National Acad Sci USA 107:18325–18330
Resnick S, Starica C (1997) Smoothing the Hill estimator. Adv Appl Probab 29:273–293
Resnick S, Starica C (1998) Tail Index Estimation for Dependent Data. The Ann Appl Probab 8:1156–1183
Silverman B (1986) Density estimation for statistics and data analysis. Chapman and Hall, London
Weron R (2001) Levy-stable distributions revisited: tail index > 2 does not exclude the Levy-stable regime. Int J Mod Phys C 12:209–223
Zipf GK (1932) Selected Studies of the Principle of Relative Frequency in Language. Librairie du Recuil Sirey, Paris
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was partially supported by the Italian Ministry of University and Research, grant PRIN 2009 “The growth of firms and countries: distributional properties and economic determinants”, prot. 2009H8WPX5.
Appendix
Appendix
To keep comparability with Gabaix and Ibragimov (2011), in Tables 4 and 5 we extend their analysis of AR(1) and MA(1) data to all the estimators considered in this article, although these types of time dependence are more compelling for applications in finance. We design the Monte Carlo exactly as in Gabaix and Ibragimov (2011).
For the case of AR(1) DGP, we generate R = 10,000 random samples of size N = 2,000 extracted from the AR(1) process
with 𝜖 extracted from Eq. 4.1, for a given combination of the values of c and ρ. On each sample we apply all the estimators for two different tail widths, i.e. including either the top–50 or the top–500 observations in the tails. We then repeat the Monte Carlo tests for different values of the parameters.
In Table 4, we report the average of point estimates across the 10,000 runs, together with asymptotic (theoretical) and sampled standard errors, as well as rejection rates of a t-test (at 5 % level) of the true null of unitary tail index performed at each run. First, consider the sensitivity to the AR(1) structure, setting aside the impact of the sub-asymptotic correction (i.e., set c = 0 and vary ρ), and take the case when the top–50 observations are considered. Although all the rejection rates are above the theoretical 5 %, the results provide a clear ranking. First, the CDF and PDF estimators both severely over-reject. Second, among the other three estimators, the Rank −1/2 is over-performing the others. However, if we take the top–500 observations in the tail, then the frequency at which the true null of unitary tail index is mistakenly rejected rapidly grows to above 50 % for all the estimators. Similar conclusions emerge when we let both c and ρ vary at the same time.
Table 5 replicates the analysis to study the properties under the MA(1) process
with 𝜖 ∼ (4.1). As before, we simulate R = 10,000 random samples of size N = 2,000 with varying c and θ, and again compare the behavior of the estimators for different tail width (top–50 and top–500 observations). The findings for θ = 0 obviously replicate the analysis on AR(1) with ρ = 0. Further, if we switch off the sub-asymptotic correction (i.e. set c = 0, and vary θ), we observe that, first, the CDF and PDF estimators are once again unreliable, with very high rejection rates. Second, although rejection rates are above the theoretical 5 % for all the methods, the Rank and Rank −1/2 estimators perform better (smaller rejection rates) than the other methods. The Rank performs slightly better if the tail includes the top-50 observations, while the Rank −1/2 is slightly better for the top–500 observations. Third, the patterns are similar when we let c and θ vary together. If anything, we notice that the rejection rates associated with all the estimators rapidly increase to above 20 % if we take the top-500 observations in the tail. Conversely, they are less dependent from the parameters in the top-50 exercise.
Rights and permissions
About this article
Cite this article
Bottazzi, G., Pirino, D. & Tamagni, F. Zipf law and the firm size distribution: a critical discussion of popular estimators. J Evol Econ 25, 585–610 (2015). https://doi.org/10.1007/s00191-015-0395-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00191-015-0395-7