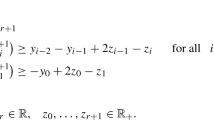First order solutions in conic programming

Abstract

We study the order of maximizers in linear conic programming (CP) as well as stability issues related to this. We do this by taking a semi-infinite view on conic programs: a linear conic problem can be formulated as a special instance of a linear semi-infinite program (SIP), for which characterizations of the stability of first order maximizers are well-known. However, conic problems are highly special SIPs, and therefore these general SIP-results are not valid for CP. We discuss the differences between CP and general SIP concerning the structure and results for stability of first order maximizers, and we present necessary and sufficient conditions for the stability of first order maximizers in CP.

1 Introduction

We consider linear conic problems (CP) of the form

where $c \in {\mathbb {R}}^n$, $B, A_1, \dots , A_n \in \mathcal {S}_{m}$ and a cone ${\mathcal {K}} \subseteq \mathcal {S}_{m}$ are given. Here, $\mathcal {S}_{m}$ denotes the set of real symmetric $m \times m$-matrices. Throughout the paper, we assume that ${\mathcal {K}}$ is a proper (i.e., full-dimensional, pointed, closed, convex) cone. The corresponding dual problem is

where $\langle B,Y \rangle := {{\mathrm{trace}}}(BY)$ denotes the inner product of $B, Y \in \mathcal {S}_{m}$, and ${\mathcal {K}}^*$ is the dual cone of ${\mathcal {K}}$, i.e. ${\mathcal {K}}^* := \{ Y \in \mathcal {S}_{m} \mid \langle Y, X\rangle \ge 0 \text { for all } X \in {\mathcal {K}} \}$.

Special choices for the cone ${\mathcal {K}}$ lead to the following well studied problem classes:

• Linear programming (LP), if ${\mathcal {K}} = {\mathcal {K}}^* = \mathcal {N}_{m} := \{ A =(a_{ij}) \in \mathcal {S}_{m} \mid a_{ij} \ge 0 \text { for all } i,j\}.$

• Semidefinite programming (SDP), if ${\mathcal {K}} = {\mathcal {K}}^* = \mathcal {S}^+_{m} := \{ A \in \mathcal {S}_{m} \mid y^T A y \ge 0 \text { for all } y \in {\mathbb {R}}^m\}$, the cone of positive semidefinite matrices.

• Copositive programming (COP), if ${\mathcal {K}} = \mathcal {COP}_{m}$ is the set of copositive matrices and ${\mathcal {K}}^* = \mathcal {CP}_{m}$ is the cone of completely positive matrices. Here $\mathcal {COP}_{m} := \{ A \in \mathcal {S}_{m} \mid y^T A y \ge 0 \text { for all } y \in {\mathbb {R}}^m_+\}$ and $(\mathcal {COP}_{m})^* = \mathcal {CP}_{m} := \{ A \in \mathcal {S}_{m} \mid A= \sum _{i=1}^N b_i b_i^T \text { with } b_i \in {\mathbb {R}}^m_+ , \; N \in \mathbb {N}\}$.

Without loss of generality, we make the following assumption throughout the paper:

Assumption 1.1

The objective vector c is nonzero and the matrices $A_1, \dots , A_n$, are linearly independent, i.e. they span an n-dimensional linear space ${\mathcal {L}} := {{\mathrm{lin}}}\{A_1, \ldots , A_n \}$ in $\mathcal {S}_{m}$.

Note that under this assumption the matrix X in the feasibility condition for (P) is uniquely determined by $x \in {\mathbb {R}}^n$. Thus, we will refer to both X and x as a feasible point of problem (P). We denote the feasible sets of (P) resp. (D) by ${\mathcal {F}}_P$ resp. ${\mathcal {F}}_D$.

In the present paper, we are interested in the so-called order of optimizers.

Definition 1.2

A feasible solution $\overline{x}$ (or ${\overline{X}}$) of (P) is called a maximizer of order $p>0$ if there exist $\gamma > 0$ and $\varepsilon > 0$ such that

$$\begin{aligned} c^T \overline{x} - c^T x \ge \gamma \Vert x - \overline{x} \Vert ^{p} \quad \text { for all } x \in {\mathcal {F}}_P \text { with } \Vert x - {\overline{x}}\Vert < \varepsilon . \end{aligned}$$

Note that if ${\overline{x}}$ is a maximizer of order $p >0$, then obviously ${\overline{x}}$ is a unique maximizer. Moreover, by definition a maximizer of order p is also a maximizer of order $p' > p$.

The order of an optimal solution provides information about its “sharpness”: the smaller the order, the sharper is the maximizer. Geometrically, the order is related to the curvature of the feasible set around the optimal solution ${\overline{x}}$. Therefore, the order of maximizers may differ depending on the geometry of the cone ${\mathcal {K}}$. The following is known:

• In LP, since there is no curvature, any unique maximizer is a first order maximizer.

• In SDP or COP, maximizers of order 1, 2 and of arbitrarily high order are possible, see Ahmed et al. (2013).

• In SDP, generically all maximizers are at least of order 2, see Shapiro (1997). We expect that this also holds for COP.

• For the case that the cone ${\mathcal {K}}$ is semialgebraic (such as the semidefinite or copositive cone), a partial genericity result with respect to the parameter c is given in Bolte et al. (2011): it is shown that in this case, for fixed B and $A_i$ generically wrt. $c \in {\mathbb {R}}^n$ the maximizers are of second order.

To explain what is meant by genericity, we have to properly define the set of problems. Given ${\mathcal {K}}$ and $n,m \in \mathbb {N}$, the set of instances of conic problems (P) and (D) is parametrized by

$$\begin{aligned} \Pi _{{{\mathrm{CP}}}} = \left\{ Q=(c,B,A_1, \ldots ,A_n) \in {\mathbb {R}}^n \times (\mathcal {S}_{m})^{n+1} \right\} \equiv {\mathbb {R}}^{n + (n+1) \cdot \frac{(m+1)m}{2}}. \end{aligned}$$

(1.1)

We endow this space with the topology given by the distance $d(Q, Q') = \Vert Q - Q' \Vert$ for $Q,Q' \in \Pi _{{{\mathrm{CP}}}}$, where $\Vert \cdot \Vert$ is some norm on $\Pi _{{{\mathrm{CP}}}}$. A property is then said to hold generically for CP if it holds for a subset $\mathcal {P}_r \subset \Pi _{{{\mathrm{CP}}}}$ such that with the Lebesgue measure $\mu$ we have

$$\begin{aligned} \mu (\Pi _{CP} \setminus \mathcal {P}_r) = 0 \quad \text { and } \quad \mathcal {P}_r \text { is open (stability)}. \end{aligned}$$

We say that a property is stable at an instance ${\overline{Q}}\in \Pi _{{{\mathrm{CP}}}}$ if the property is satisfied for all $Q \in \Pi _{{{\mathrm{CP}}}}$ in an open neighborhood of ${\overline{Q}}$. By a slight abuse of terminology, we will call X a stable maximizer of order p for some instance ${\overline{Q}}$, if X is a maximizer of order p of the corresponding program (P) and for sufficiently small perturbations of ${\overline{Q}}$ the maximizer of the resulting problem is also of order p.

As mentioned above, in a semidefinite program generically an optimal solution is at least of order two. However, stable first order maximizers do occur (see Examples in Sect. 3 and Remark 3.9). We expect the same situation for general non-polyhedral semialgebraic cones such as the copositive cone. In this respect, first order maximizers are especially “nice”, sharp maximizers which also may occur in the generic situation. Therefore, in what follows we are particularly interested in characterizations of optimizers of order 1 and their stability.

In semi-infinite optimization (SIP), characterizations of first order solutions as well as their stability properties are well-studied, see e.g., Fischer (1991), Goberna and Lopez (1998), Nürnberger (1985), Hettich and Kortanek (1993), Helbig and Todorov (1998). Since CP is a special case of SIP, one might expect that these results can be directly translated to CP. It turns out that this is indeed the case for characterizations of first order optimizers, but since CP is a very specially structured subclass of SIP, this is not true for stability statements.

The aim of this paper is to express and interpret the characterizations of first order maximizers for SIP in the context of conic programming, and to analyse the stability behaviour of first order maximizers. In particular, we show how the SIP-conditions for stability have to be modified in the CP context.

The paper is organized as follows. In Sect. 2, we give a short introduction to conic and semi-infinite programming and provide useful definitions. In Sect. 3, we discuss different characterizations of first order maximizers in terms of conic programming. Section 4 recalls the stability results for first order maximizers in general SIP and shows why these results are not valid in CP. We present approriate conditions for CP and provide necessary and sufficient conditions for the stability of first order maximizers in CP. Finally, in Sect. 5, we shortly discuss first order minimizers for the dual problem (D).

2 Preliminaries

In this section, we consider CP as a special case of linear semi-infinite programming and provide definitions used later on.

We denote the interior, relative interior, boundary, convex conic hull, linear span and dimension of a set S as ${{\mathrm{int}}}S$, ${{\mathrm{ri}}}S$, ${{\mathrm{bd}}}S$, ${{\mathrm{cone}}}S$, ${{\mathrm{lin}}}S$, and $\dim S$, respectively.

A continuous linear semi-infinite program (SIP) is a problem of the form

$$\begin{aligned} (SIP): \quad \max \; c^Tx \quad \text {s.t.} \quad b(Y) - a(Y)^T x \ge 0 \quad \text { for all } Y \in Z, \end{aligned}$$

(2.1)

where $Z \subset {\mathbb {R}}^M$ is a compact infinite or finite index set and $a: Z \rightarrow {\mathbb {R}}^n, \; b: Z \rightarrow {\mathbb {R}}$ are continuous functions. Since the cone ${\mathcal {K}}$ is closed, we can write the feasibility conditions for $X:= B- \sum _{i=1}^n x_i A_i$ in (P) as

$$\begin{aligned} \langle X, Y \rangle \ge 0 \;\text { for all }\; Y \in Z = {\mathcal {K}}^*_1 := \{ Y \in {\mathcal {K}}^* \mid \Vert Y\Vert =1 \}. \end{aligned}$$

Here $\Vert Y\Vert$ denotes a norm on $\mathcal {S}_{m}$ (e.g., the Frobenius norm $\Vert Y \Vert = {{\mathrm{trace}}}(YY)$). Using $\langle X, Y \rangle = \langle B, Y \rangle - \sum _{i=1}^n x_i \langle A_i, Y \rangle$, the primal conic program (P) can obviously be written equivalently in form of a SIP as in (2.1) with the special functions

$$\begin{aligned} b(Y) := \langle B , Y \rangle \quad \text {and} \quad a(Y) := ( \langle A_1, Y \rangle , \dots , \langle A_n, Y \rangle )^T \end{aligned}$$

(2.2)

which are linear in Y. Note that for general linear SIP of the form (2.1) the function a(Y) can be any continuous function.

For $X \in {\mathcal {F}}_P$, we define the set of active indices I(X) and the so-called moment cone M(X) by

$$\begin{aligned} I(X) := \{ Y \in {\mathcal {K}}^*_1 \mid \langle X, Y \rangle =0 \} \quad \text {and} \quad M(X):= {{\mathrm{cone}}}\{ a(Y_j) \mid Y_j \in I(X) \}. \end{aligned}$$

(2.3)

Definition 2.1

 [Slater condition]  The Slater condition is said to hold for (P), resp. (D), if there exist $X \in {\mathcal {F}}_P$, resp. $Y \in {\mathcal {F}}_D$ such that

$$\begin{aligned} X \in {{\mathrm{int}}}{\mathcal {K}}, \quad \text { resp. }\quad Y \in {{\mathrm{int}}}{\mathcal {K}}^*. \end{aligned}$$

In linear continuous SIP, we say that the feasible set ${\mathcal {F}}_{SIP}$ of (2.1) satisfies the Slater condition if there exists $x_0$ such that

$$\begin{aligned} b(Y) - a(Y)^T x_0 > 0 \quad \text { for all } Y \in Z. \end{aligned}$$

It is not difficult to show (see Ahmed et al. 2013) that for the SIP formulation of CP with a(Y) and b(Y) as in (2.2) this is equivalent to the primal Slater condition in Definition 2.1.

As usual, we say with respect to the SIP formulation that ${\overline{x}}\in {\mathcal {F}}_P$ or ${\overline{X}}\in {\mathcal {F}}_P$ satisfies the Karush–Kuhn–Tucker condition (KKT), if there exist $k \in \mathbb {N}$, $Y_j \in I(\overline{X})$ and multipliers $y_j > 0$, $j=1, \ldots , k$, such that

$$\begin{aligned} c = \sum _{j=1}^k y_j a(Y_j) \qquad \text {or equivalently} \qquad c \in M({\overline{X}}). \end{aligned}$$

(2.4)

Note that if ${\overline{X}}\in {\mathcal {F}}_P$ satisfies the KKT condition, then ${\overline{X}}$ is a maximizer of (P), and since $\langle {\overline{X}}, \sum _{j=1}^k y_j Y_j \rangle = 0$, the matrix

$$\begin{aligned} {\overline{Y}}:= \sum \limits _{j=1}^k y_j Y_j \in {\mathcal {F}}_D \end{aligned}$$

is a complementary optimal solution of (D). It is well-known that under the primal Slater condition, the KKT condition is also necessary for optimality of ${\overline{X}}\in {\mathcal {F}}_P$.

Now let us introduce some definitions from conic programming. Given $X \in {\mathcal {K}}$, we denote the minimal face of the cone ${\mathcal {K}}$ containing X by ${{\mathrm{face}}}( X, {\mathcal {K}} )$, and the minimal face of ${\mathcal {K}}^*$ containing $Y \in {\mathcal {K}}^*$ by ${{\mathrm{face}}}(Y, {\mathcal {K}}^*)$, and we define

$$\begin{aligned} {{\mathrm{J}}}(X) := {{\mathrm{face}}}( X, {\mathcal {K}} ) \quad \text { and }\quad {{\mathrm{G}}}(Y) := {{\mathrm{face}}}(Y, {\mathcal {K}}^*). \end{aligned}$$

Clearly, we have $X \in {{\mathrm{ri}}}{{\mathrm{J}}}(X)$ for each $X \in {\mathcal {K}}$.

The complementary face of ${{\mathrm{J}}}(X)$ is defined as ${{\mathrm{J}}}^{\triangle }(X) := \{ Y \in {\mathcal {K}}^* \mid \langle Y, Z \rangle = 0 \text { for all } Z \in {{\mathrm{J}}}(X) \}$. It is easy to see that the complementary face of ${{\mathrm{J}}}(X)$ is also given by

$$\begin{aligned} {{\mathrm{J}}}^{\triangle } (X) = \{ Y \in {\mathcal {K}}^* \mid \langle Y, X \rangle =0 \}. \end{aligned}$$

(2.5)

The complementary face ${{\mathrm{G}}}^{\triangle } (Y)$ of ${{\mathrm{G}}}(Y)$ is defined analogously. From (2.5) and the definition of the active index set I(X) it is clear that for any ${X} \in {\mathcal {F}}_P$ we have

$$\begin{aligned} {{\mathrm{J}}}^{\triangle }(X) = {{\mathrm{cone}}}I (X). \end{aligned}$$

(2.6)

Recall that $X \in {\mathcal {F}}_P$, $Y \in {\mathcal {F}}_D$ are called complementary if $\langle X, Y \rangle =0$, i.e., $Y \in {{\mathrm{J}}}^\triangle (X)$. By weak duality, the matrices X and Y must then be optimal solutions of (P) and (D).

Definition 2.2

The solutions $X \in {\mathcal {F}}_P$ and $Y \in {\mathcal {F}}_D$ are called strictly complementary, if

$$\begin{aligned} X \in {{\mathrm{ri}}}{{\mathrm{J}}}(X) \quad \text { and }\quad Y \in {{\mathrm{ri}}}{{\mathrm{J}}}^{\triangle }(X). \end{aligned}$$

Note that equivalently we can call X, Y strictly complementary, if ${{\mathrm{J}}}^{\triangle }(X) = {{\mathrm{G}}}(Y)$ (see Lemma 2.4a).

Definition 2.3

A feasible matrix $X \in {\mathcal {F}}_P$ is called nondegenerate if

$$\begin{aligned} {\mathcal {L}}^\perp \cap {{\mathrm{lin}}}{{\mathrm{J}}}^{\triangle } (X) = \{ 0 \} \end{aligned}$$

(here ${\mathcal {L}} = {{\mathrm{lin}}}\{A_1, \ldots , A_n \}$, as before) and X is called a basic solution if

$$\begin{aligned} {\mathcal {L}} \cap {{\mathrm{lin}}}{{\mathrm{J}}}(X) = \{0 \}. \end{aligned}$$

We say that $Y \in {\mathcal {F}}_D$ is a nondegenerate resp. a basic solution, if the corresponding dual conditions hold for Y.

The next lemma collects some auxiliary results.

Lemma 2.4

Let ${\overline{X}}\in {\mathcal {F}}_P$, ${\overline{Y}}\in {\mathcal {F}}_D$ be complementary solutions of (P) and (D). Then we have:

• (a) ${{\mathrm{G}}}({\overline{Y}}) \subseteq {{\mathrm{J}}}^\triangle ({\overline{X}})$, and these sets are equal if and only if ${\overline{X}}$ and ${\overline{Y}}$ are strictly complementary.

• (b) If ${\overline{X}}$ is a unique maximizer of (P), then ${\overline{X}}$ is a basic solution. If ${\overline{Y}}$ is nondegenerate, then ${\overline{X}}$ is unique. Corresponding statements also hold for the dual problem.

• (c) Let the KKT condition $c = \sum _{j=1}^k y_j a(Y_j)$ hold with $y_j > 0$, $Y_j \in I({\overline{X}})$, and let ${\overline{Y}}:= \sum _{j=1}^k y_j Y_j$. Suppose that ${{\mathrm{lin}}}\{Y_1, \ldots , Y_ k \} = {{\mathrm{lin}}}I({\overline{X}})$. Then

  $$\begin{aligned} {{\mathrm{lin}}}\{Y_1, \ldots , Y_k \} = {{\mathrm{lin}}}{{\mathrm{G}}}({\overline{Y}}) = {{\mathrm{lin}}}{{\mathrm{J}}}^\triangle ({\overline{X}}). \end{aligned}$$

  In particular, $\overline{X}$ and $\overline{Y}$ are strictly complementary.

Proof

For the proofs of (a) and (b), we refer to Pataki and Tunçel (2001, p. 452), and Pataki and Tunçel (2001, Theorems 1 and 2). To prove (c), observe that the linear hull of the minimal face ${{\mathrm{G}}}({\overline{Y}})$ is given by ${{\mathrm{lin}}}{{\mathrm{G}}}({\overline{Y}}) = \{Y \in {\mathcal {K}}^* \mid {\overline{Y}}\pm \lambda Y \in {\mathcal {K}}^* \text { for some } \lambda > 0 \}$ (cf., Pataki and Tunçel 2001, p. 451). Since the coefficients in the representation of ${\overline{Y}}$ satisfy $y_j > 0$, we must have $Y_j \in {{\mathrm{G}}}({\overline{Y}})$ for all j. Together with (a) and (2.6) this gives

$$\begin{aligned} {{\mathrm{lin}}}I(\overline{X}) = {{\mathrm{lin}}}\{ Y_1, \ldots , Y_k \} \subseteq {{\mathrm{lin}}}{{\mathrm{G}}}({\overline{Y}}) \subseteq {{\mathrm{lin}}}{{\mathrm{J}}}^\triangle ({\overline{X}}) = {{\mathrm{lin}}}I(\overline{X}), \end{aligned}$$

so equality must hold for all these sets. Using ${{\mathrm{lin}}}\{ Y_1, \ldots , Y_k \} = {{\mathrm{lin}}}I({\overline{X}})$, we also have ${\overline{Y}}\in {{\mathrm{ri}}}{{\mathrm{cone}}}I(\overline{X}) = {{\mathrm{ri}}}{{\mathrm{J}}}^\triangle ({\overline{X}})$. By Definition 2.2, the complementary solutions $\overline{X}$ and $\overline{Y}$ are strictly complementary. $\square$

3 First order solutions in conic programming

In this section, we consider first order maximizers of (P). We translate well-known characterizations of first order solutions from semi-infinite programming to the special case of conic programs and provide a geometrical interpretation. We further present some examples of first order maximizers for SDP and COP.

The following necessary and sufficient conditions for first order maximizers are well-known, see e.g., (Goberna et al. 1995, Theorem 4.1) or (Fischer 1991, Theorem 3.1).

Theorem 3.1

  [SIP-result]   Let ${\overline{X}}\in {\mathcal {F}}_P$. Then we have with the moment cone $M({\overline{X}})$ as in (2.3):

• (1) If $c \in {{\mathrm{int}}}M({\overline{X}})$, then ${\overline{X}}$ is a first order maximizer. Conversely, if the Slater condition holds for (P) and ${\overline{X}}$ is a first order maximizer, then $c \in {{\mathrm{int}}}M({\overline{X}})$.

• (2) The following conditions are equivalent.

  • (a) $c \in {{\mathrm{int}}}M({\overline{X}})$

  • (b) $c = \sum \limits _{j=1}^k y_j a(Y_j)$ with $y_j > 0$, $Y_j \in I({\overline{X}})$, and ${{\mathrm{lin}}}\{ a(Y_1), \ldots , a(Y_k) \} = {\mathbb {R}}^n$.

In order to formulate these conditions in terms of conic programs, we need an auxiliary lemma.

Lemma 3.2

Let $A_1, \ldots , A_n \in \mathcal {S}_{m}$ be linearly independent matrices, and let $Y_1, \ldots , Y_k \in \mathcal {S}_{m}$. As before, let ${\mathcal {L}} = {{\mathrm{lin}}}\{A_1,\ldots , A_n \}$. Define $\mathcal {R} := {{\mathrm{lin}}}\{Y_1, \ldots , Y_k \}$ and $T:= \left( \langle A_i, Y_j \rangle \right) _{i,j} \in {\mathbb {R}}^{n \times k}$. Then we have:

$$\begin{aligned} {{\mathrm{rank}}}T = n \quad \Longleftrightarrow \quad {\mathcal {L}} \cap \mathcal {R}^\perp = \{ 0 \} \;\;\text { and }\;\; \dim \mathcal {R} \ge n + \dim ( {\mathcal {L}}^\perp \cap \mathcal {R}). \end{aligned}$$

Proof

Denote $i_1 := \dim ( {\mathcal {L}} \cap \mathcal {R}^\perp )$ and $j_1 := \dim ( {\mathcal {L}}^\perp \cap \mathcal {R})$. Without loss of generality, we can assume that the matrices $Y_j$ are linearly independent, and that they are ordered according to

$$\begin{aligned} {{\mathrm{lin}}}\{ Y_{1}, \ldots , Y_{k-j_1} \} \cap {\mathcal {L}}^\perp = \{ 0 \} \quad \text { and } \quad {{\mathrm{lin}}}\{ Y_{k-j_1+1}, \ldots , Y_k \} \subseteq {\mathcal {L}}^\perp . \end{aligned}$$

Then $\mathcal {R}$ is decomposed as $\mathcal {R} = {{\mathrm{lin}}}\{ Y_{1}, \ldots , Y_{k-j_1} \} \oplus {{\mathrm{lin}}}\{ Y_{k-j_1+1}, \ldots , Y_k \}$. Similarly, we may assume that

$$\begin{aligned} {{\mathrm{lin}}}\{ A_{1}, \ldots , A_{n-i_1} \} \cap \mathcal {R}^\perp = \{ 0 \} \quad \text { and } \quad {{\mathrm{lin}}}\{ A_{n-i_1+1}, \ldots , A_n \} \subseteq \mathcal {R}^\perp . \end{aligned}$$

Then ${\mathcal {L}}$ is decomposed as ${\mathcal {L}} = {{\mathrm{lin}}}\{ A_{1}, \ldots , A_{n-i_1} \} \oplus {{\mathrm{lin}}}\{ A_{n-i_1+1}, \ldots , A_n \}.$

By removing all zero rows and columns from T, we obtain a matrix $\widetilde{T} := \left( \langle A_i, Y_j \rangle \right) _{i,j}$ for $i = 1, \ldots , n-i_1$ and $j =1, \ldots , k - j_1$ which obviously has ${{\mathrm{rank}}}\widetilde{T} = {{\mathrm{rank}}}T$.

$(\Rightarrow )$:   If $n= {{\mathrm{rank}}}T = {{\mathrm{rank}}}\widetilde{T}$, then we immediately get that $n- i_1 \ge n$ and $k-j_1 \ge n$. Hence $i_1= 0$, which implies that ${\mathcal {L}} \cap \mathcal {R}^\perp =\{0\}$, and from $k-j_1 \ge n$ we conclude that $\dim \mathcal {R} \ge n + \dim ( {\mathcal {L}}^\perp \cap \mathcal {R})$.

$(\Leftarrow )$:   Let ${\mathcal {L}} \cap \mathcal {R}^\perp = \{ 0 \}$ and $\dim \mathcal {R} \ge n + \dim ( {\mathcal {L}}^\perp \cap \mathcal {R})$. To prove that ${{\mathrm{rank}}}T = n$, it is sufficient to show that $d^T T = 0$ implies $d=0$. By contradiction, assume that $d \ne 0$ solves $d^T T = 0$. Then $0 \ne D := \sum _{i=1}^{n} d_i A_i \in {\mathcal {L}}$. Since ${\mathcal {L}} \cap \mathcal {R}^\perp = \{ 0 \}$, we have $D \notin \mathcal {R}^\perp$. Hence there exists an index $j_0$ such that for the corresponding unit basis vector $e_{j_0}$ we have $0 \ne \langle D, Y_{j_0} \rangle = d^T T e_{j_0}$. Therefore, we have $d^T T \ne 0$, a contradiction. $\square$

We can now restate the SIP-condition from Theorem 3.1(2) in terms of CP.

Theorem 3.3

The following conditions are equivalent for ${\overline{X}}$ in ${\mathcal {F}}_P$.

• (a) $c \in {{\mathrm{int}}}M({\overline{X}})$.

• (b) There exist $Y_j \in I({\overline{X}})$ and multipliers $y_j > 0$ such that ${\overline{Y}}:= \sum _{j=1}^k y_j Y_j$ is an optimal solution of (D), and we have

  $$\begin{aligned} {\mathcal {L}} \cap \mathcal {R}^\perp = \{ 0 \} \quad \text { and } \quad \dim \mathcal {R} \ge n + \dim ( {\mathcal {L}}^\perp \cap \mathcal {R} ). \end{aligned}$$

  (3.1)

  Here again ${\mathcal {L}} = {{\mathrm{lin}}}\{A_1, \ldots , A_n \}$ and $\mathcal {R} = {{\mathrm{lin}}}\{Y_1, \ldots , Y_k \}$.

Proof

The proof follows directly from Theorem 3.1(2) and Lemma 3.2 by noticing that $a(Y_1), \ldots , a(Y_k)$ are the columns of the matrix T. $\square$

Suppose now that ${\overline{X}}\in {\mathcal {F}}_P$ and ${\overline{Y}}\in {\mathcal {F}}_D$ satisfy the conditions of Theorem 3.3(b). By the arguments in the proof of Lemma 2.4(c) the relations

$$\begin{aligned} \mathcal {R} \subseteq {{\mathrm{lin}}}{{\mathrm{G}}}({\overline{Y}}) \subseteq {{\mathrm{lin}}}{{\mathrm{J}}}^\triangle ({\overline{X}}) = {{\mathrm{lin}}}I({\overline{X}}) \end{aligned}$$

(3.2)

hold, and the inequality in (3.1) implies that $n \le \dim \mathcal {R}$. In view of Theorem 3.1, this immediately yields:

(3.3)

Suppose in addition that ${\overline{X}}$ is nondegenerate, i.e., ${\mathcal {L}}^\perp \cap {{\mathrm{lin}}}{{\mathrm{J}}}^\triangle ({\overline{X}}) = \{0\}$. Since $\dim {\mathcal {L}}^\perp = \frac{1}{2}m(m+1) - n$, we obtain $\dim {{\mathrm{J}}}^\triangle ({\overline{X}}) \le n$. Combining this with (3.2), we conclude that if ${\overline{X}}$ is nondegenerate, then $n \le \dim \mathcal {R} \le \dim {{\mathrm{G}}}({\overline{Y}}) \le \dim {{\mathrm{J}}}^\triangle ({\overline{X}}) \le n$. This implies $\mathcal {R} = {{\mathrm{lin}}}{{\mathrm{G}}}({\overline{Y}}) = {{\mathrm{lin}}}{{\mathrm{J}}}^\triangle ({\overline{X}})$, and by Lemma 2.4(c), the matrices ${\overline{X}}$ and ${\overline{Y}}$ are strictly complementary. So under the conditions of Theorem 3.3(b) we have

$$\begin{aligned} \text {if } {\overline{X}}\text { is nondegenerate, then } \dim {{\mathrm{G}}}({\overline{Y}}) = n \;\text { and }\; {\overline{X}}, {\overline{Y}}\text { are strictly complementary}. \end{aligned}$$

(3.4)

Note, however, that the conditions for first order maximizers in Theorem 3.3(b) allow that $\dim \mathcal {R} > n$, in which case ${\overline{X}}$ is degenerate. Recall that even in LP a unique (thus first order) maximizer may be degenerate.

We now state the main result of this section.

Corollary 3.4

Let ${\overline{X}}\in {\mathcal {F}}_P$ be a nondegenerate maximizer of (P) and let ${\overline{Y}}$ be the optimal solution of (D) which is unique by Lemma 2.4(b). Then ${\overline{X}}$ is a first order maximizer if and only if $\dim {{\mathrm{G}}}({\overline{Y}}) = n$ and ${\overline{X}}, {\overline{Y}}$ are strictly complementary.

Proof

$(\Rightarrow )$   It is known (see Dür et al. 2014) that if there exists a nondegenerate ${\overline{X}}\in {\mathcal {F}}_P$, then the primal Slater condition holds. By Theorem 3.1(1), we have $c \in {{\mathrm{int}}}M({\overline{X}})$ and thus the conditions of Theorem 3.3(b) hold. With (3.4) this proves the statement.

$(\Leftarrow )$   By strict complementarity, we have ${{\mathrm{G}}}({\overline{Y}}) = {{\mathrm{J}}}^\triangle ({\overline{X}}) = {{\mathrm{cone}}}I({\overline{X}})$. Hence ${\overline{Y}}\in {{\mathrm{ri}}}{{\mathrm{J}}}^\triangle ({\overline{X}})$, and therefore there exist $Y_j \in I({\overline{X}})$, $y_j > 0$ ($j = 1, \ldots , k$) such that ${\overline{Y}}= \sum _{j=1}^k y_j Y_j$ and

$$\begin{aligned} \mathcal {R} := {{\mathrm{lin}}}\{ Y_1, \ldots , Y_k \} = {{\mathrm{lin}}}{{\mathrm{J}}}^\triangle ({\overline{X}}) \end{aligned}$$

(3.5)

with $\dim \mathcal {R} = \dim {{\mathrm{G}}}({\overline{Y}}) = n$. By Theorems 3.1 and 3.3, it suffices to show that (3.1) is satisfied. Nondegeneracy of ${\overline{X}}$ together with (3.5) implies that $\{ 0 \} = {\mathcal {L}}^\perp \cap {{\mathrm{lin}}}{{\mathrm{J}}}^\triangle ({\overline{X}}) = {\mathcal {L}}^\perp \cap \mathcal {R}$. Using $\dim \mathcal {R} = n$, we see that the second condition in (3.1) is valid. Since $\dim {\mathcal {L}}^\perp = \frac{1}{2}m(m+1)-n$ and $\dim \mathcal {R} =n$, we get from $\{ 0 \} = {\mathcal {L}}^\perp \cap \mathcal {R}$ that ${\mathcal {L}}^\perp + \mathcal {R} = \mathcal {S}_{m}$, and thus ${\mathcal {L}} \cap \mathcal {R}^\perp = \{ 0 \}$. $\square$

Remark 3.5

From Corollary 3.4, we conclude that if ${\overline{X}}$ is a nondegenerate first order maximizer of (P), then the unique minimizer ${\overline{Y}}$ of (D) is strictly complementary. For non-first order maximizers this need not be the case, even if both ${\overline{X}}$ and ${\overline{Y}}$ are nondegenerate, see Alizadeh et al. (1997, p. 117) for a counterexample in SDP.

We now present some examples of first order maximizers in SDP and COP. Note that it is geometrically clear that for the case $n=1$, i.e., $\dim {\mathcal {L}} = 1$, under the conditions $\emptyset \ne {\mathcal {F}}_P \nsubseteq {{\mathrm{bd}}}{\mathcal {K}}$ and $c \ne 0$, any maximizer is of first order. So we give examples with $n \ge 2$.

Example 3.6

  [SDP with $n=m=2$]    Consider

$$\begin{aligned} (P) \quad \!&\max \; (1,1) x \quad \! \text {s.t.} \quad \! X := \begin{pmatrix} 1 &{} 0 \\ 0 &{} 1 \end{pmatrix} - x_1 \begin{pmatrix} 1 &{} 0 \\ 0 &{} 0 \end{pmatrix} - x_2 \begin{pmatrix} 0 &{} 0 \\ 0 &{} 1 \end{pmatrix} = \begin{pmatrix} 1-x_1 &{} 0 \\ 0 &{} 1-x_2 \end{pmatrix} \in \mathcal {S}^+_{2}. \\ (D) \quad&\min \; \left\langle \begin{pmatrix} 1 &{} 0 \\ 0 &{} 1 \end{pmatrix}, Y \right\rangle \quad \text {s.t.} \quad y_{11} = 1, \; y_{22} = 1, \; Y \in \mathcal {S}^+_{2}. \end{aligned}$$

The solution of (P) is ${\overline{x}}=(1,1)$ or ${\overline{X}}=0$, and all matrices of the form

$$\begin{aligned} Y= \begin{pmatrix} 1 &{} y_{12} \\ y_{12} &{} 1 \end{pmatrix} \end{aligned}$$

with $-1 \le y_{12} \le 1$ are optimal solutions of (D). With $I({\overline{X}})= \{ Y \in \mathcal {S}^+_{2} \mid \Vert Y\Vert = 1 \}$, we see that the assumptions of Theorem 3.3(b) are satisfied for

$$\begin{aligned} {\overline{Y}}:= \begin{pmatrix} 1 &{} 0 \\ 0 &{} 1 \end{pmatrix} = 1 \cdot Y_1 + 1 \cdot Y_2, \qquad \text { with } \qquad Y_1 = \begin{pmatrix} 1 &{} 0 \\ 0 &{} 0 \end{pmatrix}, \; Y_2 = \begin{pmatrix} 0 &{} 0 \\ 0 &{} 1 \end{pmatrix} \in I({\overline{X}}). \end{aligned}$$

So ${\overline{X}}= 0$ is a first order maximizer. However, for the solution ${\overline{Y}}$ of (D) we have here $\dim {{\mathrm{G}}}({\overline{Y}})=3$, so ${\overline{X}}$ is degenerate. We will see later that the first order maximizer ${\overline{X}}$ is not stable in this example (cf. Example 4.2 and Remark 3.9). $\square$

Example 3.7

  [COP with $n=m=2$]    It is known that $\mathcal {COP}_{2} = \mathcal {N}_{2} + \mathcal {S}^+_{2}$ and $(\mathcal {COP}_{2})^* = \mathcal {CP}_{2} = \mathcal {N}_{2} \cap \mathcal {S}^+_{2}$, see Maxfield and Minc (1962). Consider

$$\begin{aligned} (P) \quad&\max (1,1)x \\&\text {s.t.} \quad \! \begin{pmatrix} 1 &{} 1 \\ 1 &{} 1 \end{pmatrix} - x_1 \begin{pmatrix} 1 &{} 0 \\ 0 &{} 0 \end{pmatrix} - x_2 \begin{pmatrix} 0 &{} 0 \\ 0 &{} 1 \end{pmatrix} = \begin{pmatrix} 1 - x_1 &{} 1 \\ 1 &{} 1-x_2 \end{pmatrix} \in \mathcal {COP}_{2} \!=\!\mathcal {N}_{2} \!+\! \mathcal {S}^+_{2}, \\ (D) \quad&\min \; \left\langle \begin{pmatrix} 1 &{} 1 \\ 1 &{} 1 \end{pmatrix}, Y \right\rangle \quad \text {s.t.} \quad y_{11} = 1, \; y_{22} = 1, \; Y \in \mathcal {CP}_{2} = \mathcal {N}_{2} \cap \mathcal {S}^+_{2}. \end{aligned}$$

The dual can be rewritten as:

$$\begin{aligned} (D) \qquad \min (2+2 y_{12}) \quad \text {s.t.} \quad Y= \begin{pmatrix} 1 &{} y_{12} \\ y_{12} &{} 1 \end{pmatrix} \in \mathcal {N}_{2} \cap \mathcal {S}^+_{2}. \end{aligned}$$

The feasibility condition for (D) is given by $0 \le y_{12} \le 1$, and the feasibility condition for (P) by $x_i \le 1$ for $i = 1,2$. So ${\overline{x}}=(1,1)$ or ${\overline{X}}= \begin{pmatrix} 0 &{} 1 \\ 1 &{} 0 \end{pmatrix}$ is the optimal solution of (P) with

The unique solution of (D) is

$$\begin{aligned} {\overline{Y}}:= \begin{pmatrix} 1 &{} 0 \\ 0 &{} 1 \end{pmatrix} = 1 \cdot Y_1 + 1 \cdot Y_2, \end{aligned}$$

so again the conditions of Thereom 3.3(b) are satisfied and ${\overline{X}}$ is a first order maximizer. It is not difficult to see that ${\overline{Y}}$ is also a first order minimizer and that both first order solutions are stable.

The next example is similar to Example 3.6 but with a stable first order maximizer.

Example 3.8

  [SDP with $n=3, m=2$]    Consider

$$\begin{aligned} (P) \quad&\max \; (1,1,1) x \\&\text {s.t.} \quad \begin{pmatrix} 1 &{} 1 \\ 1 &{} 1 \end{pmatrix} - x_1 \begin{pmatrix} 1 &{} 0 \\ 0 &{} 0 \end{pmatrix} - x_2 \begin{pmatrix} 0 &{} 0 \\ 0 &{} 1 \end{pmatrix} - x_3 \begin{pmatrix} 0 &{} 1 \\ 1 &{} 0 \end{pmatrix} = \begin{pmatrix} 1-x_1 &{} 1-x_3 \\ 1-x_3 &{} 1-x_2 \end{pmatrix} \in \mathcal {S}^+_{2},\\ (D) \quad&\min \;\left\langle \begin{pmatrix} 1 &{} 1 \\ 1 &{} 1 \end{pmatrix}, Y \right\rangle \quad \text {s.t.} \quad y_{11} = 1, \; y_{22} = 1,\; y_{12} = \tfrac{1}{2}, \; \; Y \in \mathcal {S}^+_{2}. \end{aligned}$$

The maximizer of (P) is ${\overline{x}}=(1,1,1)$ (or ${\overline{X}}=0$) and the minimizer of (D) is

$$\begin{aligned} {\overline{Y}}= \begin{pmatrix} 1 &{} 1/2 \\ 1/2 &{} 1 \end{pmatrix} \in {{\mathrm{int}}}\mathcal {S}^+_{2} \end{aligned}$$

with $\dim G({\overline{Y}}) = 3$. It is not difficult to see that the optimal solutions ${\overline{X}}$ of (P) and ${\overline{Y}}$ of (D) are both of first order, as they are given by the unique solutions of the linear systems

$$\begin{aligned} B - x_1 A_1 - x_2 A_2 - x_3 A_3 = 0 \quad \text {and} \quad \langle A_i , Y \rangle = c_i, \; i =1,2,3. \end{aligned}$$

Also here, the first order solutions ${\overline{X}}$ and ${\overline{Y}}$ are stable.

For the SDP case, the result in Corollary 3.4 can be further specified.

Remark 3.9

 [SDP] Let ${\mathcal {K}} = \mathcal {S}^+_{m}$, and denote the rank of the optimal solutions ${\overline{X}}$ of (P) and ${\overline{Y}}$ of (D) by ${{\mathrm{rank}}}\overline{X} =: k$ and ${{\mathrm{rank}}}\overline{Y} =: s$. Strict complementarity is equivalent to $m=k+s$ (see Pataki 2000, Example 3.2.2), and it is known that $\dim {{\mathrm{G}}}({\overline{Y}})= \frac{1}{2}s(s+1)$ (cf. Pataki 2000, Corollary 3.3.1). By applying Corollary 3.4, we obtain: If ${\overline{X}}$ is a nondegenerate maximizer of (P), then

$$\begin{aligned} \overline{X} \text { is of first order } \quad \Leftrightarrow \quad \tfrac{1}{2}s(s+1) = \tfrac{1}{2}(m-k)(m-k+1) = n. \end{aligned}$$

(3.6)

By this formula, nondegenerate first order maximizers are excluded for many choices of n. We have:

(3.7)

Table 1 gives a list of pairs (s, n) such that $\tfrac{1}{2}s(s+1) = n$.

Table 1 Pairs (s, n) such that the right-hand side in (3.7) holds

Note that for the numbers n in Table 1, stable first order maximizers are possible for all $m \ge s$. Recall that nondegeneracy and strict complementarity are generically fullfilled in SDP (see Alizadeh et al. 1997; Dür et al. 2014), and hence first order maximizers of (P) are generically excluded for numbers n not satisfying the right-hand side condition of (3.7).

The cones $\mathcal {COP}_{m}$ and $\mathcal {CP}_{m}$ have much richer structure than $\mathcal {S}^+_{m}$. Therefore, in contrast to SDP, we expect that in COP stable first order maximizers occur for any n. For instance, the maximizer in Example 3.7 with $n=m=2$ is stable.

We close this section with some remarks on related properties. As usual, we define the tangent space of ${\mathcal {K}}$ at $X \in {\mathcal {K}}$ as

$$\begin{aligned} {{\mathrm{tan}}}(X,{\mathcal {K}}) = \{ Y \in \mathcal {S}_{m} \mid {{\mathrm{dist}}}(X \pm t Y, {\mathcal {K}}) = o(t) \}. \end{aligned}$$

The tangent space is the subspace of directions where the boundary of ${\mathcal {K}}$ at X is smooth. The smaller the dimension of ${{\mathrm{tan}}}(X,{\mathcal {K}})$, the higher the non-smoothness (“kinkiness”) of ${\mathcal {K}}$ at X. For a so-called nice cone (see Pataki 2000, 2013; Roshchina 2014), the relation ${{\mathrm{J}}}^\triangle (X)^\perp = {{\mathrm{tan}}}(X,{\mathcal {K}})$ holds.

We next introduce the order of kinkiness. Defining ${\overline{m}}:= \frac{1}{2}m(m+1)$, we say that the cone ${\mathcal {K}}$ has a kink at ${\overline{X}}\in {\mathcal {K}}$ of order $k = {\overline{m}}- p$ (i.e., a kink of co-order p), if $\dim ({{\mathrm{tan}}}({\overline{X}},{\mathcal {K}}))=p$.

Clearly, there is a relation between the order of a kink at ${\overline{X}}\in {\mathcal {K}}$ and the fact that ${\overline{X}}$ is a first order maximizer. Assume ${\mathcal {K}}$ is a nice cone. Let (P) satisfy the Slater condition and let ${\overline{X}}$ be a first order maximizer with unique strictly complementary solution ${\overline{Y}}\in {\mathcal {F}}_D$. Then by (3.3) we obtain that $\dim {{\mathrm{J}}}^\triangle ({\overline{X}}) = \dim {{\mathrm{G}}}({\overline{Y}}) \ge n$, and since ${\mathcal {K}}$ is nice, this implies

$$\begin{aligned} \dim ({{\mathrm{tan}}}({\overline{X}},{\mathcal {K}})) = \dim ({{\mathrm{J}}}^\triangle ({\overline{X}})^\perp ) \le {\overline{m}}-n. \end{aligned}$$

If moreover ${\overline{X}}$ is nondegenerate, we deduce from (3.4) that $\dim ({{\mathrm{G}}}({\overline{Y}})) = n$, and thus

$$\begin{aligned} \dim ({{\mathrm{tan}}}({\overline{X}},{\mathcal {K}}))= \dim ({{\mathrm{J}}}^\triangle ({\overline{X}})^\perp ) = {\overline{m}}-n. \end{aligned}$$

4 Stability of first order maximizers

In this section, we study the stability of first order maximizers of conic programs. We show that the characterization of stability of first order solutions for general SIP is no more valid for CP, and we indicate how the conditions have to be modified in the CP context. Then we present sufficient and necessary conditions for the stability of first order maximizers of CP.

Starting with the paper Nürnberger (1985), the stability of first order maximizers of SIP was studied in several papers (see e.g., Helbig and Todorov 1998; Goberna et al. 2012). In Nürnberger (1985), Helbig and Todorov (1998), the set

$$\begin{aligned} \Pi := \{ (a,b,c) \in C(Z)^n \times C(Z) \times {\mathbb {R}}^n\} \end{aligned}$$

has been considered as the set of input data for SIP of the general form (2.1), where $Z \subset {\mathbb {R}}^M$ and C(Z) denotes the set of continuous functionals on Z. In these papers, the set $\Pi$ is endowed with the topology given by

$$\begin{aligned} d \big ( (a,b,c), (\tilde{a},\tilde{b},\tilde{c}) \big ) := \max _{Y \in Z} \Vert a(Y) - \tilde{a}(Y)\Vert + \max _{Y \in Z} | b(Y) - \tilde{b}(Y)| + \Vert c - \tilde{c} \Vert . \end{aligned}$$

For general linear SIP, the following stability results have been proven in Nürnberger (1985), Helbig and Todorov (1998) for the subsets ${\mathcal {U}}, {\mathcal {U}}_1 \subset \Pi$ defined as

$$\begin{aligned} {\mathcal {U}}&:= \{ (a,b,c) \in \Pi \mid \text { the maximizer } {\overline{x}}\hbox {of the corresponding SIP is unique} \}, \\ {\mathcal {U}}_1&:= \{ (a,b,c) \in \Pi \mid \text { the maximizer } {\overline{x}}\hbox {of the corresponding SIP is of first order} \}. \end{aligned}$$

Theorem 4.1

Let $\pi = (a,b,c) \in \Pi$ satisfy the Slater condition and let $0 \ne c \in {\mathbb {R}}^n$. Then the following statements are equivalent:

• (a) $\pi \in {{\mathrm{int}}}{\mathcal {U}}_1$,

• (b) $\pi \in {{\mathrm{int}}}{\mathcal {U}}$,

• (c) there exist ${\overline{x}}\in {\mathcal {F}}_{SIP}$ and $Y_j \in I({\overline{x}})$, $y_j > 0$ ($j =1, \ldots , n$) such that $c = \sum _{j=1}^n y_j a(Y_j)$, and for every selection $\widetilde{Y}_j \in I({\overline{x}})$ ($j =1, \ldots , n$) with $c = \sum _{j=1}^n \tilde{y}_j a(\widetilde{Y}_j), \; \tilde{y}_j \ge 0$, any subset of n vectors from

  $$\begin{aligned} c , \; a(\widetilde{Y}_j), \; (j =1, \ldots , n) \quad \text {are linearly independent.} \end{aligned}$$

  (4.1)

  Here, $I({\overline{x}})$ denotes again the active index set $I({\overline{x}}) \!=\! \{ Y \!\in \! Z \mid b(Y)- a(Y)^T {\overline{x}}\!=\! 0 \}$.

As we shall see in a moment, this result for general SIP is not true for CP. The reason for this is that the set $\Pi _{{{\mathrm{CP}}}}$ [as defined in (1.1)] of CP programs given by the linear functions a(Y), b(Y) in (2.2) is only a small subset of the set $\Pi$ of general SIP problems. It is clear that the topology in $\Pi$ allows more (also nonsmooth) perturbations, such that roughly speaking we have:

• Sufficient conditions for stability in general SIP also hold in the special case of CP, but the necessary conditions in SIP are too strong for CP.

Even worse, the conditions in Theorem 4.1(c) can never hold at first order maximizers of CP if $n >1$: Note that the condition (4.1) states in particular that the KKT relations $c = \sum _{j=1}^k y_j a(Y_j)$ cannot be fulfilled with $k<n$. However, given any first order optimizer ${\overline{x}}$ (or ${\overline{X}}$) of CP, the linearity of $b(Y) - a(Y)^Tx = \langle (B - \sum _i x_i A_i), Y \rangle$ in Y implies that if $c = \sum _{j=1}^k y_j a(Y_j)$ with $Y_j \in I({\overline{X}}), y_j > 0$ for $j=1, \ldots , k$, then with the solution ${\overline{Y}}:= \sum _{j=1}^k y_j Y_j$ of (D) we have (assuming ${\overline{Y}}\ne 0$):

$$\begin{aligned} \widetilde{Y} : = \frac{1}{\Vert {\overline{Y}}\Vert } {\overline{Y}}\in I({\overline{X}}) \quad \text { and }\quad c = \Vert {\overline{Y}}\Vert \cdot a(\widetilde{Y}). \end{aligned}$$

Consequently, the KKT condition holds with $k=1$, and for $n > 1$ the condition (4.1) in Theorem 4.1(c) always fails.

Next, we discuss how the conditions for stability of first order maximizers in Theorem 4.1(c) have to be modified in conic programming in order to obtain necessary and sufficient conditions for the stability of first order maximizers in CP. Recall that a property is said to be stable at a problem instance $\overline{Q} = (\overline{c}, \overline{B}, \overline{A}_1, \ldots , \overline{A}_n) \in \Pi _{{{\mathrm{CP}}}}$, if there exists $\varepsilon > 0$ such that the property holds for all $Q \in \Pi _{{{\mathrm{CP}}}}$ with $\Vert Q - \overline{Q}\Vert < \varepsilon$.

As an illustrative example, we go back to the SDP problem of Example 3.6.

Example 4.2

  [Example 3.6 continued]   The SDP instance with $n=m=2$ is given by

$$\begin{aligned} {\overline{Q}}= ({\overline{c}}, {\overline{B}}, {\overline{A}}_1,{\overline{A}}_2) \quad \text { with } \quad {\overline{c}}= \begin{pmatrix} 1 \\ 1 \end{pmatrix}, \; {\overline{B}}= \begin{pmatrix} 1 &{} 0 \\ 0 &{} 1 \end{pmatrix}, \; {\overline{A}}_1 = \begin{pmatrix} 1 &{} 0 \\ 0 &{} 0 \end{pmatrix}, \; {\overline{A}}_2 = \begin{pmatrix} 0 &{} 0 \\ 0 &{} 1 \end{pmatrix}. \end{aligned}$$

Recall that the primal maximizer wrt. ${\overline{Q}}$ is given by ${\overline{X}}= 0$, ${\overline{x}}=(1,1)$, and the corresponding set of dual optimal solutions is

$$\begin{aligned} S_D({\overline{X}})= \left\{ {\overline{Y}}= \begin{pmatrix} 1 &{} y_{12} \\ y_{12} &{} 1 \end{pmatrix} \mid -1 \le y_{12} \le 1 \right\} . \end{aligned}$$

For $y_{12}= \pm 1$, we obtain solutions on the boundary of $\mathcal {S}^+_{2}$:

$$\begin{aligned} {\overline{Y}}_+ := \begin{pmatrix} 1 &{} 1 \\ 1 &{} 1 \end{pmatrix}, \quad {\overline{Y}}_- := \begin{pmatrix} 1 &{} -1 \\ -1 &{} 1 \end{pmatrix}. \end{aligned}$$

Both are extreme rays satisfying $\dim {{\mathrm{G}}}({\overline{Y}}_\pm ) =1 < n$. Choose one of them, say ${\overline{Y}}_+$, and consider for small $\varepsilon >0$ the perturbed instance

$$\begin{aligned} Q_\varepsilon = ({\overline{c}}, B_\varepsilon , {\overline{A}}_1,{\overline{A}}_2) \quad \text { with } \quad B_\varepsilon = {\overline{B}}+ \varepsilon {\overline{Y}}_+ = \begin{pmatrix} 1+\varepsilon &{} \varepsilon \\ \varepsilon &{} 1+\varepsilon \end{pmatrix}. \end{aligned}$$

The primal feasibility condition now changes from $x_1 \le 1, \; x_2 \le 1$ (for ${\overline{Q}}$ which corresponds to $\varepsilon =0$) to

$$\begin{aligned} B_\varepsilon - x_1 {\overline{A}}_1 - x_2 {\overline{A}}_2 = \begin{pmatrix} 1+\varepsilon - x_1 &{} \varepsilon \\ \varepsilon &{} 1+\varepsilon - x_2 \end{pmatrix} \in \mathcal {S}^+_{2} \end{aligned}$$

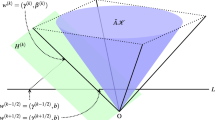
for $Q_\varepsilon$, i.e.,

$$\begin{aligned}&x_1 \le 1+\varepsilon \\&x_2 \le 1 + \varepsilon \\&(1+\varepsilon - x_1)(1 + \varepsilon - x_2) \ge \varepsilon ^2, \end{aligned}$$

Fig. 1

Perturbed and unperturbed feasible set

as displayed in Fig. 1. The primal maximizer wrt. $Q_\varepsilon$ is now given by

$$\begin{aligned} {\overline{x}}_\varepsilon = (1,1), \quad {\overline{X}}_\varepsilon = \begin{pmatrix} \varepsilon &{} \varepsilon \\ \varepsilon &{} \varepsilon \end{pmatrix} \quad \text { with } \quad {{\mathrm{J}}}^\triangle ({\overline{X}}_\varepsilon ) = \left\{ \gamma \begin{pmatrix} 1 &{} -1 \\ -1 &{} 1 \end{pmatrix} \mid \gamma \ge 0 \right\} . \end{aligned}$$

The corresponding dual problem has the unique minimizer

$$\begin{aligned} {\overline{Y}}_\varepsilon = {\overline{Y}}_- = \begin{pmatrix} 1 &{} -1 \\ -1 &{} 1 \end{pmatrix} \quad \text { with } \quad \dim {{\mathrm{G}}}({\overline{Y}}_\varepsilon ) = 1 < n. \end{aligned}$$

Note that the primal program satisfies the Slater condition, so in view of (3.3) the solution ${\overline{X}}_\varepsilon$ is not a first order minimizer for $\varepsilon > 0$. From Fig. 1, we see that the maximizer ${\overline{x}}_\varepsilon$ is of second order for any $\varepsilon > 0$.

Let us now consider a general instance ${\overline{Q}}\in \Pi _{{{\mathrm{CP}}}}$. If ${\overline{Q}}$ satisfies the primal Slater condition and a solution ${\overline{X}}$ of (P) exists, then by strong duality a complementary dual solution ${\overline{Y}}$ exists and thus the set $S_D({\overline{X}}) := \{ {\overline{Y}}\in {\mathcal {F}}_D \mid \langle {\overline{Y}}, {\overline{X}}\rangle = 0 \}$ of dual optimal solutions is nonempty and compact (see e.g., Goberna and Lopez 1998, Theorem 9.8). The analysis in Example 4.2 now suggests to replace the condition in Theorem 4.1(c) by the following condition.

• C1. There is no dual solution ${\overline{Y}}\in S_D({\overline{X}})$ such that with the minimal exposed face $F \subset {\mathcal {K}}^*$ containing ${{\mathrm{G}}}({\overline{Y}})$ we have $\dim F < n$.

Note that since the set ${{\mathrm{J}}}^\triangle ({\overline{X}})$ is an exposed face of ${\mathcal {K}}^*$ and ${{\mathrm{G}}}({\overline{Y}}) \subseteq {{\mathrm{J}}}^\triangle ({\overline{X}})$, this minimal face F must satisfy $F \subseteq {{\mathrm{J}}}^\triangle ({\overline{X}})$. It turns out that condition C1 is necessary for the stability of the first order maximizer.

Theorem 4.3

Assume that ${\overline{Q}}= (\overline{c}, \overline{B}, \overline{A}_1, \dots , \overline{A}_n) \in \Pi _{{{\mathrm{CP}}}}$ satisfies the primal Slater condition, and let ${\overline{X}}$ be the first order maximizer of the corresponding primal program. If the first order maximizer is stable, then condition C1 holds.

Proof

Assume by contradiction that there exist ${\overline{Y}}\in S_D({\overline{X}})$ and a minimal exposed face F such that ${{\mathrm{G}}}({\overline{Y}}) \subseteq F \subseteq {{\mathrm{J}}}^\triangle ({\overline{X}})$ and $\dim F < n$. Since $F \subset {\mathcal {K}}^*$ is an exposed face, there exists a supporting hyperplane $H = \{ Y \in \mathcal {S}_{m} \mid \langle S, Y \rangle = 0 \}$ with normal vector $0 \ne S \in {\mathcal {K}}$ such that $F = H \cap {\mathcal {K}}^*$, i.e.,

$$\begin{aligned} \langle S, Y \rangle= & {} 0 \quad \text {for all } Y \in F, \nonumber \\ \langle S, Y \rangle> & {} 0 \quad \text {for all } 0 \ne Y \in {\mathcal {K}}^* \setminus F. \end{aligned}$$

(4.2)

For small $\varepsilon > 0$ consider the perturbed instance

$$\begin{aligned} Q_\varepsilon = (\overline{c}, {B_\varepsilon }, \overline{A}_1, \ldots , \overline{A}_n) \qquad \text { with } \quad B_\varepsilon = {\overline{B}}+ \varepsilon S. \end{aligned}$$

Letting ${\overline{X}}_\varepsilon : = {\overline{X}}+ \varepsilon S \in {\mathcal {K}}$, we find by (4.2) and $F \subset {{\mathrm{J}}}^\triangle ({\overline{X}})$ that for any $Y \in {\mathcal {K}}^*$ we have:

$$\begin{aligned} \langle {\overline{X}}_\varepsilon , Y \rangle = \langle {\overline{X}}, Y \rangle + \varepsilon \langle S, Y \rangle = 0 \quad \Leftrightarrow \quad Y \in F. \end{aligned}$$

So wrt. $Q_\varepsilon$ the matrix ${\overline{X}}_\varepsilon$ is a maximizer with dual complementary solution ${\overline{Y}}$ such that ${{\mathrm{G}}}({\overline{Y}}) \subseteq F = {{\mathrm{J}}}^\triangle ({\overline{X}}_\varepsilon )$. Furthermore, note that any dual solution $\widetilde{Y}$ with respect to $Q_{\varepsilon }$ must be contained in $F = {{\mathrm{J}}}^\triangle ({\overline{X}}_\varepsilon )$ and thus satisfies

$$\begin{aligned} \dim {{\mathrm{G}}}(\widetilde{Y}) \le \dim F < n. \end{aligned}$$

Since the primal Slater condition holds at ${\overline{Q}}$, it also holds for $Q_\varepsilon$ for $\varepsilon$ small enough (if $X^0 := {\overline{B}}- \sum _i x_i^0 {\overline{A}}_i \in {{\mathrm{int}}}{\mathcal {K}}$, then also $X^0_\varepsilon := B_\varepsilon - \sum _i x_i^0 {\overline{A}}_i \in {{\mathrm{int}}}{\mathcal {K}}$). So by (3.3), the maximizer ${\overline{X}}_\varepsilon$ cannot be of first order, i.e., first order stability fails. $\square$

We now turn to sufficient conditions for stability of a first order maximizer ${\overline{X}}$ of CP. We look for natural assumptions such as nondegeneracy of ${\overline{X}}$, or conditions on ${{\mathrm{G}}}({\overline{Y}})$. Let again ${\overline{Q}}\in \Pi _{{{\mathrm{CP}}}}$ be fixed with a first order maximizer ${\overline{X}}$ and a unique complementary minimizer ${\overline{Y}}$ with $\dim {{\mathrm{G}}}({\overline{Y}}) =n$. Let ${\overline{Q}}$ satisfy the Slater condition and assume that uniqueness of the primal and dual optimizers are stable at ${\overline{Q}}$, i.e., for Q in a neighbourhood of ${\overline{Q}}$ there are unique complementary solutions $X=X(Q), Y= Y(Q)$. Since the Slater condition is stable, we infer from (3.3) that there exists an $\varepsilon > 0$ such that for any first order maximizer $X=X(Q)$ we have

$$\begin{aligned} \dim {{\mathrm{G}}}(Y) \ge n = \dim {{\mathrm{G}}}({\overline{Y}}) \quad \text { for }\quad Y=Y(Q), \; \Vert Q - {\overline{Q}}\Vert < \varepsilon . \end{aligned}$$

This means that the function $\dim {{\mathrm{G}}}(Y)$ is lower semicontinuous at ${\overline{Y}}$. So we consider the lower semicontinuity of the set-valued minimal face mapping

$$\begin{aligned} {{\mathrm{G}}}: {\mathcal {K}}^* \rightrightarrows {\mathcal {K}}^*, \quad {{\mathrm{G}}}(Y) = {{\mathrm{face}}}(Y, {\mathcal {K}}^*). \end{aligned}$$

Definition 4.4

A set-valued mapping ${{\mathrm{G}}}: {\mathcal {K}}^* \rightrightarrows {\mathcal {K}}^*$ is called lower semicontinuous (lsc) at ${\overline{Y}}\in {\mathcal {K}}^*$, if for any open set $V \subset \mathcal {S}_{m}$ there exists $\delta > 0$ such that

$$\begin{aligned} {{\mathrm{G}}}({\overline{Y}}) \cap V \ne \emptyset \quad \Rightarrow \quad {{\mathrm{G}}}(Y) \cap V \ne \emptyset \quad \text { for all } Y \text { with } \Vert Y - {\overline{Y}}\Vert < \delta . \end{aligned}$$

It is easy to see that lower semicontinuity of ${{\mathrm{G}}}$ implies lower semicontinuity of $\dim {{\mathrm{G}}}$: if G is lsc at ${\overline{Y}}$, then there exists $\delta > 0$ such that $\dim {{\mathrm{G}}}(Y) \ge n= \dim {{\mathrm{G}}}({\overline{Y}})$ for all $Y \in {\mathcal {K}}^*$ with $\Vert Y - {\overline{Y}}\Vert < \delta$. By these arguments it is clear that the lower semicontinuity of ${{\mathrm{G}}}$ is a natural condition for stable first order maximizers at ${\overline{Q}}$.

We now give a sufficient condition for the stability.

Theorem 4.5

Let ${\overline{Q}}\in \Pi _{{{\mathrm{CP}}}}$ and let ${\overline{X}}$ be a corresponding nondegenerate primal first order maximizer. (Then there is a unique dual optimal solution ${\overline{Y}}$ with $\dim {{\mathrm{G}}}({\overline{Y}}) =n$.) Assume in addition that primal uniqueness and nondegeneracy are stable at ${\overline{Q}}$ and that the minimal face mapping ${{\mathrm{G}}}$ is lsc at ${\overline{Y}}$. Then the first order maximizer ${\overline{X}}$ is stable at ${\overline{Q}}$.

Proof

Stability of nondegeneracy of the maximizer at ${\overline{Q}}$ implies stability of the primal Slater condition (see Dür et al. 2014). Since ${\overline{X}}$ is a maximizer of order $p > 0$ and the Slater condition holds, standard results in parametric LSIP (see e.g., Goberna and Lopez 1998, Theorem 10.4 or Bonnans and Shapiro 2000, Proposition 4.41) yield the continuity condition (upper semicontinuity) for the unique solutions $X_\nu$ of any sequence $Q_\nu \rightarrow {\overline{Q}}$:

$$\begin{aligned} X_\nu \rightarrow {\overline{X}}. \end{aligned}$$

The stability of the Slater condition implies that for $Q \approx {\overline{Q}}$ the solution set of the dual is nonempty and compact (see e.g., Goberna and Lopez 1998, Theorem 9.8), and the stability of primal nondegeneracy assures that there is a unique dual solution $Y = Y(Q)$ (cf., Lemma 2.4). Since there is no duality gap for the problems $Q_\nu$ and the primal optimal solutions $X_\nu$ converge to ${\overline{X}}$, the corresponding unique dual solutions $Y_\nu$ are bounded. Therefore, $Y_\nu$ must converge to ${\overline{Y}}$ as well.

Now assume that the first order maximizer is not stable at ${\overline{Q}}$. Then there exists a sequence $Q_\nu =(c^\nu , B^\nu , A_1^\nu , \ldots , A_n^\nu )$ with $Q_\nu \rightarrow {\overline{Q}}$ such that

$$\begin{aligned} \text {the maximizers } X_\nu \hbox { wrt. } Q_\nu \,\hbox { are not of first order. } \end{aligned}$$

(4.3)

Since ${\overline{X}}$ is a first order maximizer, we have by (3.4) that $\dim {{\mathrm{G}}}({\overline{Y}}) = n$ and strict complementarity holds for ${\overline{X}}, {\overline{Y}}$. Consider now the unique dual solutions $Y_\nu$ wrt. $Q_\nu$. Since ${{\mathrm{G}}}$ is lsc at ${\overline{Y}}$, it follows that $\dim {{\mathrm{G}}}(Y_\nu ) \ge n$. Since $Y_\nu \in {{\mathrm{ri}}}{{\mathrm{G}}}(Y_\nu )$, for any fixed $\nu$ there exist linearly independent matrices $V_j^\nu \in {{\mathrm{G}}}(Y_\nu )$ and scalars $v_j^\nu > 0$ (for $j = 1, \ldots , k_\nu$ with $k_\nu \ge n$) such that

$$\begin{aligned} Y_\nu = \sum _{j = 1}^{k_\nu } v_j^\nu V_j^\nu . \end{aligned}$$

Put ${\mathcal {L}}_\nu : = {{\mathrm{lin}}}\{A_1^\nu , \ldots , A_n^\nu \}$ and $\mathcal {R}_\nu := {{\mathrm{lin}}}\{V_1^\nu , \ldots , V_{k_\nu }^\nu \}$ with $\dim \mathcal {R}_\nu = k_\nu \ge n$. We will show that (3.1) is satisfied for $X_\nu , Y_\nu$, so that by Theorems 3.1 and 3.3 the maximizers $X_\nu$ are of first order in contradiction to (4.3). To do so, note that $\mathcal {R}_\nu \subseteq {{\mathrm{G}}}(Y_\nu ) \subseteq {{\mathrm{J}}}^{\triangle } (X_\nu )$, and the stable nondegeneracy of $X_\nu$ gives

$$\begin{aligned} {\mathcal {L}}_\nu ^\perp \cap {{\mathrm{lin}}}{{\mathrm{J}}}^{\triangle } (X_\nu ) = \{ 0 \} \quad \Rightarrow \quad {\mathcal {L}}_\nu ^\perp \cap \mathcal {R}_\nu = \{ 0 \}. \end{aligned}$$

This immediately gives that $\dim \mathcal {R}_\nu \ge n = n + \dim ({\mathcal {L}}_\nu ^\perp \cap \mathcal {R}_\nu )$.

Finally, as in the proof of Corollary 3.4, using $\dim {\mathcal {L}}_\nu ^\perp = \frac{1}{2}m(m+1) - n$ and ${\mathcal {L}}_\nu ^\perp \cap \mathcal {R}_\nu = \{ 0 \}$, we find that $\dim \mathcal {R}_\nu \le n$, and thus $\dim \mathcal {R}_\nu = n$. With $\{ 0 \} = {\mathcal {L}}^\perp _\nu \cap \mathcal {R}_\nu$, we obtain ${\mathcal {L}}^\perp _\nu + \mathcal {R}_\nu = \mathcal {S}_{m}$, and thus ${\mathcal {L}}_\nu \cap \mathcal {R}^\perp _\nu = \{0\}$. Hence, the conditions in (3.1) are satisfied. $\square$

We shortly discuss a sufficient condition for the lower semicontinuity of the mapping ${{\mathrm{G}}}$. This condition only depends on the structure of the cone ${\mathcal {K}}^*$.

Definition 4.6

 (see Papadopoulou 1977, Definition 3.1)  The closed convex cone ${\mathcal {K}}^*$ is called stable at $Y_0 \in {\mathcal {K}}^*$, if the mapping $h: {\mathcal {K}}^* \times {\mathcal {K}}^* \rightarrow {\mathcal {K}}^*, \; h(V,W) = \frac{1}{2} ( V+W)$ is open at $Y_0$.

The following result has been proven in Papadopoulou (1977, Proposition 3.3):

Theorem 4.7

Let ${\mathcal {K}}^*$ be a closed convex set, and let $Y_0 \in {\mathcal {K}}^*$. If ${\mathcal {K}}^*$ is stable at $Y_0$, then ${{\mathrm{G}}}$ is lsc at $Y_0$.

For compact convex sets, the stability of ${\mathcal {K}}^*$, the lower semicontinuity of ${{\mathrm{G}}}$, and the closedness of the so-called k-skeletons are equivalent conditions (see Papadopoulou 1977). That paper also gives an example of a convex compact set where these conditions fail.

Let us come back to sufficient conditions for stable first order maximizers. In SDP, it is known that there is a generic subset $\mathcal {P}_r \subset \Pi _{{{\mathrm{CP}}}}$ of problem instances such that for any ${\overline{Q}}\in \mathcal {P}_r$ nondegeneracy and uniqueness are stable at ${\overline{Q}}$ (see Alizadeh et al. 1997; Dür et al. 2014). The lower semicontinuity of ${{\mathrm{G}}}$ follows from the lower semicontinuity of the rank-function. So for SDP, Theorem 4.5 yields the following:

Corollary 4.8

Consider an SDP instance ${\overline{Q}}$ in the generic set $\mathcal {P}_r$. Suppose the unique maximizer ${\overline{X}}$ wrt. ${\overline{Q}}$ is of first order. Then the first order maximizer is a stable at ${\overline{Q}}$.

This result also follows from Dür et al. (2014, Proposition 5.1), where it has been shown that in SDP for any first order maximizer ${\overline{X}}$ of ${\overline{Q}}$ in the generic set $\mathcal {P}_r$, the condition $\frac{1}{2}(m-k)(m-k+1) = n$ for the rank k of ${\overline{X}}$ is stable, and thus with the stability of $\dim {{\mathrm{G}}}(Y)$ also the first order maximizers (as well as the second (non-first) order maximizers) are stable.

We finally emphasize that this means that also the relation ${\overline{Q}}\in {{\mathrm{int}}}{\mathcal {U}} \Leftrightarrow {\overline{Q}}\in {{\mathrm{int}}}{\mathcal {U}}_1$ of Theorem 4.1 is not true for CP. We give a simple counterexample in SDP.

Example 4.9

  [SDP, stable second order (non-first order) maximizer]   Consider the program

$$\begin{aligned}&(P) \quad \max \; (0,1) x\\&\quad \text {s.t.} \quad X := \begin{pmatrix} 1 &{} 0 \\ 0 &{} 1 \end{pmatrix} - x_1 \begin{pmatrix} 1 &{} 0 \\ 0 &{} -1 \end{pmatrix} - x_2 \begin{pmatrix} 0 &{} 1 \\ 1 &{} 0 \end{pmatrix} = \begin{pmatrix} 1-x_1 &{} -x_2 \\ -x_2 &{} 1+x_1 \end{pmatrix} \in \mathcal {S}^+_{2}. \end{aligned}$$

It is not difficult to see that this program is equivalent to

$$\begin{aligned} \max \; x_2 \quad \text {s.t.} \quad x_1^2 + x_2^2 \le 1, \quad -1 \le x_1 \le 1. \end{aligned}$$

The solution ${\overline{x}}=(0,1)$ or ${\overline{X}}= \begin{pmatrix} 1 &{} -1 \\ -1 &{} 1 \end{pmatrix}$ is not of first order, but of second order. It is not difficult to see that this second (non-first) order maximizer is stable for $Q \approx {\overline{Q}}= ({\overline{c}}, {\overline{B}}, {\overline{A}}_1, {\overline{A}}_2)$ with

$$\begin{aligned} {\overline{c}}= \begin{pmatrix} 0 \\ 1 \end{pmatrix}, \quad {\overline{B}}= \begin{pmatrix} 1 &{} 0 \\ 0 &{} 1 \end{pmatrix}, \quad {\overline{A}}_1 = \begin{pmatrix} 1 &{} 0 \\ 0 &{} -1 \end{pmatrix}, \quad {\overline{A}}_2 = \begin{pmatrix} 0 &{} 1 \\ 1 &{} 0 \end{pmatrix}. \end{aligned}$$

5 First order minimizers of (D)

Finally, in this short section, we finish with some remarks on first order solutions for the dual problem (D). We can apply the results for the first order maximizers ${\overline{X}}$ of (P) to the dual. To do so, define $N:= \frac{1}{2}m(m+1) - n$ and choose (under Assumption 1.1) a basis $\{A_1^\perp , \ldots , A_N^\perp \}$ of ${\mathcal {L}}^\perp$. Any solution Y of the system $\langle A_i, Y \rangle = c_i$ ($i = 1, \ldots , n$) can be written as $Y = C + \sum _{j=1}^N y_j A_j^\perp$, where $C \in \mathcal {S}_{m}$ is some solution of $\langle A_i, C \rangle = c_i$ ($i = 1, \ldots , n$). Then by defining $b := (\langle B, A_1^\perp \rangle , \ldots , \langle B, A_N^\perp \rangle )$, the dual (D) can be equivalently written in form of a “primal”:

$$\begin{aligned} (D_P) \quad \min b^T y \quad \text {s.t.} \quad Y = C + \sum _{j=1}^N y_j A_j^\perp \in {\mathcal {K}}^*, \end{aligned}$$

with corresponding “dual” problem (P). We can now apply all results of the previous sections to $(D_P)$, we only have to make the obvious changes, e.g., we have to replace ${{\mathrm{G}}}({\overline{Y}})$ by ${{\mathrm{J}}}({\overline{X}})$ and n by N.

As an example, we formulate Corollary 3.4 in terms of the dual.

Corollary 5.1

Let ${\overline{Y}}\in {\mathcal {F}}_{D_P}$ be a nondegenerate minimizer of $(D_P)$ and let ${\overline{X}}$ be the optimal solution of (P) which is unique by Lemma 2.4(b). Then ${\overline{Y}}$ is a first order minimizer if and only if $\dim {{\mathrm{J}}}({\overline{X}}) =\frac{1}{2}m(m+1) - n$ and ${\overline{X}}, {\overline{Y}}$ satisfy the dual strict complementarity condition ${{\mathrm{J}}}({\overline{X}}) = {{\mathrm{G}}}^\triangle ({\overline{Y}})$.

Remark 5.2

  [SDP]   Again we can be more specific in the case of ${\mathcal {K}} = {\mathcal {K}}^* = \mathcal {S}^+_{m}$. As before, denote the rank of the optimal solutions ${\overline{X}}$ of (P) and ${\overline{Y}}$ of $(D_P)$ by $k := {{\mathrm{rank}}}\overline{X}$ and $s := {{\mathrm{rank}}}\overline{Y}$, and recall that strict complementarity is equivalent to $m = k+s$. We obtain: if ${\overline{Y}}$ is a nondegenerate minimizer of $(D_P)$, then

$$\begin{aligned} \overline{Y} \text { is of first order } \quad \Leftrightarrow \quad \tfrac{1}{2}(m-s)(m-s+1) = \tfrac{1}{2}m(m+1) - n. \end{aligned}$$

Moreover, under primal and dual nondegeneracy and strict complementarity, we have for the optimal solutions ${\overline{X}}, {\overline{Y}}$ that

$$\begin{aligned} {\overline{X}}, \; \overline{Y} \text { are both of first order } \quad \!\Leftrightarrow \! \quad \tfrac{1}{2}s(s+1) \!=\! n \;\;\text { and }\;\; \tfrac{1}{2}k(k+1) \!=\! \tfrac{1}{2}m(m\!+\!1) \!-\!n. \end{aligned}$$

Note that this is only possible for $k=m$ and $s=n=0$ or for $s=m$ and $k=0$ (see also Example 3.8).