Universally optimal designs under mixed interference models with and without block effects

Abstract

The literature on neighbor designs as introduced by Rees (Biometrics 23:779–791, 1967) is mainly devoted to construction methods, providing few results on their statistical properties, such as efficiency and optimality. A review of the available literature, with special emphasis on the optimality of neighbor designs under various fixed effects interference models, is given in Filipiak and Markiewicz (Commun Stat Theory Methods 46:1127–1143, 2017). The aim of this paper is to verify whether the designs presented by Filipiak and Markiewicz (2017) as universally optimal under fixed interference models are still universally optimal under models with random interference effects. Moreover, it is shown that for a specified covariance matrix of random interference effects, a universally optimal design under mixed interference models with block effects is universally optimal over a wider class of designs. In this paper the method presented by Filipiak and Markiewicz (Metrika 65:369–386, 2007) is extended and then applied to mixed interference models without or with block effects.

1 Introduction

Neighbor designs are widely used in many areas, such as serology, agriculture, horticulture, forestry, medicine, etc., for experiments in which the response to a treatment may be affected by other treatments applied to neighboring experimental units. The class of neighbor designs was defined by Rees (1967) as the class of balanced designs in which every treatment applied to the unit affects equally the treatments on the left or right neighbor units. Following Hwang (1973) a neighbor design can be defined as a design in which treatments are arranged in blocks containing the same number of experimental units in such a way that each treatment appears the same number of times (but not necessarily on different blocks) and is a neighbor of every other treatment equally often. Both authors recommended the use of neighbor designs for experiments in which blocks do not have to be factors. Nevertheless, if blocks are also factors in the design d, then the requirement that d be a balanced incomplete block design is added.

Most papers about neighbor designs have been devoted to construction methods, with only a few providing results concerning the statistical properties, such as efficiency and optimality, of proposed neighbor designs. Filipiak and Markiewicz (2017) gave a review of the available literature, with special emphasis on the optimality of neighbor designs under various fixed effects interference models. Moreover, they proved the universal optimality of specified circular neighbor designs under interference models without block effects. Recently, the optimality of designs, circular or not, under various fixed interference models, e.g. models with carry-over effect, models with left- and right-neighbor effects (equal or not), with observations correlated or not, has been widely studied in the literature; cf. e.g. Druilhet (1999), Kunert and Martin (2000), Kunert et al. (2003), Filipiak and Markiewicz (2004, 2005, 2012), Filipiak (2012), Sharma (2013), Wilk and Kunert (2015) and Bailey et al. (2017). Nevertheless, there are few results on the optimality of neighbor designs under interference models with random neighbor effects; cf. Filipiak and Markiewicz (2003, 2007, 2014). In all of those papers block effects are assumed to be a factor in the experiment. The purpose of this paper is to verify which of the universally optimal designs presented by Filipiak and Markiewicz (2017) are still optimal under models with random neighbor effects. In this paper the method presented by Filipiak and Markiewicz (2007) will be extended and then applied to mixed interference models without block effects.

Note also that Azaïs and Druilhet (1997) consider designs with random neighbor effects but in a different way: the randomness comes from the randomization process.

We organize this paper as follows. First we give some preliminary results on universal optimality under a mixed linear model, and then, in Sect. 3, we specify the models and the designs which are known to be universally optimal under fixed/mixed interference models. In Sect. 4 we give an overview study of the universal optimality of designs under mixed one-sided interference models with and without block effects, two-sided interference models with equal neighbor effects with and without block effects, and two-sided interference models with and without block effects. Possible extensions of the classes under which the considered designs are universally optimal under mixed interference models with specified covariance matrix are given in Sect. 5.

2 Preliminaries

Consider the linear model associated with the design $d\in \mathcal{D}$

$$\begin{aligned} {\mathbf{y}} = {\mathbf{X}}_{1,d}\varvec{\vartheta }_1 + {\mathbf{X}}_{2,d}\varvec{\vartheta }_2 + {\mathbf{X}}_{3}\varvec{\vartheta }_3 + \varvec{\varepsilon } , \end{aligned}$$

(1)

where ${\mathbf{X}}_{i,d}\in {\mathbb {R}}^{n\times p_i}, \; i=1,2$, are known matrices which depend on d, ${\mathbf{X}}_{3}\in {\mathbb {R}}^{n\times p_3}$ is a known matrix which does not depend on d, and $\varvec{\varepsilon }$ is a vector of random errors with expectation zero. Further, $\varvec{\vartheta }_1$ is the vector of parameters of interest and $\varvec{\vartheta }_i$, $i=2,3$, are vectors of nuisance parameters. All errors are assumed to be uncorrelated with a common variance, say equal to 1. We will assume that $\varvec{\vartheta }_2$ is a vector of random effects with covariance matrix ${\mathbf{V}}$, and that it is uncorrelated with the random error $\varvec{\varepsilon }$.

Let ${\mathbf{C}}_{d,V}$ denote the information matrix of d for estimating $\varvec{\vartheta }_1$ in model (1) with random effect $\varvec{\vartheta }_2$ under normality. Recall that for a given nonnegative-definite $m \times m$ partitioned matrix ${{\mathbf{A}}} = ({{\mathbf{A}}}_{i,j})_{1\le i,j\le 2}$, the Schur complement of ${\mathbf{A}}_{22}$ in ${{\mathbf{A}}}$ is

$$\begin{aligned}{}[{{\mathbf{A}}}/{{\mathbf{A}}}_{22}] = {{\mathbf{A}}}_{11} - {{\mathbf{A}}}_{12}{\mathbf{A}}_{22}^{-}{{\mathbf{A}}}_{21}, \end{aligned}$$

where ${{\mathbf{A}}}_{22}^{-}$ is a g-inverse of ${{\mathbf{A}}}_{22}$. Markiewicz (1997) investigates the properties of an information matrix ${\mathbf{C}}_{d}$ for estimating $\varvec{\vartheta }_1$ in model (1) with fixed effects $\varvec{\vartheta }_2$ as functions of the matrix

$$\begin{aligned} {\mathbf{W}}_{d } = \left[ {\mathbf{M}}_d / {\mathbf{X}}_3'{\mathbf{X}}_3 \right] = \left( \mathbf{X}_{1,d}:{\mathbf{X}}_{2,d}\right) '{\mathbf{Q}}_{X_3}\left( {\mathbf{X}}_{1,d}:\mathbf{X}_{2,d}\right) , \end{aligned}$$

where ${\mathbf{M}}_d =\left( {\mathbf{X}}_{1,d}:{\mathbf{X}}_{2,d}:{\mathbf{X}}_3\right) '\left( {\mathbf{X}}_{1,d}:{\mathbf{X}}_{2,d}:{\mathbf{X}}_3\right)$. ${\mathbf{W}}_{d}$ is the information matrix for simultaneously estimating $\varvec{\vartheta }_1$ and $\varvec{\vartheta }_2$ in model (1) with fixed effects $\varvec{\vartheta }_2$. In particular ${\mathbf{C}}_{d}$ can be expressed as

$$\begin{aligned} {\mathbf{C}}_{d}=\left[ {\mathbf{W}}_{d}/ {\mathbf{X}}_{2,d}'{\mathbf{Q}}_{X_3}{\mathbf{X}}_{2,d} \right] . \end{aligned}$$

Moreover, the information matrix of d for estimating $\varvec{\vartheta }_1$ in model (1) with random effects $\varvec{\vartheta }_2$ is

$$\begin{aligned} {\mathbf{C}}_{d,V} = \left[ {\mathbf{W}}_{d,V}/ {\mathbf{V}}^{1/2} {\mathbf{X}}_{2,d}'\mathbf{Q}_{X_3}{\mathbf{X}}_{2,d}{\mathbf{V}}^{1/2} + {\mathbf{I}}_{p_2} \right] , \end{aligned}$$

where

$$\begin{aligned} {\mathbf{W}}_{d,V} = {\varvec{\varLambda }}{\mathbf{W}}_{d}{\varvec{\varLambda }}+ \text{ diag }(\mathbf{0},{\mathbf{I}}_{p_2}) \end{aligned}$$

with ${\varvec{\varLambda }}= \text{ diag }({\mathbf{I}}_t,{\mathbf{V}}^{1/2})$; cf. Markiewicz (1997).

We consider such designs that the n-dimensional vector of ones, $\mathbf{1}_n$, belongs to the column space of ${\mathbf{X}}_{1,d}$ and $\mathbf{X}_3$. Thus, the space of all estimable functions of $\varvec{\vartheta }_1$ is the same as in model (1) premultiplied by ${\mathbf{Q}}_{1_n}$. Moreover, for any design $d\in {\mathcal {D}}$, both matrices ${\mathbf{C}}_d$ and ${\mathbf{C}}_{d,V}$ have row and column sums zero. Now assume that we have a design $d^*\in {\mathcal {D}}$ such that ${\mathbf {C}}_{d^*}$ is completely symmetric and $\mathrm{tr} \mathbf C_{d^*}$ is maximal over $d\in {\mathcal {D}}$. Then design $d^*$ is universally optimal in Kiefer’s sense (Kiefer 1975). Recall that a matrix is completely symmetric if all of its diagonal elements are equal and all of its off-diagonal elements are equal. Since the information matrix ${\mathbf{C}}_{d^*}$ is a function of the block matrix ${\mathbf{W}}_{d^*}$, it is obvious that the complete symmetry of every block of ${\mathbf{W}}_{d^*}$ (complete symmetry of ${\mathbf{W}}_{d^*}$ with respect to the group ${\mathbf{I}}_2\otimes \mathcal{P}_t$, where $\mathcal{P}_t$ is the set of $t\times t$ permutation matrices and $\otimes$ denotes the Kronecker product) implies the complete symmetry of $\mathbf{C}_{d^*}$.

To determine a universally optimal design, we shall briefly describe a method presented in Filipiak and Markiewicz (2007).

According to Filipiak and Markiewicz (2007), for a $pr\times pr$ block matrix ${\mathbf{A}}$ with $p\times p$ blocks $A_{ij}$ we use a partial trace matrix of ${\mathbf{A}}$, originally defined by Bhatia (2003) as

$$\begin{aligned} \mathrm{Tr}_p{\mathbf{A}}=(\mathrm{tr}{\mathbf{A}}_{ij})_{1\le i,j\le r}, \end{aligned}$$

that is, the partial trace matrix is obtained by replacing every block of ${\mathbf{A}}_{ij}$, $i=1,2,\dots ,r$, by its trace. Moreover, by $\widetilde{{\mathbf{A}}}$ we denote the matrix $({\mathbf{I}}_r\otimes \mathbf{Q}_{1_p}){\mathbf{A}}({\mathbf{I}}_r\otimes {\mathbf{Q}}_{1_p})$.

We now recall two corollaries from Filipiak and Markiewicz (2007), presented here as propositions.

Let ${\mathbf{X}}_{1,d},{\mathbf{X}}_{2,d}\in {\mathbb {R}}^{n\times t}$. Then $\mathbf{W}_d$ can be represented as a $2t\times 2t$ block matrix, with blocks of order t. For a design $d \in \mathcal{D}$ we define $\text{ Tr }_t\widetilde{{\mathbf{W}}}_{d}=(c_{dij})_{1\le i,j\le 2}$. Moreover, let us assume that ${\mathbf{V}}$ is a fixed completely symmetric matrix.

Proposition 1

(Filipiak and Markiewicz 2007, Corollary 3) If there exists a design $d^*\in \mathcal{D}$ such that the matrix $\mathbf{W}_{d^*}$ is completely symmetric with respect to the group $\mathbf{I}_2\otimes \mathcal{P}_t$ and the matrix

$$\begin{aligned} \mathrm{Tr}_t {\mathbf{W}}_{d^*}-\mathrm{Tr}_t {\mathbf{W}}_{d} \end{aligned}$$

is nonnegative definite for every design $d\in \mathcal{D}$ or the matrix

$$\begin{aligned} \left( \begin{array}{cc} 1 &{}\quad 0 \\ 1 &{}\quad x_{\#} \end{array}\right) (\mathrm{Tr}_t {\mathbf{W}}_{d^*}-\mathrm{Tr}_t {\mathbf{W}}_{d}) \left( \begin{array}{cc} 1 &{}\quad 1 \\ 0 &{}\quad x_{\#} \end{array}\right) , \end{aligned}$$

where $x_{\#}=-c_{d^*12}c^{-1}_{d^*22}$, is nonnegative for every design $d\in \mathcal{D}$, then $d^*$ is universally optimal for estimating $\varvec{\vartheta }_1$ in model (1) with a fixed completely symmetric nonnegative definite ${\mathbf{V}}$.

Let us now consider model (1) with ${\mathbf{X}}_{2,d}=(\mathbf{X}_{2,d}^{(1)},{\mathbf{X}}_{2,d}^{(2)})$, where $\mathbf{X}_{2,d}^{(i)}\in {\mathbb {R}}^{n\times t}$, $i=1,2$. Then ${\mathbf{W}}_d$ can be represented as a $3t\times 3t$ block matrix, with blocks of order t, and we define $\text{ Tr }_t\widetilde{{\mathbf{W}}}_{d}=(c_{dij})_{1\le i,j\le 3}$. Let us now denote the $2t\times 2t$ block matrix of ${\mathbf{W}}_d$ corresponding to ${\mathbf{X}}_{2,d}$ by ${\mathbf{Z}}_d$. For a design $d^*$ let

$$\begin{aligned} (x_*,y_*)'=-(\text{ Tr }_t\widetilde{{\mathbf{Z}}}_{d^*})^{+}(c_{d^*12}, c_{d^*13})'. \end{aligned}$$

(2)

Let us assume that $\mathcal{V}$ is a fixed completely symmetric matrix with respect to the group ${\mathbf{I}}_2\otimes \mathcal{P}_t$. Let

$$\begin{aligned} \mathbf{\Gamma }_{\#}\! = \! \left( \! \begin{array}{cccc} 1 &{}\quad 1 &{}\quad 1 &{}\quad 1\\ -y_*/2 &{}\quad x_*-y_*/2 &{}\quad x_*+y_*/2 &{}\quad y_*/2 \\ x_*/2 &{}\quad x_*/2+y_* &{}\quad -x_*/2+y_* &{}\quad -x_*/2 \end{array} \! \right) , \end{aligned}$$

(3)

where $(x_*,y_*)'$ is defined in (2).

Proposition 2

(Filipiak and Markiewicz 2007, Corollary 2) If there exists a design $d^*\in \mathcal{D}$ such that ${\mathbf{W}}_{d^*}$ is completely symmetric with respect to the group ${\mathbf{I}}_3\otimes \mathcal{P}_t$, and such that for every design $d\in \mathcal{D}$ the matrix

$$\begin{aligned} \mathbf{\Gamma }_{\#}'(\mathrm{Tr}_t{\mathbf{W}}_{d^*}- \mathrm{Tr}_t{\mathbf{W}}_{d})\mathbf{\Gamma }_{\#} \end{aligned}$$

is copositive, then $d^*$ is universally optimal for estimating $\varvec{\vartheta }_1$ in model (1) for any fixed ${\mathbf{V}}$ completely symmetric with respect to the group ${\mathbf{I}}_2\otimes \mathcal{P}_t$.

Recall that a real symmetric matrix ${\mathbf{A}}$ of order n is said to be copositive if ${\mathbf{x}}' \mathbf{Ax} \ge 0$ for ${\mathbf{x}} =(x_1,x_2, \ldots ,x_n)'\in {\mathbb {R}}^n$ such that $x_i\ge 0$ for every $i=1,2,\ldots ,n$. A sufficient condition for a matrix to be copositive is its nonnegative-definiteness (cf. Andersson et al. 1995). Hence, a sufficient condition for Proposition 2 is the nonnegative-definiteness of the matrix $\text{ Tr }_t{\mathbf{W}}_{d^*}-\text{ Tr }_t{\mathbf{W}}_{d}$ or its respective principal submatrices when $x_*=0$ or $y_*=0$. This problem was studied in a more general setting in Markiewicz (1997), and for the case of a circular interference model in Filipiak and Markiewicz (2003).

3 Interference models

Let ${\mathcal {D}}_{t,b,k}$ be the class of designs with t treatments and n experimental units, which are grouped into b homogeneous blocks with k experimental units per block. If all of the experimental units are homogeneous (block effects are not significant) then such a set of designs is denoted by $\mathcal D_{t,n}$ with $n=bk$. For a design $d\in {\mathcal {D}}_{t,b,k}$ let d(i, j) be the treatment assigned to plot j of block i ($j=1,\dots ,k$, $i=1,\dots ,b$). The response on plot j of block i can be written as follows:

$$\begin{aligned} y_{i,j}=\mu +\tau _{d(i,j)}+\lambda _{d(i,j-1)}+\rho _{d(i,j+1)}+\beta _i+\varepsilon _{i,j}, \end{aligned}$$

(4)

where $\mu$ is an overall mean, $\tau _{d(i,j)}$ is the effect of treatment d(i, j), $\lambda _{d(i,j-1)}$ and $\rho _{d(i,j+1)}$ are the left- and right-neighbor effects of the treatment d(i, j), which in particular may be equal, $\beta _i$ is the effect of block i, and $\varepsilon _{i,j}$ is the random error. All errors are assumed to be uncorrelated with common variance, say equal to 1. We consider a circular interference model, that is, we assume that in a design every treatment has a left and right neighbor, and $d(i,0)=d(i,k)$, $d(i,k+1)=d(i,1)$. This situation may occur if each block of the design has the form of a circle. If plots in blocks are arranged in linear forms, we can obtain the effect of circularity by adding border plots at the beginning of each block, where the treatment at the border plot is the same as the treatment at the opposite end of the block (for more details see e.g. Druilhet 1999). Border plots are not used for measuring the response variables. Following Druilhet (1999) we assume $t\ge 3$.

In particular we consider model (4) with or without block effects and with or without right-neighbor effects.

Let ${\varvec{\lambda }}$ and ${\varvec{\rho }}$ be $t\times 1$ vectors of left- and right-neighbor effects. We will assume that $({\varvec{\lambda }}',{\varvec{\rho }}')'$ is a vector of random effects with covariance matrix ${\mathbf{V}}$, and that it is uncorrelated with a random error.

Let $\mathbf {T}_{du}$ be the design matrix of treatment effects in block u, $1\le u\le b$. Further, define $\mathbf {T}_d=(\mathbf {T}'_{d1}:\dots :\mathbf {T}'_{db})'$ as the design matrix of treatment effects. For each u define the left- and right-neighbor incidence matrices as, respectively, $\mathbf L_{du}={\mathbf {H}}_k\mathbf {T}_{du}$ and ${\mathbf {R}}_{du}={\mathbf {H}}'_k \mathbf {T}_{du}$, where ${\mathbf {H}}_k$ denotes the $k\times k$ permutation matrix with the element $h_{i,j}$ equal to 1 if $i-j=1$, $h_{1,k}=1$, and 0 otherwise. This form of the matrix ${\mathbf {H}}_k$ follows from the assumption that each treatment has a left neighbor.

The design matrix of block effects, ${\mathbf {B}}$, has the form ${\mathbf {I}}_b\otimes \mathbf 1_k$ while ${\mathbf {L}}_d=(\mathbf L'_{d1}:\dots :{\mathbf {L}}'_{db})'=({\mathbf {I}}_b\otimes \mathbf H_k)\mathbf {T}_d$ and ${\mathbf {R}}_d=({\mathbf {R}}'_{d1}:\dots :\mathbf R'_{db})'=({\mathbf {I}}_b\otimes {\mathbf {H}}'_k)\mathbf {T}_d$ are, respectively, the design matrices of left- and right-neighbor effects.

Now, in vector notation, model (4) can be written as

$$\begin{aligned} {\mathbf {y}} = \mu \mathbf 1_n+\mathbf {T}_d \varvec{\tau } + {\mathbf {L}}_d \varvec{\lambda } + {\mathbf {R}}_d \varvec{\rho } + {\mathbf {B}}\varvec{\beta } + \varvec{\varepsilon }, \end{aligned}$$

(5)

where ${\varvec{\tau }}$ is a $t \times 1$ vector of treatment effects, ${\varvec{\beta }}$ is a $b \times 1$ vector of block effects, and ${\varvec{\varepsilon }}$ is a $bk\times 1$ vector of random errors with $\mathrm{E}({\varvec{\varepsilon }})=0$ and $\text{ Cov }({\varvec{\varepsilon }})=\mathbf{I}_{bk}$. The covariance matrix of neighbor effects, ${\mathbf{V}}$, is usually $\text{ diag }(\sigma _L^2 {\mathbf{I}}_t, \sigma _R^2 {\mathbf{I}}_t)$. Observe, that if ${\mathbf{V}}$ is completely symmetric with respect to the group ${\mathbf{I}}_2\otimes \mathcal{P}_t$, the variances of left-neighbor effects and right-neighbor effects are respectively $\sigma _L^2$ and $\sigma _R^2$, and the off-diagonal blocks of ${\mathbf{V}}$ are proportional to $\mathbf{1}_t\mathbf{1}'_t$, then the estimator of treatment effects and its information matrix are the same as in the model with ${\mathbf{V}}=\text{ diag }(\sigma _L^2 {\mathbf{I}}_t, \sigma _R^2 {\mathbf{I}}_t)$. The optimality results presented by Filipiak and Markiewicz (2007) correspond to the more general case when ${\mathbf{V}}$ is completely symmetric with respect to the group ${\mathbf{I}}_2\otimes \mathcal{P}_t$. Thus, we will retain this assumption.

Model (5) with random neighbor effects ${\varvec{\lambda }}$ and ${\varvec{\rho }}$ is called a mixed effects model. Following Jones et al. (1992), a fixed interference model is a model (5) in which variances tend to infinity ($\sigma _L^2=\infty$ and $\sigma _R^2=\infty$) in such a way that the difference between the variances and the covariances goes to infinity. On the other hand, if $\sigma _L^2=\sigma _R^2=0$, model (5) is a model without nuisance parameters (other than block effects). Also if $\sigma _L^2\not =0$ ($\sigma _L^2=\infty$) and $\sigma _R^2=0$, model (5) has random (fixed) left-neighbor effects and has no right-neighbor effects.

Since $\mathbf 1_n$ belongs to the column-space of ${\mathbf{T}}_d$, $\mathbf{L}_d$, ${\mathbf{R}}_d$, and ${\mathbf {B}}$, we have ${\mathbf{T}}_d\mathbf{1}_t={\mathbf{L}}_d\mathbf{1}_t={\mathbf{R}}_d\mathbf{1}_t={\mathbf{B}}\mathbf{1}_t=\mathbf{1}_n$ and ${\mathcal {R}}(\mathbf{1}_n,\mathbf{B})={\mathcal {R}}({\mathbf{B}})$. Thus, we may consider the universal optimality of d (with respect to the estimation of treatment effects) in Kiefer’s sense. Moreover, we consider the class of connected designs, i.e., designs for which all treatment contrasts are estimable, which is equivalent to the condition that the rank of the information matrix for $\varvec{\tau }$ be equal to $t-1$. In such a case the spaces of all estimable functions of $\varvec{\tau }$ in models with ${\mathbf{X}}_3={\mathbf{B}}$ and ${\mathbf{X}}_3=(\mathbf{1}_n,{\mathbf{B}})$ are equal.

Based on (5) let us define the following interference models:

$$\begin{aligned} \begin{array}{llll} {\mathcal {M}}_{1A}: \qquad &{} {\mathbf{X}}_{1,d}={\mathbf{T}}_d, \;\;\; &{} {\mathbf{X}}_{2,d}={\mathbf{L}}_d, \;\;\; &{} {\mathbf{X}}_{3}={\mathbf{B}},\\ {\mathcal {M}}_{1B}: \qquad &{} {\mathbf{X}}_{1,d}={\mathbf{T}}_d, \;\;\; &{} {\mathbf{X}}_{2,d}={\mathbf{L}}_d, \;\;\; &{} {\mathbf{X}}_{3}=\mathbf{1}_n,\\ {\mathcal {M}}_{2A}: \qquad &{} {\mathbf{X}}_{1,d}={\mathbf{T}}_d, \;\;\; &{} {\mathbf{X}}_{2,d}={\mathbf{L}}_d+{\mathbf{R}}_d, \;\;\; &{} {\mathbf{X}}_{3}={\mathbf{B}},\\ {\mathcal {M}}_{2B}: \qquad &{} {\mathbf{X}}_{1,d}={\mathbf{T}}_d, \;\;\; &{} {\mathbf{X}}_{2,d}={\mathbf{L}}_d+{\mathbf{R}}_d, \;\;\; &{} {\mathbf{X}}_{3}=\mathbf{1}_n,\\ {\mathcal {M}}_{3A}: \qquad &{} {\mathbf{X}}_{1,d}={\mathbf{T}}_d, \;\;\; &{} {\mathbf{X}}_{2,d}=({\mathbf{L}}_d:{\mathbf{R}}_d), \;\;\; &{} {\mathbf{X}}_{3}={\mathbf{B}},\\ {\mathcal {M}}_{3B}: \qquad &{} {\mathbf{X}}_{1,d}={\mathbf{T}}_d, \;\;\; &{} {\mathbf{X}}_{2,d}=({\mathbf{L}}_d:{\mathbf{R}}_d), \;\;\; &{} {\mathbf{X}}_{3}=\mathbf{1}_n. \end{array} \end{aligned}$$

The (i, j)th entry of $\mathbf {T}'_d{\mathbf {L}}_d$ denotes the number of occurrences of treatment i with treatment j as left neighbor in a design d, and is called a left-neighboring matrix of design d; cf. Filipiak et al. (2008). We denote $\mathbf {T}'_d{\mathbf {L}}_d$ by ${\mathbf {S}}_d$ with elements $s_{d,ij}$. Similarly, the (i, j)th entry of ${\mathbf {L}}'_d\mathbf R_d$ denotes the number of occurrences of treatment i with treatment j as left neighbor at distance 2 in a design d. We denote ${\mathbf {L}}'_d{\mathbf {R}}_d$ by ${\mathbf {U}}_d$. Note that for every Rees’ (1967) neighbor design ${\mathbf{S}}_d+{\mathbf{S}}'_d$ is completely symmetric with zero diagonal and ${\mathbf{S}}_d\mathbf{1}_t={\mathbf{S}}'_d\mathbf{1}_t=r\mathbf{1}_t$, where r is the number of replications of a treatment (the same for every treatment) in a design d.

Throughout this paper we use some properties of a balanced block design (BBD), i.e. such a design $d\in {\mathcal {D}}_{t,b,k}$ for which (i) all $n_{d,ij}=\lfloor k/t \rfloor$ or $\lfloor k/t \rfloor +1$, (ii) all $r_{d,i}$ are equal, and (iii) every pair of distinct treatments occurs together in the same number of blocks, where $\lfloor x \rfloor$ is the largest integer not exceeding x, $r_{d,i}$ is the number of replications of the ith treatment in d, and ${\mathbf{N}}_d={\mathbf{T}}'_d{\mathbf{B}}=(n_{d,ij})$ (Kiefer 1958). A BBD reduces to a balanced incomplete block design (BIBD) when $k < t$. All designs satisfying (i) are called binary designs, while designs satisfying (ii) are called equireplicated designs. The class of BIBDs in ${\mathcal {D}}_{t,b,k}$ will be denoted by $\mathcal B_{t,b,k}$.

We also use the following designs.

Definition 1

(Druilhet 1999) A circular binary block design in $\mathcal D_{t,b,k}$ which is a balanced block design in the usual sense, and is such that for each ordered pair of distinct treatments there exist exactly l inner plots which receive the first chosen treatment and which have the second one as right neighbor, is called a circular neighbor balanced design (CNBD).

Definition 2

(Druilhet 1999) A circular neighbor balanced design such that for each ordered pair of distinct treatments there exist exactly l inner plots that have the first chosen treatment as left neighbor and the second one as right neighbor is called a circular neighbor balanced design at distances 1 and 2 (CNBD2).

It is clear that a CNBD2 is a CNBD. A catalogue of CNBD2s is given in Azaïs et al. (1993).

4 Universal optimality

Druilhet (1999) showed the universal optimality of CNBD and CNBD2 under fixed interference models $\mathcal{M}_{1A}$ and $\mathcal{M}_{3A}$ over the class $\mathcal{D}_{t,b,k}$ and over the class $\mathcal{D}_{t,b,k}$ with no treatment preceded by itself, respectively. The universal optimality of CNBD2 under a fixed interference model $\mathcal{M}_{2A}$ over the class $\mathcal{D}_{t,b,k}$ and the class $\mathcal{D}_{t,b,k}$ with no treatment preceded by itself is proved in Filipiak (2012). Filipiak and Markiewicz (2017) presented an overview study on the universal optimality of some circular neighbor balanced designs under the fixed interference models $\mathcal{M}_{1B}$, $\mathcal{M}_{2B}$, and $\mathcal{M}_{3B}$. They proved the universal optimality of some equireplicated circular neighbor balanced designs over the class $\mathcal{D}_{t,b,k}$ with no treatment preceded by itself under $\mathcal{M}_{1B}$, and over the class $\mathcal{D}_{t,b,k}$ with no treatment preceded by itself at distances 1 and 2 under $\mathcal{M}_{2B}$ and $\mathcal{M}_{3B}$.

The aim of this section is to give an overview study on the universal optimality of some circular neighbor balanced BIB/equireplicated designs under mixed models $\mathcal{M}_{1A}$–$\mathcal{M}_{3B}$.

4.1 Mixed interference models without block effects

It can be easy calculated that $\mathbf {T}'_d\mathbf Q_{1_n}\mathbf {T}_d={\mathbf {L}}'_d{\mathbf {Q}}_{1_n}{\mathbf {L}}_d=\mathbf R'_d{\mathbf {Q}}_{1_n}{\mathbf {R}}_d$ and $\mathbf {T}'_d\mathbf Q_{1_n}{\mathbf {L}}_d=(\mathbf {T}'_d{\mathbf {Q}}_{1_n}{\mathbf {R}}_d)'=\mathbf{S}_d-\frac{1}{n}{\mathbf {r}}_d{\mathbf {r}}'_d$, ${\mathbf {L}}'_d\mathbf Q_{1_n}{\mathbf {R}}_d={\mathbf{U}}_d-\frac{1}{n} {\mathbf {r}}_d{\mathbf {r}}'_d$, where ${\mathbf {r}}_d$ is a $t\times 1$ vector of replications of treatments in the design d. The components of ${\mathbf{r}}_d$ are replications of treatments, $r_{d,i}$, $i=1,\dots ,t$. We obtain:

$$\begin{aligned} \begin{array}{l} \mathrm{tr}({\mathbf{T}}'_d{\mathbf{Q}}_{1_n}{\mathbf{T}}_d)=\mathrm{tr}({\mathbf{L}}'_d{\mathbf{Q}}_{1_n}{\mathbf{L}}_d)=\mathrm{tr}({\mathbf{R}}'_d{\mathbf{Q}}_{1_n}{\mathbf{R}}_d)=n-\frac{1}{n}\sum \limits _{i=1}^{t}r_{d,i}^2,\\ \mathrm{tr}({\mathbf{T}}'_d{\mathbf{Q}}_{1_n}{\mathbf{L}}_d)=\mathrm{tr}({\mathbf{T}}'_d{\mathbf{Q}}_{1_n}{\mathbf{R}}_d)=\mathrm{tr}{\mathbf{S}}_d-\frac{1}{n}\sum \limits _{i=1}^{t}r_{d,i}^2,\\ \mathrm{tr}({\mathbf{L}}'_d{\mathbf{Q}}_{1_n}{\mathbf{R}}_d)=\mathrm{tr}{\mathbf{U}}_d-\frac{1}{n}\sum \limits _{i=1}^{t}r_{d,i}^2, \end{array} \end{aligned}$$

and hence

$$\begin{aligned} \begin{array}{l} \mathrm{tr}({\mathbf{T}}'_d{\mathbf{Q}}_{1_n}({\mathbf{L}}_d+{\mathbf{R}}_d))=2\left( \mathrm{tr}{\mathbf{S}}_d-\frac{1}{n}\sum \limits _{i=1}^{t}r_{d,i}^2\right) ,\\ \mathrm{tr}(({\mathbf{L}}_d+{\mathbf{R}}_d)'{\mathbf{Q}}_{1_n}({\mathbf{L}}_d+{\mathbf{R}}_d))=2\left( n-\frac{2}{n}\sum \limits _{i=1}^{t}r_{d,i}^2+\mathrm{tr}{\mathbf{U}}_d\right) . \end{array} \end{aligned}$$

Observe that if $d^*$ is an equireplicated design, then $\mathbf {T}'_d\mathbf {T}_d=\frac{n}{t}{\mathbf {I}}_t=r{\mathbf {I}}_t$. Moreover, if a design $d^*$ does not have any selfneighbors, then

$$\begin{aligned} \begin{array}{l} \mathrm{tr}({\mathbf{T}}'_{d^*}{\mathbf{Q}}_{1_n}{\mathbf{T}}_{d^*})=\mathrm{tr}({\mathbf{L}}'_{d^*}{\mathbf{Q}}_{1_n}{\mathbf{L}}_{d^*})=\mathrm{tr}({\mathbf{R}}'_{d^*}{\mathbf{Q}}_{1_n}{\mathbf{R}}_{d^*})=n\left( 1-\frac{1}{t}\right) ,\\ \mathrm{tr}({\mathbf{T}}'_{d^*}{\mathbf{Q}}_{1_n}{\mathbf{L}}_{d^*})=\mathrm{tr}(\mathbf{T}'_{d^*}{\mathbf{Q}}_{1_n}{\mathbf{R}}_{d^*})=-\frac{n}{t}. \end{array} \end{aligned}$$

and, if a design $d^*$ has no selfneighbors at distance 2, then

$$\begin{aligned} \begin{array}{l} \mathrm{tr}({\mathbf{L}}'_{d^*}{\mathbf{Q}}_{1_n}{\mathbf{R}}_{d^*})=-\frac{n}{t}. \end{array} \end{aligned}$$

Hence,

$$\begin{aligned} \begin{array}{l} \mathrm{tr}({\mathbf{T}}'_{d^*}{\mathbf{Q}}_{1_n}({\mathbf{L}}_{d^*}+{\mathbf{R}}_{d^*}))=-\frac{2n}{t},\\ \mathrm{tr}(({\mathbf{L}}_{d^*}+{\mathbf{R}}_{d^*})'{\mathbf{Q}}_{1_n}({\mathbf{L}}_{d^*}+{\mathbf{R}}_{d^*}))=2n\left( 1-\frac{2}{t}\right) . \end{array} \end{aligned}$$

Observe that $\frac{1}{n}\sum _{i=1}^{t}r_{d,i}^2 \ge \frac{n}{t}$, with equality for equireplicated designs. For convenience we use the notation $\alpha ={-\frac{n}{t}+\frac{1}{n}\sum \nolimits _{i=1}^{t}r_{d,i}^2}$.

We can now prove the following theorems.

Theorem 1

If there exists an equireplicated design with no treatment preceded by itself, $d^*\in {\mathcal {D}}_{t,b,k}$, such that ${\mathbf {S}}_{d^*}$ is completely symmetric, then $d^*$ is universally optimal in the estimation of treatment effects under the mixed model ${\mathcal {M}}_{1B}$ with arbitrary, fixed completely symmetric ${\mathbf{V}}$, over the class $\mathcal{D}_{t,b,k}$ with no treatment preceded by itself.

Proof

Assume that $d^*$ is an equireplicated design with no treatment preceded by itself, such that ${\mathbf {S}}_{d^*}$ is completely symmetric. Due to Proposition 1 it is enough to show that the difference $\text{ Tr }_t{\mathbf{W}}_{d^*}-\text{ Tr }_t{\mathbf{W}}_{d}$ is nonnegative definite for every $d\in \mathcal{D}_{t,b,k}$ with no treatment preceded by itself. Observe that

$$\begin{aligned} c_{d,11}=c_{d,22}=n-\frac{1}{n}\sum _{i=1}^{t}r_{d,i}^2,\quad c_{d,12}=\mathrm{tr}{\mathbf{S}}_d-\frac{1}{n}\sum _{i=1}^{t}r_{d,i}^2, \end{aligned}$$

and

$$\begin{aligned} c_{d^*,11}=c_{d^*,22}=n\left( 1-\frac{1}{t}\right) ,\quad c_{d^*,12}=-\frac{n}{t}. \end{aligned}$$

Further, we can write

$$\begin{aligned} \text{ Tr }_t{\mathbf{W}}_{d^*}-\text{ Tr }_t{\mathbf{W}}_{d}=\left( \begin{array}{cc} \alpha &{}\quad \alpha -\text{ tr }{\mathbf{S}}_d \\ \alpha -\text{ tr }{\mathbf{S}}_d &{}\quad \alpha \\ \end{array} \right) . \end{aligned}$$

For every design $d\in \mathcal{D}_{t,b,k}$ with no treatment preceded by itself the diagonal entries of ${\mathbf{S}}_d$ are equal to zero. Thus, $\text{ Tr }_t{\mathbf{W}}_{d^*}-\text{ Tr }_t{\mathbf{W}}_{d}=\alpha \mathbf{1}_2\mathbf{1}'_2$ which is nonnegative definite. $\square$

Theorem 2

If there exists an equireplicated design with no treatment preceded by itself at distances 1 and 2, $d^*\in {\mathcal {D}}_{t,b,k}$, such that ${\mathbf {S}}_{d^*}+{\mathbf{S}}'_{d^*}$ and ${\mathbf{U}}_{d^*}+\mathbf{U}'_{d^*}$ are completely symmetric, then $d^*$ is universally optimal in the estimation of treatment effects under the mixed model ${\mathcal {M}}_{2B}$ with arbitrary, fixed completely symmetric $\mathbf{V}$, over the class $\mathcal{D}_{t,b,k}$ with no treatment preceded by itself at distances 1 and 2.

Proof

Assume that $d^*$ satisfies the conditions of the theorem. Then $\mathbf{W}_{d^*}$ is completely symmetric with respect to the group $\mathbf{I}_2\otimes \mathcal{P}_t$. Due to Proposition 1 it is enough to show that the difference $\text{ Tr }_t{\mathbf{W}}_{d^*}-\text{ Tr }_t{\mathbf{W}}_{d}$ is nonnegative definite for every $d\in \mathcal{D}_{t,b,k}$ with no treatment preceded by itself at distances 1 and 2. Observe that

$$\begin{aligned} \begin{array}{l} c_{d,11}=n-\frac{1}{n}\sum \limits _{i=1}^{t}r_{d,i}^2,\quad c_{d,12}=2\left( \mathrm{tr}{\mathbf{S}}_d-\frac{1}{n}\sum \limits _{i=1}^{t}r_{d,i}^2\right) , \\ c_{d,22}=2\left( \mathrm{tr}\mathbf{U}_d+n-\frac{2}{n}\sum \limits _{i=1}^{t}r_{d,i}^2\right) , \end{array} \end{aligned}$$

and

$$\begin{aligned} c_{d^*,11}=n\left( 1-\frac{1}{t}\right) , \quad c_{d^*,12}=-\frac{2n}{t}, \quad c_{d^*,22}=2n\left( 1-\frac{2}{t}\right) . \end{aligned}$$

Further, we can write

$$\begin{aligned} \text{ Tr }_t{\mathbf{W}}_{d^*}-\text{ Tr }_t{\mathbf{W}}_{d}=\left( \begin{array}{cc} \alpha &{} 2(\alpha -\text{ tr }{\mathbf{S}}_d) \\ 2(\alpha -\text{ tr }{\mathbf{S}}_d) &{} 2(2\alpha -\text{ tr }{\mathbf{U}}_d) \end{array} \right) . \end{aligned}$$

For every design $d\in \mathcal{D}_{t,b,k}$ with no treatment preceded by itself at distances 1 and 2 the diagonal entries of ${\mathbf{S}}_d$ and ${\mathbf{U}}_d$ are equal to zero. Thus,

$$\begin{aligned} \text{ Tr }_t{\mathbf{W}}_{d^*}-\text{ Tr }_t{\mathbf{W}}_{d}=\left( \begin{array}{cc} \alpha &{}\quad 2\alpha \\ 2\alpha &{}\quad 4\alpha \end{array} \right) , \end{aligned}$$

which is nonnegative definite. $\square$

Theorem 3

If there exists an equireplicated design with no treatment preceded by itself at distances 1 and 2, $d^*\in {\mathcal {D}}_{t,b,k}$, such that ${\mathbf {S}}_{d^*}$ and ${\mathbf{U}}_{d^*}$ are completely symmetric, then $d^*$ is universally optimal in the estimation of treatment effects under the mixed model ${\mathcal {M}}_{3B}$ with arbitrary, fixed ${\mathbf{V}}$, completely symmetric with respect to the group ${\mathbf{I}}_2\otimes \mathcal{P}_t$, over the class $\mathcal{D}_{t,b,k}$ with no treatment preceded by itself at distances 1 and 2.

Proof

Assume that $d^*$ satisfies the conditions of the theorem. Then $\mathbf{W}_{d^*}$ is completely symmetric with respect to the group $\mathbf{I}_3\otimes \mathcal{P}_t$. Due to Proposition 2 we need to construct the matrix $\varvec{\Gamma }_{\#}$ and show that $\varvec{\Gamma }_{\#}(\text{ Tr }_t{\mathbf{W}}_{d^*}-\text{ Tr }_t{\mathbf{W}}_{d})\varvec{\Gamma }_{\#}$ is copositive for every $d\in \mathcal{D}_{t,b,k}$ with no treatment preceded by itself at distances 1 and 2. Observe that

$$\begin{aligned} \begin{array}{l} c_{d,11}=c_{d,22}=c_{d,33}=n-\frac{1}{n}\sum \limits _{i=1}^{t}r_{d,i}^2,\quad c_{d,12}=c_{d,13}=\mathrm{tr}{\mathbf{S}}_d-\frac{1}{n}\sum \limits _{i=1}^{t}r_{d,i}^2, \\ c_{d,23}=\mathrm{tr}{\mathbf{U}}_d-\frac{1}{n}\sum \limits _{i=1}^{t}r_{d,i}^2, \end{array} \end{aligned}$$

and

$$\begin{aligned} c_{d^*,11}=c_{d^*,22}=c_{d^*,33}=n\left( 1-\frac{1}{t}\right) , \quad c_{d^*,12}=c_{d^*,13}=c_{d^*,23}=-\frac{n}{t}. \end{aligned}$$

According to (2) and (3)

$$\begin{aligned} \left( \begin{array}{c} x^* \\ y^* \end{array}\right) =-\left( \begin{array}{cc} c_{d^*,22} &{}\quad c_{d^*,23}\\ c_{d^*,23} &{}\quad c_{d^*,33} \end{array} \right) ^{-1} \left( \begin{array}{c} c_{d^*,12} \\ c_{d^*,13} \end{array}\right) =\frac{1}{t-2}\mathbf{1}_2 \end{aligned}$$

and

$$\begin{aligned} \mathbf{\Gamma }_{\#} = \frac{1}{2(t-2)} \left( \! \begin{array}{cccc} 2(t-2) &{}\quad 2(t-2) &{}\quad 2(t-2) &{}\quad 2(t-2)\\ -1 &{}\quad 1 &{}\quad 3 &{}\quad 1 \\ 1 &{}\quad 3 &{}\quad 1 &{}\quad -1 \end{array} \! \right) . \end{aligned}$$

For every design $d\in \mathcal{D}_{t,b,k}$ with no treatment preceded by itself at distances 1 and 2 we have $\text{ tr }{\mathbf{S}}_d=\text{ tr }{\mathbf{U}}_d=0$ and

$$\begin{aligned} \varvec{\Gamma }_{\#}(\text{ Tr }_t{\mathbf{W}}_{d^*}-\text{ Tr }_t{\mathbf{W}}_{d})\varvec{\Gamma }_{\#} =\frac{\alpha }{(t-2)^2}\left( \begin{array}{cccc} (t-2)^2 &{}\quad t(t-2) &{}\quad t(t-2) &{}\quad (t-2)^2\\ t(t-2) &{}\quad t^2 &{}\quad t^2 &{}\quad t(t-2) \\ t(t-2) &{}\quad t^2 &{}\quad t^2 &{}\quad t(t-2) \\ (t-2)^2 &{}\quad t(t-2) &{}\quad t(t-2) &{}\quad (t-2)^2 \end{array} \right) . \end{aligned}$$

The above matrix is nonnegative, which implies its copositivity. $\square$

The conditions of Theorem 1 are satisfied by every CNBD, and every CNBD2 satisfies the conditions of Theorems 2 and 3. For a mixed interference model $\mathcal{M}_{2B}$, in some particular cases, for example if t is prime and $k=t$, the number of blocks can be reduced to half of the blocks in a CNBD2 by choosing half arbitrary (but different) blocks. For more details see Filipiak (2012). Moreover, if we arrange the blocks of a CNBD2 with $t=k$ or a design as described above in such a way that every block starts with the same treatment, and then we stack all the blocks side by side, then the obtained design also satisfies the conditions of Theorem 2. For more detailed examples see Filipiak and Markiewicz (2017).

4.2 Mixed interference models with block effects

Theorem 4

(Filipiak and Markiewicz 2007, Proposition 4) A BBD $d^*\in {\mathcal {D}}_{t,b,k}$ such that ${\mathbf {S}}_{d^*}$ is completely symmetric is universally optimal in the estimation of treatment effects under the mixed interference model $\mathcal M_{1A}$ with arbitrary, fixed completely symmetric V over the class ${\mathcal {D}}_{t,b,k}$.

Theorem 5

A BBD $d^*\in {\mathcal {D}}_{t,b,k}$ such that ${\mathbf {S}}_{d^*}+{\mathbf {S}}'_{d^*}$ and ${\mathbf {U}}_{d^*}+{\mathbf {U}}'_{d^*}$ are completely symmetric is universally optimal in the estimation of treatment effects under the mixed interference model ${\mathcal {M}}_{2A}$ with arbitrary, fixed completely symmetric V over the class ${\mathcal {D}}_{t,b,k}$ with no treatment preceded by itself.

Proof

From the equality ${\mathbf {Q}}_B={\mathbf {I}}_b\otimes {\mathbf {Q}}_{1_k}$ and, since ${\mathbf {H}}_k$ is orthogonal, it follows that $\mathbf {T}'_d{\mathbf {Q}}_B\mathbf {T}_d={\mathbf {L}}'_d{\mathbf {Q}}_B{\mathbf {L}}_d={\mathbf {R}}'_d{\mathbf {Q}}_B{\mathbf {R}}_d$. Moreover, since the matrices ${\mathbf {H}}_k$ and ${\mathbf {Q}}_{1_k}$ commute, $\mathbf {T}'_d{\mathbf {Q}}_B{\mathbf {L}}_d=(\mathbf {T}'_d{\mathbf {Q}}_B{\mathbf {R}}_d)'= \mathbf {T}'_d{\mathbf {L}}_d-\frac{1}{k}\sum _{i=1}^b {\mathbf {r}}_{d,i}{\mathbf {r}}'_{d,i}$, ${\mathbf {L}}'_d{\mathbf {Q}}_B{\mathbf {R}}_d={\mathbf {L}}'_d{\mathbf {R}}_d-\frac{1}{k}\sum _{i=1}^b {\mathbf {r}}_{d,i}{\mathbf {r}}'_{d,i}$, where ${\mathbf {r}}_{d,i}$ is a $t\times 1$ vector of replications of treatments in the ith block of a design d. Moreover, observe that for BIB designs $\mathbf {T}'_d\mathbf {T}_d=\frac{bk}{t}{\mathbf {I}}_t=r{\mathbf {I}}_t$.

Define ${\mathbf {F}}_{u}=\mathbf {T}_{du}\mathbf {T}'_{du}-{\mathbf {I}}_k$ for $u=1,\dots ,b$. Observe that the diagonal entries of ${\mathbf {F}}_u$ are zero and the off-diagonal entries are

$$\begin{aligned} f_{ij}=\left\{ \begin{array}{l l} 0 \qquad &{}\quad \text{ if } \text{ the } \text{ treatments } \text{ on } \text{ units }\, i\, \text{ and }\, j\, \text{ are } \text{ different };\\ 1 &{}\quad \text{ otherwise }. \end{array} \right. \end{aligned}$$

Note that $\mathbf {T}_{du}\mathbf {T}'_{du}$ depends only on the arrangement of treatments on the ordered units 1 to k.

From the symmetry of ${\mathbf {F}}_{u}$, $u=1,\dots ,b$, it follows that $\mathrm{tr}({\mathbf {H}}'_k{\mathbf {F}}_u)=\mathrm{tr}({\mathbf {H}}_k{\mathbf {F}}_u)$ and $\mathrm{tr}({{\mathbf {H}}'_k}^2{\mathbf {F}}_u)=\mathrm{tr}({\mathbf {H}}_k^2{\mathbf {F}}_u)$. Thus,

$$\begin{aligned} c_{d,11}= & {} \mathrm{tr} (\mathbf {T}'_d{\mathbf {Q}}_B\mathbf {T}_d) =\sum _{u=1}^b \mathrm{tr} ({\mathbf {Q}}_{1_k}({\mathbf {F}}_{u}+{\mathbf {I}}_k))\\= & {} b(k-1)-\frac{1}{k}\sum _{u=1}^b\mathrm{tr} (\mathbf 1_k\mathbf 1'_k{\mathbf {F}}_{u}),\\ c_{d,12}= & {} \mathrm{tr} (\mathbf {T}'_d{\mathbf {Q}}_B({\mathbf {L}}_d+{\mathbf {R}}_d))=\sum _{u=1}^b \mathrm{tr} \left( {\mathbf {Q}}_{1_k}({\mathbf {H}}_k+{\mathbf {H}}'_k)({\mathbf {F}}_{u}+{\mathbf {I}}_k)\right) \\= & {} -2\left( b-\sum _{u=1}^{b}\mathrm{tr}({\mathbf {H}}_k{\mathbf {F}}_{u})+\frac{1}{k}\sum _{u=1}^b\mathrm{tr} (\mathbf 1_k\mathbf 1'_k{\mathbf {F}}_{u})\right) ,\\ c_{d,22}= & {} \mathrm{tr} (({\mathbf {L}}_d+{\mathbf {R}}_d)'{\mathbf {Q}}_B({\mathbf {L}}_d+{\mathbf {R}}_d)) \\= & {} \sum _{u=1}^b \mathrm{tr}(({\mathbf {H}}_k+{\mathbf {H}}'_k){\mathbf {Q}}_{1_k}({\mathbf {H}}_k+{\mathbf {H}}'_k)({\mathbf {F}}_{u}+{\mathbf {I}}_k))\\= & {} 2\left( b(k-2)+\sum _{u=1}^b\mathrm{tr} ({\mathbf {H}}_k^2{\mathbf {F}}_{u})-\frac{2}{k}\sum _{u=1}^b\mathrm{tr} (\mathbf 1_k\mathbf 1'_k{\mathbf {F}}_{u})\right) . \end{aligned}$$

Since for binary designs ${\mathbf{F}}_u$ is a zero matrix,

$$\begin{aligned} c_{d^*,11}=b(k-1),\qquad c_{d^*{12}}=-2b,\qquad c_{d^*,22}=2b(k-2). \end{aligned}$$

Due to Proposition 1 we calculate

$$\begin{aligned}&\text{ Tr }_t{\mathbf{W}}_{d^*}-\text{ Tr }_t{\mathbf{W}}_{d}\\&\quad = \left( \begin{array}{cc} \displaystyle {\frac{1}{k}\sum _{i=1}^b \text{ tr }(\mathbf{1}_k\mathbf{1}'_k{\mathbf{F}}_u)} &{}\quad \displaystyle {\frac{1}{k}\sum _{u=1}^b\mathrm{tr} (\mathbf 1_k\mathbf 1'_k{\mathbf {F}}_{u})-\sum _{u=1}^b\mathrm{tr} ({\mathbf {H}}_k{\mathbf {F}}_{u}) }\\ \displaystyle {\frac{1}{k}\sum _{u=1}^b\mathrm{tr} (\mathbf 1_k\mathbf 1'_k{\mathbf {F}}_{u})-\sum _{u=1}^b\mathrm{tr} ({\mathbf {H}}_k{\mathbf {F}}_{u})} &{}\quad \displaystyle {\frac{2}{k}\sum _{u=1}^b\mathrm{tr} (\mathbf 1_k\mathbf 1'_k{\mathbf {F}}_{u})-2\sum _{u=1}^b\mathrm{tr} ({\mathbf {H}}^2_k{\mathbf {F}}_{u})} \end{array} \right) . \end{aligned}$$

For every design $d\in \mathcal{D}_{t,b,k}$ with no treatment preceded by itself at distances 1 and 2 $\mathrm{tr} ({\mathbf {H}}_k{\mathbf {F}}_{u})=\mathrm{tr} ({\mathbf {H}}^2_k{\mathbf {F}}_{u})=0$ and

$$\begin{aligned} \text{ Tr }_t{\mathbf{W}}_{d^*}-\text{ Tr }_t{\mathbf{W}}_{d}= \frac{1}{k}\sum _{i=1}^b \text{ tr }(\mathbf{1}_k\mathbf{1}'_k{\mathbf{F}}_u) \left( \begin{array}{cc} 1 &{}\quad 1\\ 1 &{}\quad 2 \end{array} \right) , \end{aligned}$$

which is nonnegative definite. Assuming that $d^*$ satisfies the conditions concerning the complete symmetry of ${\mathbf{S}}_{d^*}+\mathbf{S}'_{d^*}$ and ${\mathbf{U}}_{d^*}+{\mathbf{U}}'_{d^*}$, we obtain the theorem. $\square$

Theorem 6

(Filipiak and Markiewicz 2007, Proposition 5) A BBD $d^*\in {\mathcal {D}}_{t,b,k}$ such that ${\mathbf {S}}_{d^*}$ and ${\mathbf {U}}_{d^*}$ are completely symmetric is universally optimal in the estimation of treatment effects under the mixed interference model ${\mathcal {M}}_{3A}$ with arbitrary, fixed V completely symmetric with respect to the group ${\mathbf{I}}_2\otimes \mathcal{P}_t$, over the class ${\mathcal {D}}_{t,b,k}$ with no treatment preceded by itself.

The conditions of Theorem 4 are satisfied by every CNBD, and every CNBD2 satisfies the conditions of Theorems 5 and 6. For a mixed interference model $\mathcal{M}_{2A}$, in some particular cases, for example if t is prime and $k=t$, the number of blocks can be reduced to half of the blocks in a CNBD2 by choosing half arbitrary (but different) blocks.

Another design for which optimality is frequently considered in the literature is an orthogonal array of type I and strength 2. Such designs are universally optimal under interference models with correlated observations. Filipiak and Markiewicz (2004) showed that orthogonal arrays can be universally optimal under a general interference model with fixed interference effects among the class of binary designs. These designs also fulfill the conditions of Propositions 1 and 2. The complete symmetry of the information matrix of such designs follows from Martin and Eccleston (1998). This implies that orthogonal arrays of type I and strength 2 are universally optimal under mixed interference models $\mathcal{M}_{1A}$, $\mathcal{M}_{2A}$ and $\mathcal{M}_{3A}$, over respective classes of designs.

5 Possible extensions for specific ${\mathbf{V}}=\text{ diag }(\sigma _L^2 {\mathbf{I}}_t, \sigma _R^2 {\mathbf{I}}_t)$

We will consider left- and right-neighbor effects such that $\text{ var }(\lambda _{d(i,j)})=\sigma _L^2$ and $\text{ var }(\rho _{d(i,j)})=~\sigma _R^2$, for $d(i,j)\in \{1,2,\dots ,t \}$, where $\sigma _L^2$ and $\sigma _R^2$ are known, and ${\varvec{\lambda }}$ and ${\varvec{\rho }}$ are uncorrelated.

Let us define circular weakly neighbor balanced designs as follows.

Definition 3

(Filipiak and Markiewicz 2012) Let $b\not =x(t-1)$, $x\in {\mathbb {N}}$. A circular binary design $d\in {\mathcal {D}}_{t,b,t}$ with $s_{d,ij}\in \left\{ x-1, x \right\}$, $i\not =j$, and completely symmetric matrix ${\mathbf{S}}_d{\mathbf{S}}'_d$ is called a circular weakly neighbor balanced design (CWNBD).

Note that for $b=x(t-1)$ we obtain the definition of a CNBD, i.e. a design with ${\mathbf{S}}_{d}=x(\mathbf{1}_t\mathbf{1}'_t-{\mathbf{I}}_t)$; cf. Druilhet (1999).

From Filipiak and Markiewicz (2012) it follows that a necessary condition for the existence of a CWNBD with $(x-1)(t-1)<b\le x(t-1)$, $x\in {\mathbb {N}}$ is

$$\begin{aligned} \frac{b(b-2x+1)}{t-1}\in {\mathbb {N}}. \end{aligned}$$

Filipiak and Markiewicz (2012) proved the universal optimality of CWNBDs under the fixed interference model ${\mathcal {M}}_{1A}$ among designs from ${\mathcal {D}}_{t,b,t}$ if $b\le t-1$, and from $\overline{{\mathcal {R}}}_{t,b,t}$ if $b>t-1$, where $\overline{{\mathcal {R}}}_{t,b,k}\subset {\mathcal {D}}_{t,b,k}$ is the class of equireplicated designs with no treatment preceded by itself.

Let ${\mathcal {R}}_{t,b,k}\subset {\mathcal {D}}_{t,b,k}$ be the class of equireplicated designs.

Theorem 7

(Filipiak and Markiewicz 2014) For every $\sigma _L^2\in (0,\infty ]$ a CWNBD is universally optimal over the class ${\mathcal {R}}_{t,b,t}$, $b<t-1$, and over the class $\overline{{\mathcal {R}}}_{t,b,t}$, $b>t-1$, under the mixed interference model ${\mathcal {M}}_{1A}$.

Using the theory presented by Kushner (1997) and developed by Kunert and Martin (2000) for fixed effect interference models and by Filipiak and Markiewicz (2007, Proposition 3) for mixed effects interference models, we can prove the following propositions.

Proposition 3

A BBD $d^*\in {\mathcal {D}}_{t,b,k}$ such that ${\mathbf {S}}_{d^*}+{\mathbf {S}}'_{d^*}$ and ${\mathbf {U}}_{d^*}+{\mathbf {U}}'_{d^*}$ are completely symmetric is universally optimal under the mixed interference model $\mathcal M_{2A}$ in the estimation of treatment effects over the class of:

• designs with no treatment preceded by itself from $\mathcal D_{t,b,k}$ for every $\sigma _L^2$;

• designs with no treatment preceded by itself at distance 2 from ${\mathcal {D}}_{t,b,k}$ if $k=2,3,4$, or if $k>4$ and $\sigma _L^2\le t/(2b\sqrt{k(k-4)})$;

• all designs from ${\mathcal {D}}_{t,b,k}$ if $k=2,3$, or if $k>3$ and $\sigma _L^2\le t/(2b\sqrt{k(k-3)})$.

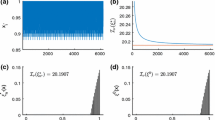
Example A CNBD2 is universally optimal over the class of designs from ${\mathcal {D}}_{t,b,k}$ for every $\sigma _L^2\le \frac{t}{2b\sqrt{k(k-3)}}$. The areas for t and $\sigma _L^2$ respectively for $k=t, b=t-1$ and $k=t-1, b=t$ are shown in Fig. 1.

Fig. 1

The areas for t and $\sigma _L^2$ respectively for $k=t, b=t-1$ and $k=t-1, b=t$

Proposition 4

A BBD $d^*\in {\mathcal {D}}_{t,b,k}$ such that ${\mathbf {S}}_{d^*}$ and ${\mathbf {U}}_{d^*}$ are completely symmetric is universally optimal under the mixed interference model ${\mathcal {M}}_{3A}$ in the estimation of treatment effects over the class of:

• designs with no treatment preceded by itself from $\mathcal D_{t,b,k}$ for every $\sigma _L^2$;

• designs with no treatment preceded by itself at distance 2 from ${\mathcal {D}}_{t,b,k}$ for every $\sigma _L^2$ and $k\le 6$;

• all designs from ${\mathcal {D}}_{t,b,k}$ if $k\le 4$.

Moreover, there exist $\sigma _L^2$ and $\sigma _R^2$ such that a design $d^*$ is universally optimal over the class of designs with no treatment preceded by itself at distance 2 from $\mathcal D_{t,b,k}$ for $k>6$, and over the class of all designs from ${\mathcal {D}}_{t,b,k}$ if $k>4$.

Example Let $k=t$ and $b=t-1$. Then a CNBD2 is universally optimal over the class of designs from $\mathcal D_{t,t-1,t}$ for every t if $\sigma _L^2$ and $\sigma _R^2$ satisfy the following inequality:

$$\begin{aligned}&2[t+(t-1)t\sigma _R^2+(t-1)^2\sigma _R^2)]+(t-1)\sigma _L^2[3t+(2t^2-t-1)\sigma _R^2)]\\&\qquad +(t-1)^2\sigma _L^4[t+1+3(t-1)\sigma _R^2)]\\&\quad \ge (t-5)(t-1)^3\sigma _L^2\sigma _R^4+(t-4)(t-1)^4\sigma _L^4\sigma _R^4. \end{aligned}$$

It can be calculated that the above inequality is usually satisfied for small $\sigma _L^2$ and $\sigma _R^2$. For example, if $\sigma _L^2=\sigma _R^2=0.1$, then a CNBD2 is universally optimal for every $t \le 23$, while for $\sigma _L^2=\sigma _R^2=0.5$ the number of treatments cannot exceed 7, for $\sigma _L^2=\sigma _R^2=1$ the number of treatments cannot exceed 5, etc. It can also be checked that the above inequality is satisfied for the following triples of parameters $(t,\sigma _L^2,\sigma _R^2)$: (10, 0.5, 0.1), (10, 10, 0.1), (15, 0.5, 0.1), (15, 2, 0.1) etc.

It is worth noting that in the case of models without blocks the results presented in Theorems 1, 2 and 3 cannot be extended. To illustrate this statement one may refer to Druilhet (1999), where examples are given of designs that are better than CNBD2 under models ${\mathcal {M}}_{2B}$ and ${\mathcal {M}}_{3B}$ with fixed neighbor effects.