Model averaging based on James–Stein estimators

Abstract

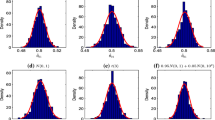
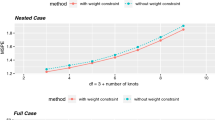
Existing model averaging methods are generally based on ordinary least squares (OLS) estimators. However, it is well known that the James–Stein (JS) estimator dominates the OLS estimator under quadratic loss, provided that the dimension of coefficient is larger than two. Thus, we focus on model averaging based on JS estimators instead of OLS estimators. We develop a weight choice method and prove its asymptotic optimality. A simulation experiment shows promising results for the proposed model average estimator.

Appendix: Proofs of theorems

Proof of Theorem 1

By the condition stated in Theorem 1 and Stein’s Lemma (Stein 1981), we have

$$\begin{aligned} E (\hat{\mu }_i^{\text {JS}}(w)-y_i)(y_i-\mu _i) = \sigma ^2E \partial (\hat{\mu }_i^{\text {JS}}(w)-y_i)/\partial y_i = \sigma ^2E \partial \hat{\mu }_i^{\text {JS}}(w)/\partial y_i -\sigma ^2. \nonumber \\ \end{aligned}$$

(5)

Using (5) and some techniques on matrix derivatives, we have

$$\begin{aligned} R^{\text {JS}}(w)&= E\Vert \hat{\mu }^{\text {JS}}(w)-\mu \Vert ^2=E\Vert \hat{\mu }^{\text {JS}}(w)-y+y-\mu \Vert ^2\nonumber \\&= E\Vert \hat{\mu }^{\text {JS}}(w)-y\Vert ^2+E\Vert y-\mu \Vert ^2+2E(\hat{\mu }^{\text {JS}}(w)-y)'(y-\mu )\nonumber \\&= E\Vert \hat{\mu }^{\text {JS}}(w)-y\Vert ^2+n\sigma ^2 +2E\sum \limits _{i=1}^n(\hat{\mu }_i^{\text {JS}}(w)-y_i)(y_i-\mu _i)\nonumber \\&= E\Vert \hat{\mu }^{\text {JS}}(w)-y\Vert ^2+n\sigma ^2 +2\sigma ^2E\text{ tr }(\partial \hat{\mu }^{\text {JS}}(w)/\partial y') -2n\sigma ^2\nonumber \\&= E\Vert \hat{\mu }^{\text {JS}}(w)-y\Vert ^2-n\sigma ^2 \!+\!2\sigma ^2E\text{ tr }\left( \partial \sum \limits _{m=1}^Mw_m\left( 1-a_mg_m(y)\right) P_my/\partial y'\right) \nonumber \\&= E\Vert \hat{\mu }^{\text {JS}}(w)-y\Vert ^2-n\sigma ^2 + 2\sigma ^2E\sum \limits _{m=1}^Mw_m(1-a_mg_m(y))\text{ tr }(P_m)\nonumber \\&+ 2\sigma ^2\sum \limits _{m=1}^Mw_mE\text{ tr }\left( P_my\left( \partial \left( 1-a_m{\Vert \hat{\mu }_m-y\Vert ^2 \over \Vert \hat{\mu }_m\Vert ^2}\right) /\partial y'\right) \right) \nonumber \\&= E\Vert \hat{\mu }^{\text {JS}}(w)-y\Vert ^2-n\sigma ^2 + 2\sigma ^2E\sum \limits _{m=1}^Mw_m(1-a_mg_m(y))k_m\nonumber \\&+2\sigma ^2\sum \limits _{m=1}^Mw_mE\text{ tr }\left( P_my\left( \partial \left( 1+a_m-a_m{y'y \over y'P_my}\right) /\partial y'\right) \right) \nonumber \\&= E\Vert \hat{\mu }^{\text {JS}}(w)-y\Vert ^2-n\sigma ^2 + 2\sigma ^2E\sum \limits _{m=1}^Mw_m(1-a_mg_m(y))k_m\nonumber \\&-2\sigma ^2\sum \limits _{m=1}^Mw_mEa_m\left( \partial \left( {y'y \over y'P_my}\right) /\partial y'\right) P_my \nonumber \\&= E\Vert \hat{\mu }^{\text {JS}}(w)-y\Vert ^2-n\sigma ^2 + 2\sigma ^2w'k-2\sigma ^2E\sum \limits _{m=1}^Mw_ma_mg_m(y)k_m\nonumber \\&-2\sigma ^2\sum \limits _{m=1}^Mw_mEa_m\left( 2(y'P_my)^{-1}y'-2y'y(y'P_my)^{-2}y'P_m \right) P_my \nonumber \\&= E\Vert \hat{\mu }^{\text {JS}}(w)-y\Vert ^2-n\sigma ^2 + 2\sigma ^2w'k-2\sigma ^2E\sum \limits _{m=1}^Mw_ma_mg_m(y)k_m\nonumber \\&-4\sigma ^2\sum \limits _{m=1}^Mw_ma_m+ 4\sigma ^2\sum \limits _{m=1}^Mw_mEa_m y'y(y'P_my)^{-1}\nonumber \\&= E\Vert \hat{\mu }^{\text {JS}}(w)-y\Vert ^2+ 2\sigma ^2w'k-2\sigma ^2E\sum \limits _{m=1}^Mw_ma_mg_m(y)(k_m-2)-n\sigma ^2\nonumber \\&= ES(w)-n\sigma ^2. \end{aligned}$$

(6)

This completes the proof. $\square$

Proof of Theorem 2

Let $U_m=(1-a_mg_m(y))P_m$, $U(w)=\sum \nolimits _{m=1}^M w_mU_m$, $\tilde{X}=[X_1,\ldots ,X_M]$, and $\tilde{P}=\tilde{X}(\tilde{X}'\tilde{X})^{-1}\tilde{X}'$. Then $\hat{\mu }^{\text {JS}}(w)=U(w)y$. It is straightforward to show that

$$\begin{aligned} \hat{S}(w)&= \Vert \hat{\mu }^{\text {JS}}(w)-\mu -e\Vert ^2+ 2\hat{\sigma }^2w'k-2\hat{\sigma }^2\sum \limits _{m=1}^Mw_ma_mg_m(y)(k_m-2)\nonumber \\&= L^{\text {JS}}(w)-2e'\hat{\mu }^{\text {JS}}(w)+ 2e'\tilde{P}\mu + 2\hat{\sigma }^2w'k-2\hat{\sigma }^2\sum \limits _{m=1}^Mw_ma_mg_m(y)(k_m-2)\nonumber \\&+\Vert e\Vert ^2 +2e'\mu -2e'\tilde{P}\mu \nonumber \\&\equiv S^*(w)+\Vert e\Vert ^2 +2e'\mu -2e'\tilde{P}\mu , \end{aligned}$$

(7)

where the last three terms are unrelated to $w$. Thus,

$$\begin{aligned} \hat{w} = \underset{w \in {{\mathcal {W}}}}{\text {argmin}} S^*(w). \end{aligned}$$

(8)

It is seen that $L^{\text {JS}}(w)- T(w) = \Vert U(w)e\Vert ^2+2\mu '(U(w)-I_n)U(w)e$ and $S^*(w)-L^{\text {JS}}(w)=-2e'U(w)e - 2e'(U(w)-\tilde{P})\mu + 2\hat{\sigma }^2w'k-2\hat{\sigma }^2\sum \nolimits _{m=1}^Mw_ma_mg_m(y)(k_m-2)$. From the proof of Theorem 3 of Liang et al. (2011), (8), and condition (C.2), the following formulas are sufficient for (3):

$$\begin{aligned}&\sup _{w\in \mathcal{W}}T^{-1}(w)\Vert U(w)e\Vert ^2\mathop {\longrightarrow }\limits ^{p}0, \end{aligned}$$

(9a)

$$\begin{aligned}&\sup _{w\in \mathcal{W}}T^{-1}(w)e'U(w)e\mathop {\longrightarrow }\limits ^{p}0, \end{aligned}$$

(9b)

$$\begin{aligned}&\sup _{w\in \mathcal{W}}T^{-1}(w)\hat{\sigma }^2w'k\mathop {\longrightarrow }\limits ^{p}0, \end{aligned}$$

(9c)

$$\begin{aligned}&\sup _{w\in \mathcal{W}}T^{-1}(w)\hat{\sigma }^2|\sum \limits _{m=1}^Mw_ma_mg_m(y)(k_m-2)| \mathop {\longrightarrow }\limits ^{p}0, \end{aligned}$$

(9d)

$$\begin{aligned}&\sup _{w\in \mathcal{W}}T^{-1}(w)|\mu '(I_n-U(w))U(w)e|\mathop {\longrightarrow }\limits ^{p}0, \end{aligned}$$

(9e)

$$\begin{aligned}&\sup _{w\in \mathcal{W}}T^{-1}(w)|e'(U(w)-\tilde{P})\mu |\mathop {\longrightarrow }\limits ^{p}0. \end{aligned}$$

(9f)

Using condition (C.1), we have

$$\begin{aligned} \hat{\sigma }^2&= y'(I_n-P_{m^*})y(n-m^*)^{-1}\le \Vert y\Vert ^2(n-m^*)^{-1}=O_p(1),\quad \quad \end{aligned}$$

(10a)

$$\begin{aligned} a_mg_m(y)&= {\Vert \hat{\mu }_m-y\Vert ^2(n-k_m+2)^{-1} \over \Vert \hat{\mu }_m\Vert ^2(k_m-2)^{-1}} = {y'(I_n-P_m)y(n-k_m+2)^{-1} \over y'P_my(k_m-2)^{-1}}\quad \quad \nonumber \\&\le {\Vert y\Vert ^2(n-k_m+2)^{-1} \over \hat{\beta }_m'X_m'X_m\hat{\beta }_m(k_m-2)^{-1}}= O_p(1),\end{aligned}$$

(10b)

$$\begin{aligned} \Vert U(w)e\Vert ^2&\le M\sum \limits _{m=1}^M w_m^2(1-a_mg_m(y))^2\Vert P_me\Vert ^2=O_p(1),\end{aligned}$$

(10c)

$$\begin{aligned} e'U(w)e&\le \sum \limits _{m=1}^M w_m|1-a_mg_m(y)|e'P_me=O_p(1),\end{aligned}$$

(10d)

$$\begin{aligned} \Vert \tilde{P}e\Vert ^2&= O_p(1). \end{aligned}$$

(10e)

From (10a)–(10d) and condition (C.2), we obtain (9a)–(9d).

In addition,

$$\begin{aligned} |\mu '(I_n-U(w))U(w)e|\le \Vert (I_n-U(w))\mu \Vert \Vert U(w)e\Vert =T^{1/2}(w)\Vert U(w)e\Vert ,\quad \quad \end{aligned}$$

(11)

which, together with (10c) and condition (C.2), implies (9e). Finally,

$$\begin{aligned} |e'(U(w)-\tilde{P})\mu |&= |e'\tilde{P}(U(w)-I_n)\mu | \le \Vert (I_n-U(w))\mu \Vert \Vert \tilde{P}e\Vert \nonumber \\&= T^{1/2}(w)\Vert \tilde{P}e\Vert , \end{aligned}$$

(12)

which, together with (10e) and condition (C.2), implies (9f). This completes the proof. $\square$