Group sequential comparison of two binomial proportions under ranked set sampling design

Abstract

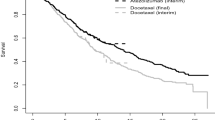
Ranked set sampling (RSS) is a technique for incorporating auxiliary (concomitant) information into estimation and testing procedures right at the design stage. In this paper, we propose group sequential testing procedures for comparing two treatments with binary outcomes under an RSS scheme with perfect ranking. We compare the power, the average sample sizes and type I errors of the proposed tests to those of the group sequential tests based on simple random sampling schemes. We illustrate the usefulness of the methodology by using data from a clinical trial on leukemia.

Appendix: Proof of the result that the test statistics are approximately Brownian motions computed at the interim analysis

• 1. First we proof result (6) for $Z_{l}^{1}$. Notice that the ranking mechanism used in this manuscript is consistent, i.e., that $\frac{1}{k}\sum _{j=1}^{m_{il}} {p_{i[r]}} =p_i$, where $p_i$ is the true proportion of the ith population and $p_{i[r]}$is the proportion of the ith population’s $r$th order statistics (see Chen et al. 2005). Therefore, since by the Weak Law of Large Numbers (WLLN)

  $$\begin{aligned} \frac{1}{m_{il} }\sum _{j=1}^{m_{il}} x_{i[r]j} {\mathop {\longrightarrow }\limits ^{p}}p_{i[r]}\quad \text{ as} m_{il} \rightarrow \infty , \end{aligned}$$

  we have by Slutsky’s theorem (Lehmann 1999) that

  $$\begin{aligned} \hat{p}_{il}^{rss} =\frac{1}{k}\sum _{r=1}^{k} \left(\frac{1}{m_{il}}\sum _{j=1}^{m_{il}}x_{i[r]j}\right) {\mathop {\longrightarrow }\limits ^{p}}\frac{1}{k} \sum _{r=1}^k {p_{i[r]}}=p_i, \end{aligned}$$

  hence, $\hat{p}_{il}^{rss}{\mathop {\longrightarrow }\limits ^{p}}p_i$. Using similar arguments,

  $$\begin{aligned} \hat{\tau }_{0l}^{2}=\frac{1}{k^{2}}\sum _{r=1}^{k}\hat{p}_{0[r]l} (1-\hat{p}_{0[r]l}){\mathop {\longrightarrow }\limits ^{p}}\tau _0^2, \end{aligned}$$

  as

  $$\begin{aligned} m_{iL} ,m_{iL} \rightarrow \infty \quad \text{ and} \quad {m_{1L}}/{m_{2L}}\rightarrow \lambda _L \in (0,1),\quad {m_{il}}/{m_{iL}} \rightarrow \lambda _{1l} \in (0,1). \end{aligned}$$

  Now we can write:

  $$\begin{aligned} Z_{l}^{1}=\frac{\hat{p}_{1l}^{rss}-\hat{p}_{2l}^{rss}}{\sqrt{\hat{\tau }}_{0l}^{2}\left(\frac{1}{m_{1l}} +\frac{1}{m_{2l}}\right)}=\frac{\sum _{j=1}^{m_{1l}}{y_{1j}} -\sum _{j=1}^{m_{2l}} {y_{2j}}}{{\sqrt{\tau _{0}^{2}\left( \frac{1}{m_{1l}}+\frac{1}{m_{2l}}\right)}}}+o_p (1), \end{aligned}$$

  where $y_{ij} =\frac{1}{k}\sum _{r=1}^k \left(x_{i[r]j} -p_{0[r]}\right)\!, p_{0[r]}$ is the proportion of success for the rth order statistic under the null hypothesis. Therefore it is enough to show the result for the vector $S^{L}=\left(S_{1}^{L}, S_2^L ,\ldots , S_L^L\right)$ with

  $$\begin{aligned} S_{l}^{L} =\frac{\sum _{j=1}^{m_{1l}}{y_{1j}}-\sum _{j=1}^{m_{2l}} {y_{2j}}}{\sqrt{\tau _0^2 \left( {\frac{1}{m_{1l} }+\frac{1}{m_{2l} }} \right)}}. \end{aligned}$$

  We can represent such vector as

  $$\begin{aligned} {\mathbf S}^{L}={\mathbf C}_1^L {\mathbf V}_1^L -{\mathbf C}_2^L {\mathbf V}_2^L \end{aligned}$$

  where $V_i^L$ for $i=1,2$ is a vector of $L$ mutually independent random variables of the form

  $$\begin{aligned} V_{il}^L =\left( {\frac{1}{\left( {m_{il}-m_{i\left( {l-1} \right)}}\right)\tau _0^2 }}\right)^{1/2}\sum _{j=m_{i\left( {l-1} \right)} }^{m_{il}} {y_{ij}}. \end{aligned}$$

  ${\mathbf C}_{i}^{L}$ are $L\times L$ matrices with elements

  $$\begin{aligned} C_{i(l,l^{\prime })}^L =\frac{\left( {m_{il^{\prime }} -m_{i(l^{\prime }-1)} } \right)^{1/2}}{m_{il} \left( {1/m_{1l} +1/m_{2l} } \right)^{1/2}} \end{aligned}$$

  for $l^{\prime }\le l$ and zero otherwise, and $y_{ij}$ is as defined above. Now thanks to the information balance assumption and hence, the assumption that $\frac{m_{il} }{m_{iL} }\rightarrow t_l ,$ we have

  $$\begin{aligned} C_{i(l,l^{\prime })}^L =\frac{(m_{il^{\prime }} -m_{i(l^{\prime }-1)})^{1/2}}{m_{il} \left( {1/m_{il} +1/m_{2l} } \right)^{1/2} }\rightarrow \frac{1}{\sqrt{2}}\left( {\frac{t_{l^{\prime }} -t_{(l^{\prime }-1)}}{t_l }} \right)^{1/2} =\frac{1}{\sqrt{2}}C^{L}_{(l,l^{\prime })}. \end{aligned}$$

  The vectors $V_{il}^L$ converge in distribution to independent multivariate standard normal variables, ${\mathbf Z}_1$ and ${\mathbf Z}_2$, and hence, by the multivariate Slutsky theorem (Lehmann 1999), we have

  $$\begin{aligned} {\mathbf S}^{L}={\mathbf C}_1^L {\mathbf V}_1^L -{\mathbf C}_2^L {\mathbf V}_2^L {\mathop {\longrightarrow }\limits ^{D}}\frac{1}{\sqrt{2}}{\mathbf C}^{L}{\mathbf Z}_1 -\frac{1}{\sqrt{2}}{\mathbf C}^{L}{\mathbf Z}_2. \end{aligned}$$

  Therefore, the asymptotic distribution of ${\mathbf S}^{L}$ is that of standardized Brownian motion computed at the interim analysis as desired.

• 2. To prove result (6) for $Z_l^2$ we notice that by large sample theory (Lehmann 1999, p. 470), asymptotically,

  $$\begin{aligned} \sqrt{m_{il} }\left(\hat{p}_{il}^{rssml}-p_i\right)\cong \frac{\sum _{j=1}^{m_{il}} {l^{{\prime }}_{ij} (p_i )} }{m_{il} I_i (p_i )} \end{aligned}$$

  in the sense of having the same asymptotic distribution, where $l^{\prime }_{ij} (p_i)$ is the first-order derivative of $l_{ij} (p_i )$ in (3) with respect to $p_i$. Also, under the null hypothesis as well as for both treatment populations all the estimators

  $$\begin{aligned} \hat{\gamma }_{il} (\hat{p}_{il}^{rssml})=I_i (\hat{p}_{il}^{rssml} ) \end{aligned}$$

  and

  $$\begin{aligned} \hat{\gamma }_{0l} (\hat{p}_{0l}^{rssml})=I_i (\hat{p}_{0l}^{rssml}) \end{aligned}$$

  are asymptotically consistent for their theoretical quantities. As a consequence, the proof of the result (6) for this case will be identical to the proof above for $Z_{l}^{1}$ by simply setting

  $$\begin{aligned} y_{ij} =l^{{\prime }}_{ij} (p_i )/I_i (p_i ). \end{aligned}$$