Abstract
Various combinations of thirteen regional climate models (RCM) and six general circulation models (GCM) were used in FP6-ENSEMBLES. The response to the SRES-A1B greenhouse gas concentration scenario over Europe, calculated as the difference between the 2021–2050 and the 1961–1990 means can be viewed as an expected value about which various uncertainties exist. Uncertainties are measured here by variance explained for temperature and precipitation changes over eight European sub-areas. Three sources of uncertainty can be evaluated from the ENSEMBLES database. Sampling uncertainty is due to the fact that the model climate is estimated as an average over a finite number of years (30) despite a non-negligible interannual variability. Regional model uncertainty is due to the fact that the RCMs use different techniques to discretize the equations and to represent sub-grid effects. Global model uncertainty is due to the fact that the RCMs have been driven by different GCMs. Two methods are presented to fill the many empty cells of the ENSEMBLES RCM × GCM matrix. The first one is based on the same approach as in FP5-PRUDENCE. The second one uses the concept of weather regimes to attempt to separate the contribution of the GCM and the RCM. The variance of the climate response is analyzed with respect to the contribution of the GCM and the RCM. The two filling methods agree that the main contributor to the spread is the choice of the GCM, except for summer precipitation where the choice of the RCM dominates the uncertainty. Of course the implication of the GCM to the spread varies with the region, being maximum in the South-western part of Europe, whereas the continental parts are more sensitive to the choice of the RCM. The third cause of spread is systematically the interannual variability. The total uncertainty about temperature is not large enough to mask the 2021–2050 response which shows a similar pattern to the one obtained for 2071–2100 in PRUDENCE. The uncertainty about precipitation prevents any quantitative assessment on the response at grid point level for the 2021–2050 period. One can however see, as in PRUDENCE, a positive response in winter (more rain in the scenario than in the reference) in northern Europe and a negative summer response in southern Europe.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In Europe the expected response of climate to an increase in greenhouse gas concentration during the 21st century is not just the typical 2–3°C warming (IPCC 2007). Many surface variables are likely to be affected by global warming. For instance, there is an agreement amongst models that precipitation should increase in the North and decrease in the South. However, an agreement on the sign of the response does not imply that all models converge towards the same numerical value. Many impacts on human environment or activities depend on thresholds. Two different models having the same sign in the response of temperature and precipitation, but different magnitudes of change, can lead to very different impacts. The evaluation of uncertainty is fundamental for any application. The primary source in terms of causality is the future of human emissions. This is a socio-economic question, not evaluable by the climate modeling community. The natural climate variability is a statistical question which can be approached by observed past series (Zhang et al. 2007; Brown et al. 2008), as long as the scope is limited to the interannual variability of the near future. Numerical climate models introduce two kinds of uncertainty, one coming from the large-scale GCMs, the other coming from the downscaling RCMs (e.g. Lenderink et al. 2007; Giorgi 2008). Since the FP5-PRUDENCE project (Christensen et al. 2002) a large number of 50 km or higher resolution simulations are available for Europe. The FP6-ENSEMBLES project (Hewitt and Griggs 2004; van der Linden and Mitchell 2009) has led to an update of the PRUDENCE database with two major improvements: a higher spatial resolution and a larger number of RCMs and driving GCMs.
In Déqué et al. (2007), referred to as D07 in the following, we attempted to quantify the different sources of uncertainty, despite the few pairs of RCM × GCM available. In D07 four sources of uncertainty were evaluated:
-
1.
the sampling uncertainty, related to the fact that the model climatology is issued from a limited number of years (30); it contributes model internal variability, which includes also longer time scales (see Sect. 5)
-
2.
the model uncertainty associated with the physics and dynamics features of the different regional climate models
-
3.
the uncertainty in the lateral boundary conditions (LBC), that is the GCM used to drive the RCM
-
4.
the uncertainty associated with the scenario (A2 or B2) of emissions of greenhouse gases (GHG)
The results showed that the largest source of uncertainty resides in the LBC applied to the RCM. However the small number of GCMs makes this conclusion preliminary at best. The aim of this study is to update the D07 results based on more models, but also with two simplifications.
-
1.
As we concentrate on the first half of the 21st century, we neglect the uncertainty due to the greenhouse gas and aerosol concentrations.
-
2.
As the modeling effort has been put on the number of RCM × GCM pairs, each pair has been run only once; we have thus approximated the model internal variability with a simple Monte-Carlo method based on limit central theorem (Gaussian distribution).
In Sect. 2, we describe the data available. In Sect. 3 we apply the D07 matrix completion method to ENSEMBLES results and make a first assessment of the partition of variance at the European level, with comparison with D07 results. Recent works on weather regimes (e.g. Sanchez-Gomez et al. 2008) suggest another method to complete the holes in the RCM × GCM matrix. This completion and the resulting new variance partition are presented in Sect. 4, with regional description for 8 sub-areas. The interannual variability as a new source of uncertainty is introduced in Sect. 5. In Sect. 6, we use the total variance of Sect. 5 to evaluate local confidence intervals over Europe. A summary of the new features brought by the ENSEMBLES project with respect to PRUDENCE is given in the conclusive Sect. 7.
2 The ENSEMBLES-RT2B database
One of the greatest successes of the PRUDENCE project is the publicly available database with a large variety of state-of-the-art RCM experiments. In D07, 10 RCMs out of this database were used (see D07 for details about the models):
CNRM, DMI, ETHZ, GKSS, HadC, ICTP, KNMI, MPI, SMHI, UCLM
These RCMs were driven by one or more of 3 GCMs:
CNRM, HadC, MPI
All were driven by HadC, some RCMs were also driven by the other two GCMs.
In ENSEMBLES, there are 13 RCMs run by 11 partners (most of them use updated versions of PRUDENCE RCMs):
-
C4I (Jones et al. 2004) uses a version of the RCM developed at the Swedish meteorological service (RCA)
-
CNRM (Radu et al. 2008) uses the RCM of French meteorological service
-
DMI (Christensen et al. 1996) uses the RCM of Danish Meteorological Institute
-
ETHZ (Böhm et al. 2006) uses the RCM of the Federal Institute of Technology in Zürich (CH)
-
HadC (Collins et al. 2006) uses the RCM of the UK Met Office. In fact, three versions have been used (HC-lo, HC-med and HC-hi)
-
ICTP (Giorgi and Mearns 1999) uses the RCM of the International Center for Theoretical Physics in Trieste (Italy)
-
KNMI (an Van Meijgaard et al. 2008) uses the RCM of the Dutch meteorological service
-
METN (Haugen and Haakensatd 2006) uses the RCM of the Norwegian meteorological service
-
MPI (Jacob 2001) uses the RCM of the Max Planck Institute for Meteorology in Hamburg (Germany)
-
SMHI (Kjellström et al. 2005) uses the RCM of the Swedish Meteorological and Hydrological Institute
-
UCLM (Sanchez et al. 2004) uses the RCM of the University of Toledo (Spain)
Out of the 13 models, 3 use the same modelling system: HC-lo, HC-med and HC-hi. These models share the same dynamics and a very similar description of the sub-grid processes. We have kept them as separate RCMs, however, because they have been produced by arbitrary perturbations of several sensitive but empirical model parameters, which lead to very different responses to GHG concentration in their GCM version (Murphy et al. 2007). Other models share some parenthood: SMHI and C4I are based on RCA; The dynamics of DMI, KNMI, METN, SMHI and C4I come from the HIRLAM forecast model.
The RCMs have been run from 1950 to 2050 (some of them to 2100) on a common domain covering the whole of Europe (from South Mediterranean coast to Cape North) at 25 km horizontal resolution. Beyond 2000 they use the A1B scenario for GHG concentration. They have been driven by one or more of 6 GCMs (again, most of them were also used in PRUDENCE at an earlier cycle of model development):
-
BCM (Furevik et al. 2004) is the GCM of the University of Bergen (Norway), the horizontal resolution is 300 km.
-
CNRM (Gibelin and Déqué 2003) uses the global version of CNRM RCM with variable resolution (300 km in the Pacific to 100 km at the lateral boundaries of the RCM).
-
HadC (Gordon et al. 2000) uses the global version of HadC RCM; 3 driving runs are available (HC-lo, HC-med and HC-hi). The resolution is 300 km.
-
MPI (Roeckner et al. 2003) uses the global version of MPI RCM. The resolution is 200 km.
Here again, we consider that the 3 versions of the HadC model are 3 different GCMs, because their climate responses are, by construction, very different. The parameter perturbations in the 3 GCMs are the same as in the 3 RCMs. One can also mention that BCM and CNRM use the same atmospheric component, namely ARPEGE, with different resolutions. Table 1 indicates which GCM is driving each RCM. One can note that all GCMs drive at least two RCMs, and three RCMs (DMI, METN and SMHI) are driven by more than one GCM. There are 3 other RCM simulations in the ENSEMBLES database, but they involve 3 other GCMs (each of them would have added a new row and a new column to Table 1): they contribute to the total spread and are therefore very important when estimating uncertainty, but they cannot help here to discriminate the respective roles of the GCM and the RCM, and have therefore been discarded. In addition, one of these RCMs uses the so-called spectral nudging technique (von Storch et al. 2000; Biner et al. 2000) and the spread due to the RCM alone would be less than in the other interior-free RCMs.
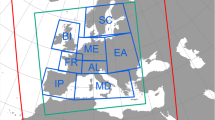
In the following we will concentrate on winter (DJF) and summer (JJA) averages of 2 m temperature and precipitation for two periods 1961–1990 (the same reference period as in PRUDENCE) and 2021–2050. The restriction to temperature and precipitation, as well as to two seasons, has been done to maintain a reasonable size for the study, whilst focussing on the most widely documented aspects of climate change. The methodology is of course suitable for wind, soil moisture, snow and other variables. The model response we analyze is the difference between the two 30-year means. We restrict this analysis to the model land grid points which fit inside one of the 8 sub-areas (aka Rockel boxes) described in figure 4 of Christensen and Christensen (2007) and already used in D07: British Isles (BI), Iberian Peninsula (IP), France (FR), Mid-Europe (ME), Scandinavia (SC), Alps (AL), Mediterranean (MD) and East-Europe (EA).
3 Analysis of variance: first method of matrix completion
As a first approach towards inter-model variance, we can calculate the variance between the GCMs driving a given RCM, repeat for the other RCMs and then average the variances obtained for all the RCMs. This is possible for 3 RCMs. We can name it inter-GCM variance. Table 2 shows the average over Europe, expressed as standard deviation for an easier interpretation. Similarly, we can calculate the variance between the RCMs driven by the same GCM, and then average over the GCMs. This is possible for all 6 GCMs. We can name it inter-RCM variance. In each case the variance is calculated with a small number of model responses (most often 2), and an unbiased estimate must be used. Table 2 shows that the inter-GCM variance is greater than the inter-RCM variance, and in half of the cases slightly greater than the total variance. The variances are calculated at each grid point of a common grid (top two rows of Table 2), and for sub-area averages (bottom two rows) for a better comparison with the following.
This basic approach does not allow to tell us how the total variance of our 18 model responses is partitioned between the inter-GCM and the inter-RCM variances, because the two contributions are not independent and calculated with different sub-samples of the ENSEMBLES database. To achieve this partition, we must use the method known as analysis of variance. In PRUDENCE, we had 10 RCMs, 3 GCMs, 2 emissions scenarios (A2 and B2) and 3 ensemble members (for the few RCMs driven by multiple GCMs members). The total variance has been decomposed as a sum of 15 positive terms representing the contribution of the 4 sources of variability (in this study variability, spread and uncertainty have the same meaning), taking into account the interactions between the 4 sources. See D07 for the full formula.
In ENSEMBLES we have a single emissions scenario A1B and a single ensemble member. We can use a simpler approach. Let i be the index of RCM (i = 1,13) and j the index of GCM (j = 1,6). Let us use the dot to represent the average with respect to the index it replaces. If Xij is the response of a model (e.g. DJF temperature scenario minus reference in BI sub-area) the total variance V can be decomposed as:
with:
where R is the term due to RCM alone, G to GCM alone, and RG the interaction term of RCM with GCM. R is the variance of the RCMs once the different GCMs have been averaged. (R + RG) is the variance of the RCMs for each GCM separately, averaged afterwards over the different GCMs. It is named the total variance due to RCM and noted V(R). Similarly, the sum G + RG is noted V(G). The difference between the computation of R and V(R) is therefore the change in the order of averaging and variance operations. In other words, R is a variance of averages and V(R) is an average of variances. Note that V(R) + V(G) is more than the total variance V because the interaction term RG is positive.
Equation 1 is an algebraic identity which assumes that all pairs (i, j) are available. In case of missing values (there are 60 holes in Table 1), we need first to fill the missing cases. In D07 the algorithm consisted of minimizing the higher interaction term RSGM (S for emissions scenario, M for ensemble member). In the present study things are much simpler because there are only two indices. Thus the D07 completion formula is derived to:
As we have at least one case for each RCM and for each GCM, Xi· and X·j can always be estimated from Table 1. Equation 5 can be easily explained as follows: to calculate the response of RCM-A driven by GCM-B, we calculate first the mean response for all RCM × GCM. Then we add the mean anomaly of the GCM-B-driven pairs with respect to this mean. Finally we add the mean anomaly of the RCM-A-driving pairs with respect to the same mean. This is equivalent to assuming that the contribution of the GCM and of the RCM are additive.
Figure 1 shows the percentage of G (top of the rectangle), RG (middle) and R (bottom) for PRUDENCE (PRP) and ENSEMBLES (ENP) experiments in the leftmost two rectangles. One can see that the RG term is small, but this is a direct consequence of Eq. 5 which assumes that RG = 0 for the missing pairs. The PRUDENCE to ENSEMBLES comparison shows the larger role of the GCM in PRUDENCE, in particular for temperature. A first possible explanation of this difference is that in PRUDENCE we focused on the end of the century with the higher A2 emissions scenario and a large SST forcing, whereas in ENSEMBLES the boundary forcing is weaker (mid-century, A1B scenario). The large-scale signal (global warming) is stronger and the spread of the 3 GCMs is larger in PRUDENCE. The “noise” introduced at smaller scale by the RCMs is thus, in terms of ratio, weaker than in ENSEMBLES. A second explanation may be that in ENSEMBLES the domains are larger and the horizontal resolution higher, which gives more degrees of freedom to the RCMs to “forget” the control exerted by the boundary forcing. The fact that the GCM explains more variance than the RCM, except for summer precipitation, was already stressed in D07 and confirms the results of Table 2.
Fraction of variance (%) explained by the RCM (bottom part of each rectangle) the GCM (top part) and interaction term (middle part): PRUDENCE (A2 scenario, 2071–2100 response) and ENSEMBLES (A1B scenario, 2021–2050 response) data over Europe for temperature (T) and precipitation (P) in DJF and JJA; the missing data have been completed with the PRUDENCE method for PRUDENCE (PRP) and ENSEMBLES (ENP), and with the weather regime method for ENSEMBLES (ENR)
Table 3 (first 6 columns) shows the mean response over Europe and the inter-model standard deviation, calculated as the quadratic average over the 8 sub-areas. The mean and standard deviation are calculated with the original (O) and the completed (P) RCM × GCM matrix. “original” means only existing RCM × GCM pairs, as in Table 2, whereas “completed” means existing and reconstructed pairs. In the case of PRUDENCE, we consider here only the A2 emissions scenario and one member per RCM × GCM (when several runs are available). One can see that the matrix completion has a marginal impact on the mean (slight reduction of the response in the case of PRUDENCE, increase in temperature response for ENSEMBLES). Its effect on the standard deviation is systematically an increase. This is easier to explain in the case of PRUDENCE, where the role of HadCM as a driving GCM is overestimated in the original matrix. In the case of ENSEMBLES, this increase shows that the reconstruction method is not just an interpolation and may produce strong responses. Because it is additive, the reconstruction can combine a GCM and an RCM which both have a high sensitivity, but have not been combined in the original matrix.
The comparison of the mean versus the standard deviation at European scale in Table 2 also shows that the signal to noise ratio is better (i.e., higher) in PRUDENCE than in ENSEMBLES for temperature. In the case of precipitation, there are compensations between sub-areas with an increase and sub-areas with a decrease. See Sects. 4 and 6 for geographical details of the response. The choice at the beginning of PRUDENCE to target the end of the 21st century is clearly justified here, at least for temperature, in terms of signal-to-noise ratio. In terms of adaptation to climate change, the choice of the ENSEMBLES period is, however, better for policy and decision making.
4 Weather regimes: second method of matrix completion
The D07 method for matrix completion is simple, but relies upon the argument that the GCM and the RCM contributions to the climate change response are independent. If we want to add more physics in the completion method, we can consider that the role of the GCM is to provide large-scale lateral advection of momentum, heat and moisture to the RCM. A concept which synthesizes this effect is the concept of weather regimes (Vautard 1990). Clustering the daily 500 hPa height values over the North Atlantic-Europe domain leads to large-scale patterns that can be linked to weather in Europe (Robertson and Ghil 1999; Yiou and Nogaj 2004). The most commonly studied are the positive and negative phases of the North Atlantic Oscillation (NAO; Hurrel et al. 2001). In winter, clustering in 4 regimes is a traditional approach since Michelangeli et al. (1995). We have applied the same k-means algorithm to ERA40 500 hPa daily data, filtered by the first 15 Empirical Orthogonal Functions (EOF) on the 90°W–30°E 20°N–80°N domain for the 4 seasons. For each season (we restrict discussion of results here to DJF and JJA for the sake of brevity), four centroids are produced, which are maps of 500 hPa height anomalies across the domain. For each RCM, we interpolate these centroids onto their native model grid. Each day is associated to regime N (N = 1, 2, 3 or 4) if the daily 500 hPa height anomaly with respect to the 1961–1990 RCM climatology is closer to centroid N than to any other centroids. This method is different from Sanchez-Gomez et al. (2008) who applied the k-means algorithm to ERA40 data on a domain intersecting all RCM domains, and interpolated all RCMs on this domain. With our method, the winter regimes are very close to the Michelangeli et al. (1995) centroids. They are more appropriate to represent the LBC forcing, and less appropriate to represent the large-scale dynamics of the individual RCMs, in particular those RCMs with westwards extension too far from Greenland.
The natural choice for the distance measure would be the euclidean distance. However, because of global warming, there is a systematic lift of the 500 hPa height. We have therefore calculated the euclidean distance to the anomaly field minus its spatial average over the RCM domain. This does not change the regime characteristics in the present climate. But in the scenario climate, the change in regime frequency is different with the simple euclidean and with the corrected euclidean distance. If, however, we use the spatial correlation (Plaut and Simmonet 2001) as a criterion to decide when a day is attributed to a given regime, the results are very similar to those obtained using the corrected euclidean distance. The RCM weather is driven by the horizontal geopotential height gradient at the lateral boundary, through the geostrophic wind, rather than by the height field itself. So we use the corrected euclidean method for regime attribution. If we consider 30-year averages, we can write, for a variable X:
Where <·> is the time average, <X|r> the conditional average of X for regime r (aka composite of regime r for variable X) and f(r) the frequency of regime r. In the scenario, both composites and frequencies may change. A simple idea for matrix completion is to write:
where the composites are calculated with RCM i and the frequencies are calculated with GCM j. We make here the hypothesis that the regime frequency is imposed by the GCM, whereas the way temperature or precipitation behaves in a given regime depends only on the RCM. There are thus two hypotheses. The first hypothesis has been partly verified in Sanchez-Gomez et al. (2008): when driven by ERA40, all ENSEMBLES RCMs have a similar regime chronology to the ERA40 one and a very similar regime frequency. The second hypothesis will be checked hereafter.
In order to further evaluate the validity of the first hypothesis, we have calculated the quadratic error E1 between the existing RCM × GCM pairs (i, j) and the reconstructed responses in which the weather regime composite comes from the same pair (i, j), but the regime frequency comes from another pair (k, j). As all GCMs have driven more than one RCM this is easy to calculate. The squared error E1 on the scenario minus reference response is averaged for the 8 sub-areas, the 2 seasons and the 18 completed RCM × GCM pairs. The reference error E1r is obtained similarly, but the weather regime frequency comes from a pair involving a different GCM. Table 4 shows that E1 is small. This error is about one third the reference error E1r, which indicates that using the weather regime frequency from an RCM × GCM pair involving the same GCM is more accurate than using the weather regime frequency from another GCM.
Symmetrically, we have tested the second hypothesis by keeping the actual weather regime frequency and taking a weather regime composite from another pair which involves the same RCM. Here we can use only 8 pairs out of 18 because only DMI, METN and SMHI RCMs have been driven by more than one GCM. The quadratic error is E2 and its reference is E2r. E2r is calculated as E2, with the same weather regime frequencies but with a weather regime composite coming from another RCM. Table 4 shows that E2 is large and close to E2r. This indicates that the assumption that the composite does not depend on the driving GCM is wrong. This implies that the precipitation response, for example, of an RCM is determined by other constraints (such as SST, continental-scale warming and moistening) coming from the driving GCM, which are not reflected in the 4 regimes.
We have thus attempted to involve the GCM in the reconstruction of the weather regime composite. In order to interpolate a missing (i, j) pair we replace \( {\left\langle {{{\text{X}}_{\text{i}} }} \mathrel{\left | {\vphantom {{{\text{X}}_{\text{i}} } {\text{r}}}} \right. \kern-\nulldelimiterspace} {\text{r}} \right\rangle } \) in Eq. 7 by:
where X stands for the temperature or precipitation mean for a given season and sub-area in the reference and in the scenario data. For example the missing composite for C4I driven by MPI is the half sum of the composite of C4I driven by HC-hi and the average of the composites involving MPI. Note that this approach is different from Eq. 5 in which the contributions of the RCM and GCM are added, whereas in Eq. 8 the two contributions are interpolated. Therefore, the missing responses, as reconstructed with the second method, are generally smaller than with the first one.
It is interesting at this stage to evaluate the validity of the reconstructions. A simple algorithm consists of comparing the original model response with a response reconstructed without the corresponding RCM × GCM pair. Unfortunately, the reconstruction error can only be calculated with 8 pairs (DMI, METN and SMHI RCMs). The mean square error is E3 for the PRUDENCE method (Eq. 5) and E4 for the weather regime method (Eqs. 7 + 8). As in the beginning of Sect. 4, a reference error (E3r) is obtained by comparing an actual response with the response from another RCM × GCM pair. This reference error is also valid for E4 (E4r = E3r). E3r is very close to E2r because we use the same pairs of models to compute the differences. The only difference is that in E2r we use the same weather regime frequency in the two responses to be subtracted. Table 4 shows that the second reconstruction method is somewhat better, and that both methods are more successful in reconstructing temperature than precipitation responses. However, since this verification is based on three RCMs only, we cannot draw a definite conclusion about which method actually performs better. As the weather regime method is more physically based, we use only this method in the rest of the paper.
The rightmost rectangles in Fig. 1 show the percentages of variance due to RCM and GCM in ENSEMBLES data completed with the weather regime method (ENR). One can first remark that the RG term (dark gray) is still small, which further justifies the PRUDENCE assumption to set this term to zero when completing the matrix. The second remark is that the weather regime method enhances the role of the GCM in the inter-model spread. Indeed, the GCM is involved both in the frequency of the weather regime and in the composite. This result is further confirmed because it is in agreement with the respective variances of Table 2, where no data completion is done, and the reconstruction error E4 (Table 4) is less than the error E3 with the PRUDENCE method. If we had used composites depending only on the RCMs (as in Eq. 7), the percentage due to the RCM would have been much larger. This is due to the fact that the climate change response is generally more a change in the composites than a change in the weather regime frequencies (Driouech et al. 2010). However, we know from Table 4 that this approach is not supported by the ENSEMBLES data. Note that in the case of summer precipitation, the GCM part remains less than the RCM part.
The last two columns of Table 3 give the mean and standard deviation calculated for each sub-area then averaged over Europe with the matrix completed by the weather regime method (R). The mean response is similar to the result with the PRUDENCE method (P) but the inter-model standard deviation is below the value with the existing pairs (O) (except in the case of winter precipitation, when they are identical), contrary to the PRUDENCE completion method which enhances the variability.
We cannot display here climate change response matrices for all sub-areas, seasons and variables. Considering the average over Europe provides a synthesis, and temperature offers the advantage that there is no spatial compensation between positive and negative responses in different sub-areas (see Sect. 6). In JJA, the spread is larger than in DJF (Tables 2, 3). Therefore, we selected this case in Table 5 which shows the full matrix. Italicized cells indicate the reconstructed values. One can see that despite the above mentioned reduction of the standard deviation (0.69–0.57°C from Table 3), the reconstructed value can produce a response of 3.3°C (HC-hi × HC-med) whereas the maximum response in the original pairs is 2.8°C (HC-med × HC-med). One should have in mind that the above standard deviations are not calculated from Table 5 cells, but separately for each sub-area.
Figure 2 gives the respective variances of RCM and GCM for the 8 sub-areas. Displaying the variance instead of its percentage, in order to identify the regions with maximum variability, would be misleading because the domains are not of the same size: East Europe (EA) is four times larger than the Alps (AL). The spatial distribution of spread is examined in Sect. 6. In winter the GCM explains about 60% of the temperature variance, rather uniformly over Europe. For winter precipitation, the percentage is more variable (50–80%) and it is hard to find a simple geographical explanation for these regional variations. Summer temperature exhibits a 60–80% variation with a larger part for the GCM in the South-West (IP, FR) than the North-East (SC, ME, EA). As in PRUDENCE, the RCM plays the major role for summer precipitation, with an exception, consistent with the temperature, in the South-West (IP, FR). It is interesting to note that even for the British Isles, which are under the constraint of the lateral boundary conditions and SST coming from the GCM, the RCM explains more than 60% of the variance of summer precipitation. The model-to-model variability for this parameter is likely produced by the convection schemes in the RCMs. If the RCM soil schemes had played a large role in the spread, a signature should have been found in the summer temperature. The fact that RCMs produce more spread in precipitation than in temperature in summer is an average feature which could mask individual behaviors. Some RCMs may have a higher summer temperature-to-precipitation dependence than others. Table 6 shows for each RCM the interseasonal (for the 1961–1990 summers) temperature-precipitation correlation. These statistical estimates are calculated from seasonal means over each sub-area, and averaged over the GCMs for DMI, METN and SMHI, and over Europe. Table 6 indicates that the negative correlation (warm and dry) for Europe (last column) varies between −0.40 (SMHI) and −0.80 (HC-lo). There is a general agreement between RCMs which share the same parameterization, the HC model being the most sensitive. There is also a region-to-region variability: on average over the 13 RCMs, the correlation varies from −0.31 over the Scandinavian area to −0.76 over the Mediterranean area. When the 2021–2050 period is considered (not shown), this regional contrast is decreased (−0.36 to −0.62), but the individual RCM correlations over Europe remain almost unchanged.
As rightmost rectangles of Fig. 1 (ENSEMBLES data reconstructed with weather regime method) for the 8 sub-areas separately: British Isles (BI), Iberian Peninsula (IP), France (FR), Mid-Europe (ME), Scandinavia (SC), Alps (AL), Mediterranean (MD), East-Europe (EA)
5 Interannual variability
Up to now, we have supposed that the 30-year means of the experiments were representative of the climatology of each model. If we had used, as in D07, several runs for each RCM × GCM pair, Eq. 1 would have been:
where M indicates the choice of ensemble member (index k and number n in the following). There are two additional interaction terms RM and GM which are defined similarly to Eqs. 2–4, and a new term:
Here we have a single member per RCM × GCM pair, but we can use the interannual variability of each single simulation as in Ferro (2004) and generate artificial ensemble members with the following simple hypothesis. The 30 year average at a single grid point, or for a sub-domain average, can be considered as the average of 30 independent variables for which the mean and variance can be easily calculated. The limit central theorem tells us that this average follows approximately a Gaussian distribution with the same mean, and a variance divided by 30. We thus generated n = 10 members by a simple Monte-Carlo procedure. If n is too small as in D07 (n = 3), the interannual variability in Eq. 9 is underestimated, because in the algebraic identity there is a division by n instead of (n − 1) which would correspond to the unbiased estimate of the variance. On the other hand, if we use unbiased estimates of the variance in Eq. 9 as we did for Table 2, the equality assumption is not satisfied. Given the number of GCMs and RCMs used here, a number n = 10 is a good compromise. Using larger values for n does not change the results dramatically.
The ENSEMBLES project offers to us a possibility to verify this Monte-Carlo method. Indeed, in the project database, we can find three simulations of the KNMI model at 50 km resolution driven by three different simulations of the MPI GCM. We have calculated the sampling variance in each sub-area by two methods: the direct one based on the 3 available ensemble members, and the indirect one using interannual variability and Monte-Carlo simulation of 10 members. For winter temperature, the average over Europe of the standard deviations is 0.46 K with the 3-member sample and 0.36 K with estimates based on the interannual variability. This indicates that our method underestimates the variability. This can be explained by the insufficient sampling of inter-decadal variability with only 30 consecutive years. However, this feature is not observed for other variables or seasons. For summer temperature, we get respectively 0.22 and 0.23 K, for winter precipitation 0.15 and 0.16 mm/day, for summer precipitation 0.11 and 0.10 mm/day. We will therefore use this method in the following to add artificial ensemble members, keeping in mind that the internal variability may be underestimated by about 30% for winter temperature. However, as we will see in the following, and in agreement with D07 results, this internal variability is one order of magnitude below the other two sources of variability, which makes our approximation acceptable.
To estimate the interannual variance, we have again the problem of missing RCM × GCM pairs. The variance is not the combination of variance per weather regime multiplied by the regime frequency as in Eq. 6. It is possible, however, to derive a formula with a sum of terms involving pairs of regimes. But the decomposition is a combination of large positive and negative terms (covariances between the regimes), and the attempts to reconstruct the variances as we did for the means led to negative variances in several cases because our samples are too short. So we used, for the interannual variances a simple interpolation as in Eq. 8.
Table 7 shows for Europe (aggregation of the 8 sub-areas) the mean, standard deviation and percentage of the variance explained by the 7 components of Eq. 9. The mean values are similar to those obtained with the data without interannual variability (Table 3). The standard deviations are larger, due to the inclusion of interannual variability. One can also remark that the combined RGM term is greater than the terms involving two sources of variability (i.e., RG, RM, GM). Thus the assumption that this term is negligible, used in D07 to fill the missing matrix data, is not supported by our analysis.
The uncertainty due to natural climate variability can be evaluated by V(M) = M+RM + GM + RGM which corresponds to the mean interannual spread of a given model. For DJF temperature V(M) is 36% of the total variance. In summer, it is only 21%. For DJF precipitation, the percentage is 58%, but this is to be compared with 72% for V(R) and 77% for V(G). In summer V(M) is 52% of the total precipitation variance. These percentages illustrate the well known feature that running several GCMs and RCMs produces a significantly larger spread in the response than running an ensemble of the same size with a single model (without perturbing the parameters as in HC-lo, HC-med and HC-hi), even for a moderate climate change like in the first half of the 21st century.
6 Spatial distribution
One of the advances of ENSEMBLES, with respect to PRUDENCE, is the production of probabilities for the projected changes. In Déqué and Somot (2010) the following probabilistic model is proposed:
-
1.
the response to climate change is one of the 18 results of the RCM × GCM matrix
-
2.
the RCMs have a probability proportional to the weight they obtain in a series of tests based on climate simulations driven by ERA40 (Christensen et al. 2010)
-
3.
the GCMs have a probability proportional to their skill in simulating weather regime frequencies over North Atlantic-Europe
-
4.
each RCM × GCM result has a probability density function (pdf) based on the limit central theorem (Gaussian law, variance of the 30-year means divided by 30)
Hypothesis 1, which is very restrictive, can be attenuated by the use of a Gaussian kernel filter designed to make a smooth transition between the maxima of the individual model pdfs.
Here we do not consider the probability of climate response (e.g. temperature change in DJF near Paris between 1961–1990 and 2021–2050) of a model drawn at random amongst the cells of the RCM × GCM matrix as is done in Déqué and Somot (2010), but rather the probability of the average of the full matrix, as is done in D07. The mean and variance we have calculated before (e.g. Table 7) can provide a confidence interval for a new RCM × GCM drawn at random from a population with the statistical properties of the ENSEMBLES models. If we take the average of n independent models, the variance is divided by n. Here the 13 × 6 responses in the matrix are not independent, because the reconstructed terms are a combination of the actual responses and additional information (the weather regime frequencies). Taking n = 18, the number of actual runs, gives a reasonable approximation for the variance of the average. Even though the pdf of a single model is not Gaussian in particular for temperature response which is skewed (see Déqué and Somot 2010), the pdf of the average can be considered as Gaussian (limit central theorem) and a confidence interval is easy to obtain.
At each grid point of a common 0.5° × 0.5° grid we have calculated a mean M and a variance V including reconstructed values. The 99% confidence interval is
Figures 3 and 4 show the lower and upper boundaries of this confidence interval for temperature. The winter pattern (Fig. 3) is very similar to the D07 pattern with a West-East gradient easy to explain by the snowline retreat in the coldest part of Europe. In the eastern part, there is also a South-North gradient which is more intense than in D07. The summer pattern (Fig. 4) is a North–South gradient as in D07. However, there is also a West-East component which was absent in D07. As a consequence, the maximum warming which was in Spain and South of France in D07 is located here in the Balkan Peninsula.
As Fig. 3 for JJA temperature
It is not possible to display similar maps for precipitation, because in both winter and summer seasons, the upper and lower boundaries of the 99% interval have an opposite sign over a large part of the domain. This means that the local response is not significant at that 99% level, contrary to D07. So a quantitative approach for precipitation is not reasonable. Instead, Fig. 5 shows the grid points for which the absolute value of the mean change is above two standard deviations, which corresponds to 95% level significance. There are 77% of such points in winter and 66% in summer, which indicates that we are analyzing a robust climate change: only 5% of the points are expected to be beyond this threshold just by chance. In addition, the winter pattern is in good agreement with Fig. 3 of D07. The summer pattern bipolar structure is different from Fig. 4 of D07 which exhibited a unipolar pattern of precipitation decrease centered at 45°N.
7 Conclusion
The most important conclusion of D07 was that for the A2 emissions scenario and 2071–2100 time slice in general the largest source of uncertainty came from the GCM. For certain sub-areas or seasons, the RCM played the major role, however. This conclusion has led to the design of the ENSEMBLES regional climate modeling study: instead of using only one GCM with all the RCMs, we have used many GCMs, distributing the RCMs amongst the driving GCMs. The result we obtain here is that for the A1B emissions scenario and 2021–2050 time slice, we confirm the larger role played by the RCMs in summer precipitation. Two different methods for filling the empty cells of the RCM × GCM matrix yield the same conclusion for this field. The first method assumes that the warming due to the GCM and RCM are additive. It produces a larger inter-model variability and shows that for the other 3 fields analysed (DJF and JJA temperature, DJF precipitation) the GCM and RCM have a similar contribution to the spread. The second method takes into account the large-scale simulation of atmospheric circulation above Europe (weather regimes) and interpolates the RCM and GCM contributions (half sum of the two). It reduces the inter-model variability and shows that, as in PRUDENCE, the GCM contributes more to the spread. When PRUDENCE and ENSEMBLES are compared with the same filling method, the contribution of the RCM is systematically enhanced. The design of a large multimodel experiment is therefore very important for analysis of the modeling uncertainties. The natural variability, which should be more important than in PRUDENCE because the signal-to-noise ratio is weaker, is still in third place.
The large spread amongst the models should not prevent us from presenting results to the impacts community as far as seasonal mean temperature is concerned. This spread provides justification for presenting them in probabilistic terms. We get spatial patterns similar to those of PRUDENCE, with an amplitude of the response coarsely divided by 2 in winter and by 3 in summer with respect to that experiment (which was for a higher emissions scenario and further into the future). In the latter season, the maximum warming is located in south-eastern Europe (compared with south-western Europe in PRUDENCE). This pattern modification between mid- and end-century in summer might be explained by the fact that the positive feedback by soil drying out with warming is not fully in place during the first half of the century. Indeed, the precipitation response is only weakly significant. Only its sign is statistically robust, with a precipitation increase in the North and a decrease in the South.
A secondary finding of this study is that two RCMs driven by the same GCM experience similar changes in weather regime frequency, as a result of global warming. However this frequency change is not sufficient to explain the temperature and precipitation changes. The changes in the conditional averages of these fields for a given weather regime depend on the RCM as well as on the driving GCM. This makes the reconstruction of the missing cells in the RCM × GCM matrix less straightforward than expected.
All the results given here depend on the ability to fill the missing values in the matrix. As we have only three RCMs driven by more than one GCM, estimating the error by removing one RCM × GCM pair and trying to reconstruct it, as was done in D07, only gives a coarse estimate of the skill. Nonetheless, such an estimation favors the second method. The results of this multi-model experiment, including the empirically reconstructed simulations, provide guidance for future model ensemble studies and the provision of better information on regional climate change responses in probabilistic terms.
References
Biner S, Caya D, Laprise R, Spacek L (2000) Nesting of RCMs by imposing large scales. In: Ritchie H (ed) Research activities in atmospheric and oceanic modelling, WMO/TD-No. 987, Report 30, pp 7.3–7.4
Böhm U, Kücken M, Ahrens W, Block A, Hauffe D, Keuler K, Rockel B, Will A (2006) CLM—the climate version of LM: brief description and long-term applications. COSMO Newslett 6
Brown SJ, Caesar J, Ferro CAT (2008) Global changes in extreme daily temperature since 1950. J Geophys Res (Atmospheres) 113(D5). doi:10.1029/2006JD008091
Christensen JH, Christensen OB (2007) A summary of the PRUDENCE model projections of changes in European climate during this century. Clim Change 81:7–30
Christensen JH, Christensen OB, Lopez P, van Meijgaard E, Botzet M (1996) The HIRHAM4 regional atmospheric climate model. Scientific report DMI, Copenhagen, Report 96-4 Available at DMI, Lyngbyvej 100, DK-2100 Copenhagen Ø, Denmark
Christensen JH, Carter TR, Giorgi F (2002) PRUDENCE employs new methods to assess European climate change. EOS 83:147
Christensen JH, Kjellström H, Giorgi F, Lenderink G, Rummukainen M (2010) Weight assignment in regional climate models. Clim Res 44:179–194
Collins M, Booth BBB, Harris GR, Murphy JM, Sexton DMH, Webb MJ (2006) Towards quantifying uncertainty in transient climate change. Clim Dyn 27:127–147
Déqué M, Somot S (2010) Weighted frequency distributions expressing modelling uncertainties in the ENSEMBLES regional climate experiments. Clim Res. doi:10.3354/cr00866
Déqué M, Rowell DP, Lüthi D, Giorgi F, Christensen JH, Rockel B, Jacob D, Kjellström E, Castro M, van den Hurk B (2007) An intercomparison of regional climate simulations for Europe: assessing uncertainties in model projections. Clim Change 81:53–70
Driouech F, Déqué M, Sánchez-Gómez E (2010) Weather regimes—Moroccan precipitation link in a regional climate change simulation. Glob Planet Change. doi:10.1016/j.gloplacha.2010.03.004
Ferro CAT (2004) Attributing variation in a regional climate change modelling experiment, PRUDENCE Technical Report. Available at Dept. of Meteorology, University of Reading, Earley Gate, PO Box 243, Reading RG6 6BB, UK, 21 pp
Furevik T, Bentsen M, Drange H, Kindem IKT, Kvamstø NG, Sorteberg A (2004) Description and evaluation of the bergen climate model: ARPEGE coupled with MICOM. Clim Dyn 21:27–51
Gibelin AL, Déqué M (2003) Anthropogenic climate change over the Mediterranean region simulated by a global variable resolution model. Clim Dyn 20:327–339
Giorgi F (2008) A simple equation for regional climate change and associated uncertainty. J Clim 21:1589–1604
Giorgi F, Mearns LO (1999) Introduction to special section: regional climate modeling revisited. J Geophys Res (Atmospheres) 104:6335–6352
Gordon C, Cooper C, Senior CA, Banks HT, Gregory JM, Johns TC, Mitchell JFB, Wood ERA (2000) The simulation of SST, sea ice extents and ocean heat transports in a version of the Hadley Centre coupled model without flux adjustments. Clim Dyn 16:147–168
Haugen JE, Haakensatd H (2006) Validation of HIRHAM version 2 with 50 and 25 km resolution. RegClim general technical report, no. 9, pp 159–173
Hewitt CD, Griggs DJ (2004) Ensembles-based predictions of climate changes and their impacts. EOS 85:566
Hurrel JW, Kushnir Y, Visbeck M (2001) The North Atlantic oscillation. Science 291(5504):603–605
IPCC (2007) Climate change 2007: the physical science basis. In: Solomon S, Qin D, Manning M, Chen Z, Marquis M, Averyt KB, Tignor M, Miller HL (eds) Contribution of working group I to the fourth assessment report of the intergovernmental panel on climate change of the intergovernmental panel of climate change. Cambridge University Press, UK 996 pp
Jacob D (2001) A note to the simulation of the annual and inter-annual variability of the water budget over the Baltic Sea drainage basin. Meteorol Atmos Phys 77(1–4):61–73
Jones CG, Willen U, Ullesrtig A, Hanssson U (2004) The Rossby Centre regional atmospheric climate model part I: model climatology and performance for the present climate over Europe. Ambio 33:199–210
Kjellström E, Bärring L, Gollvik S, Hansson U, Jones C, Samuelsson P, Rummukainen M, Ullersig A, Willen U, Wyser K (2005) A 140-year simulation of European climate with the new version of the Rossby Centre regional atmospheric climate model (RCA3). Reports meteorology and climatology, 108, SMHI, SE-60176 Norrkoping, Sweden, 54 pp
Lenderink G, van Ulden A, van den Hurk B, Keller F (2007) A study on combining global and regional climate model results for generating climate scenarios of temperature and precipitation for the Netherlands. Clim Dyn 29:157–176
Michelangeli P, Vautard R, Legras B (1995) Weather regimes: recurrence and quasi stationarity. J Atmos Sci 52:1237–1256
Murphy JM, Booth BBB, Collins M, Harris GR, Sexton D, Webb M (2007) A methodology for probabilistic predictions of regional climate change from perturbed physics ensembles. Phil Trans R Soc A 365:1993–2028
Plaut G, Simmonet E (2001) Large-scale circulation classification, weather regimes and local climate over France, the Alps and Western Europe. Clim Res 17:303–324
Radu R, Déqué M, Somot S (2008) Spectral nudging in a spectral regional climate model. Tellus A 60:898–910
Robertson AW, Ghil M (1999) Large-scale weather regimes and local climate over the Western United States. J Clim 12:1796–1813
Roeckner E, Bäuml G, Bonaventura L, Brokopf R, Esch M, Giorgetta M, Hagemann S, Kirchner I, Kornblueh L, Manzini E, Rhodin A, Schlese U, Schulzweida U, Tompkins A (2003) The atmospheric general circulation model ECHAM5. Part I: model description. Max Planck Institute for Meteorology Rep. 349. Available from MPI for Meteorology, Bundesstr 53, 20146 Hamburg, Germany, 127 pp
Sanchez E, Gallardo C, Gaertner MA, Arribas A, Castro M (2004) Future climate extreme events in the Mediterranean simulated by a regional climate model: a first approach. Glob Planet Change 44:163–180
Sanchez-Gomez E, Somot S, Déqué M (2008) Ability of an ensemble of regional climate models to reproduce the weather regimes during the period 1961–2000. Clim Dyn 33:723–736
van der Linden P, Mitchell JFB (eds) (2009) E ENSEMBLES: climate change and its impacts: summary of research and results from the ENSEMBLES project. Met Office Hadley Centre, FitzRoy Road, Exeter EX1 3 PB, UK. 160 pp
Van Meijgaard E, van Ulft LH, van de Berg WJ, Bosveld FC, van den Hurk BJJM, Lenderink G, Siebesma AP (2008) The KNMI regional atmospheric climate model RACMO, version 2.1. KNMI publication: TR-302, 43 pp
Vautard R (1990) Multiple weather regimes over the north Atlantic: analysis of precursors and successors. Mon Wea Rev 118:2056–2081
von Storch H, Langenberg H, Feser F (2000) A spectral nudging technique for dynamical downscaling purposes. Mon Wea Rev 128:3664–3673
Yiou P, Nogaj M (2004) Extreme climate events and weather regimes over the North Atlantic: when and where? Geophys Res Lett 3(L0):7202. doi:10.1029/2003GL019119
Zhang XB, Zwiers FW, Hegerl GC, Lambert FH, Gillett NP, Solomon S, Stott PA, Nozawa T (2007) Detection of human influence on twentieth-century precipitation trends. Nature 448(7152). doi:10.1038/nature06025
Acknowledgments
This work was supported by the European Commission Programme FP6 under contract GOCE-CT-2006-037005 (ENSEMBLES). This analysis has been made possible thanks to all modeling contributors to ENSEMBLES-RT2B (and RT2A for driving GCM runs). They cannot be all co-authors, but their work is strongly acknowledged here (see http://ensemblesrt3.dmi.dk/).
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Déqué, M., Somot, S., Sanchez-Gomez, E. et al. The spread amongst ENSEMBLES regional scenarios: regional climate models, driving general circulation models and interannual variability. Clim Dyn 38, 951–964 (2012). https://doi.org/10.1007/s00382-011-1053-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-011-1053-x