Introduction

The arterial endothelial layer plays a critical role in angiogenesis, vasomotion, and vascular inflammation. Endothelial cells (ECs) respond to blood flow in a wide variety of ways ranging from rapid, localized responses, such as ion channel gating and integrin activation, to slow, global responses, such as cytoskeletal reorganization and morphological changes.1,12,13,28 Importantly, ECs respond differently to different types of flow (for recent reviews see Chien6–8). For instance, relatively high levels of steady shear stress and non-reversing pulsatile flow induce an anti-inflammatory endothelial phenotype, whereas low shear stress and oscillatory flow induce a pro-inflammatory and dysfunctional profile. This has been demonstrated in vitro 19,23 and it may be the basis for the preferred localization of early atherosclerotic lesions in arterial regions of disturbed flow such as branches and bifurcations in vivo.24,35 Indeed, it has been suggested that oscillatory flow elicits abnormalities in EC adaptive responses to flow, leading to cellular dysfunction and disease.19,23

Although a number of candidate mechanoreceptors have been proposed and various mechanosensitive signaling pathways described, much remains unknown about how ECs sense, transmit, and transduce mechanical forces. Furthermore, how ECs distinguish among different types of flow remains completely unknown, although recent studies on flow-activated ion channels have suggested a possible role for these channels in endowing ECs with the ability to discriminate between steady and oscillatory flow.3,20,29 To complement experimental investigations, mathematical models of EC responsiveness to flow have been developed. While some models have focused on the processes of EC flow sensing and intracellular force transmission,2,31 others have explored flow-induced morphological changes43 or flow-mediated activation of biochemical pathways, especially calcium signaling37,38,46 and ATP/ADP concentration at the EC surface.9,26,42

Although flow in the arterial system is mostly laminar (even in disturbed flow zones), turbulence occurs in vivo in specific situations. For instance, a short-lived burst of turbulence is observed at peak systole in the aorta under normal conditions.33 Turbulence is also observed under certain pathological conditions such as severe arterial stenoses and regurgitant aortic valves.21,27 ECs respond differently to turbulent flow than they do to laminar flow. For instance, while turbulent flow stimulates EC proliferation, steady laminar flow has no effect on cell turnover rates.14 Turbulent flow also affects EC morphology and gene expression differently from laminar flow.14,18

Turbulent flow is inherently “noisy” in the sense that random fluctuations in basic fluid mechanical properties such as pressure and velocity are always present. These fluctuations typically have a wide range of possible frequencies and amplitudes. To our knowledge, there has been no theoretical investigation of mechanical signal transduction in noisy flow. The aim of this study is to investigate the effect of signal noise on mechanical force transmission in ECs, to develop insight into which cell components are most responsive to noisy flow, and to establish whether certain intracellular structures act as noise “filters” or “amplifiers.”

Computational Methods

ECs as a Network of Linear Viscoelastic Kelvin Bodies

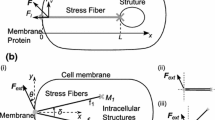
Based on earlier studies,12,13,45 the authors consider flow-mediated mechanotransduction in ECs to involve force sensing by structures on the cell surface which act as flow sensors followed by direct force transmission via cytoskeletal components to various intracellular transduction sites including a cell–cell adhesion protein (CCAP), the nucleus, and a focal adhesions site (Fig. 1a). It is understood that the CCAP and focal adhesion site as modeled here represent either individual such proteins or clusters of these proteins. Typically, the authors assume the cytoskeletal connections to consist of actin filaments; however, in some of the simulations, the authors also investigate a network in which the nucleus is connected to the flow sensor through microtubules (while the other connections consist of actin). To study intracellular deformations due to the applied force on the cell surface, the authors follow earlier studies2,31 and represent each element in the cellular network as a linear viscoelastic material whose mechanical behavior can be modeled as a spring in parallel with a spring–dashpot element (a Kelvin body; Fig. 1a).

Figure 1
figure 1

(a) Schematic representation of an endothelial cell consisting of a flow sensor (FS), cytoskeletal elements (actin filaments (A) or microtubules (M)), a nucleus (N), cell–cell adhesion protein (CCAP), and focal adhesion site (FAS). The effect of actin or microtubule connections of the nucleus on the flow sensor was examined. The inset shows a Kelvin-body representation and the viscoelastic parameters for FAS. (b) Mathematical representation of the endothelial cell components in panel a. Each cell component corresponds to a viscolelastic Kelvin body, coupled to each other according to the diagram shown. Actin and the CCAP connected in series are referred to as branch 1, actin/microtubule in series with the nucleus is branch 2, and actin and the FAS in series is branch 3

Full size image

Based on this formulation, the authors arrive at a representation of a model cell as a network of viscoelastic Kelvin bodies arranged as two bodies on three rows, each body with its two spring coefficients (k 1, k 2) and a viscosity parameter, (μ) (Fig. 1b). The viscoelastic parameters for each body are obtained from various experimental studies as described elsewhere31 and are summarized in Table 1. As detailed in our previous study,31 the following three constraints apply: (1) the sum of the forces acting on the three branches in Fig. 1b must equal the total force imposed on the network, (2) the sum of the deformations in each branch must be the same as that in every other branch, and (3) within a branch, each body experiences the same force. Mathematically, if the force on the ith branch is F i and the deformation of the jth body on the ith row is u ij , then

Table 1 Viscoelastic properties of the various cell components used in the simulations
Full size table
$$ \sum\limits_{i = 1}^{3} {F_{i} = F} $$
(1)

and

$$ {u = u_{11} + u_{12} = u_{21} + u_{22} = u_{31} + u_{32} }. $$
(2)

The following differential equation holds for each of the Kelvin bodies17

$$ {F_{i} + {\frac{{\mu^{ij} }}{{k_{2}^{ij} }}}\,\,{\frac{{{\text{d}}F_{i} }}{{{\text{d}}t}}} = k_{1}^{ij} u_{ij} + \mu^{ij} \left( {1 + {\frac{{k_{1}^{ij} }}{{k_{2}^{ij} }}}} \right){\frac{{{\text{d}}u_{ij} }}{{{\text{d}}t}}}} $$
(3)

where the viscoelastic parameters associated with the jth body on the ith row are \( k_{1}^{ij} \), \( k_{2}^{ij} \) and μ ij. In the particular system depicted in Fig. 1, the authors arrive at six linear differential equations. The deformations of the bodies and the forces on each branch are unknown; however, using the constraints from Eqs. (1) and (2), the authors are able to eliminate some of the unknowns and arrive at

$$ A{\frac{{{\text{d}}x}}{{{\text{d}}t}}} = Bx + c $$
(4a)

with initial conditions

$$ x\left( 0 \right) = x_{0} . $$
(4b)

Here the authors have defined \( x = \left[ {\begin{gathered} u_{11} \\ u_{21} \\ u_{31} \\ u \\ F_{1} \\ F_{2} \\ \end{gathered} } \right],\quad A = \left[ {\begin{array}{*{20}c} { - \alpha_{11} } & 0 & 0 & 0 & {\beta_{11`} } & 0 \\ {\alpha_{12} } & 0 & 0 & { - \alpha_{12} } & {\beta_{12} } & 0 \\ 0 & { - \alpha_{21} } & 0 & 0 & 0 & {\beta_{21} } \\ 0 & {\alpha_{22} } & 0 & { - \alpha_{22} } & 0 & {\beta_{22} } \\ 0 & 0 & { - \alpha_{31} } & 0 & { - \beta_{31} } & { - \beta_{31} } \\ 0 & 0 & {\alpha_{32} } & { - \alpha_{32} } & {\beta_{32} } & {\beta_{32} } \\ \end{array} } \right], \) \( B = \left[ {\begin{array}{*{20}c} {k_{1}^{11} } & 0 & 0 & 0 & { - 1} & 0 \\ { - k_{1}^{12} } & 0 & 0 & {k_{1}^{12} } & { - 1} & 0 \\ 0 & {k_{1}^{21} } & 0 & 0 & 0 & { - 1} \\ 0 & { - k_{1}^{22} } & 0 & {k_{1}^{22} } & 0 & { - 1} \\ 0 & 0 & {k_{1}^{31} } & 0 & 1 & 1 \\ 0 & 0 & { - k_{1}^{32} } & {k_{1}^{32} } & 1 & 1 \\ \end{array} } \right]\,{\text{and}} \quad c = \left[ {\begin{gathered} \hfill 0 \\ \hfill 0 \\ \hfill 0 \\ \hfill 0 \\ \hfill - F - \beta_{31} {\frac{{{\text{d}}F}}{{{\text{d}}t}}} \\ \hfill - F - \beta_{32} {\frac{{{\text{d}}F}}{{{\text{d}}t}}} \\ \end{gathered} } \right]. \) In these matrices, the authors introduced the following new notation for convenience: \( {\alpha_{ij} = \mu^{ij} \left( {1 + {\frac{{k_{1}^{ij} }}{{k_{2}^{ij} }}}} \right)} \) and \( \beta_{ij} = {\frac{{\mu^{ij} }}{{k_{2}^{ij} }}}. \)

Finally, the initial conditions for our system of equations need to be defined. In general, the initial deformation of any body is given by \( {u_{ij} \left( 0 \right) = {\frac{{F_{i} \left( 0 \right)}}{{k_{1}^{ij} + k_{2}^{ij} }}}.} \) As before, the authors interpret F 3 as F − F 1 − F 2. From Eq. (2), we know that u(0) = u 11(0) + u 12(0); thus, after we find the initial force in branch 1, we can also find the initial condition for u. Finding the initial conditions for the force in each branch requires the constraints from Eqs. (1) and (2) and some algebra. Ultimately, this leads to \( {F_{1} \left( 0 \right) = F\left( 0 \right){\frac{{s_{2} s_{3} }}{{s_{1} s_{2} + s_{2} s_{3} + s_{1} s_{3} }}}} \) and, similarly, \( {F_{2} \left( 0 \right) = F\left( 0 \right){\frac{{s_{1} s_{3} }}{{s_{1} s_{2} + s_{2} s_{3} + s_{1} s_{3} }}}.} \) Here, it is defined as \( {s_{i} = {\frac{1}{{k_{1}^{i1} + k_{2}^{i1} }}} + {\frac{1}{{k_{1}^{i2} + k_{2}^{i2} }}}.} \) Now we have the entire system with the appropriate initial conditions, and so we can rearrange the system and solve Eq. (5):

$$ {{\frac{{{\text{d}}x}}{{{\text{d}}t}}} = A^{ - 1} Bx + A^{ - 1} c} $$
(5)

with the appropriate initial conditions using a fourth-order Runge–Kutta method implemented in Matlab.

A few words are in order with regard to the parameter values. The parameter values used in the simulations are listed in Table 1. These values come from a variety of sources and are based on in vitro measurements. How different these values are from their in vivo counterparts remains unknown. To our knowledge, measuring these parameters in vivo is currently not feasible. The authors have also assumed that the viscoelastic parameters remain constant. That these properties change with sustained flow is evident.40 However, the time constant characterizing these changes appears to be on the order of several hours. In this study, we are primarily concerned with the effect of high-frequency noise (20–500 Hz) characterizing turbulence. Therefore, from the perspective of the time constant characterizing turbulence, EC viscoelastic parameters can be viewed as constant for any one simulation. In our previous study,31 the authors had performed a detailed study of the sensitivity of the computed deformations to the various viscoelastic parameters. In this study, the authors decided to confine this sensitivity analysis to the nucleus because changes in nuclear mechanical properties have been linked to particular pathologies.10

Representation of the Noisy Flow

The authors are interested in determining the deformations of the constituent Kelvin bodies of the network in Fig. 1 in response to turbulent (or noisy) flow on the cell surface. To describe the turbulent flow signal, the authors resort to prior experimental measurements on dog aortas33,36 demonstrating turbulent frequencies of 25–500 Hz, with an onset of turbulence just after the peak forward velocity and either decaying rapidly or persisting until the blood virtually halts in diastole.36 Although the amplitude of the turbulent oscillations was difficult to measure because of the positioning of the probe,31 reported peak velocities in horse carotid arteries ranging from 30 to 60 cm/s. Based on this, the authors allowed the noise amplitude to be varied by as much as the full amplitude of the no-noise oscillations and noise duration be varied from a small fraction to the full period of the pulsatile cycle.

The details of the turbulent (or noisy) force signal used in the present simulations are schematically depicted in Fig. 2. The authors took a non-reversing sinusoidal pulse of the form F(t) = F 0 + F 0 cos(2πt) and superimposed random noise on it. In most of the simulations, the authors varied either the duration or the maximal amplitude of the noise while maintaining the noise frequency at 20 Hz. A separate parameter study on noise frequency was conducted. The noise amplitude was a uniformly distributed random number with a zero mean and whose extreme values were set as a fraction of the amplitude of oscillations of the sinusoidal no-noise signal. For example, if F 0 = 100 and let us set the fraction of the maximal amplitude to be 1, then the noise was drawn from a uniform distribution on [−100, 100]. At any instant in time, the noise amplitude was defined as the difference between the noisy force and the no-noise sinusoidal force (see Fig. 2). The noise duration was determined as a fraction of the period of the oscillations of the sinusoidal flow. Thus, a noise duration of 0.25 indicated that the force was noisy for a quarter of a period or 0.25 s. The noise always began at the peak of the sinusoidal cycle.31 The baseline values of the noise duration and amplitude were 0.25, i.e., the maximal noise amplitude was as large as 25% of the amplitude of the no-noise signal, and the noise persisted for the first quarter of the cycle.

Figure 2
figure 2

An example of two full periods of the noisy force used in our simulations. Sinusoidal pulsatile flow (F(t) = F 0 + F 0 cos (ωt) with F 0 = 100 in arbitrary units and ω = 2π is shown with a dashed line, and superimposed on it is the noisy flow solid line. In most simulations, the noise frequency is 20 Hz, and the amplitude or the duration of the noise varies. The noise duration is given as a fraction of the period of oscillations of the no-noise sinusoidal flow, and the maximal noise amplitude is a fraction of the amplitude of the no-noise flow. Under baseline conditions, the amplitude of the noise is chosen from a uniform distribution between 0 and 25% of the amplitude of the no-noise force, and the noise duration is set to be 25% of the period of pulsatile flow. These values are close to experimentally found ranges34,36

Full size image

Results

Intracellular Deformations and Force Distribution

Figure 3 depicts the mean deformations of the three intracellular transduction sites CCAP, nucleus (N), and focal adhesion site (FAS) and the mean forces experienced by each of these sites as a function of time during the pulsatile cycle under no-noise conditions. Panels a and b are for the cases of all cytoskeletal connections being actin filaments, whereas panels c and d are for the cases of microtubule connection to the nucleus and actin connections to CCAPs and focal adhesion sites. As expected, each component undergoes an instantaneous deformation jump at the time of force application (t = 0) because of the elastic portion of the mechanical response. This is followed by relatively slow viscous creeping toward the steady-state response.

Figure 3
figure 3

Mean deformation and mean forces of our network under a no-noise sinusoidal flow. (a) Mean deformation of CCAP (solid line), nucleus (dashed line) and FAS (dash-dot line) as a function of time when the cytoskeletal element connecting the nucleus to the flow sensor is actin. (b) Mean forces acting on the CCAP (branch 1), nucleus (branch 2) and FAS (branch 3) as a function of time for the all-actin network. (c). Mean deformation of CCAP (solid line), nucleus (dashed line), and FAS (dash-dot line) in a network containing a microtubule connection between the flow sensor and the nucleus. (d) Mean forces acting on the CCAP (branch 1), nucleus (branch 2), and FAS (branch 3) as a function of time for the network containing a microtubule connection between the flow sensor and the nucleus

Full size image

When all connections are actin (Fig. 3a), the nucleus, because of its large coefficient of viscosity (see Table 1), takes considerably longer to reach its steady-state deformation than the other transduction sites. Because it is also the softest body, it attains a higher level of deformation. The CCAP and focal adhesion site reach steady state very rapidly with the stiffer focal adhesion site deforming less than the CCAP. The force divisions among the three branches are determined by the relative stiffness of the transduction sites; therefore, branch 2 requires the least force because of the softness of the nucleus and branch 3 requires the most force because of the stiffness of the focal adhesion site (Fig. 3b).

When the flow sensor is connected to the nucleus (branch 2) via microtubules instead of actin filaments, there occurs a redistribution of the force from the nucleus to the CCAP and the focal adhesion site because of the softness of the flow sensor–nucleus connection (compare Figs. 3b and 3d). Consequently, the steady-state nuclear deformation is significantly smaller (compare Figs. 3a and 3c), implying that signaling pathways that depend on direct force transmission to the nucleus would behave differently depending on the detailed intracellular cytoskeletal architecture. Two additional trends are observed when the flow sensor is coupled to the nucleus via microtubules: (1) the deformation of the nucleus exhibits an initial transient rise followed by a progressive decline to a very small steady-state value (Fig. 3c), suggesting a biphasic behavior of signaling events that depend directly on nuclear deformation. (2) The deformations of the intracellular transduction sites occur on a much longer time scale (on the order of 12 h) when the nucleus is connected to the flow sensor via microtubules (vs. ~0.5 h for an all-actin network), suggesting that the time required for steady-state signaling depends critically on the detailed cytoskeletal organization.

Signal-to-Noise Ratio

In all of the present simulations, let us collect the time series data of deformations and forces and then compute the mean, variance, and maximal value of these quantities. In order to analyze the effect of signal noise on the deformation of intracellular transduction sites, the “signal-to-noise ratio” or SNR was computed. This measure is frequently used in signal processing and is defined as the mean of the signal divided by its standard deviation.41 A small SNR indicates a large deviation from the mean, thus a highly variable or polluted signal. In order to develop a meaningful measure, let us only focus on the steady-state deformation after all initial transients have died out. This is accomplished by running the simulations sufficiently long for the system to reach a steady state and then focusing on the last 15 cycles of the simulations for which the ratio of mean to standard deviation was computed to define the SNR. The standard deviation of the deformations in sinusoidal flow is non-zero; comparing the no-noise and noise results for SNR allows determination of the effect of noise on the system.

Effect of Noise on Intracellular Deformations

The effects of noise amplitude and noise duration on the SNR in two basic networks (actin-only network, and network with microtubule connection to the nucleus and the other connections actin) were examined. Figure 4 shows that, as expected, the SNR decreases with increasing noise amplitude or duration. Interestingly, the SNR is largest for the nucleus and is largely similar for the CCAP and the FAS (slightly larger for the CCAP). Another general observation is that changes in noise amplitude (Figs. 4a, 4c, and 4e) have a larger overall effect on the SNR than changes in noise duration (Figs. 4b, 4d, and 4f). The actin-only network yields a higher SNR for both the nucleus and CCAP and a slightly lower value for the FAS.

Figure 4
figure 4

Effect of varying noise amplitude or noise duration on the “signal-to-noise ratio” (SNR; defined as the mean over the standard deviation of the steady-state deformation) of intracellular transduction sites. Each panel shows results using an all-actin network (solid line, filled dots) or a network containing a microtubule connection between the flow sensor and the nucleus (dashed line, filled triangles). Panels on the left panels show the SNR of the CCAP (a), nucleus (c), and the FAS (e) when the noise duration is fixed at 25% of the period of the no-noise pulsatile flow and the maximal noise amplitude is varied (as a fraction of the amplitude of the pulsatile flow). Panels on the right show the SNR of the CCAP (b), nucleus (d), and FAS (f) when the maximum noise amplitude is fixed at 25% of the amplitude of the pulsatile flow and the noise duration is varied

Full size image

The first data point in each of the panels of Fig. 4 corresponds to the no-noise scenario. Thus, even in the absence of noise, the SNR has a different baseline for the different intracellular transduction sites that were examined. The relatively large SNR in the nucleus is attributable to the comparatively small standard deviation in its deformation, because of the large spring constant k 222 characterizing the nucleus (see Table 1). When the network includes microtubules, the means of the deformations are smaller (see Fig. 3); thus, the SNR is smaller as well. The FAS and CCAP have very similar viscoelastic properties (Table 1); however, one of the spring coefficients associated with FAS (k 321 ) is larger, resulting in a slightly smaller mean steady-state deformation value and thus a smaller SNR.

In order to compare the effect of noise on the different intracellular transduction sites more quantitatively, the percent decreases in the SNR for all the three transduction sites and both network types under fixed values of noise amplitude and duration were computed. The results, summarized in Table 2, confirm that the SNR is significantly less sensitive to noise duration than to noise amplitude as noted above. The FAS is nearly twice as sensitive to noise as the CCAP, with the nucleus exhibiting intermediate sensitivity. Both the CCAP and the nucleus are slightly more sensitive to noise when microtubules connect the nucleus to the flow sensor than in the case of the all-actin connections. The opposite is true, however, for the FAS. These findings suggest that, in addition to their structural role, cytoskeletal connections contribute to the propagation of blood flow-derived noisy signals within ECs and that the effectiveness of this propagation is affected by both the nature of the cytoskeletal connections and the target intracellular transduction site.

Table 2 Maximal percent decrease in SNR observed in the simulations. The values represent the percent difference between the last (maximum noise) and first (no noise) data points in Fig. 4
Full size table

Sensitivity of Intracellular Transduction Sites to Noise Frequency

As already mentioned, experimental measurements of turbulence in large arteries have demonstrated turbulent frequencies ranging from 25 to 500 Hz36; therefore, the sensitivity of the intracellular deformations to noise frequency was explored (while maintaining the frequency of oscillations of the pulsatile flow at a physiological 1 Hz). In these simulations, the noise amplitude and noise duration at their baseline levels were maintained. At high noise frequencies, the time steps of our simulations had to be made very small. This, combined with the long time required to bring a network containing microtubules to steady state, rendered our parameter study unfeasible for the entire range of noise frequencies for the network including microtubules and limited our simulations on such networks to the noise frequency range of 20–125 Hz.

As illustrated in Fig. 5, the SNR for both the CCAP and the nucleus is virtually insensitive to noise frequency for both networks. In the case of the FAS, however, there is a decline in SNR at low frequencies, including the 20-Hz frequency used as our baseline value. Given that baseline value results in this study corresponded to a low frequency, it can be concluded that the method used in this study slightly underestimated the SNR in FAS in a high-frequency noise environment.

Figure 5
figure 5

The signal-to-noise ratio (SNR) of the CCAP (a), nucleus (b), and FAS (c) as a function of noise frequency (the frequency of the pulsatile flow is fixed at 1 Hz). The figure shows simulations of the all-actin network (solid line, filled dots) or the network containing a microtubule connection between the flow sensor and the nucleus (dashed line, filled triangles). Owing to computational constraints, the noise frequency for the network containing microtubules was only varied over a smaller range of frequency

Full size image

Effect of Changes in Viscoelastic Properties of the Nucleus on Intracellular Noise Propagation

A recent study has shown that the viscoelastic properties of the nucleus change when cells are exposed to flow.15 The mechanical behavior of the nucleus may also be significantly altered in certain diseases (review in Dahl et al.10). The sensitivity of the nucleus SNR to the viscoelastic parameters of the nucleus was investigated. Each of the parameters (k 1, k 2, and μ) of the nucleus over two orders of magnitude (from one tenth of the baseline values to ten times the baseline values) for each of the two networks was varied. According to the network developed here, these parameters can be denoted as k 221 , k 222 , and μ 22. Alternately, the same parameters (for example, in Fig. 6) are referred to as k 1,N , k 2,N , and μ N to emphasize that the parameters associated with the nucleus are referred to. As depicted in Fig. 6a, the SNR exhibits considerable sensitivity to the first spring coefficient of the nucleus, k 221 for both networks. As k 221 decreases below its baseline value, i.e., as the nucleus becomes more compliant, the SNR of the nucleus increases rapidly for both networks although the increase is larger for the microtubule-containing network than for the all-actin network. On the other hand, the SNR in both networks decreases as k 221 increases, i.e., as the nucleus hardens, and the decrease is equally rapid in both networks. This decrease is attributable simply to the fact that mean deformations are smaller in stiffer nuclei, leading to smaller SNR values.

Figure 6
figure 6

Effect of the viscoelastic parameters associated with the nucleus, k 1,N (panel a), k 2,N (b) and μ N (c) on the SNR of the nucleus when the nucleus is connected to the flow sensor via actin (solid line, filled dots) or microtubules (dashed line, filled triangles). The original parameter values of k 1, k 2, and μ associated with the nucleus are indicated by the arrows

Full size image

Interestingly, changing k 222 (Fig. 6b) has a very different effect: when the nucleus is soft, the SNR of the nucleus is relatively small and independent of the cytoskeletal elements used. However, increasing this spring coefficient leads to a large increase in the SNR in the microtubule-including network (due to a significant decline in the standard deviation of the fluctuations of the deformations) but has no effect on the SNR of the actin-only network. The SNR of the nucleus does not change with the coefficient of viscosity (Fig. 6c). As discussed previously, the actin-only network leads to a higher SNR. Physically, this is an intuitive result, as the steady-state deformation of the nucleus is independent of this parameter.

The different effects of k 221 and k 222 on the SNR of the nucleus may be explained as follows: If nuclear hardening results in smaller mean nuclear deformations than baseline accompanied by oscillations having the original amplitude (as occurs when k 221 increases), then the SNR will decrease, i.e., nuclear sensitivity to turbulence will diminish. On the other hand, if nuclear hardening leads to smaller oscillations around the original mean (as occurs when k 222 increases), then the SNR increases, leading to greater nuclear sensitivity to turbulent flow.

Discussion

In vivo, turbulence is present in large arteries under both normal and pathological conditions. The aim of this study was to understand the effect of turbulence on mechanotransduction in vascular ECs. To that end, the effect of a noisy force field on the deformations of various intracellular transduction sites known to be involved in EC flow signaling including the nucleus, CCAP, and FAS was investigated. The results of this study indicate that the peak deformations of the various transduction sites are more sensitive to the amplitude of oscillations in the noisy or turbulent flow than to the duration of these oscillations. Given the relative insensitivity of intracellular deformations to noise duration, our model predicts that the effect of short bursts of turbulence (as occurs in the aorta at peak systole under normal conditions) on intracellular deformations, and hence possibly on mechanosensitive cell signaling, will largely be similar to those of more persistent noise (as occurs in severe stenoses).

A significant implication of this study is that FAS, due to their relatively high sensitivity to noise, are prime candidates for acting as cellular “noise detectors.” There are two facets of FAS sensitivity to noisy flow: (1) the SNR increases with noise frequency, signifying a greater ability of FAS to detect signals as the environment becomes noisier. This increase is the most prevalent as the frequency goes from about 25–75 Hz, i.e., at the low frequency end of turbulent flow. (2) FAS exhibit greater sensitivity to noise than to either the nucleus or CCAP, suggesting that the precise character of turbulent flow has a more pronounced effect on processes mediated by FAS such as cellular adhesion, migration, and cell–matrix communication than on processes mediated by the nucleus or CCAP such as changes in mRNA and protein expression or cell–cell communication. These conclusions appear to hold whether all the cytoskeletal connections consist of actin filaments or if the nucleus is connected to the cell surface via microtubules.

Another finding of this study is that the sensitivity of the nucleus to noise exhibits a marked dependence on the viscoelastic properties of the nucleus, although this dependence appears complex. This is important in light of data demonstrating that the mechanical environment at the cell surface and certain pathologies affect the mechanical properties of the nucleus. For instance, exposure of ECs to sustained flow leads to stiffer nuclei.15 Mouse embryo studies have shown that lack of emerin, a protein of the inner nuclear membrane, leads to a greater tendency of shear deformation of the nucleus which possibly contributes to the development of Emery-Dreifuss muscular dystrophy.39 Mutations in lamin A, which cause Hutchinson Gilford progeria syndrome, lead to stiffer nuclei (review in Dahl et al.10). Our results suggest that in scenarios where the nucleus hardens, the nucleus’ response to turbulent hemodynamics depends on whether the nuclear response is a diminished deformation or a diminished amplitude of oscillations. In the former case, we expect the nucleus to “lose” its sensitivity to turbulence, whereas in the latter case, the nucleus will exhibit a significantly heightened sensitivity to the turbulent flow.

This study makes significant simplifications in its treatment of mechanical force transmission in ECs. Similar to previous studies,2,31 the authors continue to assume linear viscoelastic behavior and to consider a greatly simplified view of intracellular organization. Although several other theoretical models of EC mechanotranduction have been proposed16,32 (see also recent review in Lim et al.30), our simple framework is considered a good starting point for testing specific hypotheses as done in this study. A second limitation of this study is that it focuses exclusively on intracellular deformations. A third limitation is the fact that the forces and deformations in our model are expressed in terms of arbitrary units, which limits our ability to make predictions that are directly physiologically relevant.

A number of considerations ignored in the current model merit future investigation. For instance, recent studies have suggested that the composition of the extracellular matrix may affect the mechanical properties of ECs.45 Therefore, coupling components of the present networks to the extracellular matrix might be an interesting extension of this study. The computations worked out in this study have ignored the effects that the cytosolic fluid might have on intracellular deformations. The cytosolic fluid is expected to provide a level of damping of intracellular deformations, and this may be effectively represented by added viscosity within the viscoelastic structures inthe current model. The authors have also ignored the possible effects of cell and nuclear membrane dynamics on the deformations of the various components in our EC networks. Subjecting ECs to flow increases cell membrane fluidity,5 which is expected to alter membrane–integrin interactions and thus to affect the resulting integrin deformations. Similarly, changes in nuclear membrane dynamics are expected to affect nuclear deformations. However, the relationship between changes in membrane dynamics and integrin (or nuclear) deformations remains unknown. In the model under this study, the computed deformations are determined entirely by the viscoelastic parameters characterizing the Kelvin bodies in our networks. Therefore, a potentially effective way of incorporating the effect of changes in membrane dynamics into the model might be to make the viscoelastic parameters functions of these dynamics. Naturally, the form of this functional dependence remains to be established. Finally, extending the current modeling framework to relate intracellular deformations to intracellular signaling events promises to significantly enhance our understanding of flow-mediated mechanotransduction in vascular endothelium.