The operational matrix of Chebyshev polynomials for solving pantograph-type Volterra integro-differential equations

Abstract

In this work, the Chebyshev collocation scheme is extended for the Volterra integro-differential equations of pantograph type. First, we construct the operational matrices of pantograph and derivative based on Chebyshev polynomials. Also, the obtained operational matrices are utilized to approximate the derivatives of unknown functions. Furthermore, a detailed analysis of convergence is discussed in the weighted square norm. We conduct some numerical experiments to verify the high performance of the suggested numerical approach. The results show that the computational scheme is accurate.

1 Introduction

The main object of this current study is to extend a Chebyshev collocation scheme to calculate the following Volterra integro-differential equation of pantograph type:

$$ \begin{aligned} y'(t)={}&a_{1}(t)y(t)+a_{2}(t)y(qt)+b(t) \\ &{}+ \int _{0}^{t}k_{1}(t,s)y(s)\,ds+ \int _{0}^{qt}k_{2}(t,s)y(s)\,ds,\quad t \in [0,T], \end{aligned} $$

(1)

with $y(0)=y_{0}$, where $0< q<1$. The kernel functions $k_{1}(t,s)$, $k_{2}(t,s)$ are defined in $D=\{(t,s): 0\leq t \leq T, 0\leq s \leq t\}$ and $D_{q}=\{(t,s): 0\leq t \leq T, 0\leq s \leq qt\}$, respectively. Assume the known functions $a_{1}(t), a_{2}(t), b(t)\in C^{m}([0,T])$, $k_{1}(t,s) \in C^{m}(D)$, and $k_{2}(t,s) \in C^{m}(D_{q})$ for $m\geq 0$. Then, for each initial value $y_{0}$, the considered problems have a unique solution $y(t)\in C^{m+1}([0,T])$ [1].

These equations appear in many fields of science, including biology, physics, finance, and so on [2]. In the past few decades, integro-differential equations have attracted widespread attention. In general, it is impossible to obtain analytical solutions to integro-differential equations. Therefore, many scholars are devoted to searching an effective approximate method to solve this class of problems. In view of numerical method, several types of integro-differential equations have been treated recently by different techniques. In [3, 4] the authors developed classic Runge–Kutta methods for the considered problems. The author of [5, 6] researched the discussed problems by means of finite element methods. Furthermore, there are a major number of research works on the spectral method for the aforementioned problem, we can refer to the works [7] and [8]. The authors of [9, 10] proposed a Legendre collocation method for multiple delays differential and integral equations. Meanwhile, Wei and Chen [11] extended successfully this method to handle the proportional delays-type Volterra integro-differential equations in detail. In addition, Zhao et al. [12] worked with a similar technique based on Legendre polynomials for nonlinear Volterra integro-differential equations with nonvanishing delays. In [13] the authors applied the sinc function and collocation method to deal with proportional delay Volterra integro-differential equation. Recently, many researchers used the operational matrix methods to solve these types of integral equations [14–16]. Furthermore, the authors in [17, 18] developed the above numerical scheme for fractional order partial integro-differential equations. More recently, the operational matrix together with the tau method was utilized to deal with the Volterra integro-differential equation with pantograph delay in [19]. Yang [20] and Deng [21] employed Jacobi polynomials and Galerkin methods to calculate this type of equations with singular and noncompact kernels, respectively. In [22] the mapped Laguerre collocation methods have been implemented for solving the types of problems with noncompact kernels.

In this paper, we develop an improved Chebyshev operational matrix method to handle the considered problem described in (1). First, we formulate the operational matrices of pantograph based on shifted Chebyshev polynomial. Then, we construct the discrete computational scheme that the variable coefficients are not approximated. We provide convergence analysis in $L^{2}$-norm in detail.

2 Shifted Chebyshev operational matrix of derivative

$T^{*}_{n}(t)$ denotes the shifted Chebyshev polynomials which are defined as follows:

$$ T^{*}_{n}(t)=T_{n}(2t/T-1), \quad n\in \mathbb{N}_{0}; t\in [0,T], $$

where $T_{n}(t)$ are the standard Chebyshev polynomials, $\mathbb{N}_{0}=\mathbb{N}\bigcup \{0\}$, and $\mathbb{N}$ denotes a set of positive integers. Also, $T^{*}_{n}(t)$ can be derived by the following recursive relationship:

$$ T^{*}_{n+1}(t)=2 ( 2t/T-1 )T^{*}_{n}(t)-T^{*}_{n-1}(t), \quad n\in \mathbb{N}, $$

where $T^{*}_{0}(t)=1$, $T^{*}_{1}(t)=2t/T-1$. Moreover, the system of $T^{*}_{n}(t)$, $n\in \mathbb{N}_{0}$ satisfies a discrete orthogonality property as follows:

(2)

where $t_{k}=\frac{T}{2}(1-\cos (k\pi /N))$, $k=0,1,\ldots ,N$.

For any function $y(t)\in C[0,T]$ can be approximated as

(3)

According to the discrete orthogonality property in (2), we can denote the coefficient $c_{k}$ as

(4)

Applying (3) and (4), we can rewrite $y_{N}(t)$ in the matrix form

$$ y_{N}(t)=\boldsymbol{T}(t)\cdot \boldsymbol{P} \cdot \boldsymbol{Y}, $$

(5)

in which

$$\begin{array}{c}\mathit{T}(t)=\left[\begin{array}{c}{T}_0^{\ast }(t),T_1^{\ast }(t),\dots ,T_{N-1}^{\ast }(t),T_N^{\ast }(t)\end{array}\right],\hfill \\ \mathit{P}=\left[\begin{array}{ccccc}\frac{1}{2N}{T}_0^{\ast }(t_0)& \frac{2}{2N}{T}_0^{\ast }(t_1)& \frac{2}{2N}{T}_0^{\ast }(t_2)& \cdots & \frac{1}{2N}{T}_0^{\ast }(t_N)\\ \frac{1}{N}{T}_1^{\ast }(t_0)& \frac{2}{N}{T}_1^{\ast }(t_1)& \frac{2}{N}{T}_1^{\ast }(t_2)& \cdots & \frac{1}{N}{T}_1^{\ast }(t_N)\\ \frac{1}{N}{T}_2^{\ast }(t_0)& \frac{2}{N}{T}_2^{\ast }(t_1)& \frac{2}{N}{T}_2^{\ast }(t_2)& \cdots & \frac{1}{N}{T}_2^{\ast }(t_N)\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ \frac{1}{2N}{T}_N^{\ast }(t_0)& \frac{2}{2N}{T}_N^{\ast }(t_1)& \frac{2}{2N}{T}_N^{\ast }(t_2)& \cdots & \frac{1}{2N}{T}_N^{\ast }(t_N)\end{array}\right],\hfill \end{array}$$

and

$$\mathit{Y}={\left[\begin{array}{c}y(t_0),y(t_1),y(t_2),\dots ,y(t_N)\end{array}\right]}^T.$$

So, the values of derivatives of $y_{N}(t)$ are simply computed by

$$ \boldsymbol{Y^{(1)}}=\boldsymbol{D^{(1)}} \cdot \boldsymbol{Y}, $$

(6)

where

$${\mathit{Y}}^{\mathbf{(}\mathbf{1}\mathbf{)}}={\left[\begin{array}{c}{y}^{\prime }(t_0),y^{\prime }(t_1),y^{\prime }(t_2),\dots ,y^{\prime }(t_N)\end{array}\right]}^T,$$

$\boldsymbol{D^{(1)}}$ is the operational matrix of derivative (see [23]).

3 Operational matrix of pantograph

In a similar manner with the operational matrix of derivative, we have

$$ \boldsymbol{Y_{q}}=\boldsymbol{Q} \boldsymbol{Y}, $$

(7)

where

$$\begin{array}{c}{\mathit{Y}}_{\mathit{q}}={\left[\begin{array}{c}y(q{t}_0),y(q{t}_1),y(q{t}_2),\dots ,y(q{t}_N)\end{array}\right]}^T,\hfill \\ \mathit{Q}={\mathit{R}}_{\mathit{q}}\cdot \mathit{P},\hfill \end{array}$$

and

$${\mathit{R}}_{\mathit{q}}=\left[\begin{array}{ccccc}{T}_0^{\ast }(q{t}_0)& T_1^{\ast }(q{t}_0)& T_2^{\ast }(q{t}_0)& \cdots & T_N^{\ast }(q{t}_0)\\ T_0^{\ast }(q{t}_1)& T_1^{\ast }(q{t}_1)& T_2^{\ast }(q{t}_1)& \cdots & T_N^{\ast }(q{t}_1)\\ T_0^{\ast }(q{t}_2)& T_1^{\ast }(q{t}_2)& T_2^{\ast }(q{t}_2)& \cdots & T_N^{\ast }(q{t}_2)\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ T_0^{\ast }(q{t}_N)& T_1^{\ast }(q{t}_N)& T_2^{\ast }(q{t}_N)& \cdots & T_N^{\ast }(q{t}_N)\end{array}\right].$$

Here, Q denotes the operational matrix of pantograph based on shifted Chebyshev polynomials.

Now, we consider handling the part of integral term in (1):

$$ \int _{0}^{t}k_{1}(t,s)y(s)\,ds \approx \int _{0}^{t}k_{1}(t,s)y_{N}(s) \,ds. $$

Then, applying (5), we get

$$ \int _{0}^{t}k_{1}(t,s)y_{N}(s) \,ds= \int _{0}^{t}k_{1}(t,s)T(s)P Y \,ds. $$

So, we approximate the first integral term

$$ \boldsymbol{K_{1}}=\boldsymbol{F}\boldsymbol{Y}, $$

(8)

where

$$ \boldsymbol{K_{1}}= \biggl[ \int _{0}^{t_{0}}k_{1}(t,s)y_{N}(s) \,ds, \int _{0}^{t_{1}}k_{1}(t,s)y_{N}(s) \,ds, \ldots , \int _{0}^{t_{N}}k_{1}(t,s)y_{N}(s) \,ds \biggr]^{T} $$

and

$$ \boldsymbol{F}=\boldsymbol{G} \boldsymbol{P} \boldsymbol{Y}, $$

where

$$\mathit{G}=\left[\begin{array}{cccc}{\int }_0^{t_0}{k}_1(t,s)T_0^{\ast }(s)ds& {\int }_0^{t_0}{k}_1(t,s)T_1^{\ast }(s)ds& \cdots & {\int }_0^{t_0}{k}_1(t,s)T_N^{\ast }(s)ds\\ {\int }_0^{t_1}{k}_1(t,s)T_0^{\ast }(s)ds& {\int }_0^{t_1}{k}_1(t,s)T_1^{\ast }(s)ds& \cdots & {\int }_0^{t_1}{k}_1(t,s)T_N^{\ast }(s)ds\\ ⋮& ⋮& \ddots & ⋮\\ {\int }_0^{t_N}{k}_1(t,s)T_0^{\ast }(s)ds& {\int }_0^{t_N}{k}_1(t,s)T_1^{\ast }(s)ds& \cdots & {\int }_0^{t_N}{k}_1(t,s)T_N^{\ast }(s)ds\end{array}\right].$$

Now we consider to calculate the element $\boldsymbol{G}_{ij}=\int _{0}^{t_{i}}k_{1}(t_{i},s)T^{*}_{j}(s)\,ds$ of the matrix G. With the help of Gaussian quadrature formulas, we have

$$ \begin{aligned} \boldsymbol{G_{ij}}&= \int _{0}^{t_{i}}k_{1}(t_{i},s)T^{*}_{j}(s) \,ds \\ &=\frac{t_{i}}{2} \int _{-1}^{1}k_{1} \biggl(t_{i}, \frac{t_{i}x+t_{i}}{2} \biggr)T^{*}_{j} \biggl( \frac{t_{i}x+t_{i}}{2} \biggr)\,dx \\ &\approx \frac{t_{i}}{2}\sum_{r=0}^{N}k_{1} \biggl(t_{i}, \frac{t_{i}x_{r}+t_{i}}{2} \biggr)T^{*}_{j} \biggl( \frac{t_{i}x_{r}+t_{i}}{2} \biggr)\omega _{r}, \end{aligned} $$

where $\{\omega _{r}\}_{r=0}^{N}$ are the Chebyshev weights. Using a similar process, the second part of integral term in (1) can be approximated

$$ \int _{0}^{qt}k_{2}(t,s)y(s)\,ds \approx \int _{0}^{qt}k_{2}(t,s)y_{N}(s) \,ds. $$

By (5) and Gauss quadrature formulas, the following operational matrix $\boldsymbol{F_{q}}$ is obtained:

$$ \boldsymbol{K_{2}}=\boldsymbol{F_{q}} \boldsymbol{Y}, $$

(9)

where

$$ \boldsymbol{K_{2}}= \biggl[ \int _{0}^{qt_{0}}k_{2}(t,s)y_{N}(s) \,ds, \int _{0}^{qt_{1}}k_{2}(t,s)y_{N}(s) \,ds, \ldots , \int _{0}^{qt_{N}}k_{2}(t,s)y_{N}(s) \,ds \biggr]^{T} $$

and

$$ \boldsymbol{F_{q}}=\boldsymbol{G_{q}} \boldsymbol{P} \boldsymbol{Y}, $$

where

$$ \boldsymbol{G_{q}}=(\boldsymbol{G_{q}})_{ij}= \int _{0}^{qt_{i}}k_{1}(t_{i},s)T^{*}_{j}(s) \,ds , \quad i,j=0,1,2,\ldots ,N, $$

and

$$ (\boldsymbol{G_{q}})_{ij}\approx \frac{qt_{i}}{2}\sum _{r=0}^{N}k_{2} \biggl(qt_{i}, \frac{qt_{i}x_{r}+qt_{i}}{2} \biggr)T^{*}_{j} \biggl( \frac{qt_{i}x_{r}+t_{i}}{2} \biggr)\omega _{r}. $$

4 Proposed numerical scheme

In this section, we are devoted to solving the considered problem (1) by previously derived operational matrix. First, substituting matrix relations (6), (7), (8), and (9) into (1), we have

$$ \bigl(\boldsymbol{D}^{(1)}-\boldsymbol{A_{1}}- \boldsymbol{A_{2}} \boldsymbol{Q}-\boldsymbol{F}-\boldsymbol{F_{q}}\bigr)\boldsymbol{Y}= \boldsymbol{B}, $$

(10)

where

$$\begin{aligned}& \boldsymbol{A_{1}}=\operatorname{diag}\bigl[a_{1}(x_{0}), a_{1}(x_{1}), a_{1}(x_{2}),\ldots , a_{1}(x_{N})\bigr],\\& \boldsymbol{A_{2}}=\operatorname{diag}\bigl[a_{2}(x_{0}), a_{2}(x_{1}), a_{2}(x_{2}),\ldots , a_{2}(x_{N})\bigr],\\& \boldsymbol{B}=\bigl[b(x_{0}), b(x_{1}),\ldots , b(x_{N})\bigr]^{T}. \end{aligned}$$

Denoting the expression in parenthesis of (10) by C, the above system of equations (10) can be written as

$$ \boldsymbol{C}\boldsymbol{Y}=\boldsymbol{B}, $$

where

$$ \boldsymbol{C}=[c_{ij}] \quad i,j=0,1,2,\ldots ,N. $$

Then we incorporate the initial value condition $y(0)=y_{0}$ in (10) and obtain

$$y(0)\left[\begin{array}{c}{c}_{01}\\ c_{02}\\ c_{03}\\ ⋮\\ c_{0N}\end{array}\right]+\left[\begin{array}{ccccc}{c}_{11}& c_{12}& c_{13}& \cdots & c_{1N}\\ c_{21}& c_{22}& c_{23}& \cdots & c_{2N}\\ c_{31}& c_{32}& c_{33}& \cdots & c_{3N}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ c_{N1}& c_{N2}& c_{N3}& \cdots & c_{NN}\end{array}\right]\left[\begin{array}{c}y(t_1)\\ y(t_2)\\ y(t_3)\\ ⋮\\ y(t_N)\end{array}\right]=\left[\begin{array}{c}b(t_1)\\ b(t_2)\\ b(t_3)\\ ⋮\\ b(t_N)\end{array}\right].$$

Thus, we can get the unknown vector Y and $y_{N}(t)$ by solving the above equations.

5 Some useful notations and lemmas

First, we present some lemmas and notations, which are necessary for the error analysis. $L_{\omega ^{\alpha ,\beta}}^{2}(I)$ denotes a space of functions u for which $\|u\|_{L_{\omega ^{\alpha ,\beta}}^{2}}<\infty$ with

$$ \Vert u \Vert _{L_{\omega ^{\alpha ,\beta}}^{2}}=\sqrt{ \int _{-1}^{1} \bigl\vert u(x) \bigr\vert ^{2} \omega ^{\alpha ,\beta}(x)\,dx}, $$

where $\omega ^{\alpha ,\beta}(x)$ is the weight function on $I:=(-1,1)$. For $m\geq 0$, $m\in \mathbb{N}_{0}$, define

$$ H^{m}_{\omega ^{\alpha ,\beta ,}}= \bigl\{ v: \partial _{x}^{k}v \in L^{2}_{ \omega ^{\alpha ,\beta}}(I), 0\leq k \leq m \bigr\} $$

and

$$ \vert v \vert _{H^{m;N}_{\omega ^{\alpha ,\beta}}}= \Biggl( \sum_{k=\min(m,N+1)}^{m} \bigl\Vert \partial _{x}^{k}v \bigr\Vert ^{2}_{L^{2}_{\omega ^{\alpha ,\beta}}} \Biggr)^{ \frac{1}{2}}. $$

Particularly, let $\omega (x)$ denote the Chebyshev weight function when $\alpha =\beta =-1/2$.

For given $N\in \mathbb{N}$, $\mathbb{P}_{N}$ denotes the set of all real polynomials of degree less than N. Given any function $u\in C[-1,1]$, the Lagrange interpolation polynomial of u is

$$ I_{N}u=\sum_{i=0}^{N}u(x_{i})F_{i}(x), $$

which satisfies

$$ I_{N}u(x_{i})=u(x_{i}), $$

where $F_{i}(x)$ and $\{x_{i}\}_{i=0}^{N}$ are the Lagrange polynomials and Chebyshev Gauss–Lobatto points, respectively.

Lemma 1

([24])

For any function $u\in H^{m}_{\omega}(I)$ with $m\geq 1$, $I_{N}u$ is its interpolation polynomial. Then we have the estimates

$$ \Vert u-I_{N}u \Vert _{L_{\omega}^{2}(I)}\leq CN^{-m} \vert u \vert _{H^{m;N}_{\omega}(I)}. $$

According to Lemma 1, the following inequality can be proved. For the Gauss-type quadrature formulas, we have

$$ \biggl\vert \int _{-1}^{1}u(x)\phi (x)\omega (x)-(u,\phi )_{N} \biggr\vert \leq CN^{-m} \vert u \vert _{H^{m;N}_{\omega}(I)} \Vert \phi \Vert _{L_{\omega}^{2}(I)}, $$

(11)

where $u\in H^{m}_{\omega}(I)$, $\phi \in \mathbb{P}_{N}$, and $(u,\phi )_{N}$ is the discrete inner product associated with a Gauss-type quadrature.

Lemma 2

([25])

For a bounded function $u(x)$, we have the following inequality:

$$ \sup_{N} \Biggl\Vert \sum_{i=0}^{N}u(x_{i})F_{i}(x) \Biggr\Vert _{L_{\omega}^{2}(I)} \leq C\max_{x\in [-1,1]} \bigl\vert u(x) \bigr\vert , $$

where $\{F_{i}(x)\}_{i=0}^{N}$ are the Lagrange interpolation polynomials.

Lemma 3

([9, 11])

Suppose $0\leq M_{1}$, $M_{2}<+\infty$ and

$$ E(x)\leq M_{1} \int _{-1}^{x}E(s)\,ds+M_{2} \int _{-1}^{x}E(qs+q-1)\,ds+H(x). $$

Assume more that $E(x)$ and $H(x)$ are nonnegative integrable functions, then

$$ \Vert E \Vert _{L^{p}}\leq C \Vert H \Vert _{L^{p}}, \quad p\geq 1. $$

6 Convergence analysis

Consider (1) again. By using $t=T(1+x) /2$, the interval $[0,T]$ can be transformed to $[-1,1]$. So (1) can be rewritten as follows:

$$\begin{aligned}& \begin{aligned} u'(x)={}&A_{1}(x)u(x)+A_{2}(x)u(qx+q-1)+B(x) \\ &{}+\frac {T}{2} \int _{0}^{\frac{T}{2}(1+x)}k_{1} \biggl( \frac {T}{2}(1+x),s \biggr)y(s)\,ds \\ &{}+\frac {T}{2} \int _{0}^{\frac{qT}{2}(1+x)}k_{2} \biggl( \frac {T}{2}(1+x), \tau \biggr)y(\tau )\,d\tau , \end{aligned} \end{aligned}$$

(12)

$$\begin{aligned}& u(-1)=u_{-1}=y_{0}, \end{aligned}$$

(13)

where

$$\begin{aligned}& u(x)=y \biggl( \frac {T}{2}(1+x) \biggr), \qquad A_{1}(x)= \frac {T}{2}a_{1} \biggl( \frac {T}{2}(1+x) \biggr),\\& A_{2}(x)=\frac {T}{2}a_{2} \biggl( \frac {T}{2}(1+x) \biggr), \qquad B(x)= \frac {T}{2}b \biggl( \frac {T}{2}(1+x) \biggr), \end{aligned}$$

where $x \in [-1,1]$. Furthermore, by using the following linear transformations:

$$\begin{aligned}& s=\frac{T}{2}(1+\theta ), \quad \theta \in [-1,x],\\& \tau =\frac{T}{2}(1+\eta ), \quad \eta \in [-1,qx+q-1], \end{aligned}$$

equation (12) can be written as follows:

$$ \begin{aligned} u'(x)={}&A_{1}(x)u(x)+A_{2}(x)u(qx+q-1)+B(x) \\ &{}+ \int _{-1}^{x}K_{1}(x, \theta )u(\theta ) \,d\theta + \int _{-1}^{qx+q-1}K_{2}(x, \eta )u(\eta )\,d \eta , \end{aligned} $$

(14)

where

$$ \begin{aligned} &K_{1}(x, \theta )=\frac{T^{2}}{4}k_{1} \biggl( \frac{T}{2}(1+x),\frac{T}{2}(1+\theta ) \biggr), \\ & K_{2}(x, \eta )=\frac{T^{2}}{4}k_{1} \biggl( \frac{T}{2}(1+x), \frac{T}{2}(1+\eta ) \biggr). \end{aligned} $$

Theorem 4

If $u_{N}(x)$ and $u(x)$ are the approximate and analytical solutions of (12) with (13), respectively, assume that $u(x)$ is sufficiently smooth, then

$$ \Vert u-u_{N} \Vert _{L^{2}_{\omega}(I)}\leq CN^{-m} \bigl(M \Vert u \Vert _{L^{2}_{ \omega}(I)}+ \bigl\vert u' \bigr\vert _{H^{m;N}_{\omega}(I)}+ \vert u \vert _{H^{m;N}_{\omega}(I)} \bigr), $$

for N sufficiently large, where $M=\max_{x\in [-1,1]}|K_{1}(x,t)|_{H_{\omega}^{m;N}(I)}+ \max_{x\in [-1,1]}|K_{2}(x,t)|_{H_{\omega}^{m;N}(I)}$.

Proof

First, we insert the Gauss–Lobatto collocation points $\{x_{i}\}_{i=0}^{N}$ into (14) and obtain

$$ \begin{aligned} u'(x_{i})={}&A(x_{i})u(x_{i})+B(x_{i})u(qx_{i}+q-1)+G(x_{i}) \\ &{}+ \int _{-1}^{x_{i}}K_{1}(x, \theta )u(\theta ) \,d\theta + \int _{-1}^{qx_{i}+q-1}K_{2}(x, \eta )u(\eta )\,d \eta \end{aligned} $$

(15)

and

$$ u(x_{i})= \int _{-1}^{x_{i}}u'(\theta )\,d\theta +u_{-1}. $$

(16)

We use $u_{N}(x_{i})$ to approximate $u(x_{i})$ and

$$ u_{N}(x)=\sum_{i=0}^{N}u(x_{i})F_{i}(x), \quad i=0,1,2,\ldots ,N, $$

where $F_{i}(x)$ is the Lagrange interpolation polynomials. Next, we consider the integral terms involved in (15)

$$ \begin{aligned} \int _{-1}^{x_{i}}K_{1}(x_{i}, \theta )u_{N}(\theta )\,d\theta &=\frac{1+x_{i}}{2} \int _{-1}^{1}K_{1}(x_{i}, \tau )u_{N}( \tau )\,d\tau \\ &\approx \frac{1+x_{i}}{2}\sum_{r=0}^{N}K_{1}(x_{i}, \tau _{r})u_{N}( \tau _{r})\omega _{r}, \end{aligned} $$

where $\{\tau _{r}\}_{r=0}^{N}$ coincides with the collocation points $\{x_{i}\}_{i=0}^{N}$. In a similar way we deal with

$$ \int _{-1}^{qx_{i}+q-1}K_{2}(x_{i}, \theta )u_{N}(\theta )\,d\theta \approx \frac{q(1+x_{i})}{2}\sum _{r=0}^{N}K_{2}(x_{i}, \tau _{r})u_{N}( \tau _{r})\omega _{r}. $$

So, our numerical scheme can be reformulated as

$$\begin{aligned}& \begin{aligned}u_{N}'(x_{i})={}& A_{1}(x_{i})u_{N}(x_{i})+A_{2}(x_{i})u_{N}(qx_{i}+q-1)+B(x_{i}) \\ &{}+\frac{1+x_{i}}{2}\sum_{r=0}^{N}K_{1}(x_{i}, \tau _{r})u_{N}(\tau _{r}) \omega _{r}+\frac{q(1+x_{i})}{2}\sum_{r=0}^{N}K_{2}(x_{i}, \tau _{r})u_{N}( \tau _{r})\omega _{r}, \end{aligned} \\& u_{N}(x_{i})= \int _{-1}^{x_{i}}u'_{N}(\theta ) \,d\theta +u_{-1}. \end{aligned}$$

(17)

For ease of analysis, the above numerical scheme can be rewritten as follows:

$$ \begin{aligned}u_{N}'(x_{i})= {}&A_{1}(x_{i})u_{N}(x_{i})+A_{2}(x_{i})u_{N}(qx_{i}+q-1)+B(x_{i}) \\ &{}+ \int _{-1}^{x_{i}}K_{1}(x, \theta )u_{N}(\theta )\,d\theta + \int _{-1}^{qx_{i}+q-1}K_{2}(x, \eta )u_{N}(\eta )\,d\eta -I_{1}(x_{i})-I_{2}(x_{i}), \end{aligned} $$

(18)

where

$$ I_{1}(x_{i})= \int _{-1}^{x_{i}}K_{1}(x_{i}, \theta )u_{N}(\theta )\,d\theta -\frac{1+x_{i}}{2}\sum _{j=0}^{N}K_{1}(x_{i}, \tau _{j})u_{N}( \tau _{j})\omega _{j} $$

and

$$ I_{2}(x_{i})= \int _{-1}^{qx_{i}+q-1}K_{2}(x_{i}, \theta )u(\theta )\,d\theta -\frac{q(1+x_{i})}{2}\sum_{j=0}^{N}K_{2}(x_{i}, \tau _{j})u_{N}( \tau _{j})\omega _{j}. $$

Applying the Lagrange interpolation operator to (18) yields

$$ \begin{aligned} u_{N}'(x)={} &I_{N}\bigl(A_{1}(x)u_{N}(x)\bigr)+I_{N} \bigl(A_{2}(x)u_{N}(qx+q-1)\bigr) \\ &{}+I_{N}\bigl(B(x)\bigr)+I_{N} \biggl( \int _{-1}^{x}K_{1}(x, \theta )u_{N}( \theta )\,d\theta \biggr) \\ &{}+I_{N} \biggl( \int _{-1}^{qx+q-1}K_{2}(x, \eta )u_{N}(\eta )\,d\eta \biggr)-J_{1}(x)-J_{2}(x), \end{aligned} $$

(19)

where

$$ J_{1}(x)=\sum_{i=0}^{N}I_{1}(x_{i})F_{i}(x), \qquad J_{2}(x)=\sum_{i=0}^{N}I_{2}(x_{i})F_{i}(x). $$

Obviously, by (14),

$$ \begin{aligned} I_{N}\bigl(u'(x) \bigr)={}&I_{N}\bigl(A_{1}(x)u(x)\bigr)+I_{N} \bigl(A_{2}(x)u(qx+q-1)\bigr) \\ &{}+I_{N}\bigl(B(x)\bigr)+I_{N} \biggl( \int _{-1}^{x}K_{1}(x, \theta )u(\theta ) \,d\theta \biggr) \\ &{}+I_{N} \biggl( \int _{-1}^{qx+q-1}K_{2}(x, \eta )u(\eta )\,d \eta \biggr). \end{aligned} $$

(20)

By subtracting (19) from (20), we can obtain

$$ \begin{aligned} e_{N}'(x)= {}&u'(x)-I_{N}\bigl(u'(x) \bigr)+I_{N}\bigl(A_{1}(x)e_{N}(x)\bigr) \\ &{}+I_{N}\bigl(A_{2}(x)e_{N}(qx+q-1) \bigr)+I_{N} \biggl( \int _{-1}^{x}K_{1}(x, \theta )e_{N}(\theta )\,d\theta \biggr) \\ &{}+I_{N} \biggl( \int _{-1}^{qx+q-1}K_{2}(x, \eta )e_{N}(\eta )\,d\eta \biggr)+J_{1}(x)+J_{2}(x), \end{aligned} $$

(21)

where $e'_{N}(x)=u'(x)-u'_{N}(x)$. Meanwhile, subtracting (17) from(16) yields

$$ u(x_{i})-u_{N}(x_{i})= \int _{-1}^{x_{i}}e'_{N}(\theta ) \,d\theta . $$

(22)

Similarly, applying the Lagrange interpolation operator to (22) yields

$$ u(x)-u_{N}(x)=u(x)-I_{N}\bigl(u(x) \bigr)+I_{N} \biggl( \int _{-1}^{x}e'_{N}( \theta )\,d\theta \biggr). $$

(23)

Consequently, we rewrite (21) as

$$\begin{aligned}& \begin{aligned} e_{N}'(x)={} &A_{1}(x)e_{N}(x)+A_{2}(x)e_{N}(qx+q-1)+ \int _{-1}^{x}K_{1}(x, \theta )e_{N}(\theta )\,d\theta \\ &{} + \int _{-1}^{qx+q-1}K_{2}(x, \eta )e_{N}(\eta )\,d\eta +\sum_{i=1}^{7} J_{i}(x), \end{aligned} \end{aligned}$$

(24)

$$\begin{aligned}& e_{N}(x)= \biggl( \int _{-1}^{x}e'_{N}(\theta ) \,d\theta \biggr)+J_{8}(x)+J_{9}(x), \end{aligned}$$

(25)

where

$$\begin{aligned}& J_{3}(x)=u'(x)-I_{N}\bigl(u'(x) \bigr),\\& J_{4}(x)=I_{N}\bigl(A_{1}(x)e_{N}(x) \bigr)-A_{1}(x)e_{N}(x),\\& J_{5}(x)=I_{N}\bigl(A_{2}(x)e_{N}(qx+q-1) \bigr)-A_{2}(x)e_{N}(qx+q-1),\\& J_{6}(x)=I_{N} \biggl( \int _{-1}^{x}K_{1}(x, \theta )e_{N}(\theta )\,d\theta \biggr)- \int _{-1}^{x}K_{1}(x, \theta )e_{N}(\theta )\,d\theta ,\\& J_{7}(x)=I_{N} \biggl( \int _{-1}^{qx+q-1}K_{2}(x, \eta )e_{N}(\eta )\,d\eta \biggr)- \int _{-1}^{qx+q-1}K_{2}(x, \eta )e_{N}(\eta )\,d\eta,\\& J_{8}(x)=u(x)-I_{N}\bigl(u(x)\bigr),\qquad J_{9}(x)=I_{N} \biggl( \int _{-1}^{x}e'_{N}( \theta )\,d\theta \biggr)- \int _{-1}^{x}e'_{N}(\theta ) \,d\theta . \end{aligned}$$

Substituting (25) into the first integral part of (24) and applying Dirichlet’s formula that $\int _{-1}^{x}\int _{-1}^{\tau}\phi (\tau ,s)\,ds\,d\tau =\int _{-1}^{x} \int _{s}^{x}\phi (\tau ,s)\,d\tau \,ds$, we obtain

$$ \begin{aligned} \int _{-1}^{x}K_{1}(x, \theta )e_{N}(\theta )\,d\theta ={}& \int _{-1}^{x} \biggl( \int _{\theta}^{x} K_{1}(x,\tau )\,d\tau \biggr) e'_{N}( \theta )\,d\theta \\ & {}+ \int _{-1}^{x}K_{1}(x, \theta ) \bigl(J_{8}(\theta )+J_{9}(\theta )\bigr)\,d\theta . \end{aligned} $$

(26)

Considering the second integral part of (24),

$$ \begin{aligned} \int _{-1}^{qx+q-1}K_{2}(x, \eta )e_{N}(\eta )\,d\eta ={}& \int _{-1}^{qx+q-1}K_{2}(x, \eta ) \biggl( \int _{-1}^{\eta}e'_{N}( \theta )\,d\theta \biggr)\,d\eta \\ &{} + \int _{-1}^{qx+q-1}K_{2}(x, \eta ) \bigl(J_{8}(\eta )+J_{9}(\eta )\bigr)\,d\eta . \end{aligned} $$

(27)

For the sake of applying Dirichlet’s formula, we transform the above equation to

$$ \begin{aligned} & \int _{-1}^{qx+q-1}K_{2}(x, \eta )e_{N}(\eta )\,d\eta \\ & \quad =q^{2} \int _{-1}^{x}K_{2}(x, q\eta +q-1) \biggl( \int _{-1}^{\eta}e'_{N}(q \theta +q-1)\,d\theta \biggr)\,d\eta \\ &\qquad {} +q \int _{-1}^{x}K_{2}(x, q\eta +q-1) \bigl(J_{8}(q\eta +q-1)+J_{9}(q\eta +q-1)\bigr)\,d\eta \\ &\quad =q^{2} \int _{-1}^{x} \biggl( \int _{\eta}^{x} K_{2}(x, q\eta +q-1)\,d\eta \biggr)e'_{N}(q\theta +q-1)\,d\theta \\ &\qquad {} +q \int _{-1}^{x}K_{2}(x, q\eta +q-1) \bigl(J_{8}(q\eta +q-1)+J_{9}(q\eta +q-1)\bigr)\,d\eta . \end{aligned} $$

(28)

Substituting (26) and (28) into (24), provided the integral exists, we obtain

$$ \begin{aligned} \bigl\vert e_{N}'(x) \bigr\vert \leq {}& M_{1} \bigl\vert e_{N}(x) \bigr\vert +(M_{2}+M_{4}) \int _{-1}^{x} \bigl\vert e'_{N}(q \eta +q-1) \bigr\vert \,d\eta \\ &{}+M_{3} \int _{-1}^{x} \bigl\vert e'_{N}( \theta ) \bigr\vert \,d\theta +\sum_{i=1}^{7} \bigl\vert J_{i}(x) \bigr\vert \\ &{}+ \int _{-1}^{x}K_{1}(x, \theta ) \bigl( \bigl\vert J_{8}(\theta ) \bigr\vert + \bigl\vert J_{9}(\theta )\bigr) \bigr\vert \,d\theta \\ &{}+q \int _{-1}^{x}K_{2}(x, q\eta +q-1)\sum _{i=8}^{9} \bigl\vert J_{i}(q \eta +q-1) \bigr\vert \,d\eta , \end{aligned} $$

(29)

where

$$\begin{aligned}& M_{1}=\max_{x\in [-1,1]} \bigl\vert A_{1}(x) \bigr\vert ,\\& M_{2}=\max_{x\in [-1,1]} \bigl\vert A_{2}(x) \bigr\vert ,\\& M_{3}=\max_{x\in D_{1}} \int _{\theta}^{x} \bigl\vert K_{1}(x,\tau ) \bigr\vert \,d\tau ,\\& M_{4}=q^{2}\max_{x\in D_{2}} \int _{\eta}^{x} \bigl\vert K_{2}(x, q \eta +q-1) \bigr\vert \,d\eta , \end{aligned}$$

and

$$\begin{aligned}& D_{1}=\bigl\{ (x,\tau ): -1\leq x\leq 1,-1\leq \tau \leq x\bigr\} ,\\& D_{2}=\bigl\{ (x,\eta ): -1\leq x\leq 1,-1\leq \eta \leq qx+q-1\bigr\} . \end{aligned}$$

By Lemma 3,

$$ \bigl\Vert e'_{N}(x) \bigr\Vert _{L^{2}_{\omega}(I)} \leq C_{1} \Biggl( \bigl\Vert e_{N}(x) \bigr\Vert _{L^{2}_{ \omega}(I)}+\sum_{i=1}^{9} \Vert J_{i} \Vert _{L^{2}_{\omega}(I)} \Biggr). $$

(30)

Using (25) gives

$$ \bigl\Vert e_{N}(x) \bigr\Vert _{L^{2}_{\omega}(I)}\leq C_{2} \bigl( \bigl\Vert e'_{N}(x) \bigr\Vert _{L^{2}_{ \omega}(I)}+ \bigl\Vert J_{8}(x) \bigr\Vert _{L^{2}_{\omega}(I)}+ \bigl\Vert J_{9}(x) \bigr\Vert _{L^{2}_{ \omega}(I)} \bigr). $$

(31)

Then, by (30), (31), and $C_{1}C_{2}<1$, we have

$$ \bigl\Vert e_{N}(x) \bigr\Vert _{L^{2}_{\omega}(I)}\leq C \sum_{i=1}^{9} \Vert J_{i} \Vert _{L^{2}_{ \omega}(I)}. $$

(32)

First, using Lemma 2 and (11) yields

$$\begin{aligned}& \begin{aligned} \Vert J_{1} \Vert _{L^{2}_{\omega}(I)}& \leq C \max_{x \in [-1,1]} \bigl\vert I_{1}(x) \bigr\vert \\ & \leq C N^{-m}\max_{x\in [-1,1]} \bigl\vert K_{1}(x,t) \bigr\vert _{H_{\omega}^{m;N}(I)}\bigl( \Vert u \Vert _{L^{2}_{\omega}(I)}+ \Vert e \Vert _{L^{2}_{\omega}(I)}\bigr), \end{aligned} \end{aligned}$$

(33)

$$\begin{aligned}& \begin{aligned} \Vert J_{2} \Vert _{L^{2}_{\omega}(I)}& \leq C \max_{x \in [-1,1]} \bigl\vert I_{2}(x) \bigr\vert \\ & \leq C N^{-m}\max_{x\in [-1,1]} \bigl\vert K_{2}(x,t) \bigr\vert _{H_{\omega}^{m;N}(I)}\bigl( \Vert u \Vert _{L^{2}_{\omega}(I)}+ \Vert e \Vert _{L^{2}_{\omega}(I)}\bigr). \end{aligned} \end{aligned}$$

(34)

Next, by Lemma 1, we have

$$ \Vert J_{3} \Vert _{L^{2}_{\omega}(I)} \leq CN^{-m} \bigl\vert u' \bigr\vert _{H^{m;N}_{\omega}(I)}, \qquad \Vert J_{8} \Vert _{L^{2}_{\omega}(I)} \leq CN^{-m} \vert u \vert _{H^{m;N}_{\omega}(I)}. $$

(35)

In addition, by Lemma 1 for $m=1$, we find that

$$\begin{aligned}& \begin{aligned} \Vert J_{4} \Vert _{L^{2}_{\omega}(I)} & \leq CN^{-1} \biggl\Vert A'(x) \int _{-1}^{x}e'(\tau )\,d\tau +A(x)e'(x) \biggr\Vert _{L^{2}_{\omega}(I)} \\ &\leq CN^{-1} \bigl\Vert e'(x) \bigr\Vert _{L^{2}_{\omega}(I)}, \end{aligned} \\& \Vert J_{5} \Vert _{L^{2}(I)} \leq CN^{-1} \bigl\Vert e'(x) \bigr\Vert _{L^{2}_{\omega}(I)},\\& \Vert J_{k} \Vert _{L^{2}(I)} \leq CN^{-1} \bigl\Vert e(x) \bigr\Vert _{L^{2}_{\omega}(I)},\quad k=6,7,9. \end{aligned}$$

Therefore, a combination of $J_{i}$, $i=1,2,\ldots ,9$, yields

$$ \Vert u-u_{N} \Vert _{L^{2}_{\omega}(I)}\leq CN^{-m} \bigl(M \Vert u \Vert _{L^{2}_{ \omega}(I)}+ \bigl\vert u' \bigr\vert _{H^{m;N}_{\omega}(I)}+ \vert u \vert _{H^{m;N}_{\omega}(I)} \bigr), $$

where $M=\max_{x\in [-1,1]}|K_{1}(x,t)|_{H_{\omega}^{m;N}(I)}+ \max_{x\in [-1,1]}|K_{2}(x,t)|_{H_{\omega}^{m;N}(I)}$. □

7 Numerical experiments

In this section, we carried out the proposed computational scheme for solving the considered problem in the form of (1).

Example 7.1

First, we investigate the problem as follows:

$$ \begin{aligned} &y'(t)=y (0.5t )+ \int _{0}^{t}y(s)\,ds+ \int _{0}^{0.5t}y(s)\,ds+1-1.5t, \quad t\in [0,T], \\ &y(0)=0. \end{aligned} $$

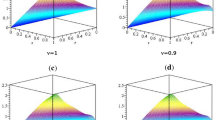
The analytical solution is $y(t)=1-e^{-t}$. We implement the proposed computational scheme to calculate the problem with various polynomial degree N. Figure 1 illustrates the absolute error function $|e_{N}(x)|=|u(x)-u_{N}(x)|$ for $N=8,16$. Table 1 provides the computational results on the interval of $[0, 10]$. From the approximate solution, one can see high accuracy of the suggested numerical scheme.

Figure 1

Absolute errors for $N=8,16$ on the interval of $[0, 1]$ for Example 7.1

Table 1 Absolute errors on the interval of $[0, 10]$ for Example 7.1

Example 7.2

We consider

$$ \begin{aligned} &y'(t)=0.5y(t)+y(0.25t)+ \int _{0}^{t}e^{t+x}y(x)\,dx+ \int _{0}^{0.25t}xy(x)\,dx+g(t), \\ & y(0)=0, \end{aligned} $$

where

$$ g(t)=0.5-0.25e^{0.25}+0.03125t^{2}-0.5e^{3t}+e^{2t}, $$

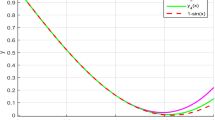
and then the analytical solution is $y(t)=e^{t}-1$. Likewise, we implement the proposed computational scheme to solve the second problem with $4\leq N\leq 20$ for $T=1$ and $16\leq N\leq 40$ for $T=10$, various values of N and T. The obtained errors are plotted in $L^{2}$-norms in Fig. 2 for $4\leq N\leq 40$. From Fig. 2, we know that the suggested numerical scheme is very effective. We compare the maximum absolute errors of our developed approach with sine collocation method [13]. The computational results are tabulated in Table 2. Moreover, a simple comparison between the two methods confirms the accuracy of the proposed computational scheme.

Figure 2

$L^{2}-$ errors obtain by using our method for $T=1,10$ for Example 7.2

Table 2 Comparison of the maximum absolute errors with various N for Example 7.1

8 Conclusion

We proposed a computational scheme for solving a class of Volterra integro-differential equations. The derivation of this scheme is based on Chebyshev operational matrices and the Gauss quadrature formula. Moreover, the convergence analysis for the present method is investigated in detail. We compare the computational results obtained in this work with other approximated methods. The comparison indicates that our approach is more accurate and efficient. Moreover, our proposed computational scheme can be extended for solving nonlinear problems of pantograph type.