Skip to main content
SpringerLink
Log in

A spectral shifted gegenbauer collocation method for fractional pantograph partial differential equations and its error analysis

  • Published:
Sādhanā Aims and scope Submit manuscript

Abstract

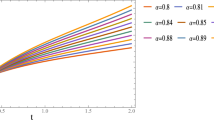
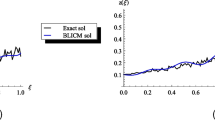
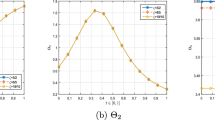
This study presents a new numerical approach for solving fractional-order pantograph partial-differential equations, in which the fractional derivatives are expressed in the Caputo sense. New operational matrices are obtained by introducing the two-variable Gegenbauer polynomials. Using these matrices with the collocation method, solving the fractional order pantograph partial differential equation is converted into solving a system of algebraic equations. An error bound is computed for this method. Also, some examples are presented that show our proposed method has a better agreement with the exact solution in comparison with methods such as the homotopy perturbation and natural decomposition methods so that we can say that it is about \(10^{3}\) times more precise than the two mentioned methods. In general, our method provides a useful tool for solving these equations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Figure 1
Figure 2
Figure 3
Figure 4
Figure 5
Figure 6
Figure 7

Similar content being viewed by others

References

  1. Podlubny I 1998 Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution, and some of their applications. Elsevier

    MATH  Google Scholar 

  2. Tarasov V E 2019 Handbook of Fractional Calculus with Applications Volume 4 Applications in Physics Part A. Walter de Gruyter GmbH & Co KG

  3. Tarasov V E 2019 Handbook of Fractional Calculus with Applications Volume 5 Applications in Physics Part B. Walter de Gruyter GmbH & Co KG

  4. Sakar M G, Uludag F and Erdogan F 2016 Numerical solution of time-fractional nonlinear PDEs with proportional delays by homotopy perturbation method. Appl. Math. Model. 40: 6639–6649

    Article  MathSciNet  MATH  Google Scholar 

  5. Shah R, Khan H, Kumam P, Arif M and Baleanu D 2019 Natural transform decomposition method for solving fractional-order partial differential equations with proportional delay. Mathematics 7(6): 1–14

    Article  Google Scholar 

  6. Ajello W, Freedman H and Wu J 1992 A model of stage structured population growth with density depended time delay. SIAM J. Appl. Math. 52: 855–869

    Article  MathSciNet  Google Scholar 

  7. Buhmann M and Iserles A 1993 Stability of the discretized pantograph differential equation. Math. Comput. 60: 575–589

    Article  MathSciNet  MATH  Google Scholar 

  8. Fox L et al. 1971 On a functional differential equation. IMA J. Appl. Math. 8: 271–307

    Article  MATH  Google Scholar 

  9. Richard O J and Tayler B A 1971 The dynamics of a current collection system for an electric locomotive. Proc. R. Soc. Lond. A 322: 447–468

    Article  Google Scholar 

  10. Wu J 1996 Theory and applications of partial functional differential equations. Springer

    Book  MATH  Google Scholar 

  11. Maleknejad Kh, Rashidinia J and Eftekhari T 2021 Numerical solutions of distributed order fractional differential equations in the time domain using the Muntz-Legendre wavelets approach. Numer. Methods Partial Differ. Equ. 37: 707–731

    Article  Google Scholar 

  12. Wang Zh 2013 A numerical method for delayed fractional-order differential equations. J. Appl. Math. 2013: 1–8

    MathSciNet  Google Scholar 

  13. Sakar M G and Ergoren H 2015 Alternative variational iteration method for solving the time-fractional Fornberg-Whitham equation. Appl. Math. Model. 39: 3972–3979

    Article  MathSciNet  MATH  Google Scholar 

  14. Zhou X and Dai Y 2022 A spectral collocation method for the coupled system of nonlinear fractional differential equations. AIMS Math. 7: 5670–5689

    Article  MathSciNet  Google Scholar 

  15. Hafez M R and Youssri Y H 2022 Shifted Gegenbauer-Gauss collocation method for solving fractional neutral functional-differential equations with proportional delays. Kragujevac J. Math. 46(6): 981–996

    Article  MathSciNet  MATH  Google Scholar 

  16. Abazari R and Ganji M 2011 Extended two-dimensional DTM and its application on nonlinear PDEs with proportional delay. Int. J. Comput. Math. 88: 1749–1762

    Article  MathSciNet  MATH  Google Scholar 

  17. Yuttanan B, Razzaghi M and Vo N T 2021 A fractional-order generalized Taylor wavelet method for nonlinear fractional delay and nonlinear fractional pantograph differential equations. Math. Methods Appl. Sci. 44: 4156–4175

    Article  MathSciNet  MATH  Google Scholar 

  18. Sadri Kh and Aminikhah H 2022Chebyshev polynomials of sixth kind for solving nonlinear fractional PDEs with proportional delay and its convergence analysis. J. Funct. Sp.. 2022: 1–20

  19. El-Hawary H M, Salim M S and Hussien H S 2000 An optimal ultraspherical approximation of integrals. Int. J. Comput. Math. 76: 219–237

    Article  MathSciNet  MATH  Google Scholar 

  20. El-Kady M, Hussien S H and Ibrahim M 2009 Ultraspherical spectral integration method for solving linear integro-differential equations. World Acad. Sci. Eng. Technol. 33: 880–887

    Google Scholar 

  21. Elgindy K 2016 High-order numerical solution of second-order one-dimensional hyperbolic telegraph equation using a shifted Gegenbauer pseudospectral method. Numer. Methods Partial Differ. Eqs. 32: 307–349

    Article  MathSciNet  MATH  Google Scholar 

  22. Elgindy K and Smith-Miles K 2013 Optimal Gegenbauer quadrature over arbitrary integration nodes. J. Comput. Appl. Math. 242: 82–106

    Article  MathSciNet  MATH  Google Scholar 

  23. Cheney W E and Kincaid D R 2009 Linear algebra: Theory and applications. Aust. Math. Soc. 110: 544–550

    MATH  Google Scholar 

  24. Guo B and Wang L 2004 Jacobi approximations in non-uniformly Jacobi-weighted Sobolev spaces. J. Approx. Theory 128: 1–41

    Article  MathSciNet  MATH  Google Scholar 

  25. Mirzaee F and Samadyar N 2020 Explicit representation of orthonormal Bernoulli polynomials and its application for solving Volterra–Fredholm–Hammerstein integral equations. SeMA J. 81–96

  26. Hass J R, Heil E C, Weir M D and Bogacki P 2022 Thomas’ Calculus: Early Transcendentals. 15th edition. Pearson

Download references

Author information

Authors and Affiliations

  1. Department of Applied Mathematics and Computer Science, Faculty of Mathematical Sciences, University of Guilan, P.O. Box 41938-19141, Rasht, Iran

    S Yaghoubi & H Aminikhah

  2. Center of Excellence for Mathematical Modelling, Optimization and Combinational Computing (MMOCC), University of Guilan, P.O. Box 41938-19141, Rasht, Iran

    H Aminikhah

  3. Department of Mathematics, Near East University TRNC, Mersin 10, Nicosia, 99138, Turkey

    K Sadri

  4. Mathematics Research Center, Near East University TRNC, Mersin 10, Nicosia, 99138, Turkey

    K Sadri

Authors
  1. S Yaghoubi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. H Aminikhah
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. K Sadri
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to H Aminikhah.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yaghoubi, S., Aminikhah, H. & Sadri, K. A spectral shifted gegenbauer collocation method for fractional pantograph partial differential equations and its error analysis. Sādhanā 48, 213 (2023). https://doi.org/10.1007/s12046-023-02270-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12046-023-02270-5

Keywords

Search

Navigation