Introduction

Structural glass is one of the most popular building materials today. Although, soda-lime-silica has a high microscopic strength, the macroscopically observed value is much smaller \(({\sim }50\hbox { MPa})\). Soda-lime-silica fractures have been studied extensively in the past century. This might indicate that it may be possible to increase the fracture resistance significantly if we understand better why there is this discrepancy. One possible explanation that this glass is considered relatively ductile at the crack tip compared to other glasses such as pure silica (Gross and Tomozawa 2008). Linear elastic fracture mechanics (Griffith 1921) was chosen to explain the observed macroscopically brittle response.

High-speed recording of edge loaded glass plates was performed. As these plates are in general use, the topic is well-researched (Haldimann et al. 2008); however, the full fragmentation process is only described in certain older works (Acloque 1963; Kerkhof 1963). Fairly recently an inspiring paper was published by Nielsen et al. (2008) about drill initiated in-plane fractures. Our analysis is similar but focused on fractures caused by a concentrated force. This is less common in production but more frequent in everyday use after installation.

During the manufacturing process frequently the glass plates are cooled rapidly to obtain an initial stress field. The aim of this process is to introduce a homogenous compressive stress at the surface. This controlled quenching makes the microscopic flaws (Molnár et al. 2012) more difficult to open.

Both United States (ASTM C1048-12e1 2012; ASTM C1279-13 2013) and European Standards (EN 1288-3:2000 2000; EN 12150-1:2000 2000; EN 12600:2002 2003; EN 356:2000 2000) require testing of strength and fracture characteristics of tempered glass elements. Using the four point bending test described in EN 1288-3:2000 (2000) the effective tensile strength can be measured, taking both tempered stress and material strength into account. Nevertheless, these tests are inaccurate because the strength of annealed (untempered) glass varies significantly (Nielsen et al. 2008). Another so-called fragment count test can be used to measure the undisturbed tempered stress field (EN 12600:2002 2003). In this case, the advantage is that the measured fracture is caused only by the initial quenching stresses. However, it is not clear how much of the potential energy stored in the glass truly relaxes during fragmentation.

Our objective is to study the fragmentation of commercially tempered glass via digital high-speed recording. With this method, insights on crack initiation and formation throughout the plate should become apparent. The test can be used to study the progression over time from initiation to final fracture pattern. Using the scattered light polariscope by GlassStress Ltd. (Anton and Aben 2003) we were able to measure the tempered stress fields. A simple method was developed using linear elastic fracture mechanics based on the modified version of the work of Warren (2001). The relative amount of dissipated energy appears to predict the tempered stress field as a function of the fracture pattern.

The two main points of the paper are the observation of the crack pattern using a high-speed camera setup and the fracture mechanics analysis relating fragment size to tempered surface stress.

Fig. 1
figure 1

Schematic illustration of the recording process (1 OLYMPUS i-SPEED 3 camera, 2 OLYMPUS ILP-2 light source (100 W), 3 Specimen, 4 INSTRON 8872 servohydraulic test system, 5 Loading wedge, 6 Dispersion sheet, 7 Loading frame)

Full size image

The frequent change between length unit m, cm and mm is employed to help the reader to understand the physical phenomena.

Experimental setup

Our goal is to describe the crack propagation of tempered glass specimens loaded in-plane with a wedge. Thus, the load is distributed equally along the thickness of the plate. The specimens used for present study were all \(300\hbox { mm}\times \,300\hbox { mm}\) commercially toughened soda-lime-silica glass with two thicknesses of 6 and 10 mm. Fracture was initiated using a sharp \(90^{\circ }\) wedge (Fig. 1), penetrating the plate at a continuous velocity of 1 mm/s. Every specimen was attached to a loading frame on both sides and bottom. To reduce the concentration of stress and distribute the force caused by the frame, thin aluminum plates were used at the bottom and under the tightening screws along the side. Aluminum was chosen because it has the same stiffness as this glass material.

The initial stress field of the samples was measured using a scattered light polariscope (SCALP-04) at 9 different points in two perpendicular directions as suggested by Nielsen et al. (2008, 2010a).

The experiments were conducted in a climate controlled chamber at \(20\pm 2^{{\,}{\circ }}\hbox {C}\) and at \(50\pm 10\,\%\) relative humidity. Both wedge displacement and loading force were registered. The fragmentation process was recorded using OLYMPUS i-SPEED 3 digital high-speed camera. To accurately capture the high speed crack 50,000 fps frame rate was used. Due to limited data storage speed, the resolution was set to \(180\times 132\) pixels. Two different perspectives were chosen to record fractures. One focused on the loading area to investigate initial crack formation. And the other gave an overview of the whole process.

The camera was perpendicular to the glass plate. The light source was placed opposite to the camera behind the glass specimen. A dispersion sheet was used on the back of the glass plate to provide a uniform light background. A \(10\times 10\hbox { mm}\) grid was printed on the dispersion foil to calculate positions and velocities of the cracks. The camera was placed further away than in the schematics (Fig. 1). Changing the zoom from close up to a long view provided the two perspectives. Figure 1 illustrates the setup used to record the failure process.

Fracture process

The stress values measured using SCALP-04 are averaged and summarized in Table 1. It is clear that the commercial tempering processes results in different tempered stress fields as a function of plate thickness. In thinner plates the residual stress is higher.

Table 1 Normal stress components measured on the plates
Full size table
Table 2 Force values measured at the first crack and at the maximum load with the corresponding wedge displacement at the maximum loading force
Full size table

The measured loading force for the first crack and the maximum load with the corresponding corrected wedge displacement is shown in Table 2. The corrected displacement takes into account the elastic response of the wedge as a function of the applied force. In Fig. 2, a typical force-displacement curve is shown. Three stages are distinguishable: an initial elastic, a continuously fracturing and a final failure mode. In the first stage the first crack shows the end of the elastic phase. The second stage shows the maximum force and the maximum load bearing capacity. Finally, in the third a reduced force value shows the initiation of the dynamic fracture. It can be seen that after the first crack the resistance of the plate increases in a stabile manner. After reaching a maximum value it begins to diminish gradually. Reaching the final load bearing limit, a dynamic failure disintegrates the glass element.

The average force measured at the first crack was 2.304 kN for 6 mm and 1.600 kN for 10 mm thick plates. By comparing the two force values, it is clear that the first fracture appears at a much smaller force for thicker plates. This phenomena can be explained by the fact that the compressive surface stress inhibits crack opening. In 6 mm thick plates the surface compressive stress was found significantly higher than in 10 mm thick ones. This gives the thin specimens a higher initial resistance.

Fig. 2
figure 2

Typical load displacement curve, showing the first crack, the maximum force, and the ultimate resistance

Full size image

However, the average maximum loading force measured was 3.222 kN for 6 mm and 7.032 kN for 10 mm thick plates. If a unified value is calculated by dividing the maximum force by the thickness of the plate, the relative resistance of the specimen is obtained. For 6 mm thick plates this resistance value was 0.537 kN/mm, for 10 mm 0.703 kN/mm. It can be seen that the final relative load bearing capacity is higher in thicker plates. The reason for this significant difference can be found in the tempered stress field as well. In Table 1 notice that the center tensile stress of 10 mm plates is much lower than for 6 mm. Therefore, at 6 mm cases it is easier to achieve the tensile limit if the wedge penetrates the tensile core.

The fracture process can be divided into two distinguishable phases. First, the edge of the glass plate is being damaged. Microscopic fragments spray from under the wedge then the edge of the specimen chips off before the process initiates the dynamic fracture (see Fig. 3). Second, when the wedge reached the inner tensile core, the elastic energy stored in the glass begins to form the crack dynamically. It was shown by several authors (Uhlmann and Kreidl 1980; Haldimann et al. 2008; Nielsen et al. 2010b that there is a compression strain field around the surface of the glass plate which tends to inhibit the opening of cracks.

The larger displacements measured at the maximum force for thicker plates suggests that the tensile core is deeper inside the glass volume in thicker specimens, preventing the crack to propagate and allowing a higher relative resistance.

The primary goal of the experiment is to record the crack pattern formation. Figure 4 shows the propagation of the crack. The velocity of the crack front was measured in two instances. For the 6 mm case the crack propagated at 1491 m/s and for the 10 mm plate with 1437 m/s which is a little bit lower than the theoretical value of 1523 m/s calculated by Acloque (1975). The crack propagates from one initiation point and spreads radially. Then radial cracks branch tangentially.

Fig. 3
figure 3

First stage of fracture

Full size image
Fig. 4
figure 4

Crack front propagation recorded with 50,000 fps on the whole specimen

Full size image

The fracture initiated from one single crack branched exponentially into two and then into four. In Fig. 5 the initial stage of crack propagation is shown. After a few bifurcations the crack pattern begins to look like a tree or a kidney. A protected zone is being formed at the side of the crack where the fragments are larger. This kind of pattern formation differs from the one observed for drilled crack initiations where two so-called whirls-fragments were the center of the crack formation.

Fig. 5
figure 5

Initial crack formation under the loading wedge

Full size image

Figure 6 shows that the fragmentation after the first crack is almost symmetric. Summing the right and left side bifurcation angles one reaches \(149^{\circ }\) and \(155^{\circ }\). The branching angle was found between \(21^{\circ }\) and \(50^{\circ }\) which is a bit less than the value observed in previous experiments (Nielsen et al. 2008). The crack opening length between two bifurcations was found quasi constant \(({\sim }6{-}8\hbox { mm})\) indicating a uniformly increasing energy release (Broek 1982).

Fig. 6
figure 6

Angles of branching under the loading wedge

Full size image

Fragment density

Many articles focused on the relation between the tempered stress field and the fragment size of toughened glass plates (Schiavonato et al. 2005; Dubru and Nugue 2005). Barsom (1968) and later Warren (2001) developed a method based on fracture mechanics. They were trying to predict the average fragment size as a function of the toughened stress field. Their experiments showed that this size is strongly underestimated by theories. They presumed that all the stored elastic energy dissipates into crack opening which is not the case (Tandon and Glass 2005). These tests were performed on 1.8–8.2 mm thick chemically tempered glass plates used for electronic purposes. The glass specimens in their work were much thinner and the fragments were much smaller than observed in typical structural glass plates.

Figure 7 shows that the fragments of the thicker plate are significantly bigger which indicates a relation between the fragment size and the glass plate thickness. It is well known (Broek 1982) that the opening of a unit of crack length in thicker plates needs a higher energy threshold because of the bigger crack surface. Also the stress field created by the tempering process is not constant as a function of thickness as it was shown in Table 1. Thicker glass plates have smaller stresses than thinner ones. Therefore, due to the smaller elastic energy and the greater need for it, fewer cracks form and the size of the fragments remain larger.

Fig. 7
figure 7

Fracture pattern for 6 and 10 mm thick glass plates (\(10\times 10\hbox { cm}\) area)

Full size image

In Table 3 the average number of fragments are shown counted in a \(10\times 10\hbox { cm}\) area far from the wedge.

Table 3 Fragment count in 6 and 10 mm thick glass plates after failure
Full size table

This section studies the experimental fracture pattern and develops a method to calculate tempered stress field using the fragment count.

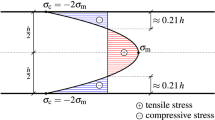
To precisely understand the governing fracture pattern, the tempered stress field had to be measured. The effects of the normal stress along the thickness (z) and all the shear stresses were found to be approximately zero \((\sigma _z \approx \tau _{xy} \approx \tau _{xz} \approx \tau _{yz} \approx 0)\). The remaining two normal stresses were considered equal. The variation of these stress components along the thickness was considered according to Eq. (1):

$$\begin{aligned} \sigma _x \left( z \right) =\sigma _y \left( z \right) =\sigma _c \left[ {\frac{1}{2}-6\left( {\frac{z}{h}} \right) ^{2}} \right] , \end{aligned}$$
(1)

where \(\sigma _c \) is the surface compression stress, h is the thickness of the plate and z is the axis perpendicular to the glass plate. Note, that the compression on the surface is twice as large as the tension in the center. To have a better understanding of the governing stress field as a function of thickness, the compression stress results of Nielsen et al. (2010a) were plotted next to this work in Fig. 8. We were able to obtain a regression on \(\sigma _c \left( h \right) \) using a hyperbolic function.

Fig. 8
figure 8

Surface compression stress with a hyperbolic fit (circles this work, crosses Nielsen et al. 2010a, b)

Full size image

Warren (2001) assumed that only tensile stress is dissipated during the fragmentation. We concluded based on our experiments and the work of Nielsen et al. (2008) that not only the inner core breaks, but the whole glass plate throughout its thickness as well. At first the core cracks creating a sharp defect in the volume. This leads to partially compressed and extended zones. This stress rearrangement causes further crack propagation until the stress decreases to the point where there is not enough energy to propagate further. The process is illustrated in Fig. 9.

Fig. 9
figure 9

Crack opening created by fracture caused by the tempered stress field

Full size image
Fig. 10
figure 10

Schematic illustration of length density as a function of cell density using Voronoi tessellation (\(\delta a=D+2\sqrt{E+\rho _{FR}}\), where \(\hbox {D} = -17.37\hbox { m}/\hbox {m}^{2}\) and \(\hbox {E} = 0.18 1/\hbox {m}^{2}\))

Full size image

Presume that the crack opens along the whole thickness. The potential energy stored in a unit volume can be calculated by:

$$\begin{aligned} \delta \Pi _b =\frac{1}{2}{{\varvec{\upsigma }} {\varvec{\upvarepsilon }} }\mathrm{d}x\mathrm{d}y\mathrm{d}z=\frac{1}{2}\left( {\sigma _x \varepsilon _x +\sigma _y \varepsilon _y } \right) \mathrm{d}x\mathrm{d}y\mathrm{d}z, \end{aligned}$$
(2)

where \(\varepsilon _{x}\) and \(\varepsilon _{y}\) are normal strains. Assuming that \(\sigma _x =\sigma _y \), and based on linear elasticity the deformation components are calculated from stresses as:

$$\begin{aligned} \varepsilon _x =\varepsilon _y =\sigma _x \frac{1-\nu }{E}=\sigma _y \frac{1-\nu }{E}, \end{aligned}$$
(3)

where E is Young’s modulus and \(\nu \) is Poisson’s ratio. Substituting Eqs. (2) to (3) the expression for the potential energy density can be expressed as the function of the normal stress as:

$$\begin{aligned} \delta \Pi _b= & {} \frac{1}{2}\frac{1-\nu }{E}\left( {\sigma _x^2 +\sigma _y^2 } \right) \mathrm{d}x\mathrm{d}y\mathrm{d}z\nonumber \\= & {} \frac{1-\nu }{E}\sigma _x^2 \mathrm{d}x\mathrm{d}y\mathrm{d}z. \end{aligned}$$
(4)

Substituting (1) in Eq. (4) and integrating along the thickness we get,

$$\begin{aligned} \delta \Pi _b^A =\int \limits _{-h/2}^{h/2} {\frac{1-\nu }{E}\sigma _{xx}^2 \mathrm{d}z\mathrm{d}y\mathrm{d}x} =\frac{1-\nu }{5E}\sigma _c^2 h\hbox { }\mathrm{d}y\mathrm{d}x,\nonumber \\ \end{aligned}$$
(5)

as the potential energy for a unit surface of the glass plate. A in the upper index means that the potential energy is normalized by area. In this manner, we obtain a so-called potential energy density which has the dimension of \(\hbox {J}/\hbox {m}^{2}\).

To calculate the crack length based on the fragment size density, one has to know the approximate geometry of the random pattern. To calculate crack length based on fragment density: a simple numerical experiment was conducted. Using a random 2D Voronoi tessellation, samples were generated for various cell densities. An average crack length distribution was calculated as a function of the cell density.

In Fig. 10a a schematic illustration is shown how the crack length was calculated. During the extraction of a, the boundaries were subtracted from the calculated length. Therefore, if only one fragment was found, no crack was calculated. After summing up the red lines, the results were divided by the size of the calculated area. Hence a length density \((\delta a)\) was defined. This quantity is shown as a function of the cell density in Fig. 10b.

Knowing the average crack length, the energy dissipated during the failure can be calculated for a unit area:

$$\begin{aligned} \delta S^{A}=2\gamma _0 \delta ah, \end{aligned}$$
(6)

where \(\gamma _{0}\) is the energy needed to cause the crack to propagate (the so-called surface energy density), \(\delta a\) is the crack length density on a unit area, and h is the thickness of the glass plate. The multiplication by 2, stands for the two sides of the crack. Determining \(\gamma _{0}\) is complicated, based on the literature its value is estimated between 0.305 and \(11\hbox { J}/\hbox {m}^{2}\) (Wiederhorn 1969). To determine the exact value is not the aim of this article, only tendencies of fragment size will be identified as a function of the tempered stress field.

Dividing the dissipated by the stored potential energy, the ratio between the two can be calculated:

$$\begin{aligned} \vartheta= & {} \frac{\delta S^{A}}{\delta \Pi _b^A }=\frac{10\gamma _0 \delta ahE}{\left( {1-\nu } \right) \sigma _c^2 h}=\frac{10\gamma _0 E}{\left( {1-\nu } \right) }\frac{\delta a}{\sigma _c^2 }=\vartheta _{mat} \frac{\delta a}{\sigma _c^2 }\nonumber \\= & {} \vartheta _{mat} \kappa , \end{aligned}$$
(7)

where the equation was normalized by subtracting the material constants (E, \(\gamma _{0}\), \(\nu \)) which are the same in all cases. The two measured quantities give a good sense how much of the stored energy is being dissipated.

Figure 11 shows \(\kappa ={\delta a}/{\sigma _c^2 }\) energy dissipation coefficient as a function of plate thickness, where \(\delta a\) and \(\sigma _{c}\) are experimentally determined parameters. The fracture density data for 6 and 10 mm glass plates were calculated by the present authors. However, results for 19 mm thick glass were taken from the work of Nielsen et al. (2010a).

Fig. 11
figure 11

Energy dissipation ratio \((\kappa )\) as a function of glass plate thickness

Full size image

It was seen that the energy dissipated during crack formation increases with thickness. Linear correlation was found between \(\kappa \) and the thickness h. Based on the equation \(\kappa ={\delta a}/{\sigma _c^2 }\) some industrial advice can be given for \(\sigma _{c}\) as a function of the counted glass fragments \((\rho _{RF})\) considering that \(\kappa \) is constant for each thickness that has practical applications. In Fig. 12 the calculation is shown. Undoubtedly, the test described in EN 12150-1:2000 (2000) can be used not only for security purposes but to approximate tempered stress field as well.

Fig. 12
figure 12

Surface compression stress as a function of the fragment count for different glass thickness

Full size image

Conclusion

The fracture of thermally toughened structural glass plates was investigated. Cracks were initiated by a concentrated force on the edge. The load was applied at a constant displacement rate by a sharp wedge. Both force and displacement was registered and the progress of the crack pattern was recorded with a high-speed camera. A novel theoretical method based on fracture mechanics was developed and verified with experimental results.

A clear correlation was found between the glass plate’s relative resistance and thickness. The first crack appeared at a lower force value in thicker glass plates because the compressive surface stress is lower. However, finally they were found to be stronger because the tempered center tensile stress is lower as well.

Fragmentation was recorded with a digital high-speed camera using 50,000 fps frame rate. A radial macroscopic crack growth was found with a quasi-constant velocity \(({\sim }1450\hbox { m}/\hbox {s})\). When focusing on the crack initiation, a symmetric bifurcation was observed with the angle of \(21^{\circ }\hbox {--}50^{\circ }\). These results would indicate a uniformly increasing energy release (Broek 1982). A protected zone formed at the entry point of the wedge, where larger fragments were found. Therefore, the crack formation is not only based on an energy principle but it is affected highly by geometry as well.

The second phase of the analysis evaluated the crack pattern far from the wedge. This pattern, formed by the quasi undisturbed tempered stress field, was measured. Using linear elastic fracture mechanics, we developed a method that established the relation between tempered stresses and fragment density. The energy release rate was linear as a function of plate thickness. Improvements were presented to the standard EN 12150-1:2000 (2000) in order to be used not only for security purposes but for tempered stress field measurement as well. A promising aspect of our work may help to reduce overhead costs for companies by eliminating the use of some expensive machines to measure stress in structural tempered glass elements.

Future work will entail verifying our method via a series of experiments to test glass plates tempered differently from the standard practices used in industry. We need to discover if the energy release rate is truly independent from the tempered stress field and only varies with the thickness.