Floer Homology: From Generalized Morse–Smale Dynamical Systems to Forman’s Combinatorial Vector Fields

Abstract

We construct a Floer type boundary operator for generalised Morse–Smale dynamical systems on compact smooth manifolds by counting the number of suitable flow lines between closed (both homoclinic and periodic) orbits and isolated critical points. The same principle works for the discrete situation of general combinatorial vector fields, defined by Forman, on CW complexes. We can thus recover the $\mathbb {Z}_2$ homology of both smooth and discrete structures directly from the flow lines (V-paths) of our vector field.

1 Introduction

One of the key ideas of modern geometry is to extract topological information about an object from a dynamical process operating on that object. For that purpose, one needs to identify the invariant sets and the dynamical relations between them. The invariant sets generate groups, and the dynamics defines boundary operators, and when one has shown that these operators square to zero, one can then define homology groups. The first such ideas may be seen in the works of Riemann, Cayley and Maxwell in the 19th century. In 1925, Morse [23] developed his famous theory where he recovered the homology of a compact Riemannian manifold M from the critical points of a smooth function f, assuming that these critical points are all non-degenerate. The dynamics in question is that of the gradient flow of f. The basic invariant sets then are precisely the critical points of f. The theory was analysed and extended by Milnor, Thom, Smale, Bott and others. In particular, Bott [4] extended the theory to the case where the gradient of f is allowed to vanish on a collection of smooth submanifolds of M.

Based on ideas from supersymmetry, Witten constructed an interpolation between de Rham and Morse homology. Floer [11] then developed the very beautiful idea that the boundary operator in Morse theory can be simply obtained from counting gradient flow lines (with appropriate orientations) between critical points of index difference one. The first systematic exposition of Floer’s ideas was given in [24] (see also [20]). The main thrust of Floer’s work was devoted to infinite dimensional problems around the Arnold conjecture, see [7,8,9,10], because for his theory, he only needed relative indices and not absolute ones, so that the theory could be applied to indefinite action functionals. But also in the original finite dimensional case, Floer’s theory advanced our insight considerably and motivated much subsequent work.

In fact, Floer [11] had been motivated by another beautiful theory relating dynamics and topology, that of Conley [6] (for more details, see [5] and for instance the presentations in [19, 28]). Conley’s theory applies to arbitrary dynamical systems, not just gradient flows. Actually, Smale [26] had already extended Morse theory to an important and general class of dynamical systems on compact Riemannian manifolds, those that besides isolated critical points are also allowed to have non-degenerate closed orbits. Similar to Morse functions, the class of Morse–Smale dynamical systems is structurally stable, that is, preserves its qualitative properties under small perturbations. It turns out, however, that these systems can also be subsumed under Morse–Bott theory. In fact, in [27] Smale proved that for every gradient-like system, there exists an energy function that is decreasing along the trajectories of the flow and Meyer [22] generalized this result to the Morse–Smale dynamical systems and defined a Morse–Bott type energy function based on the flows. Such an energy function would then be constant on the periodic orbits, and they can then be treated as critical submanifolds via Morse–Bott theory. Banyaga and Hurtubise [1, 2, 18] then constructed a general boundary operator for Morse–Bott systems that put much of the preceding into perspective (see also the detailed literature review in [18]).

There is still another important extension of Morse theory, the combinatorial Morse theory of Forman [14] on simplicial and cell complexes. Here, a function assigns a value to every simplex or cell, and certain inequalities between the values on a simplex and on its facets are required that can be seen as analogues of the non-degeneracy conditions of Morse theory in the smooth setting. As shown in [3], this theory recovers classical Morse theory by considering PL triangulations of manifolds that admit Morse functions. This theory has found various practical applications in diverse fields, such as computer graphics, networks and sensor networks analysis, homology computation, astrophysics, neuroscience, denoising, mesh compression, and topological data analysis. (For more details on smooth and discrete Morse theory and their applications see [21, 25]). In [13], Forman also extended his theory to combinatorial vector fields.

In the first chapter of this part, we extend Floer’s theory into the direction of Conley’s theory. More precisely, we shall show that one can define a boundary operator by counting suitable flow lines not only for Morse functions, but also for Morse–Smale dynamical systems and in fact, we more generally also allow for certain types of homoclinic orbits in the dynamical system. Perhaps apart from this latter small extension, our results in the smooth setting readily follow from the existing literature. One may invoke [22] to treat it as a Morse–Bott function with the methods of [18]. Alternatively, one may locally perturb the periodic orbits into heteroclinic ones between two fixed points by a result of Franks [17] and then use [27] to treat it like a Morse function. In some sense, we are also using such a perturbation. Our observation then is that the collection of gradient flow lines between the resulting critical points has a special structure which in the end will allow us to directly read off the boundary operator from the closed (or homoclinic) orbits and the critical points. It remains to develop Conley theory in more generality from this perspective. Moreover, our approach also readily extends to the combinatorial situation of [13, 14]. Again, it is known how to construct a Floer type boundary operator for a combinatorial Morse function, and an analogue of Witten’s approach had already been developed in [15]. Our construction here, however, is different from that of that paper. In fact, [15] requires stronger assumptions on the function than the Morse condition, whereas our construction needs no further assumptions. What we want to advocate foremost, however, is that the beauty of Floer’s idea of counting flow lines to define a boundary operator extends also to dynamical systems with periodic orbits, in both the smooth and the combinatorial setting, and that a unifying perspective can be developed.

We should point out that in this part and for both of the next chapters, we only treat homology with $\mathbb {Z}_2$ coefficients. Thus, we avoid having to treat the issue of orientations of flow lines. This is, however, a well established part of the theory, see [12] or also the presentations in [20, 24]. The structure of this paper is as follows:

In Sect. 2, after reviewing basic notions, we introduce the generalized Morse–Smale systems and we define a boundary operator based on these systems by which we can compute the homology groups. In Sect. 3, we turn to the discrete settings and present such a boundary operator for general combinatorial vector fields by which we can compute the homology of finite simplicial complexes. Both sections finish with some concrete examples of computing homology groups based on our Floer type boundary operators.

2 Generalized Smooth Morse–Smale Vector Fields

2.1 Preliminaries

We consider a smooth m dimensional manifold M that is closed, oriented and equipped with a Riemannian metric whose distance function we denote by d. Let X be a smooth vector field on M and $\phi _t : M\longrightarrow M$ be the flow associated with X. We first recall some basic terminology. For $p\in M$, $\gamma (p) = \cup _{t} \phi _t(p)$ will denote the trajectory of X through p. Then, for each $p \in M$ we define the limit sets of $\gamma (p)$ as

$$\begin{aligned} \alpha (p):= & {} \cap _ {s \le 0} \overline{ \cup _ {t \le s} \phi _t(p)},\\ \omega (p):= & {} \cap _ {s \ge 0} \overline{ \cup _ {t \ge s} \phi _t(p)}. \end{aligned}$$

Definition 2.1

If $f: M\rightarrow M$ is a diffeomorphism, then $x \in M$ is called chain recurrent if for any $\varepsilon > 0$, there exist points $x_1 = x, x_2,\ldots ,x_n= x$ (n depends on $\varepsilon$) such that $d(f (x_i), x_{i+1}) < \varepsilon$ for $1 \le i \le n$. For a flow $\phi _t$, $x \in M$ is chain recurrent if for any $\varepsilon > 0$, there exist points $x_1 = x, x_2,\ldots ,x_n= x$ and real numbers $t(i)\ge 1$ such that $d( \phi _{t(i)}(x_i), x_{i+1}) < \varepsilon$ for $1 \le i \le n$. The set of chain recurrent points is called the chain recurrent set and will be denoted by R(X).

The chain recurrent set R(X) is a closed submanifold of M that is invariant under $\phi _t$. We can think of R(X) as the points which come within $\varepsilon$ of being periodic for every $\epsilon > 0$. A Morse–Smale dynamical system, as introduced by Smale [26], has the fundamental property that it does not have any complicated recurrent behaviour and the $\alpha$ and $\omega$ limit sets of every trajectory can only be isolated critical points p or periodic orbits O. Morse–Smale dynamical systems are the simplest structurally stable types of dynamics; that is, if X is Morse–Smale and $X'$ is a sufficiently small $C^1$ perturbation of X then there is a homeomorphism $h: M\rightarrow M$ carrying orbits of X to orbits of $X'$ and preserving their orientation. (Such a homeomorphism is called a topological conjugacy and we say that the two vector fields or their corresponding flows are topologically conjugate.) Here, we shall consider a somewhat more general case where we allow for a certain type of homoclinic rest points and their homoclinic orbits.

Definition 2.2

A periodic orbit of the flow $\phi _t$ on M is hyperbolic if the tangent bundle of M restricted to O, $TM_O$, is the sum of three derivative $D\phi _t$ invariant bundles $E^c\oplus E^u \oplus E^s$ such that:

• 1. $E^c$ is spanned by the vector field X, tangent to the flow.

• 2. There are constants $C, \lambda >0$, such that $\Vert D\phi _t(v) \Vert$ $\ge$ $Ce^{\lambda t} \Vert v \Vert$ for $v\in E^u$, $t \ge 0$ and $\Vert D\phi _t(v) \Vert$ $\le$ $C^{-1}e^{-\lambda t} \Vert v \Vert$ for $v \in E^s, t \ge 0$, where $\Vert . \Vert$ is some Riemannian metric.

A rest (also called critical) point p for a flow $\phi _t$ is called hyperbolic provided that $T_pM= E^u \oplus E^s$, and the above conditions are valid for $v \in E^u$ or $E^s$.

The stable and unstable manifolds of a hyperbolic periodic orbit O are defined by:

$W^{s}(O)= \lbrace x\in M \mid d(\phi _tx, \phi _ty) \rightarrow 0 \text { as } t\rightarrow \infty$ for some $y\in O \rbrace$ and $W^{u}(O)= \lbrace x\in M \mid d(\phi _tx, \phi _ty) \rightarrow 0 \text { as } t\rightarrow -\infty$ for some $y\in O \rbrace$. And for a rest point and a homoclinic orbit, we define the stable and unstable manifolds analogously. Also the index of a rest point or a closed orbit is defined to be the dimension of $E^u$. We denote an arbitrary point in a homoclinic orbit H by $H_k^0$, where k is the index of the homoclinic orbit H and the homoclinic orbit itself is denoted by $H_k^1$ as it is homeomorphic to a circle and therefore is one-dimensional. Similarly by $O_k^0$, we mean an arbitrary point in a periodic orbit O of index k and by $O_k^1$ we mean the orbit itself as a one dimensional structure, homeomorphic to a circle. In the following definition, we extend the definition of Morse–Smale vector fields.

Definition 2.3

We call a smooth flow $\phi _t$ on M generalised Morse–Smale if :

• 1. The chain recurrent set of the flow consists of a finite number of hyperbolic rest points $\beta _1(p)$,...$\beta _k(p)$ and/or hyperbolic periodic orbits $\beta _{k+1}(O)$,...$\beta _n(O)$.

• 2. R(X) furthermore may have a finite number of homoclinic orbits $\beta _{n+1} (H)$,...$\beta _l (H)$ that can be obtained via local bifurcation from hyperbolic periodic orbits $\beta _{n+1}(O),\ldots , \beta _l (O)$.

• 3. For each $\beta _i (p), 1 \le i \le k$ and each $\beta _i (O), k+1 \le i \le l$ the stable and unstable manifolds $W^{s} ({\beta _i })$ and $W^{u} ({\beta _i})$ associated with $\beta _i$ intersect transversally.

  (Here, two such submanifolds intersect transversally if for every $x \in W^{u}({\beta _i}) \cap W^{s} ({\beta _j})$ we have: $T_x (M) = T_x W^{u} ({\beta _i}) \bigoplus T_ x W^{s} ({\beta _j})$.)

Note that the only difference between generalised Morse–Smale flows as defined here and standard Morse–Smale flows is the possible existence of homoclinic points and orbits. In the standard case, one simply excludes the second condition.

Therefore, a generalised Morse–Smale flow can be perturbed to a corresponding Morse–Smale flow, where all of the homoclinic orbits $\beta _i (H), n+1 \le i \le l$, are substituted by periodic orbits $\beta _i (O)$. For any two distinct $\beta _i$ and $\beta _j$ in the above definition, we consider $W(\beta _i, \beta _ j )= W^{u} (\beta _ i)\cap W^{s} (\beta _ j)$. Then, based on the transversality condition, this intersection is either empty (if there is no flow line from $\beta _i$ to $\beta _j$) or a submanifod of dimension $\lambda _{\beta _i} - \lambda _{\beta _j} + \dim \beta _i$, where the index of $\beta _k$ is denoted by $\lambda _{\beta _k}$ [1]. In the second case, the flow $\phi _t$ induces an ${\mathbb {R}}$-action on $W(\beta _i, \beta _j)= W^{u} (\beta _i)\cap W^{s} (\beta _j)$. Let

$$\begin{aligned} M(\beta _i, \beta _j)= (W(\beta _i, \beta _j))/ {\mathbb {R}}) \end{aligned}$$

be the quotient space by this action of the flow lines from $\beta _i$ to $\beta _j$.

Remark 2.4

In the definition of standard Morse–Smale flow, the condition (1) above could be replaced by $(1')$:

All periodic orbits and rest points of the flow are hyperbolic, and there exists a Morse–Bott type energy function (as defined by Meyer [22]).

2.2 The Chain Complex for Generalized Morse–Smale Vector Fields

Suppose X is a generalized Morse–Smale vector field over M. To motivate our construction, we first observe that by a slight extension of a result of Franks [17], we can replace every periodic or homoclinic orbit by two non-degenerate critical points, without changing the flow outside some small neighbourhood of that orbit.

Lemma 2.5

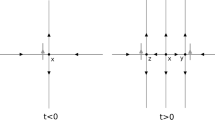
Suppose $\phi _t$ is a generalized Morse–Smale flow on an orientable manifold with a periodic or homoclinic orbit of index k. Then, for any neighbourhood U of that orbit, there exists a new generalized Morse–Smale flow $\phi '_t$ whose vector field agrees with that of $\phi _t$ outside U and which has rest points t and $t'$ of index $k+1$ and k in U, but no other chain recurrent points in U.

Proof

In [17], Franks proved that for a Morse–Smale flow $\phi _t$ on an orientable manifold with a closed periodic orbit O of index k and a given neighbourhood U of O, there exists a new Morse–Smale flow $\phi '_t$ whose vector field agrees with that of $\phi _t$ outside U and which has rest points $q_1$ and $q_2$ of index k and $k+1$ in U, but no other chain recurrent points in U.

For the generalized Morse–Smale flow, we note that each homoclinic orbit is by definition obtained in a continuous local bifurcation of a periodic orbit. Therefore, if we use this bifurcation in the reverse direction and substitute again any such homoclinic orbit with its corresponding periodic orbit we can use Franks’ argument for replacing all the periodic and homoclinic orbits with two rest points and two heteroclinic orbits between them. $\square$

Remark 2.6

In the above figure, the qualitative features of the three cases outside the grey annulus are the same. In particular, we can bifurcate two heteroclinic orbits between two critical points (in the right) to get a homoclinic orbit and a homoclinic critical point (in the middle) by bringing the two critical points closer and closer and then bifurcate the homoclinic orbit to a periodic orbit (in the left).

With this lemma, we can turn our flow into one that has only non-degenerate critical points. We could then simply utilize the Floer boundary operator for that flow. In fact, that motivates our construction, but we wish to define a Floer type boundary operator directly in terms of the periodic and homoclinic orbits and the critical points. Our simple observation is that a Floer boundary operator resulting from the replacement that Franks proposed has some additional structure that is derived from the orbits that have been perturbed away. This allows for an arrangement of the flow lines between the critical points of the perturbed flow that leads to the definition of the boundary operator in the presence of those orbits. That is, we can read off the boundary operator directly from the relations between the orbits and the critical points without appealing to that perturbation, although the perturbation helps us to see why this boundary operator squares to 0.

We define the Morse–Floer complex $(C_*(X), \partial )$ of X as follows. Let $C_k$ denote the finite vector space (with coefficients in $\mathbb {Z}_2$) generated by the following set of rest points/orbits of the vector field:

$$\begin{aligned} \left( p_k, O^0_ {k}, O^1_ {k-1}, H_ {k}^0, H_ {k-1}^1 \right) . \end{aligned}$$

The differential $\partial _k : C_k(X) \longrightarrow C_{k-1}(X)$ counts the number of connected components of $M(\beta _i, \beta _ j )$ (mod 2), where $\beta _i$ and $\beta _j$ are isolated rest points $p_k$ or closed orbits (either homoclinic orbits H or periodic orbits O). Here, each such orbit, carrying topology in two adjacent dimensions, corresponds to two elements in the boundary calculus. More precisely, a periodic orbit $O_{k}$ of index k generates an element $O_k^1$ in dimension $k+1$ and an element $O_{k}^0$ in dimension k, and analogously for the homoclinics. Thus, our boundary operator is:

$$\begin{aligned} \partial p_k= & {} \sum \alpha (p_k, p_{k-1}) p_{k-1} + \sum \alpha (p_k, O_{k-2}) O^1_{k-2}\\ {}{} & {} \quad +\, \sum \alpha (p_k, H_ {k-2}) H_ {k-2}^1, \\ \partial O^0_{k}= & {} \sum \alpha ( O_{k}, O_{k-1}) O^0_{k-1}+ \sum \alpha ( O_{k}, H_ {k-1}) H_ {k-1}^0 \\ {}{} & {} \quad +\, \sum \alpha ( O_{k}, p_{k-1}) p_{k-1}, \\ \partial O^1_{k-1}= & {} \sum \alpha ( O_{k-1}, O_{k-2}) O^1_{k-2} + \sum \alpha ( O_{k-1}, H_ {k-2}) H_ {k-2}^1, \\ \partial H_ {k}^0= & {} \sum \alpha ( H_ {k}, H_ {k-1}) H_ {k-1}^0+ \sum \alpha ( H_ {k}, O_ {k-1}) O_ {k-1}^0 \\ {}{} & {} \quad +\, \sum \alpha ( H_ {k}, p_{k-1}) p_{k-1}, \\ \partial H_ {k-1}^1= & {} \sum \alpha ( H_ {k-1}, H_ {k-2}) H_ {k-2}^1+ \sum \alpha ( H_ {k-1}, O_{k-2}) O^1_{k-2}. \end{aligned}$$

In this definition, the sums extend over all the elements on the right hand side; for instance, the first sum in the first line is over all critical points $p_{k-1}$ of index $k-1$. $\alpha (p_k, p_{k-1})$, similar to the classical Morse–Floer theory (where there is no closed orbit and therefore, the vector field is up to topological conjugacy, gradient-like), is the number of flow lines from $p_k$ to $p_{k-1}$. We observe some terms do not appear; for instance, we do not have terms with coefficients of the form $\alpha (p_k, O_{k-1})$, nor of the form $\alpha (p_k, H_{k-1})$. This will be important below in the proof of Theorem 2.8. The reason why such a term does not show up is that if there were a flow line from some $p_k$ to some $O_{k-1}^0$, then there would also be a flow to the corresponding $O_{k-1}^1$ which comes from the same closed orbit. But $O_{k-1}^1$ and $p_k$ are the elements of the same $C_k$, and by the Morse–Smale condition, there are no flow lines between critical elements of the same $C_k$. Analogously for homoclinics.

Remark 2.7

Note that in defining the chain complex and the corresponding boundary operator $\partial$ for X, we could first replace all the homoclinic orbits with bifurcated periodic orbits and present our definitions for the simpler case where all the closed orbits are periodic. Then, we would have just three generators

$$\begin{aligned} \left( p_k, O^0_ {k}, O^1_ {k-1} \right) \end{aligned}$$

for $C_k(X)$. However, here we choose not to do this to emphasize that we can construct the boundary operator also for homoclinic orbits as long as our operator is defined based on the flow lines outside the tubular neighbourhoods of orbits.

Theorem 2.8

$\partial ^ 2 = 0$.

In classical Morse–Floer theory, one assumes that there are only isolated critical points and no closed or homoclinic orbits, and therefore, all the $\alpha$ coefficients in the definition of $\partial$ except the first one (in the first row) are zero; there to prove $\partial ^ 2 = 0$ one can then use the classification theorem of one-dimensional compact manifolds, where the number of connected components of their boundary mod two is zero (see [20]). Here, as $W(\beta _i, \beta _ {i-1} )$ might have dimension bigger than one, the number of connected components of the boundary of compact two-dimensional manifolds might vary. For our generalized Morse–Smale flows, however, we use Lemma 2.5 to replace any orbit of index k (both periodic $O_ {k}$ and homoclinic $H_ {k}$) by a rest point of index k and one of $k+1$ which are joined by two heteroclinic orbits. When replacing $H_ {k}$, the resulting rest point of higher index can be taken to be the point h itself, which then will be no longer homoclinic.

Proof

By the above replacement, we get a vector field Y which has no periodic and homoclinic orbits and is therefore gradient-like (up to topological conjugacy [16]). This Y has all the isolated rest points of X, two isolated rest points $q^{\textrm{up}}_k$ and $q'^{\textrm{down}}_{k-1}$ instead of every periodic orbit $O_{k-1}$ of index $k-1$ and two isolated rest points $t^{\textrm{up}}_k$ and $t'^{\textrm{down}}_{k-1}$ instead of every homoclinic orbit $H_ {k-1}$ of index $k-1$. We note that all the critical points in Y are isolated and for each index k, they can be partitioned into five different sets $p_k, t^{\textrm{up}}_k, t'^{\textrm{down}}_k , q^{\textrm{up}}_k, q'^{\textrm{down}}_k$. This partitioning is possible because orbits and isolated rest points have pairwise empty intersection. The proof will now consist of the following main steps:

• 1. We define $C_k(Y)$ to be the finite vector space (with coefficients in $\mathbb {Z}_2$) generated by

  $$\begin{aligned} \left( p_k, q^{\textrm{up}}_k, q'^{\textrm{down}}_{k} , t^{\textrm{up}}_k, t'^{\textrm{down}}_{k} \right) . \end{aligned}$$

• 2. We define a boundary operator $\partial '$ and consequently a chain complex corresponding to $(Y,C_*(Y), \partial ')$.

• 3. And then we prove there is an isomorphism (chain map) $\varphi _* : C_*(X) \longrightarrow C_*(Y)$. Since $\varphi$ is an isomorphism, we get our desired equality $\partial ^ 2 = 0$ as $\partial = \varphi _* ^{-1} \partial ' \varphi _*$ and $\partial ^ 2=\varphi _* ^ {-1} { \partial '}^2\varphi _*$

  • 1) We note that in $C_k(Y)$, $q^{\textrm{up}}_k$ comes from a periodic orbit of index $k-1$ and $q'^{\textrm{down}}_{k}$ comes from the replacement of a periodic orbit of index k. Similarly, $t^{\textrm{up}}_k$ is obtained from replacing a homoclinic orbit of index $k-1$ and $t'^{\textrm{down}}_{k}$ comes from a homoclinic orbit of index k.

  • 2) We define $\partial '_k : C_k(Y) \longrightarrow C_{k-1} (Y)$ as follows:

    $$\begin{aligned} \partial ' p_k= & {} \sum \alpha (p_k, p_{k-1}) p_{k-1} + \sum \alpha (p_k, q^{\textrm{up}}_{k-1}) q^{\textrm{up}}_{k-1} \\ {}{} & {} \quad +\, \sum \alpha (p_k, t^{\textrm{up}}_{k-1}) t^{\textrm{up}}_{k-1},\\ \partial ' q'^{\textrm{down}} _{k}= & {} \sum \alpha (q'^{\textrm{down}} _{k}, q'^{\textrm{down}} _{k-1}) q'^{\textrm{down}} _{k-1} \\ {}{} & {} \quad +\, \sum \alpha (q'^{\textrm{down}} _{k}, t'^{\textrm{down}} _{k-1}) t'^{\textrm{down}} _{k-1} \\{} & {} \quad +\, \sum \alpha (q'^{\textrm{down}} _{k}, p_{k-1}) p_{k-1}, \\ \partial 'q^{\textrm{up}} _{k}= & {} \sum \alpha (q^{\textrm{up}} _{k}, q^{\textrm{up}} _{k-1}) q^{\textrm{up}} _{k-1} \\ {}{} & {} \quad +\, \sum \alpha (q^{\textrm{up}} _{k}, t^{\textrm{up}} _{k-1}) t^{\textrm{up}} _{k-1}, \\ \partial ' t'^{\textrm{down}} _{k}= & {} \sum \alpha (t'^{\textrm{down}} _{k}, t'^{\textrm{down}} _{k-1}) t'^{\textrm{down}} _{k-1} \\ {}{} & {} \quad +\,\sum \alpha (t'^{\textrm{down}} _{k}, q'^{\textrm{down}} _{k-1}) q'^{\textrm{down}} _{k-1} \\ {}{} & {} \quad +\, \sum \alpha (t'^{\textrm{down}} _{k}, p_{k-1}) p_{k-1}, \\ \partial 't^{\textrm{up}} _{k}= & {} \sum \alpha (t^{\textrm{up}} _{k}, t^{\textrm{up}} _{k-1}) t^{\textrm{up}} _{k-1} \\{} & {} \quad +\, \sum \alpha (t^{\textrm{up}} _{k}, q^{\textrm{up}} _{k-1}) q^{\textrm{up}} _{k-1}. \end{aligned}$$

  These sums extend over all the elements on the right hand side, and $\alpha$ is the number of gradient flow lines (mode 2) between the corresponding critical points. We want to prove ${\partial '}^ 2 = 0$ over $C_k(Y)$ by equating $\partial '$ with the boundary operator $\partial ^M$ of Floer theory which is of the form $\partial ^M (s_k) = \sum \alpha (s_k, s_{k-1}) s_{k-1}$ for a gradient vector field and counts the number of gradient flow lines $\alpha$ (mod 2) between two rest points with relative index difference one, without any partitioning on the set of isolated rest points $s_k$ of index k. In our case, we have such a partitioning and therefore more refined relationships in the definition of $\partial '$. And then, for all the generators of $C_*(Y)$, $\partial ' = \partial ^M$; we show this equality for $p_k,q^{\textrm{up}} _{k}, t'^{\textrm{down}} _{k}$ as for the other cases it can be similarly proved. If we consider such a partitioning on the set of rest points of our vector field, we have:

  $$\begin{aligned} \partial ^M (p_k)= & {} \sum \alpha (p_k, p_{k-1}) p_{k-1} + \sum \alpha (p_k, q^{\textrm{up}}_{k-1}) q^{\textrm{up}}_{k-1} \\ {}{} & {} \quad +\, \sum \alpha (p_k, q'^{\textrm{down}}_{k-1}) q'^{\textrm{down}}_{k-1} + \sum \alpha (p_k, t^{\textrm{up}}_{k-1}) . t^{\textrm{up}}_{k-1} \\ {}{} & {} \quad +\, \sum \alpha (p_k, t'^{\textrm{down}}_{k-1}) t'^{\textrm{down}}. \end{aligned}$$

  Comparing this formula with that of $\partial ' p_k$, we see that we have two extra terms in the latter; as we have explained after the definition of $\partial$, the 3th and the 5th term are not present in the former case. To have $\partial ^M(q^{\textrm{up}} _{k}) = \partial '(q^{\textrm{up}} _{k})$, the three coefficients

  $$\begin{aligned} \alpha (q^{\textrm{up}} _{k}, q'^{\textrm{down}} _{k-1}), \alpha (q^{\textrm{up}} _{k}, t'^{\textrm{down}} _{k-1}), \alpha (q^{\textrm{up}} _{k}, p_{k-1}) \end{aligned}$$

  need to be zero. The first one is zero since there are exactly two gradient flow lines (heteroclinic orbits) from $q^{\textrm{up}} _{k}$ to $q'^{\textrm{down}} _{k-1}$ which correspond to replacement of an orbit $O_{k-1}$. We note that for the other $q'^{\textrm{down}} _{k-1}$ coming from other orbits $\alpha$ is zero by definition of $\partial$ over $C_k(X)$ as otherwise in X we would have flow lines between two orbits of the same index which is not possible by the Morse–Smale condition. For the same reason, the second element is also zero since there is no flow line from $q^{\textrm{up}}_k$ to $t'^{\textrm{down}} _{k-1}$. Also the last $\alpha$ is zero as otherwise there would be flow lines from a periodic orbit of index $k-1$ to an isolated rest point with index $k-1$ in X, again violating Morse–Smale. Finally, $\partial ^M(t'^{\textrm{down}} _{k}) = \partial '(t'^{\textrm{down}} _{k})$ if we show that $\alpha (t'^{\textrm{down}} _{k}, t^{\textrm{up}} _{k-1})$ and $\alpha (t'^{\textrm{down}}, q^{\textrm{up}} _{k-1})$ are zero. If not, there would be two orbits in X with index difference two which are the boundaries of a cylinder, which is not possible. Therefore, over $C_*(Y)$, $\partial ^M= \partial '$ and hence $\partial '^ 2 = 0$ by classical Morse–Floer theory. 3) We now define $\varphi _* : C_*(X) \longrightarrow C_*(Y)$. For $0\le k \le m$, we put

  $$\begin{aligned} \varphi _*( p_k)= p_k,\quad \varphi _* (O^0_ {k}) = q'^{\textrm{down}}_k ,\quad \varphi _*( O^1_ {k-1})= q^{\textrm{up}}_k , \\ \quad \varphi _*( H_ {k}^0)= t'^{\textrm{down}}_k ,\quad \varphi _*( H_ {k-1}^1)= t^{\textrm{up}}_k. \end{aligned}$$

  $\varphi _*$ is an isomorphism by the above construction of the rest points of Y. To prove $\varphi _*$ is a chain map from $C_*(X)$ to $C_*(Y)$, we should have $\partial ' \varphi _* = \varphi _* \partial$. Here, we show this equality for one of the generators of $C_k(X)$ and for the others it can be similarly obtained. For $O^1_ {k-1}$, we have:

  $$\begin{aligned} \begin{aligned} \varphi _* \partial ( O^1_ {k-1})&= \varphi _* \left( \sum \alpha ( O_{k-1}, O_{k-2}) . O^1_{k-2} + \sum \alpha ( O_{k-1}, H_ {k-2}) . H_ {k-2}^1 \right) \\ {}&= \sum \alpha (q^{\textrm{up}} _{k}, q^{\textrm{up}} _{k-1}) . q^{\textrm{up}} _{k-1} + \sum \alpha (q^{\textrm{up}} _{k}, t^{\textrm{up}} _{k-1}) . t^{\textrm{up}} _{k-1}\\ {}&= \partial 'q^{\textrm{up}} _{k}\\ {}&= \partial ' \varphi _* ( O^1_ {k-1}). \end{aligned} \end{aligned}$$

  Therefore, $\partial ' \varphi _* = \varphi _* \partial$ and since ${\partial '}^2 = 0$ and $\partial ^ 2 =\varphi _*^{-1} {\partial '}^ 2 \varphi _*, \partial ^ 2 = 0$. $\square$

We can then define $\mathbb {Z}_2$ Morse–Floer homology of M by putting for each $k, 0 \le k \le m$,

$$\begin{aligned} H_k (M, \mathbb {Z}_2) = \frac{\textrm{ker} (\partial _k) }{\textrm{image} (\partial _{k+1})}. \end{aligned}$$

Remark 2.9

Although here we do not treat orientations, we observe from the following figure that in the above equalities, $\varphi _*$ preserves the parity of $\alpha$ as each connected component of $M(O_{k-1}, O_{k-2})$ corresponds to exactly one gradient flow line from $q^{\textrm{up}} _{k}$ to $q^{\textrm{up}} _{k-1}$ (and exactly one flow line from $q'^{\textrm{down}} _{k-1}$ to $q'^{\textrm{down}} _{k-2}$). Similarly the same happens when we consider connected components of $M(O_{k-1}, H_{k-2})$.

2.3 Computing Homology Groups of Smooth Manifolds

We shall now illustrate the simple computation of Floer homology for some smooth vector fields.

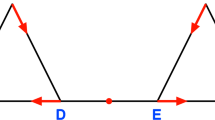
1. Let the sphere $S^2$ be equipped with a vector field V which has two isolated rest points of index zero at the north (N) and the south (S) pole, and one periodic orbit O of index one on the equator. Then,

$$\begin{aligned} C_2= & {} \left( O^1_{1}\right) , \\ C_1= & {} \left( O^0_ {1} \right) , \\ C_0= & {} \left( N_0, S_0 \right) . \end{aligned}$$

$\partial _2 O^1_{1} =0$ since there is no closed orbit of index 0 and therefore, $O^1_{1}$ is the only generator for $H_2(M, \mathbb {Z}_2)$.

$\partial _1 O^0_{1}= \alpha ( O_{1}, N_{0}) .N_{0} + \alpha ( O_{1}, S_{0}) .S_{0} = N_0+S_0 \ne 0$ and therefore, $O^0_{1}$ does not contribute to $H_1(M, \mathbb {Z}_2)$ and $H_1(M, \mathbb {Z}_2)=0$. $\partial _0 N_0= 0=\partial _0 S_0$, but since $N_0+S_0$ is in the image of $\partial _1$, therefore we have a single generator for $H_0(M, \mathbb {Z}_2)$.

2. If we reverse the orientation of flow lines in the previous example, the isolated rest points at the north and south pole will get index two and the index of the periodic orbit becomes zero. Therefore:

$$\begin{aligned} C_2= & {} \left( N_2, S_2 \right) , \\ C_1= & {} \left( O^1_{0}\right) , \\ C_0= & {} \left( O^0_ {0} \right) . \end{aligned}$$

$\partial _2 N_2= O^1_{0}=\partial _0 S_2$ and $N_2-S_2$ is the generator for $H_2(M, \mathbb {Z}_2)$.

Also $\partial _1 O^1_{1} =0$ but since $O^1_{1}$ is in the image of $\partial _2$, it does not contribute to $H_1(M, \mathbb {Z}_2)$. Finally, $\partial _0 O^0_{0}= 0$ and therefore, $O^0_{0}$ is the only generator for $H_0(M, \mathbb {Z}_2)$.

3. Consider $S^2$ with a vector field V which has two isolated rest points, at the north pole of index zero and at the south pole of index two, one orange homoclinic orbit H of index one and one yellow periodic orbit O of index zero.

$$\begin{aligned} C_2= & {} \left( S_2, H_{1}^1 \right) , \\ C_1= & {} \left( H_ {1}^0, O^1_ {0} \right) , \\ C_0= & {} \left( O^0_ {0}, N_0 \right) . \end{aligned}$$

$\partial _2 S_2= O^1_ {0}= \partial _2 H_{1}^1$ and therefore, $S_2- H_{1}^1$ is the only generator for $H_2(M, \mathbb {Z}_2)$.

$\partial _1 H_ {1}^0= \alpha ( H_ 1, O_{0}) .O^0_ {0} + \alpha ( H_ 1, N_{0}) .N_{0} =O^0_{0} + N_{0} \ne 0$ and therefore, $H_ {1}^0$ does not contribute to $H_1(M, \mathbb {Z}_2)$. On the other hand, $\partial _1 O^1_ {0}= 0$ but since $O^1_ {0}$ is in the image of $\partial _2$, it does not contribute to $H_1(M, \mathbb {Z}_2)$ and therefore, $H_1(M, \mathbb {Z}_2)=0$. $\partial _0 N_0= 0=\partial _0 O^0_ {0}$ but since $O^0_ {0} + N_{0}$ is in the image of $\partial _1$, therefore we have just one generator for $H_0(M, \mathbb {Z}_2)$.

4. Finally, a two-dimensional Torus $T^2$ with a vector field V with two periodic orbits $O_1$ and $O'_0$:

$$\begin{aligned} C_2= & {} \left( O^1_{1}\right) \\ C_1= & {} \left( O^0_ {1}, O'^1_{0} \right) \\ C_0= & {} \left( O'^0_ {0} \right) \end{aligned}$$

$\partial _2 O^1_{1}= 2. O'^1_{0}= 0$ therefore, $O^1_{1}$ is the generator for $H_2(M, \mathbb {Z}_2)$. $\partial _1 O^0_{1}= 2. O'^0_{0}= 0$ so $O^0_{1}$ is a generator for $H_1(M, Z)$. Also, $\partial _1 O'^1_{0}= 0$ and therefore, $O'^1_{0}$ is another generator for $H_1(M, \mathbb {Z}_2)=0$.

Finally, $\partial _0 O'^0_ {0}= 0$ and therefore, we have one generator for $H_0(M, \mathbb {Z}_2)$.

Remark 2.10

For a computation of the homology groups of the first two examples via Morse–Bott theory (after turning the periodic orbits into critical submanifolds of a gradient flow), see [1].

3 Combinatorial Vector Fields

3.1 Preliminaries

Forman introduced the notion of a combinatorial dynamical system on CW complexes [13]. He developed discrete Morse theory for the gradient vector field of a combinatorial Morse function and studied the homological properties of its dynamic [14] . For the general combinatorial vector fields where as opposed to gradient vector fields, the chain recurrent set might also include closed paths, he studied some homological properties by generalizing the combinatorial Morse inequalities. It remains, however, to construct a Floer type boundary operator for these general combinatorial vector fields. We define a Morse–Floer boundary operator for combinatorial vector fields on a finite simplicial complex. With this tool, we no longer need a Morse function to compute the Betti numbers of the complex. Combinatorial vector fields can be considered as the combinatorial version of smooth Morse–Smale dynamical systems on finite dimensional manifolds; here, in contrast to the smooth case we cannot have homoclinic points and homoclinic orbits as here, we cannot have a continuous bifurcation between a pair of heteroclinic orbits and a closed one, and in particular none with a homoclinic orbit in the middle.

We now recall some of the main definitions that Forman introduced. Let M be a finite CW complex of dimension m, with K the set of open cells of M and $K_p$ the set of cells of dimension p. If $\sigma$ and $\tau$ are two cells of M, we write $\sigma _p$ if $\dim (\sigma ) = p$ and $\sigma < \tau$ if $\sigma \subseteq {\overline{\tau }}$, where ${\overline{\tau }}$ is the closure of $\tau$ and we call $\sigma$ a face of $\tau$.

Suppose $\sigma _p$ is a face of $\tau _{p+1}$, B is a closed ball of dimension $p+1$ and $h: B\rightarrow M$, the characteristic map for $\tau$, i.e., a homeomorphism from the interior of B onto $\tau$.

Definition 3.1

$\sigma _p$ is a regular face of $\tau _{p+1}$ if

• $h^{-1} (\sigma ) \rightarrow \sigma$ is a homeomorphism.

• $\overline{h^{-1} (\sigma )}$ is a closed p-ball.

Otherwise, we say $\sigma$ is an irregular face of $\tau$. If M is a regular CW complex (such as a simplicial or a polyhedral complex), then all its faces are regular.

Definition 3.2

A combinatorial vector field on M is a map $V : K \rightarrow K \cup {0}$ such that

• For each p, $V(K_p) \subseteq K_{p+1} \cup {0}$.

• For each $\sigma _p \in K_p$, either $V(\sigma )= 0$ or $\sigma$ is a regular face of $V(\sigma )$.

• If $\sigma \in \textrm{Image}(V)$, then $V(\sigma ) = 0$.

• For each $\sigma _p \in K_p$, $\sharp \lbrace u_{p-1} \in K_{p-1} \mid V(u)= \sigma \rbrace \le 1$.

To present the vector field on M for any $\sigma \in K$, where $V(\sigma ) \ne 0$, we usually draw an arrow on M whose tail begins at $\sigma$ and extend this arrow into $V (\sigma )$. Thus, for each cell $\sigma _p$, there are precisely 3 disjoint possibilities:

• $\sigma$ is the head of an arrow $(\sigma \in Image(V))$.

• $\sigma$ is the tail of an arrow ($V(\sigma ) \ne 0)$.

• $\sigma$ is neither the head nor the tail of any arrow $(V (\sigma ) = 0$ and $\sigma \not \in \textrm{Image}(V )$.

In the last case, we call such a $\sigma _p$ a zero or rest point of V of index p. Cells which are not rest points occur in pairs ($\sigma ,V(\sigma )$) with $\dim V (\sigma ) = \dim \sigma + 1$. From now on and for simplicity, we restrict ourselves to the special case of simplicial complexes, instead of CW complexes. As the combinatorial version of closed periodic orbits in smooth manifolds, we have the next definition:

Definition 3.3

Define a V-path of index p to be a sequence $\gamma : \sigma _p^0,\tau ^0_{p+1},\sigma _p^1,\tau _{p+1}^1,\ldots , \tau ^{r-1}_{p+1},\sigma ^{r}_p$ such that for all $i = 1, . . . , r-1:$ $V(\sigma ^i)= \tau ^i$ and $\sigma ^i \ne \sigma ^{i+1} < \tau ^i$.

A closed path $\gamma$ of length r is a V-path such that $\sigma _p^0=\sigma _p^r$. Also, $\gamma$ is called non-stationary if $r > 0$.

Forman showed that there is an equivalence relation on the set of closed paths by considering two paths $\gamma$ and $\gamma '$ to be equivalent if $\gamma$ is the result of varying the starting point of $\gamma '$. An equivalence class of closed paths of index k will be called a closed orbit of index k and denoted by $O_k$.

Definition 3.4

We call an orbit $O_p$ twisted if in its corresponding closed path

$$\begin{aligned} \gamma :\sigma _p^0,\tau ^0_{p+1},\sigma _p^1,\tau _{p+1}^1,\ldots ,\tau ^{r-1}_{p+1},\sigma ^{r}_p =\sigma _p^0, \end{aligned}$$

there is at least one vertex of $\sigma _p^0$ that does not attach to itself in $\sigma ^{r}_p$ (for example see Remark 3.10). Otherwise, we call the orbit simple.

Definition 3.5

The combinatorial chain recurrent set R(V) for a combinatorial vector field V on M is defined to be the set of simplices $\sigma _p$ which are either rest points of V or are contained in some non-stationary closed path $\gamma$ ($\gamma$ must have index either $p-1$ or p).

The chain recurrent set can be decomposed into a disjoint union of basic sets $R(M)=\cup _{i} \Lambda _i$, where two simplices $\sigma , \tau \in R(V)$ belong to the same basic set if and only if there is a closed non-trivial V-path $\gamma$ which contains both $\sigma$ and $\tau$. Forman proved that if there are no non-stationary closed paths then V is the combinatorial negative gradient vector field of a combinatorial Morse function. However, when V has closed paths then it cannot be the gradient of a function. Subsequently, he defined a combinatorial ”Morse-type” function on K called a Lyapunov function, which is constant on each basic set and has the property that away from the chain recurrent set, V is the negative gradient of f.

Remark 3.6

This Lyapunov function can be considered as the combinatorial analogue of the Morse–Bott energy function which Meyer defined for Morse–Smale dynamical systems.

3.2 The Chain Complex of Combinatorial Vector Fields

Forman obtained Morse–type inequalities based on the basic sets of V and showed that these sets control the topology of M [13]. In this section, we present a direct way of recovering the homology of the underlying complex from the chain recurrent set of a combinatorial vector field on M from our Floer type boundary operator; our main restriction is that the chain recurrent set should not have twisted orbits. Our operator acts on chain groups generated by the basic sets and counts the number of suitable V-paths between elements of the chain recurrent set. We consider V to be a combinatorial vector field on a finite simplicial complex M, where R(V) does not include twisted orbits.

We define the Morse–Floer complex of V denoted by $(M, C_*(V), \partial )$ as follows. Let $C_k$ denote the finite vector space (with coefficients in $\mathbb {Z}_2$) generated by the set of rest points $p_k$ and closed orbits $O_{k-1}$ of the vector field:

$$\begin{aligned} \left( p_k, O^1_{k-1}, O^0_ {k} \right) \end{aligned}$$

in which by $O^1_{k-1}$ we mean the whole closed orbit $O_{k-1}$ of index ${k-1}$ and by $O^0_ {k}$ we mean an arbitrary simplex with dimension k in the closed orbit $O_k$. Similar to the smooth case, each such orbit carries topology in two adjacent dimensions, namely a closed orbit $O_k$ generates an element $O^1_{k}$ in $C_{k+1}$ and an element $O^0_{k}$ in $C_{k}$. We note that here, by definition of combinatorial vector fields, we do not have any V-path between the elements of the same $C_k$; but in order to get a Floer type boundary operator in the same way as in the smooth setting we have to exclude three different cases in our vector field; we assume:

• 1. There is no V-path from a face of a critical simplex $p_k$ to a $(k-1)$-dimensional simplex in an orbit $O_{k-1}$.

• 2. There is no V-path from a face of a k-dimensional simplex of an orbit of index $k-1$ to a critical simplex of dimension $k-1$.

• 3. There is no V-path from a face of a k-dimensional simplex of an orbit of index $k-1$ to a $(k-1)$-dimensional simplex of another orbit of index $k-1$.

This will be used in the proof of Theorem 3.7. In the smooth setting, the excluded cases cannot occur because of the Morse–Smale transversality condition.

To be able to define the combinatorial Floer-type boundary operator, we have to transfer the idea of the number of connected components of the moduli spaces of flow lines to our combinatorial setting. As we see, the number of these components (mod 2) plays a key rule in the definition of the boundary operator in the smooth setting. In the sequel, for two simplices of the same dimension q and $q'$, by $q \perp q'$, we mean that q and $q'$ are lower adjacent, i.e., they have a common face.

We have V-paths between closed orbits and rest points which make different following cases: For two orbits $O_ {k-1}$ and $O_ {k-2}$, we define the set $VP(O_ {k-1} , O_ {k-2})$ as the set of all V-paths starting from the faces of $(k-1)$- and k-dimensional simplices of $O_ {k-1}$ and go to, respectively, $(k-2)$- and $(k-1)$- dimensional simplices of $O_ {k-2}$.

If $VP(O_ {k-1} , O_ {k-2})$ is non-empty, for $O^1_{k-1}$ and $O^1_{k-2}$, we define the higher dimensional spanned set of V-paths in $VP(O_ {k-1} , O_ {k-2})$, denoted by $SVP(O^1_ {k-1} , O^1_ {k-2})$ to be

$$\begin{aligned} \lbrace q \in K_{k}, q \in \textrm{Image} (V) \mid \exists \gamma \in VP(O_ {k-1} , O_ {k-2}), q \in \gamma \rbrace . \end{aligned}$$

On this set, we can then define a relation as follows. We say q and $q'$ in $SVP(O^1_ {k-1} , O^1_ {k-2})$ are related ($q\sim q'$) if q and $q'$ belong, respectively, to two V-paths $\gamma : \alpha _{k-1}^0,\ldots ,q_k,\ldots ,\alpha ^{r}_{k-1}$ and $\gamma ' : \beta _{k-1}^0,\ldots ,q'_k,\ldots ,\beta ^{s}_{k-1}$, where $\alpha _{k-1}^0$ and $\beta _{k-1}^0$ are faces of k-dimensional simplices of $O_ {k-1}$ and $\alpha _{k-1}^r$ and $\beta _{k-1}^s$ are some $k-1$ dimensional simplices in $O_ {k-2}$ such that one of the following situations happens:

• Either $\alpha _{k-1}^0$ and $\beta _{k-1}^0$ coincide (and therefore $\gamma$ and $\gamma '$ are the same) or

• $\alpha _{k-1}^0\perp \beta _{k-1}^0$ or

• There is a sequence of $k-1$ dimensional simplices $\theta _{k-1}^0,\ldots \theta _{k-1}^z$, where $\theta _{k-1}^0,\ldots \theta _{k-1}^z$ are the faces of k dimensional simplices in $O_ {k-1}$ such that $\alpha _{k-1}^0 \perp \theta _{k-1}^0$, $\beta _{k-1}^0 \perp \theta _{k-1}^z$ and for each i, $\theta _{k-1}^i \perp \theta _{k-1}^ {i+1}$ and $\theta _{k-1}^i$ is the starting simplex of some $\gamma \in VP(O_ {k-1} , O_ {k-2})$.

It is straightforward to check that $\sim$ is an equivalence relation on $SVP(O^1_ {k-1} , O^1_ {k-2})$.

On the other side for two arbitrary simplices of dimension $k-1$ and $k-2$ in, respectively, $O_ {k-1}$ and $O_ {k-2}$, we consider the following equivalence relation ($\sim '$) on $SVP(O^0_ {k-1}, O^0_ {k-2})$ which is defined as follows:

$$\begin{aligned} \lbrace q \in K_{k-1}, q \in {\textrm{Image} (V)} \mid \exists \gamma \in VP(O_ {k-1} , O_ {k-2}), q \in \gamma \rbrace . \end{aligned}$$

We say q and $q'$ in $SVP(O^0_ {k-1} , O^0_ {k-2})$ are related ($q \sim ' q'$) if there are w and $w'$ in $SVP(O^1_ {k-1} , O^1_ {k-2})$ such that $q<w$ and $q'<w'$ and $w\sim w'$. By definition, $\sim '$ is also an equivalence relation on $SVP(O^0_ {k-1} , O^0_ {k-2})$ and the number of its equivalence classes is exactly the number of equivalence classes of $\sim$ over $SVP(O^1_ {k-1} , O^1_ {k-2})$.

For instance, consider the following triangulation of the torus which has two closed orbits of index one and index zero, respectively, shown by green and red arrows. Here, $SVP(O^1_ {k-1} , O^1_ {k-2})$ is the set of all the two-dimensional coloured simplices and based on the above equivalence relation, this set is partitioned into two sets of yellow and pink two-dimensional simplices. Also, $SVP(O^0_ {k-1} , O^0_ {k-2})$ is the set of all marked (with cross sign) edges which is partitioned into two sets, represented by orange and purple signs.

If for two orbits, $O_ {k-1}$ and $O_ {k-2}$, $VP(O_ {k-1} , O_ {k-2})$ is empty and some of the faces of $O_ {k-1}$ (faces of both $k-1$ and k-dimensional simplices) coincide with $k-2$ and $k-1$ dimensional simplices in $O_ {k-2}$, we say $O_ {k-2}$ is attached to $O_ {k-1}$. In the tetrahedron shown below, the bottom faces of the closed red orbit of index one are the closed orbit of index zero with purple arrows:

Also, we could have V-paths, $VP(p_ k , O_{k-2})$, from the faces of a critical simplex $p_k$ of index k which go to the $k-1$ dimensional simplices of some orbit of index $k-2$; we define the span set of these V-paths, denoted by $SVP(p_ {k} , O^1_ {k-2})$ to be

$$\begin{aligned} SVP(p_ {k} , O^1_ {k-2}): = \lbrace q \in K_{k}, q \in \textrm{Image} (V) \mid \exists \gamma \in VP(p_ {k} , O_ {k-2}), q \in \gamma \rbrace . \end{aligned}$$

As above, we can define an equivalence relation on this set in which the equivalence classes are obtained based on the following relation:

$q\sim q'$ if they belong, respectively, to two V-paths $\gamma : \alpha _{k-1}^0,\ldots ,q_k,\ldots ,\alpha ^{r}_{k-1}$ and $\gamma ' : \beta _{k-1}^0,\ldots ,q'_k,\ldots ,\beta ^{s}_{k-1}$ such that either $\alpha _{k-1}^0$ and $\beta _{k-1}^0$ coincide or $\alpha _{k-1}^0\perp \beta _{k-1}^0$ or there is a sequence of $k-1$ dimensional simplices $\theta _{k-1}^0,\ldots \theta _{k-1}^z$, where $\theta _{k-1}^0,\ldots \theta _{k-1}^z$ are the faces of $p_k$ such that $\alpha _{k-1}^0 \perp \theta _{k-1}^0$, $\beta _{k-1}^0 \perp \theta _{k-1}^z$ and for each i, $\theta _{k-1}^i \perp \theta _{k-1}^ {i+1}$. We note that here, $\alpha _{k-1}^0$ and $\beta _{k-1}^0$ are faces of $p_k$ and $\alpha _{k-1}^r$ and $\beta _{k-1}^s$ are some $k-1$ elements of $O_ {k-2}$.

Also for V on M, for some rest point $p_k$ and some closed orbit $O_{k-2}$, the faces of $p_ {k}$ and $k-1$ dimensional simplices in $O_ {k-2}$ might coincide; for instance in the above tetrahedron the faces of orange 2-d rest simplex coincides with the one-dimensional simplices in the closed orbit of index zero with purple arrows. We consider this again as an attachment.

In the third possible case, V-paths start from the faces of k-dimensional simplices of a closed orbit of index k, $O_k$, and go to a rest simplex of index $k-1$, $p_{k-1}$. We denote the set of such V-paths by $VP(O_ {k} , p_ {k-1})$ and we consider $SVP(O^0_ {k} , p_ {k-1}): = \lbrace q \in K_{k}, q \in \textrm{Image} (V) \mid \exists \gamma \in VP(O_ {k} , p_ {k-1}), q \in \gamma \rbrace$. In this set, we call two simplices q and $q'$ equivalent if either q and $q'$ coincide or $q \perp q'$ or we can find a sequence of simplices in $SVP(O^0_ {k} , p_ {k-1})$ such as $\theta _{k}^0,\ldots \theta _{k}^z$, such that $q \perp \theta _{k}^0$, $q' \perp \theta _{k}^z$ and for each i, $\theta _{k}^i \perp \theta _{k}^ {i+1}$. Here, we have to exclude $p_ {k-1}$ for determining lower adjacency of k-dimensional simplices in $SVP(O^0_ {k} , p_{k-1})$, namely if $q \cap q' = p_ {k-1}$, they belong to different classes. As an example, consider the following triangulation for the torus with four orange rest simplices, one of index two, two of index one and another one of index zero, and a closed red orbit of index one. Here, the edges marked by cross signs are the edges in $SVP(O^0_ {1} , p_ {0})$, which is portioned into two pink and yellow marked edges. If $VP(O_ {k} , p_{k-1})$ is empty, but $O_k$ and $p_ {k-1}$ have a non-empty intersection, we have another type of attachment. For an example of this case, see the top critical vertex and the red $O_1$ in the above tetrahedron.

Finally, if we substitute $O_ {k}(O^0_ {k})$ in the third case by a rest point of index k, $p_k$, we count the number of equivalence classes of $SVP(p_ {k} , p_ {k-1}): = \lbrace q \in K_{k}, q \in \textrm{Image} (V) \mid \exists \gamma \in VP(p_ {k} , p_ {k-1}), q \in \gamma \rbrace$, where $VP(p_ {k} , p_ {k-1})$ is the set of all V-paths starting from the faces of $p_k$ and go to $p_ {k-1}$ by passing through k-dimensional simplices, based on the following relation:

We say q and $q'$ in $SVP(p_ {k} , p_ {k-1})$ are related ($q\sim q'$) if there is a V-path in $VP(p_ {k} , p_ {k-1})$ which includes both q and $q'$. Therefore, the number of equivalence classes here is the number of V-paths starting from the faces of $p_k$ which go to $p_ {k-1}$.

The differential $\partial _k : C_k(V) \longrightarrow C_{k-1}(V)$ counts the number of the above equivalence classes mod 2, denoted by $\alpha$, and for the three types of attachments we consider $\alpha = 1$. That is,

$$\begin{aligned} \partial p_k= & {} \sum \alpha (p_k, p_{k-1}) p_{k-1} + \sum \alpha (p_k, O^1_{k-2}) O^1_{k-2},\\ \partial O^0_{k}= & {} \sum \alpha ( O^0_{k}, O^0_{k-1}) O^0_{k-1}+ \sum \alpha ( O^0_{k}, p_{k-1}) p_{k-1}, \\ \partial O^1_{k-1}= & {} \sum \alpha ( O^1_{k-1}, O^1_{k-2}) O^1_{k-2}, \end{aligned}$$

where the sums extend over all the elements on the right hand side; for instance, the second sum in the first line is over all closed orbits $O^1_{k-2}$ of index $k-2$. In Forman’s discrete Morse theory where there is no closed orbit (and therefore the combinatorial vector field is the negative gradient of a discrete Morse function), $\alpha (p_k, p_{k-1})$ is the number of gradient V-paths from the faces of the rest point $p_k$ of higher dimension to the rest point of lower dimension $p_{k-1}$ (in this case, all the coefficients in the above formula except the first coefficient in the first line are zero).

Theorem 3.7

$\partial ^ 2 = 0$.

To prove this theorem similarly to Theorem 2.8 in the smooth case, we introduce a procedure to replace any closed path of index p (correspondingly its orbit of index p, $O_{p})$ with a rest point of index p and one of index $p+1$ which are joined by two gradient V-paths starting from the faces of a higher dimensional rest point and going to the lower dimensional rest point.

We assume V has a finite number of simple closed non-stationary paths (orbits) and rest simplices. Choose arbitrarily one of these closed paths $\gamma$ of index p, $\gamma : \sigma _p^0,\tau ^0_{p+1},\sigma _p^1,\tau _{p+1}^1,\ldots ,\tau ^{r-1}_{p+1},\sigma ^{r}_p = \sigma _p^0$. $\gamma$ is a sequence of p and $(p+1)$ dimensional simplices. Take one of the $p+1$ dimensional simplices $\tau ^{k}_{p+1}$ where $k\ne r-1$. (Note that for non-stationary closed paths such a $\tau ^{k}$ always exists). We consider the following two sets of the simplices of $\gamma$ by preserving the orders in each of the sets:

$$\begin{aligned} \sigma ^{0}_p,\ldots , \tau ^{k-1}_{p+1}, \sigma ^{k}_p, \tau ^{k}_{p+1} \textrm{and} \\ \tau ^{k}_{p+1}, \sigma ^{k+1}_p, \tau ^{k+1}_{p+1}, \ldots , \sigma ^{r}_p = \sigma _p^0, \end{aligned}$$

where the union of the elements in these sets consists of all the simplices of $\gamma$ and their intersection is the starting simplex of the closed path $\sigma _p^0$ and the one of higher dimension that we took $\tau ^{k}_{p+1}$.

We keep the arrows in the second set as they are in $\gamma$ and in the first set we reverse the direction of V-path from $\sigma _p^0$ to $\tau ^{k}_{p+1}$. Namely instead of a pair $(\sigma ^{s}_p, \tau ^{s}_{p+1})$ in $\gamma$ (for $0\le s \le k$) we will have $( \sigma ^{s}_p, \tau ^{s-1}_{p+1})$ in our vector field, where the two simplices $\sigma _p^0$ and $\tau ^{k}_{p+1}$ will no longer be the tail and head of any arrow; therefore by definition both of them become rest points and there is no other rest point in $\gamma$ created in this process. We note that in this procedure we just change the arrows in O and the other pairs of the vector field (outside O) are not changed.

Proof of Theorem 3.7

If by the help of above procedure, we replace all the closed paths (orbits) by two rest points whose indices (dimensions) differ by one we get a vector field $V'$ which has no closed path (orbit) and therefore, there is a discrete Morse function on M whose gradient is $V'$. $V'$ has all the rest points of V and two rest points $q^{\textrm{up}}_k$ (the simplex of higher index) and $q'^{\textrm{down}}_{k-1}$ (the simplex of lower index) instead of every orbit $O_{k-1}$ of index $k-1$. Then, we have the following three steps to prove the theorem:

• 1. We consider $C_k(V')$ to be the finite vector space (with coefficients in $\mathbb {Z}_2$) generated by

  $$\begin{aligned} \left( p_k, q^{\textrm{up}}_k, q'^{\textrm{down}}_{k} \right) , \end{aligned}$$

  where in this set $q^{\textrm{up}}_k$ comes from an orbit of index $k-1$ and $q'^{\textrm{down}}_{k}$ comes from the replacement of an orbit of index k.

• 2. We define a boundary operator $\partial '$ and consequently a chain complex corresponding to $(V',C_*(V'), \partial ')$.

• 3. Then, we prove there is an isomorphism (chain map) $\varphi * : C_*(V) \longrightarrow C_*(V')$ .

Since $\varphi *$ is an isomorphism, we get our desired equality $\partial ^ 2 = 0$ as $\partial = \varphi ^{-1} \partial '$ and $\partial ^ 2=\varphi ^ {-1} {\partial '} ^ 2$.

• 1) All the elements of the chain recurrent set of $V'$ are rest simplices and for each index k they can be partitioned into three different sets $p_k, q^{\textrm{up}}_k, q'^{\textrm{down}}_k$. Here, in contrast to the smooth case, orbits and rest points can have non-empty intersections; in particular for different types of attachments, the pairwise intersections are non-empty. However, partitioning of rest simplices is possible since the indices of the rest simplices are the same as their dimensions and after converting orbits into two rest simplices, they will belong to different chain groups (in adjacent dimensions).

• 2) We define $\partial ' : C_k(V') \longrightarrow C_{k-1} (V')$ as follows:

  $$\begin{aligned} \partial ' p_k= & {} \sum \alpha (p_k, p_{k-1}) \cdot p_{k-1} + \sum \alpha (p_k, q^{\textrm{up}}_{k-1}) . q^{\textrm{up}}_{k-1}, \\ \partial ' q'^{\textrm{down}} _{k}= & {} \sum \alpha (q'^{\textrm{down}} _{k}, q'^{\textrm{down}} _{k-1}) \cdot q'^{\textrm{down}} _{k-1} \\ {}{} & {} \quad +\, \sum \alpha (q'^{\textrm{down}} _{k}, p_{k-1}) \cdot p_{k-1}, \\ \partial 'q^{\textrm{up}} _{k}= & {} \sum \alpha (q^{\textrm{up}} _{k}, q^{\textrm{up}} _{k-1}) \cdot q^{\textrm{up}} _{k-1}. \\ \end{aligned}$$

  To prove $\partial '^ 2 = 0$ over $C_k(V')$, we want to equate $\partial '$ with the discrete Morse–Floer boundary operator $\partial ^M$ of a combinatorial gradient vector field of the form $\partial ^M (s_k) = \sum \alpha (s_k, s_{k-1}) s_{k-1}$. There we count the number of gradient V-paths $\alpha$ (mod 2) between two rest points of relative index difference one without any such partitioning on the set of rest simplices $s_k$ of index k. In our case, where we have such kind of partitioning we should show that for all the generators of $C_*(V')$, $\partial ' = \partial ^M$. After the preceding procedure, we have:

  $$\begin{aligned} \partial ^M (p_k)= & {} \sum \alpha (p_k, p_{k-1}) \cdot p_{k-1} + \sum \alpha (p_k, q^{\textrm{up}}_{k-1}) \cdot q^{\textrm{up}}_{k-1} \\ {}{} & {} \quad +\, \sum \alpha (p_k, q'^{\textrm{down}}_{k-1}) \cdot q'^{\textrm{down}}_{k-1} ; \end{aligned}$$

  comparing this formula with that of $\partial ' p_k$ in the above formula. We see that there is one extra term in the latter; because we exclude case (1) in our vector field, the third sum is not present in the former case. As in the previous discussion to have $\partial ^M(q^{\textrm{up}} _{k}) = \partial '(q^{\textrm{up}} _{k})$, the following two coefficients should be zero: $\alpha (q^{\textrm{up}} _{k}, q'^{\textrm{down}} _{k-1}), \alpha (q^{\textrm{up}} _{k}, p_{k-1})$. In the first case, if $q^{\textrm{up}} _{k}$ and $q'^{\textrm{down}} _{k-1}$ are coming from replacement of the same orbit $O_{k-1}$, we will have exactly two $V'$-paths from the faces of $q^{\textrm{up}} _{k}$ to $q'^{\textrm{down}} _{k-1}$ and it is zero mud 2. If they are not obtained from replacement of the same orbit $O_{k-1}$, $\alpha$ is zero as otherwise in V we would have V-paths between two orbits of the same index which either contradicts the non-existence of V-paths between elements of the same chain group or violates our exclusion (3) on the vector field. On the other hand, the second $\alpha$ is zero as otherwise it violates our assumption (exclusion 2) on the vector field. Finally, $\partial ^M(q'^{\textrm{down}} _{k}) = \partial '(q'^{\textrm{down}} _{k})$ if $\alpha (q'^{\textrm{down}} _{k}, q^{\textrm{up}} _{k-1})$ is zero; if not, we would have two closed orbits O and $O'$ in V such that the faces of O are connected to $O'$ by some V-paths and their indices differ by two which is not possible. Therefore, on $C_*(V)$, $\partial ^M= \partial '$ and $\partial '^ 2 = 0$ since by Morse–Floer theory for combinatorial gradient vector fields $(\partial ^M)^2 = 0$.

• 3) We define $\varphi * : C_*(V) \longrightarrow C_*(V')$ as follows. For $0\le k \le m$,

  $$\begin{aligned} \varphi _*( p_k)= p_k,\quad \varphi _* (O^0_ {k}) = q'^{\textrm{down}}_k ,\quad \varphi _*( O^1_ {k-1})= q^{\textrm{up}}_k. \end{aligned}$$

  $\varphi _*$ is an isomorphism by the above partitioning method for the set of rest points of $V'$. To prove $\varphi _*$ is a chain map from $C_*(V)$ to $C_*(V')$, we should have $\partial ' \varphi _* = \varphi _* \partial$. Here, we show the equality for $O^1_ {k-1}$ and for the other generators of $C_k(V)$, it can be similarly obtained:.

  $$\begin{aligned} \begin{aligned} \varphi _* \partial ( O^1_ {k-1})&= \varphi _* (\sum \alpha ( O^1_{k-1}, O^1_{k-2}) . O^1_{k-2} \\&= \sum \alpha (q^{\textrm{up}} _{k}, q^{\textrm{up}} _{k-1}) . q^{\textrm{up}} _{k-1} \\&= \partial 'q^{\textrm{up}} _{k}\\&= \partial ' \varphi _* ( O^1_ {k-1}). \end{aligned} \end{aligned}$$

  In the second equality, $\varphi _*$ preserves the parity of $\alpha ( O^1_{k-1}, O^1_{k-2})$ since each equivalence class of $SVP(O^1_ {k-1} , O^1_ {k-2})$ corresponds to exactly one gradient V-path from $q^{\textrm{up}} _{k}$ to $q^{\textrm{up}} _{k-1}$ (and one gradient V-path from $q'^{\textrm{down}} _{k-1}$ to $q'^{\textrm{down}} _{k-2}$).

  Therefore, $\partial ' \varphi _* = \varphi _* \partial$ and since $\partial ^{'2} = 0$ and $\partial ^ 2 =\varphi _*^{-1} \partial ^{'2} \varphi _*, \partial ^ 2 = 0$. $\square$

Remark 3.8

For the three types of attachments in the above equality, after replacing orbits with two rest simplices and two gradient V-paths between them, $\alpha (p_k, q^{\textrm{up}}_{k-1})$, $\alpha (q^{\textrm{up}} _{k}, q^{\textrm{up}} _{k-1})$, $\alpha (q'^{\textrm{down}} _{k}, q'^{\textrm{down}} _{k-1})$ and $\alpha (q'^{\textrm{down}} _{k}, p _{k-1})$ are also one. For instance, in the left tetrahedron below, we have two orange rest simplices, one of index two $B_2$ at the bottom and one of index zero at the top $T_0$ and two red and purple closed orbits of indices one and zero. If we convert the red orbit into two rest simplices, marked with red crosses, one of index two $R_2$ and the other one of index one $R_1$ and similarly turn the purple orbit into two rest simplices, marked with purple crosses, one of index one $P_1$ and the other one of index zero $P_0$ (shown in the right figure), we have $\alpha (B_2, P_1)=1$, $\alpha (R_2, P_1) = 1$, $\alpha (R_1, P_0) =1$ and $\alpha (R_1, T_0) = 1$ (Also $\alpha (R_2, R_1) = 0$, $\alpha (P_1, P_0) =0$).

We can then define the $\mathbb {Z}_2$ Morse–Floer homology of M, for each $k, 0 \le k \le m$ by

$$\begin{aligned} H_k (M, \mathbb {Z}_2) = \frac{\textrm{ker} (\partial _k) }{\textrm{image} (\partial _{k+1})}. \end{aligned}$$

In [13], Forman proved Morse inequalities for general combinatorial vector fields based on his combinatorial Morse type Lyapunov function.

There the main components are rest points and orbits in basic sets. Here, we want to present these inequalities in a much shorter way based on the idea of changing every orbit of index $k-1$, $O_{k-1}$ to two rest points of index k and $k-1$ as above. The following result can be considered as the combinatorial version of what Franks proved for smooth Morse–Smale dynamical systems [17].

Theorem 3.9

Let V be a combinatorial vector field over a finite simplicial complex M with $c_k$ rest points of index k and $A_k$ orbits of index k. Then,

$$\begin{aligned} c_k-c_{k-1}+\cdots \pm c_0 + A_k \ge \beta _k- \beta {k-1}+\cdots \pm \beta _0, \end{aligned}$$

where $\beta _k = \dim H_k(M, \mathbb {Z}_2)$.

Proof

We create a new vector field $V'$ over M by replacing each closed orbit with two rest points as above. Since there is no closed orbit in $V'$, based on what Forman showed in [14], $V'$ is the gradient of some combinatorial Morse function on M. On the other hand, the indices of rest points do not change when turning V to $V'$ and $V'$ has $c'_k$ rest points of index k, where $c'_k = c_k+ A_k+ A_{k-1}$. Applying the Morse inequalities for gradient vector fields, to $c'_k$ in $V'$ gives us the desired inequalities. $\square$

Remark 3.10

If a simplicial complex is obtained by triangulation of a non-orientable manifold, we might not get the correct ($\mathbb {Z}_2$) homology groups when the chain recurrent set of our combinatorial vector field has non-stationary closed V-paths. However, for computing the $\mathbb {Z}_2$ homology, we can turn each orbit into two rest simplices and two V-paths between them as above to get a combinatorial gradient vector field on the simplex and use the classical discrete Floer-Morse theory. For instance, consider a triangulation of the Klein which has two closed orbits represented by red and blue arrows of index one and zero, respectively, as shown in the left diagram below. We note that the red orbit is twisted. Here, by turning orbits into two rest simplices and two V-paths between them we get the correct $\mathbb {Z}_2$-homology of the Klein bottle which is the same as the $\mathbb {Z}_2$-homology of the triangulated torus as $\mathbb {Z}_2$-homology cannot distinguish between orientable and non-orientable surfaces.

Remark 3.11

Orientability of a simplicial complex is not a necessary condition for defining the Floer boundary operator for general combinatorial vector fields. For instance in the following diagram, we have a non-orientable simplex as each vertex is the intersection of three different edges. Here, the chain recurrent set has an orbit of index zero with red arrows, as well as three critical edges and one critical vertex in the middle. If we use Theorem 3.7 to compute the $\mathbb {Z}_2$ homology of M based on this vector field, we get $H_0(M, \mathbb {Z}_2)=1$ and $H_1(M, \mathbb {Z}_2)=3$.

3.3 Computing Homology Groups of Simplicial Complexes

We now present the computation of Floer homology groups for some CW complexes.

1. Consider the tetrahedron as a symmetric triangulation of the Sphere $S ^ 2$, equipped with a vector field V which has two rest simplices, one of index (dimension) zero $(p_0)$ (the vertex at the top corner) and another of index two $\tau _2$ (the simplex at the bottom), shown in orange, and a closed red orbit $O_1$ of index one and one of index zero $O'_0$ in purple.

$$\begin{aligned} C_2= & {} \left( \tau _2, O^1_{1}\right) ,\\ C_1= & {} \left( O^0_ {1}, O'^1_ {0} \right) , \\ C_0= & {} \left( O'^0_ {0}, p_0 \right) . \end{aligned}$$

$\partial _2 \tau _2= O'^1_ {0}$ as this is an attachment where the faces of $\tau _2$ and edges in $O^1_ 0$ coincide. On the other hand, $\partial _2 O^1_{1}$ is also equal to $O'^1_ {0}$ (another type of attachment) and therefore, $\tau _2- O^1_{1}$ is the only generator for $H_2(M, \mathbb {Z}_2)$. $\partial _1 O^0_ {1}= \alpha ( O^0_ {1}, O'^0_ {0}) .O'^0_ {0} + \alpha ( O^0_ {1}, p_{0}) .p_{0} = O'^0_ {0} + p_{0} \ne 0$ and $O^0_ {1}$ does not contribute to $H_1(M, \mathbb {Z}_2)$. Also, $\partial _1 O'^1_ {0}= 0$ but since $O'^1_ {0}$ is in the image of $\partial _2$, it does not contribute to $H_1(M, \mathbb {Z}_2)$ and $H_1(M, \mathbb {Z}_2)=0$ Finally, $\partial _0 p_0= 0=\partial _0 O'^0_ {0}$, but since $O'^0_ {0} + p_{0}$ is in the image of $\partial _1$, we have just one generator for $H_0(M, \mathbb {Z}_2)$.

2. Let $T ^ 2$ at right be a triangulation of the two-dimensional torus equipped with a vector field which has two closed orbits $O_1$ and $O'_0$ with green and red arrows.

Since this case is actually a discrete version of example 4 in the previous section, we have analogous structures for the chain complexes and boundaries; $SVP(O^1_1 , O'^1_ 0)$ is partitioned into two equivalence classes and therefore, $\alpha ( O^1_1, O'^1_0)= \alpha ( O^0_1, O^0_0)= 0$ and all of the generators of $C_k$ for $k=0, 1, 2$ contribute to the corresponding homology groups.

3. Consider another combinatorial vector field on the triangulated torus, where V has four orange rest simplices, one of index zero $(p_0)$, a vertical edge $ve_1$ of index one, a horizontal edge $he_1$ of index one and one rest simplex $\tau _2$ of index two and also, a red orbit O of index one. We have

$$\begin{aligned} C_2= & {} \left( \tau _2, O^1_{1}\right) ,\\ C_1= & {} \left( ve_1, he_1, O^0_ {1} \right) , \\ C_0= & {} \left( p_o \right) . \end{aligned}$$

$\partial _2 \tau _2 = 1. ve_1 + 1. he_1 \ne 0$; also, $\partial _2 O^1_{1}=0$ as there is no orbit of index zero here. Therefore, $O^1_{1}$ is the only generator for $H_2(M, \mathbb {Z}_2)$.

$\partial _1 ve_1 = 2. p_0 =0 =\partial _1 he_1$ but since $ve_1 + he_1$ is in the image of $\partial _2$, $ve_1 - he_1$ is one generator for $H_1(M, \mathbb {Z}_2)$. $\partial _1 O^0_ {1}= 2. p_0 =0$ and therefore, $O^0_ {1}$ is the other generator of $H_1(M, \mathbb {Z}_2)$. $\partial _0 p_0= 0$ and it is the generator for $H_0(M, \mathbb {Z}_2)$.

4. Finally, to compute the Floer homology groups of the depicted cube, we consider a vector field V that has two (orange and yellow) rest simplices of index two at the top $\tau ^N_2$ and at the bottom $\tau ^S_2$ and three different orbits, one blue orbit $(bO)_0$ of index zero, one green orbit $(gO)_0$ of index zero and a red orbit $(rO)_1$ of index one.

$$\begin{aligned} C_2= & {} \left( \tau ^N_2, \tau ^S_2, (rO)^1_{1}\right) , \\ C_1= & {} \left( (rO)^0_ {1}, (bO)^1_ {0}, (gO)^1_ {0} \right) , \\ C_0= & {} \left( (bO)^0_ {0}, (gO)^0_ {0} \right) . \end{aligned}$$

$\partial _2 \tau ^N_2 = 1. (gO)^1_ {0} \ne 0$; $\partial _2 \tau ^S_2 = 1. (bO)^1_ {0} \ne 0$; $\partial _2(rO)^1_{1}= 1. (gO)^1_ {0} + 1. (bO)^1_ {0} \ne 0$ but $\partial _2 ( \tau ^N_2 + \tau ^S_2 - (rO)^1_{1})= 0$ and therefore, we have one generator for $H_2(M, \mathbb {Z}_2)$.

$\partial _1 (rO)^0_ {1}= 1. (bO)^0_ {0} + 1. (gO)^0_ {0} \ne 0$. $\partial _1 (bO)^1_ {0} = 0= \partial _1 (gO)^1_ {0}$, but since both $(bO)^1_ {0}$ and $(gO)^1_ {0}$ are in the image of $\partial _2$, we have no generator for $H_1(M, \mathbb {Z}_2)$. Finally, $\partial _0 (bO)^0_ {0}= 0 = \partial _0 (gO)^0_ {0}$, but as $(bO)^0_ {0} + (gO)^0_ {0}$ is in the image of $\partial _1$, we have one single generator for $H_0(M, \mathbb {Z}_2)$.