Introduction

The Black–Scholes model has been introduced based on the geometric Brownian motion to providing a closed-form pricing formula for the European options and describing the behavior of underlying asset prices [1,2,3]. The assumptions of the Black–Scholes model are unrealistic due to its inability to generate volatility satisfying the market observations, being nonnegative and mean-reverting [4,5,6]. To overcome this limitation, in 1993, Heston suggested Heston’s stochastic volatility (HSV) model [6]. The HSV model has been extended in finance for modeling the dynamics of implied volatilities and providing their user with simple breakeven accounting conditions for the profit and loss (S&P) of a hedged position [2, 7,8,9,10,11,12,13,14,15,16,17].

The HSV model, in the risk-neutral measure, is presented as follows

$$\begin{aligned} \left( \begin{array}{c} {{\mathscr {D}}}_{t}S(t)\\ {{\mathscr {D}}}_{t}V(t)\\ \end{array} \right) =\left( \begin{array}{c} rS(t) \\ \kappa (\theta -V(t)) \\ \end{array} \right) +\left( \begin{array}{cc} \sqrt{V(t)}S(t) &{} 0 \\ \rho \sigma \sqrt{V(t)} &{} \sigma \sqrt{V(t)(1-\rho ^2)} \\ \end{array} \right) \left( \begin{array}{c} \frac{{\text {d}}\omega _1}{{\text {d}}t} \\ \frac{{\text {d}}\omega _2}{{\text {d}}t} \\ \end{array} \right) , \end{aligned}$$
(1)

where \({{\mathscr {D}}}_{t}[\cdot ]\equiv \frac{{\text {d}}}{{\text {d}}t}[\cdot ]\) is the integer-order derivative operator, S(t) denotes the stock price, and V(t) denotes it’s return variance at time t that referred to in the literature as volatility [18]. The parameters r and \(\theta\) show the risk-free rate and the volatility long-run mean, respectively. Moreover, the parameter \(\kappa\) reveals the mean reversion rate toward \(\theta\) that controls the speed volatility going back to its average value. The volatility of volatility, \(\sigma\), is a significant risk factor that depicts the kurtosis in the stock return rate distribution. The Brownian motions, \(\omega _1(t)\) and \(\omega _2(t)\) with correlation coefficient, \(\rho \in [-1,1]\), are in the risk-neutral measure.

Despite its popularity, research on efficient discretizations of the continuous time dynamics of the Heston model has generated less attention by researchers. In 2006, an exact simulation technique was suggested by Broadie and Kaya for the HSV model [19]. Subsequently, in [20], a simulation scheme including the quadratic-exponential technique has been developed, and in [21], a second-order discretization scheme has been discussed. Along the same line of thought, the drift-implicit Milstein algorithm for the volatility [22], a Euler discretization for the log-Heston price [16] and an analytic approach for degenerate parabolic problem associated with the HSV model [17] were presented.

In the last decades, the theory of fractional calculus was motivated as a useful mathematical tool to handle application of associated concepts in the areas of physics, chemistry, economics, finance and engineering sciences [23,24,25,26,27,28,29,30,31,32,33,34]. To the author’s best knowledge, while numerous stochastic volatility models driven by fractional Brownian motion have been considered [35,36,37,38], stochastic volatility models with fixed-order and variable-order fractional derivative operators have not been carried out and this topic is far from being fully explored. More recently, just a numerical discretization technique has been proposed for approximation of a class of fractional stochastic differential equations driven by Brownian motion [39].

In this work, we assume that Brownian motions, \(\omega _1(t)\) and \(\omega _2(t)\), \(t\ge 0\), be real continuous functions that defined on a filtered probability space \(({\varOmega }, {\mathcal {F}}, {\mathbb {P}})\) with a normal filtration \(({\mathcal {F}}_t)_{t\ge 0}\). We consider the variable-order fractional HSV (VOF-HSV) model as

$$\begin{aligned} \left( \begin{array}{c} {_{0}^{\nu o}{\mathscr {D}}^{\gamma (\cdot )}_{t}}S(t)\\ {_{0}^{\nu o}{\mathscr {D}}^{\beta (\cdot )}_{t}}V(t)\\ \end{array} \right) =\left( \begin{array}{c} rS(t) \\ \kappa (\theta -V(t)) \\ \end{array} \right) +\left( \begin{array}{cc} \sqrt{V(t)}S(t) &{} 0 \\ \rho \sigma \sqrt{V(t)} &{} \sigma \sqrt{V(t)(1-\rho ^2)}\\ \end{array} \right) \left( \begin{array}{c} \frac{{\text {d}}\omega _1}{{\text {d}}t} \\ \frac{{\text {d}}\omega _2}{{\text {d}}t} \\ \end{array} \right) , \end{aligned}$$
(2)

where \(\frac{1}{2}<\gamma (t),\beta (t)\le 1\). The symbols \({_{0}^{\nu o}{\mathscr {D}}^{\gamma (\cdot )}_{t}}[\cdot ]\) and \({_{0}^{\nu o}{\mathscr {D}}^{\beta (\cdot )}_{t}}[\cdot ]\) are the fractional derivative operators of variable-order \(\gamma (t)\in {\mathbb {R}}^+\) and \(\beta (t)\in {\mathbb {R}}^+\), respectively. In general, variable-order fractional derivative operator was defined by Lorenzo and Hartley as [40]

$$\begin{aligned} {}_{0}^{\nu o}{{\mathscr {D}}}^{\gamma (\cdot )}_{t}u(t)=\frac{1}{{\varGamma }(m-\gamma (t))}\int _{0}^t\frac{u^{(m)}(\zeta ){\mathrm {d}{\zeta }}}{(t-\zeta )^{\gamma (t)+1-m}}\qquad m-1<\gamma (\cdot )\le m, \end{aligned}$$
(3)

where u(t) is \((m-1)\), \(m\in {\mathbb {N}}\), times continuously differentiable and \(u^{(m)}(t)\) is once integrable, \(\zeta\) is an auxiliary variable that belongs to the interval [0, t], and \({\varGamma }(\cdot )\) denotes the Gamma function. The concept and properties of variable-order fractional derivative operators and their application have been discussed in [41,42,43,44,45].

The outline of the paper is organized as follows. In “Optimal VOF-HSV model” section, the tuning technique is described for designing optimal VOF-HSV model for US stock market. For this propose, a discretization algorithm for the VOF-HSV model is proposed and followed by an optimization technique, genetic algorithm (GA), for tuning the unknown parameters in the VOF-HSV model. The advantages of using the VOF-HSV model are shown and verified by considering different performance criteria in “Numerical results” section. Finally, “Conclusion” section draws the conclusions.

Optimal VOF-HSV model

Throughout this paper, we let \({\varLambda }=[0,T]\) with a uniform grid \(t_{j}=jh\), \(j=0,1,\ldots ,n\), \(n\in {\mathbb {Z}}^+\), such that \(n+1=\frac{T}{h}\), and \(\gamma _n=\gamma (t_n)\), \(\beta _n=\beta (t_n)\), \(S_n=S(t_n)\) and \(V_n=V(t_n)\). In this section, an optimization strategy is formulated based on discretizing the equations in (2) and minimizing performance index under the following propositions.

Proposition 2.1

[46] The discretized expression of variable-order fractional derivative \(_{0}^{\nu o}{\mathscr {D}}^{\gamma (\cdot )}_{t} [\cdot ]\) in (3) is obtained by the forward finite-difference approximation (M-algorithm) as

$$\begin{aligned} {}_{0}^{\nu o}{\mathscr {D}}^{\gamma (\cdot )}_{t_{n+1}}u(t)=\frac{h^{-\gamma _{n+1}}}{{\varGamma }(m+1-\gamma _{n+1})}\sum _{j=0}^{n}\psi _{m,n,j}{\varDelta }_h^{m}u_{n-j}+ {\mathcal {O}}(h^{m+1-\gamma _n}), \end{aligned}$$
(4)

where h denotes the uniform step size, \(\psi _{m,n,j}=[{(j+1)}^{m-\gamma _n}-j^{m-\gamma _n}]\),

$$\begin{aligned} {\varDelta }_{h}^{m}u(t)=\sum _{i=0}^m(-1)^i\Bigg (\begin{array}{cc} m\\ i \end{array}\Bigg )u(t+(m-i)h), \end{aligned}$$

where \({\mathcal {O}}(\cdot )\) denotes convergence order of approximation.

Proposition 2.2

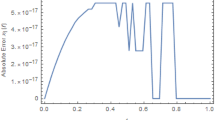
Let \(0<\gamma (t)\le 1\). Assume that u(t) be a function in \({\mathbb {L}}^2({\varOmega }, {\mathcal {F}}_t,{\mathbb {P}})\) and for every subinterval \(t\in [t_j,t_{j+1}]\subseteq {\varLambda }\), \(u(t)\in C^2[t_j,t_{j+1}]\) and \(\Vert u''(t)\Vert \le \varrho\), \(j=0,1,\ldots ,n\). Then, there exists an \(\gamma _{n+1}\) dependent constant, i.e., \(C_{\gamma _{n+1}}>0\), such that the truncated error of the variable-order fractional derivative operator obtained by the M-algorithm satisfies

$$\begin{aligned} {\mathbb {E}}\left[ \left| {_{0}^{\nu o}{\mathscr {D}}^{\gamma (\cdot )}_{t_{n+1}}}u(t)-{\left( {_{0}^{\nu o}{\mathscr {D}}^{\gamma (\cdot )}_{t_{n+1}}{u}(t)}\right) _{M-algorithm}}\right| \right] \le {C_{\gamma _{n+1}}}{h}^{2-\gamma _{n+1}}= {\mathcal {O}}(h^{2-\gamma _{n+1}}), \end{aligned}$$
(5)

where \(\displaystyle {C_{\gamma _{n+1}}=\frac{{(n+1)}^{1-\gamma _{n+1}}\varrho }{2{\varGamma }(2-\gamma _{n+1})}}\).

Proof

Assume that \(u_j\) be an approximation of \(u_j(t)\) in the subinterval \([t_j,t_{j+1}]\subseteq [0,t_{n+1})=[0,T),~j=0,1,\ldots ,n\) and

$$\begin{aligned} {\mathscr {E}}_j(t)=u'_{j}-u'_j(t)=\frac{h}{2}u''_j(t). \end{aligned}$$

Let \({\mathscr {E}}(t)\) be the error function in the interval \((0,t_n]\); therefore,

$$\begin{aligned}&{\mathbb {E}}\left[ \left| {{}_{0}^{\nu o}{\mathscr {D}}^{\gamma (\cdot )}_{t_{n+1}}}u(t)-{\left( {_{0}^{\nu o}{\mathscr {D}}^{\gamma (\cdot )}_{t_{n+1}}{u}(t)}\right) _{M-algorithm}}\right| \right] \\&=\frac{1}{{\varGamma }(1-\gamma _{n+1})}{\mathbb {E}}\left[ \sum _{j=0}^{n}\int ^{t_{j+1}}_{t_j} \Vert \frac{{\mathscr {E}}_j(\zeta )}{(t_{n+1}-\zeta )^{\gamma _{n+1}}}\Vert d\zeta \right] \\&= \frac{1}{{\varGamma }(1-\gamma _{n+1})}{\mathbb {E}}\left[ \sum _{j=0}^{n}\int ^{t_{j+1}}_{t_j} \Vert \frac{h u''_j(t)}{2(t_{n+1}-\zeta )^{\gamma _{n+1}}}\Vert d\zeta \right] \\&\le \frac{ht_{n+1}^{1-\gamma _{n+1}}\varrho }{2{\varGamma }(2-\gamma _{n+1})}\\&= \frac{{(n+1)}^{1-\gamma _{n+1}}\varrho h^{2-\gamma _{n+1}}}{2{\varGamma }(2-\gamma _{n+1})}= {\mathcal {O}}({h}^{2-\gamma _{n+1}}). \end{aligned}$$

\(\square\)

Using Propositions 2.1, the discretized equations of VOF-HSV model (2) are derived as follows

\(\displaystyle {\left( \begin{array}{c} S_{n+1}\\ V_{n+1}\\ \end{array} \right) =\left( \begin{array}{c} \left( rh^{\gamma _n}{\varGamma }(2-\gamma _n)+1\right) S_n-{\varPsi }_{h,n,j}\\ \kappa h^{\beta _n}{\varGamma }(2-\beta _n)(\theta -V_n)+V_n-{\varPhi }_{h,n,j}\\ \end{array} \right) }\)

$$\begin{aligned} \qquad \qquad \qquad +\left( \begin{array}{cc} h^{\gamma _n-1}{\varGamma }(2-\gamma _n)\sqrt{V_n}S_n &{} 0 \\ \rho \sigma h^{\beta _n-1}{\varGamma }(2-\beta _n)\sqrt{V_n}\qquad &{} \sigma h^{\beta _n-1}{\varGamma }(2-\beta _n)\sqrt{V_n(1-\rho ^2)}\\ \end{array} \right) \left( \begin{array}{c} {\varDelta }_h\omega _{1,n} \\ {\varDelta }_h\omega _{2,n}\\ \end{array} \right) . \end{aligned}$$
(6)

where \({\varPsi }_{h,n,j}=\sum _{j=1}^{n}\psi _{1,n,j}{\varDelta }_hS_{n-j}\) and \({\varPhi }_{h,n,j}=\sum _{j=1}^{n}\psi _{1,n,j}{\varDelta }_hV_{n-j}\).

There are different performance criteria for measuring goodness of fit typically summarizing discrepancy between observed values and estimated values by the prediction model. We analyze the performance of proposed models, in the viewpoint of root-mean-square error (RMSE) or the residual standard deviation defined as

$$\begin{aligned} \text {RMSE}=\frac{\text {RSS}}{\sqrt{N-p-1}}, \end{aligned}$$
(7)

where \(\text {RSS}\) denotes the square root of residual sum of squares, N and p are the number of observations and parameters in the equation, respectively [47].

For estimating the Bayesian information criterion (BIC), we apply the following formula [47]

$$\begin{aligned} \text {BIC}=N\times \ln \left( \frac{\text {RSS}}{N}\right) +2\ln (N). \end{aligned}$$
(8)

Moreover, the relative quality of statistical models for a given set of data can be analyzed in the perspective of the Akaike information criterion (AIC) defined as [48]

$$\begin{aligned} \text {AIC}=N\times \ln (\text {RSS})+2p. \end{aligned}$$
(9)

A lower \(\text {RMSE}\), \(\text {BIC}\) or \(\text {AIC}\) value indicates a better fit.

Numerical results

In this section, fixed-order and VOF-HSV models are used to estimate the behavior of the price of S&P 500 index of American options. The S&P 500 is a US stock market index that covers all the large market public companies recorded on the New York Stock Exchange (NYSE) or National Association of Securities Dealers Automated Quotations (NASDAQ) [49]. For practical applicability, in this work, the parameters of the financial market model are chosen based on [50]. In [50], authors obtained estimate values of parameters for the typical Heston model by considering S&P 500 index returns. Throughout the numerical analysis, the main parameters satisfy that the mean reversion rate converges to \(\kappa =2.75\), the long-run mean of the volatility converges to \(\theta =0.035\), the volatility of volatility converges to \(\sigma =0.425\), and the correlation coefficient converges to \(\rho =-0.4644\).

For constructing VOF-HSV model, \(\gamma (t)=c_1+c_2t\) and \(\beta (t)=c_3+c_4t\) functions where \(0\le {c_i}\le 1\), \(i=1,\ldots ,4\), with four unknown parameters being considered. Next, an optimization method, GA, is used to find the optimal values of the unknowns \(c_i\), \(i=1,\ldots ,4\), by minimizing the mean absolute error (MAE) at the discretized points goodness, that is, by minimizing \(\text {MAE}=\frac{1}{N}\sum _{n=1}^{N}|S(t_n)-\hat{S}_n|\), where \(S(t_n)\) and \(\hat{S}_n\) are the discretized value of the model and experimental value, respectively. The optimization algorithm is based on discretizing  (6) by using the M-algorithm formulated in Propositions 2.1 with \(n =1227\) equal mesh points, corresponding to observed data, so that approximation error can be determined by using Proposition  2.2. All the computations are performed under Maple v18 on an Intel (R) Core (TM) i7-7500U CPU @ 2.70 GHz machine.

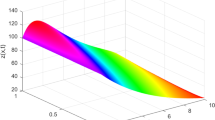
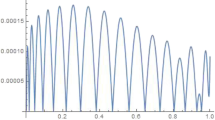
Table 1 shows the obtained values for the unknown parameters of the integer-order (i.e., \(c_1=c_3=1\) and \(c_2=c_4=0\)), the fixed-order fractional (i.e., \(c_2=c_4=0\)), and the VOF-HSV models when \(t \le 1\). In Table 2, the results in the perspective of the indices \({\text {RMSE}}\), \(\text {AIC}\) and \({\text {BIC}}\) reveal that there is evidence of positive serial correlation in all considered cases of HSV models and the variable-order fractional model gives the best fitting out of the all proposed models. Moreover, there is a significant improvement in the response estimation by using the fractional HSV models. Figures 1 and 2 depict the numerical simulations of stock price, S(t), and it’s return variance, V(t), with integer-order (i.e., \(\gamma (t)=\beta (t)=1\)), the fixed-order fractional (i.e., \(\gamma (t)=0.8960\) and \(\beta (t)=0.9292\)), and the variable-order fractional (i.e., \(\gamma (t)=0.9010+0.0890t\) and \(\beta (t)=0.9088+0.0869t\)) HSV models with \(n =1227\) equal mesh points in the interval [0, 1].

Table 1 The MAEs and optimal parameters of the integer-order, the fixed-order fractional and VOF-HSV models for \(\gamma (t)=c_1+c_2t\) and \(\beta (t)=c_3+c_4t\) in the interval [0, 1]
Full size table
Table 2 Comparison of RMSE, AIC and BIC of integer-order and optimal fixed- and VOF-HSV models with \(n =1227\) equal mesh points in the interval [0, 1]
Full size table
Fig. 1
figure 1

The experimental stock price and the variation of the orders \(\gamma (t)\) and \(\beta (t)\) in the approximated HSV models for the experimental stock price tests

Full size image
Fig. 2
figure 2

The experimental stock price volatility and the variation of the orders \(\gamma (t)\) and \(\beta (t)\) in the approximated HSV models for the experimental volatility tests

Full size image

Since proposed models cannot be solved analytically using the standard mathematical techniques, the upper 95% confidence interval (CI) was utilized to predict the behavior of sample trajectories of solutions by means of the approximated HSV models. Moreover, the statistical analysis of the process is provided in Table 3. In Table 3, the approximation values of the mean, median, first and third quartiles, kurtosis, skewness, standard deviation (STD) and 95% CI of the 50 simulated trajectories in time for several variation of orders for stock prices are listed.

Table 3 Approximation values of the mean, median, first and third quartiles, kurtosis, skewness, STD and 95% CI of the 50 simulated trajectories for stock prices for various values of \(\gamma (t)\) and \(\beta (t)\), with \(h =\frac{1}{1227}\) at \(T=1\)
Full size table

The comparison of experimental stock price and simulation results of 50 trajectories of the stock prices of proposed HSV models is shown in Fig. 3. In Fig. 3, the red circles indicate the trajectories corresponding to the observed stock price. The blue lines represent the simulation results of 50 trajectories of the approximated stock prices (Fig. 3, left column). The black and green lines indicate the 95% CI area of the 50 trajectories and the empirical mean of the process (Fig. 3. right column), respectively, for proposed HSV models. The purple lines are first and third quartiles of these models.

Fig. 3
figure 3

The red circles indicate the trajectories corresponding to the observed stock price. The blue lines represent the simulation results of 50 trajectories of the approximated stock prices for proposed HSV models (left column). The black and the purple lines indicate the 95% CI and first and third quartiles area of the 50 trajectories, respectively, and green line is the empirical mean of the process (right column), for proposed HSV models

Full size image

Conclusion

It has been shown that using fixed-order and variable-order fractional derivative operators instead of an integer-order derivative operator in models can apparently lead to better results since one has an extra freedom degree. In this paper, the objective of introducing modified Heston model was to capture the complexities in simulating the scenarios of equity movement in finance. The proposed Heston’s stochastic volatility models, due to random volatility and memory or hereditary properties, have more flexibility with market data than the constant volatility models. In this study, an optimization technique, genetic algorithm, was utilized to find an optimal set of unknown parameters of models. For this propose, an explicit numerical technique has been developed for solving Heston’s stochastic volatility models. Furthermore, experimental stock price tests of a US stock market were used to estimate fixed-order and variable-order fractional Heston’s stochastic volatility models. It was also shown that proposed fractional Heston’s stochastic volatility models are significantly better in estimating the stock price in comparison to integer-order Heston’s stochastic volatility models. Moreover, variable-order fractional Heston’s stochastic volatility model is superior to fixed-order fractional Heston’s stochastic volatility model.