Quintic B-spline method for time-fractional superdiffusion fourth-order differential equation

Abstract

The main objective of this paper is to obtain the approximate solution of superdiffusion fourth-order partial differential equations. Quintic B-spline collocation method is employed for fractional differential equations (FPDEs). The developed scheme for finding the solution of the considered problem is based on finite difference method and collocation method. Caputo fractional derivative is used for time fractional derivative of order $\alpha$, $1<\alpha <2$. The given problem is discretized in both time and space directions. Central difference formula is used for temporal discretization. Collocation method is used for spatial discretization. The developed scheme is proved to be stable and convergent with respect to time. Approximate solutions are examined to check the precision and effectiveness of the presented method.

Introduction

The idea of differentiation and integration to non integer order has been studied in fractional calculus. The subject fractional calculus is the generalized form of classical calculus. It is as old as classical calculus but getting more attention these days due to its applications in various fields, such as science and engineering. Oldham and Spanier [1], Podlubny [3], and Miller and Ross [2] provide the history and a comprehensive treatment of this subject.

In recent decades, it has been observed by many mathematicians, scientists, and researchers that non-integer operators (differential and integral) play an important role in describing the properties of physical phenomena. Fractional derivatives and integrals efficiently describe the history and inherited properties of different processes and equipments. It has further been observed that fractional models are more efficient and accurate than already developed classical models. The mathematical modeling of real world problems, such as earthquake, traffic flow, fluid flow, signal processing, and viscoelastic problems, results in FPDEs.

A fourth-order linear PDE is defined as

$$\begin{aligned} \nonumber \frac{\partial ^{2}v}{\partial t^{2}} +\nu \frac{\partial ^{4}v}{\partial z^{4}}=h(z,t). \end{aligned}$$

The fourth-order problems play a significant role for the development of engineering and modern science. For example, window glasses, floor systems, bridge slabs, etc. are modeled by fourth-order PDEs. It also represents beam problem where v is the transversal displacement of the beam, $\nu$ is the ratio of flexural rigidity of the beam to its mass per unit length, t is time, and x is space variable, h(x, t) is the dynamic driving force acting per unit mass.

The considered equation, is the superdiffusion fourth-order partial differential equation, which has the following form

$$\begin{aligned} \frac{\partial ^{\alpha }v}{\partial t^{\alpha }}+\nu \frac{\partial ^{4} v}{\partial z^{4}}= q(z,t),\quad z\in [a,b]=\Omega ,\quad t_{0}<t\le t_{f}, 1<\alpha <2, \end{aligned}$$

(1.1)

where $t_{0}, t_{f}$ represents initial and final time, respectively.

The time-fractional superdiffusion fourth-order problems play an important role in modern science and engineering. For example, airplane wings and transverse vibrations of sustained tensile beam can be modeled as plates with different boundary supports which are successfully governed by superdiffusion fourth-order differential equations.

The given problem is solved with initial conditions

$$\begin{aligned} v(z,t_{0})= f_{0}(z), \quad v_{t}(z,t_{0})=f_{1}(z), \quad a\le z\le b. \end{aligned}$$

Following three boundary conditions are used for solving Eq. (1.1)

• I.
  $$\left\{ \begin{array}{ll} v(a,t)=v(b,t)=0,\\ v_{z}(a,t)=v_{z}(b,t)=0, \quad t_{0}\le t\le t_{f}. \end{array}\right.$$
• II.
  $$\left\{ \begin{array}{ll} v(a,t)=v(b,t)=0,\\ v_{zz}(a,t)=v_{zz}(b,t)=0, \quad t_{0}\le t\le t_{f}. \end{array}\right.$$
• III
  $$\left\{ \begin{array}{ll} v(a,t)=v(b,t)=0,\\ v_{zz}(a,t)-Q v_{z}(a,t)=v_{zz}(b,t)-Q v_{z}(b,t)=0, \quad t_{0}\le t\le t_{f}, \end{array}\right.$$

where Q is an arbitrary constant.

Caputo fractional derivative is defined as

$$\frac{\partial ^{\alpha }v(z,t)}{\partial t^{\alpha }}= \left\{ \begin{array}{ll} \frac{1}{\Gamma (2-\alpha )}\int _{0}^{t} \frac{\partial ^{2} v(z,s)}{\partial s^{2}} \frac{d s}{(t-s)^{\alpha -1}} ,& \quad 1< \alpha < 2,\\ \frac{\partial ^{2} v(z,t)}{\partial t^{2}}, & \quad \alpha =2. \end{array}\right.$$

Collocation method is widely used to provide the solution of partial differential equations. Depending on the situation, some times, it is useful to find the solution of FPDEs at various locations in the given problem domain, then the spline solutions guarantee to give the information of spline interpolation between mesh points.

In many situations, it is harder to calculate the analytical solutions of fractional PDEs using analytical methods. Due to this reason, the mathematicians are motivated to develop numerical methods for the approximate solution of FPDEs. The approximate methods for solving FPDEs have become popular among the researchers in the last 10 years. A variety of approximate techniques were used for finding the solution of FPDEs, such as the FDM, FEM, FVM, and the collocation method etc.

Many authors applied different numerical methods to find the solution of fractional PDEs.

Siddiqi and Arshed [7] developed a numerical scheme for the solution of time-fractional fourth-order partial differential equation with fractional derivative of order $\alpha$ $(0<\alpha <1)$. Lin and Xu [6] developed a numerical scheme for time-fractional diffusion equation with fractional derivative of order $\alpha , (0<\alpha <1)$. Yang et al. [11] developed a novel numerical scheme for solving fourth-order partial integro-differential equation with a weakly singular kernel. Yang et al. [8] developed a quasi-wavelet-based numerical method for solving fourth-order partial integro-differential equations with a weakly singular kernel. Khan et al. [9], proposed a numerical method for the solution of time-fractional fourth-order differential equations with variable coefficients using Adomian decomposition method (ADM) and He’s variational iteration method (HVIM). Zhang and Han [10] developed a quasi-wavelet-based numerical method for time-dependent fractional partial differential equation. Zhang et al. [12] proposed quintic B-spline collocation method for the numerical solution of fourth-order partial integro-differential equations with a weakly singular kernel. Khan et al. [4] used sextic spline solution for solving fourth-order parabolic partial differential equation. Dehghan [5] used finite difference techniques for the numerical solution of partial integro-differential equation arising from viscoelasticity. In [15], Bhrawy and Abdelkawy used fully spectral collocation approximation for solving multi-dimensional fractional Schrodinger equations. Bhrawy et al. [16] proposed a new formula for fractional integrals of Chebyshev polynomials and application for solving multi-term fractional differential equations. Bhrawy [17] developed a new spectral algorithm for a time-space fractional partial differential equations with subdiffusion and superdiffusion. In [18], Bhrawy et al. gave a review of operational matrices and spectral techniques for fractional calculus. Bhrawy et al. [19] proposed Chebyshev–Laguerre Gauss–Radau collocation scheme for solving time fractional sub-diffusion equation on a semi-infinite domain. Bhrawy [20] developed a space-time collocation scheme for modified anomalous subdiffusion and nonlinear superdiffusion equations. In [21], Doha et al. developed an efficient Legendre Spectral Tau matrix formulation for solving fractional sub-diffusion and reaction sub-diffusion equations. Bhrawy [22] proposed a highly accurate collocation algorithm for 1 + 1 and 2 + 1 fractional percolation equations. In [23], Bhrawy and Zaky used fractional-order Jacobi tau method for a class of time-fractional PDEs with variable Coefficients.

This paper is designed to determine the approximate solution of superdiffusion fourth order PDEs. The approximate solution is based on central difference formula and B-spline collocation method.

The paper is divided into six sections. The quintic B-spline basis function is given in Sect. 2. The finite difference approximation for time discretization of the given problem is discussed in Sect. 3. The stability and convergence of temporal discretization are established. Space discretization based on B-spline collocation technique is discussed in Sect. 4. Approximate solutions are obtained in Sect. 5 which support the theoretical results. The conclusion is given is Sect. 6.

Quintic B-spline

The problem domain [a, b] has been subdivided into N elements having uniform step size h with knots $z_{j}, j=0,1,2,\ldots ,N$ such that $\{a=z_{0}<z_{1}<z_{2}<\ldots <z_{N}=b\}$, $h= z_{j}-z_{j-1}$, $j=1, 2,\ldots , N$.

To define basis functions for quintic B-spline, it is first needed to introduce ten additional knots, $z_{-5},z_{-4},z_{-3},z_{-2},z_{-1},z_{N+1},z_{N+2},z_{N+3},z_{N+4},z_{N+5}$ such that $z_{-5}<z_{-4}<z_{-3}<z_{-2}<z_{-1}<z_{0}$ and $z_{N}<z_{N+1}<z_{N+2}<z_{N+3}<z_{N+4}<z_{N+5}.$

The quintic B-spline basis functions $Q_{j}(z)$, $j=-2, \ldots ,N+2$ are defined as

$$Q_{j} (z)=\left\{ \begin{array}{ll} \sum\limits_{s=j-3}^{s=j+3}\frac{(z_{s}-z)_{+}^{5}}{\prod '(z_{s})}, & z\in [z_{j-3},z_{j-3}],\\ 0 , & \text {otherwise} \end{array}\right.$$

The approximate solution $V^{k+1}(z)$ at $k+1$ time level to the exact solution $v^{k+1}(z)$ is obtained as a linear combination of quintic B-spline basis functions $Q_{j}(z)$ as

$$\begin{aligned} V^{k+1}(z)=\sum ^{N+2}_{j=-2}c_{j}(t)Q_{j}(z), \end{aligned}$$

(2.1)

where $c_{j}$ are unknowns. Using Eq. (2.1) and basis functions, the approximate solution V and its derivatives at the nodes $z_{j}$, can be calculated as

$$\begin{aligned} V(z_{j}) & = c_{j+2}+26c_{j+1}+66c_{j}+26c_{j-1}+c_{j-2},\\ V^{(1)}(z_{j}) & = \frac{5}{h}\left( c_{j+2}+10c_{j+1}-10c_{j-1}-c_{j-2}\right) ,\\ V^{(2)}(z_{j}) & = \frac{20}{h^{2}}\left( c_{j+2}+2c_{j+1}-6c_{j}+2c_{j-1}+c_{j-2}\right) ,\\ V^{(3)}(z_{j}) & = \frac{60}{h^{3}}\left( c_{j+2}-2c_{j+1}+2c_{j-1}-c_{j-2}\right) ,\\ V^{(4)}(z_{j}) & = \frac{120}{h^{4}}\left( c_{j+2}-4c_{j+1}+6c_{j}-4c_{j-1}+c_{j-2}\right) . \end{aligned}$$

Time discretization

Caputo fractional derivative is used for temporal discretization. Let $t_{k}=k\Delta t$, $k=0,1,2,\ldots ,K$, where $\Delta t=\frac{t_{f}}{K}$ is the time step size and $t_{f}$ be the final time. Caputo fractional derivative is discretized using central difference approximation as

$$\begin{aligned} \frac{\partial ^{\alpha }v(z,t_{k+1})}{\partial t^{\alpha }}= & {} \frac{1}{\Gamma (2-\alpha )}\int _{0}^{t_{k+1}} \frac{\partial ^{2} v(z,s)}{\partial s^{2}} \frac{d s}{(t_{k+1}-s)^{\alpha -1}}\nonumber \\= & {} \frac{1}{\Gamma (2-\alpha )}\sum ^{n}_{l=0}\int _{t_{l}}^{t_{l+1}}\frac{\partial ^{2} v(z,s)}{\partial s^{2}} \frac{ds}{(t_{k+1}-s)^{\alpha -1}},\nonumber \\= & {} \frac{1}{\Gamma (2-\alpha )}\sum ^{k}_{l=0}\frac{v(z,t_{l+1})-2v(z,t_{l})+v(z,t_{l-1})}{\Delta t^{2}}\int _{t_{l}}^{t_{l+1}} \frac{ds}{(t_{k+1}-s)^{\alpha -1}}+r^{k+1}_{\Delta t},\nonumber \\= & {} \frac{1}{\Gamma (2-\alpha )}\sum ^{k}_{l=0}\frac{v(z,t_{l+1})-2v(z,t_{l})+v(z,t_{l-1})}{\Delta t^{2}}\int _{t_{k-l}}^{t_{k+1-l}} \frac{d\tau }{\tau ^{\alpha -1}}+r^{k+1}_{\Delta t},\nonumber \\= & {} \frac{1}{\Gamma (2-\alpha )}\sum ^{k}_{l=0}\frac{v(z,t_{k+1-l})-2v(z,t_{k-l})+v(z,t_{k-l-1})}{\Delta t^{2}}\int _{t_{l}}^{t_{l+1}} \frac{d\tau }{\tau ^{\alpha -1}}+r^{k+1}_{\Delta t},\nonumber \\= & {} \frac{1}{\Gamma (3-\alpha )}\sum ^{k}_{l=0}\frac{v(z,t_{k+1-l})-2v(z,t_{k-l})+v(z,t_{k-l-1})}{\Delta t^{\alpha }}\left( (l+1)^{2-\alpha }-l^{2-\alpha }\right) +r^{k+1}_{\Delta t},\nonumber \\= & {} \frac{1}{\Gamma (3-\alpha )}\sum ^{k}_{l=0}b_{l}\frac{v(z,t_{k+1-l})-2v(z,t_{k-l})+v(z,t_{k-l-1})}{\Delta t^{\alpha }}+r^{k+1}_{\Delta t}, \end{aligned}$$

(3.1)

where $b_{l}=(l+1)^{2-\alpha }-l^{2-\alpha }$ and $b_{0}=1$ and $\tau =(t_{k+1}-s)$.

and

$$\begin{aligned} -b_{k}+(2b_{k}-b_{k-1})+\sum ^{k-1}_{l=1}\left( -b_{l-1}+2b_{l}-b_{l+1}\right) +(2b_{0}-b_{1})=1. \end{aligned}$$

The time discrete operator is represented by $D^{\alpha }$ and defined as

$$\begin{aligned} D^{\alpha }v(z,t_{k+1}):=\frac{1}{\Gamma (3-\alpha )}\sum ^{k}_{l=0}b_{l}\frac{v(z,t_{k+1-l})-2v(z,t_{k-l})+v(z,t_{k-l-1})}{\Delta t^{\alpha }}. \end{aligned}$$

Then Eq. (3.1) can be written as

$$\begin{aligned} \frac{\partial ^{\alpha }v(z,t_{k+1})}{\partial t^{\alpha }} &= D^{\alpha }v(z,t_{k+1})+r^{k+1}_{\Delta t}. \end{aligned}$$

(3.2)

The second order approximation of Caputo derivative as discussed in [13] is given as

$$\begin{aligned} \left| r^{k+1}_{\Delta t}\right|\le & {} E\Delta t^{2}, \end{aligned}$$

(3.3)

where E is a constant.

After approximating $\frac{1}{\Gamma (2-\alpha )}\int _{0}^{t_{k+1}} \frac{\partial ^{2} v(z,s)}{\partial s^{2}} \frac{d s}{(t_{k+1}-s)^{\alpha -1}}$ by $D^{\alpha }v(z,t_{k+1})$, the finite difference scheme according to (1.1) can be written as

$$\begin{aligned} D^{\alpha }v(z,t_{k+1})+\nu \frac{\partial ^{4} v(z,t_{k+1})}{\partial z^{4}}=q(z,t_{k+1}), \end{aligned}$$

$$\begin{aligned} \frac{1}{\Gamma (3-\alpha )}\sum ^{n}_{l=0}b_{l}\frac{v(z,t_{k+1-l})-2v(z,t_{k-l})+v(z,t_{k-l-1})}{\Delta t^{\alpha }}+\nu \frac{\partial ^{4} v(z,t_{k+1})}{\partial z^{4}}=q(z,t_{k+1}). \end{aligned}$$

The above equation can be rewritten as

$$\begin{aligned} v^{k+1}(z)+\alpha _{0}\nu ~\frac{\partial ^{4} v^{k+1}}{\partial z^{4}}= & {} -\,b_{k}v^{-1}(z)+(2b_{k}-b_{k-1})v^{0}(z)+\nonumber \\&+\,\sum ^{k-1}_{l=1}\left( -b_{l-1}+2b_{l}-b_{l+1}\right) v^{l}(z) +(2b_{0}-b_{1})v^{k}(z)\nonumber \\&+\,\alpha _{0}q^{k+1}(z),\qquad k=1,2,\ldots ,K-1 \end{aligned}$$

(3.4)

where $v^{k+1}(x)=v(x,t_{k+1})$ and $\alpha _{0}= \Gamma (3-\alpha )\Delta t^{\alpha }$,

Using the following initial conditions and the boundary conditions $(\mathrm{I, II, III})$

$$\begin{aligned} v(z,t_{0})=f_{0}(z),\quad z\in [a,b], \end{aligned}$$

(3.5)

$$\begin{aligned} \frac{\partial v(z,t_{0})}{\partial t}=f_{1}(z),\quad z\in [a,b], \end{aligned}$$

(3.6)

The developed method is a three time level method. To implement the developed method, it is first required to calculate $(v^{-1})$ and $(v^{0})$.

$$\begin{aligned} v^{-1}(z)=v(z,t_{0})-\Delta t v_{t}(z,t_{0}). \end{aligned}$$

$$\begin{aligned} v^{-1}(z)=f_{0}(z)-\Delta tf_{1}(z). \end{aligned}$$

In particular, for $k=0$, the scheme simply leads to

$$\begin{aligned} v^{1}(z)+\alpha _{0}~\nu \frac{\partial ^{4} v^{1}}{\partial z^{4}} =-b_{0}v^{-1}(z)+2b_{0}v^{0}(z)+\alpha _{0}q^{1}(z), \end{aligned}$$

(3.7)

where $v^{0}(z)=v(z,t_{0})=f_{0}(z)$.

Equations (3.4) and (3.7), along with initial conditions (3.5) and (3.6) and boundary conditions $(\mathrm I,II,III)$ form a whole set of the time-discrete problem of Eq. (1.1).

$r^{k+1}$ is the error term can be defined as

$$\begin{aligned} r^{k+1}:=\left( \frac{\partial ^{\alpha }v(z,t_{k+1})}{\partial t^{\alpha }}-D^{\alpha }v(z,t_{k+1})\right) . \end{aligned}$$

(3.8)

Using Eq. (3.3),

$$\begin{aligned} \left| r^{k+1}\right| =\left| r^{k+1}_{\Delta t}\right| \le E \Delta t^{2}, \end{aligned}$$

(3.9)

Some functional spaces endowed with standard norms and inner products, to be used hereafter, are defined as under

$$\begin{aligned} H^{2}(\Omega )=\left\{ w \in L^{2}(\Omega ),\frac{\mathrm{d} w}{\mathrm{d}x},\frac{\mathrm{d}^{2}w}{\mathrm{d}x^{2}}\in L^{2}(\Omega )\right\} , \end{aligned}$$

$$\begin{aligned} H_{0}^{2}(\Omega )=\left\{ w \in H^{2}(\Omega ),w|_{\partial \Omega }=0,\frac{\mathrm{d}w}{\mathrm{d}x}|_{\partial \Omega }=0\right\} , \end{aligned}$$

$$H^{m} (\Omega ) = \left\{ {w \in L^{2} (\Omega ),\frac{{{\text{d}}^{k} w}}{{{\text{d}}x^{k} }}{\text{for}}\;{\text{all}}\;{\text{positive}}\;{\text{integer}}\;k \le m} \right\},$$

where $L^{2}\left( \Omega \right)$ is the space of measurable functions whose square is Lebesgue integrable in $\Omega$. The inner products of $L^{2}\left( \Omega \right)$ and $H^{2}(\Omega )$ are defined, respectively, by

$$\begin{aligned} \left( v,w\right) =\int _{\Omega } wv \mathrm{d}x,\qquad \left( v,w\right) _{2}=\left( v,w\right) +\left( \frac{\mathrm{d}v}{\mathrm{d}x},\frac{\mathrm{d}w}{\mathrm{d}x}\right) +\left( \frac{\mathrm{d}^{2}v}{\mathrm{d}x^{2}},\frac{\mathrm{d}^{2}w}{\mathrm{d}x^{2}}\right) , \end{aligned}$$

and the corresponding norms by

$$\begin{aligned} \left\| w\right\| _{0}=\left( w,w\right) ^{\frac{1}{2}},\quad \quad \left\| w\right\| _{2}=\left( w,w\right) ^{\frac{1}{2}}_{2}. \end{aligned}$$

The norm $\left\| .\right\|$ of the space $H^{m}\left( \Omega \right)$ is defined as

$$\begin{aligned} \left\| w\right\| _{m}=\left( \sum _{k=0}^{m}\left\| \frac{\mathrm{d}^{k}w}{\mathrm{d}x^{k}}\right\| ^{2}_{0}\right) ^{\frac{1}{2}}. \end{aligned}$$

Instead of using the above standard $H^{2}$-norm, it is preferred to define $\Vert .\Vert _{2}$

$$\begin{aligned} \Vert w\Vert _{2}=\left( \Vert w\Vert _{0}^{2}+\alpha _{0}\nu \left\| \frac{\mathrm{d}^{2} w}{\mathrm{d} x^{2}}\right\| _{0}^{2}\right) ^{1/2}, \end{aligned}$$

(3.10)

where $\alpha _{0}= \Gamma (2-\alpha )\Delta t^{\alpha }$.

For the convergence and stability analysis, the following weak formulation of Eqs. (3.4) and (3.7) is needed, i.e., finding $v^{k+1} \in H_{0}^{2}(\Omega )$, such that for all $w \in H_{0}^{2}(\Omega )$,

$$\begin{aligned} \left( v^{k+1},w\right) +\alpha _{0} \nu \left( \frac{\partial ^{4}v^{k+1}}{\partial x^{4}},w\right)= & {} -b_{k}\left( v^{-1},w\right) +(2b_{k}-b_{k-1})\left( v^{0},w\right) \nonumber \\&+ \sum ^{k-1}_{l=1}\left( -b_{l-1}+2b_{l}-b_{l+1}\right) \left( v^{j},w\right) +(2b_{0}-b_{1})\left( v^{k},w\right) \nonumber \\&+\,\alpha _{0}\left( q^{k+1},w\right) , \end{aligned}$$

(3.11)

and

$$\begin{aligned} (v^{1},w)+\alpha _{0}\nu \left( \frac{\partial ^{4} v^{1}}{\partial x^{4}},w\right)= & {} -b_{0}(v^{-1},w)+2b_{0}(v^{0},w)+\alpha _{0}(q^{1},w). \end{aligned}$$

(3.12)

Discrete Gronwall inequality

If the sequences $\{a_{l}\}$ and $\{z_{l}\}$, $jl=1,2,$..., n, satisfy inequality

$$\begin{aligned} z_{l} \le \left( \sum _{j=1}^{l-1}a_{j}z_{j}+b\right) ,~~~l= 1, 2,\ldots , n \end{aligned}$$

where $a_{l}\ge 0$, $b\ge 0$, then the inequality

$$\begin{aligned} z_{l} \le b.\exp \left( \sum _{j=1}^{l-1}a_{j}\right) ,~~~l= 1, 2,\ldots , n. \end{aligned}$$

(3.13)

Stability and convergence analysis

Theorem 1

The proposed time-discrete scheme (3.6) is stable, if for all $\Delta t >0$, the following relation holds

$$\begin{aligned} \left\| v^{k+1}\right\| _{2} \le c\left( \left\| f_{0}\right\| _{0}+\Delta t \left| f_{1}\right\| _{0} +\alpha _{0}q^{k+1}\right) ,~~~k=0, 1, 2,\ldots , K-1, \end{aligned}$$

(3.14)

where $\Vert .\Vert _{2}$ is defined in (3.10).

Proof

For $k=0$, let $w=v^{1}$ in Eq. (3.11),

Equation (3.11) takes the following form

$$\begin{aligned} \left( v^{1},v^{1}\right) +\alpha _{0}\nu \left( \frac{\partial ^{4}v^{1}}{\partial x^{4}},v^{1}\right)= & {} -b_{0}\left( v^{-1},v^{1}\right) +2b_{0}\left( v^{0},v^{1}\right) +\alpha _{0}\left( q^{1},v^{1}\right) . \end{aligned}$$

Integrating the above equation, we have

$$\begin{aligned} (v^{1},v^{1})+\alpha _{0}\nu \left( \frac{\partial ^{2}v^{1}}{\partial x^{2}}, \frac{\partial ^{2}v^{1}}{\partial x^{2}}\right)= & {} -b_{0}(v^{-1},v^{1})+2b_{0}(v^{0},v^{1})+\alpha _{0}(q^{1},v^{1}) \end{aligned}$$

(3.15)

Due to boundary conditions on w all the boundary contributions disappeared.

Using the inequality $\Vert w\Vert _{0}\le \Vert w\Vert _{2}$ and Schwarz inequality Eq. (3.15) takes the following form

$$\begin{aligned} \left\| v^{1}\right\| _{2}^{2}\le & {} \left\| v^{-1}\right\| _{0}\left\| v^{1}\right\| _{0}+2\left\| v^{0}\right\| _{0}\left\| v^{1}\right\| _{0} +\alpha _{0}\left\| h^{1}\right\| _{0}\left\| v^{1}\right\| _{0} \\\le & {} \left\| v^{-1}\right\| _{0}\left\| v^{1}\right\| _{2}+2\left\| v^{0}\right\| _{0}\left\| v^{1}\right\| _{2} +\alpha _{0}\left\| q^{1}\right\| _{0}\left\| v^{1}\right\| _{2} \end{aligned}$$

$$\begin{aligned} \Vert v^{1}\Vert _{2}\le & {} \Vert v^{-1}\Vert _{0}+2\Vert v^{0}\Vert _{0}+\alpha _{0}\Vert q^{1}\Vert _{0} \end{aligned}$$

$$\begin{aligned} \Vert v^{1}\Vert _{2}\le & {} \left( \Vert f_{0}\Vert |_{0}+\Delta t\Vert f_{1}\Vert _{0}\right) +2\Vert f_{0}\Vert _{0}+\alpha _{0}\Vert q^{1}\Vert _{0} \end{aligned}$$

$$\begin{aligned} \Vert v^{1}\Vert _{2}\le & {} 3\Vert f_{0}\Vert _{0}+\Delta t\Vert f_{1}\Vert _{0}+\alpha _{0}\Vert q^{1}\Vert _{0} \end{aligned}$$

hence

$$\begin{aligned} \Vert v^{1}||_{2}\le & {} c(\Vert f_{0}\Vert _{0}+\Delta t\Vert f_{1}\Vert _{0}+\alpha _{0}\Vert q^{1}\Vert _{0}). \end{aligned}$$

Suppose that the result hold for $w=v^{l}$ i.e.

$$\begin{aligned} \Vert v^{l}\Vert _{2}\le & {} c(\Vert f_{0}\Vert _{0}+\Delta t\Vert f_{1}\Vert _{0}+\alpha _{0}\Vert q^{l}\Vert _{0})\qquad l=2, 3, \ldots , k. \end{aligned}$$

(3.16)

Taking $w=v^{k+1}$ in Eq. (3.11), it can be written as

$$\begin{aligned} \left( v^{k+1},v^{k+1}\right) +\alpha _{0}\nu \left( \frac{\partial ^{4}v^{k+1}}{\partial x^{4}},v^{k+1}\right)= & {} -b_{k}\left( v^{-1},v^{k+1}\right) +(2b_{k}-b_{k-1})\left( v^{0},v^{k+1}\right) \\&+\, (2b_{0}-b_{1})\left( v^{k},v^{k+1}\right) \\&+\,\sum ^{k-1}_{l=1}\left( -b_{l-1}+2b_{l}-b_{l+1}\right) \left( v^{l},v^{k+1}\right) \\&+\,\alpha _{0}\left( q^{k+1},v^{k+1}\right) . \end{aligned}$$

Integrating the above equation, we get

$$\begin{aligned} \left( v^{k+1},v^{k+1}\right) +\alpha _{0}\nu \left( \frac{\partial ^{2}v^{k+1}}{\partial x^{2}},\frac{\partial ^{2}v^{k+1}}{\partial x^{2}}\right)= & {} -b_{k}\left( v^{-1},v^{k+1}\right) + (2b_{k}-b_{k-1})\left( v^{0},v^{k+1}\right) \\&+\, (2b_{k}-b_{k-1})\left( v^{0},v^{k+1}\right) \\&+\,\sum ^{k-1}_{l=1}\left( -b_{l-1}+2b_{l}-b_{l+1}\right) \left( u^{l},u^{k+1}\right) \\&+\,\alpha _{0}\left( q^{k+1},v^{k+1}\right) . \end{aligned}$$

Using the Schwarz inequality and the inequality $\Vert w\Vert _{0}\le \Vert w\Vert _{2}$ the above equation can be written as

$$\begin{aligned} \left\| v^{k+1}\right\| _{2}^{2}\le & {} b_{k}\left\| v^{-1}\right\| _{0}\left\| v^{k+1}\right\| _{0}+(2b_{k}-b_{k-1})\left\| v^{0}\right\| _{0}\left\| v^{k+1}\right\| _{0} \\&+\sum _{l=1}^{k-1}\left( -b_{l-1}+2b_{l}-b_{l+1}\right) \left\| v^{l}\right\| _{0}\left\| v^{k+1}\right\| _{0}+(2b_{0}-b_{1})\left\| v^{k}\right\| _{0}\left\| v^{k+1}\right\| _{0}\\&+\,\alpha _{0}\left\| q^{k+1}\right\| _{0}\left\| v^{k+1}\right\| _{0}, \end{aligned}$$

$$\begin{aligned} \left\| v^{k+1}\right\| _{2}^{2}\le & {} b_{k}\left\| v^{-1}\right\| _{0}\left\| v^{k+1}\right\| _{2}+(2b_{k}-b_{k-1})\left\| v^{0}\right\| _{0}\left\| v^{k+1}\right\| _{2} \\&+\sum _{l=1}^{k-1}\left( -b_{l-1}+2b_{l}-b_{l+1}\right) \left\| v^{l}\right\| _{2}\left\| v^{k+1}\right\| _{2}+(2b_{0}-b_{1})\left\| v^{k}\right\| _{2}\left\| v^{k+1}\right\| _{2} \\&+\,\alpha _{0}\left\| q^{k+1}\right\| _{0}\left\| v^{k+1}\right\| _{2}, \end{aligned}$$

$$\begin{aligned} \left\| v^{k+1}\right\| _{2}\le & {} b_{k}\left\| v^{-1}\right\| _{0}+(2b_{k}-b_{k-1})\left\| v^{0}\right\| _{0} +\sum _{l=1}^{k-1}\left( -b_{l-1}+2b_{l}-b_{l+1}\right) \left\| v^{l}\right\| _{2}\\&+\,(2b_{0}-b_{1})\left\| v^{k}\right\| _{2} +\alpha _{0}\left\| q^{k+1}\right\| _{0}, \end{aligned}$$

Using (3.13) we have

$$\begin{aligned} \left\| v^{k+1}\right\| _{2}\le & {} \left( (2b_{k}-b_{k-1})\left\| v^{0}\right\| _{0}+b_{k}\left\| v^{-1}\right\| _{0} +\alpha _{0}\left\| q^{k+1}\right\| _{0}\right) \\&\exp \left( \left( 2b_{0}-b_{1}\right) +\sum _{l=1}^{k-1}\left( -b_{l-1}+2b_{l}-b_{l+1}\right) \right) , \end{aligned}$$

$$\begin{aligned} \left\| v^{k+1}\right\| _{2}\le & {} \left( \left\| v^{0}\right\| _{0}+\left\| v^{-1}\right\| _{0} +\alpha _{0}\left\| q^{k+1}\right\| _{0}\right) \exp \left( 1+b_{k-1}-b_{k}\right) , \end{aligned}$$

$$\begin{aligned} \left\| v^{k+1}\right\| _{2}\le & {} \left( \left\| f_{0}\right\| _{0}+\left\| f_{0}\right\| _{0}+\Delta t\left\| f_{1}\right\| _{0} +\alpha _{0}\left\| q^{k+1}\right\| _{0}\right) \exp \left( 1+b_{k-1}-b_{k}\right) , \end{aligned}$$

$$\begin{aligned} \left\| v^{k+1}\right\| _{2}\le & {} c\left( \left\| f_{0}\right\| _{0}+\Delta t\left\| f_{1}\right\| _{0} +\alpha _{0}\left\| q^{k+1}\right\| _{0}\right) . \end{aligned}$$

$\square$

Theorem 2

The numerical solution obtained by the proposed method converges the exact solution, if the following relation holds

$$\begin{aligned} \left\| v(t_{k})-v^{k}\right\| _{2}\le & {} E \Delta t^{2},\qquad k=1, 2,\ldots , K. \end{aligned}$$

(3.17)

where E is a constant and $E=(1+b_{k})\exp (1+b_{k-1}-b_{k}).$

Proof

Let $s^{k}=v(z,t_{k})-v^{k}(z)$, for $k=1$, by combining Eqs. (1.1), (3.11), the error equation becomes

$$\begin{aligned} \left( s^{1},v\right) +\alpha _{0}\nu \left( \frac{\partial ^{2} s^{1}}{\partial z^{2}},\frac{\partial ^{2} v}{\partial z^{2}}\right)= & {} -\left( s^{-1},v\right) +2b_{0}\left( s^{0},v\right) +\left( r^{1},v\right) ,\quad \quad \forall v \in H^{2}_{0}(\Omega ). \end{aligned}$$

using Schwarz inequality and the inequality $\Vert w\Vert _{0}\le \Vert w\Vert _{2}$

Let $v=s^{1}$, noting $s^{0}=0$, the above equation takes the following form

$$\begin{aligned} \left\| s^{1}\right\| _{2}^{2}\le \left\| s^{-1}\right\| _{0}\left\| s^{1}\right\| _{0} +\left\| r^{1}\right\| _{0}\left\| s^{1}\right\| _{0}. \end{aligned}$$

$$\begin{aligned} \left\| s^{1}\right\| _{2}^{2}\le \left\| s^{-1}\right\| _{0}\left\| s^{1}\right\| _{2} +\left\| r^{1}\right\| _{0}\left\| s^{1}\right\| _{2}. \end{aligned}$$

$$\begin{aligned} \left\| s^{1}\right\| _{2}\le \left\| s^{-1}\right\| _{0} +\left\| r^{1}\right\| _{0}. \end{aligned}$$

since

$$\begin{aligned} \Vert s^{-1}\Vert \le \Delta t^{2} \end{aligned}$$

Using Eq.(3.9), it leads to

$$\begin{aligned} \left\| v(t_{1})-v^{1}\right\| _{2}\le 2\Delta t^{2}.\nonumber \\ \left\| v(t_{1})-v^{1}\right\| _{2}\le E\Delta t^{2}. \end{aligned}$$

(3.18)

Hence (3.19) is proved for the case $k=1$.

For inductive part, suppose (3.19) holds for $l=1, 2, 3,\ldots , k$, i.e.

$$\begin{aligned} \left\| v(t_{j})-v^{j}\right\| _{2}\le E \Delta t^{2}. \end{aligned}$$

(3.19)

For $k=s+1$ the Eqs. (1.1), (3.11) are used and the error equation can be written, for all $v\in H^{2}_{0}(\Omega )$, as

$$\begin{aligned} \left( s^{k+1},v\right) +\alpha _{0}\mu \left( \frac{\partial ^2 s^{k+1}}{\partial z^2},\frac{\partial ^2 v}{\partial z^2}\right)= & {} -b_{k}\left( e^{-1},v\right) +(2b_{k}-b_{k-1})\left( s^{0},v\right) \\&+\sum ^{k-1}_{l=1}\left( -b_{l-1}+2b_{l}-b_{l+1}\right) \left( s^{l},v\right) \\&+\,(2b_{0}-b_{1})\left( s^{k},v\right) +\alpha _{0}\left( r^{k+1},v\right) . \end{aligned}$$

using $\Vert w\Vert _{0}\le \Vert w\Vert _{2}$ and Schwarz inequality the above equation, for $v=s^{k+1}$, can be written as

$$\begin{aligned} \left\| s^{k+1}\right\| ^{2}_{2}\le & {} b_{k}\left\| s^{-1}\right\| _{0}\left\| s^{k+1}\right\| _{0}+(2b_{k}-b_{k-1})\left\| s^{0}\right\| _{0}\left\| s^{k+1}\right\| _{0} \\&+\sum ^{k-1}_{l=1}\left( -b_{l-1}+2b_{l}-b_{l+1}\right) \left\| s^{l}\right\| _{0}\left\| s^{k+1}\right\| _{0} +(2b_{0}-b_{1})\left\| s^{k}\right\| _{0}\left\| s^{k+1}\right\| _{0}\\&+\left\| r^{k+1}\right\| _{0}\left\| s^{k+1}\right\| _{0}, \end{aligned}$$

$$\begin{aligned} \left\| s^{k+1}\right\| _{2}\le & {} b_{k}\left\| s^{-1}\right\| _{0} +\sum ^{k-1}_{l=1}\left( -b_{l-1}+2b_{l}-b_{l+1}\right) \left\| s^{l}\right\| _{2} +(2b_{0}-b_{1})\left\| s^{k}\right\| _{2}+\left\| r^{k+1}\right\| _{0}. \end{aligned}$$

Using (3.15)

$$\begin{aligned} \left\| s^{k+1}\right\| _{2}\le & {} \left( b_{k}\left\| s^{-1}\right\| _{0}+\left\| r^{k+1}\right\| _{0}\right) \exp \left[ \sum ^{k-1}_{l=1}\left( -b_{l-1}+2b_{l}-b_{l+1}\right) +2b_{0}-b_{1}\right] , \end{aligned}$$

$$\begin{aligned} \left\| s^{k+1}\right\| _{2}\le & {} \left( b_{k}\left\| s^{-1}\right\| _{0}+\left\| r^{k+1}\right\| _{0}\right) \exp \left( 1+b_{k-1}-b_{k}\right) , \end{aligned}$$

$$\begin{aligned} \left\| s^{k+1}\right\| _{2}\le & {} \left( b_{k}\Delta t^{2}+\Delta t^{2}\right) \exp \left( 1+b_{k-1}-b_{k}\right) , \end{aligned}$$

$$\begin{aligned} \left\| s^{k+1}\right\| _{2}\le & {} E\Delta t^{2}. \end{aligned}$$

$\square$

Space discretization

Collocation method with quintic B-spline basis functions is employed for space discretization. Putting Eq. (2.1) into Eq. (3.4), we obtain the following equation

$$\begin{aligned}&\left( c_{j-2}^{k+1}+26c_{j-1}^{k+1}+66c_{j}^{k+1}+26c_{j+1}^{k+1}+c_{j+2}^{k+1}\right) \\&+\,\alpha _{0}\nu \frac{120}{h^{4}}\left( c_{j-2}^{k+1}-4c_{j-1}^{k+1}+6c_{j}^{k+1}-4c_{j+1}^{k+1} +c_{j+2}^{k+1}\right) \\= & {} -b_{k}(c_{j-2}^{-1}+26c_{j-1}^{-1}+66c_{j}^{-1}+26c_{j+1}^{-1}+c_{j+2}^{-1}) \\&+\,(2b_{k}-b_{k-1})(c_{j-2}^{0}+26c_{j-1}^{0}+66c_{j}^{0}+26c_{j+1}^{0}+c_{j+2}^{0})\\&+\,\sum ^{k-1}_{l=1}\left( -b_{l-1}+2b_{l}-b_{l+1}\right) (c_{j-2}^{l}+26c_{j-1}^{l}+66c_{j}^{l} +26c_{j+1}^{l}+c_{j+2}^{l})\\&+\,(2b_{0}-b_{1})(c_{j-2}^{k}+26c_{j-1}^{k}+66c_{j}^{k}+26c_{j+1}^{k} +c_{j+2}^{k})+\alpha _{0}q^{k+1}. \end{aligned}$$

The above equation can be rewritten as

$$\begin{aligned}&\left( 1+\alpha _{0}\nu \frac{120}{h^{4}}\right) c_{j-2}^{k+1} +\left( 26-4\alpha _{0}\nu \frac{120}{h^{4}}\right) c_{j-1}^{k+1}\\&+\,\left( 66+6\alpha _{0}\nu \frac{120}{h^{4}}\right) c_{j}^{k+1} +\left( 26-4\alpha _{0}\nu \frac{120}{h^{4}}\right) c_{j+1}^{k+1}+\left( 1+\alpha _{0}\nu \frac{120}{h^{4}}\right) c_{j+2}^{k+1} \\&=\,&-b_{k}\left( c_{j-2}^{-1}+26c_{j-1}^{-1}+66c_{j}^{-1}+26c_{j+1}^{-1}+c_{j+2}^{-1}\right) \\&+\,(2b_{k}-b_{k-1})\left( c_{j-2}^{0}+26c_{j-1}^{0}+66c_{j}^{0}+26c_{j+1}^{0}+c_{j+2}^{0}\right) \\&+\,\sum ^{k-1}_{l=1}\left( -b_{l-1}+2b_{l}-b_{l+1}\right) \left( c_{j-2}^{l}+26c_{j-1}^{l}+66c_{j}^{l} +26c_{j+1}^{l}+c_{j+2}^{l}\right) \\&+\,(2b_{0}-b_{1})\left( c_{j-2}^{k}+26c_{j-1}^{k}+66c_{j}^{k}+26c_{j+1}^{k} +c_{j+2}^{k}\right) +\alpha _{0}q^{k+1}. \end{aligned}$$

The above equation can be rewritten as a system of linear equations

$$\begin{aligned}&\left( 1+\alpha _{0}\nu \frac{120}{h^{4}}\right) c_{j-2}^{k+1} +\left( 26-4\alpha _{0}\nu \frac{120}{h^{4}}\right) c_{j-1}^{k+1}\\&+\left( 66+6\alpha _{0}\nu \frac{120}{h^{4}}\right) c_{j}^{k+1} +\left( 26-4\alpha _{0}\nu \frac{120}{h^{4}}\right) c_{j+1}^{k+1}+\left( 1+\alpha _{0}\nu \frac{120}{h^{4}}\right) c_{j+2}^{k+1} =F_{j}, \end{aligned}$$

where

$$\begin{aligned} F_{j}= & {} -b_{k}\left( c_{j-2}^{-1}+26c_{j-1}^{-1}+66c_{j}^{-1}+26c_{j+1}^{-1}+c_{j+2}^{-1}\right) \\&+(2b_{k}-b_{k-1})\left( c_{j-2}^{0}+26c_{j-1}^{0}+66c_{j}^{0}+26c_{j+1}^{0}+c_{j+2}^{0}\right) \\&+\sum ^{k-1}_{l=1}\left( -b_{l-1}+2b_{l}-b_{l+1}\right) \left( c_{j-2}^{l}+26c_{j-1}^{l}+66c_{j}^{l} +26c_{j+1}^{l}+c_{j+2}^{l}\right) \\&+(2b_{0}-b_{1})\left( c_{j-2}^{k}+26c_{j-1}^{k}+66c_{j}^{k}+26c_{j+1}^{k} +c_{j+2}^{k}\right) +\alpha _{0}q^{k+1}. \end{aligned}$$

This system has $N+1$ equations in $N+5$ unknowns $c^{k+1}_{-2},c^{k+1}_{-1},\ldots ,c^{k+1}_{N+1},c^{k+1}_{N+2}$. Unique solution of the above system is obtained by eliminating the unknowns $c_{-2}^{k+1},c_{-1}^{k+1},c_{N+1}^{k+1}$, and $c_{N+2}^{k+1}$ using boundary conditions.

Numerical results

In this section, two examples are considered to check the accuracy and efficiency of the proposed method. The main objective of these examples is to verify the rate of convergence of the approximate results for $\alpha$. From the following Tables 1 and 2, it is clear that the approximate results support the theoretical estimates.

Example 1

Consider the following superdiffusion PDE of fourth order

$$\begin{aligned} \frac{\partial ^{1.75}v}{\partial t^{1.75}}+0.05\frac{\partial ^{4} v}{\partial z^{4}}= & {} q(z,t),\quad z\in [0,4\pi ],\quad t_{0}=0<t\le t_{f}=T, \end{aligned}$$

with initial condition

$$\begin{aligned} v(z,0)= & {} 2 \sin ^{2} z,\quad z\in [0,4\pi ], \end{aligned}$$

and boundary condition $\mathrm {I}$

$$\begin{aligned} v(0,t)= & {} v(4\pi ,t)=0,\\ v_{z}(0,t)= & {} v_{z}(4\pi ,t)=0,\quad 0\le t\le T \end{aligned}$$

The exact solution of the problem is

$$\begin{aligned} v(z,t)= & {} 2\left( t+1\right) \sin ^{2} z. \end{aligned}$$

The error norms $L_{\infty }$ and $L_{2}$ are calculated for $N=100$ and different temporal step sizes. The temporal rate of convergence at $t_{f}=1.0$ is presented in Table 1. The temporal rate of convergence obtained by the proposed method support the theoretical results.

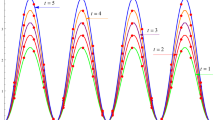
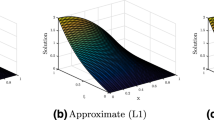
To indicate the effects of the proposed method for larger time level K, the exact solution and the approximate solution are plotted using $N=50$, $K=1000$ and $\Delta t=0.00001$ as shown in Fig. 1. It is clear from the Fig. 1 that the numerical solution is highly consistent with the exact solution, which indicates that the proposed method is very effective. In Fig. 2, the exact solution is represented by solid line and the numerical solution is represented by dotted line at $K=1000$ time level.

The temporal rate of convergence of $L_{2}$ norm error as a function of the time step $\Delta t$ for $\alpha = 1.50$ is shown in Fig. 3.

Table 1 The errors $\Vert s_{K}\Vert _{\infty }$ and $\Vert s_{K}\Vert _{2}$ for different values of time $\Delta t$ with $N=100$

Fig. 1

The results at $N=50$, $K=1000$ and $\Delta t =0.00001$ for Example 1

Fig. 2

The exact and numerical solutions at $K=1000$. Dotted line numerical solution, solid line exact solution

Fig. 3

Errors as a function of the time $\Delta t$ for $\alpha =1.50$

Example 2

Consider the following superdiffusion PDE of fourth order

$$\begin{aligned} \frac{\partial ^{1.50}v}{\partial t^{1.50}}+0.05 \frac{\partial ^{4} v}{\partial z^{4}} &= q(z,t),\quad z\in [0,1],\quad 0<t\le T, \end{aligned}$$

with the initial condition

$$\begin{aligned} v(z,0)= & {} \left( \pi ^{5}\sin \pi z+\frac{1}{\pi ^{5}}\cos \pi z-\frac{1}{\pi ^{5}}\cos 3\pi z\right) ,\quad z\in [0,1], \end{aligned}$$

and boundary condition III

$$\begin{aligned} v(0,t) &= v(1,t)=0,\\ v_{zz}(0,t)-\frac{8}{\pi ^{9}} v_{z}(0,t) &= v_{zz}(1,t)-\frac{8}{\pi ^{9}}g_{z}(1,t)=0,\quad 0\le t\le T. \end{aligned}$$

The exact solution of the problem is

$$\begin{aligned} v(z,t)= & {} \left( t+1\right) \left( \pi ^{5}\sin \pi z+\frac{1}{\pi ^{5}}\cos \pi z-\frac{1}{\pi ^{5}}\cos 3\pi z\right) . \end{aligned}$$

The error norms $L_{\infty }$ and $L_{2}$ are calculated for $N=80$ and different temporal step sizes. The temporal rate of convergence at $t_{f}=1.0$ is presented in Table 2. The temporal rate of convergence obtained by the proposed method support theoretical results.

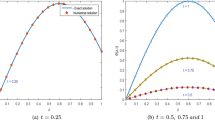
To indicate the effects of the proposed method for larger time level, the exact solution and the approximate solution are plotted using $N=80$, $K=1000$, and $\Delta t=0.00001$ as shown in Fig. 4. It is clear from the Fig. 4 that the numerical solution is highly consistent with the exact solution, which indicates that the proposed method is very effective. In Fig. 5, the exact solution is represented by solid line and the numerical solution is represented by dotted line at $K=1000$ time level.

The temporal rate of convergence of $L_{2}$ norm error as a function of the time step $\Delta t$ for $\alpha = 1.75$ is shown in Fig. 6.

Table 2 The errors $\Vert s_{K}\Vert _{\infty }$ and $\Vert s_{K}\Vert _{2}$ for different values of $\Delta t$ with $N=80$

Fig. 4

The results at $N=80$, $K=1000$ and $\Delta t =0.00001$ for Example 2

Fig. 5

The exact and numerical solutions at $K=1000$. Dotted line numerical solution, solid line exact solution

Fig. 6

Errors as a function of the time step $\Delta t$ for $\alpha = 1.75$

Conclusion

The solution of superdiffusion fourth order equation has been developed. Central difference formula and quintic B-spline are used for discretizing time and space variables, respectively. The proposed method is stable and the approximate results approach the analytical results with order $O(\Delta t^{2})$. The approximate results obtained by the suggested method support the theoretical estimates.