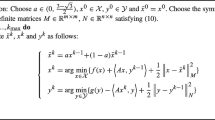1 Introduction

Bisymmetric matrices, that is, symmetric and persymmetric matrices, have been extensively discussed since 1931, which are very effective in engineering problems and have practical applications in information theory, communication theory, quantum physics, linear system theory, numerical analysis and statistics. Some results for the inverse problem of bisymmetric matrices have been obtained in [1, 11, 13]. The least squares bisymmetric and partially bisymmetric solutions have been studies by [9, 19]. Other problems related to bisymmetric matrices have been studies by [7, 14, 21]. The persymmetric Hankel and symmetric Toeplitz matrices are special forms of bisymmetric matrices that usually appear in different applications, such as vibration in structures, matching filters and estimates of shaping [4, 6].

In some of these application areas, it is required to evaluate the nearest positive semi-definite bisymmetric matrix to a given data matrix. The required matrix has no restriction on its rank. An existence theorem for the problem solutions is given in [20], and the general expression of the solutions is derived using Newton method. Similar problems containing structured covariance estimation were studied in [2,3,4].

Interior point algorithms can solve semi-definite programming problems efficiently in polynomial time [5]. This motivates us to construct the problem as mixed second-order cone and semi-definite programming problem. The constraints in this problem are constraints over the second-order cone and the positive semi-definite cones. The software SDPT3 by Toh et al. [17] is an efficient software for implementation of primal-dual path-following methods that will be used to solve the problem.

There are many similar semi-definite programming problems, for example Todd [16] formulated the optimization of the spectral norm of a special matrix as a semi-definite programming problem. Later, some other problems were compiled as mixed semi-definite and second-order cone optimization problems [15]. The special structure of our problem is an advantage, however, none of the above formulations utilized it.

To take advantage of bisymmetric structure, an isometry operator bvec is introduced. The isometry operator, bvec takes \(n\times n\) bisymmetric matrices into r vectors, where r given (1.3) and it is much smaller than \(n^2\). This operator will give our methods an advantage over the other methods.

Some notations are introduced now that will be used throughout the paper. The set of all \(n\times n\) real symmetric matrices will be denoted by \({{\mathcal {S}}}_{n}\). The cone of all \(n\times n\) real symmetric positive semi-definite matrices will be denoted by \({{\mathcal {S}}}_{n}^{+}\), where

$$\begin{aligned} {{\mathcal {S}}}_{n}^+ ~=~ \{A : A \in \mathrm{IR}^{n \times n},~ \mathrm{and} ~ z ^ T A z ~\ge ~ 0, \quad \forall ~ z \in \mathrm{IR}^ n \} \end{aligned}$$
(1.1)

is a convex cone of dimension \( ~ n (n+1)/2 \). \({{\mathcal {Q}}}_{h}\) is a second-order cone of dimension h, and is defined as

$$\begin{aligned} {{\mathcal {Q}}}_{h} = \{ {y} \in I\!\!R^{h} : \Vert {y}_{2:h}\Vert _{2} \le y_{1} \}, \end{aligned}$$

where \(\Vert .\Vert _{2}\) stands for the Euclidean distance norm defined as \(\Vert {y}\Vert _{2}= \sqrt{\sum _{i=1}^{n} y_{i}^{2}}\), \(\forall {y} \in I\!\!R^{n} \) and \({x}_{2:h}=[x_2,x_2,\ldots ,x_h]^T\). The set of all \(n\times n\) real bisymmetric matrices will be denoted by \({{\mathcal {B}}}_{n}\), where

$$\begin{aligned} {{\mathcal {B}}}_{n} ~=~ \{B(b) : B(b) \in \mathrm{IR}^ {n \times n},~ B(b)~\mathrm{is~bisymmetric} \}, \end{aligned}$$
(1.2)

which is a subspace of dimension r. In the following, the structure of an \(n \times n\) real bisymmetric matrix B(b):

$$\begin{aligned} B(b)=\left[ \begin{array}{llll} b_1&{}b_2&{}\cdots &{}b_n\\ b_2&{}b_{n+1}&{}\cdots &{}b_{n-1}\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ b_{n-1}&{}b_{2n-2}&{}\cdots &{}b_2 \\ b_n&{}b_{n-1}&{}\cdots &{}b_1\end{array} \right] ,~~ b\in I\!\!R^r, \end{aligned}$$
(1.3)

where \(r=mn-k, ~ m=n/2\) and \(k=n(n-2)/4\) if n is even and \(m=(n+1)/2\) and \(k=(n-1)(n+1))/4\) if n is odd. It is obvious that \({{\mathcal {B}}}_{n} \subset {{\mathcal {S}}}_{n}\). The norm defined on \({{\mathcal {S}}}_{n}\) is the Frobenius norm expressed as follows:

$$\begin{aligned} \Vert W \Vert _{F} = \sqrt{W \bullet W} = \Vert {\textbf {vec}}^{T}(W) {\textbf {vec}}(W)\Vert _{2}, ~ \forall ~ W \in {{\mathcal {S}}}_{n}. \end{aligned}$$
(1.4)

Here \(W \bullet W = \text {trace}(W\cdot W) =\sum _{i,j}^{n} W_{i,j}^{2}\), \({\textbf {vec}}(W)\) means vectorization operator founded by putting all columns of the matrix W on top of each other as one column and \({\textbf {vec}}^{T}\) is the transpose of \({\textbf {vec}}\). We denote the partial ordering on \({{\mathcal {S}}}_{n}^{+}\) and \({{\mathcal {Q}}}_{h}\) on \({{\mathcal {S}}}_{n}\) and \(I\!\!R^{h}\), respectively, by \(\succeq \) and \(\ge _{Q}\). That is,

$$\begin{aligned} W \succeq P ~ ~ \Leftrightarrow ~ ~ W -P \in {{\mathcal {S}}}_{n}^{+}, ~ ~ \forall ~ W, ~ P \in {{\mathcal {S}}}_{n} \end{aligned}$$

and

$$\begin{aligned} {w} \ge _{Q} {p} \Leftrightarrow ~ ~ {w}-{p} \in ~ {{\mathcal {Q}}}_{h}, ~ ~ \forall ~ {w}, ~ {p} ~ \in I\!\!R^{k}, \end{aligned}$$

where \( {y} \ge 0\) for a vector \({y} \in I\!\!R^{n}\) stands for each component of y being nonnegative. We denote the zero and identity matrices by 0 and I, respectively.

We can now describe our problem in mathematical notation as follows: Given a data matrix \(G \in I\!\!R^{n\times n}\), find the closest positive semi-definite bisymmetric matrix B(b) to G such that \(\Vert G-B(b)\Vert _{F}\) is minimal. Thus, we have the following minimization problem:

(1.5)

In Sect. 2, we describe briefly the alternating projection method. Although the rate of convergence is slow, the modified alternating projection method converges globally to the optimal solution. We can compare the results achieved by alternating projection method with our methods in Sects. 3 amd 4, since alternating projection method provides us with an accurate solutions. A brief description of semi-definite and second-order cone minimization problems alongside the interior point formulas of problem (1.5) in the formation of the relevant class will be given in Sects. 3 and  4, respectively. The performance of these primal-dual path-following methods against the alternating projection method is shown in numerical results Sect. 5.

2 The alternating projection method

The algorithm of this section is obtained from modified alternating projection method that are originally proposed by von Neumann [18] for finding the minimum distance from a given fixed point to an intersection of convex sets.

When applying the projection method to approximate a bisymmetric matrices, it is convenient to use the Frobenius norm, as expressed (1.4). To apply projection method, the projection maps \(P_{\mathcal {S}}(.)\) and \( P_{\mathcal {B}}(.)\) are needed. These projections are the maps from \(K=\{G:\;G\in \mathrm{IR}^{n\times n} \} \) on to \( {\mathcal {S}}_n^+ \) and \( {\mathcal {B}}_n\). The projection mapping \(~P_{\mathcal {S}}(G)~\) on to \(~{\mathcal {S}}_n^+~\) is given by the formula [10]

$$\begin{aligned} P_{\mathcal {S}}~(G)~= U \Lambda ^ + U ^ T, \end{aligned}$$
(2.1)

where

$$\begin{aligned} \Lambda ^+~=~\left[ \begin{matrix} \Lambda _ r &{}\mathbf{{0}}\\ \mathbf{{0}}&{} \mathbf{{0}} \\ \end{matrix} \right] , \end{aligned}$$

and \(~ \Lambda _ r~=~\mathrm{diag}~[\lambda _1,~\lambda _2,~\ldots ,~\lambda _r]~\) is the diagonal matrix consisting from the nonnegative eigenvalues of \( \Lambda \).

The mapping \(~P_{\mathcal {B}}(G)~\) formula onto \(~{\mathcal {B}}_n~\) is now given by

$$\begin{aligned} P_{\mathcal {B}}(G)~=\mathrm{Bis}(b_1,b_2, \ldots , b_{r}) , \end{aligned}$$
(2.2)

where \( b_p\) in the (i, j) position of the matrix (1.3) is given by

$$\begin{aligned} b_p=(G_{i,j}+G_{j,i}+G_{(n-i+1,n-j+1)}+G_{(n-j+1,n-i+1)})/4. \end{aligned}$$

The single valued projection mappings \(P_{\mathcal {S}}(G)\) and \( P_{\mathcal {B}}(G)\) given in (2.1) and (2.2) can now be used to execute the Dykstra algorithm. A data matrix \(G\in \mathrm{IR}^{n\times n}\) is given, then the method is initialized by \(G^{(0)}=G\). The iteration algorithm is given now by:

$$\begin{aligned} G^{(k+1)}=G^{(k)}+ (P_{\mathcal {B}}(P_{\mathcal {S}}(G^{(k)})))-P_{\mathcal {S}}(G^{(k)}). \end{aligned}$$
(2.3)

Both sequences \(\{P_{\mathcal {S}}(G^{(k)})\}\) and \(\{ P_{\mathcal {B}}(P_{\mathcal {S}}( G^{(k)})) \}\) produced by (2.3) converge globally to the optimal solution \(B^*\) of (1.5), [8].

3 Semidefinite programming approach

The primal standard form for semi-definite programming (SDP) problem is given by:

$$\begin{aligned} (P) ~~&{minimize}_X&D \bullet X \nonumber \\&{subject\, to}&A_{i} \bullet X=b_{i},~~i = 1,2,\dots , m, ~~~ X \succeq 0, \end{aligned}$$
(3.1)

where all \(A_{i}, ~D \in {{\mathcal {S}}}_{n},~ b \in I\!\!R^{m}\) are given and the variable is \(X \in {{\mathcal {S}}}_{n}\). This minimization problem (3.1) is a convex minimization problem since its constraint and objective are convex. The dual problem of (3.1) is

(3.2)

where the variable is \({y} \in I\!\!R^{m}\). Many problems are special cases of problems (3.1) and (3.2) and there are many applications, in particular (1.5). The following lemma is useful in writing (1.5) in the form of (3.2):

Lemma 3.1

(Schur Complement) If

$$\begin{aligned}N=\left[ \begin{matrix} B&{}D \\ D^{T}&{} C \\ \end{matrix} \right] \end{aligned}$$

where \(B \in {{\mathcal {S}}}_{n}^{+}\) is nonsingular matrix and \(C \in {{\mathcal {S}}}_{n}\), then the matrix N is positive (semi)definite if and only if the matrix \(C-D^{T}B^{-1}D\) is positive (semi)definite.

This matrix \(C-D^{T}B^{-1}D\) is called the Schur complement of B in N.

3.1 Formulation I (SDV)

Letting \(\Vert G-B(b)\Vert _{F}^{2} \le t\), where t is a real nonnegative scalar and observing that:

$$\begin{aligned} \Vert G-B(b)\Vert _{F}^{2} = {\textbf {vec}}^{T}(G-B(b)){\textbf {vec}}(G-B(b)), \end{aligned}$$

we have:

$$\begin{aligned}&{\textbf {vec}}^{T}(G-B(b)){\textbf {vec}}(G-B(b)) \le t \\ \Leftrightarrow ~&t- {\textbf {vec}}^{T}(G-B(b))I {\textbf {vec}}(G-B(b)) \ge 0 \\ \Leftrightarrow ~&\left[ \begin{matrix} I&{} {\textbf {vec}}(G-B(b))\\ {\textbf {vec}}^{T}(G-B(b))&{} t \\ \end{matrix} \right] \succeq 0. \end{aligned}$$

We can deduce from Lemma 3.1 the equivalency in the above inequalities. Therefore, we can write (1.5) as follows

$$\begin{aligned} (SDV) ~~&{minimize}~~&t, \nonumber \\&{subject\,\, to}&\left[ \begin{matrix} t&{}0&{}0 \\ 0&{} B(b)&{} 0 \\ 0&{}0&{}U \\ \end{matrix} \right] \succeq 0, \end{aligned}$$
(3.3)

where

$$\begin{aligned} U = \left[ \begin{matrix} I&{} {\textbf {vec}}(G-B(b))\\ {\textbf {vec}}^{T}(G-B(b))&{} t \\ \end{matrix} \right] , \end{aligned}$$

this is an SDP problem in the dual form (3.2) and the dimensions of this problem are \(r+1\) (see (1.3) number of variables) and \(n^{2}+n+2\) (size of the matrices).

3.2 Formulation II (SDB)

Now, the SDP problem (3.3) is very huge even for a modest data matrix G. For example, a \(30 \times 30\) matrix G will make the problem grow to a problem with dimensions 240 and 932, thus it is not efficient to solve (1.5) using formulation (3.3). Furthermore, the structure of the matrix B(b) being bisymmetric is not utilized. An alternative approach is to develop an SDP problem with acceptable dimensions and utilizes the bisymmetric structure of B(b). This can now be achieved by means of the following isometry operator.

Definition 3.2

Let \({\textbf {bvec}}: {{\mathcal {B}}}_{n} \longrightarrow I\!\!R^{r}\) be defined as \({\textbf {bvec}}(U) = [\sqrt{2} u_{1,1} ~ \sqrt{4}u_{2,1} ~ \cdots ~ \sqrt{4}u_{n-1,1} ~ \sqrt{2}u_{n,1} ~ \sqrt{2}u_{2,2} ~\sqrt{4}u_{3,2} ~\cdots ~ \sqrt{4}u_{n-1,2} ~~\cdots ~ \sqrt{g} u_{m,m}]^{T}\) for any \(U \in {{\mathcal {B}}}_{n}\), where \( m=n/2\) and \(g=2\) if n is even and \(m=(n+1)/2\) and \(g=4\) if n is odd.

It is clear that \({\textbf {bvec}}\) is a linear operator taking the set of all \(n\times n\) real bisymmetric matrices to \(I\!\!R^r\). The characterizations of \({\textbf {bvec}}\) are given by the following lemma:

Lemma 3.3

Given the operator \({\textbf {bvec}}\), defined in the above definition, the following conditions hold: For any \(W, P \in {{\mathcal {B}}}_{n}\)

  1. (1)

    \( W \bullet W= {\textbf {bvec}}^{T}(W){\textbf {bvec}}(W)\).

  2. (2)

    \(\Vert W-P\Vert ^{2}_{F}={\textbf {bvec}}^{T}(W-P){\textbf {bvec}}(W-P)\).

Proof

It is clear from the definition of the operator bvec that Part 1 is satisfied. Part 2 is a consequence of Part 1. \(\square \)

From Part 1, it is clear that bvec is an isometry. To take advantage of the above lemma, we need G to be bisymmetric. Projecting G onto \({{\mathcal {B}}}_{n}\) using the above orthogonal projection given in (2.2) makes a bisymmetric matrix, say \(\bar{G}\). In the following proposition, we show that the closest bisymmetric positive semi-definite matrix to \(\bar{G}\) is also the nearest to G.

Proposition 3.4

Given an orthogonal projection \(\bar{G}\) of G onto \({{\mathcal {B}}}_{n}\) and let B(b) be the closest bisymmetric positive semi-definite matrix to \(\bar{G}\), then B(b) is so for G.

Proof

The proof is complete if \(\bar{G}\) is positive semi-definite. If not, then for any \(T \in {{\mathcal {B}}}_{n}\), we have \(~ (G-\bar{G})^{T}\bullet (\bar{G}-T)=0 ~\). This is true because \(\bar{G}\) is the orthogonal projection of G. Thus, \(~\Vert G-T\Vert ^{2}_{F} = \Vert G-\bar{G}\Vert ^{2}_{F}+\Vert \bar{G}-T\Vert ^{2}_{F}.~\) \(\square \)

As a result of this proposition, the following problem is equivalent to (1.5):

$$\begin{aligned}&\mathrm{minimize }~~~\Vert \bar{G}-B(b) \Vert _{F} ~~~~~~~~~~~~~~ \nonumber \\&\mathrm{subject ~~ to }~~ B(b) \in {{\mathcal {B}}}_{n}, ~~~~ B(b) \succeq 0. \end{aligned}$$
(3.4)

From Lemma 3.1, the following are equivalences (for \(t \ge 0 \in I\!\!R\)):

$$\begin{aligned}&\Vert \bar{G}-B(b) \Vert _{F}^{2}\le t ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\ \Leftrightarrow ~~&{\textbf {bvec}}^{T}(\bar{G}-B(b)) {\textbf {bvec}}(\bar{G}-B(b))\le t ~~~{ {by ~~Lemma ~{3.3}{FPar3}}3.3} ~~~\\ \Leftrightarrow ~~&t-{\textbf {bvec}}^{T}(\bar{G}-B(b))I {\textbf {bvec}}(\bar{G}-B(b))\le 0 ~~~\\ \Leftrightarrow ~~&\left[ \begin{array}{cc} I&{} {\textbf {bvec}}(\bar{G}-B(b))\\ {\textbf {bvec}}^{T}(\bar{G}-B(b))&{} t \\ \end{array} \right] \succeq 0 ~~~{by ~~Lemma~~3.1} .~~~ \end{aligned}$$

Therefore, we have the following SDP problem:

$$\begin{aligned} (SDB) ~~&{minimize}~~&t, \nonumber \\&{subject \,\, to}&\left[ \begin{matrix} t&{}0&{}0 \\ 0&{} B(b)&{} 0 \\ 0&{}0&{}\bar{V} \\ \end{matrix} \right] \succeq 0 , \end{aligned}$$
(3.5)

where

$$\begin{aligned} \bar{V} = \left[ \begin{matrix} I&{} {\textbf {bvec}}(\bar{G}-B(b))\\ {\textbf {bvec}}^{T}(\bar{G}-B(b))&{} t \\ \end{matrix} \right] . \end{aligned}$$

The dimensions of this problem are r and \(n+r+2 \). These dimensions are much better than (3.3) where \(r=mn-k, ~ m=n/2\) and \(k=n(n-2)/4\) if n is even and \(m=(n+1)/2\) and \(k=(n-1)(n+1))/4\) if n is odd.

3.3 Formulation III (SDQ)

An alternative method for formulating (1.5) is by means of the Frobenius norm definition:

$$\begin{aligned} \Vert G-B(b)\Vert _{F}^{2} = {y}^{T}P{y} + 2{{q}}^{T}{y} + s , \end{aligned}$$

where

$$\begin{aligned} {y}= & {} [b_{1}~ b_{2} \cdots ~ b_{r}]^{T},\\ ~P= & {} \text {diag}([2~ 4~ \cdots 4 ~2~ 2~4~ ~ ~ \cdots 2]) ~~~ \text {and} ~~~ s=\Vert G\Vert _{F}^{2} \\ q= & {} [-2G_{1,1},-4G_{1,2} \cdots -2G_{1,n},~-2G_{2,2},~-4G_{2,3} \cdots -2G_{r,r}]. ~\end{aligned}$$

For a nonnegative real scalar t, we have the following problem:

$$\begin{aligned}&\Vert G-B\Vert _{F}^{2} \le t \\ \Leftrightarrow ~ ~&{y}^{T}P{y} + 2q^{T}{y} + s \le t \\ \Leftrightarrow ~ ~&(P^{1/2}{y})^{T}(P^{1/2}{y}) + 2q^{T}{y} + s \le t \\ \Leftrightarrow ~ ~&t - 2q^{T}{y} - s - (P^{1/2}{y})^{T}I(P^{1/2}{y}) \ge 0 \\ \Leftrightarrow ~ ~&\left[ \begin{matrix} I &{} (P^{1/2}{y})\\ (P^{1/2}{y})^{T} &{} t - 2q^{T}{y} - s \\ \end{matrix} \right] \succeq 0. \end{aligned}$$

Therefore, we deduce the following SDP problem:

$$\begin{aligned} (SDQ) ~~&{minimize} ~~&t, \nonumber \\&{subject\, to}&\left[ \begin{matrix} t&{}0&{}0 \\ 0&{} B(b)&{} 0 \\ 0&{}0&{}Q \\ \end{matrix} \right] \succeq 0, \end{aligned}$$
(3.6)

where

$$\begin{aligned} Q=\left[ \begin{matrix} I &{} (P^{1/2}{y})\\ (P^{1/2}{y})^{T} &{} t - 2q^{T}{y} - s \\ \end{matrix} \right] . \end{aligned}$$

This is an SDP problem in the dual form (3.2) and the dimensions of this problem are \(r+1\) and \(n+r+2\). In spite of the fact that the dimensions of problem (3.5) is the same as the dimensions of problem (3.6), the latter is less efficient if we solve it using SDP method, especially when G is large in size. It has been found that in practice, as we will see later in Sect. 5, the performance of SDQ formula is not as efficient as in SDB formula. The reason for this inefficiency is the matrix P being of full rank which makes the system badly conditioned. We can develop a more efficient method for this formula by reformulating it over the second-order cone as described in Sect. 4, (see [12]).

Formula SDQ appears to be straightforward. Nonetheless, we found that using this SDQ formula to solve related problems was not an adequate option. In the next section, we will explain the cause for that when we speak about mixed SDP and second-order cone programming method. In Sect. 5, we will understand this fact about SDQ formula when we use the formula to solve large numerical examples with \(n > 50\). The SDV formula does not contend favorably with the other two SDB and SDQ formulations due to the quantity of work per one iteration of interior-point method which solve SDV formula. It is \({{\mathcal {O}}}(n^6)\), where n in the dimension of G and \({{\mathcal {O}}}(.)\) is the order of convergence. The SDV formulation is even slower than the projection method in some cases. Hence, using the SDV formulation to solve (1.5) is time consuming. The above discussion makes SDB formula as the best choice since we anticipate good performance while it does not have the illness of SDQ nor the large size of SDV.

4 Mixed semidefinite and second-order cone approach

Now, we explain the primal and the dual mixed semi-definite and second-order cone problem (SOCP) which is of the form:

$$\begin{aligned} (P')~~&{minimize}~ ~&C_{S} \bullet X_{S} +C^{T}_{Q}X_{Q} \nonumber \\&{subject\, to}&~~ (D_{S})_{i} \bullet X_{S} + (D_{Q})^{T}_{i} X_{Q} =b_{i}, ~ ~ i = 1,2,\dots , m \nonumber \\&\qquad \qquad X_{S} \succeq 0, X_{Q} \ge _{Q} 0. \end{aligned}$$
(4.1)

The variables are \(X_{S}\in {{\mathcal {S}}}_{n}\) and \(~ X_{Q}\in I\!\!R^{k}\). The given data matrices are \(C_{S},~ (D_{S})_{i}\) \(\in {{\mathcal {S}}}_{n}\) and \(C_{Q},~ (D_{Q})_{i}\) \( \in I\!\!R^{k}, \) \(\forall i\). In the two above inequalities each has a different explication : \( X_{S} \succeq 0\) means \(X_{S}\in {{\mathcal {S}}}_{n}^{+}\) and \(X_{Q} \ge _{Q} 0\) means that \(X_{Q}\in {{\mathcal {Q}}}_{k}\).

The dual problem of (4.1) is:

$$\begin{aligned} (D') ~ ~&{maximize}~ ~&{b}^{T}{y} \nonumber \\&{subject\, to}&\sum _{i=1}^{m}y_{i}(D_{S})_{i} \preceq C_{S} \nonumber \\&\sum _{i=1}^{m}y_{i}(D_{Q})_{i} \le _{Q} C_{Q} . \end{aligned}$$
(4.2)

Here, \({y} \in I\!\!R^{m}\) is the variable.

The objective function of problem (1.5) can now be rewritten as a dual SOCP in three different ways.

4.1 Formulation IV (SQV)

One direction is to define \(\Vert G-B(b)\Vert _{F}\) as

$$\begin{aligned} \Vert G-B(b)\Vert _{F}=\Vert {\textbf {vec}}(G-B(b))\Vert _{2}. \end{aligned}$$

Hence, if we place \(\Vert G-B(b)\Vert _{F}\le t\) for t belong to \(I\!\!R^{+}\), the second-order cone definition gives us

$$\begin{aligned} \left[ \begin{matrix} t \\ {\textbf {vec}}(G-B(b)) \end{matrix} \right] \in {{\mathcal {Q}}}_{1+n^2}. \end{aligned}$$

Therefore, we have the following equivalent problem to (1.5):

$$\begin{aligned} (SQV) ~~&{minimize} ~~ t, \nonumber \\&{subject\, to} \left[ \begin{matrix} t &{} 0 \\ 0&{} B(b) \\ \end{matrix} \right] \succeq 0 \left[ \begin{matrix} t \\ {\textbf {vec}}(G-B(b)) \\ \end{matrix} \right] \ge _{Q} 0, \end{aligned}$$
(4.3)

where \(t\in I\!\!R^{+}\). The above problem is in the shape of problem (4.2). The second-order cone constraint is the difference between this form and SDV. The dimensions of this SQV problem are \(r+1\), the SDP part is \(n+1\) and the SOCP part is \(n^2+1\). This makes us anticipate much less efficiency from SQV when we execute it.

4.2 Formulation V (SQQ)

The second formula is as established in Sect. 3.3, i.e.

$$\begin{aligned} \Vert G-B(b)\Vert _{F}^2~~ ={y}^{T}P{y}+2{q}^{T}{y}+s. \end{aligned}$$

Therefore, we have the following problem which is equivalent to problem (1.5)

$$\begin{aligned}&{minimize} ~ ~&{y}^{T}P{y}+2{q}^{T}{y}+s \nonumber \\&{subject\, to}&B(b)~ \in ~ {{\mathcal {B}}}_{n},~~ B(b)\succeq 0. \end{aligned}$$
(4.4)

But

$$\begin{aligned} {y}^{T}P{y}+2{q}^{T}{y}+s = \Vert P^{1/2}{y}+P^{-1/2}{q}\Vert _{2}^{2}+s-{q}^{T}P^{-1}{q}. \end{aligned}$$

Now, we optimize \(\Vert G-B(b)\Vert _{F}^{2}\) by minimizing \(\Vert P^{1/2}{y}+P^{-1/2}{q}\Vert _{2}\). Then, we have the following equivalent problem:

$$\begin{aligned} (SQQ) ~~&{minimize} ~ ~&t, \nonumber \\&{subject\, to} \left[ \begin{matrix} t &{} 0 \\ 0&{} B(b) \\ \end{matrix} \right] \succeq 0&\left[ \begin{matrix} t \\ P^{1/2}{y}+P^{-1/2}{q} \\ \end{matrix} \right] \ge _{Q} 0 , \end{aligned}$$
(4.5)

where \(t\in I\!\!R^{+}\). The above problem is in the shape of problem (4.2). The second-order cone constraint is the difference between this form and SDQ. The dimensions of this SQQ problem are \(r+1\), the SDP part is \(n+1\) and the SOCP part is \(r+1\). It may be noticed that we did not speak about the constraint of B(b) being bisymmetric. This is because the structure of the bisymmetric matrix B(b) is embedded inside the other constraints.

4.3 Formulation VI (SQB)

The last formula will take advantage and feature the bisymmetric structure of B(b) explicitly. In Sect. 3, we introduced the operator vectorization \(\mathbf {bvec}\) on bisymmetric matrices. This operator will be used to develop SQB formula. Lemma 3.3 gives us the following:

$$\begin{aligned} \Vert \bar{G}-B(b)\Vert _{F}=\Vert {\textbf {bvec}}(\bar{G}-B(b))\Vert _{2} \end{aligned}$$

where \(\bar{G}=P_{\mathcal {B}}(G)\), which leads to:

$$\begin{aligned} (SQB) ~~&{minimize} ~ ~\quad t, \nonumber \\&{subject\, to} \left[ \begin{matrix} t &{} 0 \\ 0&{} B(b) \\ \end{matrix} \right] \succeq 0&\left[ \begin{matrix} t \\ {\textbf {bvec}}(\bar{G}-B(b)) \\ \end{matrix} \right] \ge _{Q} 0. \end{aligned}$$
(4.6)

The second-order cone dimension in this form is \(r+1\), which is the same as that of SQQ.

The mixed formulations are expected to be more efficient in practice than SDP-only formulas, particularly the SQQ and SQB which have the least dimension in the second-order cone constraint. For interior point method, the SOCP has superior worst-case complexity more than the SDP method. Nevertheless, SDB has a much less SDP dimension with no weakness like SDQ has, and that causes SDB a preferable choice among other SDP. This is due to the economical vectorization operator \(\mathbf {bvec}\). It was clear from practical experiments that the SQB formula shows competitive behaviour over SQQ and similar to SDB (see Sect. 5).

5 Numerical results

In this section, we compare and present the performance of the methods we discussed in previous sections. First, we present numerical results for the projection method and then we use NT-direction of the interior-point primal-dual path-following method. Next, we present numerical results for all the six different formulas of Sects. 3and  4, and compare them with the alternating projection method.

To implement the modified alternating projection method, a Matlab code was written and the iteration is stopped when \(\Vert P_{\mathcal {B}} (P_{\mathcal {S}}(G_{j}))-P_{\mathcal {S}}(G_{j})\Vert _F \le 10^{-5}\). For the six SDP and SOCP formulas, we used the software SDPT3 ver. 3.0 [17] because of its stability and its ability to utilize sparsity very efficiently.

Problem (1.5) was transformed into six different formulas as explained in Sects. 3 and  4. For each formula, we wrote a Matlab code. This Matlab code transforms the problem and passes it through to SDPT3 for a first run. A second run is done with the minimal iterate from the first run being the starting initial point. We repeat this process until no more progress is detected. We execute all the numerical experiment in this section using Matlab 9.0.

Table 1 \(\Vert G-B^*\Vert _F\) among all methods
Full size table

We applied all approaches to problems starting from small dense problems with \(n=10\) up to a large problems with \(n=150.\) We apply the methods to obtain results as follows: we construct a matrix B positive definite bisymmetric randomly, then we perturb this matrix by adding random noise matrix N to B, where elements of B changes between \(-10.0\) and 10.0. Then, the problem is to retrieve the matrix before the matrix noise was added. The optimal solution is found for all the cases with high accuracy, at least seven decimals, except for the projection method where we stop with five decimals of accuracy. Table 1 shows how close, in Frobenius norm for selected test problem and the minimal solution of each method, \(B^*\) to the data matrix G. We show in Fig. 1 the comparison results, comparing the CPU time in ln of seconds against the size of the data matrix G. The correlation between the size of the matrix and the CPU time is shown in Fig. 1.

Fig. 1
figure 1

Comparing CPU time in minutes for all seven approaches

Full size image

The SDV formulation does not compete favorably with the other formulations due to the volume of work at each iteration of interior-point methods which solve SDV formula in \({{\mathcal {O}}}(n^6)\), where \({{\mathcal {O}}}(.)\) is the order of convergence. The SDV formulation is even sometimes slower than the projection method. Hence, using the SDV formulation to solve (1.5) is time consuming. This leaves us with SDB and SQB formula in which we anticipate good performance since it does not have the weakness of SDQ or SQQ nor the huge size of SDV or SQV. However, we practically found that all formulations work well except for the SDV and SQV.