Blood flow analysis with considering nanofluid effects in vertical channel

Abstract

Manipulation of heat convection of copper particles in blood has been considered peristaltically. Two-phase flow model is used in a channel with insulating walls. Flow analysis has been approved by assuming small Reynold number and infinite length of wave. Coupled equations are solved. Numerical solution are computed for the pressure gradient, axial velocity function and temperature. Influence of attention-grabbing parameters on flow entities has been analyzed. This study can be considered as mathematical representation to the vibrance of physiological systems/tissues/organs provided with medicine.

Introduction

Fluids are mostly used as energy (heat) carriers. For efficient heat transfer, low thermal conductivity of fluid is major constraint. As a result, engineering fluids are developed with suspensions of metallic particles. The word nanofluid was initially used by Choi (1995). Fluids like water, engine oil, ethylene glycol, some lubricants, blood and polymer solutions have low thermal conductivity as compared to solids. By adding solid particles of higher thermal conductivity to these fluid, raises the thermal conductivity of these fluids. These solid particles are usually of the size of the order of 1–100 nanometers and known as nanoparticles are mostly of materials, such as metals (Ag, Au, Cu, Fe), nitride ceramics (AlN, SiN), oxide ceramics (Al$_{2}$O$_{3}$, CuO), carbide ceramics (SiC, TiC), semiconductors (TiO$_{2}$) and single-, double- or many-walled carbon nanotubes (DWCNT, SWCNT, MWCNT). The base fluids in which these particles are added are termed as nanofluids. Nanofluids carry up to a $5\%$ volume fraction $\epsilon$ of nanoparticles to guarantee effective heat transfer enhancement. The nanofluid is composed of three different types of magnetic (cobalt ferrite CoFe$_{2}$O$_{4}$, magnetitie Fe$_{3}$O$_{4}$, and Mn–Zn ferrite Mn–ZnFe$_{2}$O$_{4}$) and non-magnetic (silver Ag, alumina Al$_{2}$O$_{3}$ and titania TiO$_{2}$) nanoparticles (Khan et al. 2014; Sheikholeslami et al. 2016; Sheikholeslami and Rashidi 2015; Malvandi and Ganji 2016; Hussanan and Salleh 2017).

Fluid flows driven by heat convection in open channels have been in progress, over the past few decades, for vertical or inclined geometries. This great interest stems from its range of utilizations, such as the chilling of electronic devices, solar chimney, solar cells, solar energy collectors and as a means of facilitating thermal performance in many other industrial processes. Flows induced by travelling sinusoidal waves on channel walls are referred as peristaltic flows. The peristaltic transport has fundamental importance due to physiological and many other applications such as urine transportation, chyme motion, spermatozoa transport, vasomotion of small blood vessels, heart–lung machine, sanitary fluid transport, hose pumps, dialysis machine, and transport of corrosive fluids in nuclear industry. Earthworms use similar system to derive their locomotion. Modern machinery imitate this design like robots. Latham (1966) was the first who discussed the peristaltic theory of viscous fluid. Meanwhile, Shapiro (1969) analyzed the peristaltic transport of viscous fluid experimentally. Afterwards, several investigators made significant researches in peristalsis by accounting various geometries and suppositions (Kothandapani and Srinivas 2008; Mekheimer and Abd elmaboud 2008; Srinivas and Kothandapani 2008; Gnaneswara et al. 2016; Asghar and Ali 2016; Ali et al. 2016; Noreen et al. 2015; Nowar 2014; Sarkar et al. 2015; Mekheimer and Abd Elmaboud 2015).

Adjacent to this, non-Newtonian fluids are habitually used for flow of alloys/metals and blood flow at low shear rate. Here heating traits in non-Newtonian fluids are inevitable. Heat transfer through nanofluid involves destruction of undesirable cancer tissues. Researches additionally trimmed down for the case of non-Newtonian fluids with nanoparticles (Noreen 2013; Reddy and Makinde 2016; Abou-zeid 2016; Mekheimer 2016; Kothandapani and Prakash 2016a, b). Excessive copper deposits in the human body is not a big deal. One omission is “Wilson’s syndrome. A number of people are born disable to remove copper from their bodies. Copper preserves in them. Excessive reservior of copper in human body can affect a person’s liver/brain/kidneys. Worse effects include mental illness/death. Luckily, this issue can be fixed. Patients are provided with chemical that combines with copper, and that is how copper’s spoiling effects on the body are narrowed down. Present article endeavor more in this course.

This work for the first time, evaluates the nano effects of copper particles on peristaltic transport of blood in the presence of heat convection. Current article aims to identify the influence of copper particles in the motion of blood in a vertical channel, and then to define modelling of blood by a non-Newtonian shear thinning fluid (Boger 1977) (considering pseudoplastic fluid as blood makes the problem more general. Such consideration is important in medical science), the detailed description of the mathematical formulation with mixed convection in vertical channels provides complete analysis of this topic in section two. Discussion of graphical results is done in division three. Conclusions are explored in division four.

Problem development and formulation

Let us consider a two-dimensional incompressible flow of copper-blood nanofluid in an asymmetric channel of thickness $d_{1}+d_{2}$. Pseudoplastic fluid is used to represent rheology of blood. Motion is induced by sinusoidal wave moving with speed $c\$ channel boundaries. Coordinates system $\left( \overline{X},\overline{Y}\right)$ with $\overline{X}$ parallel and $\overline{Y }\$perpendicular to the course of wave is projected. The wave geometry is taken as

$$\begin{aligned} \overline{h}_{1}(\overline{X},\overline{t}) & = {} \overline{a}_{1}\cos \left( \frac{2\pi }{\lambda } \left( \overline{X}-c\overline{t}\right) \right) +\overline{d}_{1}, \qquad \qquad \text {upper\; wall,} \nonumber \\ \overline{h}_{2}(\overline{X},\overline{t}) & = {} -\overline{b}_{1}\cos \left( \frac{2\pi }{\lambda }\left( \overline{X}-c\overline{t}\right) +\Omega \right) -\overline{d}_{2} \quad \; \; \text {lower\; wall,} \end{aligned}$$

(1)

where phase difference $\Omega$ varies in the limit $0\le \Omega \le \pi$ and $\overline{a}_{1,\ }b_{1,\ }$ are the amplitudes of travelling waves. The case $\Omega =0$ matches to the symmetric channel. Additionally, $\overline{t}$ the time, $\lambda$ is the wavelength. Symbolizing components $\overline{U}$ and $\overline{V}$ in $\overline{X}$ and $\overline{Y}$-directions in the fixed frame, the velocity field $\mathbf {V}$ is

$$\begin{aligned} \mathbf {V}=[\overline{U}(\overline{X},\overline{Y},\overline{t}),\overline{V}(\overline{X},\overline{Y},\overline{t} ),0]. \end{aligned}$$

(2)

The governing equations for the present flow problem are:

$$\begin{aligned} \nabla \cdot \mathbf {V=}\,0, \end{aligned}$$

(3)

$$\begin{aligned} \rho _\mathrm{ef}\frac{\mathrm{d}\mathbf {V}}{\mathrm{d}t}=\text {div}\mathbf {T}\,+\,g\left( \rho \beta \right) _\mathrm{ef}(T-T_{0}), \end{aligned}$$

(4)

$$\begin{aligned} \left( \rho C\right) _\mathrm{ef}\frac{\mathrm{d}T}{\mathrm{d}t}=\kappa _\mathrm{ef}\nabla ^{2}T+\mathbf {T}. \mathbf {L}. \end{aligned}$$

(5)

Here T the temperature, $\mathrm{d}/\mathrm{d}t$ the material derivative. For copper-blood nanofluid $\rho _\mathrm{ef}$ is the effective density, $C_\mathrm{p}$ the specific heat, and $\kappa _\mathrm{ef}$ the effective thermal conductivity are adopted in the following form:

$$\begin{aligned} (\rho C)_\mathrm{ef}=(1-\epsilon )(\rho C)_\mathrm{f}+\epsilon (C\rho )_\mathrm{p}, \end{aligned}$$

(6)

$$\begin{aligned} \rho _\mathrm{ef}\,=(1-\epsilon )\rho _\mathrm{f}+\epsilon \rho _\mathrm{p}, \end{aligned}$$

(7)

$$\begin{aligned} \left( \rho \beta \right) _\mathrm{ef}\,=(1-\epsilon )(\rho \beta )_\mathrm{f}+\epsilon (\rho \beta )_\mathrm{p} \end{aligned}$$

$$\begin{aligned} k_\mathrm{ef}=\frac{2k_\mathrm{f}+k_\mathrm{p}+2\epsilon (k_\mathrm{p}-k_\mathrm{f})}{2k_\mathrm{f}+k_\mathrm{p}-\epsilon (k_\mathrm{p}-k_\mathrm{f})}k_\mathrm{f} \end{aligned}$$

(8)

$$\begin{aligned} \mu _\mathrm{ef}=\frac{1}{(1-\epsilon )^{2.5}} \end{aligned}$$

(9)

where f and p, respectively, refer to fluid and nanoparticle, $\rho _\mathrm{f}$ is the density of the base fluid, $\rho _\mathrm{p}$ is the density of the nanoparticle, $k_\mathrm{f}$ is the fluid thermal conductivity, $k_\mathrm{p}$ is the thermal conductivity of the nanoparticles, and $C_\mathrm{p}$ and $C_\mathrm{f}$ are the heat capacities of the nanoparticle and the base fluid, respectively, and $\epsilon$ is the volume fraction of the nanoparticles. This is also known as Brinkmann model.

Cauchy stress tensor for pseudoplastic fluid is Boger (1977)

$$\begin{aligned} \mathbf {\overline{T}}=\mathbf {\overline{S}}-p\mathbf {\overline{I},} \end{aligned}$$

(10)

$$\begin{aligned} \overline{\lambda }_{1}\mathbf {\overline{S}}^{\nabla }+\mathbf {\overline{S}}+\frac{1}{2} \left( \mathbf {\overline{A}}_{1}\mathbf {\overline{S}+\overline{S}\ \overline{A}}_{1}\right) \left( \overline{\lambda }_{1}-\overline{\mu }_{1}\right) =\mu \mathbf {\overline{A}}_{1}, \end{aligned}$$

(11)

$$\begin{aligned} \mathbf {\overline{S}}^{\nabla }=-\mathbf {\overline{S}\overline{L}}^{T}+\frac{\mathrm{d}\mathbf {\overline{S }}}{\mathrm{d}t}-\mathbf {\overline{L}\overline{S},\ \ \overline{L}}=\nabla \mathbf {\overline{V},} \end{aligned}$$

(12)

in which $\mathbf {\overline{I}}$ identity tensor, $\mathbf {\overline{S} }$ extra stress tensor, $\mu$ dynamic viscosity, p pressure, $\mathbf {\overline{S}}^{\nabla }$ upper-convected derivative and $\overline{\mu } _{1}$ and $\overline{\lambda }_{1}$ represents relaxation times. Introducing the transformations

$$\begin{aligned} \xi & = {} \overline{X}-c\overline{t},\quad \eta =\overline{Y}, \nonumber \\ \overline{u}(\overline{\xi },\overline{\eta }) & = {} \overline{U}-c,\quad \overline{v}(\overline{\xi },\overline{\eta })=\overline{V}, \end{aligned}$$

(13)

Equations (1)–(12) in terms of above transformations give

$$\begin{aligned} \frac{\partial \overline{u}}{\partial \overline{\overline{\xi }}}+\frac{\partial \overline{v} }{\partial \overline{\eta }}=0, \end{aligned}$$

(14)

$$\begin{aligned} \rho _\mathrm{ef}\left( (\overline{u}+c)\frac{\partial }{\partial \overline{\xi }}+\overline{v} \frac{\partial }{\partial \overline{\eta }}\right) (\overline{u}+c)+\frac{\partial \overline{p}}{\partial \overline{\overline{\xi }}}=\frac{\partial \overline{S}_{ \overline{\xi }\overline{\overline{\xi }}}}{\partial \overline{\xi }}+\frac{\partial \overline{ S}_{\overline{\xi }\overline{\eta }}}{\partial \overline{\eta }}+g(\rho \beta )_\mathrm{ef}\left( \overline{T}-T_{0}\right) \end{aligned}$$

(15)

$$\begin{aligned} \rho _\mathrm{ef}\left( (\overline{u}+c)\frac{\partial }{\partial \overline{\xi }}+\overline{v} \frac{\partial }{\partial \overline{\eta }}\right) \overline{v} \, + \, \frac{\partial \overline{p}}{\partial \overline{\overline{\eta }}}=\frac{\partial \overline{S}_{ \overline{\xi }y}}{\partial \overline{\overline{\xi }}}+\frac{\partial \overline{S}_{ \overline{\eta }\overline{\eta }}}{\partial \overline{\eta }}, \end{aligned}$$

(16)

$$\begin{aligned} (\rho C_\mathrm{p})_\mathrm{ef}\left[ (\overline{u}+c)\frac{\partial }{\partial \overline{\xi }}+\overline{ v}\frac{\partial }{\partial \overline{\eta }}\right] \overline{T}=\kappa _\mathrm{ef}\left[ \frac{\partial ^{2}\overline{T}}{\partial \overline{\xi }^{2}}+\frac{\partial ^{2}\overline{T }}{\partial \overline{\eta }^{2}}\right] +\overline{S}_{\overline{\xi }\overline{\xi }}\frac{ \partial \overline{u}}{\partial \overline{\xi }}+\overline{S}_{\overline{\eta }\overline{\eta }} \frac{\partial \overline{v}}{\partial \overline{\eta }}+\overline{S}_{\overline{\xi }\overline{\eta }}\left[ \frac{\partial \overline{v}}{\partial \overline{\xi }}+\frac{\partial \overline{u}}{ \partial \overline{\eta }}\right] , \end{aligned}$$

(17)

Defining dimensionless wave ($\delta ),$ Prandtl ($\Pr$), Reynolds (Re),  Eckert (Ec), amplitude ratio ($\alpha )$, temperature ($\Pi$), stream function ($\psi$), relaxation times ($\lambda _{1}$, $\mu _{1}$), and wall temperature ($T_{0}$, $\ T_{1})$:

$$\begin{aligned} \lambda _{1} & = {} \frac{\overline{\lambda }_{1}c}{a},\ \xi =\frac{\overline{\xi }}{\lambda },\ y=\frac{\overline{y}}{a},\ t=\frac{c\overline{t}}{\lambda },\ p=\frac{a^{2} \overline{p}}{c\lambda \mu },\ \ u=\frac{\overline{u}}{c},\ v=\frac{\overline{v}}{c},Gr= \frac{\rho _\mathrm{f}g\beta _\mathrm{f}T_{0}a^{2}}{c\mu _\mathrm{f}} \nonumber \\ \delta & = {} \frac{a}{\lambda },\ \overline{S}_{ij}=\frac{a\overline{S}_{ij}}{ \mu _\mathrm{f}c}\ \left( \text { for }\ i,j\ =1,2,3\right) ,\ \mu _{1}=\frac{\overline{ \mu }_{1}c}{a},\ \Pi =\frac{\overline{T}-T_{0}}{T_{1}-T_{0}},\ Re=\frac{ca\rho _\mathrm{f}}{\mu _\mathrm{f}} \nonumber \\ Ec & = {} \frac{c^{2}}{\left( C\right) _\mathrm{f}(T_{1}-T_{0})},\ \Pr =\frac{\mu _\mathrm{ef}\left( C_\mathrm{p}\right) _\mathrm{f}}{\kappa _\mathrm{ef}},\ b=\frac{\overline{b}_{1}}{\overline{d} _{1}},\ h_{1}=\frac{\overline{h}_{1}}{\overline{d}_{1}},\ h_{2}=\frac{\overline{h}_{2}}{ \overline{d}_{1}},\ a=\frac{\overline{a}_{1}}{\overline{d}_{1}}, \end{aligned}$$

(18)

the wall surfaces are

$$\begin{aligned} h_{1} & = {} 1+a\cos \left( 2\pi \xi \right) , \nonumber \\ h_{2} & = {} -d-b\cos \left( 2\pi \xi +\Omega \right) . \end{aligned}$$

(19)

Introducing

$$\begin{aligned} v=-\delta \frac{\partial \Psi }{\partial \xi },u=\frac{\partial \Psi }{ \partial \eta }\ , \end{aligned}$$

(20)

continuity equation (14) is identically satisfied and Eqs. (15)–(17) yield

$$\begin{aligned}&-\text {Re}\delta ^{3}\left( (1-\phi _{1})+\frac{\phi _{1}\rho _\mathrm{p}}{\rho _\mathrm{f}}\right) \left( -\left( \frac{\partial \Psi }{\partial \eta }+1\right) \frac{\partial ^{2}\Psi }{\partial \xi ^{2}}+\frac{\partial \Psi }{\partial \xi }\frac{\partial ^{2}\Psi }{\partial \eta \partial \xi }\right) \nonumber \\&\quad =-\frac{\partial p}{\partial \eta }-\frac{\delta ^{2}}{K(1-\phi _{1})^{2.5} }+\frac{\delta }{(1-\phi _{1})^{2.5}}\left( -\delta ^{2}\frac{\partial ^{3}\Psi }{\partial \xi ^{3}}-\delta \frac{\partial ^{3}\Psi }{\partial \xi \partial \eta ^{2}}\right) \end{aligned}$$

(21)

$$\begin{aligned}&\text {Re}\delta \left( (1-\epsilon )+\frac{\epsilon \rho _\mathrm{p}}{\rho _\mathrm{f}} \right) \left( \left( \frac{\partial \Psi }{\partial \eta }+1\right) \frac{ \partial ^{2}\Psi }{\partial \xi \partial \eta }-\frac{\partial \Psi }{ \partial \xi }\frac{\partial ^{2}\Psi }{\partial \eta ^{2}}\right) +\frac{ \partial p}{\partial \xi } \nonumber \\&\quad =\frac{\partial S_{\xi \eta }}{\partial \eta } +Gr\ \left[ (1-\epsilon )+\epsilon \left( \frac{(\rho \beta )_\mathrm{p}}{(\rho \beta )_\mathrm{f}}\right) \right] \Pi +\delta \frac{\partial S_{\xi \xi }}{\partial \xi } \end{aligned}$$

(22)

$$\begin{aligned} -Re\delta ^{2}\left( (1-\epsilon )+\frac{\epsilon \rho _\mathrm{p}}{\rho _\mathrm{f}} \right) \left( \frac{\partial \Psi }{\partial \eta }\frac{\partial }{ \partial \xi }-\frac{\partial \Psi }{\partial \xi }\frac{\partial }{\partial \eta }\right) \frac{\partial \Psi }{\partial \xi }+\frac{\partial p}{ \partial \eta }=\delta \left( \delta \frac{\partial S_{\eta \xi }}{\partial \xi }+\frac{\partial S_{\eta \eta }}{\partial \eta }\right) , \end{aligned}$$

(23)

$$\begin{aligned}&c\delta d_{1}(1-\phi _{1})(\rho c)_\mathrm{f}+\phi _{1}(\rho C)_\mathrm{p}\left[ \left( \frac{\partial \Psi }{\partial \eta }+1\right) \frac{\partial \Pi }{\partial \xi }-\frac{\partial \Psi }{\partial \xi }\frac{\partial \Pi }{\partial \eta }\right] \nonumber \\&= K_\mathrm{eff}\delta ^{2}\frac{\partial ^{2}\Pi }{\partial \xi ^{2}}+ \frac{\partial ^{2}\Pi }{\partial \eta ^{2}} +Ec\Pr \frac{1}{(1-\epsilon )^{2.5}} \times \delta (S_{xx}-S_{\eta \eta })\frac{\partial ^{2}\Psi }{\partial \xi \partial \eta } + \left( \frac{\partial ^{2}\Psi }{\partial \eta ^{2}}-\delta ^{2}\frac{\partial ^{2}\Psi }{\partial \xi ^{2}} \right) S_{\xi \eta } \end{aligned}$$

(24)

$$\begin{aligned} \frac{1}{(1-\epsilon )^{2.5}}\left( 2\delta \frac{\partial ^{2}\Psi }{ \partial \eta \partial \xi }\right) & = {} S_{\xi \xi }+\lambda _{1}\left[ \left( \delta \frac{\partial \Psi }{\partial \eta }\frac{\partial }{\partial \xi }+\frac{\partial \Psi }{\partial \xi }\frac{\partial }{\partial \eta } \right) S_{\xi \xi }-2\left( \delta \frac{\partial ^{2}\Psi }{\partial \xi \partial \eta }S_{xx}+\frac{\partial ^{2}\Psi }{\partial \eta ^{2}}S_{\xi \eta }\right) \right] \nonumber \\& \quad +\frac{1}{2}\left( \lambda _{1}-\mu _{1}\right) \left( 4\delta S_{\xi \xi } \frac{\partial ^{2}\Psi }{\partial \xi \partial \eta }+2S_{\xi \eta }\left( \frac{\partial ^{2}\Psi }{\partial \eta ^{2}}-\delta ^{2}\frac{\partial ^{2}\Psi }{\partial \xi ^{2}}\right) \right) , \end{aligned}$$

(25)

$$\begin{aligned} -\frac{1}{(1-\epsilon )^{2.5}}\left( 2\delta \frac{\partial ^{2}\Psi }{ \partial \eta \partial \xi }\right) & = {} S_{\eta \eta }+\lambda _{1}\left[ \delta \left( \frac{\partial \Psi }{\partial \eta }\frac{\partial }{\partial \xi }-\frac{\partial \Psi }{\partial \xi }\frac{\partial }{\partial \eta } \right) S_{\eta \eta }+2\delta \left( \delta \frac{\partial ^{2}\Psi }{ \partial \xi ^{2}}S_{\xi \eta }+\frac{\partial ^{2}\Psi }{\partial \xi \partial \eta }S_{\eta \eta }\right) \right] \nonumber \\& \quad +\frac{1}{2}\left( \lambda _{1}-\mu _{1}\right) \left[ 2S_{\xi \eta }\left( \frac{\partial ^{2}\Psi }{\partial \eta ^{2}}-\delta ^{2}\frac{ \partial ^{2}\Psi }{\partial \xi ^{2}}\right) -4\delta S_{yy}\frac{\partial ^{2}\Psi }{\partial \xi \partial \eta }\right] , \end{aligned}$$

(26)

$$\begin{aligned} \frac{1}{(1-\epsilon )^{2.5}}\left( \frac{\partial ^{2}\Psi }{\partial \eta ^{2}}-\delta ^{2}\frac{\partial ^{2}\Psi }{\partial \xi ^{2}}\right) & = {} +\lambda _{1}\left[ \delta \left( \frac{\partial \Psi }{\partial \eta } \frac{\partial }{\partial \xi }-\frac{\partial \Psi }{\partial \xi }\frac{ \partial }{\partial \eta }\right) S_{\xi \eta }-\left( \frac{\partial ^{2}\Psi }{\partial \eta ^{2}}S_{\eta \eta }-\delta ^{2}\frac{\partial ^{2}\Psi }{\partial \xi ^{2}}S_{xx}\right) \right] \nonumber \\& \quad +S_{\xi \eta }+\frac{1}{2}\left( \lambda _{1}-\mu _{1}\right) \left[ \left( S_{xx}+S_{\eta \eta }\right) \left( \frac{\partial ^{2}\Psi }{ \partial \eta ^{2}}-\delta ^{2}\frac{\partial ^{2}\Psi }{\partial \xi ^{2}} \right) \right] . \end{aligned}$$

(27)

Assuming that peristaltic wave is of infinite length

$$\begin{aligned} \frac{\partial p}{\partial \xi }=\frac{1}{(1-\epsilon )^{2.5}}\frac{\partial S_{\xi \eta }}{\partial y}+Gr\ \left[ (1-\epsilon )+\epsilon \left( \frac{ (\rho \beta )_\mathrm{p}}{(\rho \beta )_\mathrm{f}}\right) \right] \Pi , \end{aligned}$$

(28)

$$\begin{aligned} \frac{\partial p}{\partial \eta }=0, \end{aligned}$$

(29)

$$\begin{aligned} \left( \frac{k_\mathrm{p}+2k_\mathrm{f}+2\epsilon (k_\mathrm{p}-k_\mathrm{f})}{k_\mathrm{p}+2k_\mathrm{f}-\epsilon (k_\mathrm{p}-k_\mathrm{f})}\right) \frac{\partial ^{2}\gamma }{\partial \eta ^{2}}+Br \frac{1}{(1-\epsilon )^{2.5}}\frac{\partial ^{2}\Psi }{\partial \eta ^{2}} S_{\xi \eta }=0, \end{aligned}$$

(30)

$$\begin{aligned} S_{\xi \xi }=\left( \lambda _{1}+\mu _{1}\right) \frac{\partial ^{2}\Psi }{ \partial \eta ^{2}}S_{\xi \eta }, \end{aligned}$$

(31)

$$\begin{aligned} S_{\eta \eta }=\left( -\lambda _{1}+\mu _{1}\right) S_{\xi \eta }\frac{ \partial ^{2}\Psi }{\partial \eta ^{2}}, \end{aligned}$$

(32)

$$\begin{aligned} (1-\epsilon )^{2.5}S_{\xi \eta }=\frac{\Psi _{yy}}{1+\chi \Psi _{\eta \eta }^{2}}, \end{aligned}$$

(33)

with $\left( \lambda _{1}^{2}-\mu _{1}^{2}\right) =\chi .$

The conditions at boundary in wave frame are

$$\begin{aligned} \Psi & = {} \frac{F}{2}, \frac{\partial \Psi }{\partial \eta }=-1, \quad \Pi =0 \quad \mathrm{at} \quad \eta =h_{1}, \nonumber \\ \Psi & = {} -\frac{F}{2}, \frac{\partial \Psi }{\partial \eta }=-1,\ \Pi =1 \quad \mathrm{at} \quad \eta =h_{2} \end{aligned}$$

(34)

where F (dimensionless time mean flow rate in moving frame) and g (dimensionless time mean flow rate in the fixed frame) are equated by $g=F+1+d$ with

$$\begin{aligned} F=\int _{h_{2}}^{h_{1}}\frac{\partial \Psi }{\partial \eta }\ \mathrm{d}\eta . \end{aligned}$$

(35)

Employing Eqs. (28) and (33), one obtains

$$\begin{aligned} \frac{\partial p}{\partial \xi }=\frac{1}{(1-\epsilon )^{2.5}}\frac{\partial }{\partial \eta }\left[ \Psi _{\eta \eta }\left\{ 1-\chi \left( \frac{ \partial ^{2}\Psi }{\partial \eta ^{2}}\right) ^{2}\right\} \right] +Gr\left[ (1-\epsilon )+\epsilon \left( \frac{(\rho \beta )_\mathrm{p}}{(\rho \beta )_\mathrm{f}} \right) \right] \ \Pi , \end{aligned}$$

(36)

Equations (29) and (36) yield

$$\begin{aligned} \frac{1}{(1-\epsilon )^{2.5}}\frac{\partial ^{4}\Psi }{\partial \eta ^{4}} -\chi \frac{1}{(1-\epsilon )^{2.5}}\frac{\partial ^{2}}{\partial \eta ^{2}} \left( \frac{\partial ^{2}\Psi }{\partial \eta ^{2}}\right) ^{3}+Gr\left[ (1-\epsilon )+\epsilon \left( \frac{(\rho \beta )_\mathrm{p}}{(\rho \beta )_\mathrm{f}} \right) \right] \frac{\partial \Pi }{\partial \eta }=0. \end{aligned}$$

(37)

Pressure rise $\Delta P_{\lambda }$

$$\begin{aligned} \Delta P_{\lambda }=\int _{0}^{1}\frac{\mathrm{d}p}{\mathrm{d}\xi }\mathrm{d}\xi .\ \end{aligned}$$

(38)

Table 1 Thermophysical properties of base fluid and nanoparticles

Results and discussion

A comparison of considered thermophysical characteristics of base fluid and nanoparticles is stated in Table 1. In this section, we have analyzed the obtained numerical results. Flow of pseudoplastic fluid with copper nanoparticles is studied. Copper is well-known thermal and electrical conductor making it ideal for markable electrical purposes. To study the influence of Grashof number Gr, relaxation time $\chi$ and volume fraction of copper nanoparticles $\epsilon$, the velocity u, pressure $\Delta P_{\lambda }$ and temperature $\Pi$ are graphically explored in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10.

Figure 1 depict the behavior of velocity for different values of the non-Newtonian fluid parameter $\chi$. It is observed that velocity profile is parabolic and its magnitude is maximum near the center of the channel. It is noticed that the velocity decreases by increasing the fluid paramater $\chi .$ Figure 2 examined the impact of copper nanoparticles. It is noticed that magnitude of velocity decreases above the centerline with an increase in the value of $\epsilon$. Copper particles concentration provide a resistance to flow, and thus hinders fluid from attaining high velocities at $\eta =0$. Velocity at channel center and wall is dissimilar. Natural tendency of fluid to migrate due to some driving force of buoyancy caused by a temperature gradient is explained by Grashof number Gr. The variations of Gr on the velocity is conspired in Fig. 3 by fixing values of $\ a=0.1,b=0.5,$ $\phi =\pi /6$ and $d=1.1$. In Fig. 3 it is discovered that the magnitude of velocity increases in region $0\le \eta \le 1.1$ and it decreases in region $-1.6\le \eta \le 0$ with a raise in Gr.

Fig. 1

Influence of $\chi$ on u

Fig. 2

Influence of $\epsilon$ on u

Fig. 3

Influence of Gr on u

Rise in pressure per wavelength against volume flow rate g is portrayed in Figs. 4, 5 and 6. Effect of $\epsilon$ on $\Delta P_{\lambda }$ is seen in Fig. 4. Copper has demonstrated its antimicrobial effectiveness in biological engineering. The effectiveness of copper and copper alloys as antimicrobial coatings on touch-surfaces has been well documented by many researchers. Here in pumping $(\Delta P_{\lambda }>0)$ and free ($\Delta P_{\lambda }=0)$ pumping section, the pumping rate enhances by rising nanoparticle volume fraction $\epsilon$. Whereas in the co-pumping section $\Delta P_{\lambda }<0,$ the pumping rate lessen down by increasing $\epsilon .$ It is found from Figs. 5 and 6 that $\Delta p_{\lambda }$ is growing function of fluid parameter $\chi$ and Grashof (Gr) number.

Fig. 4

Influence of $\chi$ on $\Delta P_{\lambda }$

Fig. 5

Influence of $\epsilon$ on $\Delta P_{\lambda }$

Fig. 6

Influence of Gr on $\Delta P_{\lambda }$

Figures 7, 8 and 9 explained the temperature distribution $\Pi$ of fluid for the significant parameters. The effect of $\chi$ on distribution $\Pi$ has been described in Fig. 7. Obviously, the magnitude of $\Pi$ decreases when $\chi$ is increased. Figures 8 and 9 that the value of temperature distribution $\Pi$ is boosted with Gr and dropped off upon increasing $\epsilon$. Hence, the toting of copper nanoparticle volume fraction, increases heat loss of fluid. High thermal conductivity of copper is the foremost reason behind it.

Fig. 7

Influence of $\chi$ on $\Pi$

Fig. 8

Influence of $\epsilon$ on $\Pi$

Fig. 9

Influence of Gr on $\Pi$

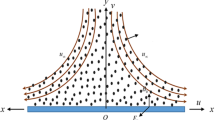
Figure 10 has demonstrated trapping analysis. Streamlines indicated the paths of fluid units in a flow regime. The development of inner mingling fluid bolus by the sealed streamlines is trapping. Flow went through a bifurcation process which has resulted in bolus. The streamlines are shown for the variations of copper particle concentration from 0, 10 and 20 cent in the pseudoplastic fluid. These figures indicate that the dimension of trapped bolus diminishes by enhancing concentration of nanoparticles. The number of closed circulating streamlines also increases.

Fig. 10

a Streamlines for $\epsilon =0.0$. b Streamlines for $\epsilon =0.1$. c Streamlines for $\epsilon =0.2$

Conclusions

The study inspects the manipulation of copper particles and heat convection on peristaltically moving pseudoplastic fluid. Two-phase flow model is used. We specifically note the following results:

• 1. Pumping rate increases with $\chi$ and Gr and decreases with$\ \epsilon$ for copper-blood fluid flow.

• 2. The velocity profile has differing behavior around walls $h_{1}$ and $h_{2}$ with an increase in Gr.

• 3. Trapping is likely perturbed by increasing concentration of copper particles in pseudoplastic fluid.

• 4. Concentration of copper nanoparticles disfavors the maximum velocity u in pseudoplastic fluid.

• 5. Gr parameter increases temperature distribution $\Pi$ in copper-blood fluid flow.

• 6. Addition of copper prevents overheating.