Convective boundary conditions effect on peristaltic flow of a MHD Jeffery nanofluid

Abstract

This work is aimed at describing the influences of MHD, chemical reaction, thermal radiation and heat source/sink parameter on peristaltic flow of Jeffery nanofluids in a tapered asymmetric channel along with slip and convective boundary conditions. The governing equations of a nanofluid are first formulated and then simplified under long-wavelength and low-Reynolds number approaches. The equation of nanoparticles temperature and concentration is coupled; hence, homotopy perturbation method has been used to obtain the solutions of temperature and concentration of nanoparticles. Analytical solutions for axial velocity, stream function and pressure gradient have also constructed. Effects of various influential flow parameters have been pointed out through with help of the graphs. Analysis indicates that the temperature of nanofluids decreases for a given increase in heat transfer Biot number and chemical reaction parameter, but it possesses converse behavior in respect of mass transfer Biot number and heat source/sink parameter.

Introduction

Nowadays, the study of nanofluids flow has created significant interest because of its wide ranging application in medical, biochemistry and industrial engineering. The nanofluids are a new class of fluids platform patterned by dispersing nanometer-sized materials in base fluids. Choi (1995) experimentally proved that the suspension of solid nanoparticles with typical length scales of 1–50 nm with high thermal conductivity enhances the effective thermal conductivity and the convective heat transfer coefficient of the base fluid. In his other work (Choi et al. 2001), it was also shown that the addition of a small amount (less than 1 % by volume) of nanoparticles to conventional heat transfer liquids increases the thermal conductivity of the fluid up to approximately two times. An elaborated analysis of nanofluids examined by Buongiorno (2006) was brought out that this massive increase in the thermal conductivity occurs owing to the presence of two main effects such as the Brownian diffusion and the thermophoretic diffusion of the nanoparticles. Masuda et al. (1993) described that the effective thermal conductivity of nanofluids is higher to enhance the heat transfer as compared to conventional heat transfer. This phenomenon suggests that the possibility of using nanofluids in advanced nuclear systems by Buongiorno and Hu (2005). Mekheimer and Abd Elmaboud (2008) have pointed out that the cancer tissues may be destroyed when the temperature reaches 42–45 °C. Some recent studies of nanofluids are given in the references (Anoop et al. 2009; Gorla and Hossain 2013; Wang and Mujumdar 2008; Kakaç and Pramuanjaroenkij 2009; Srinivasacharya and Surender 2014; Ellahi et al. 2014).

The field of peristaltic flow is another significant area, which has lately been paying attention of many researchers. Peristalsis is a mechanism, which is formed by successive waves of contraction/expansion that pushes fluid (or fluid-like contents) forward. The first investigation as peristaltic motion was done by Latham (1966). The phenomenon of peristalsis mechanism has been analyzed in detail by various researchers for different fluids under different conditions with references to physiological and mechanical situation (Fung and Yih 1968; Shapiro et al. 1969; Akbar and Nadeem 2012; Mekheimer 2002; Kothandapani and Srinivas 2008a; Vajravelu et al. 2012; Hayat et al. 2011a, 2012). Recently, attention (Akbar et al. 2012a; Srinivas and Kothandapani 2009; Kothandapani and Srinivas 2008b; Srinivas et al. 2009; Hayat et al. 2011b) has been extended on the study of peristaltic flow in the presence of heat transfer. At present, only a few numbers of studies of peristaltic transport of nanofluids are available, however in the literature, despite important applications in medical and industrial engineering systems. In view of the application of endoscope, peristaltic flow of a nanofluid between two concentric tubes has been investigated by Akbar and Nadeem (2011). The influences of wall properties on the peristaltic flow of a nanofluid have been studied by Mustafa et al. (2012). Akbar et al. 2012b, c investigated peristaltic flow of a nanofluid with slip effects using a homotopy perturbation method. They indicated that the pressure rise decreases with the increase in thermophoresis parameter, whereas increasing in the Brownian motion parameter and the thermophoresis parameter induces a rise in temperature of the nanofluids. Mixed convection peristaltic flow of magnetohydrodynamic (MHD) nanofluid was analyzed by Hayat et al. (2014a). Consequence of their investigation (Hayat et al. 2014b), the peristaltic transport of viscous nanofluid in an asymmetric channel has been presented in account of the convective conditions. Akbar et al. (2014) studied the wall-generated fluid motion of a Newtonian nanofluid in an asymmetric channel in the presence of thermal and velocity slip effects. Nadeem et al. (2014) examined the peristaltic flow of Williamson nanofluid in a curved compliant wall.

More recently, to simulate the intrauterine fluid motion in a sagittal cross section of the uterus, the induced fluid flow in a finite tapered asymmetric channel has been modeled (Eytan et al. 2001). In support of extension of our earlier works (Kothandapani and Prakash 2015a, b, c the effect of chemical reaction and convective boundary conditions on the peristaltic flow of Jeffery nanofluids is taken into the account. Even the study of peristaltic flow of an electrically conducting Jeffery nanofluid including the slip effect in the tapered asymmetric channel is also not available. In this paper, we have discussed the influence of nanofluids on peristaltic transport of a Jeffery fluid model under the effects of slip, magnetic field, chemical reactions, heat source/sink parameter and thermal radiation parameter. The paper is arranged as: the mathematical formulation of the present problem is given in “Mathematical formulation of the problem”. In “Solutions procedure”, analytical solutions are evaluated for the velocity, nanoparticles temperature and concentration with the help of homotopy perturbation method. The graphical results of the problem are represented in “Results and discussion”. Final section contains “Concluding remarks”.

Mathematical formulation of the problem

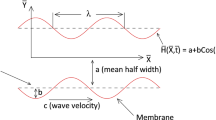
We consider the peristaltic transport of incompressible non-Newtonian nanofluids (Jeffery model) in an infinite two-dimensional tapered asymmetric channel. The tapered channel asymmetry is produced due to non-uniform channel having different amplitudes and phase difference with the same speed of peristaltic waves. We denote axial and transverse directions by $\bar{X}$ and $\bar{Y}$, respectively. Here, $\bar{U}$ and $\bar{V}$ are components of velocity in the axial and transverse directions, respectively. Let $\bar{Y} = \bar{H}_{1}$ and $\bar{Y} = \bar{H}_{2}$ be the right and left boundaries of walls (see Fig. 1). the ambient values of $T$ and $C$ as y tend to $H_{1}$ are denoted by $T_{0}$ and $C_{0}$ and y tend to $H_{2}$ are denoted by $T_{1}$ and $C_{1} .$ These are defined by

$$\bar{H}_{1} (\bar{X},\,t') = - d - m'\bar{X} - a_{1} \sin \left[ {\frac{2\pi }{\lambda }\left( {\bar{X} - ct'} \right) + \phi } \right],$$

(1a)

$$\bar{H}_{2} (\bar{X}\,,t') = d + m'\bar{X} + a_{2} \sin \left[ {\frac{2\pi }{\lambda }\left( {\bar{X} - ct'} \right)} \right],$$

(1b)

where $d$ is the half-width of the channel at the inlet of flow, $a_{1}$ and $a_{2}$ are the amplitudes of right and left walls, respectively, $c'$ is the phase speed of the wave, $m'\left( { < < 1} \right)$ is the non-uniform parameter, $\lambda$ is the wavelength, the phase difference $\phi$ is the phase difference which varies in the range $0 \le \phi \le \pi$ when $\phi = 0$ then channel is out of phase. Further $a_{1} ,$ $a_{2} ,$ $d$ and $\phi$ satisfy the condition

$$a_{1}^{2} + a_{2}^{2} + 2a_{1} a_{2} \cos (\phi ) \le (2d)^{2} .$$

(2)

Fig. 1

Geometry of the problem

The expression for Jeffery nanofluids is

$${\mathbf{T}} = - p{\mathbf{I}} + {\mathbf{S}}\;,$$

(3)

$${\mathbf{S}} \, = \, \frac{\mu }{{ 1+ \lambda_{ 1} }}\left( {\dot{\gamma } + \lambda_{2} \ddot{\gamma }} \right)\;.$$

where ${\mathbf{T}}\,$ and ${\mathbf{S}}$ are Cauchy stress tensor and extra stress tensor, respectively, $p$ is the pressure, ${\mathbf{I}}$ is the identity tensor, $\lambda_{1}$ is the ratio of relaxation to retardation times, $\lambda_{2}$ is the retardation time, $\mu$ is the coefficient of viscosity of the fluid, $\dot{\gamma }$ is the shear rate and dots over the quantities indicate differentiation with respect to time.

The governing equations the balance of mass, momentum, nanoparticle temperature and nanoparticle volume fraction for an incompressible nanofluid under the effect of chemical reaction, magnetic field, thermal radiation and heat source/sink parameter are given by (Akbar et al. 2012b; Mustafa et al. 2012)

$$\frac{{\partial \bar{U}}}{{\partial \bar{X}}}\, + \,\frac{{\partial \bar{V}}}{{\partial \bar{Y}}}\, = \,0\,,$$

(4)

$$\begin{aligned} \rho_{f} \left( {\frac{\partial }{{\partial t^{\prime}}} + \bar{U}\frac{\partial }{{\partial \bar{X}}} + \bar{V}\frac{\partial }{{\partial \bar{Y}}}} \right)\bar{U} = - \frac{{\partial \bar{P}}}{{\partial \bar{X}}} + \frac{\partial }{\partial X}\left( {\bar{S}_{{\bar{X}\bar{X}}} } \right) + \frac{\partial }{\partial Y}\left( {\bar{S}_{{\bar{X}\bar{Y}}} } \right) - \sigma^{\prime}B_{0}^{2} \bar{U} + (1 - C_{0} )\rho_{f} \alpha g\left( {\bar{T} - T_{0} } \right) + (\rho_{p} - \rho_{f} )\beta 'g\left( {\bar{C} - C_{0} } \right), \hfill \\ \end{aligned}$$

(5)

$$\rho_{f} \left( {\frac{\partial }{{\partial t^{\prime}}} + \bar{U}\frac{\partial }{{\partial \bar{X}}} + \bar{V}\frac{\partial }{{\partial \bar{Y}}}} \right)\bar{V} = - \frac{{\partial \bar{P}}}{{\partial \bar{Y}}} + \frac{\partial }{\partial X}\left( {\bar{S}_{{\bar{X}\bar{X}}} } \right) + \frac{\partial }{\partial Y}\left( {\bar{S}_{{\bar{X}\bar{Y}}} } \right),$$

(6)

$$\begin{aligned} (\rho c')_{f} \left[ {\frac{{\partial \bar{T}}}{{\partial t^{\prime}}} + \bar{U}\frac{{\partial \bar{T}}}{{\partial \bar{X}}} + \bar{V}\frac{{\partial \bar{T}}}{{\partial \bar{Y}}}} \right] = \kappa \left[ {\frac{{\partial^{2} \bar{T}}}{{\partial \bar{X}^{2} }} + \frac{{\partial^{2} \bar{T}}}{{\partial \bar{Y}^{2} }}} \right] + (\rho c')_{p} \left[ {D_{B} \left( {\frac{{\partial \bar{C}}}{{\partial \bar{X}}}\frac{{\partial \bar{T}}}{{\partial \bar{X}}} + \frac{{\partial \bar{C}}}{{\partial \bar{Y}}}\frac{{\partial \bar{T}}}{{\partial \bar{Y}}}} \right)} \right]- \frac{{\partial q_{r} }}{{\partial \bar{Y}}} + Q_{0} + \frac{{D_{T} }}{{T_{m} }}\left[ {\left( {\frac{{\partial \bar{T}}}{{\partial \bar{X}}}} \right)^{2} + \left( {\frac{{\partial \bar{T}}}{{\partial \bar{Y}}}} \right)^{2} } \right]\; \\ \end{aligned}$$

(7)

$$\left[ {\frac{{\partial \bar{C}}}{{\partial t^{\prime}}} + \bar{U}\frac{{\partial \bar{C}}}{{\partial \bar{X}}} + \bar{V}\frac{{\partial \bar{C}}}{{\partial \bar{Y}}}} \right] = D_{B} \left[ {\frac{{\partial^{2} \bar{C}}}{{\partial \bar{X}^{2} }} + \frac{{\partial^{2} \bar{C}}}{{\partial \bar{Y}^{2} }}} \right] + \frac{{D_{T} }}{{T_{m} }}\left[ {\frac{{\partial^{2} \bar{T}}}{{\partial \bar{X}^{2} }} + \frac{{\partial^{2} \bar{T}}}{{\partial \bar{Y}^{2} }}} \right] - k_{1} (\bar{C} - C_{0} )\;,$$

(8)

where $\mu$ is the coefficient of viscosity of the fluid, the volumetric volume expansion coefficient $c'$, $T_{m}$ is the fluid mean temperature, $\rho_{f}$ is the density of the base fluid, $\rho_{p}$ is the density of the particle, $\kappa$ is the thermal conductivity of the nanofluids, ${\partial \mathord{\left/ {\vphantom {\partial {\partial t}}} \right. \kern-0pt} {\partial t}}'$ represents the material time derivative, $\bar{P}$ is the pressure, $\bar{T}$ is the nanoparticle temperature, $\bar{C}$ is the nanoparticle concentration, $D_{B}$ is the Brownian diffusion coefficient, $D_{T}$ is the themophoretic diffusion coefficient, $k_{1}$ is the chemical reaction parameter, $Q_{0}$ is the constant heat addition/absorption, the radioactive heat flux $q_{r}$, $\alpha$ is the thermal expansion coefficient and $\beta '$ is the coefficient of expansion with concentration.

Convective boundary conditions

The appropriate boundary conditions are given by (Parti 1994)

$$\bar{U} = \frac{{\sqrt {k'} }}{\alpha '}\frac{{\partial \bar{U}}}{{\partial \bar{Y}}}, - k_{h} \frac{{\partial \bar{T}}}{{\partial \bar{Y}}} = h_{h} \left( {T_{0} - \bar{T}} \right)\,{\text{and}} - k_{m} \frac{{\partial \bar{C}}}{{\partial \bar{Y}}} = h_{m} \left( {C_{0} - \bar{C}} \right)\;{\text{at}}\;\bar{Y} = \bar{H}_{1} ,$$

(9a)

$$\bar{U} = - \frac{{\sqrt {k'} }}{\alpha '}\frac{{\partial \bar{U}}}{{\partial \bar{Y}}}, - k_{h} \frac{{\partial \bar{T}}}{{\partial \bar{Y}}} = h_{h} \left( {\bar{T} - T_{1} } \right)\,{\text{and}} - k_{m} \frac{{\partial \bar{C}}}{{\partial \bar{Y}}} = h_{m} \left( {\bar{C} - C_{1} } \right){\text{at }}\bar{Y} = \bar{H}_{2} ,$$

(9b)

where $k'$ is the permeability of the porous walls (Darcy number), $\alpha '$ is slip coefficient at the surface of the porous walls, $h_{h}$ and $h_{m}$ are the heat and mass transfer coefficients, respectively, the thermal conductivity $k_{h}$ and the mass conductivity $k_{m}$.

Non-dimensional quantities

We introduce the following non-dimensional quantities in Eqs. 4, 5, 6, 7 and 8, we get

$$x = \frac{{\bar{X}}}{\lambda }\;,\,\,y = \frac{{\bar{Y}}}{d}\;,\,\,t = \frac{{ct^{\prime}}}{\lambda }\;,\,\,u = \frac{{\bar{U}}}{c}\;,\,\,v = \frac{{\bar{V}}}{c}\;,\,\,\delta = \frac{d}{\lambda }\;,\,\,h_{1} = \frac{{\bar{H}_{1} }}{d}\;,\,\,h_{2} = \frac{{\bar{H}_{2} }}{d},\,\,\theta = \frac{{\bar{T} - T_{0} }}{{T_{1} - T_{0} }},\,\,a = \frac{{a_{1} }}{d},\,\,{\text{Sc}} = \frac{v}{{D_{B} }},$$

$$b = \frac{{a_{2} }}{d},\;m = \frac{\lambda m'}{d},\;\sigma = \frac{{\bar{C} - C_{0} }}{{C_{1} - C_{0} }},\;R = \frac{{\rho_{f} cd}}{\mu },\;G_{r} = \frac{{(1 - C_{0} )\rho_{f} g\alpha d^{2} (T_{1} - T_{0} )}}{c\mu },\;\beta = \frac{{Q_{0} d^{2} }}{{(T_{1} - T_{0} )\nu c_{p} }},$$

$$P_{r} = \frac{{\mu c_{f} }}{\kappa },\;N_{b} = \frac{{\tau D_{B} (C_{1} - C_{0} )}}{\nu },\;N_{t} = \frac{{\tau D_{T} (C_{1} - C_{0} )}}{{T_{0} \nu }},\;M = \sqrt {\frac{{\sigma^{\prime}}}{\mu }} dB_{0} ,\;R_{n} = \frac{{16\sigma \; \times \;T_{0}^{3} }}{{3k\; \times \;\mu c_{f} }},\;K = \frac{k}{{d^{2} }},$$

$$B_{r} = \frac{{(\rho_{p} - \rho_{f} )g\beta 'd^{2} (C_{1} - C_{0} )}}{c\mu },\;p = \frac{{d^{2} \bar{P}}}{c\lambda \mu },\;B_{h} \, = \,\frac{{h_{h} d}}{{k_{h} }},\;B_{m} = \frac{{h_{m} d}}{{k_{m} }},\;s = \frac{d}{\mu c}\bar{S}\,,\;L = \frac{\sqrt k }{d\alpha '},\;u = \frac{\partial \psi }{\partial y}\;{\text{and}}\,v = - \delta \frac{\partial \psi }{\partial x}.$$

$$R\delta \left[ {\psi_{y} \psi_{xy} - \psi_{x} \psi_{yy} } \right] = - \frac{\partial p}{\partial x} + \delta \frac{\partial }{\partial x}\left( {s_{xx} } \right) + \frac{\partial }{\partial y}\left( {s_{xy} } \right) - M^{2} \frac{\partial \psi }{\partial y} + G_{r} \theta + B_{r} \sigma ,$$

(11)

$$R\delta^{3} \left[ { - \psi_{y} \psi_{xy} + \psi_{x} \psi_{yy} } \right] = - \frac{\partial p}{\partial y} + \delta^{2} \frac{\partial }{\partial x}\left( {s_{yx} } \right) + \delta \frac{\partial }{\partial y}\left( {s_{yy} } \right),$$

(12)

$$R\delta \left[ {\frac{\partial \theta }{\partial t} + \psi_{y} \frac{\partial \theta }{\partial x} - \delta \psi_{x} \frac{\partial \theta }{\partial y}} \right] = \frac{1}{{P_{r} }}\left[ {\delta^{2} \frac{{\partial^{2} \theta }}{{\partial x^{2} }} + \frac{{\partial^{2} \theta }}{{\partial y^{2} }}} \right] + R_{n} \frac{{\partial^{2} \theta }}{{\partial y^{2} }} + N_{b} \left[ {\delta^{2} \frac{\partial \sigma }{\partial x}\frac{\partial \theta }{\partial x} + \frac{\partial \sigma }{\partial y}\frac{\partial \theta }{\partial y}} \right]\,\, + N_{t} \left[ {\delta^{2} \left( {\frac{\partial \theta }{\partial x}} \right)^{2} + \left( {\frac{\partial \theta }{\partial y}} \right)^{2} } \right]\;,$$

(13)

$$R\delta \,{\text{Sc}}\left[ {\frac{\partial \sigma }{\partial t} + \;\psi_{y} \frac{\partial \sigma }{\partial x} + \,\delta \psi_{x} \frac{\partial \sigma }{\partial y}} \right] = \delta^{2} \frac{{\partial^{2} \sigma }}{{\partial x^{2} }} + \frac{{\partial^{2} \sigma }}{{\partial y^{2} }} + \frac{{N_{t} }}{{N_{b} }}\left[ {\delta^{2} \frac{{\partial^{2} \theta }}{{\partial x^{2} }} + \frac{{\partial^{2} \theta }}{{\partial y^{2} }}} \right]\;,$$

(14)

where

$$s_{xx} = \frac{2\delta }{{1 + \lambda_{1} }}\left[ {1 + \frac{{\delta \lambda_{2} c}}{d}\left( {\frac{\partial \psi }{\partial y}\frac{\partial }{\partial x} - \frac{\partial \psi }{\partial x}\frac{\partial }{\partial y}} \right)} \right]\frac{{\partial^{2} \psi }}{\partial x\partial y},$$

$$s_{xy} = \frac{1}{{1 + \lambda_{1} }}\left[ {1 + \frac{{\delta \lambda_{2} c}}{d}\left( {\frac{\partial \psi }{\partial y}\frac{\partial }{\partial x} - \frac{\partial \psi }{\partial x}\frac{\partial }{\partial y}} \right)} \right]\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }} - \delta^{2} \frac{{\partial^{2} \psi }}{{\partial x^{2} }}} \right),$$

$$s_{yy} = - \frac{2\delta }{{1 + \lambda_{1} }}\left[ {1 + \frac{{\delta \lambda_{2} c}}{d}\left( {\frac{\partial \psi }{\partial y}\frac{\partial }{\partial x} - \frac{\partial \psi }{\partial x}\frac{\partial }{\partial y}} \right)} \right]\frac{{\partial^{2} \psi }}{\partial x\partial y},$$

and continuity equation is automatically satisfied.

Using the long-wavelength approximation, neglecting the wave number, one can find from Eqs. 11, 12, 13 and 14 that

$$\frac{\partial p}{\partial x} = \frac{\partial }{\partial y}\left( {\frac{1}{{1 + \lambda_{1} }}\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right) - M^{2} \frac{\partial \psi }{\partial y} + G_{r} \theta + B_{r} \sigma ,$$

(15)

$$\frac{\partial p}{\partial y} = 0,$$

(16)

$$\left( {\frac{{1 + R_{n} P_{r} }}{{P_{r} }}} \right)\frac{{\partial^{2} \theta }}{{\partial y^{2} }} + N_{b} \left( {\frac{\partial \sigma }{\partial y}\frac{\partial \theta }{\partial y}} \right) + N_{t} \left( {\frac{\partial \theta }{\partial y}} \right)^{2} + \beta = 0,$$

(17)

$$\frac{{\partial^{2} \sigma }}{{\partial y^{2} }} + \frac{{N_{t} }}{{N_{b} }}\frac{{\partial^{2} \theta }}{{\partial y^{2} }} - \gamma \sigma = 0\;.$$

(18)

Further, Eq. 16 indicates $p \ne p(y).$

From Eqs. 15 and 16, we have

$$\frac{{\partial^{2} }}{{\partial y^{2} }}\left( {\frac{1}{{1 + \lambda_{1} }}\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right) - M^{2} \frac{{\partial^{2} \psi }}{{\partial y^{2} }} + G_{r} \frac{\partial \theta }{\partial y} + B_{r} \frac{\partial \sigma }{\partial y} = 0,$$

(19)

where $M$ is the Hartmann number, $K$ is the permeability parameter, R is the Reynolds number, $p$ is the dimensionless pressure, $a$ and $b$ are amplitudes of left and right walls, respectively, Sc is the Schmidt number, $\delta$ is wave number, $m$ is the non-uniform parameter, Reynolds number $R$, $\nu$ is the nanofluid kinematic viscosity, stream function $\psi$, $\theta$ is the dimensionless temperature, $\sigma$ is the dimensionless rescaled nanoparticle volume fraction, Prandtl number $P_{r}$, β is the non-dimensional heat source/sink parameter, $G_{r}$ is the local temperature Grashof number, $B_{r}$ is the local nanoparticle Grashof number, $N_{b}$ is the Brownian motion parameter, $B_{h}$ is the heat transfer Biot number, $B_{m}$ is the mass transfer Biot number, $L$ is the slip parameter,$N_{t}$ is the thermophoresis parameter, the chemical reaction parameter $\gamma$, Jeffrey parameter $\lambda_{1}$ and the thermal radiation parameter $R_{n} .$

From Eq. 9a, 9b, we get,

$$\psi = - \frac{F}{2},\frac{\partial \psi }{\partial y} = L\frac{{\partial^{2} \psi }}{{\partial y^{2} }},\frac{\partial \theta }{\partial y} = B_{h} \theta \;{\text{and}}\;\frac{\partial \sigma }{\partial y} = B_{m} \sigma {\text{ at }}y = h_{1} ,$$

(20a)

$$\psi = \frac{F}{2},\frac{\partial \psi }{\partial y} = - L\frac{{\partial^{2} \psi }}{{\partial y^{2} }},\;\frac{\partial \theta }{\partial y} = B_{h} (1 - \theta )\;\frac{\partial \sigma }{\partial y} = B_{m} (1 - \sigma )\;{\text{at}}\;y = h_{2}$$

(20b)

in which $h_{1}$ and $h_{2}$ represent the dimensionless form of the surfaces of the peristaltic walls,

$$h_{1} = - 1 - mx - a\sin (2\pi (x - t) + \phi )\;{\text{and}}\;h_{2} = 1 + mx + b\sin (2\pi (x - t)).$$

(21)

It is observed that the instantaneous average volume rate of the flow $F(x,t)$ periodic in $\left( {x - t} \right),$ (Srivastava et al. 1983; Srivastava and Srivastava 1988; Kothandapani and Srinivas 2008c; Gupta and Sheshadri 2008; Kothandapani and Prakash 2015c) as

$$F(x,t) = \varTheta + a\sin 2\pi \left( {x - t} \right) + b\sin \left[ {2\pi \left( {x - t} \right) + \phi } \right]$$

(22)

in which

$$F = \int\limits_{{h_{1} }}^{{h_{2} }} u \text{d}y.$$

Solutions procedure

The computations of Eqs. 17, 18 are made through homotopy perturbation method (HPM) (He 2003; Wazwaz 2002; Abbasbandy 2006) with appropriate boundary condition Eq. 20a, 20b. For that, we write

$$H(\theta ,\tilde{p}) = (1 - \tilde{p})\left( {L(\theta ) - L(\theta_{0} )} \right) + \tilde{p}\left( {L(\theta ) + A_{1} \frac{\partial \theta }{\partial y}\frac{\partial \sigma }{\partial y} + A_{2} \left( {\frac{\partial \theta }{\partial y}} \right)^{2} + A_{3} } \right),$$

(23)

$$H(\sigma ,\tilde{p}) = (1 - \tilde{p})\left( {L(\sigma ) - L(\sigma_{0} )} \right) + \tilde{p}\left( {L(\sigma ) + \frac{{N_{t} }}{{N_{b} }}\frac{{\partial^{2} \theta }}{{\partial y^{2} }} - \gamma \sigma } \right).$$

(24)

Let us write

$$\theta = \theta_{0} + \tilde{p}\theta_{1} + \tilde{p}^{2} \theta_{2} + \cdots ,$$

(25)

$$\sigma = \sigma_{0} + \tilde{p}\sigma_{1} + \tilde{p}^{2} \sigma_{2} + \cdots$$

(26)

The solutions of temperature and nanoparticle volume fraction phenomena (for $\tilde{p} \to 1$) are constructed as

$$\theta = A_{13} + A_{12} y + \frac{{A_{9} y^{2} }}{2} + \frac{{A_{10} y^{3} }}{6} + \frac{{A_{11} y^{4} }}{12} + \frac{{B_{h} (y - h_{1} ) + 1}}{{B_{h} (h_{2} - h_{1} ) + 2}} + \frac{{A_{4} (h_{1} - h_{2} )}}{{2B_{h} }} + \frac{{A_{4} (h_{1} - y)(h_{2} - y)}}{2},$$

(27)

$$\sigma = A_{8} + A_{15} + (A_{7} + A_{14} )y + \frac{{B_{m} (y - h_{1} ) + 1}}{{B_{m} (h_{2} - h_{1} ) + 2}} - \frac{{y^{2} (A_{4} N_{t} - A_{7} A_{8} N_{b} \gamma )}}{{2N_{b} }} + \frac{{A_{6} y^{2} }}{2} + \frac{{A_{5} y^{3} }}{6} + \frac{{A_{6} \gamma y^{4} }}{24} + \frac{{A_{5} \gamma y^{5} }}{120}.$$

(28)

Using Eqs. 27 and 28, the exact solutions of Eqs. 19 and 15 and with corresponding boundary conditions Eq. 20a, 20b are obtained as

$$\begin{aligned} \psi (y) = A_{21} + \frac{{24A_{16} }}{{N^{8} }} + \frac{{2A_{18} }}{{N^{6} }} + \frac{{A_{20} }}{{N^{4} }} + y\left( {A_{22} + \frac{{6A_{17} + N^{2} A_{19} }}{{N^{6} }}} \right) + e^{ - Ny} \left( {A_{23} + A_{24} e^{2Ny} } \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + y^{2} \left( {\frac{{12A_{6} + N^{2} A_{18} }}{{N^{6} }} + \frac{{A_{20} }}{{2N^{2} }}} \right) + y^{3} \left( {\frac{{A_{17} }}{{N^{4} }} + \frac{{A_{19} }}{{6N^{2} }}} \right) + y^{4} \left( {\frac{{A_{16} }}{{N^{4} }} + \frac{{A_{18} }}{{12N^{2} }}} \right) + \frac{{A_{16} y^{6} }}{{30N^{2} }} + \frac{{A_{17} y^{5} }}{{20N^{2} }}, \hfill \\ \end{aligned}$$

(29)

$$\begin{aligned} u(y) = A_{22} - N\left( {A_{23} e^{ - Ny} - A_{24} e^{Ny} } \right) + \frac{1}{{N^{2} }}\left( {\frac{{A_{16} y^{5} }}{5} + \frac{{A_{17} y^{4} }}{4} + \frac{{A_{18} y^{3} }}{3} + \frac{{A_{19} y^{2} }}{2} + A_{20} y} \right) + \frac{{6A_{17} + 24A_{16} y}}{{N^{6} }} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{1}{{N^{4} }}\left( {4A_{16} y^{3} + 3A_{17} y^{2} + 2A_{18} y + A_{19} } \right), \hfill \\ \end{aligned}$$

(30)

$$\frac{\partial p}{\partial x} = - A_{22} N^{2} - A_{20} y - \frac{{A_{16} y^{5} }}{5} - \frac{{A_{17} y^{4} }}{4} - \frac{{A_{18} y^{3} }}{3} - \frac{{A_{19} y^{2} }}{2} + G_{r} \theta + B_{r} \sigma ,$$

(31)

where $N = M\sqrt {1 + \lambda_{1} } .$

The coefficient of heat transfer at the right wall is given by

$$Z = h_{1x} \theta_{y} .$$

(32)

Results and discussion

To discuss the influences of various parameters of interest on flow variables qualitatively such as the nanoparticles velocity, temperature, volume fraction and heat transfer coefficient, we have prepared the Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25 and 26 at the fixed values of $x = 0.5$ and $t = 0.2$

Fig. 2

Axial velocity profile $u(y)$ for $N_{b}$

Fig. 3

Axial velocity profile $u(y)$ for $R_{n}$

Fig. 4

Axial velocity profile $u(y)$ for $\gamma$

Fig. 5

Axial velocity profile $u(y)$ for $M$

The effects of Brownian motion and thermal radiation parameters on the amplitude of velocity are displayed in Figs. 2 and 3. It is viewed that the profiles of axial velocity are parabolic in nature and the amplitude of velocity field increases at the center part of the channel with increasing Brownian motion and thermal radiation parameters. Figure 4 presents the influence of chemical reaction parameter $\gamma \,$ with constant values of other parameters. It shows that the effect of increasing $\gamma \,$ leads to decrease in velocity of nanofluids in the core part of the channel. The behavior of velocity distribution for various valued of the Hartmann number (M) is shown in Fig. 5. It is observed that an increase in M causes a decrease in magnitude of axial velocity u. The instillation of magnetic nanoparticles in glioblastoma multiforme (GBM) patients induced the uptake of nanoparticles in macrophages to a major extent, and the uptake was further promoted by magnetic fluid hyperthermia (MFH) therapy (Landeghem et al. 2009). Figure 6 is prepared to study the effect of Jeffery parameter $(\lambda_{1} )$ on the magnitude of velocity field $u$. It is seen that an increase in $\lambda_{1}$ supports the amplitude of velocity of the fluid near the channel walls, and then, the situation is changed in the middle of the channel. The effect of $m$ on amplitude of velocity distribution is displayed in Fig. 7. It is expressed that the behavior of axial velocity near the channel walls and at center is not similar, also the maximum velocity of the nanoparticles always occurs at the heart part of the channel, decaying smoothly to zero at the periphery (channel wall). Perhaps, the axial velocity of the nanofluid in a uniform channel is higher than non-uniform channel. Figures 8 and 9 are included to study the effects of slip and thermophoresis parameters on the amplitude of velocity field $u$. It is observed that an increase in $L$ and $N_{t}$ supports the velocity of the fluid near the channel walls, but the situation changes in the core part of the channel.

Fig. 6

Axial velocity profile $u(y)$ for $\lambda_{1}$

Fig. 7

Axial velocity profile $u(y)$ for $m\,$

Fig. 8

Axial velocity profile $u(y)$ for $L$

Fig. 9

Axial velocity profile $u(y)$ for $N_{t}$

The temperature and volume fraction of nanoparticles distributions are illustrated in Figs. 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20 and 21 for various values of the parameters $\gamma ,$ $B_{h} ,$ $R_{n} ,$ $B_{m} ,$ $P_{r}$ and $\beta$. It is clear from Fig. 10 that decrease in chemical reaction lead to decrease in the temperature of the nanofluid. The effects of increasing heat transfer Biot number $B_{h}$ on $\theta$ are plotted in Fig. 11. We notice that amplitude of the temperature distribution decreases as $B_{h}$ increases. The distribution of temperature is plotted against y for the different value of $R_{n}$ in Fig. 12. It is renowned that the temperature decreases with increasing radiation parameter $(R_{n} ).$ The effect of mass transfer Biot number $(B_{m} )$ on $\theta$ is shown in Fig. 13. It is seen that the temperature profiles are almost parabolic in nature and get increases as $B_{m}$ increases. One can see from Fig. 14 that as the value of Prandtl number increases, the temperature profile also increases. Figure 15 clearly indicates that the effect of $\beta$ on temperature field. Here, the temperature profile is increased when $\beta$ is increased. Figures 16, 17, 18, 19, 20 and 21 reveal that the concentration of nanofluid decreases when chemical reaction, heat source/sink parameter, heat transfer Biot number and Prandtl number are increased and it increases when there is an increase in the value of mass transfer Biot number and thermal radiation parameter.

Fig. 10

Temperature profile $\theta (y)$ for $\gamma$

Fig. 11

Temperature profile $\theta (y)$ for $B_{h}$

Fig. 12

Temperature profile $\theta (y)$ for $R_{n}$

Fig. 13

Temperature profile $\theta (y)$ for $B_{m}$

Fig. 14

Temperature profile $\theta (y)$ for $P_{r}$

Fig. 15

Temperature profile $\theta (y)$ for $\beta$

Fig. 16

Nanoparticle volume fraction $\sigma (y)$ for $\gamma$

Fig. 17

Nanoparticle volume fraction $\sigma (y)$ for $\beta$

Fig. 18

Nanoparticle volume fraction $\sigma (y)$ for $B_{h}$

Fig. 19

Nanoparticle volume fraction $\sigma (y)$ for $P_{r}$

Fig. 20

Nanoparticle volume fraction $\sigma (y)$ for $B_{m}$

Fig. 21

Nanoparticle volume fraction $\sigma (y)$ for $R_{n}$

The impacts of various physical parameters of heat transfer coefficient are shown in Figs. 22, 23, 24 and 25. It is observed that the heat transfer coefficient is in oscillatory behavior which may due to contraction and expansion of the walls. The absolute values of heat transfer coefficient increases with increase of heat transfer Biot number $(B_{h} )$ and heat source/sink parameter $(\beta )$, while it get decreased with increasing thermal radiation parameter $(R_{n} )$ and chemical reaction$(\gamma )$.

Fig. 22

Heat transfer coefficient profile $Z(x)$ for $B_{h}$

Fig. 23

Heat transfer coefficient profile $Z(x)$ for $\beta$

Fig. 24

Heat transfer coefficient profile $Z(x)$ for $\gamma$

Fig. 25

Heat transfer coefficient profile $Z(x)$ for $R_{n}$

An added interesting phenomenon in the peristaltic transport is trapping, and it is mainly the formation of an internally circulating bolus of fluid by the closed streamlines. This trapped bolus pushed ahead along peristaltic waves and also the variation of circulating bolus is represented for various pertinent parameters. Figure 26a, b illustrates the influence of chemical reaction $(\gamma )$ on the streamlines for the fixed values of other parameters. It is observed that the size of the trapped bolus is decreased on both walls of the channel with the increase in $\gamma$. The effects of slip parameter $(L)$ on trapping are shown in Fig. 26b, c. It is noted that the circulating trapped bolus decreases in size and number with increase in the slip parameter. Figure 26c, d displays that the influence of flow rate $(\varTheta )$ on the streamline for fixed values of other parameters. When increase in $\varTheta$ size of the trapped bolus occurring at the walls increases. Figure 26d, e are plotted for various values of Hartmann number $\left( M \right)$ on the streamlines. We notice that while Hartmann number is increased, the size of internal bolus decreases. Figure 26e, f indicates that the trapped bolus size is increased inside and number as non-uniform parameter is increased.

Fig. 26

Streamlines when $a = 0.3,$ $b = 0.2,$ $\phi = \pi /4,$ $N_{t} = 0.5,$ $N_{b} = 0.8,$ $R_{n} = 0.1,$ $P_{r} = 0.3,$ $G_{r} = 1,$ $B_{r} = 0.5,$ $\beta = 0.3,$ $B_{m} = 1,$ $B_{h} = 0.5,$ $\lambda_{1} = 1,$ $t = 0.2,$ a $\gamma = 0.4,$ $L = 0.1,$ $\varTheta = 1.6,$ $M = 1,$ $m = 0.25,$ b $\gamma = 3,$ $L = 0.1,$ $\varTheta = 1.6,$ $M = 1,$ $m = 0.25,$ c $\gamma = 3,$ $L = 0.3,$ $\varTheta = 1.6,$ $M = 1,$ $m = 0.25,$ d $\gamma = 3,$ $L = 0.3,$ $\varTheta = 1.7,$ $M = 1,$ $m = 0.25,$ e $\gamma = 3,$ $L = 0.3,$ $\varTheta = 1.7,$ $M = 3,$ $m = 0.25$ and f $\gamma = 3,$ $L = 0.3,$ $\varTheta = 1.7,$ $M = 3,$ $m = 0.4$

The comparisons between the analytical solutions obtained by using HPM and numerical solutions solved by employing MATLAB through BVP command have also been made. It has been observed from Table 1 that numerical solution in respect of the temperature of the fluid greatly agrees with the analytical solution for the entire values of width of the channel. Moreover, it has been noticed that our results in the limiting cases $\left( {G_{r} = 0,\,\;B_{r} = 0,\;\,m = 0} \right)$ are in very good agreement with the previous studies (Kothandapani and Srinivas 2008c) when slip parameter approaches to zero.

Table 1 Comparison between analytical solution and numerical solution for different value of y when $a = 0.3,$ $b = 0.1,$ $m = 0.1,$ $\phi = \pi /2,$ $P_{r} = 1,$ $N_{t} = 0.3,$ $N_{b} = 0.1,$ $R_{n} = 2,$ $\beta = 0.1,$ $\gamma = 0.1,$ $B_{m} = 0.1,$ $B_{h} = 0.2,$ $x = 0.3$ and $t = 0.3$

Concluding remarks

In this paper, a mathematical model to study the peristaltic transport of an electrically conducting nanofluid in a vertical tapered symmetric channel in the presence of slip effect, chemical reactions, thermal radiation and heat source/sink parameters has been presented. Under the assumptions of long-wavelength and low-Reynolds number, analytic solutions have been derived for the amplitude of velocity, temperature, nanoparticles volume fraction and stream function. Interaction of various emerging parameters with peristaltic transport is discussed. The main results can be summarized as follows:

• The velocity of nanofluid decreases at the central part of channel when $L$ and $N_{t}$ are increased as expected.

• The nanoparticles temperature and volume fraction distributions are decreased with the increase in chemical reaction and heat transfer Biot number.

• The volume of trapped channel decreases with increasing chemical reaction and slip parameter, but it shows the opposite behavior with the non-uniform parameter.

Appendix

$$A_{1} = \frac{{N_{b} P_{r} }}{{1 + R_{n} P_{r} }},\;A_{2} = \frac{{N_{t} P_{r} }}{{1 + R_{n} P_{r} }},A_{3} = \frac{{\beta P_{r} }}{{1 + R_{n} P_{r} }},A_{5} = \frac{{B_{m} \gamma }}{{B_{m} (h_{2} - h_{1} ) + 2}},A_{6} = - \frac{{\gamma (B_{m} h_{1} - 1)}}{{B_{m} (h_{2} - h_{1} ) + 2}},$$

$$A_{4} = - A_{3} - \frac{{A_{2} B_{h}^{2} }}{{(B_{h} (h_{2} - h_{1} ) + 2)^{2} }} - \frac{{A_{1} B_{m} B_{h} }}{{(B_{m} (h_{2} - h_{1} ) + 2)(B_{h} (h_{2} - h_{1} ) + 2)}}$$

$$A_{7} = \frac{{A_{5} (h_{1} - h_{2} )^{2} }}{{6(B_{m} (h_{1} - h_{2} ) - 2)}} - \frac{{A_{6} (h_{2} + h_{1} )}}{2} - \frac{{A_{5} (h_{1}^{2} + h_{2}^{2} + h_{1} h_{2} )}}{6},$$

$$A_{8} = \frac{{h_{1} h_{2} (3A_{6} + A_{5} (h_{1} + h_{2} ))}}{6} + \frac{{(h_{1} - h_{2} )(2A_{6} + A_{5} (h_{1} + h_{2} ))}}{{4B_{m} }} - \frac{{A_{5} (h_{1}^{2} - h_{2}^{2} )(h_{1} - h_{2} )}}{{12(B_{m} (h_{1} - h_{2} ) - 2)}},$$

$$A_{9} = \frac{{A_{2} A_{4} B_{h} (h_{1} + h_{2} )}}{{B_{h} (h_{2} - h_{1} ) + 2}} - A_{1} \left( {\frac{{A_{7} B_{h} }}{{B_{h} (h_{2} - h_{1} ) + 2}} - \frac{{A_{4} B_{m} (h_{1} + h_{2} )}}{{2(B_{m} (h_{2} - h_{1} ) + 2)}}} \right),$$

$$A_{10} = - A_{1} \left( {\frac{{A_{4} B_{m} }}{{B_{m} (h_{2} - h_{1} ) + 2}} + \frac{{A_{6} B_{h} }}{{B_{h} (h_{2} - h_{1} ) + 2}}} \right) - \frac{{2A_{2} A_{4} B_{h} }}{{B_{h} (h_{2} - h_{1} ) + 2}},A_{11} = - \frac{{A_{1} A_{5} B_{h} }}{{2B_{h} (h_{2} - h_{1} ) + 4}},$$

$$A_{12} = - \frac{{12A_{9} (h_{1} + h_{2} ) + 6A_{10} (h_{1}^{2} + h_{2}^{2} ) + 4A_{11} (h_{1}^{3} + h_{2}^{3} ) - 6A_{9} B_{h} (h_{1}^{2} - h_{2}^{2} ) - 2A_{10} B_{h} (h_{1}^{3} - h_{2}^{3} ) - A_{11} B_{h} (h_{1}^{4} - h_{2}^{4} )}}{{12B_{h} (h_{2} - h_{1} ) + 24}},$$

$$\begin{aligned} A_{13} = \frac{{h_{1} h_{2} (A_{11} (h_{1}^{2} + h_{1} h_{2} + h_{2}^{2} ) + 2A_{10} (h_{1} + h_{2} ) + 6A_{9} )}}{12} - \frac{{(h_{1}^{2} - h_{2}^{2} )(h_{1} - h_{2} )(A_{10} + A_{11} (h_{1} + h_{2} ))}}{{12(B_{h} (h_{1} - h_{2} ) - 2)}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\, + \frac{{(h_{1} - h_{2} )(2A_{11} (h_{1}^{2} + h_{1} h_{2} + h_{2}^{2} ) + 3A_{10} (h_{1} + h_{2} ) + 6A_{9} )}}{{12B_{h} }}, \hfill \\ \end{aligned}$$

$$\begin{aligned} A_{14} = \frac{{A_{4} N_{t} (h_{1} + h_{2} )}}{{2N_{b} }} - \left( {\gamma (5A_{5} (h_{1}^{4} + h_{2}^{4} ) + 20A_{6} (h_{1}^{3} + h_{2}^{3} ) + 120A_{7} A_{8} (h_{1} + h_{8} ) - A_{5} B_{m} (h_{1}^{5} - h_{2}^{5} )} \right. \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,{{\left. { - 5A_{6} B_{m} (h_{1}^{4} - h_{2}^{4} ) - 60A_{7} A_{8} B_{m} (h_{1}^{2} - h_{2}^{2} )} \right)} \mathord{\left/ {\vphantom {{\left. { - 5A_{6} B_{m} (h_{1}^{4} - h_{2}^{4} ) - 60A_{7} A_{8} B_{m} (h_{1}^{2} - h_{2}^{2} )} \right)} {(120(B_{m} (h_{2} - h_{1} ) + 2)}}} \right. \kern-0pt} {(120(B_{m} (h_{2} - h_{1} ) + 2)}}), \hfill \\ \end{aligned}$$

$$\begin{aligned} A_{15} &= \frac{{h_{1} h_{2} }}{{120N_{b} }}\left( {A_{5} N_{b} \gamma (h_{1}^{3} + h_{1}^{2} h_{2} + h_{1} h_{2}^{2} + h_{2}^{3} ) + 5A_{6} N_{b} \gamma (h_{1}^{2} + h_{1} h_{2} + h_{2}^{2} ) - 60(A_{4} N_{t} - A_{7} A_{8} N_{b} \gamma )} \right) \\ &\quad+ \frac{{(h_{1} - h_{2} )}}{{48BcN_{b} }}\left( {A_{5} N_{b} \gamma (h_{1}^{3} + h_{1}^{2} h_{2} + h_{1} h_{2}^{2} + h_{2}^{3} ) + 4A_{6} N_{b} \gamma (h_{1}^{2} + h_{1} h_{2} + h_{2}^{2} ) - 24(A_{4} N_{t} - A_{7} A_{8} N_{b} \gamma )} \right) \\&\quad- \frac{{\gamma (h_{1}^{2} - h_{2}^{2} )(h_{1} - h_{2} )}}{{240(Bc(h_{1} - h_{2} ) - 2)}}\left( {3A_{5} h_{1}^{2} + 4A_{5} h_{1} h_{2} + 10A_{6} h_{1} + 3A_{5} h_{2}^{2} + 10A_{6} h_{2} } \right), \hfill \\ \end{aligned}$$

$$A_{16} = \frac{{A_{5} B_{r} \gamma (1 + \lambda_{1} )}}{24},A_{17} = \frac{{(2A_{11} G_{r} + A_{6} B_{r} \gamma )(1 + \lambda_{1} )}}{6},A_{18} = \frac{{(A_{5} B_{r} + A_{10} G_{r} )(1 + \lambda_{1} )}}{2},$$

$$A_{19} = (1 + \lambda_{1} )G_{r} (A_{4} + A_{9} ) + B_{r} (1 + \lambda_{1} )\left( {A_{6} + A_{7} A_{8} \gamma - \frac{{A_{4} N_{t} }}{{N_{b} }}} \right),$$

$$A_{20} = (1 + \lambda_{1} )G_{r} \left( {A_{12} - \frac{{A_{4} (h_{1} + h_{2} )}}{2} + \frac{{B_{h} }}{{B_{h} (h_{2} - h_{1} ) + 2}}} \right) + B_{r} (1 + \lambda_{1} )\left( {A_{7} + A_{14} + \frac{{B_{m} }}{{B_{m} (h_{2} - h_{1} ) + 2}}} \right),$$

$$\begin{aligned} A_{21} = \frac{F}{2} - A_{22} h_{2} - A_{23} e^{{ - Nh_{2} }} - A_{24} e^{{Nh_{2} }} - A_{25} h_{2}^{2} - A_{26} h_{2}^{3} - A_{27} h_{2}^{4} - A_{28} h_{2}^{5} - A_{29} h_{2}^{6} \hfill \\ \,\,\,\,\,\,\,\,\,\,\, - \frac{{(A_{20} + A_{19} h_{2} )N^{4} + (2A_{18} + 6A_{17} h_{2} )N^{2} + 24A_{16} }}{{N^{8} }}, \hfill \\ \end{aligned}$$

$$A_{22} = - \frac{{A_{19} N^{2} + 6A_{17} }}{{N^{6} }} + 2A_{25} L - A_{30} + A_{23} e^{{ - Nh_{1} }} (N + LN^{2} ) - A_{24} e^{{Nh_{1} }} (N - LN^{2} ),$$

$$A_{23} = \frac{{A_{33} A_{37} - A_{34} A_{36} }}{{A_{32} A_{36} - A_{33} A_{35} }},\;A_{24} = - \frac{{A_{32} A_{37} - A_{34} A_{35} }}{{A_{32} A_{36} - A_{33} A_{35} }},\;A_{25} = \frac{{12A_{16} }}{{N^{6} }} + \frac{{A_{18} }}{{N^{4} }} + \frac{{A_{20} }}{{2N^{2} }},\;A_{26} = \frac{{A_{17} }}{{N^{4} }} + \frac{{A_{19} }}{{6N^{2} }},$$

$$A_{27} = \frac{{A_{16} }}{{N^{4} }} + \frac{{A_{18} }}{{12N^{2} }},\;A_{28} = \frac{{A_{17} }}{{20N^{2} }},\;A_{29} = \frac{{A_{16} }}{{30N^{2} }},$$

$$A_{30} = 6A_{29} h_{1}^{5} + (5A_{28} - 30A_{29} L)h_{1}^{4} + (4A_{27} - 20A_{28} L)h_{1}^{3} + (3A_{26} - 12A_{27} L)h_{1}^{2} + (2A_{25} - 6A_{26} L)h_{1} ,$$

$$A_{31} = 6A_{29} h_{2}^{5} + (5A_{28} + 30A_{29} L)h_{2}^{4} + (4A_{27} + 20A_{28} L)h_{2}^{3} + (3A_{26} + 12A_{27} L)h_{2}^{2} + (2A_{25} + 6A_{26} L)h_{2} ,$$

$$A_{32} = e^{{ - Nh_{2} }} - e^{{ - Nh_{1} }} - e^{{ - Nh_{1} }} (LN^{2} + N)(h_{1} - h_{2} ),A_{33} = e^{{Nh_{2} }} - e^{{Nh_{1} }} - e^{{Nh_{1} }} (N - LN^{2} )(h_{1} - h_{2} ),$$

$$\begin{aligned} A_{34} = A_{30} (h_{1} - h_{2} ) - A_{25} (2L(h_{1} - h_{2} ) + h_{1}^{2} - h_{2}^{2} ) - F - A_{26} (h_{1}^{3} - h_{2}^{3} ) - A_{27} (h_{1}^{4} - h_{2}^{4} ) - A_{28} (h_{1}^{5} - h_{2}^{5} ) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,A_{29} (h_{1}^{6} - h_{2}^{6} ), \hfill \\ \end{aligned}$$

$$A_{35} = e^{{ - Nh_{2} }} (N - LN^{2} ) - e^{{ - Nh_{1} }} (N + LN^{2} ),A_{36} = e^{{Nh_{1} }} (N - LN^{2} ) - e^{{Nh_{2} }} (N + LN^{2} ),A_{37} = A_{30} - A_{31} - 4A_{25} L.$$