Estimates of Size of Cycle in a Predator-Prey System

Abstract

We consider a Rosenzweig–MacArthur predator-prey system which incorporates logistic growth of the prey in the absence of predators and a Holling type II functional response for interaction between predators and preys. We assume that parameters take values in a range which guarantees that all solutions tend to a unique limit cycle and prove estimates for the maximal and minimal predator and prey population densities of this cycle. Our estimates are simple functions of the model parameters and hold for cases when the cycle exhibits small predator and prey abundances and large amplitudes. The proof consists of constructions of several Lyapunov-type functions and derivation of a large number of non-trivial estimates which are of independent interest.

Introduction and Main Results

The dynamical relationship between predators and preys, most simply described by Lotka–Volterra type ordinary differential equations, has been investigated widely in recent years. One well known mathematical model describing this relationship is the Rosenzweig–MacArthur extension of the classical Lotka–Volterra model, see e.g. [7, 17, 21, 23, 25, 26], in which various interaction rates between the populations have nonlinear dependence on the prey density according to

$$\begin{aligned} \frac{dS}{dt}&\,=\, r S \left( 1-\frac{S}{K}\right) - \frac{q X S}{H + S},\nonumber \\ \frac{dX}{dt}&\,=\, \frac{p X S}{H + S} - d X. \end{aligned}$$

(1.1)

Here, $S \,=\, S\left( t\right)$ and $X \,=\, X\left( t\right)$ denotes the population densities of prey and predator, respectively, and r, K, q, H, p and d are positive parameters. The biological meanings of the parameters are the following: r is the intrinsic growth rate of the prey; K is the prey carrying capacity; q is the maximal consumption rate of predators; H is the amount of prey needed to achieve one-half of q; d is the per capita death rate of predators; and p is the efficiency with which predators convert consumed prey into new predators.

In this paper, we prove analytical estimates of the size of a limit cycle in the following version of system (1.1):

$$\begin{aligned} \frac{ds}{d\tau }&\,=\, \left( h\left( s\right) -x\right) \,s, \nonumber \\ \frac{dx}{d\tau }&\,=\, \left( s-\lambda \right) \,x, \quad \text {where}\quad h\left( s\right) \,=\,\left( 1-s\right) \left( s+a\right) \end{aligned}$$

(1.2)

and $s \,=\, s\left( \tau \right)$ and $x \,=\, x\left( \tau \right)$ denote the prey and predator, respectively. We will focus on the dynamics of system (1.2) when the parameters a and $\lambda$ take on small values, namely, we assume

$$\begin{aligned} a \,<\, 0.1 \quad \text{ and } \quad \lambda \,<\, 0.1. \end{aligned}$$

(1.3)

In order to describe the simple relation between the above Rosenzweig–MacArthur system in (1.2) and the more standard version given in (1.1), we observe that by introducing the scaled time $\tau$, the state variables $s \,=\, s\left( \tau \right)$ and $x \,=\, x\left( \tau \right)$ and the parameters a, b and $\lambda$ according to

$$\begin{aligned} \tau \,=\, \int \frac{r K}{H + S\left( t\right) } dt, \quad s \,=\, \frac{S}{K}, \quad x \,=\, \frac{q X}{r K}, \quad a \,=\, \frac{H}{K}, \quad b \,=\, \frac{p - d}{r} \quad \text {and} \quad \lambda \,=\, \frac{d H}{r K}, \end{aligned}$$

(1.4)

the standard system in (1.1) transforms to system (1.2) when $b \,=\, 1$.

Rosenzweig–MacArthur systems incorporate logistic growth of the prey in the absence of predators and a Holling type II functional response (Michaelis-Menten kinetics) for interaction between predators and preys. A literature survey shows that the model has been widely used in real life ecological applications, see e.g. [5, 17,18,19,20], including the spatiotemporal dynamics of an aquatic community of phytoplankton and zooplankton [22] as well as dynamics of microbial competition [1, 8, 24].

From a mathematical point of view, the dynamics of systems of type (1.1) and (1.2) has been frequently studied, see e.g. [2,3,4, 6, 9, 11,12,13,14,15] and the references therein. In particular, system (1.2) always has a unique positive equilibrium at $\left( x,s\right) \,=\, \left( \left( 1-\lambda \right) \left( \lambda + a\right) , \lambda \right)$ which attracts the whole positive space when $2\lambda + a \,>\, 1$. At $2\lambda + a \,=\, 1$ there is a Hopf bifurcation in which the equilibrium loses stability and a stable limit cycle, surrounding the equilibrium, is created. In particular, for $2\lambda + a \,<\, 1$ the equilibrium is a source and the cycle attracts the whole positive space (except the source) [2].

Our main results are analytical estimates of the size of this unique limit cycle when a and $\lambda$ are small. Namely, we assume (1.3) and prove that in such cases the amplitude of the cycle becomes large and x and s become very small during a portion of the cycle, see Theorem 1 below. Biologically, this means that the modeled population exhibits very small predator and prey abundances during a portion of the cycle, indicating that the population suffers a relatively high risk of going extinct because of random perturbations, see Fig. 1a, b. From (1.4) it is clear that an increase the carrying capacity K (when other parameters are fixed) implies a decrease in both parameters a and $\lambda$. Thus, if K is large enough then assumption (1.3) will be satisfied. Our results therefore show that the population becomes small, and hence vulnerable, when the carrying capacity K becomes large. This result is in line with the paradox of enrichment [17]. Indeed, Rosenzweig argues that enrichment of the environment (larger carrying capacity K) leads to destabilization.

Fig. 1

a, b The limit cycle of system (1.2) for $a = \lambda = 0.2$ (red, dotted) and for $a = 0.1$ and $\lambda = 0.05$ (black, solid). c The function $\kappa _1$ for $a=0.1$, 0.08, 0.06, 0.04, 0.02 and $a = 0.001$ (steepest curve). d The functions $\kappa _2$ (blue, dashed) and $\kappa _3$ (black, solid) for $a=0.1$, 0.08, 0.06, 0.04, 0.02 and $a = 0.001$ (lowest curve)

The above observations underscore the importance of understanding the dynamics of systems of type (1.2) under assumption (1.3). To further motivate our analytical estimates, we mention that it is nontrivial to obtain accurate numerical results by integrating the Eqs. (1.2) using standard numerical methods when a and $\lambda$ are small, see section on numerical results in the end of the paper.

A nice and interesting study close to ours is [10] in which Hsu and Shi give estimates of the period of the cycle, and estimates of parts of this period when population is very small, large, increasing and decreasing. When death rate of predators tends to zero (which implies $\lambda \rightarrow 0$), they show that the limit cycle behaves similar to a nonlinear relaxation oscillator. When both $\lambda$ and a tend to zero, they show that the prey (s) exhibits slow time scales when $s \approx 0$ as well as when $s \approx 1$. Hsu and Shi also show, without imposing restrictions on parameter values, that the prey is of order $O(\lambda /b)$ (in our notations) and the predator is of order O(a) for a time scale of $O(b/\lambda )$.

Before stating our main results, let us note that the above Rosenzweig–MacArthur systems are very simplified models of reality and therefore usually not directly applicable in biology without modifications. For example, it is clear from our main results that in model (1.2) predator and prey populations can decrease to unacceptable low abundances and still survive. However, even though our estimates are proved for such simple models, we believe that they are “good” in the sense of being useful when investigating dynamics also in more complex and realistic systems, such as, e.g., systems modeling the interactions of several predators and one prey, or seasonally dependent systems, see e.g. [1, 4, 16].

Our main results are summarized in the following theorem.

Theorem 1

Let $x_{max}$ and $s_{max}$ be the maximal x- and s-values and let $x_{min}$ and $s_{min}$ be the minimal x- and s-values in the unique limit cycle of system (1.2) under assumption (1.3). Then the predator satisfies

$$\begin{aligned} 1 \,<\, x_{max} \,<\, 1.6 \quad \text {and} \quad \exp {\left( -\frac{x_{max}}{a}\right) } \,<\, x_{min} \,<\, \exp {\left( -\frac{x_{max}}{a\kappa _1}\right) }, \end{aligned}$$

and the prey satisfies

$$\begin{aligned} 0.9 \,<\, s_{max} \,<\, 1 \quad \text {and} \quad \exp {\left( -\frac{ x_{max}}{\lambda \kappa _2}\right) } \,<\, s_{min} \,<\, \exp {\left( -\frac{ x_{max}}{\lambda \kappa _3}\right) }, \end{aligned}$$

where

$$\begin{aligned} 1\,<\, \kappa _1 \,=\, \frac{1 + e^{-2}\frac{\lambda }{a}}{1 - 2.1 \lambda - 0.31 a} \,<\, 1.32 \left( 1 + e^{-2}\frac{\lambda }{a}\right) , \end{aligned}$$

$$\begin{aligned} 1 \,>\, \kappa _2 \,=\, \frac{1}{1 +\lambda \left( 1-\ln \left( \lambda \right) \right) } \,>\, 0.75 \quad \text {and} \quad 1 \,<\, \kappa _3 \,=\, \frac{1}{1 - 0.3\lambda - a \left( 1.3 - \ln \left( a\right) \right) } \,<\, 1.64. \end{aligned}$$

From the expressions for $\kappa _1, \kappa _2$ and $\kappa _3$ in Theorem 1 we conclude that

$$\begin{aligned}&\kappa _1 \searrow 1 \quad \text {if} \quad a \rightarrow 0 \quad \text {and} \quad \frac{\lambda }{a} \rightarrow 0,\\&\kappa _2 \nearrow 1 \quad \text {if} \quad \lambda \rightarrow 0,\\&\kappa _3 \searrow 1 \quad \text {if} \quad a \rightarrow 0 \quad \text {and} \quad \lambda \rightarrow 0. \end{aligned}$$

These limiting properties of $\kappa _1, \kappa _2$ and $\kappa _3$, which we illustrate in Fig. 1c, d, clarify that Theorem 1 yields the following remark.

Remark 1

Let $x_{max}$ and $s_{max}$ be the maximal x- and s-values and let $x_{min}$ and $s_{min}$ be the minimal x- and s-values in the unique limit cycle of system (1.2) under assumption (1.3). If both a and $\frac{\lambda }{a}$ are small, then the estimate

$$\begin{aligned} x_{min} \,\approx \, \exp \left( {-\frac{x_{max}}{a}}\right) \end{aligned}$$

is “good” for the minimal predator abundance of the unique limit cycle. Similarly, if both a and $\lambda$ are small, then the estimate

$$\begin{aligned} s_{min} \,\approx \, \exp \left( {-\frac{x_{max}}{\lambda }}\right) \end{aligned}$$

is “good” for the minimal prey abundance of the unique limit cycle.

In the last section of the paper we give some numerical results illustrating the precision of the estimates stated in Remark 1, see Figs. 9 and 10.

Before discussing the outline of the proof of Theorem 1, we state its analogue for the more standard version of the Rosenzweig–MacArthur system given in (1.1) as a corollary. In this setting, assumption (1.3) takes the form

$$\begin{aligned} \frac{H}{K} \,<\, 0.1, \quad \frac{d H}{r K} \,<\, 0.1 \quad \text {and} \quad \frac{p - d}{r} \,=\, 1. \end{aligned}$$

(1.5)

The biological meaning of the first two inequalities is that the half-saturation constant for predators (H) is assumed small compared to the carrying capacity of the prey (K), and that the death rate of predators (d) is assumed small compared to the growth rate of the prey (r) times K / H. The third assumption in (1.5) says that the growth rate of the prey (r) equals the difference between the efficiency of the predators (p) and the death rate of predators (d). Theorem 1 immediately implies the following result.

Corollary 1

Let $X_{max}$ and $S_{max}$ be the maximal predator and prey densities and let $X_{min}$ and $S_{min}$ be the minimal predator and prey densities of the unique limit cycle in system (1.1) under assumption (1.5). Then the predator satisfies

$$\begin{aligned} 1 \,<\, \frac{q X_{max}}{r K} \,<\, 1.6 \quad \text {and} \quad \exp {\left( -\frac{q X_{max}}{r H}\right) } \,<\, \frac{q X_{min}}{r K} \,<\, \exp {\left( -\frac{q X_{max}}{r H \kappa _1}\right) }, \end{aligned}$$

and the prey satisfies

$$\begin{aligned} 0.9 \,<\, \frac{S_{max}}{K} \,<\, 1 \quad \text {and} \quad \exp {\left( -\frac{q X_{max}}{d H \kappa _2}\right) } \,<\, \frac{S_{min}}{K} \,<\, \exp {\left( -\frac{q X_{max}}{d H\kappa _3}\right) }, \end{aligned}$$

where $\kappa _1$, $\kappa _2$ and $\kappa _3$ are given by Theorem 1 with $a \,=\, \frac{H}{K}$ and $\lambda \,=\, \frac{d H}{r K}$.

Moreover, if $\frac{H}{K}$ and $\frac{d}{r}$ are small, then the estimate $X_{min} \approx \frac{r K }{q}\exp {\left( -\frac{q X_{max}}{r H}\right) }$ is good for the minimal predator density, and if $\frac{H}{K}$ and $\frac{dH}{rK}$ are small, then the estimate $S_{min} \approx K \exp {\left( -\frac{ q X_{max}}{d H }\right) }$ is good for the minimal prey density.

The proof of Theorem 1 consists of constructions of several Lyapunov-type functions and derivation of a large number of non-trivial estimates. We believe that these methods and constructions have values also beyond this paper as they present methods and ideas that, potentially, can be useful for proving analogous results for dynamics in similar systems as well as in more complex systems.

The proof is constructed in a way such that Theorem 1 is a direct consequence of four statements, namely Statements 1–4, which we prove in the following section. In addition to the estimates in Theorem 1 it is also possible to find, from these statements and lemmas, a positively invariant region trapping the unique limit cycle inside. In fact, the limit cycle will be inside an outer boundary consisting of the part of a trajectory ${\hat{T}}$ with initial condition $x\left( 0\right) \,=\,1.6, \, s\,=\,\lambda$ and the part of $s\,=\,\lambda$ between $\left( 1.6, \lambda \right)$ and the next intersection with $s\,=\,\lambda$ when $x\,>\,h\left( \lambda \right)$. It will also be outside an inner boundary consisting of the part of a trajectory $\check{T}$ with initial condition $x\left( 0\right) \,=\,1, \, s\,=\,\lambda$ and the part of $s\,=\,\lambda$ between $\left( 1, \lambda \right)$ and the next intersection with $s\,=\,\lambda$ when $x\,>\,h\left( \lambda \right)$. Estimates for these boundaries can be found from given statements and lemmas, even if we do not write them explicitly here. We also point out that better but more complicated estimates than those summarized in Theorem 1 follow from lemmas which are used for the proofs of Statements 1–4 and Theorem 1.

The following section is devoted to the proof of Theorem 1, while we end the paper by giving a section on numerical results.

Proof of Theorem 1

To outline the proof of Theorem 1 we first observe that the coordinate axes are invariant, and hence the region $x,s \,>\, 0$ is also invariant. Therefore, we consider solutions only for positive s and x. Moreover, system (1.2) has isoclines at $x \,=\, h\left( s\right)$ and $s \,=\, \lambda$, which lead us to split the proof by introducing the following four regions:

• Region 1, where $x\,>\,h\left( s\right) , \ s\,>\,\lambda$ and x is growing and s decreasing.

• Region 2, where $x\,>\,h\left( s\right) ,\ s\,<\,\lambda$ and both x and s decrease.

• Region 3, where $x\,<\,h\left( s\right) ,\ s\,<\,\lambda$ and x decreases and s grows.

• Region 4, where $x\,<\,h\left( s\right) ,\ s\,>\,\lambda$ and both x and s increase.

Fig. 2

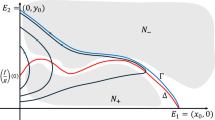
Notations of the four Regions 1-4, the points $P_1$-$P_8$ on a trajectory T (blue, solid), and the isoclines $x \,=\, h(s)$ and $s \,=\, \lambda$ (red, dotted) of system (1.2)

Any trajectory starting in Region 1 will enter Region 2 from where it will enter Region 3 and then Region 4 and finally Region 1 again, and the behaviour repeats infinitely. Figure 2 illustrates the four regions together with isoclines and points which will be used in the proof of Theorem 1. Behaviour and estimates for trajectories in different regions are examined in different subsections. The main results in Regions 1–4 will be concluded in Statements 1–4.

Estimates in Region 1

We begin this section by proving a lemma which gives a bounded region into which all trajectories will enter after sufficient time and which will be used in several places in the proof of Theorem 1.

Lemma 1

Consider the function

$$\begin{aligned} V_g\left( s\right) \,=\, \frac{\alpha \left( 1-s\right) }{1+\beta \left( 1-s\right) } \quad \text {where} \quad \alpha \,=\, 2-\lambda +a \quad \text {and} \quad \beta \,=\,\frac{\lambda +1}{a-2\lambda +3}. \end{aligned}$$

All solutions of system (1.2) under condition (1.3) with positive initial values will enter into the region determined by the inequalities $x \,<\, V_g\left( s\right)$, $x \,>\, 0$, $s \,>\, 0$ and remain there.

Fig. 3

Geometry in the proof of Lemma 1

Proof of Lemma 1

Let $U\,=\,x-\alpha \left( 1-s\right)$. Differentiation with respect to time and using (1.2) yield

$$\begin{aligned} U'\,=\,-\left( 1-s\right) ^2 \left( s+\lambda \right) \,\alpha +\gamma \, \left( \lambda s -s -as -\lambda \right) \,<\,0 \end{aligned}$$

for $\gamma \,\ge \, 0$ when $x\,=\,\alpha \left( 1-s\right) +\gamma$. Thus all trajectories will enter the region $x \,<\, \alpha \left( 1-s\right)$ and remain there, see Fig. 3. Let also

$$\begin{aligned} V\,=\,\left( 1+\beta \left( 1-s\right) \right) x -\alpha \left( 1-s\right) , \end{aligned}$$

and notice that $\frac{\partial V}{\partial x} , \frac{\partial V}{\partial s} \,>\, 0$ since $0 \,<\, \beta \,<\, 1 \,<\, \alpha$ and, after sufficient time, $s \,<\, 1$ and $x \,<\, \alpha$. Calculating the derivative of V with respect to time we get

$$\begin{aligned} V'\,=\,-\frac{\alpha \,{\left( 1-s\right) }^{3}\,S }{{\left( 4-\lambda \,s-s+a-\lambda \right) }^{2}} \end{aligned}$$

at $x \,=\, V_g$, where

$$\begin{aligned} S\,=\,\left( \lambda +1\right) \,\left( a-3\,\lambda +2\right) \,s+\lambda \,{\left( a-\lambda +4\right) }^{2}. \end{aligned}$$

Because $S\,>\,0$ for $a,\lambda \,<\,0.1$ we get $V'\,\le \, 0$ for $0\,<\,s\,\le \, 1$ and $V'\,=\,0$ only for $s\,=\,1$. Because $\beta \,>\,0$ we have $V_g\,<\,\alpha \left( 1-s\right)$ and since $h\left( s\right) \,<\, V_g\left( s\right)$ for $0\,<\,s\,<\,1$ all trajectories entering $x\,<\,\alpha \left( 1-s\right)$ also enter region $x\,<\,V_g$, where they remain because of the sign of $V'$.

The maximal x-value for a trajectory is attended when it escapes from Region 1 to Region 2. In this section we will give estimates for maximal x-value, when trajectory starts on boundary of Region 1.

Statement 1

Any trajectory starting on the isocline $x \,=\, h\left( s\right) , s \,>\, \lambda$ has a maximum $x_0$ before it enters Region 2 and $x_0 \,<\, 1.6$. Moreover, if the trajectory starts from a point where $s \,>\, 0.9$, then $x_0 \,>\, 1$.

We formulate the last part of the statement as a lemma with an own proof.

Lemma 2

Any trajectory starting on the isocline $x\,=\,h\left( s\right) , s \,>\, 0.9$ has a maximum $x_0$ before it enters Region 2 and $x_0\,>\,1$.

Proof of Lemma 2

In Region 1 the x-value on the trajectory is growing while the s-value is decreasing, and $x'$ is smallest for greatest $\lambda$ and $s'$ is smallest for smallest a. This implies that in Region 1, for any $a, \lambda \in [0,0.1)$, the x-value for a trajectory of system (1.2) is always growing stronger than the x-value for a trajectory of the system obtained for $a\,=\,0$ and $\lambda \,=\, 0.1$, since $\vert \frac{dx}{ds}\vert$ will then be smallest. By this fact we are able to construct a bound for the minimal value of $x_0$ by using system (1.2) with $a\,=\,0$ and $\lambda \,=\, 0.1$ fixed.

We define the continuous function f by

$$\begin{aligned} f\left( s\right) \,=\,\left\{ \begin{array}{ll} 0.513+1.33 s - 2 s^2 &{}\quad 0.7\,<\,s\,\le \, 0.9 \\ 1.045-0.13s-s^2 &{}\quad 0.5\,<\,s\,\le \, 0.7 \\ 1.08-0.2s-s^2 &{}\quad 0.3\,<\,s\,\le \, 0.5 \\ 0.975+0.45s-2s^2 &{}\quad 0.1\,\le \, s\,\le \, 0.3 \end{array} \right. \end{aligned}$$

and consider the function Y defined by $Y\left( x,s\right) \,=\,x-f\left( s\right)$. The derivative of Y with respect to time, considering system (1.2) with $a\,=\,0,\ \lambda \,=\,0.1$ and substituting $x\,=\,f\left( s\right)$, is a fourth order polynomial on each piece of definition. By standard techniques it can be shown that this derivative is positive on each piece. Thus, x grows faster than $f\left( s\right)$ on the curve $x\,=\,f\left( s\right)$.

Fig. 4

Geometry in the proof of Lemma 2

Moreover, for $s\,=\,0.9$ we get $f\left( s\right) \,=\,0.09$, meaning that the point $\left( f\left( s\right) ,s\right) \,=\, \left( 0.09, 0.9\right)$ is on the isocline $x \,=\, h\left( s\right)$ because $h\left( 0.9\right) \,=\, 0.09$, see Fig. 4. We conclude that trajectories intersect the pieces of $x\,=\,f\left( s\right)$ transversally going from the region defined by $x\,<\,f\left( s\right)$ to region where $x\,>\,f\left( s\right)$. The isocline of any system (1.2) under condition (1.3) is above the isocline for the system we considered, meaning x is greater and also trajectories cannot intersect $x\,=\,f\left( s\right)$ before $s\,<\,0.1$. Moreover $f\left( 0.1\right) \,=\,1$. Thus any trajectory for any $a,\lambda \in [0,0.1)$ under our conditions that start on the isocline $x\,=\,h\left( s\right)$, $s \,>\, 0.9$, will at $s\,=\,0.1$ have an x-value greater than 1 and consequently this holds also at $s\,=\,\lambda$. Therefore, $x_0 \,>\, 1$ and the proof of Lemma 2 is complete.

Proof of Statement 1

We first recall the notations from Lemma 1 and also the fact that the maximum of a trajectory taken for $s \,=\, \lambda$ before it enters Region 2 is less than $V_g\left( \lambda \right)$, and

$$\begin{aligned} V_g\left( \lambda \right) \,=\,-\frac{\left( \lambda -1\right) \,\left( a-2\,\lambda +3\right) \,\alpha }{a-{\lambda }^{2}-2\,\lambda +4}. \end{aligned}$$

For $a,\lambda \in (0, 0.1]$, the derivative of $V_g\left( \lambda \right)$ with respect to a is

$$\begin{aligned} \frac{\left( 1-\lambda \right) \,\left( {a}^{2}-2\,{\lambda }^{2}\,a-4\,\lambda \,a+8\,a+3\,{\lambda }^{3}-{\lambda }^{2}-15\,\lambda +14\right) }{{\left( a-{\lambda }^{2}-2\,\lambda +4\right) }^{2}}\,>\,0, \end{aligned}$$

and derivative of $V_g\left( \lambda \right)$ with respect to $\lambda$ is

$$\begin{aligned} -\frac{{a}^{3}+{\lambda }^{2}\,{a}^{2}-8\,\lambda \,{a}^{2}+10\,{a}^{2}+20\,{\lambda }^{2}\,a-52\,\lambda \,a+35\,a-2\,{\lambda }^{4}-8\,{\lambda }^{3}+55\,{\lambda }^{2}-84\,\lambda +40}{{\left( a-{\lambda }^{2}-2\,\lambda +4\right) }^{2}}\,<\,0. \end{aligned}$$

Thus, $V_g\left( \lambda \right)$ is less than its value for $a \,=\, 0.1$ and $\lambda \,=\, 0$, which is less than 1.588. Since the estimate from below follows from Lemma 2, the proof of Statement 1 is complete. $\square$

Estimates in Region 2 and Region 3

We consider a trajectory T of system (1.2) under condition (1.3) with initial condition $x\left( 0\right) \,=\,x_0, \, s\left( 0\right) \,=\,\lambda$, where $1\,<\,x_0\,<\,1.6$. We suppose $c_1$ and $c_2$ are such that $0\,<\,c_2\,<\,c_1\,<\,\lambda$. If T intersects $s\,=\,c_2\lambda$ before escaping Region 2 we denote the point of first intersection with $s\,=\,c_1\lambda$ by $P_1\,=\,\left( x_1, c_1\lambda \right)$ and the point of first intersection with $s\,=\,c_2\lambda$ by $P_2\,=\,\left( x_2, c_2\lambda \right)$. We denote the next intersection with the isocline $x\,=\,h\left( s\right)$ by $P_3\,=\,\left( x_3, s_3\right)$, where $x_3\,=\,h\left( s_3\right)$. The second intersection with $s\,=\,c_2\lambda$ we denote by $P_4\,=\,\left( x_4, c_2\lambda \right)$ and the second intersection with $s\,=\,c_1\lambda$ by $P_5\,=\,\left( x_5, c_1\lambda \right)$. The next intersection with $s\,=\,\lambda$ we denote by $P_6\,=\,\left( x_6, \lambda \right)$. The lowest s-value of the trajectory before it escapes to Region 4 will be at $P_3$ and the lowest x-value at $P_6$. The notations are illustrated in Fig. 2, where there are added also points used in Region 4. We point out that trajectory T is normally not a cycle, even though such case is illustrated in Fig. 2.

The main results in this section are given in Statements 2 and 3 which give main estimates in Regions 2 and 3. Statement 2 gives a lower and upper bound for minimal x-value and Statement 3 gives a lower and upper bound for minimal s-value of the part of the trajectory in Regions 2 and 3. Lemma 3 gives a better upper estimate for lowest x-value which is needed also in for the estimates in Region 4. These estimates will also serve as upper and lower estimates for the unique cycle of system (1.2) under condition (1.3). In the proofs of Statement 2 and Lemma 3 we assume $c_1\,=\,e^ {-2},\, c_2\,=\,e^{-4}$.

We here give these three main results of this section.

Lemma 3

Trajectory T intersects $s\,=\,e^{-4}\lambda$ before escaping Region 2 and for $x_6$ we have the estimate

$$\begin{aligned} x_6 \,<\, 1.015\, e^{-2A-\frac{\theta \left( {\tilde{x}_2}\right) }{a+e^{-4}\lambda }} \end{aligned}$$

(2.1)

where

$$\begin{aligned} {\tilde{x}_2}\,=\,x_0 -3.8\, \lambda , \quad \theta \left( {\tilde{x}_2}\right) \,=\, {\tilde{x}_2} - \left( a+e^{-4}\lambda \right) \ln \left( \tilde{x}_2\right) ,\quad A\,=\,\frac{\left( 1-e^{-2}\right) \lambda }{a+e^{-2}\lambda }. \end{aligned}$$

More general estimates than in Lemma 3 and Statement 2 are given in Lemmas 4 and 5. These are formulated for general choices of parameters $c_1$ and $c_2$, which are fixed in proofs of Lemma 3 and Statement 2.

Statement 2

For the intersection of trajectory T with the isocline $s \,=\, \lambda$ at $P_6 \,=\, \left( x_6, s_6\right)$ the following estimates are valid for the x-value.

$$\begin{aligned} e^{-\frac{x_0}{a}} \,<\, x_6 \,<\, e^{-\frac{x_0}{a\kappa _1}}, \end{aligned}$$

(2.2)

where

$$\begin{aligned} 1 \,<\, \kappa _1 \,<\, \frac{1 + e^{-2}\frac{\lambda }{a}}{1 - 2.1 \lambda - 0.31 a} \,<\, 1.32 \left( 1 + e^{-2}\frac{\lambda }{a}\right) . \end{aligned}$$

(2.3)

From Statement 2 it follows that for small $\frac{\lambda }{a}$ and a the estimate $e^{-\frac{x0}{a}}$ is good for the minimal x-value on trajectory T.

Statement 3

For the intersection of trajectory T with the isocline $x \,=\, h\left( s\right)$ at $P_3 \,=\, \left( x_3, s_3\right)$ the following estimates are valid for the s-value.

$$\begin{aligned} e^{-\frac{x_0}{\lambda \kappa _2}} \,<\,s_3 \,<\, e^{-\frac{x_0}{\lambda \kappa _3}}, \end{aligned}$$

(2.4)

where

$$\begin{aligned} 1 \,>\, \kappa _2 \,>\, \frac{1}{1 +\lambda \left( 1-\ln \left( \lambda \right) \right) } \,>\, 0.75, \end{aligned}$$

and

$$\begin{aligned} 1 \,<\, \kappa _3 \,<\, \frac{1}{1 - 0.3\lambda - a \left( 1.3 - \ln \left( a\right) \right) } \,<\, 1.64. \end{aligned}$$

From Statement 3 we see that for small $\lambda ,\, a$ the estimate $e^{-\frac{x0}{\lambda }}$ is good for the minimal s-value on T.

The proof of Statement 2 is following from Lemma 3 and Statement 1 and a short Lemma 14. The proofs of Lemmas 3–5 are built on Lemmas 6–9. Lemmas 6–7 give estimates for trajectory from start to $P_2$ ($c_2\lambda \,<\,s\,<\, \lambda$ in Region 2). Lemma 8 gives estimate of the behaviour between $P_2$ and $P_4$ ($s\,<\,c_2\lambda$) and Lemma 9 for the behaviour between $P_4$ and $P_5$ ($c_2\lambda \,<\,s\,<\, c_1\lambda$ in Region 3). Lemmas 6–9 use more new lemmas about which we inform later. The section ends with the proof of Statement 3.

Before we start with the proofs of the Statements and Lemma 3 we introduce Lemmas 4 and 5. Lemma 5 can be seen as corollary from Lemma 4. The proof of Lemma 3 is very similar to proof of Lemma 4. We wish to formulate the most general upper estimate for $x_6$ in Lemma 4. We find such an estimate in the case T intersects $s\,=\,c_2\lambda$ before escaping Region 2 using auxiliary estimates for $x_1, \, x_2, \, x_4$ and $x_5$. For the estimate we need some notations and assumptions.

We introduce the following notations

$$\begin{aligned} C_1\,=\,\left( 1-c_1+ \ln \left( c_1\right) \right) \lambda ,\quad C_2\,=\,\left( c_1-c_2 +\ln \left( \frac{c_2}{c_1}\right) \right) \lambda , \end{aligned}$$

(2.5)

and notice that $C_1,\, C_2\,<\,0$. Moreover, we let

$$\begin{aligned} H_0\,=\,a+\lambda ,\quad H_1\,=\,a+c_1\lambda ,\quad H_2\,=\,a+c_2\lambda . \end{aligned}$$

(2.6)

Next, we assume that

$$\begin{aligned} C_1 \,>\, - \left( \sqrt{x_0} -\sqrt{H_0}\right) ^2, \end{aligned}$$

(2.7)

and defined the function $Q_1$ by

$$\begin{aligned} Q_1\left( x\right) \,=\, x^2 - \left( H_0+C_1+x_0\right) x + H_0 x_0. \end{aligned}$$

(2.8)

If (2.7) is satisfied, then $Q_1$ has a unique root $x^+_1$ in the interval $\left( \sqrt{H_0 x_0}, x_0\right)$. Similarly, we assume that

$$\begin{aligned} C_2 \,>\, - \left( \sqrt{x^+_1} -\sqrt{H_1}\right) ^2, \end{aligned}$$

(2.9)

and define the function $Q_2$ by

$$\begin{aligned} Q_2\left( x\right) \,=\,x^2 -\left( H_1+C_2+x^+_1\right) x + H_1 x^+_1. \end{aligned}$$

(2.10)

Again, if (2.9) is satisfied we note that then $Q_2$ has a unique root $x^+_2$ in the interval $\left( \sqrt{H_1 x^ +_1}, x^+_1\right)$. We also introduce a function $\theta$ and a number $\tilde{C}$ by

$$\begin{aligned} \theta \left( x\right) \,=\, x - H_2 \ln \left( x\right) , \quad {\tilde{C}}\,=\,\theta \left( x^+_2\right) . \end{aligned}$$

(2.11)

We make one more assumption

$$\begin{aligned} k \,=\, H_2\, e^\frac{\tilde{C}}{H_2} \,>\, 4. \end{aligned}$$

(2.12)

Also the following notations are needed

$$\begin{aligned} {\hat{z}} \,=\,\frac{1}{\sqrt{k^ 2-4k}},\quad M\,=\,\frac{c_2}{c_1} \quad \text {and} \quad A\,=\,\frac{\left( 1-c_1\right) \lambda }{H_1}. \end{aligned}$$

(2.13)

With these assumptions and notations we can formulate an upper estimate for $x_6$.

Lemma 4

Suppose assumptions (2.7), (2.9) and (2.12) are satisfied. Then the trajectory T intersects $s\,=\,c_2\lambda$ before escaping Region 2 and for $x_6$ we have the estimate

$$\begin{aligned} x_6 \,<\, \left( 1+\hat{z}\right) M^A e^{-\frac{\tilde{C}}{H_2}}. \end{aligned}$$

From the definition of $x^+_1$ and $x^+_2$, we obtain, for $i \,=\, 1,2$, that $x^+_i \,>\, x^*_i$ where $x^*_i$ is the value of $x^+_i$ for $a \,=\, 0.1,\, \lambda \,=\, 0.1$ and $x_0 \,=\, 1$. This will give us a new estimate as a corollary which we call Lemma 5. To formulate the lemma we need the notation

$$\begin{aligned} D^*_1\,=\,1-\frac{H^*_0}{x^*_1}, \quad D^*_2\,=\,1-\frac{H^*_1}{x^*_2}, \end{aligned}$$

where $H^*_i$ are the values of $H_i$, $i \,=\, 0,1$, when $a \,=\, \lambda \,=\, 0.1$, that is, $H_0^* \,=\, 0.2$ and $H_1^* \,=\, \left( 1 + c_1\right) \cdot 0.1$. With these notations we can formulate next lemma.

Lemma 5

Suppose assumptions (2.7), (2.9) and (2.12) are satisfied. Then the trajectory T intersects $s\,=\,c_2\lambda$ before escaping Region 2 and for $x_6$ we have the estimate

$$\begin{aligned} x_6 \,<\, \left( 1+{\hat{z}}\right) M^A e^{-\frac{\theta \left( {\tilde{x}_2}\right) }{H_2}}, \end{aligned}$$

where

$$\begin{aligned} {\tilde{x}_2}\,=\,x_0 + \frac{C_1}{D^*_1} + \frac{C_2}{D^*_2}. \end{aligned}$$

Because $C_i, \, i\,=\,1,2$ depend only on $\lambda$, $D^*_i$ only on $\lambda$ and $c_1$, $\tilde{x}_ 2$ does not depend on a, only on $\lambda ,\, c_1$ and $x_0$. If we choose $c_1\,=\,e^{-2},\,c_2\,=\,e^{-4}$ we are able to prove that assumptions (2.7), (2.9) and (2.12) are satisfied and get Lemma 3.

Lemma 4 is based on Lemmas 6, 8 and 9. We now give these lemmas and also Lemma 7 needed for Lemma 3. Lemma 7 can be seen as a corollary of Lemma 6.

Lemma 6

Suppose assumptions (2.7) and (2.9) are satisfied. Then the trajectory T intersects $s\,=\,c_i\lambda , \, i\,=\,1,2$, before escaping Region 2 at points $P_1\,=\,\left( x_1,c_1\lambda \right)$ and $P_2\,=\,\left( x_2,c_2\lambda \right)$, where

$$\begin{aligned} x_1 \,>\, x_0 +\frac{C_1}{1-\frac{H_0}{x^+_1}} \quad \text {and} \quad x_2 \,>\, x_0 +\frac{C_1}{1-\frac{H_0}{x^+_1}} +\frac{C_2}{1-\frac{H_1}{x^+_2}}. \end{aligned}$$

(2.14)

Moreover, if $x_i^*$ are the values for $x_i^+$, $i\,=\,1,2$, when $a\,=\,\lambda \,=\,0.1$ and $x_0\,=\,1$, then the inequalities in (2.14) remain valid for all $a,\lambda \,<\,0.1$ if $x_i^+$ are replaced by $x_i^*$.

Using Lemma 6 for special values of $c_i$ after calculating some quantities we get a corollary.

Lemma 7

Suppose that $c_1\,=\,e^{-2}$ and $c_2\,=\,e^{-4}$. Then the trajectory T intersects $s\,=\,c_2\lambda$ before escaping Region 2 at point $P_2\,=\,\left( x_2,c_2\lambda \right)$, where

$$\begin{aligned} x_2 \,>\, x_0 - 3.8 \lambda . \end{aligned}$$

Lemma 8

Let $T^*$ be a trajectory of system (1.2) under conditions (1.3) with initial conditions $x\left( 0\right) \,=\,u, \, s\left( 0\right) \,=\,\lambda ^* \,<\, \lambda , \, u\,>\,2.5H^*$ and $H^*\,=\,a+\lambda ^*\,>\,h\left( \lambda ^*\right)$. Then the trajectory $T^*$ next time intersects $s\,=\,\lambda ^*$ at a point $P\,=\,\left( v,\lambda ^*\right)$ where

$$\begin{aligned} v\,<\,\left( 1+{\hat{z}}\right) e^{-\frac{\tilde{\theta }\left( u\right) }{H^*}}, \end{aligned}$$

and where

$$\begin{aligned} \tilde{\theta }\left( u\right) \,=\,u-H^* \ln \left( u\right) ,\quad \hat{z} \,=\,\frac{1}{\sqrt{\tilde{k}^ 2-4\tilde{k}}} \quad \text {and} \quad \tilde{k}\,=\,\frac{H^*}{u} e^\frac{u}{H^*}. \end{aligned}$$

Lemma 9

Let $T^*$ be a trajectory of system (1.2) under conditions (1.3) with initial conditions $x\left( 0\right) \,=\,u, \, s\left( 0\right) \,=\,c_2\lambda , \, u\,<\,h\left( c_2\lambda \right)$. The trajectory $T^*$ next time intersects $s\,=\,c_1\lambda$ at a point $P_v\,=\,\left( v,c_1\lambda \right)$ where

$$\begin{aligned} v\,<\,u M^A. \end{aligned}$$

We now proceed to prove these lemmas. We start with Lemmas 6 and 7. The proof of Lemma 6 is based on Lemmas 10 and 11 which we give here, before the proofs of Lemma 8 and 9. We consider a trajectory $T_2$ of system (1.2) under conditions (1.3) with initial condition $x\left( 0\right) \,=\,u\,>\,h\left( c_1^*\lambda \right) , \, s\left( 0\right) \,=\, c_1^*\lambda ,\, 0\,<\,c_1^*\,\le \, 1$. Let $c_2^*$ be a number less than $c_1^*$. We introduce the quantities C and H and the function R by

$$\begin{aligned} C\,=\,\left( c_1^*-c_2^* + \ln \left( \frac{c_2^*}{c_1^*}\right) \right) \lambda , \quad H\,=\,a+c_1^*\lambda ,\quad R\left( x\right) \,=\,x-u- H\ln \left( \frac{x}{u}\right) . \end{aligned}$$

We are interested in whether $T_2$ intersects $s\,=\,c_2^*\lambda$ before escaping Region 2. We are also interested in a lower estimate for the x-value of such an intersection. Lemma 10 gives an answer to these questions and Lemma 11 gives a more explicit estimate.

Lemma 10

If the equation $R\left( x\right) \,=\,C$ has a solution $x\,=\,{\bar{x}}$, $H \,<\, {\bar{x}} \,<\, u$, then the trajectory $T_2$ intersects $s\,=\,c_2^*\lambda$ before escaping Region 2 at a point $\tilde{P} \,=\,\left( \tilde{x}, c_2^*\lambda \right)$, where ${\tilde{x}} \,>\, \bar{x}$.

Suppose H, C and u satisfy the following assumptions

$$\begin{aligned} 0\,<\,H\,<\,0.2, \quad H\,<\,u, \quad -\left( \sqrt{u}-\sqrt{H}\right) ^2 \,<\, C \,<\,0, \end{aligned}$$

(2.15)

and define

$$\begin{aligned} {\tilde{R}}\left( x\right) \,=\,\left( 1-\frac{H}{x}\right) \left( x-u\right) . \end{aligned}$$

Then $Q\left( x\right) \,=\, \left( {\tilde{R}}\left( x\right) -C\right) x \,=\, x^2-\left( H+C+u\right) x + Hu \,=\, 0$ has a unique root $x_+ \in \left( \sqrt{Hu}, u\right)$ and the following holds.

Lemma 11

If (2.15) is satisfied, then equation $R\left( x\right) \,=\,C$ has exactly one solution ${\bar{x}}$ for $x\,>\,H$ and

$$\begin{aligned} {\bar{x}} \,>\, x_+ \,=\, u+ \frac{C}{1-\frac{H}{x_+}}. \end{aligned}$$

(2.16)

Further if $H\,<\,H_m$ and $x_m$ is the root of Q between $\sqrt{Hu}$ and u for $H\,=\,H_m$ and $u\,=\,1$, then

$$\begin{aligned} {\bar{x}} \,>\, u + \frac{C}{1-\frac{H_m}{x_m}}. \end{aligned}$$

(2.17)

Proof of Lemma 10

We notice that the equation $R\left( x\right) \,=\,C$ is equivalent to $U\left( x,c_2^*\lambda \right) \,=\, U\left( u,c_1^*\lambda \right)$, where

$$\begin{aligned} U\left( x,s\right) \,=\, x - H \ln \left( x\right) + s - \lambda \ln \left( s\right) . \end{aligned}$$

(2.18)

Because the equation has a solution ${\bar{x}}$, $H \,<\, {\bar{x}} \,<\, u$, and U is increasing in x and decreasing in s in Region 2 as long as $H \,<\, x$, the equation $U\left( x,s\right) \,=\, U\left( u,c_1^*\lambda \right)$ has a unique solution $x\left( s\right)$ for any s between $c_2^*\lambda$ and $c_1^*\lambda$ and $x\left( s\right)$ is increasing in s and $x\left( c_2^*\lambda \right) \,=\, \bar{x}$ and $x\left( c_1^*\lambda \right) \,=\, u$, see Fig. 5.

Fig. 5

Geometry in the proof of Lemma 10

Derivation with respect to time gives $U'\left( x,s\right) \,=\, \left( h\left( s\right) -H\right) \left( s-\lambda \right) \,>\,0$ in Region 2. Thus, because $U\left( x,s\right)$ increases in x, the trajectory $T_2$ will remain in the region defined by $x\,>\,x\left( s\right)$ until it intersects $s\,=\,c_2^*\lambda$ at ${\tilde{P}}$ with ${\tilde{x}}\,>\, {\bar{x}}$. On trajectory part $U\left( x,s\right) \,>\,U\left( x\left( s\right) ,s\right) \,=\,U\left( u,c_1^*\lambda \right)$. $\square$

Proof of Lemma 11

We now use the auxiliary function ${\tilde{R}}\left( x\right) \,=\,\left( 1-\frac{H}{x}\right) \left( x-u\right)$. From $\ln \left( \frac{x}{u}\right) \,>\, \frac{1}{x} \left( x-u\right)$ it follows that $R\left( x\right) \,<\,{\tilde{R}}\left( x\right)$ for $x \,<\, u$. Equation $\tilde{R}\left( x\right) \,=\, C$ has a unique solution $x_+$ in $\left( \sqrt{Hu},u\right)$ when (2.15) is satisfied. (${\tilde{R}}$ has a global minimum ${\tilde{R}}\left( \sqrt{Hu}\right) \,=\, -\left( \sqrt{u}-\sqrt{H}\right) ^2$ and ${\tilde{R}} \left( u\right) \,=\,0$). Because ${\tilde{R}}\left( x\right) \,=\, C$ is equivalent with $Q\left( x\right) \,=\, 0$, $x_+$ is also the greatest root of Q. Equation $R\left( x\right) \,=\, C$ has a unique solution ${\bar{x}}$ in $\left( H,u\right)$ such that $x_+\,<\,{\bar{x}}\,<\,u$, because $R\left( u\right) \,=\, 0$ and $R\left( x_+\right) \,<\, {\tilde{R}}\left( x_+\right) \,=\, C$ and R is growing for $x \,>\, H$. Now we notice that $Q\left( x\right) \,=\,0$ is equivalent to

$$\begin{aligned} x\,=\,u+\frac{C}{1-\frac{H}{x}}, \end{aligned}$$

from which we get (2.16).

To prove the second inequality we note that the function Q is increasing in H for $x\,<\,u$ and decreasing in u for $x\,>\,H$, from which we conclude that $x_+$ is decreasing in H and increasing in u and, therefore, $\frac{H_m}{x_m}\,>\,\frac{H}{x_+}$ which implies (2.17). Thus, both inequalities of the lemma are proved and the proof is complete. $\square$

We can now prove Lemma 6.

Proof of Lemma 6

From Lemmas 10 and 11 with $c_1^*\,=\,1, \, c_2^*\,=\,c_1, C\,=\,C_1,\, H\,=\,H_0, \, u\,=\,x_0$ it follows that the trajectory T intersects $s\,=\,c_1\lambda$ before escaping Region 2, and that for this intersection the first inequality in Lemma 6 holds. Using Lemmas 10 and 11 once again, this time with $c_1^*\,=\,c_1, \, c_2^*\,=\,c_2,\, C\,=\,C_2,\, H\,=\,H_1, \, u\,=\,x_1$, we conclude that T also intersects $s\,=\,c_2\lambda$ before escaping Region 2, and that for this intersection the second inequality in Lemma 6 holds. Indeed, to see that we can apply Lemma 11 here we observe that $u \,=\, x_1 \,>\, x_1^+ \,>\, \sqrt{H_0 x_0} \,>\, a + \lambda \,>\, H_1.$ Finally, we notice that $H_0$ and $H_1$ take their maximal values for $a\,=\,\lambda \,=\,0.1$. Thus, the possibility to replace $x_i^+$ by $x_i^*$ follows from inequality (2.17). $\square$

Proof of Lemma 7

We intend to use Lemma 6. Let $c_1 \,=\, e^{-2}$ and $c_2 \,=\, e^{-4}$. Using (2.5) and (2.6) we find $C_1 \,>\, -1.135 \lambda ,C_2 \,>\, -1.883 \lambda ,H_0 \,<\, 0.2$ and $H_1 \,<\, 0.1136$. Equation (2.8) with $x_0 \,=\, 1$ yields $x_1^* \,>\, 0.851$ and (2.10) with $x_1^+ \,=\, 0.851$ yields $x_2^* \,>\, 0.620$. Using these estimates we obtain $D_1 \,=\, 1 - \frac{H_0}{x_1^*} \,>\, 0.764, \, D_2\,=\, 1 - \frac{H_1}{x_2^*} \,>\, 0.816$ and $\frac{C_1}{D_1} + \frac{C_2}{D_2} \,>\, -3.8 \lambda$. Now, we note that the above estimates imply assumptions (2.7) and (2.9), and Lemma 7 now follows by an application of Lemma 6. $\square$

We have now proved Lemmas 6 and 7 and proceed to the proof of Lemma 8. Proof of Lemma 8 is based on Lemmas 12 and 13, we now introduce. We consider a trajectory $T^*$ of system (1.2) under conditions (1.3) with initial conditions $x\left( 0\right) \,=\,u, \, s\left( 0\right) \,=\, \lambda ^*\,<\,\lambda , \, u \,>\, a + \lambda ^*.$ Suppose $P\,=\,\left( v,\lambda ^*\right)$ is the next intersection with $s\,=\,\lambda ^*$. Let further

$$\begin{aligned} \theta \left( x\right) \,=\,x- H\ln \left( x\right) . \end{aligned}$$

The following lemma which will also be used for Statement 3, gives estimates for v.

Lemma 12

Let ${\hat{x}}$ be the solution to $\theta \left( x\right) \,=\,\theta \left( u\right) , \, x\,<\,H\,=\,a+\lambda ^*$ and $\check{x}$ the solution to $\theta \left( x\right) \,=\,\theta \left( u\right) , \, x\,<\,H\,=\,a$. Then for the next intersection of trajectory $T^*$ with $s \,=\, \lambda ^*$ at $P\,=\,\left( v,\lambda ^*\right)$, it holds that $\check{x}\,<\,v\,<\,{\hat{x}}$.

Next lemma gives estimate for the equation in previous lemma.

Lemma 13

Suppose that C is a number such that $C\,>\,\theta \left( H\right)$ and suppose

$$\begin{aligned} k\,=\,He^{C/H}\,>\,4, \quad 0\,<\,H\,<\,0.2. \end{aligned}$$

Then the equation

$$\begin{aligned} \theta \left( x\right) \,=\,C,\quad x\,<\,H, \end{aligned}$$

(2.19)

has a unique solution $\bar{x}$ such that

$$\begin{aligned} e^{-C/H} \,<\, {\bar{x}}\,<\, \left( 1+{\hat{z}}\right) \, e^{-C/H}, \end{aligned}$$

where ${\hat{z}} \,=\,\frac{1}{\sqrt{k^2-4k}}$.

Proof of Lemma 12

The trajectory $T^*$ escapes from Region 2 at a minimal s to Region 3, where s grows and after some time $T^*$ intersects $s\,=\,\lambda ^*$ at $P\,=\,\left( v,\lambda ^*\right)$, see Fig. 6.

Fig. 6

Geometry in the proof of Lemma 12

As in the proof of Lemma 10 we will make use of the function U defined in (2.18) to construct barriers for the trajectory $T^*$. We note that U is decreasing in s, increasing in x for $x \,>\, H$ and decreasing in x for $x \,<\, H$. Moreover, $\theta \left( x\right) \,=\, U\left( x,\lambda ^*\right)$.

We first prove the upper bound $v \,<\, \hat{x}$. Let $H\,=\,a+\lambda ^*$ and let ${\bar{s}}\left( x\right)$ be the level curve to U such that $U\left( x, {\bar{s}}\left( x\right) \right) \,=\, \theta \left( u\right)$. The curve ${\bar{s}}\left( x\right)$ will have a minimum at $x \,=\, H \,=\, a+\lambda ^*$ and intersect $\lambda ^*$ at $x \,=\, {\hat{x}}$ and also at $x \,=\, u$. Observe that, since $h\left( s\right) \,<\, h\left( \lambda ^*\right) \,<\, \lambda ^* + a \,=\, H$, the derivative of U with respect to time is positive: $U'\,=\,\left( h\left( s\right) -H\right) \left( s-\lambda \right) \,>\, 0$. Therefore, the trajectory $T^*$ must stay below the curve ${\bar{s}}\left( x\right)$. On trajectory $T^*$ we have $U\left( x,s\right) \,>\, U\left( x, {\bar{s}}\left( x\right) \right) \,=\, \theta \left( u\right) \,=\, \theta \left( {\hat{x}}\right)$. Hence, recalling that U is decreasing in x for $x\,<\,H$, we have $v \,<\, {\hat{x}}$ and the upper bound follows.

The proof of the lower bound $\check{x} \,<\, v$ is similar. Let $H \,=\, a$ and let $\underline{s}\left( x\right)$ be the level curve to U such that $U\left( x, \underline{s}\left( x\right) \right) \,=\, \theta \left( u\right)$. In this case, the derivative of U with respect to time is negative, and thus the trajectory $T^*$ must stay above the curve $\underline{s}\left( x\right)$. On trajectory $T^*$ we have $U\left( x,s\right) \,<\, U\left( x, \underline{s}\left( x\right) \right) \,=\, \theta \left( u\right) \,=\, \theta \left( \check{x}\right)$, and it follows also that $\check{x} \,<\, v$.

Proof of Lemma 13

It is clear that Eq. (2.19) must have a solution because $\theta \left( H\right) \,<\,C$ and $\theta \left( x\right) \rightarrow \infty$ for $x\rightarrow 0_+$. The solution is unique because $\theta$ is decreasing for $x\,<\,H$. Moreover, since $e^{-C/H} \,<\, H$ and $C \,<\, \theta \left( e^{-C/H}\right)$, a solution ${\bar{x}}$ of $\theta \left( x\right) \,=\, C$ must satisfy ${\bar{x}} \,>\, e^{-C/H}$, which proves the first inequality in Lemma 13.

Substitution of $x\,=\,\left( 1+z\right) e^{-C/H}$ into $\theta \left( x\right)$ gives $\bar{\theta }\left( z\right) +C$ where $\bar{\theta }\left( z\right) \,=\, \left( 1+z\right) e^{-C/H} - H\ln \left( 1+z\right)$. Thus Eq. (2.19) is equivalent to $\bar{\theta }\left( z\right) \,=\,0$. Let ${\bar{z}}$ be the z-value corresponding to the solution ${\bar{x}}$ (${\bar{x}}\,=\,\left( 1+{\bar{z}}\right) e^{-C/H}$). For $z\,=\,0$ we get $\theta \left( x\right) \,=\,x+C\,>\,C$, so clearly ${\bar{z}} \,>\,0$. We wish to find an upper estimate for ${\bar{z}}$. From $\ln \left( 1+z\right) \,>\, \frac{z}{1+z}$ it follows that $\bar{\theta }\left( z\right) \,<\, \left( 1+z\right) e^{-C/H} - \frac{Hz}{1+z} \,=\, \frac{ e^{-C/H}}{1+z} \tilde{\theta }\left( z\right)$, where $\tilde{\theta }\left( z\right) \,=\,\left( 1+z\right) ^ 2 -kz,\, k\,=\,H\, e^{C/H}$. The function $\tilde{\theta }\left( z\right)$ has two roots because $k\,>\,4$. We denote the smallest one by ${\tilde{z}}$. Clearly ${\tilde{z}} \,<\,\frac{k-2}{2}$, and $1+{\tilde{z}} \,<\, k/2 \,<\,k$ which is equivalent to ${\tilde{x}} \,=\, \left( 1+{\tilde{z}}\right) e^{-C/H} \,<\, H$. Because $\bar{\theta }\left( {\tilde{z}}\right) \,<\,\tilde{\theta }\left( {\tilde{z}}\right) \,=\,0$ and $\bar{\theta }$ is decreasing in $\left( 0,{\tilde{z}}\right)$ we must have ${\bar{z}} \,<\, {\tilde{z}}$. Using the assumption $k \,>\, 4$ and the mean value theorem, we get an estimate for ${\tilde{z}}$:

$$\begin{aligned} {\tilde{z}}= & {} \frac{k-2}{2}\left( 1- \sqrt{1-\frac{4}{\left( k-2\right) ^ 2}}\right) \,<\, \frac{k-2}{2}\cdot \frac{4}{\left( k-2\right) ^ 2}\cdot \frac{1}{2\sqrt{1-\frac{4}{\left( k-2\right) ^ 2}}} \\= & {} \frac{1}{\sqrt{k^ 2-4k}}\,=\, \hat{z}. \end{aligned}$$

Now we conclude $0\,<\,{\bar{z}}\,<\,{\hat{z}}$ and thereby $e^{-C/H} \,<\, {\bar{x}} \,<\,\left( 1+{\hat{z}}\right) e^{-C/H}$ and the lemma is proved. $\square$

We are now ready with the proofs of Lemma 12 and 13 and can use them for proving Lemma 8. $\square$

Proof of Lemma 8

The result follows from Lemmas 12 and 13 by taking $H \,=\, H^*$ and $C \,=\, \tilde{\theta }\left( u\right)$. We observe that we will have ${\tilde{k}} \,>\,4$ because $u\,>\,2.5H^*$.

Now only Lemma 9 is left to be proved in order to give the proofs of Lemmas 3–5.

Proof of Lemma 9

The part of the trajectory between $P_u\,=\,\left( u,c_2\lambda \right)$ and $P_v$ is in Region 3, where $s'\,>\,0\,>\,x'$ and moreover $s\,<\,c_1\lambda$. There we get the following inequalities

$$\begin{aligned} \frac{dx}{ds} \,<\, \frac{\max x'}{\max s'} \,=\, \frac{\left( c_1-1\right) \lambda x}{\left( h\left( c_1\lambda \right) -x\right) s} \,<\,\frac{\left( c_1-1\right) \lambda x}{\left( a+c_1\lambda \right) s}. \end{aligned}$$

Integrating and using $u \,<\, c_2 \lambda$ we get

$$\begin{aligned} \int _u^ v \frac{1}{x} dx \,<\, \int _{c_2\lambda }^{c_1\lambda } \frac{\left( c_1-1\right) \lambda }{a+c_1\lambda } \cdot \frac{1}{s} ds, \end{aligned}$$

and, by using the notation in (2.13) we have $\ln \left( v\right) - \ln \left( u\right) \,<\, - A \ln \left( M^{-1}\right)$ from which Lemma 9 follows. $\square$

We have now finished the proofs of all auxiliary results needed for Lemmas 3-5 and we will now continue by proving these lemmas.

Proof of Lemma 4

From Lemma 6 follows that the trajectory T intersects $s\,=\,c_2\lambda$ before escaping Region 2 at a point $P_2\,=\,\left( x_2,c_2\lambda \right)$ where $x_2 \,>\, x_2^+$. From Lemma 7 it follows that $x_2^+ \,>\, x_0 - 3.8 \lambda \,>\, 0.6$, and, therefore, we can apply Lemma 8 with $H^*\,=\,H_2 \,=\, a + c_2 \lambda$. In particular, from Lemma 8 with $H^*\,=\,H_2$ and $\lambda ^* \,=\, c_2\lambda$ it follows that the trajectory with initial condition $x\left( 0\right) \,=\,x_2^+,\,s\left( 0\right) \,=\,c_2\lambda \,=\,\lambda ^*$ next time intersects $s\,=\,c_2\lambda$ at a point ${\tilde{P}}_4\,=\,\left( {\tilde{x}}_4,c_2\lambda \right)$ where ${\tilde{x}}_4\,<\, \left( 1+{\hat{z}}\right) e^{-\frac{\theta \left( x_2^ +\right) }{H_2}}$. Thus trajectory T intersects $s\,=\,c_2\lambda$ at a point $P_4\,=\,\left( x_4,c_2\lambda \right)$, where $x_4\,<\,{\tilde{x}}_4$. From Lemma 9 follows that a trajectory with initial condition $x\left( 0\right) \,=\,{\tilde{x}}_4,\, s\left( 0\right) \,=\,c_2\lambda$ next time intersects $s\,=\,c_1\lambda$ at a point ${\tilde{P}}_5\,=\,\left( {\tilde{x}}_5,c_1\lambda \right)$, where ${\tilde{x}}_5\,<\,{\tilde{x}}_4 M^A$. Thus trajectory T intersects $s\,=\,c_1\lambda$ next time at a point $P_5\,=\,\left( x_5,c_1\lambda \right)$, where $x_5\,<\,\tilde{x}_5$. Finally, because at $P_6\,=\,\left( x_6,\lambda \right)$ (next intersection of T with $s\,=\,\lambda$), $x_6\,<\,x_5$ we get

$$\begin{aligned} x_6\,<\,x_5\,<\,{\tilde{x}}_5\,<\,{\tilde{x}}_4 M^A \,<\,\left( 1+{\hat{z}}\right) M^A e^{-\frac{\theta \left( x_2^+\right) }{H_2}} \end{aligned}$$

The proof of Lemma 4 is complete. $\square$

Proof of Lemma 5

The proof is analogous to the proof of Lemma 4. We only use Lemma 6 so that we replace $x_2^+$ by $x_2^*$ and modify it by taking as $H_0$ and $H_1$ the values they get for $a\,=\,\lambda \,=\,0.1$.

Proof of Lemma 3

The proof is analogous to proof of Lemma 4, we only use Lemma 7 instead of Lemma 6. In particular, from Lemma 7 it follows that the trajectory T intersects $s \,=\, e^{-4}\lambda$ before escaping Region 2 at a point $P_2\,=\,\left( x_2, e^{-4}\lambda \right)$, where

$$\begin{aligned} x_2 \,>\, {\tilde{x}}_2 \,=\, x_0 - 3.8 \lambda . \end{aligned}$$

We now use Lemma 8 with $H^* \,=\, a + \lambda ^*$, $\lambda ^* \,=\, e^{-4}\lambda$ and $u \,=\, {\tilde{x}}_2$ to obtain $x_4 \,<\, {\tilde{x}}_4 \,=\, \left( 1 + {\hat{z}}\right) e^{-\frac{ {\tilde{\theta }} \left( {\tilde{x}}_2\right) }{a + e^{-4}\lambda }}.$ To estimate ${\hat{z}}$, we carefully observe that the largest $\hat{z}$ is obtianed by setting $a \,=\, \lambda \,=\, 0.1$ and $x_0 \,=\, 1$. Indeed, we obtian $\hat{z} \,<\, 0.015$ and so

$$\begin{aligned} x_4 \,<\, {\tilde{x}}_4 \,=\, 1.015 e^{-\frac{\tilde{\theta } \left( {\tilde{x}}_2\right) }{a + e^{-4}\lambda }}. \end{aligned}$$

From Lemma 9 follows that a trajectory with initial condition $x\left( 0\right) \,=\,\tilde{x}_4,\, s\left( 0\right) \,=\,e^{-4} \lambda$ next time intersects $s\,=\,e^{-2}\lambda$ at a point $\tilde{P}_5\,=\,\left( \tilde{x}_5, e^{-2}\lambda \right)$, where $\tilde{x}_5 \,<\, \tilde{x}_4 M^A \,=\, \tilde{x}_4 e^{-2 A}$. Thus trajectory T intersects $s \,=\, e^{-2} \lambda$ next time at a point $P_5 \,=\, \left( x_5, e^{-2}\lambda \right)$, where $x_5 \,<\, \tilde{x}_5$. Finally, because at $P_6\,=\,\left( x_6,\lambda \right)$ we have $x_6 \,<\, x_5$, we get

$$\begin{aligned} x_6\,<\,x_5\,<\,{\tilde{x}}_5\,<\,{\tilde{x}}_4 e^{-2 A} \,<\, 1.015 e^{-2 A - \frac{\tilde{\theta } \left( {\tilde{x}}_2\right) }{a + e^{-4}\lambda }}, \end{aligned}$$

which proves Lemma 3. $\square$

In order to prove Statement 2 we need one more lemma. The proof of it follows by using Lemma 13 with $C \,=\, \theta \left( u\right)$ and $H \,=\, a$, but it can also be proved shortly directly.

Lemma 14

Equation $\theta \left( x\right) \,=\,\theta \left( u\right) , \, u\,>\,1$, where $\theta \left( x\right) \,=\,x- a\ln \left( x\right) , \, a\,<\,0.1$, has a unique solution $\bar{x}$ in $\left( 0,a\right)$ and ${\bar{x}} \,>\, e^{-\frac{u}{a}} \,=\, \check{x}$.

Proof

We first note that $\theta$ is decreasing in $\left( 0,a\right)$ and that $\theta$ has its global minimum at a. Moreover, $\theta \left( u\right) \,=\, u - a \ln \left( u\right) \,<\, u/a + e^{-u/a} \,=\, \theta \left( \check{x}\right)$. Therefore, $\theta \left( a\right) \,<\, \theta \left( u\right) \,<\, \theta \left( \check{x}\right)$ and thus there is a unique solution to $\theta \left( x\right) \,=\, \theta \left( u\right)$ between $\check{x}$ and a. $\square$

We have now finished the proofs of all auxiliary lemmas and will proceed to the proofs of our main results for this section; Statements 2 and 3.

Proof of Statement 2

Lemmas 12 and 14 together give the lower estimate in Statement 2 if we use $\lambda ^*\,=\,\lambda$ and $u\,=\,x_0$.

To prove the upper bound we first observe that from Statement 1 and Lemma 3 it follows that $x_0 - 3.8 \lambda \,<\, {\tilde{x}}_2 \,<\, 1.6$, where ${\tilde{x}}_2$ is as defined in Lemma 3. Using this estimate we conclude, since $\frac{\ln \left( 1.6\right) }{1.6} \,<\, 0.294$, that

$$\begin{aligned} \theta \left( \tilde{x}_2\right) \,=\, \tilde{x}_2 \left( 1 - H_2 \frac{\ln \left( \tilde{x}_2\right) }{\tilde{x}_2}\right) \,>\, \tilde{x}_2\left( 1 - 0.294 H_2\right) \,>\, \left( x_0 - 3.8 \lambda \right) \left( 1 - 0.294 H_2\right) . \end{aligned}$$

From (2.1) in Lemma 3, using that $H_2 \,<\, H_1$, we get

$$\begin{aligned} \ln \left( x_6\right)&\,<\, -2A-\frac{\theta \left( {\tilde{x}}_2\right) }{H_2} + \ln \left( 1.015\right) \\&\,<\, \frac{-2\left( 1-c_1\right) \lambda }{H_1} - \frac{\left( x_0-3.8\lambda \right) \left( 1-0.294\, H_2\right) - H_2\ln \left( 1.015\right) }{H_2} \\&\,<\, \frac{-2\left( 1-c_1\right) \lambda - \left( x_0-3.8\lambda \right) \left( 1-0.294\, H_2\right) + \left( a+c_2\lambda \right) \ln \left( 1.015\right) }{H_1}, \end{aligned}$$

and hence, using that $1 \,<\, x_0$,

$$\begin{aligned} \ln \left( x_6\right)&\,<\, \frac{-x_0 + \left( 3.8 - 2\left( 1-c_1\right) + c_2\ln \left( 1.015\right) + 0.294 c_2 x_0\right) \lambda + \left( 0.294 x_0 + \ln \left( 1.015\right) \right) a}{H_1} \\&\,<\, \frac{-x_0 \left( 1 - 2.1\lambda - 0.31 a\right) }{H_1} \,<\, -\frac{x_0}{1.32 H_1}. \end{aligned}$$

The above inequality gives the upper estimate in Statement 2 and the proof is complete. $\square$

Proof of Statement 3

We denote by $S_2$ the part of the trajectory T between the initial point $\left( x_0,\lambda \right)$ and $P_6 \,=\, \left( x_6, \lambda \right)$. Let $U\left( x,s\right) \,=\,x - H \, \ln \left( x\right) + s- \lambda \, \ln \left( s\right)$. We denote by $\check{s}$ the solution to

$$\begin{aligned} U\left( x_0,\lambda \right) \,=\,U\left( a,s\right) ,\quad H\,=\,a. \end{aligned}$$

(2.20)

The function U, for $H\,=\,a$, is decreasing in s ($s\,\le \, \lambda$), decreasing in x for $x\,<\,a$ and increasing in x for $x\,>\,a$. Thus the solutions to $U\left( x_0,\lambda \right) \,=\,U\left( x,s\right)$, $s \,\le \, \lambda$, form a curve $\check{S}_2$ given by $s\,=\,\check{\sigma }\left( x\right) ,\, x_6\,\le \, x \,\le \, x_0$, where $\check{\sigma }$ has a minimum for $x\,=\,a$ and is increasing for $x\,>\,a$ and decreasing for $x\,<\,a$. Differentiating U with respect to time gives $U'\,=\,\left( h\left( \lambda \right) -H\right) \left( s-\lambda \right) \,<\,0$ for $s\,<\,\lambda$ and $U\left( x,s\right) \,<\, U\left( x,\check{\sigma }\left( x\right) \right)$ and $s \,>\, \check{\sigma }\left( x\right)$ for $\left( x,s\right)$ on trajectory T.

We denote by $\hat{s}$ the solution to

$$\begin{aligned} U\left( x_0,\lambda \right) \,=\,U\left( a + \lambda ,s\right) ,\quad H\,=\,a+\lambda . \end{aligned}$$

(2.21)

Analogously we find that the solutions to $U\left( x_0,\lambda \right) \,=\,U\left( x,s\right)$, $s \,\le \, \lambda$ form a curve $\hat{S}_2$ given by $s\,=\,\hat{\sigma }\left( x\right) ,\, x_6\,\le \, x \,\le \, x_0$, where $\hat{\sigma }$ has a minimum for $x\,=\,a+\lambda$ and is increasing for $x\,>\,a+\lambda$ and decreasing for $x\,<\,a+\lambda$. We now get $U'\,>\,0$ for $s\,<\,\lambda$ and hence $U\left( x,s\right) \,>\, U\left( x,\hat{\sigma }\left( x\right) \right)$ and $s \,<\, \hat{\sigma }\left( x\right)$ for $\left( x,s\right)$ on trajectory T. We conclude that $\hat{S}_2$ and $\check{S}_2$ together form a closed region and $S_2$ is wholly inside this region. The s-values on $\hat{S}_2$ are greater than the corresponding s-values for T and the s-values on $\check{S}_2$ are less than the corresponding s-values for T, except at the coinciding endpoints of the curves $S_2$, $\check{S}_2$ and ${\hat{S}}_2$.

The minimum s-value on $\check{S}_2$ is $\check{s}$ and it must be less than the minimal s-value on $S_2$ and we get $\check{s} \,<\,s_3$. Analogously we get ${\hat{s}} \,>\, s_3$, where ${\hat{s}}$ is the minimum s-value on $\hat{S}_2$. We will now find an estimate for the solution $\check{s}$ to Eq. (2.20). To do so we first note that Eq. (2.20) is equivalent to

$$\begin{aligned} s-\lambda \ln \left( s\right) \,=\, x_0 - a\ln \left( x_0\right) + \rho \left( \lambda \right) -\rho \left( a\right) \,=\, L, \end{aligned}$$

where $\rho \left( x\right) \,=\,x\left( 1-\ln \left( x\right) \right)$. Because $-\lambda \ln \left( s\right) \,<\, s-\lambda \ln \left( s\right)$ and, since $1 \,<\, x_0$,

$$\begin{aligned} \hat{L}\,=\,x_0 +\rho \left( \lambda \right) -\rho \left( a\right) \,>\,L \end{aligned}$$

and since $s-\lambda \ln \left( s\right)$ decreases in s, we get $\check{s} \,>\, e^{-\frac{\hat{L}}{\lambda }}$. Moreover, from $\rho \left( a\right) \,>\,0$ and $x_0\,>\,1$ it follows that ${\hat{L}} \,<\, x_0 +\rho \left( \lambda \right) \,<\, x_0 \left( 1+\rho \left( \lambda \right) \right)$ and thus

$$\begin{aligned} s_3 \,>\, \check{s} \,>\, e^{-\frac{\hat{L}}{\lambda }} \,>\, e^{-\frac{x_0}{\lambda \kappa _2}}, \end{aligned}$$

where $\kappa _2 \,>\, \frac{1}{1 + \lambda \left( 1 - \ln \left( \lambda \right) \right) }$. This proves the lower estimate in Statement 3.

To prove the upper estimate in Statement 3 we will now find an estimate for the solution $\hat{s}$ to Eq. (2.21). To do so we first note that this equation is equivalent to

$$\begin{aligned} s-\lambda \ln \left( s\right) \,=\,x_0 - H \ln \left( x_0\right) + \rho \left( \lambda \right) -\rho \left( a+\lambda \right) \,=\, \check{L}. \end{aligned}$$

(2.22)

To estimate the solution of (2.22) we will make use of Lemma 13. In particular, Lemma 13 with $H \,=\, \lambda$ and $C \,=\, \check{L}$ gives

$$\begin{aligned} {\hat{s}} \,<\, \left( 1 + {\hat{z}}\right) e^{-\frac{\check{L}}{\lambda }}\quad \text {where} \quad {\hat{z}} \,=\, \frac{1}{\sqrt{k^2 - 4k}}. \end{aligned}$$

(2.23)

Next, we find a lower estimate of k. Using the inequality $\check{L} \,>\, 1 + \rho \left( \lambda \right) - \rho \left( a + \lambda \right) \,=\, {\tilde{L}}$, we see that $k \,=\, \lambda e^{\frac{\check{L}}{\lambda }} \,>\, \lambda e^{\frac{\tilde{L}}{\lambda }} \,=\, {\tilde{k}}$. The derivative with respect to a of ${\tilde{k}}$ is of the same sign as the derivative of $-\rho \left( a+\lambda \right)$ with respect to a which is negative. ${\tilde{k}}$ can also be written in form

$$\begin{aligned} {\tilde{k}}\,=\,e^{\frac{1}{\lambda }-\frac{a}{\lambda } +\left( 1+ \frac{a}{\lambda } \right) \ln \left( a+\lambda \right) } \end{aligned}$$

and the derivative of $\tilde{k}$ with respect to $\lambda$ can be seen to be

$$\begin{aligned} \frac{\partial {\tilde{k}}}{\partial \lambda } \,=\, \frac{\tilde{k}}{\lambda ^2} \left( \lambda + a-1 - a \ln \left( a+\lambda \right) \right) \end{aligned}$$

which again is negative for our values of a and $\lambda$. Thus, ${\tilde{k}}$ is greater than the value ($>324$) it takes of $a\,=\,\lambda \,=\,0.1$ and it follows that $\hat{z}\,<\, \frac{1}{\sqrt{\tilde{k}^2 -4{\tilde{k}}}} \,<\, 0.004$. Using this estimate and (2.23) we conclude that ${\hat{s}} \,<\, 1.004 e^{-\frac{\check{L}}{\lambda }}$.

For trajectory T we have $x_0 \,<\, 1.6$ and therefore $x_0 - H\ln \left( x_0\right) \,>\, x_0\left( 1-0.294 \,H\right)$. Moreover, $\rho \left( a+\lambda \right) -\rho \left( \lambda \right) \,<\,\rho \left( a\right)$ and we obtain

$$\begin{aligned} \ln \left( {\hat{s}}\right) \,<\, -\frac{x_0\left( 1-0.294\, H\right) -\rho \left( a\right) }{\lambda } + \ln \left( 1.004\right) , \end{aligned}$$

and so

$$\begin{aligned} \ln \left( \hat{s}\right)&\,<\, -\frac{x_0}{\lambda }\left( 1-0.294\, H -\rho \left( a\right) -\lambda \ln \left( 1.004\right) \right) \\&\,<\, -\frac{x_0}{\lambda }\left( 1 - 0.3\, \lambda -a\left( 1.3 - \ln \left( a\right) \right) \right) . \end{aligned}$$

Thus $s_3\,<\, {\hat{s}} \,<\, e^{-\frac{x_0}{\lambda \kappa _3}}$, where $\kappa _3$ is as in Statement 3, and the proof is complete. $\square$

Estimates in Region 4

We again consider a trajectory T of system (1.2) under conditions (1.3) with initial condition $x\left( 0\right) \,=\,x_0\,>\,1, \, s\left( 0\right) \,=\,\lambda$. We are interested in the behaviour of the trajectory in Region 4. The trajectory enters Region 4 at point $P_6\,=\,\left( x_6,\lambda \right)$. We are interested in the next intersection of the trajectory with $s\,=\,s_7\,>\,0.5$ at point $P_7\,=\,\left( x_7,s_7\right)$ (if it occurs before escaping Region 4) and of the next intersection with the isocline $x\,=\,h\left( s\right)$ at $P_8\,=\,\left( x_8,s_8\right)$, where $x_8\,=\,h\left( s_8\right)$. Lemma 3 from previous section gives an estimate for $x_6$ and we are able to show that for such $x_6$ the trajectory will intersect $s\,=\,0.8$ before escaping Region 4 and the escaping occurs at $P_8$, where $s_8\,>\,0.9$.

The main result is Statement 4 which is based on the following two lemmas.

Lemma 15

The trajectory T after intersecting $s\,=\,\lambda$ next time always intersects $s\,=\,0.8$ at a point $P_7\,=\,\left( x_7,0.8\right)$, where $x_7 \,<\, 0.012$, before escaping Region 4.

Lemma 16

If trajectory T after intersecting $s\,=\,\lambda$ next time intersects $s\,=\,0.8$ at a point $P_7\,=\,\left( x_7,0.8\right)$ where $x_7 \,<\, 0.012$ then it intersects the isocline $s'\,=\, 0$ next time for an s-value greater than 0.9.

From these lemmas follows

Statement 4

Trajectory T after intersecting $s\,=\,\lambda$ at $P_4$ escapes from Region 4 at an s-value greater than 0.9.

The trajectory in Region 4 is well estimated by $x\,=\,x_6 B$ for $s\,<\,0.8$, where B is defined in (2.26). For $s\,>\,0.8$ expression (2.35) gives a one-sided estimate for the trajectory while remaining in Region 4 and (2.36) gives an estimate for $s_8$ substituting $m\,=\,0.8$.

The proof of Lemma 16 is at the end of the section. The proof of Lemma 15 is based on some lemmas we provide here. Lemma 15 uses Lemma 18 and Lemma 19. Lemma 18 gives us necessary conditions in form of inequalities for the trajectory to intersect $s\,=\,s_7$ before escaping Region 4 and an estimate for x-value at intersection point $P_7$. Lemma 19 tells us that we have to check the inequalities only for $a,\lambda \,=\,0.1$ to be sure they hold for all other parameters. Lemma 18 is based on Lemmas 17 and  3, where Lemma 17 gives estimates in Region 4 and Lemma 3 takes care of estimates for trajectory in Regions 2 and 3. Lemma 17 is based on Lemmas 20 and 21. Lemma 20 gives us estimates for trajectory in a part of Region 4 and Lemma 21 tells us that we need to check these estimates only for $s\,=\,\lambda$ and $s\,=\,s_7$ in order to be sure the trajectory will stay in the region.

We now give Lemmas 17–19. Lemma 19 can be proved directly, but the proof of Lemma 17, which is needed for proving Lemma 18, needs more lemmas and is given later.

Lemma 17

Suppose $0\,<\,k\,<\,1$ and $s_7\,\ge \, 0.5$. If

$$\begin{aligned} x_6\, K_7 \left( \frac{1}{a+\lambda }\right) ^{\frac{1}{k}}\,<\,\left( 1-k\right) \, h\left( s_7\right) \end{aligned}$$

(2.24)

where $K_7 \,=\, \left( e^{\frac{\lambda }{s_7}} \frac{s_7+a}{1-s_7} \right) ^{\frac{1}{k}}$ and $x_6 \,<\, \left( 1-k\right) \, h\left( \lambda \right)$, then the trajectory T intersects $s \,=\, s_7$ before escaping Region 4 and at the intersection $P_7\,=\,\left( x_7,s_7\right)$ the estimate

$$\begin{aligned} x_7 \,<\, x_6\, K_7 \left( \frac{1}{a+\lambda }\right) ^{\frac{1}{k}} \end{aligned}$$

is satisfied.

Lemma 3 gives estimate for $x_6$ and thus from Lemmas 3 and 17 we get a new statement. For this we introduce the function $\eta \left( a, \lambda \right)$ to find out whether inequality (2.24) holds.

$$\begin{aligned} \eta \left( a,\lambda \right) \,=\, K_7 \left( \frac{1}{a+\lambda }\right) ^{\frac{1}{k}}1.015\, e^{-2A-\frac{\theta \left( {\tilde{x}}_2\right) }{H_2}} \end{aligned}$$

(Notations from Lemma 3 are used here).

Lemma 18

Suppose $0\,<\,k\,<\,1$ and $s_7\,\ge \, 0.5$. If

$$\begin{aligned} \eta \left( a,\lambda \right) \,<\,\left( 1-k\right) \, h\left( s_7\right) \end{aligned}$$

(2.25)

and $x_6\,<\,\left( 1-k\right) \, h\left( \lambda \right)$, then the trajectory T intersects $s \,=\, s_7$ before escaping Region 4 and at the intersection $P_7\,=\,\left( x_7,s_7\right)$ the estimate $x_7\,<\,\eta \left( a,\lambda \right)$ holds.

Proof

The statement follows directly from Lemmas 17 and 3. $\square$

The following Lemma tells us that to prove that (2.25) holds for all $a, \lambda \in [0,0.1)$, it is enough to prove the inequality for $a \,=\, \lambda \,=\, 0.1$ fixed in the left hand side, i.e., $\eta \left( 0.1, 0.1\right) \,<\, \left( 1-k\right) \, h\left( s_7\right)$.

Lemma 19

The derivatives of $\eta \left( a,\lambda \right)$ with respect to a and $\lambda$ are positive if $k\,\ge \, 0.9$.

Proof

Calculations give $\frac{\partial \eta }{\partial \lambda } \,=\, \xi _\lambda \eta \left( a,\lambda \right)$, where

$$\begin{aligned} \xi _\lambda \,=\, \frac{1}{s_7} - \frac{1}{k\left( a+\lambda \right) }-2\frac{\partial A}{\partial \lambda } + 3.8 \left( \frac{1}{H_2} -\frac{1}{\tilde{x}_2}\right) + \frac{\tilde{x}_2 c_2}{H^2_2} \end{aligned}$$

and

$$\begin{aligned} \frac{\partial A}{\partial \lambda } \,=\, \frac{\left( 1-c_1\right) a}{H_1^2}\,<\,\frac{0.9a}{H_1^2} \,<\, \frac{0.9}{H_1}. \end{aligned}$$

For $\xi _\lambda$ we get the estimate

$$\begin{aligned} \xi _\lambda \,>\, -\frac{1}{k\left( a+\lambda \right) } - \frac{1.8}{H_1} + \frac{3.8}{H_2} - \frac{3.8}{0.6} \,>\, -\frac{3}{H_2} + \frac{3.8}{H_2} - \frac{3.8}{0.6}\,>\, \frac{0.8}{H_2} - \frac{3.8}{0.6} \,>\, 0, \end{aligned}$$

because $H_2\,<\,0.11$. Thus, since $\eta \left( a,\lambda \right) \,>\, 0$ we conclude that $\eta \left( a,\lambda \right)$ is increasing in $\lambda$. Calculations also give $\frac{\partial \eta }{\partial a} \,=\, \xi _a \eta \left( a,\lambda \right)$, where

$$\begin{aligned} \xi _a \,=\, \frac{1}{k \left( s_7 + a\right) } - \frac{1}{k\left( a+\lambda \right) }+ 2\frac{\left( 1-c_1\right) \lambda }{H_1^2} + \frac{\tilde{x}_2 }{H^2_2}. \end{aligned}$$

For $\xi _a$ we get the estimate

$$\begin{aligned} \xi _a \,>\, -\frac{1}{k\left( a+\lambda \right) } + \frac{{\tilde{x}}_2 }{H^2_2} \,>\, -\frac{1}{k\, H_2}+ \frac{0.6 }{H^2_2} \,=\, \frac{1}{H_2}\left( \frac{0.6}{H_2} - \frac{1}{k}\right) \,>\, 0. \end{aligned}$$

Thus, $\eta \left( a,\lambda \right)$ is increasing also in a and the proof of the Lemma 19 is complete.

We now proceed to the proof of Lemma 17, which follows from Lemmas 20 and 21. These lemmas we formulate now. For the statements we need the following notations:

$$\begin{aligned} B\,=\,E_1\, E_2\, E_3\, E_4, \end{aligned}$$

(2.26)

where

$$\begin{aligned} E_1\,= & {} \,\left( \frac{s+a}{s} \right) ^{k_2}, \quad E_2\,=\,\left( \frac{\lambda }{a+\lambda } \right) ^{k_2}, \quad \end{aligned}$$

(2.27)

$$\begin{aligned} E_3\,= & {} \,\left( \frac{\left( s+a\right) \left( 1-\lambda \right) }{1-s} \right) ^{k_3}, \quad E_4\,=\,\left( \frac{1}{a+\lambda } \right) ^{k_3}, \end{aligned}$$

(2.28)

$$\begin{aligned} k_2\,=\,\frac{\lambda }{a} \quad \text {and} \quad k_3\,=\,\frac{1-\lambda }{1+a}. \end{aligned}$$

Lemma 20

Suppose that $x_6\,<\,\left( 1-k\right) \, h\left( \lambda \right)$. Then as long as the trajectory stays in the region determined by $x\,<\,\left( 1-k\right) \, h\left( s\right)$ the following estimates are valid:

$$\begin{aligned} x\,<\,x_6B^{\frac{1}{k}} \end{aligned}$$

(2.29)

and, when $s \,\ge \, 0.5$,

$$\begin{aligned} x\,<\,x_6\, K \left( \frac{1}{a+\lambda } \right) ^{\frac{1}{k}}\quad \text {where}\quad K\,=\,\left( e^{\frac{\lambda }{s}} \cdot \frac{s+a}{1-s}\right) ^{\frac{1}{k}}. \end{aligned}$$

(2.30)

Lemma 21

Suppose $x_6\,<\,\left( 1-k\right) \, h\left( \lambda \right)$ and $x_6 \left( B_7 \right) ^{\frac{1}{k}}\,<\, \left( 1-k\right) \, h\left( s_7\right)$, where $B_7$ is the value B takes for $s\,=\,s_7\,\ge \, 0.5$. Then the trajectory T intersects $x\,=\,\left( 1-k\right) \, h\left( s\right)$ next time after $P_6$ for $s\,>\,s_7$ and is inside the region determined by $x\,<\,\left( 1-k\right) \, h\left( s\right)$ before it intersects $s\,=\,s_7$.

Proof of Lemma 20

When $x\,<\,\left( 1-k\right) \, h\left( s\right)$ we have $s'\,>\,k h\left( s\right) s\,>\,0$ and $x'\,>\,0$. Thus we get the inequality

$$\begin{aligned} \frac{dx}{ds} \,<\, \frac{\left( s-\lambda \right) s}{k h\left( s\right) s}. \end{aligned}$$

Integrating gives

$$\begin{aligned} x\,<\, x_6 \left( \frac{F\left( s\right) }{F\left( \lambda \right) }\right) ^{\frac{1}{k}}\quad \text {where}\quad F\left( y\right) \,=\,\frac{\left( y+a\right) ^{k_1}}{y^{k_2} \left( 1-y\right) ^{k_3}} \end{aligned}$$

(2.31)

and where $k_1\,=\,\frac{a+\lambda }{a\left( a+1\right) }$. But

$$\begin{aligned} \frac{F\left( s\right) }{F\left( \lambda \right) }\,=\, \left( \frac{s+a}{\lambda +a}\right) ^{k_1} \left( \frac{\lambda }{s}\right) ^{k_2} \left( \frac{1-\lambda }{1-s}\right) ^{k_3} \end{aligned}$$

and because $k_1\,=\,k_2+k_3$ we get

$$\begin{aligned} \frac{F\left( s\right) }{F\left( \lambda \right) }\,=\, \left( \frac{s+a}{s}\right) ^{k_2} \left( \frac{\lambda }{\lambda +a}\right) ^{k_2} \left( \frac{\left( 1-\lambda \right) \left( s+a\right) }{1-s}\right) ^{k_3} \left( \frac{1}{\lambda +a}\right) ^{k_3}. \end{aligned}$$

Choosing $B \,=\, \frac{F\left( s\right) }{F\left( \lambda \right) } \,=\, E_1 E_2 E_3 E_4$ we get estimate (2.29).

To prove (2.30) we note that for $E_i, \, i\,=\,1,2,3,4$ we get the following estimates

$$\begin{aligned} E_1\,= & {} \, \left( \left( 1+ \frac{1}{\frac{s}{a}}\right) ^\frac{s}{a} \right) ^\frac{\lambda }{s} \,<\, e^\frac{\lambda }{s},\quad E_2\,=\,\frac{1}{\left( 1+\frac{1}{k_2}\right) ^{k_2}}\,<\,1 \\ k_3\,< & {} \,1,\quad E_3\,<\, \left( \frac{s+a}{1-s}\right) ^{k_3} \,<\, \frac{s+a}{1-s},\quad E_4\,<\, \frac{1}{\lambda +a}. \end{aligned}$$

All these estimates together give (2.30).

Proof of Lemma 21

We first claim that the assumptions in the lemma implies

$$\begin{aligned} \frac{B\left( s\right) ^{\frac{1}{k}}}{h\left( s\right) } \,<\, \frac{1-k}{x_6} \quad \text {for all} \quad s \in [\lambda , s_7]. \end{aligned}$$

(2.32)

Next, assume, by way of contradiction, that the trajectory T intersects the curve $x \,=\, \left( 1-k\right) h\left( s\right)$ for some $s \in [\lambda , s_7]$. Using claim (2.32) we then obtain $x_6 B\left( s\right) ^{\frac{1}{k}} \,<\, x$ for the point of intersection. But from (2.29) in Lemma 20 it follows that $x \,<\, x_6 B\left( s\right) ^{\frac{1}{k}}$ as long as T stays in the region defined by $x \,<\, \left( 1-k\right) h\left( s\right)$. Using continuity this leads to a contradiction. Hence, we conclude that the trajectory T intersects $x\,=\,\left( 1-k\right) \, h\left( s\right)$ next time, after $P_6$, for $s\,>\,s_7$ and T is inside the region determined by $x\,<\,\left( 1-k\right) \, h\left( s\right)$ before it intersects $s\,=\,s_7$.

To finish the proof of Lemma 21 it remains to prove that claim (2.32) holds true. To do so we observe that differentiating $G\left( s\right) \,=\,\frac{F\left( s\right) ^\frac{1}{k}}{h\left( s\right) }$ with respect to s, where $F\left( s\right)$ is given by (2.31), gives

$$\begin{aligned} G'\left( s\right) \,=\,\frac{F\left( s\right) ^\frac{1}{k}}{k\left( 1-s\right) ^2 s \left( s+a\right) ^2} G^*\left( s\right) , \end{aligned}$$

where

$$\begin{aligned} G^*\left( s\right) \,=\,2ks^2 +\left( ak-k+1\right) s-\lambda . \end{aligned}$$

We conclude that $G\left( s\right)$ has a unique minimum between $s\,=\,\lambda$ and $s\,=\,0.5$, when $a,\lambda \,<\, 0.1$ and $0\,<\,k\,<\,1$, because

$$\begin{aligned} \frac{9\lambda \left( a+2\lambda -1\right) }{10} \,=\, G^*\left( \lambda \right) \,<\, 0 \,<\, G^*\left( 0.5\right) \,=\, \frac{9a-20\lambda +10}{20}, \end{aligned}$$

and $G^*$ is increasing in s. Thus, the maximal value of G in $[\lambda ,s_7]$ is either $G\left( \lambda \right)$ or $G\left( s_7\right)$. Claim (2.32) now follows since $\frac{G\left( s\right) }{F\left( \lambda \right) ^{\frac{1}{k}}} \,=\, \frac{B\left( s\right) ^\frac{1}{k}}{h\left( s\right) }$ and the assumptions in the lemma equals

$$\begin{aligned} \frac{B\left( \lambda \right) ^\frac{1}{k}}{h\left( \lambda \right) } \,<\, \frac{1-k}{x_6} \quad \text {and} \quad \frac{B\left( s_7\right) ^\frac{1}{k}}{h\left( s_7\right) } \,<\, \frac{1-k}{x_6}. \end{aligned}$$

The proof of Lemma 21 is complete. $\square$

We are now ready with proofs of Lemmas 20 and 21 and can use them for getting proofs of Lemmas 17 and 18.

Proof of Lemma 17

The proof follows from Lemmas 20 and 21. Lemma 21 tells that the trajectory will be inside the region $x\,<\,\left( 1-k\right) \, h\left( s\right)$ and then Lemma 20 gives us the necessary estimates. $\square$

Finally, we are ready with all proofs of auxiliary results and can prove the main Lemmas 15 and 16 from which Statement 4 follows.

Proof of Lemma 15

We choose $k\,=\,0.9$ and $s_7\,=\,0.8$ and calculate $\eta \left( 0.1,0.1\right) \,<\, 0.012 \,<\, \left( 1-k\right) \, h\left( s_7\right)$ and then from Lemma 19 it follows that inequality (2.25) holds for all $a,\lambda \in [0,0.1)$. Since $\eta \left( a,\lambda \right) \,<\, 0.012$ it follows that $x_6\, K_7 \left( \frac{1}{a+\lambda }\right) ^{\frac{1}{k}} \,<\, 0.012$ and because $K_7 \,>\, 1$ we also get, using $k \,=\, 0.9$, that $x_6 \,<\, 0.012 \cdot \left( a+\lambda \right) \,<\, \left( 1-k\right) \, h\left( \lambda \right)$. Lemma 15 now follows by an application of Lemma 18. $\square$

Proof of Lemma 16

We consider trajectories of system (1.2) in region

$$\begin{aligned} E_{m,s_7} \,=\,\lbrace \left( x,s\right) \vert \, 0\,<\,x\,<\,m\left( 1-s\right) , s\,>\,s_7\rbrace , \end{aligned}$$

where $m\,\le \, s_7$. Observe that

$$\begin{aligned} m\left( 1-s\right) \,\le \, s_7\left( 1-s\right) \,<\,s\left( 1-s\right) \,<\,\left( s+a\right) \left( 1-s\right) \,=\,h\left( s\right) . \end{aligned}$$

In $E_{m,s_7}$ we get the estimates

$$\begin{aligned} s'\,>\,\left( m\left( 1-s\right) -x\right) s, \quad x'\,<\,sx \quad \text {and\;hence} \quad \frac{ds}{dx} \,>\, \frac{m\left( 1-s\right) - x}{x}. \end{aligned}$$

(2.33)

Let us consider a trajectory with initial condition $x\left( 0\right) \,=\,x_7,\, s\left( 0\right) \,=\,s_7$, where $x_7\,<\,m\left( 1-s_7\right)$. Using (2.33), we conclude that as long as this trajectory remains in $E_{m,s_7}$, it will be in the subregion bounded by the trajectory of the linear system

$$\begin{aligned} s'\,=\, m\left( 1-s\right) -x,\quad x'\,=\,x, \end{aligned}$$

(2.34)

with initial condition $x\left( 0\right) \,=\,x_7, s\left( 0\right) \,=\,s_7$ and the lines $x\,=\,m\, \left( 1-s\right)$ and $x\,=\,0$. Solving system (2.34) we find that the trajectory follows the curve

$$\begin{aligned} s\,=\,d\left( \frac{x_7}{x} \right) ^m +1 -\frac{x}{1+m} \quad \text {with} \quad d\,=\,s_7+\frac{x_7}{1+m} -1. \end{aligned}$$

(2.35)

The trajectory leaves $E_{m,s_7}$ when $x\,=\,m\, \left( 1-s\right)$. (Observe that then $s'\,=\,0$ for (2.34)). Substituting $x\,=\,m\, \left( 1-s\right)$ into (2.35) we get

$$\begin{aligned} \frac{d x_7^m}{m^m\left( 1-s\right) ^m} +1-s -\frac{m}{m+1} \left( 1-s\right) \,=\, 0, \end{aligned}$$

which is equivalent to

$$\begin{aligned} 1-s \,=\, \frac{\left( -d\right) ^\frac{1}{m+1} x_7^\frac{m}{m+1}}{m^\frac{m}{m+1}} \left( 1+m\right) ^\frac{1}{m+1}. \end{aligned}$$

(2.36)

The above expression for $1-s$ increases with $x_7$, for all $m \,\ge \, 0$, because

$$\begin{aligned} \frac{\partial }{\partial x_7} \left( -d x_7^m\right) \,=\, - \left( \frac{x_7}{1+m} + m\left( s_7 +\frac{x_7}{m+1} -1\right) \right) x_7^{m-1} \,=\, x_7^{m-1} \left( m\left( 1-s_7\right) -x_7\right) \,>\, 0. \end{aligned}$$

Thus, a lower boundary for the maximal s can be calculated from (2.36) for given $\left( x_7,s_7\right)$ choosing $m \,=\, s_7$. Calculations show that if $s_7 \,=\, 0.8$ and $x_7 \,<\, 0.012$, then the maximal s is greater than 0.9379. We observe that system (2.34) is not depending on a or $\lambda$. Hence, the results are independent of these parameters. The proof of Lemma 16 is complete.

Fig. 7

The maximal x- and s-values as functions of the parameters a and $\lambda$. a and c $\lambda \,=\, 0.1$ (green, dashed), $\lambda \,=\, 0.05$ (blue, dashdot), $\lambda \,=\, 0.01$ (red, dotted). b and d $a \,=\, 0.1$ (green, dashed), $a \,=\, 0.05$ (blue, dashdot), $a \,=\, 0.01$ (red, dotted). Black solid lines show analytical estimates for $x_{max}$ and $s_{max}$ from Theorem 1

Fig. 8

The minimal x- and s-values as functions of the parameters a and $\lambda$ (red, dotted): a and c $\lambda \,=\, 0.1$. b and d $a \,=\, 0.1$. Grey dashed curves show analytical estimates for $x_{min}$ and $s_{min}$ given in Theorem 1 using $\kappa _1$, $\kappa _2$ and $\kappa _3$, while black solid curves show estimates produced by using the bounds of $\kappa _1$, $\kappa _2$ and $\kappa _3$ given in Theorem 1

Numerical Results

Before comparing our analytical estimates to numerical simulations, let us mention that to achieve accurate numerics of system (1.2) under assumption (1.3) we recommend transforming the equations (e.g. log transformations) to avoid variables taking on very small values. Imposing linear approximations near the unstable equilibria at $(x,s) = (0,0)$ and $(x,s) = (0,1)$ are also helpful. Indeed, using e.g. the MATLAB ode-solver ODE45 directly on system (1.2) may result in trajectories not satisfying Theorem 1, when $a \,\le \, 0.2$ and $\lambda \,\le \, 0.2 a$, unless tolerance settings are forced to minimum values. The true trajectory approaches much smaller population densities and also spend more time at these very low population abundances. Therefore, one has to be careful, since such misleading numerical results would give, e.g., a far to good picture of the populations chances to survive from any perturbation.

In Fig. 7 the maximal predator and prey abundances, $x_{max}$ and $s_{max}$, are plotted for the unique limit cycle as functions of the parameters a and $\lambda$, together with the analytical estimates given in Theorem 1. We can observe that the maximal predator abundance $x_{max}$ slightly decreases as a approaches zero, but increases as $\lambda$ approaches zero, see Fig. 7a, b. Moreover, the maximal prey abundance $s_{max}$ stays very close to 1 as a approaches zero, as well as when $\lambda$ approaches zero, see Fig. 7b, c. Our analytical results in Theorem 1 ensure that $1< x_{max} < 1.6$ and $0.9< s_{max} < 1$ whenever $a, \lambda < 0.1$.

Fig. 9

Level curves of a $\tau _s$ and b $\tau _x$ as functions of a and $\lambda$. Observe the nonlinear steps between curves for $\tau _x$. The function $\tau _s$ is closest to one when $a \approx \lambda$, while $\tau _x$ is closest to one when $\lambda \approx 0.01$

Fig. 10

The functions $\tau _s$ and $\tau _x$ as functions of $\lambda$ (red, dotted): a and c $a \,=\, 0.1$, b and d $a \,=\, 0.05$. Grey dashed curves show analytical estimates for $\tau _x$ and $\tau _s$ given by $\kappa _1$, $\kappa _2$ and $\kappa _3$ in Theorem 1, while the black solid curves show analytical estimates produced by using the bounds of $\kappa _1$, $\kappa _2$ and $\kappa _3$ given in Theorem 1

In Fig. 8 the minimal predator and prey abundances, $x_{min}$ and $s_{min}$, are plotted for the unique limit cycle. We observe that the minimal predator and prey abundances decrease as a approaches zero, as well as when $\lambda$ approaches zero. The analytical estimates for $x_{min}$ and $s_{min}$ are produced by using the corresponding estimate for the maximal x-value, $1< x_{max} < 1.6$, given in Theorem 1.

Suppose now that $\left( x_{max},\lambda \right)$, $\left( h(s_{min}),s_{min}\right)$ and $\left( x_{min},\lambda \right)$ are points on the simulated limit cycle and let $\tau _s$ and $\tau _x$ be such that

$$\begin{aligned} s_{min} \,=\, \exp \left( {-\frac{x_{max}}{\tau _s\lambda }}\right) \quad \text {and} \quad x_{min} \,=\, \exp \left( {-\frac{x_{max}}{\tau _x a}}\right) . \end{aligned}$$

We can thus say that $\tau _s$ and $\tau _x$ are measures of how good the approximations

$$\begin{aligned} s_{min} \,\approx \, \exp \left( {-\frac{x_{max}}{\lambda }}\right) \quad \text {and} \quad x_{min} \,\approx \, \exp \left( {-\frac{x_{max}}{a}}\right) , \end{aligned}$$

stated in Remark 1, are. Figure 9 shows level curves of the functions ${\tau _{s}}$ and ${\tau _{x}}$ in the $a \lambda$-plane for $a,\lambda \in (0.01,0.1)$. From Fig. 9a we can observe that the approximation for $s_{min}$ is good for $a \approx \lambda$, while Fig. 9b shows that the approximation for $x_{min}$ is good for $\lambda \approx 0.01$.

We end this section by plotting the functions ${\tau _{x}}$ and ${\tau _{s}}$, for small values of a, as functions of $\lambda$ in Fig. 10 together with the analytical estimates for ${\tau _{x}}$ and ${\tau _{s}}$ given by $\kappa _1$, $\kappa _2$ and $\kappa _3$ in Theorem 1. As $\lambda$ and $\frac{\lambda }{a}$ approaches zero, the lower estimate for $\tau _s$ approaches 1 ($\kappa _2 \rightarrow 1$) while $\kappa _1$ and $\kappa _3$, giving upper estimates of ${\tau _{x}}$ and ${\tau _{s}}$, stays a bit away from 1 for all $\lambda$.