Periodic Solutions in Kolmogorov-Type Predator–Prey Systems

Abstract

We consider a class of prey-predator models, i.e., a Kolmogorov-type system. We are interested in their dynamics when a certain parameter (that can be viewed as the death rate of the predator) changes from zero value to positive. By utilizing alternative but simple techniques, including a sub- and super-solutions method, we establish the existence of periodic solutions when some conditions are satisfied. We also prove that the solutions are bounded by a non-periodic trajectory when the parameter vanishes. We give an example to illustrate our results.

Introduction

Consider system

$$\begin{array}{*{20}c} {\dot{x} = xf(x) - xyg(x),} \\ {\dot{y} = - \delta y + xyh(x),} \\ {x,y \ge 0} \\ \end{array} {\text{ }}$$

(1)

where $\delta \ge 0$ is a parameter. System (1) is referred as a Kolmogorov-type system [3]. Interpreting it as a prey-predator model, x and y represent the population of prey and predator, respectively, and $\delta$ can be viewed as the death rate of the latter. Overdot is the derivative with respect to the temporal variable t.

The aim of this paper is to describe changes in the dynamics of the system when $\delta \ge 0$ changes from zero value to positive. Note that when $\delta =0$ we have a special case where the y-axis becomes equilibria of (1). Under conditions 1-3 below, we will prove that if $\delta >0$ is small then the system (1) possesses periodic trajectories. We will also prove that such trajectories are uniformly bounded by a non-periodic trajectory of (1) for $\delta =0$.

The system (1) is a special case of Gause-type predator–prey systems. Problems concerning global stability of the positive equilibrium (i.e. the equilibrium lying in the positive cone), existence and uniqueness of periodic trajectories in such a system have been studied by many authors and various results are known. It was proven that under certain conditions, the positive equilibrium is globally asymptotically stable in the positive cone, see [10] and references therein. In [9], a criterion for existence and uniqueness of a periodic orbit was proven; see also [1].

In our present paper, for the specific class of predator–prey systems (1), we obtain results on its periodic solutions using alternative but standard techniques, i.e., system linearization, sub- and super-solution methods, and the Poincare-Bendixson theorem or Dulac-Bendixson criterion. Its relevance in the context of population biology will be discussed later in the Example section.

Fig. 1

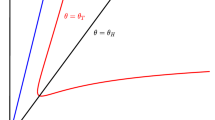
Sketch of the phase portrait of the system (1) for $\delta =0$. See the text for the meaning of the symbols

Preliminaries

Throughout the whole paper, we will assume that the functions f, g, h satisfy the following conditions:

• 1. There exists some $x_{0}>0$ such that $f(x)>0$ for $x\in [0,x_{0})$ and $f(x_{0})=0$.

• 2. The functions f, g, h are continuously differentiable in $[0,x_{0}]$ and g, h are positive in $[0,x_{0}]$.

• 3. It holds that $(xh)'(x)>0$ for $x\in [0,x_{0}]$, $f'(x_{0})<0$, and $\left( {\frac{f}{g}}\right) ^{\prime }(0)>0$.

Let us look at the dynamics of the system (1). Denote

$$\begin{aligned} N:= & {} \left\{ {(x,y)\in \mathbb {R}^{2};\; x,y>0}\right\} \\ N_+:= & {} \left\{ {(x,y)\in N;\; y<\left( {\frac{f}{g}}\right) (x),\; x\in [0,x_0]}\right\} ,\\ N_-:= & {} \left\{ {(x,y)\in N;\; y>\left( {\frac{f}{g}}\right) (x),\; x\in [0,x_0]}\right\} \end{aligned}$$

and

$$\begin{aligned} \Delta := \left\{ {(x,y)\in N;\; y=\left( {\frac{f}{g}}\right) (x),\; x\in [0,x_0]}\right\} . \end{aligned}$$

If $\delta =0$, then the y-axis is a line of equilibria of (1). Point $E_{1}:=(x_{0},0)$ is also an equilibrium. Note that $\dot{x}>0$ in $N_+$, $\dot{x}<0$ in $N_-$, $\dot{x}=0$ in $\Delta$ and any solution that starts in $N_{+}$ moves away from the y-axis, crosses $\Delta$ and continues to $N_{-}$. Such solutions are bounded from above by a heteroclinic trajectory $\Gamma$ that connects $E_{1}$ and an equilibrium on y-axes; see Theorem 1 and its proof. Since $\Delta$ is actually a graph of differentiable function $y(x)=\left( {\frac{f}{g}}\right) (x)$, any solution of (1) crosses $\Delta$ transversely. It is clear that such system does not have any periodic trajectory. The situation is illustrated in Fig. 1.

If $\delta >0$ is sufficiently small, then the assumption $(xh)'>0$ assures that there exists some $x_\delta >0$ such that $\delta = x_\delta h( x_\delta )$ and $x_\delta$ moves from left to right if $\delta$ increases. Denote $y_\delta =\left( {\frac{f}{g}}\right) ( x_\delta )$. Observe that the point $E:=(x_\delta ,y_\delta )$ that lies in $\Delta$ is an equilibrium of the system (1). In Theorem 1, we will prove that there exists a periodic trajectory $P_{\delta }$ that orbits around E; see Fig. 2.

Fig. 2

Sketch of the phase portrait of the system (1) for sufficiently small $\delta >0$

In the paper, we will use the following results.

Proposition 1

(Poincare-Bendixson Theorem). A nonempty compact $\omega$- or $\alpha$-limit set of a planar flow, which contains no equilibria, is a periodic trajectory.

Proposition 1 will be used to prove the existence of a periodic solution of system (1) under conditions 1-3. The result is well-known and can be found in literature concerning dynamical systems such as [5, 6]. The next result is an application of Dulac criterion for nonexistence of periodic trajectories in a region.

Proposition 2

Consider system (1) and let the conditions 1-3 be valid. For $\lambda \in \mathbb {R}$ fixed, we define the function $S_{\lambda }$ by

$$\begin{aligned} S_{\lambda }(x):=x\left( {\frac{f}{g}}\right) ^{\prime }(x) +\lambda \frac{xh(x)-\delta }{g(x)}. \end{aligned}$$

Assume that there exists an open interval $I\subset (0,\infty )$ and $\lambda \in \mathbb {R}$ such that $S_{\lambda }(x)$ does not change sign for all $x \in I$, and all its zeroes are isolated. Then the system (1) does not have any periodic solutions totally included in the strip $I\times (0,\infty )$.

Proposition 2 is a special case of a result from [1]; see also [10].

Results

The proof of Theorem 1 relies on basic knowledge regarding dynamical systems and periodic solutions such as investigation of linearizations of the system (1) at equilibrium points. The following lemma will be useful for such investigation.

Lemma 1

Let $\left( {\begin{matrix} a &{} b \\ c &{} d \end{matrix}}\right)$ be a real matrix and $\lambda _{k}$, $k=1,2$ be its eigenvalues. Denote $\alpha _{k}$ as the real part of $\lambda _{k}$ for $k=1,2$.

• 1. Let $(a+d)^{2}\le 4(ad-bc)$. If $a+d>0$ then $\alpha _{k}>0$ for $k=1,2$.

• 2. Let $(a+d)^{2} > 4(ad-bc)$. Then $\lambda _{k}$, $k=1,2$ are real numbers. If $a+d>0$ and $ad-bc>0$ then $\alpha _{k}>0$ for $k=1,2$. If $ad-bc<0$ then one of the values $\alpha _{1},\alpha _{2}$ is positive and one is negative.

One can prove the lemma by a straightforward calculation.

Theorem 1

Let functions f, g, h satisfy conditions 1 - 3.

• 1. Let $\delta =0$. Then there exists a nonempty open bounded invariant set $\Omega$ of the system (1) that is a subset of N. The set $\Omega$ is bounded by the axes and a heteroclinic trajectory $\Gamma$.

• 2. There exists $\delta _0>0$ such that for every $\delta \in (0,\delta _0)$ there exists a periodic trajectory $P_{\delta }$ of system (1).

Proof

We start with the proof of the assertion 1. The linearization of (1) at point $E_{1}$ is

$$\left( {\begin{array}{*{20}c} {x_{0} f(x_{0} )} & { - x_{0} g(x_{0} )} \\ 0 & {x_{0} h(x_{0} )} \\ \end{array} } \right){\text{ }}$$

(2)

Due to the assumption $f'(x_{0})<0$ and Lemma 1, the matrix (2) has one positive and one negative eigenvalue. Hence there exists a trajectory $\Gamma$ of system (1) that starts at $E_1$. This trajectory represents a global solution (x, y) of (1), i.e. $\Gamma (t):=(x,y)(t)$ for $t\in \mathbb {R}$.

We prove that $\Gamma$ is a heteroclinic trajectory and connects $E_{1}$ with a point $E_{2}:=(0,y_{0})$ for some $y_{0}>0$. First, we prove that $\Gamma$ lies entirely in $N_-$. Since the linearization with matrix (2) is locally equivalent to the system (1), trajectory $\Gamma$ continues to the region $N_-$, more precisely, there exists some $t_0\in \mathbb {R}\cup \infty$ such that $\Gamma (t)\in N_-$ for $t<t_0$. We claim that $t_0=\infty$. If not, then $\Gamma$ crosses $\Delta$ at $t_0\in \mathbb {R}$ transversely and there exists some $t_1<t_0$ such that $\Gamma (t_1)\in N_+$ what is not possible.

Second, we show that the trajectory $\Gamma (t):=(x,y)(t)$ is bounded for $t\in \mathbb {R}$ and x(t) converges to 0 as $t\rightarrow \infty$. Since $\dot{x}(t)>0$ for every $t\in \mathbb {R}$ there exist $a\in [0,x_0)$ and a function $\varphi$ defined in interval $(a,x_0)$ such that $y=\varphi (x)$ and for its derivative, it holds

$$\begin{aligned} \varphi '(x)=\frac{\dot{y}}{\dot{x}}=\frac{yh(x)}{f(x)-yg(x)}. \end{aligned}$$

The derivative of $\varphi$ is clearly negative and bounded from below for y large enough. This means that $\varphi$ is defined in interval $(0,x_0)$, i.e., $a=0$ and $\varphi (x)$ converges to some $y_0>0$ as $x\rightarrow 0$. The point $E_{2}=(0,y_0)$ is an equilibrium point of system (1) for $\delta =0$ and the solution represented by trajectory $\Gamma$ converges to $E_2$ and so $\Gamma$ is a bounded trajectory.

Finally, the heteroclinic trajectory $\Gamma$, the line segments between origin and $E_1$, and between origin and $E_2$ bound the invariant set $\Omega$ of system (1) for $\delta =0$. Clearly, this set is nonempty, open and bounded.

Now, we prove the assertion 2. Let $\Gamma$ and $\varphi$ be as in the previous part of the proof and let $\delta >0$ be fixed. Our first goal is to prove that for such $\delta$, $\Omega$ is an invariant set of the system (1). Let $F:=(x_{1},y_{1})$ be an arbitrary point that lies in $\Gamma$ and (x, y) be the solution of (1) that starts at F. Since $F\in N_-$, there exists a positive differentiable function $\psi$ defined on some neighborhood of $x_{1}$ such that $y=\psi (x)$. Note that such function exists as long as the solution (x, y) stays in $N_-$ and fails to exist if (x, y) crosses $\Delta$. For the derivative of $\psi$, it holds

$$\begin{aligned} \psi '(x)=\frac{\dot{y}}{\dot{x}}=\frac{-\delta y + xyh(x)}{xf(x)-xyg(x)}=\frac{\delta }{x}\frac{ \psi (x)}{\psi (x)g(x)-f(x)}+\frac{\psi (x)h(x)}{f(x)-\psi (x)g(x)}. \end{aligned}$$

(3)

Thus $\psi$ is a solution of the equation (3). Observe that $\varphi$ is a solution of equation

$$\begin{aligned} \varphi '(x)=\frac{\varphi (x)h(x)}{f(x)-\varphi (x)g(x)}. \end{aligned}$$

(4)

From (3), we see that

$$\begin{aligned} \psi '(x)>\frac{\psi (x)h(x)}{f(x)-\psi (x)g(x)}. \end{aligned}$$

This inequality along with (4) implies that $\psi (x)<\varphi (x)$ for $x<x_{1}$ (note that every solution moves from right to left in $N_-$), and so the solution corresponding to $\psi$ lies in $\Omega$. Moreover, any other solution of (1) that starts in $\Omega$ cannot cross $\Gamma$.

A simple computation shows that the linearization of (1) at point E is

$$\begin{aligned} \left( {\begin{matrix} x_\delta g(x_\delta )\left( {\frac{f}{g}}\right) ^\prime (x_\delta ) &{} x_\delta g(x_\delta ) \\ y_\delta (xh)^\prime (x_\delta ) &{} 0 \end{matrix}}\right) . \end{aligned}$$

(5)

Due to our assumptions and the smoothness of the function $\frac{f}{g}$, there exists some $\delta _{0}>0$ sufficiently small such that $\left( {\frac{f}{g}}\right) ^\prime (x_\delta )>0$ and the determinant of the matrix of (5) is positive for every $\delta \in (0,\delta _{0})$. Thus Lemma 1 implies that E is a repellent, i.e. every trajectory of the system (1) moves away from E.

Trajectories of the system (1) remain in a compact set that is a subset of $\Omega$ and does not contain E. Such a compact set does not contain any equilibria, and due to Proposition 1, there exists a periodic trajectory $P_{\delta }$ of (1). $\square$

Remark

From the proof of Theorem, it is clear that if $(xh)'(x_\delta )>0$ and $\left( {\frac{f}{g}}\right) ^{\prime }(x_\delta )>0$ for some $\delta >0$ then the system (1) possesses a periodic trajectory that lies in $\Omega$. These assumptions can be verified easily if one is able to obtain $x_\delta$ as the solution of the equation $xh(x)=\delta$.

The following lemma provides a sub- and super-solution method that is used the proof of Theorem 2. We refer the reader to [5] for more details on this method in differential inequalities.

Lemma 2

Assume that the conditions 1-3 are valid. Consider system

$$\begin{array}{*{20}c} {\dot{z}} & = & {z(F - Gy),} \\ {\dot{y}} & = & {x_{\delta } Hy(z - 1),} \\ {z,y} & \ge & 0 \\ \end{array} {\text{ }}$$

(6)

where F, G and H are positive constants. Let (z, y) be a periodic solution of the system (6) that orbits around the equilibrium $\left( {1,\frac{F}{G}}\right)$. Let $\delta _{0}>0$ be such that $x_\delta$ exists for $\delta \in (0,\delta _{0}]$. Denote $y_{\delta ,1},y_{\delta ,2}$ ($y_{\delta ,1}>\frac{F}{G}>y_{\delta ,2}$) to be the intersections of (z, y) with line $z=1$ and $z_{\delta ,1}$ ($z_{\delta ,1}<1$) to be the left intersection of (z, y) with line $y=\frac{F}{G}$. Then the following statements are equivalent:

• i. There exists $\alpha >\frac{F}{G}$ such that $y_{\delta ,1}\le \alpha$ for all $\delta \in (0,\delta _{0})$.

• ii. There exists $\beta >0$ such that $e^{-\frac{\beta }{x_{\delta }}}\le z_{\delta ,1}$ for all $\delta \in (0,\delta _{0})$.

• iii. There exists $\gamma >0$ such that $y_{\delta ,2}\ge \gamma$ for all $\delta \in (0,\delta _{0})$.

Remark

The system (6) was studied by several authors. In [10], it was proven that if $x_\delta >0$ then every solution lying in the positive cone is periodic except the equilibrium $\left( {1,\frac{F}{G}}\right)$.

Proof of Lemma 2

First, let us prove that i and ii are equivalent. Denote $\varphi$ to be the solution of equation

$$\begin{aligned} \varphi '(y)=\frac{\dot{z}}{\dot{y}}=\frac{\varphi (y)}{1-\varphi (y)}\frac{Gy-F}{x_\delta H y} \end{aligned}$$

that satisfies the condition $\varphi (y_{\delta ,1})=1$. Such solution exists for $y\in \left[ { y_{\delta ,2},y_{\delta ,1} }\right]$ and it holds that $\varphi (y_{\delta ,1})=\varphi (y_{\delta ,2})$. By a simple computation, we find that

$$\begin{aligned} \varphi (y)=\Psi ^{-1}\left( {\frac{\Phi (y)-\Phi (y_{\delta ,1})}{x_\delta H}}\right) \end{aligned}$$

where $\Phi (\tau )=G\tau -F\text{ ln }(\tau )$ for $\tau >0$, $\Psi (\tau )=\text{ ln }(\tau )+1-\tau$ for $\tau \in (0,1]$, and $\Psi ^{-1}$ is the inverse function of $\Psi$. Observe that for $\xi <0$ bounded away from zero, it holds that

$$\begin{aligned} e^{c\xi }\le \Psi ^{-1}(\xi )\le e^{\xi } \end{aligned}$$

(7)

for some $c>1$.

It is clear that $\varphi$ attains its minimum at $y=\frac{F}{G}$ and $\varphi \left( {\frac{F}{G}}\right) =z_{\delta ,1}$. Assume that i is valid. Since $\Phi$ is increasing in $\left( {\frac{F}{G},\infty }\right)$ it holds $\Phi \left( {\frac{F}{G}}\right) -\Phi (\alpha )\le \Phi \left( {\frac{F}{G}}\right) -\Phi (y_{\delta ,1})<0$.

Note that $\frac{\Phi \left( {\frac{F}{G}}\right) -\Phi (\alpha )}{ x_\delta H}$ is negative and bounded away from zero since $x_\delta <x_{0}$ for $\delta \in (0,\delta _{0})$. Hence it is possible to use the estimate (7) and if we set $\beta :=c\frac{\Phi (\alpha )-\Phi \left( {\frac{F}{G}}\right) }{H}$, the assertion ii follows. Conversely, if we assume ii, then similar estimates as in the first part of the proof yield i.

Now, we prove that i and iii are equivalent. This is obvious since if $\varphi (y_{\delta ,1})=\varphi (y_{\delta ,2})=1$ then due to the expression of $\varphi$, it follows that $\Phi (y_{\delta ,2})=\Phi (y_{\delta ,1})$. This actually means that $y_{\delta ,1}$ is bounded if and only if $y_{\delta ,2}$ is bounded away from zero; see the definition of $\Phi$. This completes the proof.

Theorem 2

Let conditions 1-3 be satisfied and let $\delta _{0}>0$ be such that for every $\delta \in (0,\delta _{0})$ exists at least one periodic solution of system (1). Denote $P_{\delta }$ to be one of periodic trajectories of (1) for corresponding $\delta$ and let $y_{\delta ,2}<y_{\delta }$ be the intersection of $P_{\delta }$ with the line $x=x_{\delta }$. Then, there exists $\delta _{1}\in (0,\delta _{0})$ such that

$$\begin{aligned} \inf \limits _{\delta \in (0,\delta _{1})}y_{\delta ,2}>0 \end{aligned}$$

(8)

and

$$\begin{aligned} \sup \limits _{\delta \in (0,\delta _{1})}y_{\delta ,2}<\left( {\frac{f}{g}}\right) (0). \end{aligned}$$

(9)

Proof

For $\delta \in (0,\delta _{0})$, denote

$$\begin{aligned} M_-:= \left\{ {(x,y)\in N;\; x<x_\delta }\right\} ,\; M_+:= \left\{ {(x,y)\in N;\; x\in (x_\delta ,x_{0})}\right\} \text{ and } M:= \left\{ {(x,y)\in N;\;x=x_\delta }\right\} . \end{aligned}$$

From the dynamics of the system (1), we see that $P_{\delta }$ circles around the equilibrium E in the anti-clockwise direction, since $\dot{x}<0<\dot{y}$ for $(x,y)\in N_{-}\cap M_{+}$, $\dot{x},\dot{y}<0$ for $(x,y)\in N_{-}\cap M_{-}$, $\dot{y}<0<\dot{x}$ for $(x,y)\in M_{-}\cap N_{+}$ and $0<\dot{x},\dot{y}$ for $(x,y)\in N_{+}\cap M_{+}$. It is clear that the x-coordinate of $P_{\delta }$ attains its minimum at some point $x_{\delta ,1}\in \Delta$ and maximum at $x_{\delta ,2}\in \Delta$, and the y-coordinate of $P_{\delta }$ attains its minimum at $y_{\delta ,2}\in M$ and maximum at $y_{\delta ,1}\in M$. Obviously, $x_{\delta ,1}<x_{\delta }<x_{\delta ,2}$ and $y_{\delta ,2}<y_{\delta }<y_{\delta ,1}$.

First, we prove (8). We introduce a new variable $z=\frac{x}{x_{\delta }}$ in the system (1). Using the definition of $x_{\delta }$, we transform the system (1) into

$$\begin{aligned} \begin{array}{rcl} \dot{z} &{}=&{} zf(x_{\delta }z)-zyg(x_{\delta }z),\\ \dot{y} &{}=&{} -x_{\delta }h(x_{\delta }) y + x_{\delta }zyh(x_{\delta }z),\\ z,y &{}\ge &{} 0. \end{array} \end{aligned}$$

Let $\varphi _{\delta }$ be the solution of equation

$$\begin{aligned} \varphi _{\delta }'(z)=\frac{\dot{y}}{\dot{z}}=\frac{x_{\delta }\varphi _{\delta }(z)(h(x_{\delta }) - zh(x_{\delta }z))}{z(g(x_{\delta }z)\varphi _{\delta }(z)-f(x_{\delta }z))} \end{aligned}$$

(10)

satisfying the initial condition $\varphi _{\delta }(1)=y_{\delta ,1}$. We recall that such solution $\varphi _{\delta }$ exists in interval $\left( {z_{\delta ,1},1}\right]$ (i.e. $\varphi _{\delta }$ is a part of $P_{\delta }$ that lies in $M_{-}\cap N_{-}$), is increasing, and its derivative is unbounded.

Our next step is to construct an upper bound for $\varphi _{\delta }$. Such bound is in fact a solution of the system (6) for suitable positive constants F, G and H. We apply the mean-value theorem in (10) and for some $c\in (x_{\delta }z,x_{\delta })$, we obtain

$$\begin{aligned} \varphi _{\delta }'(z)= \frac{x_{\delta }(1-z)}{z}\frac{\varphi _{\delta }(z)(zh)^{\prime }(c)}{g(x_{\delta }z)\varphi _{\delta }(z)-f(x_{\delta }z)}. \end{aligned}$$

Observe that we can choose $\varepsilon >0$ such that

$$0<f(0)-\varepsilon<f(x_\delta z),\;g(x_\delta z)<g(0)+\varepsilon \text{ and } 0<(zh)^{\prime }(0)-\varepsilon< (zh)^{\prime }(c)<(zh)^{\prime }(0)+\varepsilon$$

for some $\delta _{1}>0$ sufficiently small, $\delta \in (0,\delta _{1})$ and $z\in (0,1)$. Hence

$$\begin{aligned} \varphi _{\delta }'(z) \ge \frac{x_{\delta }(1-z)}{z}\frac{\varphi _{\delta }(z)((zh)^{\prime }(0)-\varepsilon )}{(g(0)+\varepsilon )\varphi _{\delta }(z)-(f(0)-\varepsilon )}. \end{aligned}$$

Such estimate is true since $\varphi _{\delta }(z)>\frac{f(x_\delta z)}{g(x_\delta z)}>\frac{f(0)-\varepsilon }{g(0)+\varepsilon }$. If $\varphi$ is the solution of the problem

$$\begin{aligned} \varphi '(z)= \frac{x_{\delta }(1-z)}{z}\frac{\varphi (z)((zh)^{\prime }(0)-\varepsilon )}{(g(0)+\varepsilon )\varphi (z)-(f(0)-\varepsilon )} \end{aligned}$$

equipped with the initial condition $\varphi (1)=y_{\delta ,1}$, then $\varphi _{\delta }$ is a super-solution of the euquation above and hence

$$\begin{aligned} \varphi _{\delta }(z)\le \varphi (z). \end{aligned}$$

(11)

Denote $z_{\delta ,1}=\frac{x_{\delta ,1}}{x_{\delta }}$; this is the point (after the transformation) where $P_{\delta }$ crosses $\Delta$ and where $\varphi _{\delta }$ fails to exist. Since $\varphi$ crosses the line $y=\frac{f(0)-\varepsilon }{g(0)+\varepsilon }$ at some $z_{\varphi }\in (0,1)$ our choice of $\varepsilon$ and the estimate (11) yield $z_{\varphi }\le z_{\delta ,1}$. We already know that the condition i from Lemma 2 is valid. This follows due the fact that all periodic trajectories $P_{\delta }$ are contained in a bounded set $\Omega$ defined in Theorem 1. Hence it holds $e^{-\frac{\beta }{x_{\delta }}}\le z_{\varphi }\le z_{\delta ,1}$ for some $\beta >0$ that may depend on $\varepsilon$ but is independent of $\delta$.

Let $\varphi _{\delta }$ be the solution of (10) that starts at $z_{\delta ,1}$ and $\varphi _{\delta }(z)<\frac{f(x_{\delta }z)}{g(x_{\delta }z)}$, i.e. $\varphi _{\delta }$ is a part of $P_{\delta }$ that lies in $M_{-}\cap N_{+}$. We can assume that $\varphi _{\delta }$ crosses $\frac{f(0)-\varepsilon }{g(0)+\varepsilon }$ at some $z\in (z_{\delta ,1},1)$ otherwise (8) would be valid. Denote $\varphi _{1}$ to be the solution of problem

$$\begin{aligned} \varphi _{1}'(z)=- \frac{x_{\delta }(1-z)}{z}\frac{\varphi _{1}(z)((zh)^{\prime }(0)+\varepsilon )}{(f(0)-\varepsilon )-(g(0)+\varepsilon )\varphi _{1}(z)},\quad \varphi _{1}(z_{\varphi })=\frac{f(0)-\varepsilon }{g(0)+\varepsilon }. \end{aligned}$$

Similar arguments as in the previous part of the proof imply that for $\delta _{1}$ is small enough, it holds that $\varphi _{\delta }$ is a super-solution for the equation above. Hence $\varphi _{\delta }(z)\ge \varphi _{1}(z)$ for every $z\le 1$ such that $\varphi _{\delta }$ exists. Since $e^{-\frac{\beta }{x_{\delta }}}\le z_{\varphi }$ for some $\beta >0$ we can use Lemma 2 and conclude that there is some $\gamma >0$ such that $\gamma \le \varphi _{1}(1)\le \varphi _{\delta }(1)$ for all $\delta \in (0,\delta _{1})$. Thus we proved (8).

Next, we prove (9). Due to the conditions 1 and 2, there exists some $\beta >0$ such that $\left( {\frac{f}{g}}\right) ^{\prime }(x)>0$ for every $x\in (0,\beta )$ and $\left( {\frac{f}{g}}\right) ^{\prime }(\beta )=0$. In such case, the function $S_{0}(x)$ defined in Preposition 2 is positive in $(0,\beta )$, and hence there is no periodic solution in strip $(0,\beta )\times (0,\infty )$. So $P_{\delta }$ cannot be totally contained in the strip and consequently, $x_{\delta ,2}\ge \beta$. Since $x_\delta \rightarrow 0$ as $\delta \rightarrow 0^{+}$, there exists some $\delta _{1}>0$ that $x_\delta <\frac{\beta }{2}$ and due to the monotonicity of $\frac{f}{g}$, there is some $\alpha >0$ such that $\left( {\frac{f}{g}}\right) (\beta )\ge \alpha +\left( {\frac{f}{g}}\right) (0)$. The trajectory $P_{\delta }$ lies in $M_{+}\cap N_{-}$ until it crosses M, thus $y_{\delta ,1}>\left( {\frac{f}{g}}\right) (\beta )\ge \alpha + \left( {\frac{f}{g}}\right) (0)$.

Let $\varphi _{\delta }$ be the solution of problem

$$\begin{aligned} \varphi _{\delta }'(x)=\frac{\varphi _{\delta }(x)(xh-\delta )}{x(f(x)-\varphi _{\delta }g(x))},\;\varphi _{\delta }(x_\delta )=y_{\delta ,2} \end{aligned}$$

and $\varphi _{\delta }<\frac{f}{g}$, i.e. $\varphi _{\delta }$ lies in $N_{+}\cap M_{+}$. Let $\eta >1$ and $c>0$ be constants such that $\eta x_\delta <\frac{\beta }{2}$ and $\min \limits _{x\in [0,x_{0}]}h(x)-\frac{h(x_\delta )}{\eta }\ge c$ for every $\delta \in (0,\delta _{1})$; taking $\delta _{1}$ lower might be needed. The constants $\eta$ and c can be chosen to be independent of $\delta$. It is clear that then it holds $\frac{xh-\delta }{x}=h-\frac{x_\delta h(x_\delta )}{x}\ge c$ for all $x\in \left[ {\eta x_\delta ,\beta }\right]$. We know that $\varphi _{\delta }\ge \gamma$ for some $\gamma >0$ for $\delta _{1}$ small due to (8). For $\varepsilon >0$, we define $F:\left[ {0,\beta }\right] \rightarrow \mathbb {R}$, $F(x)=\frac{f(x)-\varepsilon }{g(x)}$. First, we choose $\varepsilon$ small enough so that the estimate $\frac{c\gamma }{\varepsilon }>\max \limits _{x\in [0,\beta ]}F'(x)$ is valid. Our goal is to prove that $\varphi _{\delta }(x)<F(x)$ for $x\in \left[ {\eta x_\delta ,\frac{\beta }{2}}\right]$ if $\varepsilon$ is small. Observe that if $\varphi _{\delta }(\xi )\ge F(\xi )$ for some $\xi \in \left( {\eta x_\delta ,\beta }\right)$ then

$$\begin{aligned} \varphi _{\delta }'(\xi )\ge \frac{c\gamma }{\varepsilon }. \end{aligned}$$

(12)

We claim that we can take $\varepsilon$ small enough so that $\varphi _{\delta }(\xi _{1})<F(\xi _{1})$ for some $\xi _{1}\in \left( {\frac{\beta }{2},\beta }\right)$. Otherwise, integrating (12) on the interval $\left( {\frac{\beta }{2},\beta }\right)$ would yield $\varphi _{\delta }(\beta )-\varphi _{\delta }\left( {\frac{\beta }{2}}\right) \ge \frac{c\gamma }{2\varepsilon }$ and this is a contradiction since $\varphi _{\delta }$ is bounded. It is now easy to deduce that $\varphi _{\delta }(x)< F(x)$ for $x\in \left[ {\eta x_\delta ,\xi _{1}}\right]$.

If we lower $\delta _{1}$ then there holds $F(\eta x_\delta )<\frac{f(0)-\frac{\varepsilon }{2}}{g(0)}$ for all $\delta \in (0,\delta _{1})$. Since $\varphi _{\delta }$ is increasing in $M_{+}\cap N_{+}$ it holds that $\varphi _{\delta }(x_\delta )<\varphi _{\delta }(\eta x_\delta )\le \frac{f(0)-\frac{\varepsilon }{2}}{g(0)}$ and the estimate (9) follows. $\square$

Fig. 3

Mutual position of periodic trajectories $P_{\delta _{1}}$ and $P_{\delta _{2}}$ for some $0<\delta _{2}<\delta _{1}$. Here‘ $P_{\delta _{2}}$ is ”close” to a trajectory of (1) for $\delta =0$

Remark

The results from Theorem 2 have the following geometrical meaning. The intersections of periodic trajectories $P_{\delta }$ and the line $x=x_\delta$ are bounded away from the x-axis and from $\Delta$ for $\delta >0$ small enough. This implies that all of $P_{\delta }$ are bounded by a trajectory (x, y) of (1) with $\delta =0$, $y(t)>0$ for $t\in \mathbb {R}$, and by a part of the y-axis. The trajectories $P_{\delta }$ are bounded away from the heteroclinic orbit $\Gamma$ (see Theorem 1). On the other hand, the right intersection of $P_{\delta }$ with $\Delta$ stays away from the y-axis, $P_{\delta }$ cannot ”shrink” to any of equilibria that lie on the y-axis. A compactness argument implies that there is a sequence $\delta _{n}$ and one corresponding $P_{\delta _{n}}$ such that $P_{\delta _{n}}$ converge locally uniformly to a trajectory of (1) for $\delta =0$ as $\delta _{n}\rightarrow 0^{+}$; see Fig. 3.

Example

Fig. 4

Dynamics of the prey-predator system (13). (a) Phase portrait of the systems with trajectories from two initial conditions (shown as solid blue curves) that tend to a limit cycle (shown as a red dashed curve). Note that the horizontal axis is plotted in a logarithmic scale for clarity. Here, $\delta =0.2630$. (b) Plot of the limit cycle in (a) obtained from solving the BVP (14)-(15). The calculated period is $T\approx 40$. (c) The limit cycle period as a function of $\delta$. The curve terminates at a Hopf point $\text {HP}$, located at $\delta =d(a-c)/(a+c)$. Note that the period $T\rightarrow \infty$ as $\delta \rightarrow 0$. (d) The same as panel (a), but with $\delta =0$. The presence of a heteroclinic trajectory $\Gamma$ connecting $E_1$, i.e., (a, 0) [13], and $(0,y_0)$ for some $y_0>0$ can be seen clearly

We consider system

$$\begin{aligned} \begin{array}{rcl} \dot{x} &{}=&{} x\left( {1-\frac{x}{a}}\right) -\frac{bxy}{c+x},\\ \dot{y} &{}=&{} -\delta y + \frac{dxy}{c+x},\\ x,y &{}\ge &{} 0 \end{array} \end{aligned}$$

(13)

where a, b, c, d are positive constants and $\delta \ge 0$ is a parameter. The system is well-known as a prey-predator model with a Holling type II functional response and death in the predator population with rate $\delta$, see, e.g., [2, 4, 7]. Similar ones were studied in various works, e.g., in [1, 11, 16]. In a recent paper, Marwan and Tuwankotta [13] studied properties of periodic solutions of (13) when $\delta$ varies by using numerical calculations. Kooi and Poggiale [8] and Poggiale et al. [14] study bifurcating limit cycles of the system as a canard phenomenon using asymptotic perturbation methods and geometrical singular perturbation theory, respectively (see also, e.g., [15]).

Note that (13) is a special case of the system (1) where $f(x)=1-\frac{x}{a}$, $g(x)=\frac{b}{c+x}$, and $h(x)=\frac{d}{c+x}$. The conditions 1 and 2 are obviously valid for $x_{0}=a$. A simple computation shows that the derivative of $\left( {\frac{f}{g}}\right) (x)=\frac{(a-x)(c+x)}{ab}$ is positive on $\left[ {0,\frac{a-c}{2}}\right)$ if $\frac{a-c}{2}>0$. Thus the condition 3 is valid if and only if $a>c$. For $\delta \in (0,d)$, there exists the unique value $x_\delta =\frac{c\delta }{d-\delta }$ and $x_\delta$ lies in the interval $\left( {0,x_{0}}\right)$ if $\delta \in \left( {0,\frac{ad}{a+c}}\right)$.

If $a\le c$ then the derivative of $\frac{f}{g}$ is non-positive. The function $S_{0}$ defined in Proposition 2 is non-positive and hence the system (13) does not possess any periodic solutions. If $a>c$ then Theorem 1 assures that for $x_\delta \in \left( {0,\frac{a-c}{2}}\right)$, there exists a periodic trajectory $P_{\delta }$ and any of the trajectories lies in $\Omega$. The set $\Omega$ is bounded by the heteroclinic trajectory $\Gamma$ and by parts of the axes. Hence these curves are bounds for $P_{\delta }$. If $\delta =d\frac{a-c}{a+c}$ (and $x_\delta =\frac{a-c}{2}$ is the corresponding x-coordinate of equilibrium E) then one can use Proposition 2 to prove that the system (13) does not have any periodic trajectories. In fact, straightforward computations show that $S_{\lambda }(x)=(2x-a+c)\left( {-\frac{x}{ab}+\lambda \frac{cd}{b(a+c)}}\right)$. Setting $\lambda =\frac{(a-c)(a+c)}{2adc}$, we have $S_{\lambda }\le 0$ on [0, a] and the result follows.

Theorem 2 implies that for all $\delta >0$ sufficiently small, $P_{\delta }$ is bounded away from the x-axis due to (9). This means that any of $P_{\delta }$ lies within a proper subset of $\Omega$. The boundary of such subset consists of a trajectory of the system (13) for $\delta =0$ and a part of the y-axis. On the other hand, $P_{\delta }$ do not ”shrink” to the equilibrium $\left( {0,\left( {\frac{f}{g}}\right) (0)}\right)$ due to (9).

We have solved the governing equations (1) numerically. Time integration has been done using the standard fourth-order Runge-Kutta method. We also solved the model for periodic solutions by transforming it into

$$\begin{aligned} \begin{array}{rcl} {x}' &{}=&{} \left( \frac{T}{2\pi }\right) \left[ x\left( {1-\frac{x}{a}}\right) -\frac{bxy}{c+x}\right] ,\\ {y}' &{}=&{} \left( \frac{T}{2\pi }\right) \left[ -\delta y + \frac{dxy}{c+x}\right] ,\\ x(0)&{}=&{}x(2\pi ),\quad y(0)\,=\,y(2\pi ), \end{array} \end{aligned}$$

(14)

where prime is the derivative with respect to a scaled time $\tau =2\pi t/T$ and T is the minimal period. We solved the boundary value problem (BVP) (14) using spectral method.

Note that if $x_0(\tau )$, $y_0(\tau )$ is a solution to the BVP, so is $x_0(\tau +\sigma )$, $y_0(\tau +\sigma )$ for any phase shift $\sigma$. To fix $\sigma$, we impose the integral phase condition

$$\begin{aligned} \int _{0}^{2\pi } w'(\tau )\,x(\tau )\,d\tau =0, \end{aligned}$$

(15)

where $w(\tau )$ is any $2\pi$-periodic smooth function. The equation (15) is a necessary condition for the $L_2$-distance between $x(\tau +\sigma )$ and $w(\tau )$, i.e., $\rho (\sigma )=\int _{0}^{2\pi }|| x(\tau +\sigma )-w(\tau ) ||^2\,d\tau$, to have a local minimum with respect to possible shifts $\sigma$ at $\sigma =0$, i.e., $\left. d\rho /d\sigma \right| _{\sigma =0}=0$ [12]. The BVP (14) with the phase condition (15) will determine the states $x(\tau )$, $y(\tau )$, and T uniquely.

We consider the model (14) with parameter values $a=6$, $b=0.75$, and $c=d=1$. We plot our results in Figure 4, where we demonstrate the presence of a (stable) limit cycle for $\delta$ small enough. The period of the limit cycle increases as the parameter $\delta$ decreases. When $\delta =0$, we have heteroclinic trajectories bounded by $\Gamma$ connecting $E_1$ and $(0,y_0)$ for a $y_0>0$.