Fractional differentiation and its use in machine learning

Abstract

This article covers the implementation of fractional (non-integer order) differentiation on real data of four datasets based on stock prices of main international stock indexes: WIG 20, S&P 500, DAX and Nikkei 225. This concept has been proposed by Lopez de Prado [5] to find the most appropriate balance between zero differentiation and fully differentiated time series. The aim is making time series stationary while keeping its memory and predictive power. In addition, this paper compares fractional and classical differentiation in terms of the effectiveness of artificial neural networks. Root mean square error (RMSE) and mean absolute error (MAE) are employed in this comparison. Our investigations have determined the conclusion that fractional differentiation plays an important role and leads to more accurate predictions in case of ANN.

1 Introduction

Many supervised machine learning algorithms are applied on financial time series data require stationarity [1]. In the process of creating a predictive model, it is assumed that a given time series is generated by a stochastic process. To make an accurate inference from such model, it is crucial that mentioned data generation process remains consistent. In statistical terms, the mean, variance and covariance should not change with time [1]. As a result in analyzed time series, a trend over time is not revealed. When this assumption is not fulfilled, the algorithm may assign a wrong prediction to a new observation.

In contrary to cross-sectional data, time series is a specific kind of data in the sense that any observation reflects a history of observations occurred in the past. The literature named it as a distinctive memory of past track record [2]. Due to the stationarity condition, this series memory is often excluded from the dataset.

The most commonly used method for non-stationarity removal is differencing up to some integer order [2]. Subtracting from each observation its predecessor, one gets the first-order differentiation. The second-order differencing is accomplished by repeating this process on obtained time series. It is similar for higher orders. Admittedly, these transformations can lead to the stationarity, but as a consequence all memory from the original series is erased [2]. On the other hand, the predictive power of machine learning algorithm is based on this memory. Lopez de Prado [3] calls it as the stationarity versus memory dilemma by asking a question whether there is a trade-off between these two concepts, in other words—does exist a solution of making the time series stationary concurrently with keeping its predictive power. One way to resolve this dilemma—fractional differentiation—has been proposed by Hosking [4]. Lopez de Prado upgraded this idea to find the optimal balance between zero differentiation and fully differentiated time series.

The remainder of the paper is organized as follows. The next section gives an overview of fractional differentiation introduced above. The data used in this research are presented in Sect. 3, and the method applied on this data is described in Sect. 4. Section 5 discusses the results, and chapter 6 concludes the paper.

2 Fractional differentiation—an overview

In this section, the concept of fractional differentiation is elaborated in more detail. Assume that a time series $X$ runs throughout time $t$ and it is not stationary:

$X = \left\{ {X_{t} , X_{t - 1} , X_{t - 2} , \ldots , X_{t - k} , \ldots } \right\}$.

As previously explained, computing the differences between consecutive observations is an approach to achieve a stationary time series [2]:

$$\nabla X_{t} = X_{t} - X_{t - 1}$$

By defining a backshift operator $B$ as $B^{k} X_{t} = X_{t - k}$ for $k \ge 0$ and $t > 1$, the above formula, first-order differentiation, can be expressed as:

$\nabla X_{t} = X_{t} - X_{t - 1} = X_{t} - BX_{t} = \left( {1 - B} \right)X_{t}$.

Concerning the situation when differenced data will not appear to be stationary, it may be demanded to difference the data a second time to obtain a stationary series:

$$\nabla^{2} X_{t} = \nabla \left( {\nabla X_{t} } \right) = \nabla (X_{t} - X_{t - 1} ) = (X_{t} - X_{t - 1} ) - (X_{t - 1} - X_{t - 2} ) = X_{t} - 2X_{t - 1} + X_{t - 2}$$

which using the backshift operator may be represented as:

$$\left( {1 - B} \right)^{2} = 1 - 2B + B^{2}$$

$$B^{2} X_{t} = X_{t - 2}$$

$$\left( {1 - B} \right)^{2} X_{t} = X_{t} - 2X_{t - 1} + X_{t - 2}$$

More generally, for order of differentiation $d$ we have:

$$\nabla^{d} X_{t} = \left( {1 - B} \right)^{d} X_{t}$$

For a real number $d$ using a binomial formula [3]:

$$\left( {1 + x} \right)^{d} = \mathop \sum \limits_{k = 0}^{\infty } \left( {\begin{array}{*{20}c} d \\ k \\ \end{array} } \right)x^{k}$$

the series can be expanded to [3]:

$$\left( {1 - B} \right)^{d} = \mathop \sum \limits_{k = 0}^{\infty } \left( { - B} \right)^{k} \mathop \prod \limits_{i = o}^{k - 1} \frac{d - i}{{k - i}} = 1 - dB + \frac{{d\left( {d - 1} \right)}}{2!}B^{2} - \frac{{d\left( {d - 1} \right)\left( {d - 2} \right)}}{3!}B^{3} + \ldots$$

The current value in time series is the function of all the past values occurred before this time point. To each past value, a weight $\omega_{k}$ is assigned [3]:

$$X_{t} = \mathop \sum \limits_{k = 0}^{\infty } \omega_{k} X_{t - k}$$

The application of fractional differentiation on time series allows to decide each weight for each corresponding value. All weights calculated by fractional derivative can be expressed as [3]:

$$\omega = \left\{ {1, - d, \frac{{d\left( {d - 1} \right)}}{2!}, - \frac{{d\left( {d - 1} \right)\left( {d - 2} \right)}}{3!}, \ldots , \left( { - 1} \right)^{k} \mathop \prod \limits_{i = 0}^{k - 1} \frac{d - i}{{k!}}, \ldots } \right\}$$

When we consider $d$ as a positive integer number, there is a point when $d$ is equal to $k$, then $d - k = 0$ and:

$$\mathop \prod \limits_{i = 0}^{k - 1} \frac{d - i}{{k!}} = 0$$

which leads to conclusion that memory beyond that point is removed. In first-order differencing ($d = 1$), weights follow as (see Fig. 1 as a confirmation):

$$\omega = \left\{ {1, - 1, 0, 0, \ldots } \right\}$$

Fig. 1

Weights of the lag coefficients for various values of $k$. Each line is related to particular order of differencing (${\text{d}} \in \left[ {0,1} \right]$)

General-purpose approach of coefficient for various orders of differencing is depicted in Fig. 1. For example, if $d = 0.25$ and $k$ is always an integer number, all weights achieved values other than 0 which means that the memory is going to be preserved.

From the above derivation, the iterative formula for the weights of the lags can be deduced [3]:

$$\omega_{k} = - \omega_{k - 1} \cdot \frac{{\left( {d - k + 1} \right)}}{k}$$

where $\omega_{k}$ is the coefficient of backshift operator $B^{k}$. For the first-order differentiation, we have: $\omega_{0} = 1$, $\omega_{1} = - 1$. $\omega_{k} = 0$ for $k > 1.$

In conclusion, the main intention to use the fractional differentiation is finding the fraction $d$, which is considered as minimum number needed to achieve stationarity, meanwhile keeping the maximum volume of memory in analyzed time series [3].

3 Data

This study uses four datasets with main stock indexes from different countries: WIG20 (Poland), S&P 500 (USA), DAX (Germany) and Nikkei 225 (Japan). The stock indexes were recorded from 1st June of 2010 to 30th June of 2020. The empirical distributions of mentioned indexes observed in each of the datasets are given in Figs. 2, 3, 4, 5.

Fig. 2

Closing price time series for WIG20 index

Fig. 3

Closing price time series for S&P 500 index

Fig. 4

Closing price time series for DAX index

Fig. 5

Closing price time series for Nikkei 225 index

Table 1 shows the results of the unit root test for all the analyzed stocks, including the augmented Dickey–Fuller (ADF) test and the Kwiatkowski–Phillips–Schmidt–Shin (KPSS) test (described in Appendix). These tests are the most widely used to determine whether a given time series is stationary [5]. The null hypothesis of the ADF test essentially assumes non-stationarity, and the null hypothesis of the KPSS test is stationarity. It can be found out that all the stock prices are non-stationary.

Table 1 The results of ADF and KPSS tests

4 Method

This section describes the selected approach used to compare statistical properties of fractional differentiation with differencing of first order.

In [6] (see also references therein) authors claim that artificial neural networks (ANN) are commonly used for forecasting stock prices indexes. In general, ANN outperforms other statistical models applied on time series due to their good nonlinear approximation ability [7]. They were inspired by the strategy human brain processes given information. One of the most frequently implemented neural networks topology is multilayer perceptron.

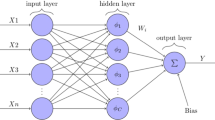
Like the human brain the neural network has single processing elements which are called neurons. They are connected to each other by weighted and directed edges (see Fig. 6). Commonly, neurons are aggregated into layers. Typical multilayer perceptron has three layers consisting of neurons: input layer, output layer and hidden layer. In the most simple case of artificial neural network, the edges between layers are limited to being forward edges (feed forward artificial neural networks). It means that any element of a current layer feeds all the elements of the succeeding layer.

Fig. 6

An example of simple ANN with input, hidden and output layers

The goal of the neural network is mapping values from input layer to values from output layer using hidden neurons in some way. This mapping is based on modifying the weights of the connections to receive a result closer to the output. To determine the value of the output applying the activation function to a weighted sum of incoming values is needed as well. The most widely used activation functions are: the logistic function and the hyperbolic tangent (used in our study) [6].

In the first step, the system takes the values of neurons in the input layer and sums them up by the assigned weights. In this first iteration, all weights are randomized. Then, for each iteration an error is calculated, which is a difference between the achieved value and the output value. This divergence between estimated and expected value is called a loss function. Calculated loss information is propagated backward then from the output layer to all the neurons in the hidden layer that contribute directly to the output.

The learning process, where the total loss should be minimized, uses the propagated information for the adjustment of the weights of connections between neurons. The search of minimum of the loss function was performed in this study by the gradient descent method. This technique calculates the derivative of the loss function to find direction of descending toward the global minimum [8]. In practice, this calculation begins from defining the initial parameter's values of loss function and uses calculus to iteratively adjust the values to minimize the given function. There are more advanced learning techniques (based on gradient descent method) used to train neural network models such as scaled conjugate gradient, one-step secant, gradient descent with adaptive learning rate and gradient descent with momentum [9].

In this study, we are focused on predicting the closing price of a stock tomorrow $\left\{ {close_{t + 1} } \right\}$ which is the output layer using the input layer consisting prices measured a day before $\left\{ {low_{t} , high_{t} , open_{t} , close_{t} } \right\}$. The structure of this ANN is presented in Fig. 6.

The performances of the resulting neural network are measured on the test set according to following metrics:

root mean square error (RMSE):

$$RMSE = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {\hat{y}_{i} - y_{i} } \right)}}{N}}$$

mean absolute error (MAE):

$$MAE = \frac{{\mathop \sum \nolimits_{i = 1}^{N} \left| {\hat{y}_{i} - y_{i} } \right|}}{N}$$

where $N$ denotes the number of observations, $\hat{y}$ is the model prediction value and $y_{i}$ is the observed value.

5 Results

In this section, the fractional differentiation method will be applied on stock indexes described in previous part. For every stock index, we are going to compute the minimum coefficient $d$ to get stationary fractionally differentiated series.

To find the minimum coefficient $d$, the combination of the augmented Dickey–Fuller test statistics and Pearson correlation coefficient was used. This concept is illustrated in Fig. 7, 8, 9, 10 and Table 333 (in Appendix). The ADF statistic is on the left y-axis, with the correlation between the original series and the fractionally differenced series on the right y-axis.

Fig. 7

ADF test statistics and Pearson correlation coefficients with the original series for various fractional orders of differencing, applied to WIG20 index

Fig. 8

ADF test statistics and Pearson correlation coefficients with the original series for various fractional orders of differencing, applied to S&P 500 index

Fig. 9

ADF test statistics and Pearson correlation coefficients with the original series for various fractional orders of differencing, applied to DAX index

Fig. 10

ADF test statistics and Pearson correlation coefficients with the original series for various fractional orders of differencing, applied to Nikkei 225 index

The original series of WIG20 index has the ADF statistics of −2.22, while the differentiated equivalent has this statistic equal to −36.02. At a 95% confidence level, the critical value of the DF t-distribution is -2.8623. This value is presented as a dotted line in Fig. 7. The ADF statistic crosses this threshold in the area close to $d = 0.1$. At this point, the correlation has the high value of 0.9975. This proves that fractionally differenced series is not only stationary but holds considerable memory of the original series as well.

Similarly, the ADF statistic S&P 500 index reaches 95% critical value when the differencing is approximately 0.4 (for DAX series $d \approx 0.3$ and Nikkei 225 $d \approx 0.4$) and the correlation between the original series and the new fractionally differenced series is over 99% (the same for DAX and Nikkei 225).

Figures 11, 12, 13, 14 contain original series with results of implementing the minimum coefficient $d$ indicated above. The high correlation indicates that the fractionally differenced time series retains meaningful memory of the original series.

Fig. 11

WIG20 index (in black, left axis) along with fractional derivatives (shades of gray, right axis)

Fig. 12

S&P 500 index (in black, left axis) along with fractional derivatives (shades of gray, right axis)

Fig. 13

DAX index (in black, left axis) along with fractional derivatives (shades of gray, right axis)

Fig. 14

Nikkei 225 index (in black, left axis) along with fractional derivatives (shades of gray, right axis)

The above-obtained time series are going to be implemented in creating multiplayer perceptrons for proposed stock indexes. To begin with, the data for all stock indexes have been normalized using the following equation:

$$price_{norm} = \frac{{price - {\text{min}}\left( {price} \right)}}{{\max \left( {price} \right) - {\text{min}}\left( {price} \right)}}$$

and divided into training and testing datasets. The first 1681 days are used for training, and the last 813 used for testing process.

Feedforward neural networks were created using Keras, open-source neural network library in Python. Every network was inputted with the low, high, opening and closing price for each day $t$. The result layer consists of closing price on next day $t + 1$:

$$\left[ {\begin{array}{*{20}c} {low_{t} } \\ {high_{t} } \\ {open_{t} } \\ {close_{t} } \\ \end{array} } \right] \to \left[ {close_{t + 1} } \right]$$

It means that artificial neural network predicts the closing price of the next days using historical data from the day before.

As it is observed in Table 2, the analysis shows that for all stock indexes fractional differentiation gives better RMSE and MAE statistics obtained on test data.

Table 2 Results of ANN on test datasets

The purpose of this research is not to evaluate the predictive performance of artificial neural networks, but rather to evaluate how much better a fractional differentiation is, compared to full differentiation.

6 Conclusions

In this study, the concept of fractional differentiation was evaluated on four time series datasets obtained from the known stock exchanges (from Poland, UK, Germany and Japan). In these fractionally differenced time series, selected orders of differencing vary from 0.12 to 0.43, which is far from integer differencing. For all of them, we have received a high level of linear correlation coefficients (above 0.99%), which means immense association with original series. Nonetheless, these fractional time series are stationary (indicated by the results of augmented Dickey–Fuller test), which proves that their means, variances and covariances are time-invariant.

Using fractional differentiation, we have made analyzed time series stationary while keeping its memory and predictive power. Therefore, this study has clearly demonstrated the potential of applying fractional differentiation on time series.

The previously discussed results clearly show the benefit of fractional differentiation compared to classical differentiation in terms of applied performance measurements on created artificial neural networks. Consequently, fractional differentiation used in preliminary data analysis has broad applications prospects in machine learning area, which was confirmed by predictive performance metrics.

Appendix

See Table

Table 3 ADF test statistics and Pearson correlation coefficients with the original series for various fractional orders of differencing, applied to selected stock indexes

3.

1.1 Tests

We assume that a time series is generated by an AR(1) process:

$$y_{t} = \alpha y_{t - 1} + \varepsilon_{t}$$

where $\varepsilon_{t}$ is a stationary disturbance term. If $\alpha = 1$, then the analyzed process is non-stationary. The Dickey–Fuller test takes the following model:

$$\Delta y_{t} = \delta y_{t - 1} + \varepsilon_{t}$$

where $\delta = \alpha - 1$ and verifies a null hypothesis that $\delta = 0$, which means that $y_{t}$ is generated by AR(1). Alternative hypothesis assumes that the time series is stationary and $\delta < 0$. The estimation of $\hat{\delta }$ is calculated then using OLS regression and divided by its standard error in computing the testing statistic. The test is a one-sided left tail test. Augmented Dickey–Fuller (ADF) test adds $p > 0$ lags of the dependent variable $\Delta y_{t}$ to make model dynamically complete.

In KPSS test, the following model is analyzed:

$$y_{t} = \beta t + r_{t} + \phi y_{t - 1} + \varepsilon_{t}$$

$$r_{t} = r_{t - 1} + u_{t}$$

where $t = 1,2, \ldots , T$ is a deterministic trend, $r_{t}$ = random walk process, $\varepsilon_{t}$ are iid $\left( {0, \sigma_{\varepsilon }^{2} } \right)$ and $\sigma_{\varepsilon }^{2} = 1$, $u_{t}$ are $\left( {0, \sigma_{u}^{2} } \right)$ and $\left| \phi \right| < 1$. If $\sigma_{u}^{2} = 0$ and the initial value of $r_{0}$ is fixed, then $y_{t}$ is a trend stationary process. If $\beta = 0$, the process is stationary around its mean ($r_{0}$) rather than around a trend. For $\sigma_{u}^{2}$ the process is non-stationary.