Introduction

Plasma spraying involves dozens of factors, which may influence the final coating quality (Ref 1). These influencing factors include, among others, the plasma torch geometry and its operating parameters, carrier gas flow rate, injection direction and velocity, particle size distribution and particle morphology, stand-off distance, temperature, velocity and turbulence profile of the plasma flow, etc. (Ref 2). With regard to the numerous influencing factors, plasma spraying process involves many sources of uncertainty or non-deterministic and random elements (Ref 3). For example, while the temperature and velocity fields are the governing plasma jet properties for particle heating and acceleration (Ref 4), individual particles will follow different trajectories and heating histories due to the effect of random turbulent fluctuations (Ref 5).

Considering the complex interactions between the various influencing parameters and the harsh spraying conditions, i.e., extremely high temperatures and velocities, the optimization of the spraying parameters using a purely empirical approach is a time-consuming and rather impractical undertaking. Numerical analysis to investigate the particle behavior in plasma jet can help understand the complex interdependencies of the plasma spraying process. Hence, particle motion in plasma jet has been intensively researched in the literature by modeling the momentum, heat, and mass transfer to injected powder particles using computational fluid dynamics (CFD) (Ref 2, 6). However, the more sophisticated CFD models have the drawback of requiring a lot of computation time, even though these techniques allow to describe very complex systems, specifically the multi-arc plasma spraying process (Ref 7). A promising approach for a fast replication of the CFD simulations in plasma spraying is to combine the simulation models of the process with Machine Learning (ML) algorithms. There are only few studies in the literature using simulation data for training ML models in Thermal Spraying, mostly aimed at providing the user with optimal process parameters (Ref 8). In a previous work (Ref 9), we developed fast and precise metamodels to predict the average particle properties near the substrate by employing two individual ML methods, namely Support Vector Machine (SVM) and Residual Neural Network (ResNet), trained with CFD simulations of the plasma jet. The results showed that the developed metamodels could predict average particle properties much more accurately than the properties of individual particles. This phenomenon is to be expected because plasma spraying is a stochastic process with many influencing factors. Therefore, individual particle behavior is substantially more random than average particle behavior.

The objective of the current work is to develop an ML approach to predict the behavior of the individual particles and replicate the simulated particle trajectories in the plasma jet. The behavior of an individual particle in this study is described by its temperatures, velocities and coordinates during flight, which are considered as the predictions of the models. The developed ML approach contains the supervised training of two consecutive ResNets, in a way that the differences between the target values and the predictions of the first ResNet for particle temperatures, velocities and coordinates are used as additional inputs for the second one. These differences are stored in a database. Hence, when a new test case with new process parameters is to be computed, the additional input values for the second ResNet can be set up by searching the database for the best-fitting values with respect to process parameters and particle sizes. To quantify the prediction accuracy of the model, we define novel metrics based on the mean absolute percentage error and the coefficient of determination (R-squared).

In the following sections, first the preparation of the simulation data as well as the architecture of the ML approach are explained in detail. Subsequently, we qualitatively and quantitatively investigate three different test cases and comment on the efficiency of our new approach in relation to the CFD simulations.

Numerical Modeling

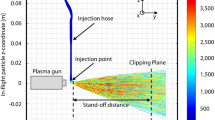
At the Surface Engineering Institute (IOT) at RWTH Aachen University, a numerical model for the simulation of the plasma spraying process was developed in previous studies (Ref 10, 11). The model, implemented using ANSYS CFX version 20.2 (ANSYS, Inc., Canonsburg, USA), is divided into two sub-models, one for the plasma generator and one for the plasma jet. First, the flow in the plasma generator is simulated. The resulting temperature, velocity, turbulent kinetic energy and turbulent dissipation rate profiles at the plasma generator outlet are then used as boundary conditions at the plasma jet inlet to couple both sub-models. In the plasma jet, the plasma-particle interaction has to be accurately reflected. For this purpose, the effects of the plasma on the particles and vice versa are taken into account in a two-way coupled manner in the plasma jet model (Ref 2). The models were validated by experiments extensively (Ref 12). Figure 1 shows the simulated particle trajectories with their temperatures inside the plasma jet exemplarily for one simulation. Please note the coordinate system, which in the following is used to determine the particle positions \({x}_{p}\), \({y}_{p}\), \({z}_{p}\) in the plasma jet.

Fig. 1
figure 1

Exemplary illustration of the plasma jet simulation

Full size image

Process parameters, which are used as input values for the simulations, are primary gas flow \({Q}_{Ar}\) (Ar for argon), electric current \(I\), carrier gas flow \({Q}_{cg}\), particle feed rate \({\dot{m}}_{p}\), and distribution of the particle size \({D}_{p}\). The input parameters for the simulations are set up using design of experiment (DOE) methods (Ref 13), in particular Latin Hypercube Sampling (LHS) (Ref 14) or Central Composite Design (CCD) (Ref 15). More information on the data preparation for the simulations can be found in (Ref 9).

The objective of this work is to develop a new sub-model of the plasma jet with a machine learning approach capable of predicting the particle temperatures \({T}_{p}\) and velocities \({v}_{p}\) as well as the particle coordinates \({x}_{p}\) and \({z}_{p}\) for a given position \({y}_{p}\) in the spray direction. This approach involves two consecutively trained neural networks. The data preparation for the neural networks is described in the following section.

Data Preparation for Neural Networks

For the training of neural networks, we use data from 40 simulations initially set up by CCD. The process parameters for these simulations are listed in Table 1. In each simulation, 2,000 particles are injected into the plasma jet, and a particular stand-off distance of the substrate (\({y}_{p}\)) is prescribed. Only the particles which reach the substrate are considered in the final simulation data.

Table 1 Process parameter inputs for training the neural networks from 40 simulations
Full size table

To keep the data manageable for the purpose of machine learning, we fix 16 equidistantly placed positions \({y}_{p}\in \left[0.12, 0.27\right]\mathrm{ m}\) along the jet, cf. Figure 1, and extract all particle data closest to these positions. With 40 simulations, up to 2,000 particle trajectories per simulation and 16 positions for each particle trajectory, we end up with approximately 1.28 million data points for the neural network training. For testing the trained neural networks, we use the data of three further simulations, which are not involved in the training. The process parameters of these test cases are given in Table 2. The same approach as described above is used for the data extraction at 16 \({y}_{p}\)-positions such that we have up to 32,000 data points per test case.

Table 2 Process parameter inputs for testing the neural networks
Full size table

Machine Learning Approach with Two Residual Neural Networks

In (Ref 9), we presented two ML approaches for the prediction of particle properties in plasma spraying on a substrate, namely an SVM and a ResNet. The inputs to these ML methods were the same process parameters as described above, i.e., primary gas flow \({Q}_{Ar}\), electric current \(I\), carrier gas flow \({Q}_{cg}\), particle feed rate \({\dot{m}}_{p}\), and distribution of the particle size \({D}_{p}\). The objective was to predict the particle properties on the substrate at a given stand-off distance. Hence, the stand-off distance was the sixth input. In plasma spraying, individual particles collide substantially with the injector wall, thus there is a random initial distribution of the particles. The collisions of the particles with the injector wall cause the final particle properties to be very sensitive to the initial position, i.e., small differences in the initial position can have a large influence on the final particle positions, velocities, and temperatures on the substrate. Hence, it is possible that two particles of nearly the same size and for the same process parameters exhibit different temperatures or velocities. As a consequence, with the two approaches in (Ref 9) it is only possible to predict the average particle behavior.

In this work, we extend the ResNet approach to a method containing two individual, consecutively trained ResNets with the aim of predicting the behavior of individual particles. The ResNets we use are fully connected without skip connections. Their forward propagation formula is given by

$${x}^{(l)}=\left\{\begin{array}{c}{x}^{\left(l-1\right)}+\sigma \left({W}^{{(l)}^{T}}{x}^{(l-1)}+{b}^{(l)}\right), l=2,\dots ,L-1,\\ \sigma \left({W}^{{(l)}^{T}}{x}^{(l-1)}+{b}^{(l)}\right), l=\{1,L\}.\end{array}\right.$$
(1)

In this formula, \({x}^{(l)}\) denotes the output of layer \(l\) of the ResNet, \(\sigma\) is the activation function, \({W}^{(l)}\) and \({b}^{\left(l\right)}\) are the weights and biases of layer \(l\), respectively, and the \(L\)th layer is the output layer (i.e., the network has \(L-1\) hidden layers). The only difference compared with a classical artificial neural network is the addition of the output \({x}^{(l-1)}\) of the respective previous layer \(l-1\) to the output of layer \(l\). This is done to improve the training of deep networks (Ref 16). More information on our ResNets, in particular regarding the backpropagation formula, can be found in (Ref 9). The structure of the two ResNets of our new approach is illustrated in Fig. 2. The last four inputs and their corresponding connections that are colored red only appear in the second ResNet, i.e., the first ResNet has the first six inputs and the second one has all the ten inputs. As shown in the illustration, we use ten hidden layers with six neurons each. This choice is discussed in Sect. “ResNet Setup”.

Fig. 2
figure 2

Structure of the two ResNets (inputs and connections in red only appear in the second ResNet) and their forward propagation procedure with comparison to a classical artificial neural network

Full size image

The whole procedure of training and testing the two ResNets of our new approach is illustrated in Fig. 3. First, we replace the sixth input quantity (stand-off distance of the substrate) used in (Ref 9) by the y-coordinate of the particles in the plasma jet \({y}_{p}\). This allows for predicting the particle properties in the whole plasma jet instead of only on the substrate. The four outputs of the ResNet are the same as in (Ref 9): particle temperature \({T}_{p}\), particle velocity \({v}_{p}\) and particle coordinates \({x}_{p}\) and \({z}_{p}\). The ResNets are trained with data from 40 simulations as described in Sect. “Data Preparation for Neural Networks” and summarized in Table 1.

Fig. 3
figure 3

Illustration of the training and testing procedure for the machine learning approach with two ResNets

Full size image

The training of the first ResNet with six inputs and four outputs results in a neural network which is capable of predicting the average particle behavior as explained above. Hence, the difference between the target values (i.e., the simulation data) and the ResNet outputs for the training data regarding particle temperatures, velocities and coordinates for an individual particle can be significant. These differences are stored in a database for each particle and for each of the four output quantities together with the corresponding process parameters. In the following, we denote these differences by

$${d}_{{T}_{p},i}={\left({t}_{i}-{p}_{i}\right)}_{{T}_{p}}, \; {d}_{{v}_{p},i}={\left({t}_{i}-{p}_{i}\right)}_{{v}_{p}}, \; {d}_{{x}_{p},i}={\left({t}_{i}-{p}_{i}\right)}_{{x}_{p}}, \; {d}_{{z}_{p},i}={\left({t}_{i}-{p}_{i}\right)}_{{z}_{p}},$$
(2)

where \({t}_{i}\) and \({p}_{i}\) are the target and prediction, respectively, of data point \(i\). The four differences describe the absolute deviation of the properties of a particle \(i\) of size \({D}_{p,i}\) at position \({y}_{p,i}\) for a fixed process (regarding \({Q}_{Ar}\), \(I\), \({Q}_{cg}\), and \({\dot{m}}_{p}\)) from the predicted average behavior of that particle.

With the information from the database, we set up a second ResNet with ten input quantities, see Fig. 2 and 3. The first six quantities are the same as the ones of the first ResNet, and the last four quantities are the differences \({d}_{{T}_{p}}\), \({d}_{{v}_{p}}\), \({d}_{{x}_{p}}\), and \({d}_{{z}_{p}}\). The second ResNet is then trained with the same training data as the first ResNet, complemented by the differences stored in the database. This leads to predictions of the second ResNet replicating the training data with a high accuracy.

The main results of the procedure explained above are the trained second ResNet and the differences stored in the database. The latter can be thought of as a substitute for the missing information regarding the random collisions of the particles with the injector wall and consequently the random initial particle distribution, which allows to predict the behavior of individual particles. The second ResNet can be used for a new process, which has not been included in the training, in the following manner: Imagine one wants to predict the particle properties for the process parameters \({Q}_{Ar}=46\) SLPM, \(I=499\) A, \({Q}_{cg}= 6\) SLPM, \({\dot{m}}_{p}=16\) g/min and \({D}_{p}\in [55, 75]\) \(\upmu\)m, which is our test case 1, see Table 2. This case is close to simulation 16 in Table 1 but differs in the particle feed rate \({\dot{m}}_{p}\), which for simulation 16 is \({\dot{m}}_{p}=24\) g/min. However, we use the differences regarding simulation 16 stored in the database to set up the inputs 7 to 10 of the second ResNet for the test case. For each particle of the test case, the input values for the four additional input quantities are determined by searching the database for the particle \((i)\) which is close to the current particle of the test case regarding its \({y}_{p}\)-position with a small tolerance and \((ii)\) whose size \({D}_{p}\) is closest to the size of the current particle. The differences stored in the database for the found particle are then used as the four additional input values. For each particle, they can be understood as the expected deviations regarding \({T}_{p}\), \({v}_{p}\), \({x}_{p}\), and \({z}_{p}\) of that particle from the average behavior. Of course, this can only be an approximation since the process parameters are similar but not exactly the same (\({\dot{m}}_{p}=16\) g/min instead of \({\dot{m}}_{p}=24\) g/min, see above). To summarize, setting up the input values for the difference inputs 7 to 10 from the database is a two-fold process: first, the best-fitting simulation regarding the process parameters has to be found. Second, from the found simulation the best-fitting particles regarding the position \({y}_{p}\) and the particle size \({D}_{p}\) have to be found. Obviously, building up a large database covering a wide range of process parameters is crucial for a good prediction accuracy of the second ResNet regarding the individual particle behavior. Of course, the first ResNet for predicting the average particle behavior can also be used for the test cases. This is only done for comparison with the second ResNet in the following, indicated by the dashed arrows in Fig. 3.

ResNet Setup

For the training of the two ResNets, we have to fix some hyperparameters. As mentioned above and shown in Fig. 2, the ResNets have ten hidden layers (i.e., \(L=11\)), and each layer has six neurons. This choice has turned out to provide ResNets within a moderate training time being deep and wide enough to accurately predict the average (first ResNet) and the individual particle behavior (second ResNet). The learning rate for the backpropagation is 0.005, and for the activation function \(\sigma\) we use the hyperbolic tangent. For the initialization of the weights and biases of the ResNets, the Glorot initialization (Ref 17) is applied. All input and target data are standardized by the z-score method, and the values of the mean and standard deviation used for standardization are stored in a file. When later applying the trained ResNet to a new data set, the values are loaded from that file to guarantee a consistent scaling of the new data set.

As explained in Sect. “Data Preparation for Neural Networks”, we use the data from 43 simulations and, consequently, we have 43 different data sets. Hence, a classical splitting into a training and a test data set, as usually done for the training of a neural network, is not necessary in our setting. We use the data of 40 simulations for training the ResNets, see Table 1, and the data of the other three simulations for testing the ResNets, see Table 2. The training is conducted with full batching such that all input data are forward propagated at once in each training iteration. The training of the first and the second ResNet is done for 1,000 and 3,000 iterations, respectively. Since the first ResNet is only capable of predicting the average particle behavior, the training converges quickly. In contrast, the second ResNet is trained to predict individual particle behavior with a high accuracy, requiring a significantly larger number of iterations. Please note that a full hyperparameter study varying the numbers of hidden layers and neurons per layer, the learning rate and the activation function or techniques such as hyperparameter tuning might slightly improve the results of the ResNets. However, with the setup described above, predictions with high accuracy are obtained as demonstrated in Sect. “Results and Discussion”.

Accuracy Metrics

Typical accuracy metrics used to evaluate the quality of the predictions of a neural network for regression problems are the mean absolute percentage error (MAPE)

$${e}_{\mathrm{MAPE}}=\frac{1}{N}\sum_{i=1}^{N}\left|\frac{{t}_{i}-{p}_{i}}{{t}_{i}}\right|,$$
(3)

where \({t}_{i}\) and \({p}_{i}\) again are the targets and predictions, respectively, for the ith of the overall \(N\) data points, and the coefficient of determination (also called R-squared)

$${R}_{\mathrm{sq}}=1-\frac{{\sum }_{i=1}^{N}{\left({t}_{i}-{p}_{i}\right)}^{2}}{{\sum }_{i=1}^{N}{\left({t}_{i}-\overline{t }\right)}^{2}},$$
(4)

where \(\overline{t }\) is the mean of all target values. The MAPE sums up the absolute values of the relative errors of the predictions and should be close to zero. In contrast, the R-squared value for a perfect prediction is one, whereas a model always predicting the mean value leads to an R-squared value of zero. If the predictions are worse than predicting the mean value, R-squared becomes negative.

We want to investigate the quality of our new ML approach with two ResNets based on the above metrics. Both formulas rely on the comparison of predictions and targets per data point. However, our objective is to predict the whole plasma jet, which not only involves the particle properties (temperature \({T}_{p}\) and velocity \({v}_{p}\)) but also their position in the jet, i.e., their coordinates \({x}_{p}\) and \({z}_{p}\). Hence, an accurate prediction of the properties and the position at the same time is crucial, whereas the data-point-wise correlation is not important. In other words, a good prediction for a particular target particle has to have temperature and velocity values being similar to the values of the target particle and to be close to the target particle regarding the coordinates. Hence, we introduce position-dependent (PD) alternatives for \({e}_{\mathrm{MAPE}}\) and \({R}_{\mathrm{sq}}\) and call them \({e}_{\mathrm{MAPE},\mathrm{PD}}\) and \({R}_{\mathrm{sq},\mathrm{PD}}\). Since we cannot expect a perfect prediction of the coordinates \({x}_{p}\) and \({z}_{p}\) based on which the position-dependent metrics for \({T}_{p}\) and \({v}_{p}\) have to be calculated, the new metrics include a tolerance regarding the predicted coordinates. The algorithm for the computation of the new metrics is given below in Algorithm 1. The setting for an exemplary target particle is schematically illustrated in Fig. 4.

Fig. 4
figure 4

Schematic illustration of the setting for computing the position-dependent accuracy metrics according to Algorithm 1

Full size image
figure a

Please note that the algorithm is given for computing the metrics with respect to the particle temperature \({T}_{p}\). The procedure for the particle velocity \({v}_{p}\) is analogous.

The algorithm proceeds as described in the following. For each data point \(i\) of the test data set (line 3), a target coordinate vector \({\overrightarrow{t}}_{\mathrm{coord},i}\) is set up (line 4) containing the target coordinates \({t}_{{x}_{p},i}\) and \({t}_{{z}_{p},i}\) and the input coordinate \({u}_{{y}_{p},i}\). Then, within a radius \(r\) defined by the user (line 1) around \({\overrightarrow{t}}_{\mathrm{coord},i}\), the best prediction for the current target \(i\) is searched for (lines 5–17). This requires an inner for-loop, which for the ease of representation here again iterates over all test data points. If the test data points are sorted according to their \({y}_{p}\)-position, in a more efficient version, the second for-loop can be restricted to a small fraction of the test data points dependent on the current input value \({u}_{{y}_{p},i}\) of the target \(i\). For each prediction \(j\) of the inner loop, the coordinate vector \({\overrightarrow{p}}_{\mathrm{coord},j}\) is set up (line 8) containing the predicted coordinates \({p}_{{x}_{p},j}\) and \({p}_{{z}_{p},j}\) and the input coordinate \({u}_{{y}_{p},j}\). If the Euclidean distance \({d}_{i,j}\) between target and predicted coordinate vector computed in line 9 is smaller than the prescribed radius \(r\) (line 10), the absolute temperature difference \({d}_{{T}_{p},i,j}\) between target \(i\) and prediction \(j\) is computed (line 11). If this difference is smaller than any temperature difference previously determined for the current target \(i\) (line 12), the minimum temperature difference \({d}_{{T}_{p},\mathrm{min}}\) is updated (line 13) and the index of the current prediction \(j\) is stored in \({j}_{\mathrm{best}}\) (line 14). If no prediction is found within the given radius \(r\), i.e., all predictions are too far away from the current target regarding their position, \({j}_{\mathrm{best}}\) still contains its initial value zero. Note that this assumes the point indexing starting at one and not at zero, which depends on the used programming language. If a prediction was found within the radius \(r\) (line 18), the position-dependent MAPE \({e}_{\mathrm{MAPE},\mathrm{PD}}\) and the numerator \({R}_{\mathrm{sq},\mathrm{PD},1}\) and denominator \({R}_{\mathrm{sq},\mathrm{PD},2}\) needed for the position-dependent R-squared \({R}_{\mathrm{sq},\mathrm{PD}}\) are updated (lines 19–21). In addition, the counter \(c\) is incremented (line 22). The final values for \({e}_{\mathrm{MAPE},\mathrm{PD}}\) and \({R}_{\mathrm{sq},\mathrm{PD}}\) are computed in lines 25–26. The number of targets for which no prediction of \({T}_{p}\) lies within radius \(r\) is stored in \({N}_{\mathrm{out}}\) in line 27.

For an exemplary target \(i\) with coordinate vector \({\overrightarrow{t}}_{\mathrm{coord},i}\), the setting is illustrated in Fig. 4. Several predictions lie within the circle with radius \(r\) around that target. One of them is prediction \(j\) with coordinate vector \({\overrightarrow{p}}_{\mathrm{coord},j}\) and distance \({d}_{i,j}\) to target \(i\). The colors of the particles represent the magnitude of the values of the considered property (temperature \({T}_{p}\) or velocity \({v}_{p}\)), where blue represents a low value and red a large value. Obviously, the best prediction for target \(i\) with respect to the considered property and within the radius \(r\) is the one marked as prediction \({j}_{best}\) because both target \(i\) and prediction \({j}_{best}\) are yellow.

The position-dependent accuracy metrics defined above can be interpreted as measuring how accurate the particle properties \({T}_{p}\) and \({v}_{p}\) can be predicted dependent on the accuracy of the prediction of the particle coordinates \({x}_{p}\) and \({z}_{p}\). An increasing radius \(r\) leads to an increasing accuracy for \({T}_{p}\) and \({v}_{p}\), a decreasing accuracy for \({x}_{p}\) and \({z}_{p}\) and a smaller number of targets \({N}_{\mathrm{out}}\) for which no prediction is close enough. Therefore, in this study we investigate the effect of the pre-defined radius on the accuracy metrics by considering two different radii, namely \(r=0.5 \mathrm{mm}\) and \(r=0.8 \mathrm{mm}\), and compare the results, see Sect. “Results for the Three Test Cases”.

Results and Discussion

In the following, we first present the results of the training of the first and the second ResNet. Subsequently, the second ResNet is tested for three different test cases not included in the training. This is done qualitatively as well as quantitatively and in comparison with results of the first ResNet. In addition, computation times of the ResNets are compared with those of the CFD simulations.

Training Results

The loss function we use for the training of the ResNets is the mean square error (MSE)

$${e}_{\mathrm{MSE}}=\frac{1}{N}\sum_{i=1}^{N}\left[{({t}_{i}-{p}_{i})}_{{T}_{p}}^{2}+{({t}_{i}-{p}_{i})}_{{v}_{p}}^{2}+{({t}_{i}-{p}_{i})}_{{x}_{p}}^{2}+{({t}_{i}-{p}_{i})}_{{z}_{p}}^{2}\right].$$
(5)

The indices denote the quantity for which the individual squared error is computed. The training with 1,000 (first ResNet) and 3,000 iterations (second ResNet) leads to the loss depicted in Fig. 5. Since the first ResNet can only predict the average particle behavior due to the missing information regarding the random initial particle distribution inside the injector, the loss cannot be further reduced.

Fig. 5
figure 5

Training loss \({e}_{\mathrm{MSE}}\) of the two ResNets on a logarithmic scale

Full size image

Figure 6 compares the predictions of the first ResNet with the target values for the particle temperatures \({T}_{p}\) for a part of the approximately 1.28 million training data points, precisely for the first 17 of the 40 simulations used for training. In addition, the mean values for each of the 17 simulations contained in the training data are depicted. The figure is intended to give an impression of the overall particle temperature distribution. The partition into the different simulations is clearly visible. It is evident that the behavior of individual particles cannot be predicted accurately by the first ResNet. For instance, for the first simulation (particles 1–32,000) the target temperatures (red) are between approximately 300 and 3,725 K, while the predictions of the first ResNet (blue) only range from 2,385 to 3,175 K. However, the mean values of the predictions show a good agreement with the mean values of the targets. On the basis of these results, the differences \({d}_{{T}_{p},i}\), \({d}_{{v}_{p},i}\), \({d}_{{x}_{p},i}\), and \({d}_{{z}_{p},i}\) for each data point \(i\) are stored in a database together with the corresponding process parameters according to the 40 different simulations as explained in Sect. “Machine Learning Approach with Two Residual Neural Networks”.

Fig. 6
figure 6

Particle temperatures predicted by the first ResNet for the training data compared with target values

Full size image

The difference data contain individual information for each particle and, hence, comprise all effects which lead to a deviation of a particle from the average behavior, especially induced by the random collisions of the particles with the injector wall. Consequently, using the stored differences as additional inputs for the second ResNet and training the second ResNet with the same training data as the first one, results in an accurate predictability of individual particle behavior, see Fig. 7. This figure again shows the target temperatures of the first 17 simulations (red) and the corresponding predictions (blue). The spread of the predictions of the second ResNet is much wider than the spread of the predictions of the first ResNet in Fig. 6 and much closer to the spread of the target temperatures. The high accuracy of the second ResNet in prediction of individual particle behavior for the training data is due to the exact differences being known from the first ResNet. This is also reflected in the accuracy metrics MAPE and R-squared according to Eq 3 and 4, respectively, which are listed in Table 3 for the training data. While the first ResNet leads to MAPEs between 18 and 20%, the second ResNet reduces these values to about 2%. The R-squared values increase from 0.521 for temperature \({T}_{p}\) and 0.77 for velocity \({v}_{p}\) to nearly one. The quality of the second ResNet when applied to unknown data with a prior search for the best-fitting differences in the database has still to be investigated. This is done in the following section.

Fig. 7
figure 7

Particle temperatures predicted by the second ResNet for the training data compared with target values

Full size image
Table 3 Accuracy for predicting the training data with the first and the second ResNet
Full size table

Results for the Three Test Cases

The ResNet results for the three test cases according to Table 2 are shown in Fig. 8, 9, and 10, on the left for the temperatures \({T}_{p}\) and on the right for the velocities \({v}_{p}\). The plots compare the predictions of the second ResNet with those of the first one and the target values. Note that for the purpose of a clear visualization not all particles are displayed. Furthermore, regarding the predictions, the left half of each plot only shows those of the second ResNet (blue), while the right half only shows those of the first ResNet (green). The particles are sorted with respect to the input particle coordinate \({y}_{p}\), also plotted in Fig. 8, 9, and 10. This explains the steplike behavior of predictions and targets occurring whenever \({y}_{p}\) is significantly increased, which is especially visible in Fig. 10 for test case 3. For all three test cases, the second ResNet predicts a considerably wider range of temperatures and velocities than the first ResNet, almost covering the whole spread of the targets. However, the close-up for 150 particles of test case 1 in Fig. 11 reveals that the predictions of individual values of the temperatures or velocities may still be inaccurate when sorted per data point. However, this is not a problem as our objective is to predict the particle properties \({T}_{p}\) and \({v}_{p}\) and the particle coordinates \({x}_{p}\) and \({z}_{p}\) at the same time. Hence, the accurate prediction of \({T}_{p}\) and \({v}_{p}\) dependent on the particle position is crucial, while the correlation with the corresponding data points is not important in terms of the process development, see also the explanation in Sect. “Accuracy Metrics”.

Fig. 8
figure 8

Test case 1: Particle temperatures (left) and velocities (right) predicted by the first and the second ResNet compared with target values

Full size image
Fig. 9
figure 9

Test case 2: Particle temperatures (left) and velocities (right) predicted by the first and the second ResNet compared with target values

Full size image
Fig. 10
figure 10

Test case 3: Particle temperatures (left) and velocities (right) predicted by the first and the second ResNet compared with target values

Full size image
Fig. 11
figure 11

Test case 1: Close-up of the particle temperatures (left) and velocities (right) for 150 particles predicted by the second ResNet compared with target values

Full size image

The whole plasma jets, i.e., the particles for the 16 \({y}_{p}\)-positions, for test cases 1 and 3 are depicted in Fig. 12 and 13, respectively. The plasma jet of test case 2 is similar to that of test case 1. In both figures, the targets are shown on the left-hand side and the predictions of the second ResNet on the right-hand side. Both the temperature \({T}_{p}\) (Fig. 12) and the velocity \({v}_{p}\) (Fig. 13) as well as the coordinates \({x}_{p}\) and \({z}_{p}\) can be well predicted with the second ResNet. The form of the free jets can be explained with the combination of the parameter sets from DOE listed in Table 2. The test cases 1 and 2 have larger particle size distributions than test case 3. Since the larger powder particles possess greater momentum, the carrier gas flow should be lower for larger particle size distributions to obtain an ideally shaped free jet, which is not the case here according to Table 2. This leads to an unconventional arc-shaped free jet for test case 1 and an ideal disk-shaped free jet for test case 3, allowing us to investigate the applicability of our new ML approach to different kinds of free jets.

Fig. 12
figure 12

Test case 1: Targets (left) and predictions of the second ResNet (right) for the particle temperatures in the whole plasma jet consisting of 16 \({y}_{p}\)-positions

Full size image
Fig. 13
figure 13

Test case 3: Targets (left) and predictions of the second ResNet (right) for the particle velocities in the whole plasma jet consisting of 16 \({y}_{p}\)-positions

Full size image

While Fig. 12 and 13 shows the whole free jet, the results of a particular spray distance for the first and second ResNet are also investigated in the following. For this purpose, approximately 2,000 particles at \({y}_{p}=0.22\) m, which corresponds to a stand-off distance of about 130 mm, are considered. Figure 14 shows the target values at that position, where this time we use the velocities \({v}_{p}\) for test case 1 (left-hand side) and the temperatures \({T}_{p}\) for test case 3 (right-hand side). The two black circles in Fig. 14 (left) illustrate the chosen radii \(r\) according to Algorithm 1 used for the computation of the position-dependent accuracy metrics that will be explained below. The predictions of the first ResNet and the second ResNet are presented in Fig. 15 and 16, respectively. We again emphasize that not only \({T}_{p}\) and \({v}_{p}\) are predicted but also the coordinates \({x}_{p}\) and \({z}_{p}\), i.e., in Fig. 14 the particles are plotted according to the target values for the coordinates, whereas in Fig. 15 and 16 they are plotted according to the predicted coordinate values.

Fig. 14
figure 14

Velocity targets of test case 1 (left) and temperature targets of test case 3 (right) at spray distance of \(y\approx 130\) mm

Full size image
Fig. 15
figure 15

Predictions of the 1st ResNet for the particle velocities of test case 1 (left) and for the particle temperatures of test case 3 (right) at spray distance of \(y\approx 130\) mm

Full size image
Fig. 16
figure 16

Predictions of the 2nd ResNet for the particle velocities of test case 1 (left) and for the particle temperatures of test case 3 (right) at spray distance of \(y\approx 130\) mm

Full size image

Since the first ResNet is only able to predict average values, which also concerns the particle coordinates \({x}_{p}\) and \({z}_{p}\), all particles are concentrated to a small region in Fig. 15 for both test cases. These results indicate that a prediction of individual particle behavior is not possible by only using the first ResNet. In contrast, the results of the second ResNet in Fig. 16 are in good agreement with the targets in Fig. 14 for both test cases, demonstrating the capability of the second ResNet to predict individual particle behavior. Of course, the spread of the particles is not exactly the same and there are visible differences in the temperatures and velocities concerning some particles, but the overall prediction of the jet is reasonable.

For a quantitative investigation of the ResNets, we study the position-dependent accuracy metrics introduced in Sect. “Accuracy Metrics”. We present results for two different radii \(r\) to assess the influence of \(r\). Tables 4 and 5 list the results for \(r=0.5 \mathrm{mm}\) and \(r=0.8 \mathrm{mm}\) for all three test cases. As mentioned above, the circles corresponding to these two radii are illustrated in Fig. 14 (left) to give a visual impression of the search radii of a particular target particle. The small circle corresponds to \(r=0.5 \mathrm{mm}\) and the large one to \(r=0.8 \mathrm{mm}\). Within the circles, the most accurate prediction with respect to the target particle is sought. Table 4 lists the fraction \({N}_{\mathrm{out}}/{N}_{\mathrm{test}}\) of the targets for which no prediction of \({T}_{p}\) or \({v}_{p}\) lies within the particular radius \(r\) regarding the particle coordinates, while Table 5 summarizes the position-dependent MAPE \({e}_{\mathrm{MAPE},\mathrm{PD}}\) and the position-dependent R-squared \({R}_{\mathrm{sq},\mathrm{PD}}\). The values \({N}_{\mathrm{out}}/{N}_{\mathrm{test}}\) only depend on the coordinates and not on the different properties, i.e., temperature \({T}_{p}\) and velocity \({v}_{p}\).

Table 4 Percentage of target particles for which no prediction is found within tolerance radius \(r=0.5 \mathrm{mm}\) or \(r=0.8 \mathrm{mm}\) when computing the position-dependent accuracy metrics (tc = test case)
Full size table
Table 5 Position-dependent accuracy metrics with tolerance radius \(r=0.5 \mathrm{mm}\) or \(r=0.8\) mm for predicting the test data with the first and the second ResNet (tc = test case)
Full size table

Directly noticeable in Table 4 are the high values for the numbers of targets for which no prediction can be found within radius \(r\) in case of the first ResNet. Considering Fig. 15, this is not surprising since the predicted particles all lie in a small region only reflecting the average positions. Since the position-dependent accuracy metrics are only calculated with those targets for which a prediction is found within radius \(r\), the meaningfulness of the accuracy results should necessarily be interpreted by considering the \({N}_{\mathrm{out}}/{N}_{\mathrm{test}}\) values. For test case 1 with \(r=0.5 \mathrm{mm}\), there is actually no target with a prediction close enough (\({N}_{\mathrm{out}}/{N}_{\mathrm{test}}\) = 100%) to even compute the position-dependent accuracy metrics. In contrast, for the second ResNet the highest value for \({N}_{\mathrm{out}}/{N}_{\mathrm{test}}\) is 11.9% for test case 1 with \(r=0.5 \mathrm{mm}\). In general, the arc-shaped free jet leads to lower numbers of predictions within the radius than the disk-shaped free jet, because the particles are less concentrated in case of the arc-shaped free jet.

Table 5 shows that, compared with the first ResNet, all values of both accuracy metrics are significantly better for the second ResNet. For the latter, the worst values of the accuracy metrics are only \({e}_{\mathrm{MAPE},\mathrm{PD}}=3.88\mathrm{ \%}\) (test case 1, \(r=0.5 \mathrm{mm}\), \({T}_{p}\)) and \({R}_{\mathrm{sq},\mathrm{PD}}=0.723\) (test case 3, \(r=0.5 \mathrm{mm}\), \({T}_{p}\)), indicating an accurate prediction. Increasing the radius to \(r=0.8 \mathrm{mm}\), i.e., allowing a larger tolerance for the position of the particles, these values are improved to \({e}_{\mathrm{MAPE},\mathrm{PD}}=2.76\mathrm{ \%}\) and \({R}_{\mathrm{sq},\mathrm{PD}}=0.877\). In general, it turns out that the velocity \({v}_{p}\) can be predicted with a higher accuracy than the temperature \({T}_{p}\). For \({v}_{p}\), especially the position-dependent R-squared is always close to one with the worst value being \({R}_{\mathrm{sq},\mathrm{PD}}=0.987\) (test cases 1 and 3, \(r=0.5 \mathrm{mm}\)). This can be explained by the strong correlation of the particle velocity with the particle size distribution and its drag force. As stated in (Ref 18), in general and for a constant drag coefficient, the particle velocity is proportional to the square root of the ratio of the distance traveled, divided by the particle diameter. On the other hand, the influencing factors on the particle temperatures are much more complicated, as radiation, heat transfer, particle vaporization, and other physicochemical mechanisms play a dominant role. Hence, considering the particle size distribution as one of the inputs of the ResNet model, it is expected to have a better prediction accuracy for particle velocities.

Comments on Computational Efficiency

In the following, we comment on the computational efficiency of our new machine learning approach and relate it to the CFD simulations. This allows to assess in which cases the application of the two-ResNet model is beneficial. An extensive study of computation times and speed-ups, however, is out of the scope of this work.

To evaluate the computational efficiency of our new ML approach, we have to split the computation times into two parts: first, the time needed for the training of the two ResNets and second, the time needed for the later application, which only involves using the database and evaluating the second ResNet. Our two-ResNet model is implemented in Matlab and uses multithreading.

The training of the two ResNets has to be done once in the beginning or, as a retraining, whenever the database is to be extended by new simulation data. The training time depends on the number of process parameter sets to be covered by the database and, hence, on the overall number of particles. Usually, it amounts to a few minutes on a cluster using 24 cores running at 2.25 GHz clock speed, where the training of the second ResNet takes longer than the training of the first one since more iterations are required, see Fig. 5.

Applying the second ResNet to a new process first requires a search of the database to set up the values for the four additional inputs. This is done in a few seconds. The evaluation of the second ResNet to compute the predictions then takes less than a second.

Of course, building up a large database covering a wide range of process parameters is crucial for the accuracy of the predictions of the second ResNet. This requires a large number of CFD simulations which take about three hours each on a cluster using 24 cores running at 2.1 GHz clock speed. However, once this is done, the second ResNet provides results within a few seconds. Compared with three hours, this is an enormous speed-up which in most cases will justify the loss of accuracy resulting from using the ML approach.

To summarize, the two-ResNet approach is particularly beneficial if the database covers the test case to be computed adequately, i.e., if a process with process parameters close to the ones of the new test case is available in the database. Otherwise, a CFD simulation should be conducted which then in turn can be used to extend the database for the second ResNet. In the long term, i.e., after a large database has been built up, the second ResNet can replace the CFD simulations, reducing computation times from hours to seconds.

Conclusions and Outlook

The objective of this study was to predict the behavior of individual particles in the plasma jet with two consecutive residual neural networks (ResNets), trained with CFD simulations of a multi-arc plasma spraying system. For this purpose, first the simulation data sets, including the input process parameters in combination with their in-flight particle temperatures, velocities and coordinates, were prepared by a design matrix based on the Central Composite Design (CCD) method. The two aforementioned ResNets were then trained consecutively with the prepared simulation data, in a way that the differences between the targets and predictions of the first ResNet were used as additional inputs for the second one. These differences can be thought of as a substitute for the missing information regarding the random initial particle distribution due to particle collisions with the injector wall, which allows to predict the behavior of individual particles. The differences were stored in a database to be able to set up the additional inputs for the second ResNet if a new test case has to be computed. To quantify the accuracy of the model in terms of replication of the simulated particle trajectories in the plasma jet, position-dependent accuracy metrics for temperatures and velocities were defined. The following conclusions can be drawn from the presented results:

  • The developed ML approach with two consecutive ResNets allows accurate prediction of individual particle properties with respect to the particle positions and, therefore, replication of the simulated particle trajectories in the plasma jet. An accurate data-point-wise prediction cannot be guaranteed.

  • The results of the newly defined position-dependent accuracy metrics for the test cases reveal a significantly better accuracy for the second ResNet compared with the first one.

  • The particle velocities can be predicted with a higher accuracy than the temperatures. This can be explained with the strong correlations of particle velocity with particle size distribution and its drag force.

  • The whole profile of the simulated plasma jets can be replicated with sufficient accuracy, indicating the capability of the developed model to substitute the CFD simulations.

  • With the developed ML approach, the particle trajectories can be replicated dramatically faster than with the computationally expensive CFD simulations.

To guarantee accurate predictions for a wide range of process parameters, building up a large database of differences is desirable. Each extension of the database requires a retraining of the two ResNets. This is a classical transfer learning task and should be done by applying efficient retraining algorithms such as ensemble Kalman filtering (Ref 19, 20).

Future studies may deal with the concept of physics-informed neural networks (PINNs) (Ref 21) to enhance the prediction accuracy of individual particle behavior. This incorporates physical laws into the learning process by adding the residuals of a system of partial differential equations (PDEs), governing the simulations, to the loss function of the applied neural network.