1 Introduction

The description of the high-temperature superconductors based on copper (cuprates) [1,2,3] is the very complicated issue. The main problem is associated with the correct determination of the pairing mechanism responsible for the condensation of the electrons into the Cooper pairs. The literature is dominated by the view that the main role is played by the strong electron correlations modeled by the Emeri Hamiltonian [4], or in the simpler manner in the framework of the Hubbard [5, 6], or t − J [7] theory. On the other hand, many experimental data also indicate the importance of the electron-phonon interactions (EPh). At this point, it is worth to mention the results of the ARPES method, which clearly indicate the existence of the kink in the energy spectrum near the phonon energy [8, 9], the data related to the isotope effect for the critical temperature in the undoped area [10], or the results obtained from the penetration depth measurements [11], and the Raman experiments [12]. The direct observation of the phonons by using the scanning tunneling microscopy [13] is even possible. Hence, it can be supposed that the full pairing mechanism in cuprates consists of the components, which are connected with the strong electron correlations and the interaction of the electrons with the phonons.

The full analysis of the pairing mechanism in cuprates is practically impossible from the mathematical side, which is caused by the need to take into account all the contributions to the self-energy coming from the strong electron correlations. Let us notice that the matter also is not so simple in the case of the electron-phonon interaction, because of the existence of the vertex corrections [14,15,16] (the value of the Fermi energy (ε F ) is low and equal to about 0.1–0.3 eV). Accordingly to the above, the partial solution appears to base the analysis on the effective model, which allows to understand the significant number of the experimental data, and at the same time it is at least approximately solvable using mathematical and computer tools.

The model, which satisfies the above conditions, is based on the Hamilton for two-dimensional (2D) system with the interaction term of the electron-phonon and electron-electron-phonon (EEPh) type [17,18,19]. In particular, two-dimensionality of the system ensures the existence of the van Hove singularity in the electron density of states at the Fermi level, which is responsible for the high values of the critical temperature (T C ), and the low values of the isotope coefficient [20,21,22]. Let us note that the van Hove singularity in cuprates is observed due to the quasi two-dimensional nature of the copper-oxygen planes. For example, the singularity in YBa2Cu4O8 compound is located about 19 meV below ε F at the Y point in the Brillouin zone [23]. The special attention is demanded to be paid on the term of the interaction of the electron-electron-phonon type. It was introduced into the model due to the experimentally observed half-value of the magnetic flux [24]. This result proves that the electron quartets form also in the superconducting state. In the simplest case, the existence of the electron correlations of such type can be reproduced with the help of the EEPh interaction (as a result of the canonical transformation eliminating the phonon degrees of freedom, the EEPh interaction transforms directly into the effective four-fermion interaction [17, 18]). Let us notice that the presented way of concluding is not new and was at first adapted by Rickayzen in the classical BCS theory in the context of the description of the alpha particle, which represents the stable system of four fermions [25]. Nowadays, the four-fermion interaction is also considered in the works [26,27,28], where there is suggested its significant meaning in the description of the high-temperature superconducting state. In relation to the classical electron-phonon interaction taking into account the additional term of the EEPh type causes that it is possible to explain the anomalously high values of the energy gap, the weak dependence of the energy gap on the temperature, and the existence of the Nernst temperature (T ⋆⋆) [17,18,19, 29,30,31,32,33,34,35].

Recently, the EPh and EEPh interactions were analyzed beyond the mean-field approximation in the framework of the Eliashberg formalism [36]. It was shown that for the relevantly large values of the EEPh potential the dependence of the order parameter on the doping has the analogous course like in cuprates (visible is even the characteristic plateau [3]), the electron density of states is asymmetric which also agrees qualitatively with the experimental data [37], and above the critical temperature exists the pseudogap, which turns out to be induced by the many-body and strong-coupling effects.

In the presented paper, we will show that beginning from the Eliashberg equations, presented in [36], one can get the generalized mean-field model. Next, we will derive the analytical formulas for the most important thermodynamic parameters of the superconducting state. In the last step, we will determine the critical temperature—Nernst temperature diagram, and we will compare the results with the experimental data for cuprates.

2 Formalism

The Eliashberg equations possess the form [36]:

$$ Z_{\textbf{k}}\left( i\omega_{n}\right)=1+\left( v_{1}+v_{2}\right)^{2}\frac{1}{\beta}\sum\limits_{\omega_{m}\textbf{q}} \frac{\omega_{m}}{\omega_{n}}P_{\textbf{q}}\left( i\omega_{n}-i\omega_{m}\right)D_{\textbf{k}-\textbf{q}}^{-1}\left( i\omega_{m}\right) Z_{\textbf{k}-\textbf{q}}\left( i\omega_{m}\right), $$
(1)
$$\begin{array}{@{}rcl@{}} \varphi_{\textbf{k}}\!\left( i\omega_{n}\right)&=& \!\left( {v_{1}^{2}}+2v_{1}v_{2}\right)\frac{1}{\beta}\sum\limits_{\omega_{m}\textbf{q}}P_{\textbf{q}}\left( i\omega_{n}-i\omega_{m}\right) D^{-1}_{\textbf{k}-\textbf{q}}\left( i\omega_{m}\right)\varphi_{\textbf{k}-\textbf{q}}\left( i\omega_{m}\right)\\ &+& \!\frac{4{v_{2}^{2}}}{\beta^{3}}\!\sum\limits_{\omega_{m_{1}}\sim\omega_{m_{3}}} \!\frac{1}{N}\!\sum\limits_{\textbf{k}_{1}}\varphi_{\textbf{k}_{1}}\!\left( i\omega_{m_{1}}\right) \!D^{-1}_{\textbf{k}_{1}}\!\left( i\omega_{m_{1}}\right) \!\frac{1}{N}\!\sum\limits_{\textbf{k}_{2}}\varphi_{\textbf{k}_{2}}\!\left( i\omega_{m_{2}}\right) \!D^{-1}_{\textbf{k}_{2}}\!\left( i\omega_{m_{2}}\right)\\ &\times& \!\sum\limits_{\textbf{q}}P_{\textbf{q}}\left( i\omega_{n}\!-i\omega_{m_{1}}\!-i\omega_{m_{2}}\!-i\omega_{m_{3}}\right) \!D^{-1}_{\textbf{k}-\textbf{q}}\left( i\omega_{m_{3}}\right)\varphi_{\textbf{k}-\textbf{q}}\left( i\omega_{m_{3}}\right), \end{array} $$
(2)

where \(Z_{\textbf {k}}\left (i\omega _{n}\right )\) denotes the wave function renormalization factor, and \(\varphi _{\textbf {k}}\left (i\omega _{n}\right )\) is the order parameter function; k and ω n represent respectively the electron momentum and the Matsubara energy: \(\omega _{n}\equiv \left (\pi /\beta \right )\left (2n-1\right )\), where \(\beta \equiv \left (k_{B}T\right )^{-1}\) (k B is the Boltzmann constant); by v 1 and v 2 are given the EPh and EEPh potentials. The phonon propagator (\(P_{\textbf {q}}\left (i\omega _{l}\right )\)) can be simplified according to the formula below:

$$ P_{\textbf{q}}\left( i\omega_{l}\right)\rightarrow 2{\int}_{0}^{\omega_{0}}d{\Omega}\frac{F\left( {\Omega} \right)}{\Omega}\equiv\overline{\lambda}^{2}, $$
(3)

where ω 0 is the maximum phonon frequency, and \(F_{\textbf {q}}\left ({\Omega } \right )\rightarrow F\left ({\Omega } \right )\) denotes the phonon density of states. Finally, \(D_{\textbf {k}}\left (i\omega _{n}\right )\equiv \left (\omega _{n}Z_{\textbf {k}}\left (i\omega _{n}\right )\right )^{2} +\varepsilon ^{2}_{\textbf {k}}+\varphi ^{2}_{\textbf {k}}\left (i\omega _{n}\right )\). We assume the electron band energy for the square lattice with the hopping integral t. In the considered case: \(\varepsilon _{\textbf {k}}=-t\gamma \left (\textbf {k}\right )\), where \(\gamma \left (\textbf {k}\right )\equiv 2\left [\cos \left (k_{x}\right )+\cos \left (k_{y}\right )\right ]\). The Eliashberg equations set is complicated and cannot be solved in the exact analytical manner. For this reason, we simplified its form, so that one can get the formulas for the thermodynamic parameters. In the first step, we assume \(Z_{\textbf {k}}\left (i\omega _{n}\right )=1\). From the physical point of view, this means that the renormalization of the electron band mass by the EPh and the EEPh interaction was omitted. Next approximation is based on the assumption that the order parameter is real, and it is independent of the wave vector and the Matsubara frequency (\(\varphi _{\textbf {k}}\left (i\omega _{n}\right )\rightarrow \varphi \)). In addition, it is convenient to introduce the designations: \(E^{2}_{\textbf {k}}\equiv \varepsilon _{\textbf {k}}^{2}+\varphi ^{2}\), \(v_{1}\overline {\lambda }\equiv v/\sqrt {N}\), and \(2v_{2}\overline {\lambda }\equiv u/\sqrt {N}\). The simple transformations lead us to the equation for the order parameter:

$$ 1=\left[{v}^{2}+vu+u^{2}\varphi^{2} \left( \frac{1}{N}\sum\limits_{\textbf{k}}\frac{\tanh\left( \frac{\beta E_{\textbf{k}}}{2}\right)}{2E_{\textbf{k}}}\right)^{2}\right] \frac{1}{N}\sum\limits_{\textbf{k}}\frac{\tanh\left( \frac{\beta E_{\textbf{k}}}{2}\right)}{2E_{\textbf{k}}}. $$
(4)

For the 2D band relation, the density of states has the form [21, 38,39,40]: \(\rho \left (\varepsilon \right )=b_{1}\ln |\frac {\varepsilon }{b_{2}}|\), where: b 1 = −0.04687 t −1 and b 2 = 21.17796 t. Hence,

$$\begin{array}{@{}rcl@{}} && 1\,=\,\left[{\!v}^{2}\,+\,vu\,+\,u^{2}\varphi^{2} \!\left( \!{\int}^{\omega_{0}}_{-\omega_{0}}d\varepsilon\rho\left( \varepsilon\right)\frac{\tanh\left( \frac{\beta \sqrt{\varepsilon^{2}+\varphi^{2}}}{2}\right)}{2 \sqrt{\varepsilon^{2}+\varphi^{2}}}\!\right)^{\!2}\right]\\ &&\qquad {\int}^{\omega_{0}}_{-\omega_{0}}d\varepsilon\rho\left( \varepsilon\right)\frac{\tanh\left( \frac{\beta \sqrt{\varepsilon^{2}+\varphi^{2}}}{2}\right)}{2 \sqrt{\varepsilon^{2}+\varphi^{2}}}. \end{array} $$
(5)

The expression (5) represents the complicated integral equation that cannot be solved analytically for any temperature. Therefore, the numerical methods were used, whereby the following was taken into account: v = 25 meV 1/2 and selected u. Additionally, it was assumed that the half-width of the electron band is equal to 1 eV, which means that the hopping integral equals 250 meV [41]. In the case of the maximum phonon frequency, it was adopted that ω 0 = 75 meV [42].

The obtained results are plotted in the Fig. 1. It has been found that for the relatively low value of u (Fig. 1a) the superconducting state characterizes with the moderate value of the critical temperature (T C = 3.1 K). Nonetheless, the twofold increase of u causes approximately tenfold increase of the critical temperature: T C = 32.1 K (Fig. 1b). For u = u C = 3.56eV 1/2, the critical temperature increases to 75.7 K (Fig. 1c). It should be further noted that the curve describing the dependence of the order parameter on the temperature clearly differs from the curve predicted by the BCS theory. In particular, the attention is drawn to the weak dependence of the order parameter on the temperature in the range from 0 to about 50 K, followed by the sharp decline of φ. For u > u C , the order parameter totally does not resemble the prediction of the BCS theory (Fig. 1d). The weak influence of the temperature on the order parameter is visible in the range of the temperatures from 0 to T C . Above T C , the values of \(\varphi \left (T\right )\) are declining much faster, while for T = 183.5 K, we observe the first order phase transition instead of the second order phase transition. Note that the change in the nature of the phase transition is induced by the applied approximations—the correct type of the phase transition is predicted on the Eliashberg equations level [36]. Interestingly, the value of the temperature, at which the transition occurs, is well defined and can be properly interpreted physically as will be discussed in the next section. In addition, we note that for T > T C and u > u C , the equation (5) really has two solutions, the so-called upper and lower branch of the order parameter. Wherein only the upper branch (shown in Fig. 1d) minimizes the thermodynamic potential which means that this is the physical solution. The curves presented in the Fig. 1 well reproduce the results contained in the publications [17,18,19], where the thermodynamic properties of the superconducting state, induced by the EPh and the EEPh interactions, were analyzed with the use of the canonical transformation. In order to quantitatively link both models, the equations, by which the order parameter was determined, have to be compared. This issue is discussed in the next section.

Fig. 1
figure 1

The dependence of the order parameter on the temperature for the selected values of u

Full size image

2.1 Presented Approach vs. Canonical Transformation Result

The equation for the order parameter derived in the papers [17,18,19] has the form (in original notation):

$$ 1=V_{tot}{\int}^{\omega_{0}}_{-\omega_{0}} d\varepsilon\rho\left( \varepsilon\right) \frac{\tanh\left( \frac{\beta}{2}E\right)}{2E}, $$
(6)

where: \(E\equiv \sqrt {\varepsilon ^{2}+{\Delta }^{2}_{tot}}\), Δ t o t ≡ V t o t |Δ|, and \(V_{tot}\equiv \overline {V}+\frac {\overline {U}}{6}|{\Delta }|^{2}\). Additionally, \({\Delta }\equiv \frac {1}{N}{\sum }^{\omega _{0}}_{\textbf {k}}\left <c_{-\textbf {k}\downarrow }c_{\textbf {k}-\uparrow }\right >\), where c k σ represents the electron annihilation operator (σ is the spin). It has been shown that the formula (6) represents the simplified form of the (5). For this purpose, the designations have to be introduced: \({\Delta }_{tot}\rightarrow \varphi \), \(\overline {V}\rightarrow v^{2}\), and \(\overline {U}/6\rightarrow u^{2}\). Hence, the (6) can be rewritten in the following manner:

$$ 1=\left[v^{2}+u^{2}|{\Delta}|^{2}\right]I\left( \varphi\right), $$
(7)

where:

$$ I\left( \varphi\right)\equiv{\int}^{\omega_{0}}_{-\omega_{0}}d\varepsilon\rho\left( \varepsilon\right)\frac{\tanh\left( \frac{\beta \sqrt{\varepsilon^{2}+\varphi^{2}}}{2}\right)}{2 \sqrt{\varepsilon^{2}+\varphi^{2}}}. $$
(8)

Let us notice that \(|{\Delta }|=\frac {\varphi }{v^{2}+u^{2}|{\Delta }|^{2}}\). On this basis, the expression (7) was transformed to the form containing the continued fraction:

$$ 1=\left[v^{2}+\left[\frac{u\varphi}{v^{2}+\left[\frac{u\varphi}{v^{2}+\left[...\right]^{2}}\right]^{2}}\right]^{2}\right]I\left( \varphi\right). $$
(9)

On the other hand, the expression (5) gives:

$$ 1=\left( v^{2}+vu+\left( u\varphi\right)^{2}I^{2}\left( \varphi\right)\right)I\left( \varphi\right). $$
(10)

Hence,

$$ I\left( \varphi\right)=\frac{1}{v^{2}+vu+\left( u\varphi\right)^{2}I^{2}\left( \varphi\right)}. $$
(11)

Using the formula (11), we can easily obtain the connection of the integral \(I\left (\varphi \right )\) with the continued fraction:

$$ I\left( \varphi\right)=\frac{1}{v^{2}+vu+\left[\frac{u\varphi}{v^{2}+vu+\left[\frac{u\varphi}{v^{2}+vu+ \left[...\right]^{2}}\right]^{2}}\right]^{2}}. $$
(12)

The last step is to insert (12) into (10), thus obtaining:

$$ 1=\left[v^{2}+vu+\left[\frac{u\varphi}{v^{2}+vu+\left[\frac{u\varphi}{v^{2}+vu+\left[...\right]^{2}}\right]^{2}}\right]^{2}\right] I\left( \varphi\right). $$
(13)

Comparing with each other (13) and (9), it can be seen that the equation determining the thermodynamic properties of the superconducting state from [17,18,19] can be obtained from the expression (5), whereas the product vu has to be omitted. Let us note that the lack of the term vu in the (9) results from the way of conducting the canonical transformation, which eliminates the phonon degrees of freedom. Namely, it was separately applied to the EPh and the EEPh interaction. In addition, note the fact that the exact value of continued fraction present in the (12) is equal to:

$$\begin{array}{@{}rcl@{}} \frac{1}{v\varphi} && \!\!\!\left[\!-\frac{2^{1/3}\left( v^{2}+vu\right)}{\left[27v\varphi+\sqrt{108\left( v^{2}+vu\right)^{3}+729v^{2}\varphi^{2}}\right]^{1/3}}\right. \\ &&\left.\quad \!\!\!+\frac{1}{3}\frac{\left[27v\varphi\,+\,\sqrt{\!108\left( v^{2}+vu\right)^{3}\,+\,729v^{2}\varphi^{2}}\right]^{\!1/3}}{2^{1/3}}\right]\!. \end{array} $$
(14)

The derivation of the formula (14) is simple. It suffices to rewrite the expression (10) in following form: \(\left (u\varphi \right )^{2}I^{3}\left (\varphi \right )+\left (v^{2}+vu\right )I\left (\varphi \right )-1=0\). The resulting equation must then be solved for \(I\left (\varphi \right )\). The result is two complex coupled roots and one real root, which determines the value of continued fraction in question.

The results presented above show that all of the results obtained in [17,18,19] can be easily reproduced by using the (5). To do this, one only needs to properly rescale the previously accepted values of the potentials v and u due to the existence of an additional pairing potential vu. From the physical standpoint, this means that the value of the temperature, wherein there is the phase transition of the first order, should be identified with the Nernst temperature. We underline that the (5) correctly binds together the experimental values of the critical temperature, the Nernst temperature, and the order parameter for T = 0 K. For the selected values of the temperature, and using the (5), one can derive the formulas, which allow to calculate the interesting thermodynamic parameters with the very good accuracy. This issue will be discussed in the following sections.

2.2 The Critical Temperature

The formula for the critical temperature is determined by adopting φ = 0. In the considered case:

$$ 1=\left( {v}^{2}+vu\right) {\int}^{\omega_{0}}_{0}d\varepsilon\rho\left( \varepsilon\right)\frac{\tanh\left( \frac{\beta\varepsilon}{2}\right)}{\varepsilon}. $$
(15)

The integral appearing in the expression (15) can be calculated analytically:

$$\begin{array}{@{}rcl@{}} &&1=b_{1}\left( {v}^{2}+vu\right) \left[\frac{1}{2}\ln^{2}\left( \frac{\omega_{0}}{2k_{B}T_{C}}\right)\right. \\ &&\qquad\qquad\qquad +\left.\ln\left( \frac{2k_{B}T_{C}}{b_{2}}\right) \ln\left( \frac{a\omega_{0}}{k_{B}T_{C}}\right)-1\right], \end{array} $$
(16)

where \(a\equiv \frac {2}{\pi }e^{\gamma }\simeq 1.13\), and γ is the Euler constant (γ ≃ 0.577). The (16) was solved with respect to k B T C :

$$ k_{B}T_{C}\!\,=\,ab_{2}\exp\!\left[\!\!-\sqrt{\ln^{2}\!\left( 2a\right)\,+\,\ln^{2}\left( \!\frac{b_{2}}{\omega_{0}}\!\right)\!\,-\, \frac{2}{\left( v^{2}\,+\,vu\right)b_{1}}\,-\,2}\right]\!. $$
(17)

When analyzing the formula for the critical temperature, it can be easily noticed that the role of the effective pairing potential is played by the expression v 2 + v u. The obtained result indicates that the high value of critical temperature does not have to be associated with the high value of the potential modeling the EPh interaction. In the considered model, the high value of T C can also induce the sufficiently high potential u. Figure 2 presents the course of the critical temperature in the dependence on u for selected v and three representative values of the maximum phonon frequency. The obtained results prove that the model predicts the sufficiently high T C to explain the experimentally observed values of the critical temperature in the cuprates.

Fig. 2
figure 2

The dependence of the critical temperature on u for the selected v and ω 0

Full size image

2.3 Order Parameter for T = 0 K

The second fundamental quantity beyond the critical temperature—describing the thermodynamic properties of the superconducting state, is the order parameter at the temperature of zero Kelvin. In the considered case, the (5) can be written as:

$$ 1=\lim\limits_{n\rightarrow+\infty}f^{\left[2n\right]} {\int}^{\omega_{0}}_{0}d\varepsilon\rho\left( \varepsilon\right)\frac{1}{\sqrt{\varepsilon^{2}+\varphi\left( 0\right)^{2}}}, $$
(18)

where the theorem presented in the Appendix was additionally used. The integral given in the (18) was calculated analytically:

$$\begin{array}{@{}rcl@{}} &&1\,=\,b_{1}\lim_{n\rightarrow+\infty}f^{\left[2n\right]} \!\left[\frac{1}{2}\ln^{2}\!\left( \!\frac{\omega_{0}}{\varphi\left( 0\right)}\!\right)\,+\, \ln\left( \!\frac{\varphi\left( 0\right)}{b_{2}}\!\right) \!\ln\!\left( \!\frac{2\omega_{0}}{\varphi\left( 0\right)}\!\right)\right. \\ &&\qquad\qquad\qquad\qquad\quad \left. - \frac{1}{2}\text{Li}_{2}\left( 1\right)-\frac{1}{2}\ln^{2}\left( \frac{1}{2}\right)\right], \end{array} $$
(19)

while \(\text {Li}_{n}\left (z\right )\) denotes the polylogarithm given by \(\text {Li}_{n}\left (z\right )\equiv {\sum }^{+\infty }_{k=1}z^{k}/k^{n}\) and \(\text {Li}_{2}\left (1\right )=\pi ^{2}/6\). Then, some simple transformations need to be carried out, as the result comes the expression for the order parameter at the temperature of zero Kelvin:

$$ \varphi\!\left( 0\right)\,=\,2\omega_{0}\exp\!\left[\!\,-\,\ln\left( \!\frac{\omega_{0}}{b_{2}}\!\right)\,-\, \sqrt{\ln^{2}\left( \!\frac{\omega_{0}}{b_{2}}\right)\,-\,\frac{2}{b_{1}\lim_{n\rightarrow+\infty}f^{\left[2n\right]}}\!-\frac{\pi^{2}}{6}}\right]\!. $$
(20)

The influence of the EEPh potential on the order parameter at the temperature of zero Kelvin is presented in the Fig. 3a–c. The selected values of v were adopted and the three phonon frequencies were taken into account. The obtained results prove that the high value of the order parameter is mainly due to the high value of u. However, the phonon frequency is also important. Let us note that \(\varphi \left (0\right )\) is most conveniently interpreted in the relation to the energy associated with the critical temperature. For this purpose, the dimensionless ratio is defined: \(R_{\varphi }\equiv 2\varphi \left (0\right )/k_{B}T_{C}\). Figure 3d–f shows the plot of R φ in the dependence on the potential u. It has been found that the ratio R φ can take the values significantly higher than the values predicted by the BCS theory (R φ = 3.53) [43, 44]. This effect is often observed in the cuprates.

Fig. 3
figure 3

a–c The dependence of the order parameter at the temperature of zero Kelvin on u for selected values of v and ω 0. d–f The dependence of the ratio R φ on potential u for selected values of v and ω 0

Full size image

2.4 Temperature Dependence of Order Parameter: u ≤ u C

With respect to the order parameter one should also note the possibility of derivation of the formula near the critical temperature. For this purpose, the (5) was written in the form, which is using the continued fraction (see also Appendix):

$$ 1=\lim_{n\rightarrow+\infty}f^{\left[2n-1\right]} {\int}^{\omega_{0}}_{0}d\varepsilon\rho\left( \varepsilon\right)\frac{\tanh\left( \frac{\beta\sqrt{\varepsilon^{2}+\varphi^{2}}}{2}\right)} {\sqrt{\varepsilon^{2}+\varphi^{2}}}. $$
(21)

For \(T\rightarrow T_{C}\), the order parameter is the quantity of small order, so it can be assumed:

$$\begin{array}{@{}rcl@{}} \frac{\tanh\left( \frac{\beta\sqrt{\varepsilon^{2}+\varphi^{2}}}{2}\right)}{2\sqrt{\varepsilon^{2}+\varphi^{2}}} \!&=& \frac{1}{\beta}\sum\limits^{+\infty}_{m=-\infty}\frac{1}{{\omega^{2}_{m}}+\varepsilon^{2}+\varphi^{2}} \simeq \frac{1}{\beta}\sum\limits^{+\infty}_{m=-\infty}\frac{1}{{\omega^{2}_{m}}+\varepsilon^{2}}\\ &-& \frac{1}{\beta}\sum\limits^{+\infty}_{m=-\infty}\frac{\varphi^{2}}{\left( {\omega^{2}_{m}}+\varepsilon^{2}\right)^{2}}. \end{array} $$
(22)

We insert the expression (22) into the (21) and we use the equation for T C . As a result we get:

$$\begin{array}{@{}rcl@{}} \left[\!1\,-\,\frac{T}{T_{C}}\!\right]\!\left[\!\frac{T}{T_{C}}\,+\,2\ln\!\left( \!\frac{k_{B}T_{C}}{ab_{2}}\!\right)\,-\,1\!\right]\!\!\!&=&\!\! \!\varphi^{2}\!\frac{u^{2}}{\left( v^{2}\,+\,vu\right)^{3}}\!\left[\!\ln^{2}\!\left( \!\frac{k_{B}T}{ab_{2}}\!\right)\,-\,\ln^{2}\!\left( \!\frac{\omega_{0}}{b_{2}}\!\right) \!\,-\,\ln^{2}\!\left( 2a\right)\,+\,2\!\right]\\ &+& \varphi^{2}\frac{4}{\beta}\sum\limits^{+\infty}_{m=-\infty}{\int}^{\omega_{0}}_{0}d\varepsilon\ln\left( \frac{\varepsilon}{b_{2}}\right) \frac{1}{\left( {\omega^{2}_{m}}+\varepsilon^{2}\right)^{2}}, \end{array} $$
(23)

where, it was adopted: \(\lim _{n\rightarrow +\infty }f^{\left [2n-1\right ]}\simeq v^{2}+vu+\left (\frac {u}{v^{2}+vu}\right )^{2}\varphi ^{2}\). Then, the value of the integral was estimated:

$$ {\int}^{\omega_{0}}_{0}\!d\varepsilon\ln\!\left( \!\frac{\varepsilon}{b_{2}}\!\right) \!\frac{1}{\left( {\omega^{2}_{m}}\,+\,\varepsilon^{2}\right)^{2}}\!\simeq\! \frac{\pi}{4}\frac{1}{|\omega_{m}|^{3}}\left[\ln|\omega_{m}|\,-\,\ln|b_{2}|\!\,-\,1\right]. $$
(24)

The simple transformations lead us to the final result:

$$ \varphi\left( T\right)= \left[ \frac {\left[1-\frac{T}{T_{C}}\right]\left[\frac{T}{T_{C}}+2\ln\left( \frac{k_{B}T_{C}}{ab_{2}}\right)-1\right]} {\frac{u^{2}}{\left( v^{2}+vu\right)^{3}}\left[\ln^{2}\left( \frac{k_{B}T}{ab_{2}}\right)-\ln^{2}\left( \frac{\omega_{0}}{b_{2}}\right) -\ln^{2}\left( 2a\right)+2\right]+ \frac{7\zeta\left( 3\right)}{\left( 2\pi k_{B}T\right)^{2}}\left[\ln\left( \frac{\pi k_{B}T}{b_{2}}\right) +\frac{\zeta_{\ln}\left( 3\right)-1}{\zeta\left( 3\right)}\right]} \right]^{1/2}, $$
(25)

where \(\zeta \left (z\right )\) denotes the Riemann zeta function \(\zeta \left (z\right )\equiv {\sum }^{+\infty }_{m=1}\left (\frac {1}{m}\right )^{z}\), and \(\zeta _{\ln }\left (z\right )\equiv \frac {8}{7}{\sum }^{+\infty }_{m=1}\frac {\ln \left (2m-1\right )}{\left (2m-1\right )^{z}}\). Taking into account the results obtained above, the question arises whether one can derive the formula for the dependence of the order parameter on the temperature over the whole range from 0 K to T C . It turns out that the answer is negative. However, such formula was able to be guessed basing on the performed numerical calculations. In the first step, let us note that the dependence of the order parameter on the temperature in the classical BCS theory is well reproduced by [45]:

$$ \varphi\left( T\right)\simeq\varphi\left( 0\right)\sqrt{1-\left( \frac{T}{T_{C}}\right)^{3}}. $$
(26)

In the case of the high-temperature superconductors, the formula (26) should be generalized to:

$$ \varphi\left( T\right)\simeq\varphi\left( 0\right)\sqrt{1-\left( \frac{T}{T_{C}}\right)^{\frac{2\varphi\left( 0\right)}{k_{B}T_{C}}}}. $$
(27)

Figure 4 presents the curves of the order parameter determined numerically in the range of the temperatures from 0 K to T C . It was adopted: v = 25 meV 1/2, ω 0 = 75 meV, and the selected values of u. In addition, the results obtained using the formulas (25) and (27) are also plotted. It can be easily seen that the analytical expressions reproduce the numerical results in the correct way.

Fig. 4
figure 4

a–c The dependence of the order parameter on the temperature for the selected values of u. The orange line represents the numerical results. The blue line was obtained using the formula (25). The circles were obtained from the formula (27)

Full size image

2.5 The Nernst Temperature

The dependence of the order parameter on the temperature for u > u C differs greatly from \(\varphi \left (T\right )\) described by the formula (27). In the considered case, using the (5), it is possible to derive the formula, which allows to calculate the value of the Nernst temperature. For this purpose, it should be noted that for T = T ⋆⋆, the derivative \(\frac {d\varphi \left (T\right )}{dT}\) is undefined. Next, we consider the (5), which was differentiated at the both sides due to the temperature:

$$\begin{array}{@{}rcl@{}} -\!&&\!\!\!\!\!\!\!\left[v^{2}+vu+3u^{2}\varphi^{2}\left( T\right)I^{2}\left( \varphi\left( T\right),T\right)\right]\frac{dI\left( \varphi\left( T\right),T\right)}{dT}\\ &=& 2u^{2}\varphi\left( T\right)I^{3}\left( \varphi\left( T\right),T\right)\frac{d\varphi\left( T\right)}{dT}, \end{array} $$
(28)

where:

$$ I\left( \varphi\left( T\right),T\right)\equiv {\int}^{\omega_{0}}_{-\omega_{0}}d\varepsilon\rho\left( \varepsilon\right)\frac{\tanh\left( \frac{\sqrt{\varepsilon^{2}+ \varphi^{2}\left( T\right)}}{2k_{B}T}\right)}{2 \sqrt{\varepsilon^{2}+\varphi^{2}\left( T\right)}}. $$
(29)

The temperature derivative of the expression (29) is equal to:

$$\begin{array}{@{}rcl@{}} \frac{dI\left( \varphi\left( T\right),T\right)}{dT}&=&\left[\frac{1}{k_{B}T}J_{A}\left( \varphi\left( T\right),T\right) -J_{B}\left( \varphi\left( T\right),T\right)\right] \\ && \varphi\left( T\right)\frac{d\varphi\left( T\right)}{dT}\,-\,\frac{1}{4k_{B}T^{2}} J_{C}\left( \varphi\left( T\right),T\right), \end{array} $$
(30)

wherein:

$$ J_{A}\left( \varphi\left( T\right),T\right)\equiv {\int}^{\omega_{0}}_{-\omega_{0}}d\varepsilon\rho\left( \varepsilon\right)\frac{\text{sech}^{2}\left( \frac{\sqrt{\varepsilon^{2}+ \varphi^{2}\left( T\right)}}{2k_{B}T}\right)}{4\left( \varepsilon^{2}+\varphi^{2}\left( T\right)\right)}, $$
(31)
$$ J_{B}\left( \varphi\left( T\right),T\right)\equiv {\int}^{\omega_{0}}_{-\omega_{0}}d\varepsilon\rho\left( \varepsilon\right)\frac{\tanh\left( \frac{\sqrt{\varepsilon^{2}+ \varphi^{2}\left( T\right)}}{2k_{B}T}\right)}{2 \left( \varepsilon^{2}+\varphi^{2}\left( T\right)\right)^{3/2}}, $$
(32)

and

$$ J_{C}\!\left( {\kern-.5pt}\varphi\!\left( {\kern-.5pt}T{\kern-.5pt}\right){\kern-.5pt},{\kern-.5pt}T{\kern-.5pt}\right)\!\equiv {\int}^{\omega_{0}}_{-\omega_{0}}d\varepsilon\rho\left( \varepsilon\right)\text{sech}^{2}\!\left( \frac{\sqrt{\varepsilon^{2}+ \varphi^{2}\left( T\right)}}{2k_{B}T}\right). $$
(33)

Hence,

$$ \frac{d\varphi\left( T\right)}{dT}\,=\, \frac{\left[v^{2}+vu+3u^{2}\varphi^{2}\left( T\right)I^{2}\left( \varphi\left( T\right),T\right)\right]\frac{1}{4k_{B}T^{2}} J_{C}\left( \varphi\left( T\right),T\right)} {\left\{\left[v^{2}+vu+3u^{2}\varphi^{2}\left( T\right)I^{2}\left( \varphi\left( T\right),T\right)\right] \left[\frac{1}{k_{B}T}J_{A}\left( \varphi\left( T\right),T\right)-J_{B}\left( \varphi\left( T\right),T\right)\right] +2u^{2}I^{3}\left( \varphi\left( T\right),T\right)\right\}\varphi\left( T\right)}. $$
(34)

As it was already mentioned, T ⋆⋆ denotes the value of the temperature, for which the denominator in the formula (34) equals zero. In addition, the integrals I, J A , and J B can be approximated as follows: \(I\left (\varphi \left (T\right ),T\right )\simeq I\left (\varphi \left (0\right ),T_{C}\right )\), \(J_{A}\left (\varphi \left (T\right ),T\right )\simeq J_{A}\left (\varphi \left (0\right ),T_{C}\right )\), and \(J_{B}\left (\varphi \left (T\right ),T\right )\simeq J_{B}\left (\varphi \left (0\right ),T_{C}\right )\). The critical temperature can be calculated from (17), while \(\varphi \left (0\right )\) should be obtained from the simplest version of the formula (20):

$$ \varphi\!\left( 0\right)\,=\,2\omega_{0}{\kern-.5pt}\exp\!\left[\!-{\kern-.5pt}\!\ln\!\left( \frac{\omega_{0}}{b_{2}}\right)\,-\, \sqrt{\ln^{2}\!\left( \!\frac{\omega_{0}}{b_{2}}\!\right)\!-{\kern-.5pt}\!\frac{2}{b{\kern-.5pt}_{1}\left( v^{2}\,+\,uv\right)}\!{\kern-.5pt}-\!\frac{\pi{\kern-.5pt}^{2}}{6}}~\right]. $$
(35)

Transforming the denominator of the expression (34), the final result can be obtained:

$$ k_{B}T^{\star\star}=\frac{ J_{A}\left( \varphi\left( 0\right),T_{C}\right)} {J_{B}\left( \varphi\left( 0\right),T_{C}\right)-\frac{2u^{2}I^{3}\left( \varphi\left( 0\right),T_{C}\right)} {v^{2}+vu+3u^{2}\varphi^{2}\left( 0\right)I^{2}\left( \varphi\left( 0\right),T_{C}\right)}}. $$
(36)

Figure 5 shows the plot of the course of the Nernst temperature in the dependence on the parameter u. It may be noted that the physical values of the Nernst temperature (T ⋆⋆ > T C ) exist only for the sufficiently large values of u in the relation to v. At the same time, not without significance is the maximum phonon frequency, which can decide, whether the Nernst phase exists or not. For example, for ω 0 equal to 25 and 50 meV, the Nernst phase has not been observed. It should be also noted that, in the extreme case \(u/v\rightarrow +\infty \), the (36) simplifies to the relationship that binds together the parameters T ⋆⋆, \(\varphi \left (0\right )\), and T C without overt presence of the potentials v and u:

$$ k_{B}T^{\star\star}=\frac{ J_{A}\left( \varphi\left( 0\right),T_{C}\right)} {J_{B}\left( \varphi\left( 0\right),T_{C}\right)-\frac{2}{3}\frac{1}{\varphi^{2}\left( 0\right)}I\left( \varphi\left( 0\right),T_{C}\right)}. $$
(37)
Fig. 5
figure 5

The dependence of the Nernst temperature and the critical temperature on u for the selected values of v and ω 0. The non-physical values of the Nernst temperature satisfy the inequality T ⋆⋆ ≤ T C .

Full size image

2.6 The General Form of the Diagram T C - T ⋆⋆

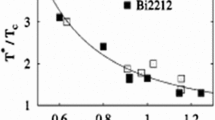
Figure 6 presents the form of the diagram T C - T ⋆⋆. The values of the critical temperature and the Nernst temperature were determined for \(v\in \left <2.5, 25\right > \mathrm {meV^{1/2}}\), \(u\in \left <5, 10\right >\) eV 1/2, and ω 0 = 60 meV. In addition, Fig. 6 shows the experimental data obtained for the selected superconductors, for which the results are also summarized in Table 1. Basing on the obtained results, we can discussed the experimental values of v and u. In particular, the maximum value of v is equal to 19.71 meV 1/2, which corresponds to the order of the value of the electron-phonon pairing potential given in the literature [52] (∼ 10 meV 1/2). The maximum value of u is much higher (\(\left [u\right ]_{\max }=9.42 \, \mathrm {eV^{1/2}}\)). From the physical point of view, this means the large change of the on-site Coulomb repulsion (U) caused by the small changes of the interatomic distance (R i j ), since in the Wannier representation u ∼ δ U/δ R i j. In our opinion, this value is to high, which may be due to the assumed approximations (the mean-field approximation, omitting the impact of the electron correlation, and taking into account only the s-wave symmetry). For this reason, the presented model is too simplistic to determine the physical values of the potentials v and u. Let us notice that the calculation of u directly from the fundamental microscopic models is extremely difficult. The preliminary considerations of this problem the reader can find in [53], where the all electronic one- and two-body terms for Hubbard dimer were taken into account. Additionally, let us note that if the hole density decreases (np. YBCO) the superconducting phase disappears and the Nernst region strongly expands. In this case, v generally decreases and u increases. The similar effect is observed for the remaining compounds—the increase of T C usually causes the increase of v and the increase of T ⋆⋆ is connected with the increase of u (see in the Table 1 the case of the disorder induced by the electron irradiation or the in-plane and out-of-plane disorder). Of course, there are slight deviations from the above rule due to the complex structure of the effective potential which depends not only on v 2 and u 2 but also on the product vu.

Fig. 6
figure 6

The T C - T ⋆⋆ diagram. The orange points represent the theoretical data. The increase of T C and T ⋆⋆ is connected both with the increase of v and u

Full size image
Table 1 The experimental values of T C and T ⋆⋆ and the calculated values of v and u for the selected high-temperature superconductors. The symbol p denotes the hole density (holes/Cu)
Full size table

The presented model also suggests that, with the increasing critical temperature, above 150 K, the values of the Nernst temperature increasingly will recede from the values of the critical temperature (the red lined area in Table 1). It is possible that this interesting behavior of the Nernst temperature was able to be observed experimentally for the superconductors with the extremely high value of T C . In our opinion, the best candidate would be the compound HgBa2Ca2Cu3O8 + y, which under the pressure at 31 GPa has the critical temperature equal to 164 K [54].

3 Summary

We have explained some anomalous properties of the high-temperature superconducting state in the cuprates. The considerations have been based on the Hamiltonian modeling the electron-phonon and the electron-electron-phonon interaction. It has been shown that the simplified form of the Eliashberg equations, boiling down to the integral equation for the order parameter, generalize the results, which can be obtained using the canonical transformation. Hence comes the immediate conclusion that the resulting model correctly associates with each other the experimental values of the critical temperature, the Nernst temperature, and the order parameter at the temperature of zero Kelvin. The equation for the order parameter resulting from the Eliashberg equations is significant, because it allows the derivation of the analytical formulas for the basic thermodynamic parameters of the superconducting state. In particular, on the basis of the formulas for the critical temperature, the Nernst temperature, and the order parameter at the temperature of zero Kelvin, the diagram binding T C and T ⋆⋆ was determined. It was shown that the existing experimental data confirm its form. Additionally, on the basis of the diagram, the limitation from below for T ⋆⋆ was set—occurring for the critical temperature higher than 150 K.