Behaviour equivalent max-plus automata for timed petri nets under open-loop race-policy semantics

Abstract

Timed Petri nets and max-plus automata are well known modelling frameworks for timed discrete-event systems. In this paper we present an iterative procedure that constructs a max-plus automaton from a timed Petri net while retaining the timed behaviour. Regarding the Petri net, we essentially impose three assumptions: (a) the Petri net must be bounded, i.e, the reachability graph must be finite; (b) we interpret the Petri net with single server semantics; and (c) the Petri net operates according to the race policy, i.e., the earliest possible transition will fire and thereby possibly consume tokens required by other competing transitions. Under these assumptions we show that the proposed procedure terminates with a finite deterministic max-plus automaton that realises the same timed behaviour as the Petri net. As a variation of the plain race policy, we also consider that a subsequently designed supervisor may temporarily disable distinguished transitions. Again, we present a terminating procedure that constructs a behaviour equivalent deterministic max-plus automaton. We demonstrate by example how the latter automaton can be utilised as an open-loop model in the context of supervisor control.

1 Introduction

Max-plus automata are defined as a generalisation of plain automata by assigning minimum durations to individual transitions, and, hence, can be used to model the behaviour of timed discrete-event systems; see Gaubert (1995). Although max-plus automata are not as expressive as general timed automata introduced by Alur and Dill (1994), they can be conveniently analysed within an algebraic setting, e.g., considering power series with coefficients from the idempotent semiring over the reals with addition and maximum as the two binary operations. Max-plus automata must not be confused with linear max-plus dynamic systems and variations thereof; see e.g. Baccelli et al. (1992) or Hardouin et al. (2018).

Max-plus automata have also been utilised in the context of supervisory control. Here, a given max-plus automaton represents the plant behaviour and one seeks to synthesise a supervisory controller such that the closed-loop behaviour satisfies a prescribed specification; e.g. Komenda et al. (2009) and Su et al. (2012). As with un-timed supervisory control introduced by Ramadge and Wonham (1989), the basic case of complete observation corresponds to a deterministic plant automaton. However, it is well known that not all max-plus automata are determinisable. Algorithms that enable determinisation of max-plus automata under restrictive conditions have been presented by Gaubert (1995) and Mohri (1997), where weighted automata are applied to speech recognition and their determinisation is possible if the so-called twin property holds. A less restrictive condition for termination of the procedure has been introduced in Lahaye et al. (2020). The classical algorithm for determinisation based on normalisation of the state vector has been extended by Kirsten (2008) for polynomially ambiguous max-plus automata, where a more general clone property guarantees the determinisation. For the more restrictive class of unambiguous max-plus automata a concept for observer construction has been proposed recently by Lai et al. (2021). Nevertheless, for non polynomially ambiguous max-plus automata even the decidability of determinisation is still open. Weighted automata have also been used in image processing; see Culik and Kari (1997).

Similar to max-plus automata, timed Petri nets are introduced by assigning durations to individual transitions in a Petri net; see Ramchandani (1973). There are a number of alternative firing rules commonly applied to plain Petri nets, and this variety is inherited by timed Petri nets. For example, Gaubert and Mairesse (1999) and Lahaye et al. (2015) consider so called safe timed Petri nets under preselection policy and show how they can be converted to behaviour equivalent max-plus automata. Although this is a relevant result for the purpose of analysis, the obtained automata in general fail to be deterministic and are, hence, of limited use in the context of controller synthesis. In contrast, Komenda et al. (2016) consider so called bounded Petri nets under race policy and provide a semi-algorithm that in the case of termination generates behaviour equivalent deterministic max-plus automata. To this end, Komenda et al. (2016), p. 427, impose a fairness condition on the Petri net and show that this condition is sufficient to imply termination of the semi-algorithm.

The present paper is based on our earlier conference contribution (Triska and Moor 2020), where we follow the line of thought by Komenda et al. (2016). However, we do propose some strategic variations of the algorithm that allow us to drop the fairness requirement. In particular, our algorithm terminates for all bounded Petri nets under race policy with rational timing parameters, and thereby generalises the results by Komenda et al. (2016). Our conversion result is still a deterministic max-plus automaton and technically can serve as the basis for a subsequent supervisory controller design. However, plain race-policy semantics leave little leverage for a supervisor to control the system under consideration. Extending our earlier conference contribution, we therefore propose to explicitly account for supervisors, that may temporarily disable distinguished transitions and thereby give priority to alternative transitions that could not occur under plain race policy. Since these considerations take place before any specific decision is made by the supervisor, we refer to our semantics as open-loop race policy. As with our base result for plain race-policy semantics, we present an algorithm for the construction of a behaviour equivalent deterministic max-plus automaton that terminates for bounded Petri nets with rational timing parameters.

The paper is organised as follows. After providing some elementary notation in Section 2, we recall common definitions regarding max-plus automata and timed Petri nets. In preparation of the following discussion, we also derive a formal representation for the behaviour of timed Petri nets. Section 4 then presents our first main result in that we construct a behaviour equivalent max-plus automaton for a given timed Petri net with race-policy semantics. Here, the discussion includes a formal proof of termination for our algorithm, provided that the Petri net is bounded. This result is extended in Section 5, where we address open-loop race-policy semantics, again including a proof of termination for bounded Petri nets. Subsequent controller design is demonstrated by a simple example in Section 6.

2 Notation

The positive integers are denoted by $\mathbb {N}$ and we let $\mathbb {N}_{0}:=\mathbb {N}\dot {\cup }\{0\}$. The rationales are denoted by $\mathbb {Q}$ and the reals $\mathbb {R}$. The non-negative rationals are denoted by $\mathbb {Q}_{\ge 0}$ and the non-negative reals $\mathbb {R}_{\ge 0}$. For a neutral element ε regarding the $\max \limits$ operation, we also consider $\mathbb {Q}_{\max \limits }:=\mathbb {Q}\dot {\cup }\{-\infty \}$ and $\mathbb {R}_{\max \limits }:=\mathbb {R}\dot {\cup }\{-\infty \}$ with $\varepsilon :=-\infty$ and the convention that x + ε = ε for all $x\in \mathbb {R}_{\max \limits }$.

An alphabet A is a finite set of symbols. We denote A^∗ the Kleene-closure of A, i.e., the set of finite-length words composed from symbols in A, including the empty word λ ∈ A^∗, λ∉A. Subsets of A^∗ are referred to as languages over A.

Throughout this paper we identify a map $f\colon X\rightarrow Y$

with the associated vector g = (g_x)_x∈X ∈ Y^X, g_x = f(x) ∈ Y for all x ∈ X; i.e., we do not distinguish between f and g and use either notation whenever convenient.

An equivalence relation ≡ on a set Q is a reflexive, symmetric and transitive relation, technically defined as a subset $\equiv \subseteq Q\times Q$. We use common infix notation $q^{\prime }\equiv q^{\prime \prime }$ for $(q^{\prime },q^{\prime \prime })\in \equiv$. The associated equivalence classes are denoted by $[q]:=\{ q^{\prime }\in Q | q\equiv q^{\prime } \}$. Given two equivalence relations $\equiv _{1},\ \equiv _{2} \subseteq Q\times Q$, we say that ≡₁ is at least as fine as ≡₂, if for all $q^{\prime },\ q^{\prime \prime }\in Q$ with $q^{\prime }\equiv _{1} q^{\prime \prime }$ we have that $q^{\prime }\equiv _{2} q^{\prime \prime }$.

3 Max-plus automata and timed petri nets

In this section we first recall common definitions regarding max-plus automata and timed Petri nets. Notational conventions are kept in line with Komenda et al. (2016). A more extensive introduction to this topic is given by Gaubert (1995) and Seatzu et al. (2012). Subsequently we demonstrate how a representation of the semantic state of a timed Petri net can be obtained and how the behaviour of the timed Petri net can be formally defined in terms thereof. This amounts to an automaton representation, which, however, at this stage may not be finite.

3.1 Deterministic max-plus automata

Max-plus automata are introduced as a generalisation of plain automata with durations assigned to transitions. We regard the timing component in $\mathbb {R}_{\max \limits }$ with the binary operations $\max \limits$ and + , which entail the respective neutral elements $\varepsilon := -\infty$ and e := 0.¹

Definition 1

A max-plus automaton is defined as a quadruple G = (Q, A, Q₀, δ), where

• Q is the set of states,

• A is the alphabet of event symbols,

• Q₀ is the set of initial states, and

• $\delta \colon Q \times A \times Q \rightarrow \mathbb {R}_{max}$ is the transition function.

The max-plus automaton G is finite if Q is a finite set.

The transition function in a max-plus automaton associates with each transition a non-negative duration and thereby generalises the common transition relation of plain automata. Technically, we require that for $q, q^{\prime } \in Q$ and a ∈ A either

$$ \delta(q,a,q^{\prime}) = d \ge 0 $$

(1)

to indicate that the respective transition takes no more than d time units, or that

$$ \delta(q,a,q^{\prime})=\varepsilon $$

(2)

to indicate that the respective transition cannot take place at all.

A path or run in the max-plus automaton G is defined as a sequence

$$ \pi=q_{0} a_{1} q_{1} a_{2} q_{2} {\cdots} a_{n} q_{n} $$

(3)

such that q₀ ∈ Q₀ and q_i ∈ Q, a_i ∈ A, δ(q_i, a_i+ 1, q_i+ 1)≠ε for all $i\in \mathbb {N}_{0}$, i < n. With the run π we associate the word w = a₁a₂⋯a_n. A word w ∈ A^∗ is recognised by G if there exists at least one run π with associated word w. Note that the empty word λ is recognised by any max-plus automaton via the trivial run π = q₀. The logical behaviour $\mathrm {L}(G)\subseteq A^{*}$ of G is then defined as the set of all words recognised by G.

A max-plus automaton is deterministic if it has exactly one initial state and if, given a state and an event symbol, there can be at most one successor state. Throughout this paper, we only consider deterministic automata. Technically, we then have that Q₀ = {q₀} and that for all $q, q^{\prime }, p^{\prime }\in Q$ and for all a ∈ A

$$ \delta(q,a,q^{\prime})\in \mathbb{R}_{\ge 0} \ \ \text{and}\ \ \delta(q,a,p^{\prime})\in \mathbb{R}_{\ge 0} \ \ \ \Longrightarrow \ \ \ \delta(q,a,q^{\prime}) = \delta(q,a,p^{\prime}) \ \ \text{and}\ \ q^{\prime}=p^{\prime} . $$

(4)

In particular, we have that for each w ∈L(G) there exists exactly one run of G with w the associated word.

The timed behaviour of max-plus automata is defined via a dater function that returns the date at which a sequence of events has definitely been executed. For the situation of deterministic max-plus automata, the technical construction simplifies considerably.

Definition 2

The behaviour $y_{G} \colon A^{*} \rightarrow \mathbb {R}_{\max \limits }$ of a deterministic max-plus automaton G = (Q, A,{q₀}, δ) is given by

$$ y_{G}(w) := \delta(q_{0},a_{1},q_{1}) + \delta(q_{1},a_{2},q_{2}) + {\dots} + \delta(q_{n-1},a_{n},q_{n}) , $$

(5)

where π = q₀a₁q₁a₂q₂⋯a_nq_n is the unique run with associated word w ∈L(G), including the special case of w = λ with the empty sum, i.e., y_G(λ) = 0. For w∉L(G), we let y_G(w) = ε.

Referring to the transition durations as weights, the timed behaviour amounts to the sum of the transition weights along the unique run associated with each individual recognised word. Taking this perspective, we define the labeled and weighted transition relation ‘→’ by letting

$$ q \xrightarrow{a/d} q^{\prime} $$

(6)

for q, $q^{\prime }\in Q$ and a ∈ A if and only if $d=\delta (q,a,q^{\prime })\ge 0$. This transition relation is commonly extended to words in A^∗ by taking the transitive closure while accumulating weights. Technically, we begin with the empty word λ ∈ A^∗ and define the transitions

$$ q \xrightarrow{\lambda/0} q , $$

(7)

for all q ∈ Q. We then iteratively define further transitions

$$ q \xrightarrow{wa/d} q^{\prime\prime} $$

(8)

with q, $q^{\prime \prime }\in Q$, w ∈ A^∗ and a ∈ A if and only if

$$ q \xrightarrow{w/d^{\prime}} q^{\prime} \ \ \ \text{and}\ \ \ q^{\prime} \xrightarrow{a/d^{\prime\prime}} q^{\prime\prime} $$

(9)

are both defined for some $q^{\prime }\in Q$ and $d=d^{\prime }+d^{\prime \prime }$.

For the deterministic max-plus automata considered in this paper, it can be seen by induction over the length of words that, given q ∈ Q and w ∈ A^∗, there exists at most one duration $d\in \mathbb {R}_{\ge 0}$ and one successor state $q^{\prime }\in Q$ such that

$$ q \xrightarrow{w/d} q^{\prime} . $$

(10)

Moreover, considering the initial state q = q₀ and a word w ∈ A^∗, the existence of d and $q^{\prime }$ that qualify for Eq. 10 is equivalent to y_G(w) = d ≥ 0.

3.2 Petri nets

A Petri net is a bipartite graph with places and transitions as nodes. Places can hold any number of tokens and the token configuration determines which transitions are enabled. We recall the formal definition and comment on aspects relevant for the present paper.

Definition 3

A Petri net is a quadruple $\mathcal {G = (P,T,F},M_{0})$, where

• $\mathcal {P}$ is a finite set of places,

• $\mathcal {T}$ is a finite set of transitions,

• $\mathcal {F \subseteq (P \times T)\cup (T \times P)}$ is the incidence relation, and

• $M_{0} \colon \mathcal {P} \rightarrow \mathbb {N}_{0}$ is the initial marking.

The configuration of a Petri net is given by a marking$M \colon \mathcal {P} \rightarrow \mathbb {N}_{0}$, which specifies the number of tokens present at each place. Whenever convenient, we identify the function M with the corresponding vector in $\mathbb {N}_{0}^{\mathcal {P}}$. The evolution of the marking over logic time adheres to the following rules:

• (S1) Transition $t\in \mathcal {T}$ is enabled by a marking M if each input place of t has at least one token; i.e., if M_p > 0 for all $p\in \mathcal {P}$ with $(p,t)\in \mathcal {F}$. This is denoted by $M \overset {t}{\rightarrow }$. Given a marking M, we write

  $$ \text{En}(M):=\{ t\in\mathcal{T} | M \overset{t}{\rightarrow}\} \subseteq\mathcal{T} $$

  (11)

  for the set of all enabled transitions.

• (S2) Considering the Petri net with marking M, an enabled transition t ∈En(M) can fire. The firing of t transforms the marking M into $M^{\prime }$, where one token is eliminated from each input place of t and, subsequently, one token is generated for each output place. Technically, we denote $\text {Elm}(M,t)\in \mathbb {N}_{0}^{\mathcal {P}}$ the intermediate marking after token elimination, i.e.,

  $$ \text{Elm}(M,t)_{p}:= \begin{cases} M_{p}-1 & \text{if } (p,t)\in\mathcal{F},\\ M_{p} & \text{else}, \end{cases} $$

  (12)

  for all $p\in \mathcal {P}$. Likewise, token generation is expressed by $\text {Gen}(M,t)\in \mathbb {N}_{0}^{\mathcal {P}}$ with

  $$ \text{Gen}(M,t)_{p}= \begin{cases} M_{p}+1 & \text{if } (t,p)\in\mathcal{F},\\ M_{p} & \text{else}, \end{cases} $$

  (13)

  for all $p\in \mathcal {P}$. Then, the successor marking $M^{\prime }$ is obtained as $M^{\prime }:= \text {Gen}(\text {Elm}(M,t))$. The overall process is denoted by $M \overset {t}{\rightarrow } M^{\prime }$.

Conforming with the above rules, a firing sequence is specified by markings $M_{i}\in \mathbb {N}_{0}^{\mathcal {P}}$, $i=0,\ldots , n\in \mathbb {N}$, and transitions $t_{i}\in \mathcal {T}$ such that $M_{i}\overset {t_{i}}{\rightarrow } M_{i+1}$ for $i=0,\ldots , n-1\in \mathbb {N}$, and we associate the word $w:=t_{0}t_{1}{\cdots } t_{n-1}\in \mathcal {T}^{*}$ with this firing sequence. The logical behaviour $\mathrm {L}(\mathcal {G})\subseteq \mathcal {T}^{*}$ of the Petri net $\mathcal {G}$ is then defined as the set of all words associated with some firing sequence.

A Petri net is called bounded if for all markings reachable by some firing sequence the token count at each place does not exceed a uniform bound.

Definition 4

The reachability graph or marking graph of a bounded Petri net $\mathcal {G}$ is the deterministic finite automaton $\text {Reach}(\mathcal {G})=({\mathscr{M}},\mathcal {T},M_{0},t_{r})$, where

• the state set ${\mathscr{M}}$ is the set of markings reachable by some firing sequence,

• the alphabet is the set of transitions $\mathcal {T}$,

• the initial state is the initial marking M₀, and

• the partial transition function $t_{r} \colon {\mathscr{M}} \times \mathcal {T} \rightarrow {\mathscr{M}}$ is defined for $M\in {\mathscr{M}}$ and $t \in \mathcal {T}$ by $t_{r}(M,t) := M^{\prime }$ if and only if $M \overset {t}{\rightarrow }$ and where $M^{\prime }\in {\mathscr{M}}$ is the unique marking with $M \overset {t}{\rightarrow } M^{\prime }$.

Note that the determinism of the reachability graph crucially depends on the direct use to the set of transitions as alphabet. When applying the same approach in the presence of explicit transition labels, such a labeling needs to be injective for us to obtain a deterministic reachability graph. Since an explicit labeling is quite common in the literature, we refer to our setting as injectively labeled.

3.3 Timed Petri nets under race policy

In the context of time extensions for Petri nets multiple approaches have been introduced that are based on assigning durations to places, transitions, or both, see e.g. Merlin (1974) and Ramchandani (1973), and Cerone and Maggiolo-Schettini (1999). In our specific setting we consider a class of timed Petri nets that is obtained from plain Petri nets by associating with each individual transition a duration. This style of generalisation is similar to when moving from plain automata to max-plus automata.

Definition 5

A timed Petri net is a pair $(\mathcal {G},\tau )$, where $\mathcal {G}$ is a Petri net with set of transitions $\mathcal {T}$ and where $\tau = (\tau _{t})_{t \in \mathcal {T}} \in \mathbb {R}_{\ge 0}^{\mathcal {T}}$ is a parameter vector representing the durations associated with each individual transition.

In contrast to the setting with max-plus automata, the duration τ_t here is interpreted as the firing time of transition $t\in \mathcal {T}$. Since holding times are not considered throughout this paper, the duration τ_t is the minimum delay between enabling and firing of t. This interpretation leads to the following informal extension of firing rules.

• (S3) The tokens belonging to the initial marking become available at time instant zero.

• (S4) All transitions are considered to be single server, meaning that a transition can only process one token from each input place at a time.

• (S5) If multiple transitions are enabled, the one that can fire the earliest has priority. This rule is also known as race policy. In the case several transitions qualify under this policy, either one can fire next.

• (S6) Transitions are fired as soon as possible, which is referred to as the earliest functioning firing rule.

These semantics are effectively the same as in Komenda et al. (2016). For a general discussion of alternative settings, such as multi server, see e.g. Seatzu et al. (2012).

At this point we are looking to find a formal representation of the timed behaviour. Our approach here is to extend the discrete state set

$$ \mathcal{M}\subseteq\mathbb{N}_{0}^{\mathcal{P}} $$

(14)

from the reachability graph by a continuous component $\boldsymbol {{\mathscr{C}}}$ to strategically encode clock values in order to address the timing rules (S3)–(S6). Technically, we let

$$ \boldsymbol{\mathscr{C}}:= (\mathbb{R}_{\ge 0}\cup\{\ddagger\})^{\mathcal{T}} $$

(15)

to maintain one clock per transition that shows the time for which the transition has been continuously enabled or, alternatively, the distinguished symbol † to explicitly indicate that the respective transition is disabled and, hence, the clock is inactive. While the initial marking M₀ is specified by the Petri net, we define the initial clock vector as $C_{0} := (c_{0,t})_{t\in \mathcal {T}} \in \boldsymbol {{\mathscr{C}}}$ with

$$ c_{0,t} := \begin{cases} 0&\text{if }M_{0}\overset{t}{\rightarrow} , \text{and} \\ \ddagger &\text{else} . \end{cases} $$

(16)

Thus, the overall set of semantic states amounts to the product ${\mathscr{M}}\times \boldsymbol {{\mathscr{C}}}$ with initial state $(M_{0},C_{0})\in {\mathscr{M}}\times \boldsymbol {{\mathscr{C}}}$. We define a number of operations on these states that turn out useful in the subsequent discussion.

• As a means to update the values of all clocks after the elapse of some finite amount of time we define the operation Inc for a clock vector $C= (c_{t})_{t\in \mathcal {T}}\in \boldsymbol {{\mathscr{C}}}$ and a duration $d\in \mathbb {R}_{\ge 0}$, that is $\text {Inc}(C,d)\in \boldsymbol {{\mathscr{C}}}$ with

  $$ \text{Inc} (C,d)_{t} := \begin{cases} c_{t}+d&\text{if }c_{t}\in \mathbb{R}_{\ge 0} \ \text{and} \\ \ddagger&\text{else} , \end{cases} $$

  (17)

  for all $t\in \mathcal {T}$.

• In the interest of comparing clock values and for better readability, we define for $d \in \mathbb {R}_{\ge 0}$

  $$ \min(\ddagger,d)= \ddagger $$

  (18)

  The $\min \limits$ operator is extended to vector valued arguments in the obvious elementwise way.

• To reset the value of specific clocks we define the operation Reset for a set of transitions $R \subseteq \mathcal {T}$ and a clock vector $C= (c_{t})_{t\in \mathcal {T}}\in \boldsymbol {{\mathscr{C}}}$. The clocks corresponding to transitions in R are reset and other clocks are not effected; that is $\text {Reset} (C,R)\in \boldsymbol {{\mathscr{C}}}$ with

  $$ \text{Reset} (C,R)_{t} := \begin{cases} 0&\text{if }t\in R , \text{and} \\ c_{t}&\text{else} , \end{cases} $$

  (19)

  for all $t\in \mathcal {T}$. The single server transition semantics are then implemented by resetting the respective clock value after every firing of a transition.

• Since the timing is only relevant for enabled transitions, we deactivate a clock referring to disabled transitions by substituting said clock with the indicator symbol †. This operation is performed by Sub, defined for $S \subseteq \mathcal {T}$ and $C= (c_{t})_{t\in \mathcal {T}}\in \boldsymbol {{\mathscr{C}}}$ with $\text {Sub} (C,S)\in \boldsymbol {{\mathscr{C}}}$ and

  $$ \text{Sub} (C,S)_{t} := \begin{cases} c_{t},&\text{if }t\in S, \text{and} \\ \ddagger&\text{else} . \end{cases} $$

  (20)

  for all $t \in \mathcal {T}$.

• In order to adequately reset and start relevant clocks, we need to identify newly enabled transitions. Given a marking $M \in {\mathscr{M}}$ with $M\overset {t}\rightarrow M^{\prime }$ for some transition $t\in \mathcal {T}$ and the unique successor marking $M^{\prime } \in {\mathscr{M}}$, a transition $t^{\prime }\in \mathcal {T}$ is obviously newly enabled if it is enabled in $M^{\prime }$ but not in M, i.e., if $t\in \text {En}(M^{\prime }) \setminus \text {En}(M)$. In this case, the corresponding entry in the clock vector shall be set to 0. However, we also need to account for the situation where the elimination of tokens as required by firing t temporally disables a transition $t^{\prime }$ which otherwise is enabled by both markings M and $M^{\prime }$. Technically, we then obtain

  $$ \text{NewEn}(M,t,M^{\prime}):=\text{En}(M^{\prime}) \setminus \text{En}(\text{Elm}(M,t))\subseteq\mathcal{T}. $$

  (21)

  Note that systematically resetting clocks of newly enabled transitions ensures that clocks of enabled transitions are always active, and hence, show a real value as opposed to the distinguished symbol †. Note also that our construct here crucially relies on the assumption of single server semantics.

• The race policy guarantees that among enabled transitions only the one(s) with the minimal remaining firing delay can be fired. With En(M) the set of transitions enabled by a marking M we define $\text {FirstFired}(M,C) \subseteq \text {En}(M)$ by

  $$ \begin{array}{@{}rcl@{}} \text{FirstFired}(M,C) &=& \{ t\in \text{En}(M) | \\ &\forall& u\in\text{En}(M) : \tau_{t}\! - c_{t}\le \tau_{u} - c_{u}\} . \end{array} $$

  (22)

  In this regard the expression d = τ_t − c_t for t ∈FirstFired(M, C) represents the minimal remaining firing delay among transitions enabled by the marking M. Hence, before the elapse of d time units, no transition can fire and after the elapse of d time units some transition a ∈FirstFired(M, C) will fire provided that En(M)≠∅.

We are now in the position to formally define the overall timed Petri nets semantics by introducing weighted transitions

$$ (M,C) \xrightarrow{a/d} (M^{\prime},C^{\prime}) , $$

(23)

between two semantic states

with $M, M^{\prime }\in {\mathscr{M}}$, $C, C^{\prime }\in \boldsymbol {{\mathscr{C}}}$, $a\in \mathcal {T}$ and $d\in \mathbb {R}_{\ge 0}$ if and only if

• (i) $M \xrightarrow {a} M^{\prime }$,

• (ii) a ∈FirstFired(M, C),

• (iii) d = τ_a − c_a,

• (iv) C⁺ = Inc(C, d),

• (v) $C^{++} = \text {Reset}(C^{+},\text {NewEn}(M,a,M^{\prime })\cup \{a\})$,

• (vi) $C^{\prime } = \text {Sub}(C^{++},\text {En}(M^{\prime }))$.

Note that the above transition relation is deterministic by construction in the sense that

$$ (M,C) \xrightarrow{a/d^{\prime}} (M^{\prime},C^{\prime}) \ \ \ \text{and}\ \ \ (M,C) \xrightarrow{a/d^{\prime\prime}} (M^{\prime\prime},C^{\prime\prime}) $$

(24)

implies $d^{\prime \prime }=d^{\prime }$, $M^{\prime \prime }=M^{\prime }$ and $C^{\prime \prime }=C^{\prime }$. In particular, the transitions can be interpreted as state transitions in a deterministic max-plus automata with state set $Q={\mathscr{M}}\times \boldsymbol {{\mathscr{C}}}$ and we will follow this up in the subsequent section. To this end, we refer to the common extension of weighted transition relations to words as presented at the end of Section 3.1 for a formal definition of the timed behaviour of the Petri net. Technically, we begin with the empty word $\lambda \in \mathcal {T}^{*}$ and define the transitions

$$ (M,C) \xrightarrow{\lambda/0} (M,C) $$

(25)

for all $M\in {\mathscr{M}}$, $C\in \boldsymbol {{\mathscr{C}}}$. Referring to Eq. 23 with conditions (i)–(vi), we then iteratively introduce further transitions

$$ (M,C) \xrightarrow{wa/d} (M^{\prime\prime},C^{\prime\prime}) $$

(26)

with $w\in \mathcal {T}^{*}$, $a\in \mathcal {T}$ and $d\in \mathbb {R}_{\ge 0}$ whenever there exist $M^{\prime }\in {\mathscr{M}}$, $C^{\prime }\in \boldsymbol {{\mathscr{C}}}$ and $d^{\prime },\ d^{\prime \prime }\in \mathbb {R}_{\ge 0}$ such that

$$ (M,C) \xrightarrow{w/d^{\prime}} (M^{\prime},C^{\prime}) \ \ \ \text{and}\ \ \ (M^{\prime},C^{\prime}) \xrightarrow{a/d^{\prime\prime}} (M^{\prime\prime},C^{\prime\prime}) . $$

(27)

and $d=d^{\prime }+d^{\prime \prime }$. Note that the determinism as observed above carries over to the extension to words. In particular, given a word $w\in \mathcal {T}^{*}$ there exists at most one matching sequence of transitions beginning at the initial state (M₀, C₀) and, if so, a unique corresponding overall duration d.

Definition 6

The behaviour of a timed Petri net $(\mathcal {G},\tau )$ is defined as the dater function $y_{\mathcal {G}}\colon \mathcal {T}^{*} \rightarrow \mathbb {R}_{max}$ with $y_{\mathcal {G}}(w):=d$ if

$$ (M_{0},C_{0}) \xrightarrow{w/d} (M^{\prime},C^{\prime}) $$

(28)

for some $M^{\prime }\in {\mathscr{M}}$ and $C^{\prime }\in \boldsymbol {{\mathscr{C}}}$, and referring to the transition relation defined by Eqs. 23–27, or, else, $y_{\mathcal {G}}(w):=\varepsilon$.

4 Finite state representation

Based on the semantics defined in the previous section, we are now looking to obtain a max-plus automaton with equal behavior to a given bounded, timed Petri net operating under race policy with single server semantics. For our main result, Theorem 1, we show that a suitable automaton with a finite number of states always exists and we demonstrate how to obtain such an automaton.

4.1 Behaviour considerations

As a first step in constructing the desired max-plus automaton we propose an initial candidate with an infinite state set that realizes the same behavior as the respective timed Petri net. This is done be re-interpreting the transition relation on the semantic states, Section 3.3, Eq. 23, as the transition function of a max-plus automaton with state set $Q={\mathscr{M}}\times \boldsymbol {{\mathscr{C}}}$, i.e., the set of all pairs of markings and clock vectors with regard to a given bounded timed Petri net $(\mathcal {G},\tau )$, $\mathcal {G} = (\mathcal {P},\mathcal {T},\mathcal {F},M_{0})$. Given a state q = (M, C) ∈ Q, we ask for all possible successor states under the restriction of the race policy and with single server semantics. Referring to the determinism of the transition relation on semantic states, Eq. 23, recall that given q = (M, C) ∈ Q and $t\in \mathcal {T}$ there exists at most one duration $d\in \mathbb {R}_{\ge 0}$ and one successor state $q^{\prime }=(M^{\prime },C^{\prime })\in Q$ such that

$$ q \xrightarrow{t/d} q^{\prime} . $$

(29)

Hence, we can define the max-plus transition function $\delta \colon Q\times \mathcal {T}\times Q\rightarrow \mathbb {R}_{\max \limits }$ by

$$ \delta(q,t,q^{\prime}) = \begin{cases} \ d,&\text{if }q \xrightarrow{t/d}q^{\prime}\ \text{for }\ d\in\mathbb{R}_{\ge0} \text{and}\\ \ \varepsilon,&\text{else}, \end{cases} $$

(30)

and consider the deterministic max-plus automaton

$$ G = (Q,\mathcal{T},\{(M_{0},C_{0})\},\delta) . $$

(31)

It is evident from the construction that the weighted transition relation, Eq. 30, associated with G matches the transition relation on the semantic states defined in Section 3.3, Eq. 23. Hence, we have that

$$ \forall w \in \mathcal{T}^{*} . y_{\mathcal{G}}(w) = y_{G}(w) . $$

(32)

In other words, the timed behaviour of the max-plus automaton G equals the behaviour of the timed Petri net $(\mathcal {G},\tau )$.

4.2 Restriction to a finite automaton

Although the state set $Q={\mathscr{M}}\times \boldsymbol {{\mathscr{C}}}$ of G is technically infinite due to the $\boldsymbol {{\mathscr{C}}}$-component, our conjecture is that the set of reachable states is only finite. In support of a formal argument, we conduct a forward-reachability analysis on G. Consider the operator

$$ \begin{array}{@{}rcl@{}} &&\text{NextState}(P) := \\ &&{\kern3em}\{ q^{\prime} \in Q | \exists t\in \mathcal{T}, q\in P . \delta(q,t,q^{\prime}) \ge 0 \} \end{array} $$

(33)

defined for sets of states $P\subseteq Q$. Then the set of reachable states in G is obtained by the following iteration

$$ \begin{array}{@{}rcl@{}} Q_{0}&:=&\{(M_{0},C_{0})\} , \end{array} $$

(34)

$$ \begin{array}{@{}rcl@{}} Q_{i+1}&:=&Q_{i} \cup \text{NextState}(Q_{i}) , \end{array} $$

(35)

$$ \begin{array}{@{}rcl@{}} Q_{*}&:=&\cup\{ Q_{i} | i\in\mathbb{N}_{0} \} , \end{array} $$

(36)

i.e., there exists a path π in G that ends in a state q ∈ Q if and only if q ∈ Q_∗. Since non-reachable states do not contribute to the behaviour, we can restrict G to the state set Q_∗. Technically, we consider the max-plus automaton

$$ G_{*} = (Q_{*},\mathcal{T},\{(M_{0},C_{0})\},\delta_{*}) , $$

(37)

where the transition function $\delta _{*}\colon Q_{*} \times \mathcal {T} \times Q_{*}\rightarrow \mathbb {R}_{\max \limits }$ equals δ on the restricted domain, i.e.,

$$ \forall (q,t,q^{\prime}) \in Q_{*} \times \mathcal{T} \times Q_{*} . ~\delta_{*}(q,t,q^{\prime})=\delta(q,t,q^{\prime}) . $$

(38)

and we conclude that $y_{\mathcal {G}}(w) = y_{G}(w)=y_{G_{*}}(w)$ for all $w \in \mathcal {T}^{*}$.

From the boundedness assumption of the Petri net $\mathcal {G}$ it follows that the set of reachable markings ${\mathscr{M}}$ in $\text {Reach}(\mathcal {G})$ is finite. In order to establish that Q_∗ is finite, we show that the range of the $\boldsymbol {{\mathscr{C}}}$-component over all states in Q_∗ is finite, too. To this end, consider the following Lemma.

Lemma 1

The entries of the clock vector C in every state (M, C) ∈ Q_∗ of the automaton G_∗ are bounded by the respective entry in the vector of transition durations $\tau \in \mathbb {R}_{\ge 0}^{\mathcal {T}}$, i.e.

$$ \forall (M,C) \in Q_{*} , t \in \mathcal{T} . c_{t}\neq\ddagger \Rightarrow c_{t}\leq \tau_{t} . $$

(39)

Proof

For the case of Q_∗ = {(M₀, C₀)} the claim is trivially true since each entry c_{0, t} of C₀ by definition either equals † or 0 ≤ τ_t, with the latter inequality as a consequence of τ_t being non negative.

For a proof by contradiction, suppose there exists a state $q^{\prime }=(M^{\prime },C^{\prime }) \in Q_{*}$ different from the initial state, and such that $c^{\prime }_{t} > \tau _{t}$ for some transition $t \in \mathcal {T}$. Since $q^{\prime }$ is not the initial state, there exists $i\in \mathbb {N}_{0}$ such that $q^{\prime }\not \in Q_{i}$ but $q^{\prime }\in Q_{i+1}$. Hence, by Eq. 35, we have that $q^{\prime }\in \text {NextState}(Q_{i})$. By the definition of NextState, Eq. 33, we can choose a predecessor state $q=(M,C)\in Q_{i}\subseteq Q_{*}$ such that $\delta (q,a,q^{\prime })=d\ge 0$ for some $a\in \mathcal {T}$. With Eq. 30 this implies

$$ (M,C) \xrightarrow{a/d} (M^{\prime},C^{\prime}) , $$

(40)

and we can refer to conditions (i)–(vi) below (23) to derive further consequences. In order for $c^{\prime }_{t}$ to be greater than zero, transition t has to be enabled for marking $M^{\prime }$ as well as the predecessor marking M, otherwise transition t would be considered obviously newly enabled or disabled and the clock value $c^{\prime }_{t}$ is reset; see conditions (v) and (vi), respectively. In particular, we have t ∈En(M). Referring to condition (i), we have a ∈En(M) and, since transition a was chosen according to the race policy semantics, condition (ii), we also have a ∈FirstFired(M, C), i.e.,

$$ d = \tau_{a} - c_{a} \le \tau_{b} - c_{b} , $$

(41)

for all b ∈En(M). From the definition of clock values via conditions (iv)–(vi), we obtain $c_{t} + d = c^{\prime }_{t}$ to conclude

$$ \begin{array}{@{}rcl@{}} c_t + d &=& c^{\prime}_t \end{array} $$

(42)

$$ \begin{array}{@{}rcl@{}} \Leftrightarrow c_t + \tau_a - c_a &=& c^{\prime}_t > \tau_t \end{array} $$

(43)

$$ \begin{array}{@{}rcl@{}} \Leftrightarrow \tau_a - c_a &>& \tau_t - c_t . \end{array} $$

(44)

As t ∈En(M) holds true, Eq. 44 constitutes a contradiction with Eq. 41. □

Regarding the above lemma we consider the restricted range of clock values

$$ \boldsymbol{\mathscr{C}}_{*}:= ([0,\tau_{\max}]\cup\{\ddagger\})^{\mathcal{T}}\subseteq \boldsymbol{\mathscr{C}} , $$

(45)

with $\tau _{\max \limits }=\max \limits _{t\in \mathcal {T}}\tau _{t}$ to observe that

$$ Q_{*}\subseteq\mathcal{M}\times\boldsymbol{\mathscr{C}}_{*} . $$

(46)

If all entries in the timing vector τ are non-negative integers, i.e., $\tau \in \mathbb {N}_{0}^{\mathcal {T}}$, then the clock vector C of any state q = (M, C) ∈ Q_∗ is also in $\mathbb {N}_{0}^{\mathcal {T}}$. Since the intersection of $\boldsymbol {{\mathscr{C}}}_{*}$ with $\mathbb {N}_{0}^{\mathcal {T}}$ is a finite set, this implies that Q_∗ is a finite set, too. For the case of a rational timing $\tau \in \mathbb {Q}_{\ge 0}^{\mathcal {T}}$, we uniformly scale clocks to refer to the least common denominator of all entries in τ to again obtain a finite set Q_∗ by the same argument. Note that this observation does not carry over to general real-valued timings $\tau \in \mathbb {R}_{\ge 0}^{\mathcal {T}}$. We now state our main result.

Theorem 1

Consider a bounded, injectively labeled, timed Petri net $(\mathcal {G},\tau )$ under race-policy and with single server semantics. Assuming a rational timing vector $\tau \in \mathbb {Q}_{\ge 0}^{\mathcal {T}}$, there exists a finite deterministic max-plus automaton with equal behaviour. One such automaton is given by

$$ G_{*} = (Q_{*},\mathcal{T},\{(M_{0},C_{0})\},\delta_{*}) , $$

(47)

as defined in Eq. 37 via the iteration (34)–(36). In particular, the iteration attains a fixpoint after finitely many steps, i.e., we have Q_∗ = Q_i for some $i\in \mathbb {N}_{0}$.

Proof

Finiteness of Q_∗ is a consequence of Lemma 1 and the discussion for rational timings thereafter. Behavioural equivalence has been discussed in Section 4.1 concluding with Eq. 32. Attaining a fixpoint Q_∗ = Q_i for some $i\in \mathbb {N}_{0}$ is a consequence of finiteness of Q_∗ and monotonicity $Q_{i}\subseteq Q_{i+1}\subseteq Q_{*}$ in the iteration (34)–(36). □

4.3 Algorithm and example

With the intent to have the necessary computational steps be clearly accessible we present an equivalent representation in the form of an algorithm; see Procedure 1.

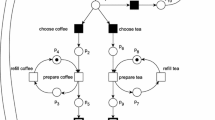
In order to illustrate the application of the proposed procedure we will detail relevant construction steps for the Petri net depicted in Fig. 1. Here, all relevant vectors are triples of single digit integers and we can concisely write xyz for the vector $(x,y,z)\in (\mathbb {N}_{0}\cup \{\ddagger \})^{3}$; i.e., for the initial state with the marking as depicted we have (M₀, C₀) = (201,0 † 0) and we start our reachability analysis with Q₀ = {(201,0 † 0)}. Following the algorithmic procedure we note that

• FirstFired(201,0 † 0) = {a},

• d = τ_a − c_a = 2 − 0 = 2,

• t_r(201, a) = 111,

• NewEn(201, a,111) = {b},

• Sub(Reset(Inc(0 † 0,2),{a, b}),{a, b, c}) = 002,

and we obtain NextState(Q₀) = {(111,002)} and thus

$$ Q_{1} = \{(201,0\!\ddagger\!0),(111,002)\}. $$

(48)

For the next iteration we additionally need to consider successors of the newly obtained state (111,002). Therefore, we note

• FirstFired(111,002) = {b, c},

• d_b = τ_b − c_b = 1 − 0 = 1,

• t_r(111, b) = 201,

• NewEn(111, b,201) = {c},

• for b: Sub(Reset(Inc(002,1),{b, c}),{a, c}) = 1 † 0,

• d_c = τ_c − c_c = 3 − 2 = 1,

• t_r(111, c) = 111,

• NewEn(111, c,111) = {b, c},

• for c: Sub(Reset(Inc(002,1),{b, c}),{a, b, c}) = 100,

to obtain

$$ \text{NextState}(\{(111,002)\}) = \{(201,1\!\ddagger\!0),(111,100)\} $$

and therefore

$$ Q_{2} = \{(201,0\!\ddagger\!0),(111,002),(201,1\!\ddagger\!0),(111,100)\}. $$

(49)

Continuing in the same vein until the termination condition is reached at Q₅ = Q₄, results in the max-plus automaton portrayed in Fig. 2.

Fig. 1

Timed Petri net $(\mathcal {G},\tau )$

Fig. 2

Resulting max-plus automaton G_∗

5 Generalisation to open-loop race-policy semantics

In oder to address subsequent supervisory controller design, we now distinguish controllable and uncontrollable transitions; i.e., we consider a Petri net $\mathcal {G = (P,T,F},M_{0})$ as in Definition 3, however, the set of transitions is composed as a disjoint union $\mathcal {T} := \mathcal {T}_{\mathrm {c}} \dot {\cup } \mathcal {T}_{\mathrm {u}}$ of controllable and uncontrollable transitions $\mathcal {T}_{\mathrm {c}}$ and $\mathcal {T}_{\mathrm {u}}$, respectively. As in the purely logical setting, a supervisor can then be designed to disable any controllable transition at any instant of time. In contrast to the purely logical setting, such a supervisor potentially enlarges the timed behaviour under race-policy: disabling a transition that would otherwise win the race effectively enables alternative transitions that are not accounted for in the timed behaviour considered so far. To obtain an open-loop model suitable as a basis for a subsequent supervisor design, such additional transitions must be included when transforming the Petri net into a max-plus automaton. In this section, we review and adapt our approach in this regard.

5.1 Behaviour considerations

Recalling the informal semantics (S1)–(S6), Section 3, we propose the below variations for (S5) and (S6) in order to address the open-loop configuration and to account for the potential effect of a supervisor. We refer to this variation as open-loop race policy.

• (S5’) As with plain race-policy semantics, a transition that can fire no later than any other enabled transition can always fire next. This accounts for supervisors, that do not disable the respective transition. Additionally, transitions that can fire no later than any uncontrollable transition can also fire next. This accounts for supervisors, that disable all earlier controllable transitions. If multiple transitions qualify under this policy, either one of them can fire next.

• (S6’) Transitions will fire as soon as possible, while respecting the priorities imposed by Rule (S5’).

Not that in the absence of controllable transitions, i.e. $\mathcal {T}_{\mathrm {c}}=\emptyset$, rule (S5’) matches plain race policy (S5) and, in turn (S6’) matches the earliest firing rule (S6). In this sense, the proposed open-loop race semantics are a generalisation of plain race semantics.

We are now in the position to set up transitions in terms of semantic states similar to the case of plain race-semantics.

Technically, we let

$$ (M,C) \xrightarrow{a/d} (M^{\prime},C^{\prime}) , $$

(50)

for $M, M^{\prime }\in {\mathscr{M}}$, $C, C^{\prime }\in \boldsymbol {{\mathscr{C}}}$, $a\in \mathcal {T}$ and $d\in \mathbb {R}_{\ge 0}$ if and only if

• (i) $M \xrightarrow {a} M^{\prime }$,

• (ii’) $\{t \in (\text {En}(M)\cap \mathcal {T}_{\mathrm {u}}) : \tau _{t} - c_{t} < \tau _{a}-c_{a} \} = \emptyset$

• (iii’) $d=\max \limits (\tau _{a} - c_{a},0)$,

• (iv) C⁺ = Inc(C, d),

• (v) $C^{++} = \text {Reset}(C^{+},\text {NewEn}(M,a,M^{\prime })\cup \{a\})$,

• (vi) $C^{\prime } = \text {Sub}(C^{++},\text {En}(M^{\prime }))$.

Here, technical condition (ii’) corresponds to rule (S5’), while (iii’) ensures non-negative weights. The latter could occur due to a supervisor disabling otherwise qualifying transitions.

The open-loop behaviour $y_{\mathcal {G}}$ of the timed Petri net $(\mathcal {G},\tau )$ under open-loop race policy is then defined literally as in the previous Definition 6, except that we now refer to the transitions defined by Eq. 50 as opposed to Eq. 23. Likewise, we set up the transition function δ literally as in Eq. 30 to obtain a behaviour equivalent max-plus automaton $G = (Q,\mathcal {T},\{(M_{0},C_{0})\},\delta )$, i.e., we again have $y_{G}(w)= y_{\mathcal {G}}(w)$ for all $w\in \mathcal {T}^{*}$; see also Section 4.1.

5.2 Finite realisation

Our aim in this section is to identify states with identical future behaviour. In order to proof that a realization of G with a finite state set exists, we show that all states of G can be assigned to a finite number of equivalence classes without changing the behaviour. Technically, our construction is based on the notion of quotient automata and language equivalent states. Both concepts are well known for plain automata (see e.g. Hopcroft and Ullman 1979), and we present a nearby adaption for our use case of deterministic max-plus automata.

Definition 7

For a given equivalence relation ≈ on the set of states Q of the max-plus automaton G = (Q, A,{q₀}, δ), we define the quotient automaton G_≈ = (Q_≈, A,{[q₀]}, δ_≈) where

• Q_≈ is the set of all equivalence classes in Q, i.e., Q_≈ := {[q]|q ∈ Q},

• A is the alphabet of event symbols,

• [q₀] is the equivalence class with the initial state q₀,

• $\delta _{\approx } \colon Q_{\approx } \times A \times Q_{\approx } \rightarrow \mathbb {R}_{max}$ is defined for arguments $([p],a,[p^{\prime }])\in Q_{\approx } \times A \times Q_{\approx }$ by

  $$ \delta_{\approx} ([p],a,[p^{\prime}]) := \max\{ \delta (q,a,q^{\prime}) | q \in [p],\ q^{\prime} \in [p^{\prime}] \} . $$

In general, a quotient automaton realizes a “larger” behaviour than the original automaton in that it (a) picks up words in the logical behaviour that are not possible in the original automaton and in that it (b) provides a pessimistic estimate on the respective minimum duration; i.e., we have $y_{G_{\approx }}(w)\ge y_{G}(w)$ for all w ∈ A^∗. However, the behaviour is maintained exactly, provided that we only merge so called behavioural equivalent states.

Definition 8

Let G = (Q, A,{q₀}, δ) be a max-plus automaton. For r, s ∈ Q we denote G_r = (Q, A, r, δ) and G_s = (Q, A, s, δ) the respective automaton obtained by substituting the initial state. Then, the two states r and s are called behavioural equivalent if $y_{G_{r}}(w) = y_{G_{s}}(w)$ for all w ∈ A^∗. This is denoted by $r\overset {\text {bhv}}{\sim } s$ and defines the behaviour equivalency $\overset {\text {bhv}}{\sim }$ on Q associated with the automaton G.

As with plain automata (see e.g. Hopcroft and Ullman 1979), it can be verified by induction over the length of words that G and $G_{\overset {\text {bhv}}{\sim }}$ and G exhibit the same behaviour; note that this fact crucially relies on determinism and does not carry over to the general case of non-deterministic max-plus automata.

Lemma 2

Let G = (Q, A,{q₀}, δ) be a max-plus automaton with behaviour equivalency $\overset {\text {bhv}}{\sim }$ on Q and consider the quotient automaton $G_{\overset {\text {bhv}}{\sim }}$. Then $y_{G_{\overset {\text {bhv}}{\sim }}}(w)= y_{G}(w)$ for all w ∈ A^∗.

Proof

As a preliminary observation, we note that $\overset {\text {bhv}}{\sim }$ is a right congruence, i.e., the equivalence of two states is retained under the execution of transitions with the same label.

For the induction hypothesis, assume that $y_{G}(w)= y_{G_{\overset {\text {bhv}}{\sim }}}(w)$ for some w ∈ A^∗. If $y_{G_{\overset {\text {bhv}}{\sim }}}(w)=y_{G}(w)\ge 0$, there exists a unique run π_G of G associated with w that ends in a final state q ∈ Q and, as part of our induction hypothesis, we assume that there also exists a unique run $\pi _{G_{\overset {\text {bhv}}{\sim }}}$ of $G_{\overset {\text {bhv}}{\sim }}$ associated with w that ends in the final state [q] ∈ Q_≈.

For the base case, we have w = λ and observe $y_{G}(\lambda )=0=y_{G_{\overset {\text {bhv}}{\sim }}}(\lambda )$ with the unique trivial runs $\pi _{G_{\overset {\text {bhv}}{\sim }}}$ and $\pi _{G_{\overset {\text {bhv}}{\sim }}}$ consisting of the respective initial states q₀ ∈ Q and [q₀] ∈ Q_≈. This established the induction hypothesis for w = λ.

For the induction step, consider the hypothesis for a specific w ∈ A^∗ and one extra symbol a ∈ A. In the case of $y_{G}(w)=y_{G_{\overset {\text {bhv}}{\sim }}}(w)=\epsilon$, there exists no matching run and we observe $y_{G}(wa)=y_{G_{\overset {\text {bhv}}{\sim }}}(wa)=\epsilon$ to conclude the induction step. From now on we consider $y_{G}(w)=y_{G_{\overset {\text {bhv}}{\sim }}}(w)=d\ge 0$, i.e., by determinism of G we have a unique run π_G of G with associated word w and some final state q ∈ Q and by the induction hypothesis we have a unique run $\pi _{G_{\overset {\text {bhv}}{\sim }}}$ of $G_{\overset {\text {bhv}}{\sim }}$ with associated word w and final state [q] ∈ Q_≈. We again distinguish two cases.

For case (a) we assume that G can execute a in state q. By the determinism of G, we pick the unique $q^{\prime }\in Q$ and $d^{\prime }\ge 0$ such that $\delta (q,a,q^{\prime })=d^{\prime }$. Thus, we obtain a run $\pi ^{\prime }_{G}$ of G with associated word wa and with final state $q^{\prime }$ and we observe that $y_{G}(wa)=d+d^{\prime }$. By the definition of $\overset {\text {bhv}}{\sim }$, we observe that $y_{G_{q}}(a)=y_{G_{p}}(a)=d^{\prime }$ for all p ∈ [q]. Now pick an arbitrary p ∈ [q]. Determinism of G then implies the unique existence of $p^{\prime }\in Q$ with $\delta (p,a,p^{\prime })=d^{\prime }$. Referring to our preliminary observation that $\overset {\text {bhv}}{\sim }$ is a right congruence, we also have $p^{\prime }\in [q^{\prime }]$. Since p ∈ [q] was chosen arbitrarily, we obtain $\delta _{\approx }([q],a,[q^{\prime }])=d^{\prime }$ and δ_≈([q], a, r) = 𝜖 for all $r\neq [q^{\prime }]$. Hence, there exists a unique run $\pi ^{\prime }_{G_{\overset {\text {bhv}}{\sim }}}$ of $G_{\overset {\text {bhv}}{\sim }}$ with associated word wa and final state $[q^{\prime }]\in Q_{\approx }$. In particular, and we have that $y_{G_{\overset {\text {bhv}}{\sim }}}(wa)=d+d^{\prime }=y_{G}(wa)$. This concludes the induction step for case (a).

For case (b), we assume that G can not execute a in state q. We then have $y_{G_{q}}(a)=\epsilon$ and, hence, y_G(wa) = 𝜖. By the definition of $\overset {\text {bhv}}{\sim }$, this implies $y_{G_{p}}(a)=\epsilon$ for any p ∈ [q] and, thus, $\delta (p,a,p^{\prime })=\epsilon$ for any p ∈ [q] and any $p^{\prime }\in Q$. Thus, we obtain $\delta _{\approx } ([q],a,[q^{\prime }])=\epsilon$ for any $q^{\prime }\in Q$. Regarding $G_{\overset {\text {bhv}}{\sim }}$, this implies $y_{G_{\overset {\text {bhv}}{\sim }}}(wa)=\epsilon$. This concludes the induction step for case (b). □

For our specific use-case, we now seek for an equivalence relation on $Q={\mathscr{M}}\times \boldsymbol {{\mathscr{C}}}$ that is (a) at least as fine as the behaviour equivalence and that (b) obviously leads to a finite quotient automaton. To this end, our conjecture is that we can limit the value c_t of each entry in the clock component by the corresponding duration parameter τ_t without affecting the future behaviour. This is expressed by the following candidate equivalence.

Definition 9

Consider the automaton $G=(Q,\mathcal {T},\{(M_{0},C_{0})\},\delta )$ derived from a timed Petri net $(\mathcal {G},\tau )$ as in Section 5.1 and with state set $Q={\mathscr{M}}\times \boldsymbol {{\mathscr{C}}}$. A pair of states $(M,C),\ (\tilde {M},\tilde {C})\in Q$ is called clock equivalent, denoted by $(M,C) \overset {\text {clk}}{\sim } (\tilde {M},\tilde {C})$, if and only if

$$ M=\tilde{M}\quad\text{and}\quad\forall t \in \mathcal{T}: \min(\tau_{t},c_{t}) = \min(\tau_{t},\tilde{c}_{t}) $$

(51)

In other words, two states are declared clock equivalent if their marking matches and if all clock entries either match exactly or are both at least as high as the corresponding timing parameter, i.e., the clock entries can only differ for two transitions which are both eligible to fire. For integer valued timing parameters, the quotient automaton w.r.t. clock equivalence $\overset {\text {clk}}{\sim }$ is obviously finite. As with pure race-semantics, this carries over to rational timing parameters by suitable scaling. The following technical lemma is in support of our main result, in which we establish that clock equivalence is indeed at least as fine as behaviour equivalence.

Lemma 3

Consider the automaton $G=(Q,\mathcal {T},\{(M_{0},C_{0})\},\delta )$ derived from a timed Petri net $(\mathcal {G},\tau )$ as in Section 5.1 and with state set $Q={\mathscr{M}}\times \boldsymbol {{\mathscr{C}}}$. Let $(M,C),\ (M,\tilde {C})\in Q$ be a pair of clock equivalent states, i.e., $(M,C) \overset {\text {clk}}{\sim } (M,\tilde {C})$. Then, for any $w \in \mathcal {T}^{*},\ d \in \mathbb {R}_{\geq 0},\ (M^{\prime },C^{\prime }) \in Q$ such that

$$ (M,C) \xrightarrow{w/d} (M^{\prime},C^{\prime}), $$

there exists some $\tilde {C}^{\prime }\in \boldsymbol {{\mathscr{C}}}$ such that $(M^{\prime },C^{\prime }) \overset {\text {clk}}{\sim } (M^{\prime },\tilde {C}^{\prime })$ and such that

$$ (M,\tilde{C}) \xrightarrow{w/d} (M^{\prime},\tilde{C}^{\prime}). $$

Proof

We will proof Lemma 3 by induction over the length of w.

Initial case: Let w = λ. Then we have d = 0 by definition and we can choose $\tilde {C}^{\prime }=C^{\prime }=C$ as a qualifying clock component. Induction hypothesis: Suppose for some specific $w \in \mathcal {T}^{*},\ d \in \mathbb {R}_{\geq 0},\ (M^{\prime },C^{\prime }) \in Q$ with

$$ \begin{array}{@{}rcl@{}} (M,C) \xrightarrow{w/d} (M^{\prime},C^{\prime}) , \end{array} $$

(52)

there exists $\tilde {C}^{\prime }\in \boldsymbol {{\mathscr{C}}}$ such that $(M^{\prime },C^{\prime }) \overset {\text {clk}}{\sim } (M^{\prime },\tilde {C}^{\prime })$ and

$$ (M,\tilde{C}) \xrightarrow{w/d} (M^{\prime},\tilde{C}^{\prime}). $$

(53)

Induction step: We now consider any $a \in \mathcal {T},\ d_{2}\ \in \mathbb {R}_{\geq 0}$ and $(M^{\prime \prime },C^{\prime \prime }) \in Q$ such that

$$ (M,C) \xrightarrow{wa/d_{2}} (M^{\prime\prime},C^{\prime\prime}) . $$

(54)

By the iterative definition of the weighted transitions for words this implies the existence of $d_{1}\in \mathbb {R}_{\geq 0}$ such that

$$ (M^{\prime},C^{\prime}) \xrightarrow{a/d_{1}} (M^{\prime\prime},C^{\prime\prime}) , $$

(55)

and, more specifically, that we must have d₂ = d + d₁. Turning to the definition of individual transitions, we observe that conditions (i)–(vi) in Eq. 50 are to be satisfied, e.g., we clearly have that $a\in \text {En}(M^{\prime })$. We now seek to establish a corresponding transition from state $(M^{\prime },\tilde {C}^{\prime })$. For an argument by contradiction, assume that transition a cannot fire in state $(M^{\prime },\tilde {C}^{\prime })$. Inspecting again conditions (i)–(vi) in Eq. 50, and recalling that $a\in \text {En}(M^{\prime })$, this implies that condition (ii’) is violated, i.e., transition a is not fast enough. Then, there exists a transition $t \in \text {En}(M^{\prime }) \cap \mathcal {T}_{\mathrm {u}}$ such that $\tau _{t} - \tilde {c}^{\prime }_{t} < \tau _{a} - \tilde {c}^{\prime }_{a}$. Since t is uncontrollable, its firing cannot be delayed or disabled and thus corresponds to race policy behaviour. With regard to Lemma 1 we conclude that $\tilde {c}^{\prime }_{t}$ is bounded by τ_t. Utilizing $(M^{\prime },C^{\prime }) \overset {\text {clk}}{\sim } (M^{\prime },\tilde {C}^{\prime } )$ we obtain $\tilde {c}^{\prime }_{t} = c^{\prime }_{t}$. Additionally

$$ 0 \leq \tau_{t} - \tilde{c}^{\prime}_{t} < \tau_{a} - \tilde{c}^{\prime}_{a} \implies \tau_{a} - \tilde{c}^{\prime}_{a} > 0 $$

(56)

and as such $\tilde {c}^{\prime }_{a} = \min \limits (\tau _{a},\tilde {c}^{\prime }_{a}) = \min \limits (\tau _{a},c^{\prime }_{a}) = c^{\prime }_{a}$. Thus, we have $\tau _{t} - c^{\prime }_{t} < \tau _{a} - c^{\prime }_{a}$, and, hence, a contradiction to Eq. 55, more specifically to condition (ii’) in Eq. 50.

This concludes our argument by contradiction, and hence there must exist some some $\tilde {d}_{1} \in \mathbb {R}_{\geq 0}$ and $\tilde {C}^{\prime \prime }\in \boldsymbol {{\mathscr{C}}}$ with

$$ (M^{\prime},\tilde{C}^{\prime}) \xrightarrow{a/\tilde{d}_{1}} (M^{\prime\prime},\tilde{C}^{\prime\prime}) . $$

(57)

To show that both durations d₁ and $\tilde {d}_{1}$ match, we refer to Eq. 50, condition (iii’), and indeed obtain by utilizing (51)

$$ \begin{array}{@{}rcl@{}} d_{1} &=& \max(\tau_{a} - c_{a}^{\prime},0) \\ &=& \tau_{a} - \min(\tau_{a},c_{a}^{\prime}) \\ &=& \tau_{a} - \min(\tau_{a},\tilde{c}_{a}^{\prime})\\ &=& \max(\tau_{a} - \tilde{c}_{a}^{\prime},0)\\ &=& \tilde{d}_{1} , \end{array} $$

and, hence,

$$ (M^{\prime},\tilde{C}^{\prime}) \xrightarrow{a/d_{1}} (M^{\prime\prime},\tilde{C}^{\prime\prime}) . $$

(58)

This in turn implies

$$ (M,C) \xrightarrow{wa/d_{2}} (M^{\prime\prime},\tilde{C}^{\prime\prime}) . $$

(59)

Observe that incrementing both clock vectors $C^{\prime }$ and $\tilde {C}^{\prime }$, see Eqs. 17 and 50, condition (iv), with the same $d_{1} \in \mathbb {R}_{\geq 0}$ retains clock equivalency. Furthermore, as the marking component initially is $M^{\prime }$ in both transitions the effect of the operators Reset and Sub, see Eqs. 19 and 20, is the same on $C^{\prime }$ and $\tilde {C}^{\prime }$. Thus we obtain $(M^{\prime \prime },C^{\prime \prime }) \overset {\text {clk}}{\sim } (M^{ \prime \prime },\tilde {C}^{\prime \prime })$. This concludes the induction step. □

As a consequence of Lemma 3 we can now formulate the main result of this section and identify classes of behaviour equivalent states.

Theorem 2

Consider the automaton $G=(Q,\mathcal {T},\{(M_{0},C_{0})\},\delta )$ derived from a timed Petri net $(\mathcal {G},\tau )$ as in Section 5.1 and with state set $Q={\mathscr{M}}\times \boldsymbol {{\mathscr{C}}}$. Then for any pair of states $(M,C),\ (M,\tilde {C})\in Q$ we have that

$$ (M,C) \overset{\text{clk}}{\sim} (M,\tilde{C}) \implies (M,C) \overset{\text{bhv}}{\sim} (M,\tilde{C}) , $$

(60)

i.e., clock equivalence is at least as fine as behaviour equivalence.

Proof

We denote r = (M, C) and $s=(M,\tilde {C})$ and consider any $w \in \mathcal {T}^{*}$. In the case of $y_{G_{r}}(w) = d\in \mathbb {R}_{\geq 0}$, we refer to Lemma 3 and choose $r^{\prime }, s^{\prime } \in Q$ such that

$$ r \xrightarrow{w/ d} r^{\prime} \quad\text{and}\quad s \xrightarrow{w/ d} s^{\prime} , $$

(61)

and, hence, $y_{G_{s}}(w) = d = y_{G_{r}}(w)$. If, on the other hand, $y_{G_{r}}(w) = \varepsilon$ we must also have $y_{G_{s}}(w) = \varepsilon$, since $y_{G_{s}}(w)\neq \varepsilon$ by Lemma 3 would imply $y_{G_{r}}(w)=y_{G_{s}}(w)\in \mathbb {R}_{\geq 0}$. In both cases, we have obtained $y_{G_{s}}(w) = y_{G_{r}}(w)$. This constitutes behaviour equivalence of r and s. □

As a consequence the quotient automaton $G_{\mathbin {\overset {\text {clk}}{\sim }}}$ realizes the same behaviour as G while having a finite set of states. The resulting upper bound on the number of states is the same as in the race policy considerations.

5.3 Algorithmic procedure

Akin to the first procedure we now present an equivalent representation in the form of an algorithm; see Procedure 2. In the iterative construction process we choose for each equivalence class one state as a representative. This is done in line 12 by imposing the transition durations as an upper bound. Note that Procedure 2 yields the same result as Procedure 1, if no transitions are considered controllable, i.e., if $\mathcal {T} = \mathcal {T}_{\mathrm {u}}$.

6 Example in the context of supervisor design

In the situation where the timed Petri net represents a plant model and if its behaviour fails to satisfy a prescribed specification, we seek a supervisory controller to enforce the specification in closed-loop configuration. As with conventional controllers, a supervisor can only restrict the plant behaviour. Hence, the latter must be given as an open-loop behaviour to serve the purpose of controller design. In this section we demonstrate by a simple engineering application how max-plus automata obtained from timed Petri nets under open-loop race policy forms an adequate basis for the design of a supervisor.

Consider the timed Petri net $(\mathcal {G},\tau )$ given by Fig. 3 as the model of a thermal cycle, where work pieces are alternatively heated or cooled. The work pieces are represented by tokens in the left loop. In compliance with single server semantics only one work piece can be processed at a time. In this regard the heating process b is only possible if a work piece has arrived and the waste heat valve is closed for two time units, indicated by a token in P₃ used by b. Thereafter the work piece has reached its desired temperature and has to leave the oven in order to avoid damage, i.e., the supervisor shall not disable transition b, hence our choice of $b\in \mathcal {T}_{\mathrm {u}}$. As a means to reset the temperature in the oven, waste heat can be removed over one time unit to be used for other purposes. The token in P₃ acting as a shared resource implements this aspect of the physical plant. Furthermore, a work piece getting cooled for longer than three time units does no harm and the valve position can be set as desired, i.e. $a,\ c \in \mathcal {T}_{\mathrm {c}}$. To this end, our transitions are partitioned by $\mathcal {T}_{\mathrm {c}} = \{a,c\}$ and $\mathcal {T}_{\mathrm {u}} = \{b\}$.

Fig. 3

A thermal cycle application modelled by $(\mathcal {G},\tau )$ with $\mathcal {T}_{\mathrm {c}} = \{a,c\}$ and $\mathcal {T}_{\mathrm {u}} = \{b\}$

We now invoke Procedure 2 to build a max-plus automaton with timed behaviour that represents all feasible sequences of transitions in the timed Petri net under open-loop race policy. The resulting max-plus automaton $G_{*}=(Q,\mathcal {T},Q_{0},\delta )$ is depicted in Fig. 4. For easier identification, the states of G_∗ are additionally labelled with Roman numerals. A path in G_∗ represents a firing sequence of transitions and the associated duration in the timed Petri net. For the given input data we observe a greatly increased behaviour compared to Procedure 1, addressing plain race policy, as in this case only transition c would ever be able to fire.

Fig. 4

max-plus automaton G_∗

To further illustrate the usage of the constructed automaton we consider the following additional requirements:

• 1) the cooling station can only accommodate one work piece, i.e., capacity of P₁ is one;

• 2) two work pieces have to remain in the left loop at all times;

• 3) the heating and cooling processes have to alternate and complete two iterations;

• 4) the process is to be executed with minimal duration.

Requirement 2) is achieved by virtue of the chosen initial marking. Upholding 3) automatically implies that 1) is guaranteed. Time optimality and 4) will be attended after the logical requirements are met. Thus, at this stage we are left to address a purely logical closed-loop language-inclusion specification given by the upper bound L_spec = (c^∗bc^∗ac^∗)², i.e., we require two cycles of transitions b followed by a and do not need to care about c. Technically, this can be expressed by the plain automaton G_spec = (X, Σ, x₀, f, X_m) with state set X = {A, B, C, D, E}, alphabet Σ = {a, b}, initial state x₀ = A, partial transition function $f \colon X \times {{\varSigma }} \rightarrow X$ and set of marked states X_m = {E}; see Fig. 5 for a graphical representation.

Fig. 5

Specification automaton G_spec

We can now use the parallel composition of G_∗ and G_spec to obtain all paths in G_∗ that satisfy the language-inclusion specification, technically defined by

$$ G_{*} \parallel G_{\text{spec}}:= (Q \times X, \mathcal{T} \cup {{\varSigma}}, (Q_{0},x_{0}),{\varrho}, Q \times X_{m} ) $$

(62)

where

$$ {\varrho}((q,x),a,(q^{\prime},x^{\prime})) = \begin{cases} \delta(q,a,q^{\prime}),&~\text{if } a \in {{\varSigma}} \text{ and } x^{\prime}=f(x,a) \\ \delta(q,a,q^{\prime}),&~\text{if } a \notin {{\varSigma}} \text{ and } x^{\prime}=x\\ \varepsilon,&~\text{else.} \end{cases} $$

(63)

The result of this operation is represented in Fig. 6. The accepted language of G_∗∥ G_spec consists of all possible open-loop sequences of transitions that fulfil the specification. Note that at this stage a supervisor at instances can also disable uncontrollable transitions by prioritising a faster alternative transition. E.g., in state II a supervisor may schedule the faster transition c and thereby disable the uncontrollabale transition b. At a final stage, we may apply Dijkstra’s algorithm in order to find time optimal solutions. In this context we are interested in the path with the lowest weight from the initial state to any accepted state. For this example, we obtain the following five time optimal paths

$$ \begin{array}{@{}rcl@{}} w_1 = bcabca,& &y_{G_* \vert \vert G_{\text{spec}}}(w_1) = 8, \end{array} $$

(64)

$$ \begin{array}{@{}rcl@{}} w_2 = bcabcac,& &y_{G_* \vert \vert G_{\text{spec}}}(w_2) = 8, \end{array} $$

(65)

$$ \begin{array}{@{}rcl@{}} w_3 = bcabcca,& &y_{G_* \vert \vert G_{\text{spec}}}(w_3) = 8, \end{array} $$

(66)

$$ \begin{array}{@{}rcl@{}} w_4 = bcabccac,& &y_{G_* \vert \vert G_{\text{spec}}}(w_4) = 8, \end{array} $$

(67)

$$ \begin{array}{@{}rcl@{}} w_5 = bcabccca,& &y_{G_* \vert \vert G_{\text{spec}}}(w_5) = 8. \end{array} $$

(68)

A supervisor that enforces any of the above sequences of transitions will guarantee that the given requirements are upheld.

Fig. 6

Parallel composition G_∗||G_spez (accessible part only)

7 Conclusion

The main technical contribution of this paper, Theorems 1 and 2, establishes terminating procedures for the conversion of a timed Petri net to a deterministic finite max-plus automaton while retaining the timed behaviour. The assumptions imposed on the Petri net are boundedness, single server semantics, injective labelling, rational timing parameters, and operation under race policy. Although our argument follows the same line of thought as Komenda et al. (2016), our result is more general in that we do not need to impose fairness requirements on the Petri net. Moreover, we optionally account for controllable transitions, i.e., transitions that can be temporarily disabled by a supervisory controller. For this situation, our algorithm constructs a deterministic finite max-plus automaton which in open-loop is behaviour equivalent to the provided timed Petri net. Hence, the automaton representation is a suitable basis for supervisory controller design. This is demonstrated by example. For future work, we envisage a more formal discussion of control objectives and the resulting controller synthesis problem.