Stochastic inverse modeling and global sensitivity analysis to assist interpretation of drilling mud losses in fractured formations

Abstract

This study is keyed to enhancing our ability to characterize naturally fractured reservoirs through quantification of uncertainties associated with fracture permeability estimation. These uncertainties underpin the accurate design of well drilling completion in heterogeneous fractured systems. We rely on monitored temporal evolution of drilling mud losses to propose a non-invasive and quite inexpensive method to provide estimates of fracture aperture and fracture mud invasion together with the associated uncertainty. Drilling mud is modeled as a yield power law fluid, open fractures being treated as horizontal planes intersecting perpendicularly the wellbore. Quantities such as drilling fluid rheological properties, flow rates, pore and dynamic drilling fluid pressure, or wellbore geometry, are often measured and available for modeling purposes. Due to uncertainty associated with measurement accuracy and the marked space–time variability of the investigated phenomena, we ground our study within a stochastic framework. We discuss (a) advantages and drawbacks of diverse stochastic calibration strategies and (b) the way the posterior probability densities (conditional on data) of model parameters are affected by the choice of the inverse modeling approach employed. We propose to assist stochastic model calibration through results of a moment-based global sensitivity analysis (GSA). The latter enables us to investigate the way parameter uncertainty influences key statistical moments of model outputs and can contribute to alleviate computational costs. Our results suggest that combining moment-based GSA with stochastic model calibration can lead to significant improvements of fractured reservoir characterization and uncertainty quantification.

Appendices

Appendix 1: Derivation of the analytical model and theoretical analysis

The momentum Eq. (1) and the strain rate tensor, $\varvec{\bar{\gamma } }$, in cylindrical coordinates read

$$\left\{ {\begin{array}{*{20}l} {\rho \frac{{dv_{r} }}{dt} = - \frac{{\partial p^{\prime}}}{\partial r} - \frac{{\partial \tau_{Y} }}{\partial r} - k\left[ {\frac{{\partial \gamma_{rr}^{m} }}{\partial r} + \frac{1}{r}\frac{{\partial \gamma_{\theta r}^{m} }}{\partial \theta } + \frac{{\partial \gamma_{zr}^{m} }}{\partial z} + \frac{1}{r}\left( {\gamma_{rr}^{m} - \gamma_{\theta \theta }^{m} } \right)} \right]} \hfill \\ {\rho \frac{{dv_{\theta } }}{dt} = - \frac{1}{r}\frac{{\partial p^{\prime}}}{\partial \theta } - \frac{1}{r}\frac{{\partial \tau_{Y} }}{\partial \theta } - k\left[ {\frac{{\partial \gamma_{r\theta }^{m} }}{\partial r} + \frac{1}{r}\frac{{\partial \gamma_{\theta \theta }^{m} }}{\partial \theta } + \frac{{\partial \gamma_{z\theta }^{m} }}{\partial z} + \frac{1}{r}\left( {\gamma_{r\theta }^{m} + \gamma_{\theta r}^{m} } \right)} \right]} \hfill \\ {\rho \frac{{dv_{z} }}{dt} = - \rho g - \frac{{\partial p^{\prime}}}{\partial z} - \frac{{\partial \tau_{Y} }}{\partial z} - k\left[ {\frac{{\partial \gamma_{rz}^{m} }}{\partial r} + \frac{1}{r}\frac{{\partial \gamma_{\theta z}^{m} }}{\partial \theta } + \frac{{\partial \gamma_{zz}^{m} }}{\partial z} + \frac{{\gamma_{rz}^{m} }}{r}} \right]} \hfill \\ \end{array} } \right.$$

(17)

$$\bar{\varvec{\gamma }} = \left[ {\begin{array}{*{20}c} {\frac{{\partial v_{r} }}{\partial r}} & {\frac{1}{2}\left( {r\frac{\partial }{\partial r}\frac{{v_{\theta } }}{r} + \frac{1}{r}\frac{{\partial v_{r} }}{\partial \theta }} \right)} & {\frac{1}{2}\left( {\frac{{\partial v_{r} }}{\partial z} + \frac{{\partial v_{z} }}{\partial r}} \right)} \\ {\frac{1}{2}\left( {r\frac{\partial }{\partial r}\frac{{v_{\theta } }}{r} + \frac{1}{r}\frac{{\partial v_{r} }}{\partial \theta }} \right)} & {\frac{1}{r}\frac{{\partial v_{\theta } }}{\partial \theta } + \frac{{\partial v_{r} }}{\partial r}} & {\frac{1}{2}\left( {\frac{{\partial v_{\theta } }}{\partial z} + \frac{1}{r}\frac{{\partial v_{z} }}{\partial \theta }} \right)} \\ {\frac{1}{2}\left( {\frac{{\partial v_{r} }}{\partial z} + \frac{{\partial v_{z} }}{\partial r}} \right)} & {\frac{1}{2}\left( {\frac{{\partial v_{\theta } }}{\partial z} + \frac{1}{r}\frac{{\partial v_{z} }}{\partial \theta }} \right)} & {\frac{{\partial v_{z} }}{\partial z}} \\ \end{array} } \right].$$

(18)

Considering laminar flow (i.e., $v_{\theta } = v_{z} = 0$), the problem is axisymmetric (i.e., $\frac{{\partial v_{r} }}{\partial \theta } = \frac{\partial p'}{\partial \theta } = 0$) and (17)–(18) reduce to

$$\left\{ {\begin{array}{*{20}l} {\rho \left( {\frac{{\partial v_{r} }}{\partial t} + v_{r} \frac{{\partial v_{r} }}{\partial r}} \right) = - \frac{{\partial p^{\prime}}}{\partial r} - k\left[ {\frac{1}{r}\frac{{\partial \left( {r\gamma_{rr}^{m} } \right)}}{\partial r} + \frac{{\partial \gamma_{zr}^{m} }}{\partial z} - \frac{{\gamma_{\theta \theta }^{m} }}{r}} \right]} \hfill \\ {} \hfill \\ {0 = - \rho g - \frac{{\partial p^{\prime}}}{\partial z} - k\left[ {\frac{{\partial \gamma_{rz}^{m} }}{\partial r} + \frac{{\gamma_{rz}^{m} }}{r}} \right]} \hfill \\ \end{array} } \right.$$

(19)

$$\bar{\varvec{\gamma }} = \left[ {\begin{array}{*{20}c} {\frac{{\partial v_{r} }}{\partial r}} & 0 & {\frac{1}{2}\frac{{\partial v_{r} }}{\partial z}} \\ 0 & {\frac{{v_{r} }}{r}} & 0 \\ {\frac{1}{2}\frac{{\partial v_{r} }}{\partial z}} & 0 & 0 \\ \end{array} } \right].$$

(20)

Substituting (20) into (19) yields

$$\left\{ {\begin{array}{*{20}l} {\rho \left( {\frac{{\partial v_{r} }}{\partial t} + v_{r} \frac{{\partial v_{r} }}{\partial r}} \right) = - \frac{{\partial p^{\prime}}}{\partial r} - k\left[ {\frac{1}{r}\frac{\partial }{\partial r}\left( {\frac{{\partial rv_{r} }}{\partial r}} \right)^{m} + \frac{\partial }{\partial z}\left( {\frac{{\partial v_{r} }}{\partial z}} \right)^{m} - \frac{1}{r}\left( {\frac{{v_{r} }}{r}} \right)^{m} } \right]} \hfill \\ {0 = - \rho g - \frac{{\partial p^{\prime}}}{\partial z} - k\left[ {\frac{\partial }{\partial r}\left( {\frac{1}{2}\frac{{\partial v_{r} }}{\partial z}} \right)^{m} + \frac{1}{r}\left( {\frac{1}{2}\frac{{\partial v_{r} }}{\partial z}} \right)^{m} } \right]} \hfill \\ \end{array} } \right..$$

(21)

Making use of mass conservation, i.e., $\left( {\partial \left( {rv_{r} } \right)} \right)/\partial r$ = 0, considering that the viscous term is dominant over the inertial one, i.e., $\rho \frac{{\partial v_{r} }}{\partial t} \ll k\left[ {\frac{\partial }{\partial z}\left( {\frac{{\partial v_{r} }}{\partial z}} \right)^{m} } \right]$, noting that $\left( {\frac{{\partial v_{r} }}{\partial r} \ll \frac{{\partial v_{r} }}{\partial z}} \right)$ and

$$\frac{\partial }{\partial r}\left( {\frac{{\partial v_{r} }}{\partial z}} \right)^{m} = m\left( {\frac{{\partial v_{r} }}{\partial z}} \right)^{m - 1} \frac{{\partial^{2} v_{r} }}{\partial r\partial z} = m\left( {\frac{{\partial v_{r} }}{\partial z}} \right)^{m - 1} \frac{\partial }{\partial z}\left( { - \frac{{v_{r} }}{r}} \right) = - \frac{m}{r}\left( {\frac{{\partial v_{r} }}{\partial z}} \right)^{m}$$

(22)

and introducing the quantity $p = p^{\prime} + \rho g$, (21) becomes

$$\left\{ {\begin{array}{*{20}l} {\frac{\partial p}{\partial r} = - k\frac{\partial }{\partial z}\left[ {\left( {\frac{{\partial v_{r} }}{\partial z}} \right)^{m} } \right]} \\ {\frac{\partial p}{\partial z} = - \frac{k}{r}\frac{{\left( {1 - m} \right)}}{{2^{m} }}\left( {\frac{{\partial v_{r} }}{\partial z}} \right)^{m} } \\ \end{array} .} \right.$$

(23)

Note that the vertical gradient of p (1) vanishes when $m = 1$ (i.e., for a Newtonian or Bingham plastic fluid) and (2) decreases as the distance from the pumping well, $r$, increases. Therefore, pressure is hydrostatic when $m = 1$ or tends to become hydrostatic (for $m$ ≠ 1) as the distance from the well increases.

The mud flow rate, $Q$, can be obtained by integrating (7) along the fracture aperture, resulting in

$$Q = \pi rw^{2} \left( {\frac{m}{2m + 1}} \right)\left[ { - \frac{w}{2k}\frac{\partial p}{\partial r}} \right]^{{\frac{1}{m}}} \left[ {1 + \frac{2}{w}\left( {\frac{2m + 1}{m + 1}} \right)\frac{{\tau_{Y} }}{{\frac{ \partial p}{\partial r}}}} \right]^{{\frac{1}{m}}} .$$

(24)

Evaluating $Q^{m}$ from (24), expanding $Q^{m}$ as a Taylor series in terms of $\tau_{Y} /\left( { - \frac{w}{2}\frac{ \partial p}{\partial r}} \right)$ and retaining only the first two terms in the expansion, yields the following approximate solution for the pressure gradient:

$$- \frac{\partial p}{\partial r} = \frac{2 }{w}\left( {\frac{{kQ^{m} }}{{\left[ { \pi r\frac{m}{2m + 1}w^{2} } \right]^{m} }} + \frac{2m + 1}{m + 1}\tau_{Y} } \right) .$$

(25)

A closed-form expression for $\Delta p = p_{w} - p_{f}$ can be obtained by integrating (25) from the wellbore radius, $r_{w}$ (with pressure p_w), to the mud front $r_{f}$ (with pressure $p_{f}$), as:

$$\Delta p = \frac{2 }{w}\frac{{k Q^{m} \left( {r_{f}^{1 - m} - r_{w}^{1 - m} } \right)^{{}} }}{{\left( {1 - m} \right)\left( { \pi \frac{m}{2m + 1} w^{2} } \right)^{m}_{ } }} + \frac{{2\tau_{Y} }}{w}\frac{2m + 1}{m + 1}\left( {r_{f} - r_{w} } \right).$$

(26)

Appendix 2: Particle swarm optimization algorithm

We start by introducing the vector x of N_p × N entries. The optimal choice for the number of particles N_p to sample the N-dimensional parameter space (N = 5 in our example) is problem-dependent. The results included in Sect. 5 have been obtained with N_p = 50, similar findings being achieved with 40 ≤ N_p ≤ 80.

PSO is implemented according to the following steps:

• 1. Step i = 0. Random selection of a number N_p of points x₀(j) with j = 1,…, N_p within the N-dimensional parameter space together with a random value of a displacement vector v₀(j).

• 2. Displace the N_p particles within the N-dimensional space as x_i+1(j) =x_i(j) +v_i(j).

• 3. Evaluate (16) and select the value of j = j_best (i.e., the particle) giving the minimum of (16) and set g_best=x_best = x(j_best).

• 4. Evaluate a new displacement v_i+1(j) = $\omega$v_i(j) + c₁U[x_best− x_i(j)] + c₂U[g_best− x_i(j)] where U is a random number uniformly distributed between 0 and 1, c₁ and c₂ are constant coefficients and $\omega$ is a step dependent variable (Lagarias et al. 1998). Here, we follow Rahmat-Samii and Michielssen (1999) and fix c₁ = c₂ = 1.495.

• 5. Update the particle position with the displacement evaluated at step 4, evaluate (16), select the value of j = j_best (i.e., the particle) rendering the minimum of (16) and set x_best = x(j_best). If (16) evaluated with x_best is smaller than (16) evaluated with g_best, set g_best = x_best, otherwise set g_best = g_best.

• 6. Set i = i + 1 and go to Step 2.

Steps 2–6 are repeated until the maximum number of prescribed displacements is reached. We set this quantity to 60 in our application. In order to avoid selection of a local minimum, PSO has been performed upon varying the initial condition x₀, for a total of 800 iterations.

Appendix 3: Acceptance-rejection sampling

The objective of the sampling algorithm ARS is to draw random samples from the posterior pdf of a parameter set collected in vector $\varvec{P},$$f_{{\varvec{P}|\varvec{V}_{m}^{*} }}$, given a vector of $n_{t}$ observed values of $\varvec{V}_{m}^{*}$. According to Bayes’ theorem

$$f_{{\varvec{P}|\varvec{V}_{m}^{*} }} \propto f_{\varvec{P}} f_{{\varvec{V}_{m}^{*} |\varvec{P}}}$$

(27)

where $f_{{\varvec{V}_{m}^{*} |\varvec{P}}}$ is the likelihood function and $f_{\varvec{P}}$ is the prior pdf of P. We assume that $f_{{\varvec{V}_{m}^{*} |\varvec{P}}}$ is multiGaussian, i.e.,

$$f_{{\varvec{V}_{m}^{*} |\varvec{P}}} = \left( {2\uppi \upsigma_{{V_{m} }}^{2} } \right)_{{}}^{{ - n_{t} /2}} {\text{exp}}\left\{ { - \frac{1}{{2\sigma_{{V_{m} }}^{2} }}\left[ {\varvec{V}_{\varvec{m}}^{\varvec{*}} - \varvec{V}_{\varvec{m}} \left( \varvec{P} \right)} \right]^{T} \left[ {\varvec{V}_{\varvec{m}}^{\varvec{*}} - \varvec{V}_{\varvec{m}} \left( \varvec{P} \right)} \right]} \right\}$$

(28)

where $\sigma_{{V_{m} }}^{{}}$ is the standard deviation of the measurement errors (which we set to $0.01$ and 0.1, for event 3 and 4, respectively, in our application example).

ARS can be used to draw samples from $f_{{\varvec{P}|\varvec{V}_{m}^{*} }}$ according to the following iterative procedure:

• 1. Sample N values from a uniform distribution in the interval (0,1) to obtain normalized parameters.

• 2. Map normalized parameters onto $\varvec{P}$.

• 3. Evaluate (8) to compute the temporal evolution of $\varvec{V}_{\varvec{m}} \left( \varvec{P} \right)$.

Evaluate $\alpha_{i}$ that is the acceptance probability of $\varvec{P}$ as

$$\alpha_{i} = \frac{{f_{{\varvec{V}_{m}^{*} |\varvec{P}}} }}{{{ \hbox{max} }\left\{ {f_{{\varvec{V}_{m}^{*} |\varvec{P}}} } \right\}}} = \exp \left\{ { - \frac{1}{{2\sigma_{{V_{m} }}^{2} }}\left[ {\varvec{V}_{\varvec{m}}^{\varvec{*}} - \varvec{V}_{\varvec{m}} \left( \varvec{P} \right)} \right]^{T} \left[ {\varvec{V}_{\varvec{m}}^{\varvec{*}} - \varvec{V}_{\varvec{m}} \left( \varvec{P} \right)} \right]} \right\}$$

(29)

• 4. Draw a random value u from a uniform distribution in the interval (0,1).

• 5. Accept current realization of $\varvec{P}$ if ${ \ln }\left( u \right) < \ln \left( {\alpha_{i} } \right),$ otherwise reject it and return to Step 1.

Steps 1–6 are repeated until a stable $f_{{\varvec{V}_{m}^{*} |\varvec{P}}}$ is obtained. In our application, convergence has been attained after about $10^{6}$ iterations.

Appendix 4: Posterior probability distribution of model parameters resulting from stochastic inverse modeling

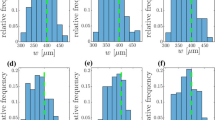
See Fig. 13.

Fig. 13

Sample pdfs of $\tau_{Y} /k\,\, [\text s^{{\text{-m}}}]$ (a, e), $\Delta p/k\,\, [\text s^{{\text{-m}}}]$ (b, f), $m$ (c, g) and $r_{w}\,\, [\text m]$ (d, h) obtained for event a–d 3 and e–h 4 by stochastic inverse modeling implemented via NMS (black dotted curves), PSO (blue curves) and ARS (red curves). Widths of the prior support have been computed from of experimental measurements taking into account measurements errors and relative error propagations