Probabilistic assessment of equivalent fracture aperture constrained on quasi-real-time drilling mud loss data

Abstract

We provide a rigorous workflow to quantify the effects of key sources of uncertainty associated with equivalent fracture aperture estimates w constrained through mud loss information acquired while drilling a well in a reservoir. A stochastic inverse modeling framework is employed to estimate the probability distribution of w. This choice is consistent with the quantity and quality of available data. The approach allows assessing the probability that values of w inferred from mud loss events exceed a given threshold. We rely on a streamlined analytical solution to model mud losses while drilling. We explicitly consider uncertainties associated with model parameters and forcing terms, including drilling fluid rheological properties and flow rates, pore fluid pressure, and dynamic drilling fluid pressure. A synthetic scenario is considered to provide a transparent reference setting against which our stochastic inverse modeling workflow can be appraised. The approach is then applied to a real-case scenario. The latter is associated with data monitored on a rig site. A direct comparison of the impact of data collected through two common techniques (respectively, relying on flow meter sensors or pump strokes) on the ensuing probability of w is provided. A detailed analysis of the uncertainty related to the level of data corruption is also performed, considering various levels of measurement errors. Results associated with the field setting suggest that the proposed workflow yields probability distribution of w that are compatible with interpretations relying on traditional analyses of image logs. Results stemming from direct and indirect flow data display similar shapes. This suggests the viability of the probabilistic inversion methodology to assist quasi-real-time identification of equivalent fracture apertures on the basis of routinely acquired information during drilling.

Introduction

Naturally fractured reservoirs (NFRs) host key hydrocarbon reserves and resources. Recent studies revealed that at least 40% of oil and gas reserves can be linked to NFRs (Zimmerman 2018). These are typically characterized by highly heterogeneous geological structures. Recovery factors associated with these types of reservoirs are often very low. This is mainly a consequence of the inherent complexity of these systems which in turn hampers accurate system characterization. Rapid production decline and early gas or water breakthrough are quite frequent under field conditions. Discriminating between the contribution to production due to the rock matrix or the fractured system component is markedly challenging. In this context, it is recognized that fracture distributions across NFRs play a significant role on flow rates, permeability anisotropy assessment, and hydrocarbon recovery (Nelson 1985). Characterizing the remarkable heterogeneity of these systems requires detailed reservoir studies and high-quality information. Seismic data and studies from analogues are widely used in large-scale field settings (Biber et al. 2018; Takam Takougang et al. 2019). Various types of data acquired while drilling are nowadays available at reservoir and borehole scales. These include, e.g., wireline logs, image logs (Maeso et al. 2015; Patria et al. 2017), core data (Lai et al. 2017), drilling parameters (Xia et al. 2015) and production data. These real- (and quasi-real-)time information can be employed to infer fracture distributions along the borehole and their equivalent aperture. Data on drilling fluid flow are usually available in real-time, mainly due to safety reasons (e.g., for early kick detection). These data play a critical role to aid monitoring drilling performances. Differences between flow in and out of the drilling mud circuit can assist identification of fluid influx into the well and/or mud losses events (Al-Muraikhi et al. 2013).

A vast majority of wells are nowadays equipped with technologies for accurate and real-time monitoring of flow in and out. As mentioned above, these data can also embed valuable information conducive to detection of the presence of fractures and their equivalent aperture. Examples of the use of these types of data in this context are offered by, e.g., Majidi et al. (2008) or Lichun et al. (2014). Analytical formulations to assess the equivalent fracture aperture and to describe the mud flow advancement within a fracture encountered while drilling are proposed by Sawaryn (2001) and Sarkar et al. (2004). A typically non-Newtonian incompressible drilling fluid is considered in a variety of (numerical and analytical) studies (Lavrov 2014; Xia et al. 2015; Salehi et al. 2016; Razavi et al. 2017; Afolabi 2018; Fakoya and Ahmed 2018). Consistent with the work of Canbolat and Parlaktuna (2019), Albattat and Hoteit (2019) introduce an analytical model that can be employed to circumvent the assumption of uniform fracture aperture employed in several studies.

The key objective of this study is to provide a methodology conducive to quasi-real-time estimates of equivalent fracture apertures. In this context, the ensuing estimates of equivalent fracture aperture correspond to a parallel plate system whose hydraulic behavior is equivalent to the one observed through monitored fluid loss rates. Thus, the concept can imbue the effect of a single fracture or of a network of (possibly micro-)fractures whose presence is imprinted onto the pattern of the observed fluid losses (e.g., Verga et al. 2000; Russian et al. 2019). The analysis workflow relies on the real-time information associated with temporal histories of drilling mud losses and on the use of a simple analytical formulation. Mud is modeled as a yield power law fluid (Majidi et al. 2010). Fractures are treated as horizontal planes, perpendicular to the wellbore, within which radial flow conditions take place. Since the parameters associated with the employed interpretive model are typically affected by uncertainty (see Russian et al. 2019), model calibration is addressed in a stochastic inverse modeling framework. As opposed to a deterministic approach which is conducive to a unique solution, a stochastic framework enables us to obtain multiple possible solutions to characterize the considered model and its outputs of interest under uncertainty. Thus, model parameters are characterized in terms of their (posterior) probability distribution, as constrained through available data. In this framework, we focus on the probabilistic assessment of equivalent fracture aperture upon leveraging on routinely monitored mud loss events. These are then used to constrain model calibration and uncertainty quantification. Two commonly used measuring techniques are here considered. We also provide an appraisal of the impact of the associated measurement uncertainty on the quality of the stochastic inversion results.

The study is structured as follows. Section 2 illustrates the employed methodological workflow, including the illustration of the considered analytical model, and the adopted stochastic inverse modeling approach. Section 3 is devoted to the quantitative assessment of our operational framework through a controlled synthetic scenario. An application to a comprehensive dataset acquired while drilling a well across a layered reservoir is illustrated in Sect. 4.

Methodology

Here, we present an overview of the methodological workflow underpinning the study. We also illustrate the key theoretical elements associated with the analytical model considered. We refer to the works of Majidi et al. (2010) and Russian et al. (2019) for the complete set of details. Application and ensuing results are then illustrated in Sects. 3 and 4.

Analytical model

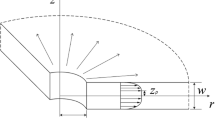
Mud losses monitored while drilling are characterized upon resting on the semi-analytical model introduced by Majidi et al. (2010). The model considers radial flow taking place between two parallel circular disks, mimicking the smooth walls of a fracture of infinite extent. Advancement of mud flow in the system is described through the momentum equation (see Russian et al. 2019 and references therein). The shear stress tensor is defined upon characterizing the mud as a Herschel-Bulkley fluid. The Herschel-Bulkley model can be considered as a generalized model to describe a non-Newtonian fluid. The temporal evolution of mud fluid volume losses, V(t), is evaluated as

$$\begin{aligned} V(t) = \pi w\left( {r_{f}^{2} (t) - r_{w}^{2} } \right) , \end{aligned}$$

(1)

where w is the width of the equivalent fracture aperture (conceptualized as described in Sect. 1), $r_f$ denotes the mud front advancement in the system, and $r_w$ is the well radius. Following Majidi et al. (2010) and Russian et al. (2019), $r_f$ is evaluated through integration of

$$\begin{aligned} \frac{dr_f}{dt}=\frac{\frac{wn}{2(2n+1)}\left( \frac{\Delta p}{k} - \frac{2\tau _Y}{wk} \left( \frac{2n+1}{n+1} \right) \left( r_f - r_w \right) \right) ^{\frac{1}{n}}\left( \frac{w}{2}\left( 1-n\right) \right) ^{\frac{1}{n}}}{r_f\left( r^{1-n}_f-r^{1-n}_w\right) ^{\frac{1}{n}}}, \end{aligned}$$

(2)

here n is an index characterizing the fluid behavior, $\tau _Y$ is the fluid yield stress, k is the fluid consistency index, and $\Delta p$ corresponds to overpressure, i.e., the difference between the dynamic mud pressure and the formation fluid pressure at the well and at the mud front.

The key assumptions underpinning this model are here briefly recounted for completeness. These include the following: (1) laminar radial flow is considered to take place, where viscous forces dominate over inertial forces, and the transverse and vertical velocity components are neglected; (2) variations of radial velocity are much stronger across the fracture thickness than along the radial direction; (3) a constant pressure drop $\Delta p$ drives the drilling fluid invading the system; (4) a quasi-steady-state approximation is invoked in Equation (2); (5) mud is incompressible and the formation fluid is ideal. It is also noted that Equation (2) also rests on several assumptions about fracture roughness, as described in Zimmerman et al. (1991).

Stochastic inverse modeling

A key objective of this study is to provide quasi-real-time estimates of equivalent fracture aperture conditional on available data acquired while drilling. We rely on the semi-analytical model illustrated in Sect. 2.1 and frame it into a proper stochastic model calibration context. We recall that a deterministic approach yields a unique model parameter set through minimization of a desired objective/cost function. Otherwise, a stochastic approach leads to the characterization of the (posterior) probability distribution associated with each model parameter, as constrained through available data. Resting on a stochastic calibration framework is fully consistent with the inherent uncertainty associated with model parameter estimates conditional on a limited amount of data.

The $n_{param} = 5$ uncertain model parameters which are subject to stochastic inverse analysis are w, $\tau _Y/k$, $\Delta p/k$, n and $r_w$. Each parameter is characterized by a uniform prior probability density function. This enables one to assign equal weight to each of the parameter values across their corresponding support (see also Russian et al. 2019 and reference therein).

Observations constraining model calibration comprise data associated with temporal evolution of mud volume losses from the well. Available information is collected in vector ${\textbf {V}}_k^* = [V^*_{k}(t_1),V^*_{k}(t_2), \ldots , V^*_{k}(t_{N_k})]$, whose entries correspond to the $N_k$ observations of mud volume losses at times $t_i$ ($i = 1, ..., N_k$) within a given fracture k. Considering a set of data associated with $N_{frac}$ mud losses events, we ground stochastic model calibration on the evaluation of the objective/cost function

$$\begin{aligned} J(\mathbf{p}_j)=\sum _{k=1}^{N_{frac}}\sqrt{\frac{\sum _{i=1}^{N_{k}}({\textbf {V}}_{k}^*(t_i)-{\textbf {V}}_{k}{(t_i,{\textbf {p}}_j)})^2}{N_k}}. \end{aligned}$$

(3)

Here, ${\textbf {V}}_{k}{(t_i,{\textbf {p}}_j)}$ is the vector collecting the values of mud volume loss for fracture k at time $t_i$ evaluated through Equation (1) whose input parameters are collected in vector ${\textbf {p}}_j$. Minimization of cost function (3) is achieved through the particle swarm optimization (PSO; see Eberhart and Kennedy 1995) technique. The latter is structured according to a series of steps which are briefly summarized in the following. At the initial step of the inversion, i.e., at step $s = s_0$, a number $N_p$ of points ${\textbf {p}}_j(s_0)$ (with $j = 1, \ldots , N_p$) termed particles is randomly sampled across the considered $n_{param}$-dimensional parameter space together with a random displacement vector ${\textbf {v}}_j(s_0)$. The latter is drawn from a uniform distribution within the unit support [0, 1]. Particle displacements are then evaluated during subsequent evolutionary steps of the algorithm to update particle locations. While an optimal value for $N_p$ depends on the scenario considered, $N_p$ is typically comprised within the range 20–50  (Rahmat-Samii and Michielssen 1999). Displacement of each selected point across the parameter space is governed by

$$\begin{aligned} {\textbf {p}}_{j}(s+1)= {\textbf {p}}_{j}(s) + {\textbf {v}}_j(s). \end{aligned}$$

(4)

Evaluation of objective function (3) is performed at particle locations, each corresponding to parameter combination ${\textbf {p}}_{j}(s+1)$.

Two reference points within the parameter space, i.e., ${\textbf {p}}_{best,j}$ and ${\textbf {g}}_{best}$, respectively, represent the location of maximum fitness (minimum distance to data; ${\textbf {p}}_{best,j}$) discovered by particle j and the location associated with the best fitness ever discovered by all particles (${\textbf {g}}_{best}$) are evaluated at each step s of the procedure. Note that, while ${\textbf {p}}_{best}$ is evaluated at each step of the inversion for each particle j, ${\textbf {g}}_{best}$ is the same for the entire particle set. Consistent with Eberhart and Kennedy (1995), updating of a particle displacement is performed upon considering ${\textbf {v}}_j(s+1)$ as a function of ${\textbf {p}}_{j}(s+1)$, ${\textbf {v}}_j(s)$, ${\textbf {g}}_{best}$, and ${\textbf {p}}_{best,j}$ according to

$$\begin{aligned} {\textbf {v}}_j(s+1)=\omega {\textbf {v}}_j(s) + c_1 U ({\textbf {p}}_{best,j}-{\textbf {p}}_{j}(s+1))+c_2 U ({\textbf {g}}_{best}-{\textbf {p}}_{j}(s+1)), \end{aligned}$$

(5)

where U is a random number uniformly distributed within the unit support; $c_1$ and $c_2$ are constant coefficients, here set as $c_1 = c_2 = 1.495$ (Rahmat-Samii and Michielssen 1999); and $\omega$ is a step-dependent variable evaluated according to Lagarias et al. (1998). In this application, we consider convergence to be achieved (in terms of minimization of Equation (3)) when (i) a minimum value of the objective function is attained or (ii) after the completion of 1000 iterations of the PSO algorithm. While the latter criterion does not ensure convergence to a global minimum, such a number of iterations are considered as a good compromise between accuracy and computational cost (see also Russian et al. 2019). Repeating this procedure for a variety of random initial parameter combinations and measurement errors (i.e., random perturbation of the entries of ${\textbf {V}}_k^*$) allows exploring the parameter and solution spaces. This yields $N_{calib}$ sets of model parameters satisfying the imposed convergence criteria. These are then analyzed through their empirical frequency distributions. As such, these results correspond to a frequentist analysis of a collection of model parameter estimates. The mud flow values employed within the inverse modeling framework can be obtained through a variety of approaches. These include, e.g., pump stroke counters, Coriolis flow meters, or electromagnetic flow meters (Singhal et al. 2019). In our application setting, the mud flow entering the mud circuit is measured through (1) electromagnetic flow meters and (2) pump strokes counters. Hereinafter, data related to electromagnetic flow meters are referred to as direct measurements and those coming from pump strokes counter as indirect measurement, respectively. Uncertainty associated with observed data is expected to be a function of the employed technique and the corresponding accuracy. We set our stochastic model calibration within the illustrated context and analyze the impact of both measurement approaches. Differences between the parameter distributions stemming from the resulting data sets are quantitatively assessed through the Kullback-Leibler divergence (KLD; Kullback and Leibler 1951). The latter is a global metric enabling one to quantify the extent at which a probability distribution differs from a second one. It is applied in a variety of fields, including, e.g., fluid mechanics, neuroscience, and machine learning (Bishop 2006). We denote the probability distribution of model parameters obtained through inverse modeling relying on direct measurements as $P_{direct}$. Otherwise, $P_{indirect}$ represents its counterpart based on pump strokes counters. Considering the case of discrete probability distributions defined on the same support X, the KLD is then defined as

$$\begin{aligned} D_{KL}(P_{direct} \parallel P_{indirect})=\sum _{x \in X} = P_{direct} (x) \log \left( {\frac{P_{direct}(x)}{P_{indirect}(x)}}\right) . \end{aligned}$$

(6)

As such, the quantity $D_{KL}(P_{direct} \parallel P_{indirect})$ is always positive and corresponds to the amount of information lost when $P_{indirect}$ is used to approximate $P_{direct}$.

Synthetic case

This section is devoted to illustrate how the approach and techniques introduced in Sect. 2 can be applied in the context of a synthetic scenario. This yields transparent comparative analyses to assess the quality of the estimated probability distributions of model parameters conditional on available data. The support across which uncertain parameters can range and the reference values are based on literature information and modeler experience. The aim is to obtain a realistic dataset that can be considered as a simplified description of a real field case. Consistent with this aim, the values of mud volume losses are evaluated from the semi-analytical model illustrated in Sect. 2.1. These results are then perturbed by applying a random measurement error, to mimic uncertainty associated with observations.

Uncertain model parameters

As discussed in Sect. 2.2, values of mud front advancement and related mud volume losses resulting from the semi-analytical model of Sect. 2.1 depend on a set of five uncertain model parameters, i.e., w, $\tau _Y/k$, $\Delta p/k$, n, and $r_w$. Table 1 lists the range of variability considered for each parameter, together with the values employed to obtain the reference synthetic dataset. As seen in Sect. 2.2, in the absence of prior information each model parameter is described by a uniform probability density across the corresponding support.

Table 1 Uncertain model parameters, corresponding reference value employed in the synthetic scenario and support (range of variability) considered in the analyses

Stochastic model calibration

In this section we present and discuss the results obtained through the application of the stochastic inverse modeling technique described in Sect. 2.2 to the synthetic dataset. As stated above, we rely on the semi-analytical model of Sect. 2.1 to mimic data sampling at a uniform time step $\Delta t = 1$ s within a 60-second temporal window. The ensuing (reference) values of mud volume loss are corrupted with a measurement error. The latter is randomly sampled from a uniform distribution. This choice is consistent with the approach employed to quantify (prior) model parameter uncertainty and enables to give equal weight to all values comprised within the support of data uncertainty. We obtain a collection of $N_{calib} = 200$ realizations of perturbed observations. The reference value at each time step is obtained through the semi-analytical formulation considered and corresponds to the mean value of the above-mentioned uniform distribution. The impact of the magnitude of the measurement error on model calibration results is probed by considering various values of the coefficient of variation (CV) of the distribution. We note that considering a Gaussian distribution for measurement errors (with the same mean and CV as their uniform counterparts) does not influence significantly the range of results of model inversion (details not shown). Figure 1 depicts the empirical frequency distributions of the values of w obtained through stochastic model inversion for scenarios characterized by $5\% \le$ CV $\le 30\%$. As stated above, each sample distribution in Fig. 1 is based on 200 inversions. The reference value employed for the analyses (green dashed lines) is here juxtaposed for completeness. These results are then complemented in Fig. 2. The latter provides a depiction of the way characteristic quantiles of the distributions of w depend on CV. The shaded area in the figure corresponds to values of w comprised between the $5{th}$ and the $95{th}$ percentile of the distribution. The median (red solid line), the lowest, and largest bounds (dashed blue lines) of the reference range of variability of w (see Table 1) are also depicted for ease of interpretation. These results show that, despite some minor differences in the overall shape of the empirical distributions resulting from stochastic model calibration, their associated maximum a posteriori (MAP) constitutes a generally good approximation for the reference value. This is noted independent of the strength of the measurement error considered, as expressed through the values adopted for CV. These results imbue us with confidence about the suitability of the considered stochastic inverse modeling technique to yield reliable posterior distributions of w in the presence of perturbed mud volume loss information. Corresponding results associated with model parameters $\tau _Y/k$, n, and $\Delta p/k$ are included in Appendix 6, for completeness.

Fig. 1

Empirical distributions of relative frequencies of equivalent fracture aperture w for CV = (a) 5%, (b) 10%, (c) 15%, (d) 20%, (e) 25%, (f) 30%. Green dashed lines represent parameter reference values employed in the analyses

Fig. 2

Median value of the equivalent fracture apertures (red solid curve) versus the value of CV considered for the stochastic inverse model calibration. The shaded area denotes values of w comprised between the $5{th}$ and the $95{th}$ percentile of the distribution; the blue dashed lines represent the lowest and largest bounds of the reference range of variability of w (see Table 1)

The inverse modeling results can be employed to assess the uncertainty associated with the desired model output conditional on the available observations. This is a key element to support risk analyses. First, we evaluate the analytical model of Sect. 2.1 upon relying on the $N_{calib}=200$ combinations of parameter values obtained through stochastic calibration procedure. We then compare the ensuing mud volume loss distributions against the corresponding reference value evaluated at times which are not employed for model inversion. This provides a perspective about model prediction assessment. As an example, Figs. 3 and 4 depict the distributions of cumulative mud loss volumes associated with six selected observation times. These range from 10.5 to 60.5 seconds and from 70 to 120 seconds, respectively, corresponding to CV = 5% and 30%. Reference values are denoted with vertical green dashed lines. The effect of the level of uncertainty associated with the value of CV is clearly visible in Figs. 3 and 4. One can evidence (a) an increased uncertainty linked to the modeled state variable and (b) differing values of the probability of exceeding given threshold values. Otherwise, it is noted that the most frequent values of both distributions are well in agreement with the corresponding reference value. Since the calibration dataset is associated with a temporal window that covers the first 60 s, the uncertainty linked to V is increasing with time, as expected. Nevertheless, our result suggests that the calibrated solutions are characterized by distributions that are compatible with the corresponding reference values also in the context of model prediction analysis.

Fig. 3

Relative frequency distributions of mud volume loss evaluated through the analytical model relying on the $N_{calib}=200$ combinations of parameters obtained via stochastic calibration. Results are related to CV= 5% (orange) and 30% (purple) and correspond to times, t, which are not considered for model inversion. Green dashed lines denote reference values

Fig. 4

Relative frequency distributions of mud volume loss evaluated through the analytical model relying on the $N_{calib}=200$ combinations of parameters obtained via stochastic calibration. Results are related to CV= 5% (orange) and 30% (purple) and correspond to times, t, extending beyond the temporal window within which calibration data are collected. Green dashed lines denote reference values

Field case scenario

In this section we showcase the application of our workflow through a set of available data associated with a real field case scenario. The drilling mud circuit is a typical closed system that is comprised by two parts. These are termed in (extending from the surface into the well) and out (encompassing the portion conveying the mud fluid from the well back to surface), respectively. Consistent with the objectives of our study, we rest on flow-out and flow-in data, hereafter termed $Q_{o}$ and $Q_{i}$, respectively. These are monitored while drilling a single well in a sequence of shale and sandstone within a layered reservoir. These data are key to enable fracture characterization while drilling. A variation in the difference between them, i.e., $\Delta Q= Q_{o}-Q_{i}$, represents the signature of an event. This is potentially due to the occurrence of a fracture or of a set of fractures (e.g., Majidi et al. 2011; Al-Adwani et al 2012; Russian et al. 2019). We consider the relative impact of relying with direct (i.e., corresponding to electromagnetic flow meters data) or indirect (i.e., corresponding to pump strokes counters) flow-in observations.

Mud loss dataset

Mud volume losses can take place when (a) the pressure of the drilling fluid exceeds that of the formation fluid (Vavik et al. 2016), and (b) there is a flow pathway (Osisanya 2002). The latter can be related, e.g., to the occurrence of an open natural fracture or to a network of (micro-)fractures. In this study, we analyze mud loss events associated with six events. These are hereinafter terms 1–6 (the numbering corresponds to increasing depths along the borehole). As stated in Sect. 1, we rely on the concept of equivalent aperture to represent the impact of a single fracture (or of a network of fractures) on the observed fluid losses.

Observations of flow-out and flow-in deriving from electromagnetic flowmeters (hereafter denoted as $Q_{o}$ and $Q_{is}$, respectively) have been collected at a uniform time step $\Delta t = 5$ seconds. Flow-in data derived from pump strokes are acquired at the same time scale as their flowmeter-based counterparts. In the case of pump strokes data, flow-in (hereafter denoted as $Q_{ip}$) can be evaluated as

$$\begin{aligned} Q_{ip}=\sum _{n=1}^{N}SPT_n\Delta v_n \eta _n, \end{aligned}$$

(7)

where N is the number of pumps installed at the rig site, $SPT_n$ is the number of strokes per unit time of the n-th pump, $\Delta v_n$ is the volume of drilling fluid displaced per stroke, and $\eta _n$ denotes pump efficiency. We denote mud losses associated with flow-in measurements derived from pump strokes and flow meter sensors as $\Delta Q_p=Q_{o} - Q_{ip}$ and $\Delta Q_s=Q_{o} - Q_{is}$, respectively.

Figure 5 depicts the temporal evolution of the six cumulative mud volume loss ($V^*$) histories considered. Figure 5a and Fig. 5b is based on electromagnetic flow-in data $\Delta Q_s$ and pump strokes counters $\Delta Q_p$, respectively. Values of $V^*$ are assessed by integrating across time the monitored mud flow rate loss $|\Delta Q|$. Events in Fig. 5 are depicted upon rescaling time with respect to the first detection time associated with each of them. Identification of the initial mud volume loss is based on observations of $\Delta Q$ prior to start evidencing a significant increase. These typically tend to oscillate around a constant mean (before yielding a sharp increase of values of $V^*$), consistent with the advancement of the drilling.

Fig. 5

Temporal evolution of mud volume losses for the six events considered in the field scale scenario. Values associated with direct and indirect measurements of flow are indicated with (a) crosses and (b) dots, respectively

Information about mud rheology, overpressure at the borehole, and geometric attributes of wellbore and fractures have been acquired for each selected event, as detailed in the following. Rheological parameters $\tau _Y$, n, and k (see Sect. 2.1) have been estimated through viscometer analysis, i.e.,

$$\begin{aligned} \tau _Y=2\theta _3-\theta _6, \ \ n=3.3219\log _{10}\frac{\theta _{600}-\tau _Y}{\theta _{300}-\tau _Y}, \ \ k=\frac{\theta _{300}-\tau _Y}{511^n}, \end{aligned}$$

(8)

where $\theta _i$ is the shear stress obtained from a coaxial cylinder viscometer operating at i rotations per minute (RP et al. 2006; Rehm et al. 2013). Overpressure ($\Delta p$) is monitored along the wellbore while drilling. Its values are assessed on the basis of the drilling mud equivalent circulating density (ECD) and pore pressure at depths corresponding to fractures. The well radius ($r_w$) is assessed through caliper log. Interpretation of electric image logs yields independent estimates of fracture apertures w. The image log tools WBI HRP have been reported to perform properly in the depth interval here considered (i.e., from 3979 m and 4078 m). According to the technical report related to downhole analyses, the tool provided a high-quality response.

Table 2 lists the main elements associated with our analysis. These include the event identifier and the number of mud loss volumes associated with sampled $\Delta Q$. These samples are attributed to a reference depth, also listed in Table 2. We note that identification along the borehole of the precise location at which mud loss takes place is inherently challenging. Thus, we consider the set of fracture aperture values obtained via microscanner data and comprised within a vertical interval of width ± 0.5 m centered around the location at which mud loss data are ascribed. The extent of this vertical interval can be deemed compatible with the observations that (a) our analysis is based on the concept of equivalent fracture aperture and (b) there can be a certain degree of uncertainty related to the acquisition of driller depth data. Image log analysis leads to detecting approximately 6–7 fractures for each event within such a range of depths. We then include in Table 2 the lower and upper bounds of the detected aperture values. These will then be employed to assess the quality of the stochastic inversion (see Sect. 4.2). Values of the other quantities of interest estimated with the techniques illustrated above are also included in Table 2. As these values are affected by uncertainty due to measurement and interpretive errors, the stochastic inverse modeling framework is employed to provide probability distribution of these quantities conditional on the available information. To this end, we consider model parameters to vary across the supports whose bounds are listed in Table 1.

Table 2 Events considered in the field scale analysis. The corresponding reference depth to which mud volume loss is ascribed, the number of available mud volume loss data, the reference value w, and minimum and maximum values (w int) of the set of fracture aperture values comprised within a vertical interval of width ± 0.5 m centered around the reference depth and evaluated through image log interpretations are shown. Values of the other quantities of interest estimated with the various standard techniques illustrated are also listed

We note that each of the events considered in this field case is characterized by a limited amount of data. These typically range between four and six observations. On the other hand, there are four uncertain model parameters, i.e., w, $\tau _Y/k$, n, and $\Delta p/k$ for each event (we assume that $r_w$ is known, as caliper log consistently renders the same value of wellbore radius along the overall depth encompassing all six events). This yields a total of 24 parameters to be estimated. In this context, inverse modeling considering each event separately could not lead to reliable results.

We circumvent this difficulty by noting that the six events are comprised within a depth of less than 100 ms (see Table 2). One can then consider mud rheological parameters to be constant for all fractures across this depth range. This significantly reduces the number of uncertain model parameters. With this assumption, we then consider all of the mud volume loss data of the six events as a unique dataset to be employed in batch in the context of the stochastic calibration process. Model parameters subject to stochastic inverse analysis then correspond to the equivalent fracture aperture $w_i$ (index $i=1,\dots ,6$ denoting each of the events), the overpressure $\Delta p_i/k$, and the rheological parameters $\tau _Y/k$ and n. This yields a total of 14 model parameters. Table 3 lists the parameters considered for the stochastic calibration process based on the analytical model formulated in Sect. 2.1.

Table 3 Parameters considered for the stochastic calibration process of the field scale setting considered, together with their corresponding support

As stated in Sect. 2.2, we compare the results stemming from stochastic inverse modeling upon relying on two types of delta flow data. These correspond to $\Delta Q_p$ and $\Delta Q_s$ associated with flow-in measurements based on pump strokes and flow meter sensors, respectively.

Since a precise quantification of data uncertainty is not available, we follow the procedure implemented in Sect. 3.2. Thus, we perturb observed values of $\Delta Q_p$ and $\Delta Q_s$ with a zero-mean random error characterized by a uniform distribution and a given coefficient of variation (CV). We explore the impact of the latter by performing inverse modeling for several scenarios. Each of these corresponds to a given value of CV, which is taken to range between 5% and 30%.

Probability distribution of equivalent fracture apertures

In this section we illustrate the results obtained from the stochastic inverse modeling approach by focusing on the probability distributions of fracture apertures. These are evaluated upon conditioning on either direct or indirect mud volume loss data. We then juxtapose independent information stemming from the microscanner analysis (see Sect. 4.1 and Table 2) to these probability distributions. The complete set of distributions including the remaining model parameters is offered in Appendix 6.

We rest on a collection of $N_{calib}$ = 200 inversions corresponding to randomized datasets and obtained through minimization of the objective function provided by Equation (3) via the PSO algorithm. The total computational cost required to obtain the resulting (conditional) empirical multivariate distributions of parameter estimates involves considering $\approx$ 10 million realizations of the semi-analytical model. This corresponds to slightly less than 24 h with an Intel ® $\hbox {Core}^{\mathrm{TM}}$ i7–6900K CPU@3.20GHz.

As a first example of the results, Fig. 6 depicts the empirical distributions of values of w associated with each of the events and corresponding to observations of $\Delta Q_s$ and $\Delta Q_p$ perturbed with CV=5%. The value of fracture aperture stemming from the interpretation of the microscanner analysis data associated with the depth at which the mud loss event is first detected is also depicted (green solid line, corresponding to the reference depth listed in Table 2). As stated in Sect. 4.1, we recall that it is very difficult to identify the precise location along the borehole at which mud loss takes place due to the presence of a fracture (or a network of fractures). Thus, we consider the set of fracture aperture values associated with a vertical interval of width ± 0.5 m centered around the location at which mud loss data are ascribed (see Table 2). We further note that our inverse modeling approach is characterized by a probabilistic nature. As such, stochastic inverse modeling results should be compared against sample (probability) distributions obtained from field observations associated with a considered depth interval. In our cases, image log analysis leads to detecting approximately 6–7 fractures for each event within such a range of depths. Since these are not conducive to reliable distributions, we limit ourselves to include in Fig. 6 the lower and upper bounds of the resulting aperture values (vertical blue dotted lines) as an additional element to assist the appraisal of the quality of the stochastic inversion.

Fig. 6

Empirical distributions of equivalent fracture aperture related to event (a) 1, (b) 2, (c) 3, (d) 4, (e) 5, and (f) 6 obtained through stochastic inverse modeling based on direct (red) and indirect (blue) mud volume loss observations perturbed considering CV=5%. Values of fracture aperture based on image log interpretations at the depth at which mud loss data are ascribed (green solid lines; Table 2) and lower and upper bounds of fracture apertures (blue dashed lines) detected within a vertical width ± 0.5 m centered around this reference depth are also depicted

Our results show that equivalent fracture aperture distributions obtained through inverse modeling are mostly comprised within the intervals identified through the image log interpretations with only a few exceptions. These typically correspond to the tails of the distributions. Distributions obtained by relying on $\Delta Q_s$ or $\Delta Q_p$ information display similar shapes. These results imbue us with confidence about the ability of the considered methodological workflow to constrain the identification of equivalent apertures on the basis of information routinely acquired while drilling. We emphasize that our results are obtained in a quasi-real-time mode and provide a full uncertainty quantification, as constrained through available information. As such, the approach provides a considerable advantage as compared against commonly employed methods of analysis based on, e.g., image logs. These requires a time-consuming postprocessing and do not take full advantage of the variety and richness of data available. We complete the analysis with the assessment of the influence of potential measurement errors associated with both methods considered for mud loss evaluation.

Figure 7 depicts the values of the Kullback-Leibler divergence $D_{KL}(P_{direct} \parallel P_{indirect})$ (see Equation (6), Sect. 2.2) evaluated considering the empirical distributions of w related to each event and assessed on the basis of direct and indirect mud flow observations. Results are depicted as a function of the values of CV associated with the available information, as described in Sect. 4.1.These results show that the value of KLD is always very small. This suggests that stochastic inversions relying on perturbed data of direct and indirect measurements lead to similar (posterior) probability distributions of w.

Fig. 7

Kullback-Leibler divergence (KLD; Equation (6)) associated with the empirical distributions obtained through model inversions conditional on pump strokes and flow meter sensor data, as a function of the coefficient of variation (CV) employed to quantify measurement uncertainty

Uncertainty propagation from input parameters to model output, i.e., mud loss volume, is then investigated upon leveraging on stochastic inverse modeling results. As an example, Fig. 8 depicts results corresponding to event # 3 (see Table 2). These correspond to the 200 stochastic model inversions associated with noisy data related to CV=30%. Figure 8a and 8b depicts results based on electromagnetic flow meter data and pump strokes information, respectively. In general, propagation of uncertainty from model parameter distributions yields temporal histories of mud losses which are consistent with those that can be observed through direct observations. At the same time, our results show that errors associated with pump strokes data tend to be conducive to mud volume loss values which are more spread around the unperturbed values (red dots) than their counterparts based on electromagnetic flow meter observations. Results of similar quality are obtained for all of the other events, as illustrated in Appendix 6.

Fig. 8

Temporal evolution of mud volume losses associated with event # 3 (i.e., $V_3$) rendered through the 200 stochastic model inversions grounded on noisy data characterized by CV=30%. The collection of model inversion solutions based on (a) $\Delta Q_s$ and (b) $\Delta Q_p$ is depicted together with the unperturbed dataset (red circles)

Conclusions

The key objective of this study is the characterization of equivalent fracture apertures on the basis of available mud loss information of the kind which is acquired in (quasi)-real-time while drilling a well in a natural formation. Our operational workflow relies on a stochastic inverse modeling framework. This yields a probabilistic assessment of w on the basis of a simple analytical model. Our analyses consider a scenario where (a) typically monitored mud loss events are available, and (b) stochastic model inversion is constrained through flow data stemming from direct and indirect information. The latter are represented by flow meter sensors and pump stroke analyses, respectively. We also perform a detailed study of the uncertainty related to corrupted data and the way this impacts the probabilistic assessment of equivalent fracture apertures. The work leads to the following key conclusions.

• 1. We rest on a straightforward analytical model to describe, in quasi-real-time and under uncertain conditions, the probability distribution of w in a sequence of sandstones and shales layers. We start by testing our technique on a streamlined synthetic scenario and quantifying the effect of uncertainty associated with measurement errors on the probability distribution of w. The maximum a posteriori (MAP) of these distributions favorably compares against the reference value employed in the setting considered for low to high levels of data corruption.

• 2. Results associated with a natural setting rely on limited amount of data monitored while drilling a single well through a reservoir mainly formed by a sequence of shale and sandstone layers. They demonstrate that the proposed procedure yields distribution of w which are compatible with interpretations based on the analysis of image logs. The quality of our results suggests that our approach is efficient and provides a detailed probabilistic characterization and uncertainty quantification of w constrained by available flow data within a quasi-real-time perspective.

• 3. We end by noting that we had the possibility to assess our stochastic modeling framework in a given geological setting, i.e., a reservoir characterized by alternation of shale and sandstone. These results can constitute a valuable basis to showcase the methodology in other setting including, e.g., carbonate reservoirs. We envision to tackle this aspect in future works, as soon as information of sufficient quality and quantity is openly available.

Appendix: Complete set of stochastic inverse modeling results

Figure 9 depicts the empirical distributions of model parameters $\tau _Y/k$, n, and $\Delta p/k$ obtained through the inverse modeling approach related to the synthetic case (see Sect. 3) for scenarios characterized by diverse coefficient of variations (i.e., CV=5% and 30%, respectively) quantifying the strength of measurement errors considered. These results are complemented by a depiction of the way selected quantiles of these distributions vary with CV. It can be noted that conclusions similar to those drawn from Figs. 1 and 2 hold for all uncertain model parameters.

Fig. 9

Empirical distributions of uncertain model parameters (a)-(b) $\tau _Y/k$, (d)-(e) n, (g)-(h) $\Delta p/k$ for (a)-(d)-(g) CV=5%, (b)-(e)-(h) CV=30% together with reference values employed (green dashed lines; Table 1). Selected quantiles versus the value of CV considered are depicted for (c) $\tau _Y/k$, (f) n, (i) $\Delta p/k$. Median values are denoted through red solid curves, the yellow shaded area denoting values of uncertain parameters comprised between the $5{th}$ and the $95{th}$ percentile of the distribution; the blue dashed lines represent the lowest and largest bounds of the reference range of model parameter variability (see Table 1)

Figure 10 depicts the empirical distributions of uncertain model parameters for each of the events considered in the field scale scenario (see Table 3) and associated with observations of $\Delta Q_s$ and $\Delta Q_p$ perturbed with CV=5%. Distributions related to $\Delta Q_s$ (red) and $\Delta Q_p$ (blue) information display compatible shapes, similar to what is observed in Fig. 6.

Fig. 10

Empirical distributions of parameter (a) $\tau _Y/k$, (b) n, (c) $\Delta p_1/k$, (d) $\Delta p_2/k$, (e) $\Delta p_3/k$, (f) $\Delta p_4/k$, (g) $\Delta p_5/k$, and (h) $\Delta p_6/k$ obtained through stochastic inverse modeling based on direct (red) and indirect (blue) mud volume loss observations perturbed with CV =5%

Figure 11 depicts results related to events 1–2–4–5–6 (see Table 2) associated with observations of $\Delta Q_s$ and $\Delta Q_p$ which are randomized considering CV=30%. The temporal evolution of mud volume losses of the six events (see Fig. 8 for event 3) considered for the field scale scenario and obtained through the results of the 200 stochastic model inversions is compatible with those observed through direct and indirect observations of flow-in data.

Fig. 11

Temporal evolution of mud loss volumes associated with event (a)-(f) 1, (b)-(g) 2, (c)-(h) 4, (d )-(i) 5, and (e)-(l) 6 rendered through the 200 stochastic model inversions associated with noisy data related to CV = 30%. Model inversion solutions based on (a)-(b)-(c)-(d)-(e) $\Delta Q_s$ and (f)-(g)-(h)-(i)-(l) $\Delta Q_p$ are depicted together with the unperturbed dataset (red circles)