Strain mode-dependent weighting functions in hyperelasticity accounting for verification, validation, and stability of material parameters

Abstract

Optimized material parameters obtained from parameter identification for verification wrt a certain loading scenario are amenable to two deficiencies: Firstly, they may lack a general validity for different loading scenarios. Secondly, they may be prone to instability, such that a small perturbation of experimental data may ensue a large perturbation for the material parameters. This paper presents a framework for extension of hyperelastic models for rubber-like materials accounting for both deficiencies. To this end, an additive decomposition of the strain energy function is assumed into a sum of weighted strain mode related quantities. We propose a practical guide for model development accounting for the criteria of verification, validation and stability by means of the strain mode-dependent weighting functions and techniques of model reduction. The approach is successfully applied for 13 hyperelastic models with regard to the classical experimental data on vulcanized rubber published by Treloar (Trans Faraday Soc 40:59–70, 1944), showing both excellent fitting capabilties and stable material parameters.

1 Introduction

1.1 State of the art on hyperelasticity

Rubber-like materials or elastomers, respectively, consist of randomly oriented chain-like macromolecules with more or less closely connected entanglements or cross-links. Two main characteristics are their ability for large deformations subject to relatively small stresses and their retaining of the initial configuration after unloading without considerable permanent deformation. This behavior is attributed to the network entropy as the orientation of chains alters with deformation. Due to these special properties, the materials have numerous technical application such as for tires, structural bearings, medical devices and base isolations of buildings; see, e.g., [7].

Numerous phenomenological and micro-mechanically motivated models have been proposed in the literature in order to capture the elastic and nearly incompressible mechanical of rubber-like materials. Moreover, the former can be classified into invariant-based and principal-stretch-based formulations, cf. e.g. [47].

Phenomenological invariant-based models are based on the theory of invariants as elaborated extensively by Spencer in [46] for anisotropic materials. For the case of isotropy, an appropriate set of invariants dependent on the right Cauchy–Green tensor are selected, which are included as polynomials with sufficiently high orders into the strain energy function, known as Rivlin’s expansion, [43]. Classical examples such as the Neo-Hooke material are of Mooney–Rivlin type, cf., e.g., [33, 40,41,42]. Since then a vast variety of models have been developed. For example, Yeoh [55] revealed that cubic terms of the first invariant are able to reproduce the highly nonlinear S-shaped uniaxial behavior of rubber, also at very large strains. Alternatively to polynomial formulations, logarithmic formulations are presented, e.g., in the Gent–Thomas model [15], the Gent model [14] or the Pucci Saccomandi model [39]. In Khajehsaeid et al. [22], the combination of polynomials, logarithmic, and exponential formulations is investigated. Another approach is given in the model of Carrol [9], which combines powers of the first invariant with the square root of the second invariant. A prominent example for a phenomenological principal-stretch-based model is presented by Ogden in [37].

Micro-mechanical models are derived from statistical mechanics arguments on networks of idealized chain molecules. In this way, they account for a lower scale insight to the physical/chemical microstructure to explain phenomenological macroscopic mechanical behavior, although this might render higher computational costs. Well known examples for micro-mechanical models are the 3-chain, the 4-chain, and the 8-chain model as well as the unit sphere (21-chain) model, cf. Arruda and Boyce [3] and Miehe et al. [32].

Many of the above-mentioned models for rubber-like materials are well advanced from the mathematical point of view, [17], and the numerical point of view [31, 45].

1.2 Criteria for a “good” parameter vector

A well accepted first step for parameter identification is based on a least-squares functional, in order to minimize the distance of simulated data and experimental data with respect to a chosen norm. However, this step leaves open the precise meaning of a “good” vector of material parameters. In this work, we follow the outline in [27] accounting for the three criteria of

• Verification

• Validation

• Stability.

Verification is related to the fit quality of a material model as a consequence of parameter identification. This step of model development assesses if the simulated outputs of the underlying model are adequate when compared to measurement data which contribute to the underlying least-squares functional. In this way, all measurement data involved in this step are known beforehand, such that more precisely it could also be termed backwards-verification. Comparative studies on verification for models in hyperelasticity have been performed for example in Marckmann and Verron [30], Boyce and Arruda [6], Seibert and Schöche [44]. Parameter identification for Rivlin and Saunders type hyperelasticity [43] has been examined, e.g., by Hartmann et al. [16]. The identification from inhomogeneous experiments on polyurethane is investigated in [53], where particular focus has been set on error-controlled adaptive mesh refinement.

Some aspects of validation and stability are outlined next.

1.3 An aspect of validation: Conformity of data sets and constitutive model

In contrast to verification, validation of material models is related to the prediction capability. Alternatively, it could also be termed forecast-verification, since this step of model development assesses whether the simulated outputs of the underlying model are adequate when compared to additional measurement data which are not known or considered, respectively, in the backwards-verification step; see, e.g., [27].

In this work, we are particularly interested in possible remedies in case of non-validity for material models in hyperelasticity. In particular, we will resort to a typical situation of laboratory testing, where a certain number of data sets each related to a certain loading scenario is available. An example for such a set of experimental data is provided by Treloar [48] for the three loading scenarios of uniaxial, biaxial, and pure shear deformations. An extensive comparative study on the fit quality of 14 material models on these data is provided by Steinmann et al. in [47]. Most of the models meet the criteria of verification, however, merely wrt to one individual loading scenario with a certain vector of optimized material parameters (occasionally with perfect agreement). Then, the same parameter vector is not able to capture different loading scenarios (occasionally even showing disappointing agreement). This lack of validity motivates the following definition:

Definition 1

(on conformity between experimental data and constitutive model) Available experimental data sets, all of them related to different loading scenarios (or stress modes, strain modes, respectively), and a constitutive model are conform, if a reduced experimental data set is sufficient to validate the material model for the remaining data sets.

Definition 1 applied to the extensive comparative study in Steinmann et al. in [47] renders, e.g., a poor conformity between the Treloar data and the Isihara model [20], while the situation improves significantly for the Carroll model [9].

It should be emphasized that Definition 1 on conformity is restricted to available data and, in this sense, constitutes only a necessary but not a sufficient condition for general validation, that is, predictive simulation for all loading cases that could be envisaged. Examples for further possible loading scenarios are hydrostatic tension, uniaxial compression, equibiaxial compression, or hydrostatic compression (although experimentally challenging) in order to get a more comprehensive (though in general still not complete) characterization of the material.¹

The experimental data sets in Definition 1 may have different origins. In practice, typically they may refer to different loading scenarios, which allows us to exploit the extensive literature for modeling asymmetric effects within the fields of plasticity and creep. Along this line constitutive equations have been formulated, e.g., in [2, 5, 25, 26, 51, 56,57,58], among others. It appears from the above mentioned references that so far no common approach exists concerning the best strategy for taking account of individual loading scenarios in the constitutive equations. A general agreement is the incorporation of odd power terms for odd invariants of stresses; see, e.g., [5]. Furthermore, a scalar variable, which is expressed in terms of the ratio of the second and third basic invariant of the deviatoric stress tensor, can be used as an indicator for detection of differences in the loading modes. This quantity, stress mode angle or Lode-factor, respectively, has been applied, e.g., in [1, 12, 25, 57]. Based on [26], extensive use of the stress mode angle has also been made by this author and co-workers for modeling asymmetric effects of experimental data in tension, compression and shear for metallic materials (such as AISI 52100) [10, 11, 29], with applications for cutting processes like hard turning [49].

Aims of present work on non-conformity A main purpose of this work is the extension of some well-known hyperelastic material models in case they fail to be conform to given data sets according to Definition 1. To this end, we make extensive use of the above-mentioned works on asymmetric effects. In particular, as a counterpart to the stress mode angle used in [1, 12, 25, 26, 57] a strain mode angle is introduced in order to characterize the individual loading scenario. The key idea consists in an additive decomposition of the logarithmic isochoric Hencky strain tensor, where each of the related quantities incorporates a weighting function dependent on the strain mode angle. The advantage of this approach is, that certain (though not all) material parameters, such as Mooney–Rivlin-type constants, can be obtained individually from specific loading modes such as uniaxial tension, equibiaxial tension and pure shear, investigated experimentally in the laboratory.

1.4 An aspect of stable material parameters: I-criteria

The solution of the underlying least-squares problem for parameter-identification might render a satisfactory agreement between simulated and experimental data; however, it might be susceptible to instability, in the sense, that a small perturbation of experimental data may lead to a large deviation of the resulting parameter solution. Two possible reasons for this undesirable effect (or even non-uniqueness) have to be distinguished: 1. Deficiency of the material model, where (too many) functional terms and/or parameters may be lead to (almost) linear dependencies within the model (overparametrization) or 2. Deficiency of experimental data, where certain material effects intended by the model are not properly activated (incomplete data). see, e.g., [27].

For detection of possible instabilities several indicators are proposed in the literature. A well-known example is the correlation matrix, which is defined, e.g., in [38]. In addition, an indicator for perturbations of the measurements is given in [50]. Alternatively, statistical methods can be considered as discussed, e.g., in [27]. Since the generation of experimental data might become costly, this approach can be supported by stochastic simulation, cf., e.g., [35, 36].

In the field of optimum experimental design a confidence matrix is introduced, which typically may be constructed in terms of the Jacobian of the underlying least-squares functional. Then, different indicator functions for evaluation of a stable solution vector are defined, known as A-,E-,D- and M-criterion and subsequently generally denoted as I-criteria; see, e.g., [4] and [24] for precise definitions. In the field of optimal control problems, the indicator function may be dependent on further design variables such that an optimality problem can be formulated, cf., e.g., [4] and [24].

Aims of present work on stable material parameters

Following [50], we perform a first-order perturbation analysis in order to investigate the influence of perturbed experimental data to the perturbation of material parameters. This analysis motivates the definition of four so-called I-criteria known from optimal control problems. In this work, these criteria will be applied, to give a stability assessment of material parameters related to the strain mode decomposition discussed above, which eventually can be exploited for model reduction.

1.5 Structure of this work

The structure of the paper is as follows: Based on the preliminaries in Sect. 2 for hyperelasticity in continuum mechanics, Sect. 3 presents a general framework for strain mode-dependent hyperelasticity. To this end, strain mode related weighting functions are introduced, which are incorporated into a new formulation of a general strain energy function. We propose a general framework for convenient implementation, including the consistent tangent modulus, for any free energy density in terms of the principal isochoric stretches, the eigenvalues and respectively the invariants of the isochoric right Cauchy–Green strain tensor. Section 4 considers aspects of stable parameter identification. We perform a perturbation analysis to motivate four different so-called I-criteria known from optimal control theory. In Sect. 5 we propose a practical guide for model development accounting for the criteria of verification, validation and stability by means of the strain mode-dependent weighting functions. In Sect. 6 the approach is applied for 13 hyperelastic models with regard to the classical experimental data on vulcanized rubber published by Treloar [48]. Detailed investigations with a focus on verification, validation and stability by means of the strain mode-dependent weighting functions and techniques of model reduction will be presented.

Notations

Square brackets $[\bullet ]$ are used throughout the paper to denote ’function of’ in order to distinguish from mathematical groupings with parenthesis $(\bullet )$.

2 Preliminaries of hyperelasticty in continuum mechanics

This section provides a brief review on the modeling of hyperelasticty in the finite strain regime of continuum mechanics. Particular interest is directed to basic kinematics, spectral decomposition, and the derivation of stress tensors and tangent operators associated to a given strain energy density.

We focus on hyperelastic properties for rubber-like materials which exhibit a decoupled response to volumetric and isochoric deformations. For this purpose, the following kinematical quantities are indispensable

$$\begin{aligned} 1.~ \mathbf {F}= \partial \varvec{\varphi }/\partial \mathbf {X}, \quad 2.~ J = \det [\mathbf {F}], \quad 3.~ \mathbf {C}= \mathbf {F}^T\mathbf {F}, \quad 4.~ \overline{\mathbf {C}}= J^{-2/3} \mathbf {C}. \end{aligned}$$

(1)

Here the material gradient $\mathbf {F}$ is defined as the partial derivative of the nonlinear deformation map $\varvec{\varphi }$ with respect to the position vector $\mathbf {X}\in \mathbb {R}^{3}$ in the Euclidean space $\mathbb {R}^{3}$, J is its determinant, $\mathbf {C}$ is the right Cauchy–Green tensor and $\overline{\mathbf {C}}$ is the isochoric right Cauchy–Green tensor, cf. e.g. [18, 19]. The decomposition (1.4) can also be derived from the multiplicative split $\mathbf {F}= (J^{1/3}\mathbf {1}) \cdot {\bar{\mathbf {F}}}$ of the deformation gradient that goes back to Flory [13] and satisfies the incompressibility condition $\det {\bar{\mathbf {F}}}~=~1$. Here, also the second-order unity tensor $\mathbf {1}$ has been used.

In the subsequent exposition, extensive use will be made of the following relations; see, e.g., [45]:

$$\begin{aligned} \begin{array}{llllllll} 1. &{} \mathbf {C}&{}=&{} \displaystyle \sum _{a=1}^3 {\Lambda }_a \mathbf {M}_{aa}, \qquad &{} 2. &{} \mathbf {M}_{aa} = \mathbf {N}_a \otimes \mathbf {N}_a ~ \Longleftrightarrow ~ \\ 3. &{} \overline{\mathbf {C}}&{}=&{} \displaystyle \sum _{a=1}^3 {{\bar{\Lambda }}}_a \mathbf {M}_{aa}, &{} 4. &{} {{\bar{\Lambda }}}_a = J^{-2/3} {\Lambda }_a. \end{array} \end{aligned}$$

(2)

Here Eq. (2.1) represents the spectral decomposition of the right Cauchy–Green tensor $\mathbf {C}$ in Eq. (1.3) with associated eigenvalues ${\Lambda }_a$ and eigenvectors $\mathbf {N}_a$, $a=1,2,3$. Analogously, Eq. (2.3) represents the spectral decomposition of the isochoric right Cauchy–Green tensor $\overline{\mathbf {C}}$ in Eq. (1.4) with associated eigenvalues ${{\bar{\Lambda }}}_a$ and eigenvectors $\mathbf {N}_a$, and where the eigenvalues ${\Lambda }_a$ and ${{\bar{\Lambda }}}_a$, $a=1,2,3$ are related by Eq. (2.4). According to standard notation, see, e.g., [19], we introduce the three principal stretches

$$\begin{aligned} 1. ~~{\lambda }_a= {\sqrt{\Lambda }_a},\quad 2. ~~\overline{{\lambda }}_a= {\sqrt{{\bar{\Lambda }}}_a} = J^{-1/3} {\lambda }_a, \quad a = 1,2,3 \end{aligned}$$

(3)

in terms of the eigenvalues ${\Lambda }_a$ and ${{\bar{\Lambda }}}_a$, respectively. Note, that ${\lambda }_a$ and $\overline{{\lambda }}_a$ are the eigenvalues of $\mathbf {F}$ and $\bar{\mathbf {F}}$, respectively.

Moreover, three invariants ${I}_1 := {{\,\mathrm{tr}\,}}[\mathbf {C}]$, ${I}_2 := \frac{1}{2}\bigl ({{\,\mathrm{tr}\,}}[\mathbf {C}]^2 - {{\,\mathrm{tr}\,}}[\mathbf {C}^2]\bigr )$ and ${I}_3 := \det (\mathbf {C})$ of the right Cauchy–Green strain tensor $\mathbf {C}$, and analogously defined for its isochoric part $\overline{\mathbf {C}}$ are written in terms of the eigenvalues ${\Lambda }_a$ and ${{\bar{\Lambda }}}_a$, respectively, as

$$\begin{aligned} \begin{array}{llllllllll} 1. \quad I_1 &{}= {\Lambda }_1 + {\Lambda }_2 + {\Lambda }_3, &{} \quad I_2 &{}= {\Lambda }_1 {\Lambda }_2 + {\Lambda }_2 {\Lambda }_3 + {\Lambda }_1 {\Lambda }_3, &{} \quad I_3 &{}= {\Lambda }_1 {\Lambda }_2 {\Lambda }_3 \\ 2. \quad {\bar{I}}_1 &{}= {{\bar{\Lambda }}}_1 + {{\bar{\Lambda }}}_2 + {{\bar{\Lambda }}}_3, &{} \quad {\bar{I}}_2 &{}= {{\bar{\Lambda }}}_1 {{\bar{\Lambda }}}_2 + {{\bar{\Lambda }}}_2 {{\bar{\Lambda }}}_3 + {{\bar{\Lambda }}}_1 {{\bar{\Lambda }}}_3, &{} \quad \bar{I}_3 &{}= {{\bar{\Lambda }}}_1 {{\bar{\Lambda }}}_2 {{\bar{\Lambda }}}_3 = 1. \end{array} \end{aligned}$$

(4)

In the last relation the condition $\det [\bar{\mathbf {F}}]) = \overline{{\lambda }}_1 \overline{{\lambda }}_2 \overline{{\lambda }}_3 = {\bar{J}} = 1$ for the isochoric incompressible material behavior has been exploited. In view of Eq. (1.4), the above invariants are related as

$$\begin{aligned} {\bar{I}}_1 = J^{-2/3} I_1,\quad {\bar{I}}_2 = J^{-4/3} I_2,\quad \bar{I}_3 = J^{-2} I_3 = 1. \end{aligned}$$

(5)

A well accepted starting point for modelling hyperelastic materials is an additive decomposition of the strain energy function into volumetric (shape preserving) and isochoric (volume preserving but shape changing) parts:

$$\begin{aligned} \psi [\mathbf {C}, \varvec{\kappa }] = {\hat{\psi }}_{\text {}}[J,\varvec{\kappa }] + \overline{\psi }[\overline{\mathbf {C}},\varvec{\kappa }]. \end{aligned}$$

(6)

Additionally, in Eq. (6) we have accounted for a vector of material parameters $\varvec{\kappa }\in \mathcal{K}\subset \mathbb {R}^{n_{\text {p}}}$, where $\mathcal{K}\subset \mathbb {R}^{n_{\text {p}}}$ denotes the $n_{\text {p}}$-dimensional space of admissible parameters, which will be investigated more deeply in the ensuing Sect. 4.

The second Piola–Kirchhoff stress tensor $\mathbf {S}$ is given as the derivative of the free energy wrt $\mathbf {C}$ multiplied by 2, that is $\mathbf {S}= 2 {\partial \psi }/{\partial \mathbf {C}}$, and a further derivative wrt $\mathbf {C}$ multiplied by a factor 2 renders the fourth-order elasticity tensor (or tangent operator) $\mathbb {C}= 2 {\partial \mathbf {S}}/{\partial \mathbf {C}} = 4 {\partial ^2 \psi }/{\partial \mathbf {C}\partial \mathbf {C}}$, cf. e.g. [45]. Exploiting the additive decomposition Eq. (6) yields the corresponding decoupled stress tensor and tangent operator as

$$\begin{aligned} 1.~\mathbf {S}= \hat{\mathbf {S}}+ \overline{\mathbf {S}}= 2 \displaystyle \frac{\partial {\hat{\psi }}_{\text {}}}{\partial \mathbf {C}} + 2 \displaystyle \frac{\partial \overline{\psi }}{\partial \mathbf {C}}, \qquad 2.~ \mathbb {C}= {\hat{\mathbb {C}}}_\text {}+ \overline{\mathbb {C}}= 2 \displaystyle \frac{\partial \hat{\mathbf {S}}}{\partial \mathbf {C}} + 2 \displaystyle \frac{\partial \overline{\mathbf {S}}}{\partial \mathbf {C}}. \end{aligned}$$

(7)

By use of the chain rule, the volumetric stress tensor can be expressed as

$$\begin{aligned} \hat{\mathbf {S}}= 2 \displaystyle \frac{\partial {\hat{\psi }}_{\text {}}(J)}{\partial J} \displaystyle \frac{\partial J }{\partial \mathbf {C}} = J p\mathbf {C}^{-1}, \qquad \text{ where }\quad p= \displaystyle \frac{\partial {\hat{\psi }}_{\text {}}(J)}{\partial J}. \end{aligned}$$

(8)

Here $p$ is known as the hydrostatic pressure and the result ${\partial J }/{\partial \mathbf {C}} = 1/2 \mathbf {C}^{-1}$ has been used, cf. e.g. [45].

3 A general framework for strain mode-dependent hyperelasticity

3.1 Strain mode-dependent energy function

Many existing hyperelastic models known from the literature are well advanced both from the mathematical and the numerical point of view and offer a convincing fit quality for a variety of nonlinear experimental stress-strain data. However, in many cases, optimized material parameters obtained for a certain strain mode (e.g., uniaxial tension) lack a general validity for different strain modes (e.g., equibiaxial tension or pure shear), and consequently are not conform according to Definition 1 in Sect. 1.3. This section presents a framework for extension of hyperelastic models for rubber-like materials exhibiting different behaviors in different loading scenarios, which can be examined individually in the laboratory.

The starting point for the strain mode related approach is the following isochoric part of the strain energy $\overline{\psi }$ in Eq. (6):

$$\begin{aligned} \begin{array}{lllllll} 1. &{} \overline{\psi }[\overline{\mathbf {C}}, \varvec{\kappa }] &{}=&{} \mathop {\sum }\limits _{i=1}^{S} w^{i}\overline{\psi }^{i}[\overline{\mathbf {C}},\varvec{\kappa }^{i}], \quad \text{ where }\quad \\ 2. &{} w^{i}&{}=&{} w^{i}[\mathbf {E}(\overline{\mathbf {C}})]. \\ \end{array} \end{aligned}$$

(9)

The above mathematical structure is identical to the one in [26] for creep simulation of asymmetric effects by use of stress mode-dependent weighting functions. Equation (9.1) represents an additive decomposition of the energy function into $S$ strain mode related quantities. Each of them incorporates a strain mode-dependent energy function $\overline{\psi }^{i}$ dependent on the isochoric right Cauchy–Green tensor $\overline{\mathbf {C}}$, and a vector of material parameters $\varvec{\kappa }^{i}$ associated to the ith strain mode investigated individually in the laboratory, such that $\varvec{\kappa }= \{\varvec{\kappa }^{i}\}_{i=1}^3$. Furthermore, in the above skeleton structure (9) a weighting function $w^{i}$ is associated to each mode $i$, which is dependent on a strain tensor $\mathbf {E}(\overline{\mathbf {C}})$, and for which it is stipulated that

$$\begin{aligned} \begin{array}{rrll} ~~~1. &{} \mathop {\sum }\limits _{i=1}^{S} w^{i}[\mathbf {E}(\overline{\mathbf {C}})] &{}=&{} 1 \\ ~~~2. &{} w^{i}[\mathbf {E}(\overline{\mathbf {C}}^{j})] &{}=&{} \delta _{ij}, \end{array} \end{aligned}$$

(10)

where $\delta _{ij}$ is the Kronecker-delta. Also, the strain tensors $\mathbf {E}(\overline{\mathbf {C}}^{j})$, $j=1,2,..,S$ refer to independent characteristic strain modes, which for example can be investigated experimentally in uniaxial tension, equibiaxial tension and pure shear, respectively. Note, that Eq. (10.1) can be regarded as a completeness condition, whereas Eq. (10.2) constitutes a normalization condition for the weighting functions. We remark also, that above Eq. (9) are restricted to isotropic materials. The aspect of anisotropy combined to strain mode-dependent material behavior is not within the scope of this paper.

3.2 Choices for strain mode related weighting functions

For illustrative purpose, we consider three independent strain modes for uniaxial tension (UT), equibiaxial tension (ET) and pure shear (PS), respectively, as published by Treloar [48] for experimental data on vulcanized rubber. For UT, only one out of three principal stretches ${\lambda }_a, a=1,2,3$ is prescribed, ${\lambda }_1 = {\lambda }$ say, for ET there are two prescribed values ${\lambda }_1 ={\lambda }_2 = {\lambda }$ say, and for PS we require ${\lambda }_1 = {\lambda }$ and ${\lambda }_2 = 1$ say. From the condition on incompressibility ${\bar{I}}_3 =$ $\overline{{\lambda }}_1^2 \overline{{\lambda }}_2^2 \overline{{\lambda }}_3^2 = 1$, and the assumption of isotropy, the complementary principal stretches follow accordingly. In summary, the corresponding deformation gradients and the right Cauchy–Green tensors are, cf. e.g. [47]:

• Uniaxial tension (UT)

  $$\begin{aligned} \begin{array}{llllllll} {\bar{\mathbf {F}}}^{\text{ UT }}&{}=&{} \left[ \begin{array}{l@{\quad }l@{\quad }l} \overline{{\lambda }}&{} 0 &{} 0 \\ 0 &{} \overline{{\lambda }}^{-1/2} &{} 0 \\ 0 &{} 0 &{} \overline{{\lambda }}^{-1/2} \end{array} \right] &{} \Longrightarrow &{} \overline{\mathbf {C}}^{\text{ UT }}&{}=&{} \left[ \begin{array}{l@{\quad }l@{\quad }l} \overline{{\lambda }}^2 &{} 0 &{} 0 \\ 0 &{} \overline{{\lambda }}^{-1} &{} 0 \\ 0 &{} 0 &{} \overline{{\lambda }}^{-1} \end{array} \right]&\end{array} \end{aligned}$$

  (11)

• Equibiaxial tension (ET)

  $$\begin{aligned} \begin{array}{lllllllll} {\bar{\mathbf {F}}}^{\text{ ET }}&{}=&{} \left[ \begin{array}{l@{\quad }l@{\quad }l} \overline{{\lambda }}&{} 0 &{} 0 \\ 0 &{} \overline{{\lambda }}^{} &{} 0 \\ 0 &{} 0 &{} \overline{{\lambda }}^{-2} \end{array} \right] &{} \Longrightarrow &{} \overline{\mathbf {C}}^{\text{ UT }}&{}=&{} \left[ \begin{array}{l@{\quad }l@{\quad }l} \overline{{\lambda }}^2 &{} 0 &{} 0 \\ 0 &{} \overline{{\lambda }}^{2} &{} 0 \\ 0 &{} 0 &{} \overline{{\lambda }}^{-4} \end{array} \right]&\end{array} \end{aligned}$$

  (12)

• Pure shear (PS)

  $$\begin{aligned} \begin{array}{lllllllll} {\bar{\mathbf {F}}}^{\text{ PS }}&{}=&{} \left[ \begin{array}{l@{\quad }l@{\quad }l} \overline{{\lambda }}&{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} \overline{{\lambda }}^{-1} \end{array} \right] &{} \Longrightarrow &{} \overline{\mathbf {C}}^{\text{ PS }}&{}=&{} \left[ \begin{array}{l@{\quad }l@{\quad }l} \overline{{\lambda }}^2 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} \overline{{\lambda }}^{-2} \end{array} \right] . \end{array} \end{aligned}$$

  (13)

The above tensors are formulated in terms of powers of $\overline{{\lambda }}$. This motivates the following choice for the strain tensor $\mathbf {E}$ in Eq. (9) as the Hencky strain tensor in logarithmic form

$$\begin{aligned} \mathbf {E}:= \displaystyle \frac{1}{2}\ln \overline{\mathbf {C}}= \displaystyle \frac{1}{2}\displaystyle \sum _{a=1}^3 \ln {{\bar{\Lambda }}}_a \mathbf {M}_{aa} = \displaystyle \sum _{a=1}^3 \ln \overline{{\lambda }}_a \mathbf {M}_{aa}, \end{aligned}$$

(14)

where $\mathbf {M}_{aa}$ is the dyadic basis in Eq. (2.2), and where the relation (3.2) has been used. Application of Eq. (14) to the three loading scenarios in Eq. (11) to Eq. (13) renders

$$\begin{aligned} \begin{array}{lllllllll} \mathbf {E}^{\text{ UT }}= \displaystyle \frac{1}{2}\ln {{\bar{\Lambda }}}\left[ \begin{array}{r@{\quad }r@{\quad }r} 1 &{} 0 &{} 0 \\ 0 &{} -1/2 &{} 0 \\ 0 &{} 0 &{} -1/2 \end{array} \right] , &{} \mathbf {E}^{\text{ ET }}= \displaystyle \frac{1}{2}\ln {{\bar{\Lambda }}}\left[ \begin{array}{r@{\quad }r@{\quad }r} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} -2 \end{array} \right] , &{} \\ \mathbf {E}^{\text{ PS }}= \displaystyle \frac{1}{2}\ln {{\bar{\Lambda }}}\left[ \begin{array}{r@{\quad }r@{\quad }r} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} -1 \end{array} \right] .&\end{array} \end{aligned}$$

(15)

Observe the property ${{\,\mathrm{tr}\,}}[\mathbf {E}^{i}] = 0$ for all three cases ${i}=$ UT, ET, PS, where the trace operator is defined by ${{\,\mathrm{tr}\,}}[\bullet ] := \mathbf {1}:[\bullet ]$. This infers $\mathbf {E}^{i}= {{\,\mathrm{dev}\,}}[\mathbf {E}^{i}]$ for all three cases, where the deviatoric operator is defined by ${{\,\mathrm{dev}\,}}[\bullet ] := \bullet - \mathbf {1}:[\bullet ] \mathbf {1}$.

With these properties at hand, we can follow the same procedure as extensively outlined by [12] for deviatoric stress tensors. The three modes in Eq. (15) are represented in the octahedral plane of the associated logarithmic isochoric strain tensor. To this end the quantities

$$\begin{aligned} \begin{array}{rrll} ~~~1. &{} \theta &{}=&{} \displaystyle \frac{1}{3} \text{ arccos } \left[ \xi \right] , \quad \text{ where }\\ ~~~2. &{} \xi &{}=&{} \displaystyle \frac{\sqrt{{27}}}{2} \displaystyle \frac{{J}_3}{{J}_2^{1.5}} \\ ~~~3. &{} {J}_k &{}=&{} \displaystyle \frac{1}{k} \mathbf {1}: \mathbf {E}^k,\qquad k = 2,3 \\ \end{array} \end{aligned}$$

(16)

are defined. Here $\theta$ shall be referred to as the strain mode angle dependent on the strain mode factor $\xi$. Furthermore, in above Eq. (16.3) ${J}_2$ and ${J}_3$ denote the second and third basic invariant of the logarithmic isochoric strain tensor $\mathbf {E}$, respectively. Exploiting the spectral decomposition of the logarithmic Hencky strain tensor in Eq. (14) renders

$$\begin{aligned} \begin{array}{lllllll} 1.~~ &{}{J}_2 &{}=&{} \displaystyle \frac{1}{2}\left( (\ln {{\bar{\Lambda }}}_1)^2 + (\ln {{\bar{\Lambda }}}_2)^2 + (\ln {{\bar{\Lambda }}}_3)^2\right) , \quad \\ 2.~~ &{}{J}_3 &{}=&{} \displaystyle \frac{1}{3} \left( (\ln {{\bar{\Lambda }}}_1)^3 + (\ln {{\bar{\Lambda }}}_2)^3 + (\ln {{\bar{\Lambda }}}_3)^3\right) . \end{array} \end{aligned}$$

(17)

Fig. 1

Top: Octahedral plane in the logarithmic isochoric strain space. Here $\ln \overline{{\lambda }}_1, \ln \overline{{\lambda }}_2, \ln \overline{{\lambda }}_3$ denote the principal logarithmic isochoric strains. Circles, squares, and triangles represent strain modes of uniaxial tension (UT), equibiaxial tension (ET) and pure shear (PS), respectively. Middle: Weighting functions (21) in terms of the strain mode angle $\theta$ for UT, ET and PS. Bottom: Weighting functions (22) in terms of the strain mode angle $\theta$ for UT and ET

A graphical interpretation of the strain mode angle $\theta$ is given at the top of Fig. 1. In particular, it becomes apparent, that the independent strain modes of UT, ET, and PS, respectively, are characterized by the strain mode angles

$$\begin{aligned} {{\begin{array}{rllllllll} ~~~1. &{} \text{ UT: } &{} \xi = 1 &{}\Longrightarrow &{} \theta _1 &{}=&{} \displaystyle \frac{2 \pi }{3} n, &{} n= 0,1,2,...&{} \\ ~~~2. &{} \text{ ET: } &{} \xi = -1 &{}\Longrightarrow &{} \theta _2 &{}=&{} \displaystyle \frac{2\pi }{3} n + \displaystyle \frac{\pi }{3}, &{} n= 0,1,2,...&{} \\ ~~~3. &{} \text{ PS: } &{} \xi = 0 &{}\Longrightarrow &{} \theta _3 &{}=&{} \displaystyle \frac{\pi }{3} n + \displaystyle \frac{\pi }{6} &{} n= 0,1,2,...&{} \end{array}}} \end{aligned}$$

(18)

and for each of the strain modes the following periodicity angles

$$\begin{aligned} {{\begin{array}{rllllll} ~~~1. &{} \text{ UT: } &{} {\tilde{\theta }}^{(1)}&{}=&{} \displaystyle \frac{2\pi }{3} \\ ~~~2. &{} \text{ ET: } &{} {\tilde{\theta }}^{(2)}&{}=&{} \displaystyle \frac{2\pi }{3}\\ ~~~3. &{} \text{ PS: } &{} {\tilde{\theta }}^{(3)}&{}=&{} \displaystyle \frac{\pi }{3} \end{array}}} \end{aligned}$$

(19)

are obtained. Based on these observations, in addition to the relations (10) the following is required for the weighting functions

$$\begin{aligned} \begin{array}{rrll} ~~~1. &{} \mathop {\sum }\limits _{{i}=1}^{S} w^{i}[\theta ] &{}=&{} 1 \\ ~~~2. &{} w^{i}[\theta ^{j}] &{}=&{} \delta _{ij} \\ ~~~3. &{} w^{i}[\theta ] &{}=&{} w^{i}[\theta + {\tilde{\theta }}^{i}]. \end{array} \end{aligned}$$

(20)

For the strain modes related to the loading scenarios of uniaxial tension, equibiaxial tension and pure shear, respectively, we set $S=3$ and the requirements (20) are satisfied by the following weighting function

$$\begin{aligned} \begin{array}{rllllll} 1. &{} \text{ UT: } &{} w^{(1)}[\theta ] = \left\{ \begin{array}{llll} \displaystyle \frac{1}{2}+ \displaystyle \frac{1}{2}\cos {3 \theta }, &{} &{}\text{ if } &{} - \displaystyle \frac{\pi }{6} + n {\tilde{\theta }}^{(1)}\le \theta \le \displaystyle \frac{\pi }{6} + n {\tilde{\theta }}^{(1)}\\ 0, &{} &{} \text{ else } &{} \\ \end{array} \right. \\ 2. &{} \text{ ET: } &{} w^{(2)}[\theta ] = \left\{ \begin{array}{llll} 0, &{} &{}\text{ if } &{} - \displaystyle \frac{\pi }{6} + n {\tilde{\theta }}^{(1)}\le \theta \le \displaystyle \frac{\pi }{6} + n {\tilde{\theta }}^{(1)}\\ \displaystyle \frac{1}{2}+ \displaystyle \frac{1}{2}\cos {3 \theta }, &{} &{} \text{ else } &{} \\ \end{array} \right. \\ 3. &{} \text{ PS: } &{} w^{(3)}[\theta ] = \displaystyle \frac{1}{2}+ \displaystyle \frac{1}{2}\cos \left( {3 \theta - {\pi } }\right) \\ \end{array} \end{aligned}$$

(21)

and where $n=0,1,2,...$ are integer values. A graphical representation of the weighting functions (21) is given in the middle graph of Fig. 1. For the case, that experimental data are available only for loading in uniaxial tension and equibiaxial tension, respectively, with $S=2$, the following weighting functions can be used

$$\begin{aligned} {{\begin{array}{rllllll} ~~1. &{} \text{ UT: } &{} w^{(1)}[\theta ] &{}=&{} \displaystyle \frac{1}{2}+ \displaystyle \frac{1}{2}\cos {3 \theta } \\ ~~2. &{} \text{ ET: } &{} w^{(2)}[\theta ] &{}=&{} \displaystyle \frac{1}{2}+ \displaystyle \frac{1}{2}\cos {\left( 3 \theta - \pi \right) }. \end{array}}} \end{aligned}$$

(22)

These functions, which are illustrated at the bottom of Fig. 1, do also satisfy the requirements (20).

Upon using the definition (16.1), alternatively the functional relationships (21) and (22) can be rewritten in terms of the strain mode factor $\xi$ as

$$\begin{aligned} {{\begin{array}{rllllll} ~~1. &{} \text{ UT: } &{} w^{(1)}[\xi ] &{}=&{} \left\{ \begin{array}{llll} \xi ^2 , &{} &{}\text{ if } &{} \xi \ge 0 \\ 0, &{} &{} \text{ else } &{} \\ \end{array} \right. \\ \\ ~~2. &{} \text{ ET: } &{} w^{(2)}[\xi ] &{}=&{} \left\{ \begin{array}{llll} 0, &{} &{}\text{ if } &{} \xi \le 0 \\ \xi ^2, &{} &{} \text{ else } &{} \\ \end{array} \right. \\ ~~3. &{} \text{ PS: } &{} w^{(3)}[\xi ] &{}=&{} 1-\xi ^2\\ \end{array}}} \end{aligned}$$

(23)

or

$$\begin{aligned} {{\begin{array}{rllllll} ~~1. &{} \text{ UT: } &{} w^{(1)}[\xi ] &{}=&{} \displaystyle \frac{1}{2}(1 + \xi ) \\ ~~2. &{} \text{ ET: } &{} w^{(2)}[\xi ] &{}=&{} \displaystyle \frac{1}{2}(1 - \xi ) \end{array}}}, \end{aligned}$$

(24)

respectively, which is more convenient for numerical implementation of the strain energy $\overline{\psi }$ in Eq. (9).

3.3 Hyperelasticity based on principal stretches

A general formulation for the strain energy function for isotropy may be written as $\overline{\psi }= \overline{\psi }[{\lambda }_a,\varvec{\kappa }]$, which we assume as continuously differentiable with respect to the three principal stretches ${\lambda }_a, a = 1,2,3$ of Eq. (3.1). In order to account for incompressibility and strain mode-dependent material behavior, the free energy density for the isochoric part in Eq. (9) is now postulated in a mixed formulation as

$$\begin{aligned} \begin{array}{lllllll} \overline{\psi }[\overline{\mathbf {C}}, \varvec{\kappa }]= & {} \displaystyle \mathop {\sum }\limits _{i=1}^{S} w^{i}[{{\bar{\Lambda }}}_a] \overline{\psi }^{i}[\overline{{\lambda }}_a,\varvec{\kappa }^{i}] \end{array} \end{aligned}$$

(25)

in terms of the eigenvalues ${{\bar{\Lambda }}}_a$ introduced in Eq. (2) and the principal isochoric stretches $\overline{{\lambda }}_a, a = 1,2,3$ of Eq. (3.2). Closed-form expressions for the related stresses and tangent moduli of $\overline{\psi }^{i}[\overline{{\lambda }}_a,\varvec{\kappa }^{i}]$ in terms of the reference configuration as well as the current configuration have been derived in [45]. A summary for the isochoric second Piola–Kirchhoff stress tensor $\overline{\mathbf {S}}$ and the corresponding tangent $\overline{\mathbb {C}}$ of Eq. (7) is provided, e.g., in [47].

A reformulation of the mixed relation (25) purely in terms of the eigenvalues ${\Lambda }_a$ requires a reparametrization of the individual energy functions from a stretch based formulation $\overline{\psi }^{i}[\overline{{\lambda }}_a,\varvec{\kappa }^{i}]$ to an eigenvalue based formulation $\overline{\psi }^{i}[{{\bar{\Lambda }}}_a,\varvec{\kappa }^{i}]$, which is easily achieved by means of the relations (3). Accordingly, straightforward differentiation renders by means of the chain rule the isochoric second Piola–Kirchhoff stress tensor in Eq. (7.1) as

$$\begin{aligned} \begin{array}{llllll} 1. &{} \overline{\mathbf {S}}&{}=&{} 2 \displaystyle \frac{\partial \overline{\psi }}{\partial \mathbf {C}} = \displaystyle \mathop {\sum }\limits _{i=1}^{S} \overline{\mathbf {S}}^{i}, \quad \text{ where }\\ 2. &{} \overline{\mathbf {S}}^{i}&{}=&{} 2 \displaystyle \frac{\partial (w^{i}\overline{\psi }^{i}) }{\partial \mathbf {C}} = \displaystyle 2 \sum _{a=1}^3 \displaystyle \frac{\partial (w^{i}\overline{\psi }^{i})}{\partial {\Lambda }_a} \displaystyle \frac{\partial {\Lambda }_a}{\partial \mathbf {C}} = \displaystyle 2 \sum _{a=1}^3 \overline{s}^{i}_a \mathbf {M}_{aa}, \quad \\ 3. &{} \overline{s}^{i}_a &{}=&{} \displaystyle \frac{\partial (w^{i}\overline{\psi }^{i})}{\partial {\Lambda }_a} = w^{i}\overline{S}^{i}_a + \overline{\psi }^{i}\overline{W}^{i}_a \\ 4. &{} \overline{S}^{i}_a &{}=&{} \displaystyle \frac{\partial \overline{\psi }^{i}}{\partial {\Lambda }_a} = \sum _{b=1}^{3} \displaystyle \frac{\partial \overline{\psi }^{i}}{\partial \overline{{\lambda }}_b} \displaystyle \frac{\partial \overline{{\lambda }}_b}{\partial {\Lambda }_a}\\ 5. &{} \overline{W}^{i}_a &{}=&{} \displaystyle \frac{\partial w^{i}}{\partial {\Lambda }_a} = \sum _{b=1}^{3} \displaystyle \frac{\partial w^{i}}{\partial {{\bar{\Lambda }}}_b} \displaystyle \frac{\partial {{\bar{\Lambda }}}_b}{\partial {\Lambda }_a} \end{array} \end{aligned}$$

(26)

where the second-order basis tensors $\mathbf {M}_{aa}$ are defined in Eq. (2.2). In Eq. (26.4) the functional relation $\overline{\psi }^{i}[\overline{{\lambda }}_a,\varvec{\kappa }^{i}]$ defined in (25) has been taken into account. Moreover, the following results are required for evaluations of Eq. (26.4–5):

$$\begin{aligned} \begin{array}{llllll} 1.~~ \displaystyle \frac{\partial \overline{{\lambda }}_a}{\partial {\Lambda }_b} = \displaystyle \sum _{c=1}^{3} \displaystyle \frac{\partial \overline{{\lambda }}_a}{\partial {{\bar{\Lambda }}}_c} \displaystyle \frac{\partial {{\bar{\Lambda }}}_c}{\partial {\Lambda }_b}, \quad \text{ where }\\ 2.~~\displaystyle \frac{\partial \overline{{\lambda }}_a}{\partial {{\bar{\Lambda }}}_b} = \left\{ \begin{array}{llll} \displaystyle \frac{1}{2\overline{{\lambda }}_b}, &{} \text{ for }~ a = b \\ 0 &{} \text{ else } \end{array} \right. \quad 3.~~\displaystyle \frac{\partial {{\bar{\Lambda }}}_a}{\partial {\Lambda }_b} = J^{-2/3} \left( \delta _{ab} - \displaystyle \frac{1}{3} \displaystyle \frac{{\Lambda }_a}{{\Lambda }_b} \right) . ~~~~ \end{array} \end{aligned}$$

(27)

3.3.1 Remarks 3.3

• 1. The coefficients $\overline{S}^{i}_a$ in (26.4) characterize the constitutive part of the hyperelastic model. The coefficients ${\partial \overline{\psi }^{i}}/{\partial \overline{{\lambda }}_b}$ must be obtained for the individual material model. Examples for some classical material models are provided in Appendix B.

• 2. Due to the same structure for $\overline{S}^{i}_a$ in Eq. (26.4) and for $\overline{W}^{i}_a$ in Eq. (26.5), the coefficients $\overline{W}^{i}_a$ can be interpreted as stress like coefficients.

• 3. Setting $S=1$ and $w^{i}=$ const in the above general structure (25) ensues $\overline{W}^{i}_a = 0$ for the stress like coefficients in Eq. (26.5), such that the stress tensor $\overline{\mathbf {S}}$ boils down to classical results as, e.g., in [45].

Similarly, the isochoric tangent operator in Eq. (7.2) is derived as

$$\begin{aligned} \begin{array}{llllll} 1. &{} \overline{\mathbb {C}}&{}=&{} 2 \displaystyle \frac{\partial \overline{\mathbf {S}}}{\partial \mathbf {C}} = \displaystyle \mathop {\sum }\limits _{i=1}^{S} \overline{\mathbb {C}}^{i}, \quad \text{ where }\\ 2. &{} \overline{\mathbb {C}}^{i}&{}=&{} 2 \displaystyle \frac{\partial \overline{\mathbf {S}}^{i}}{\partial \mathbf {C}} = 4 \displaystyle \sum _{a=1}^3\sum _{b=1}^3 c_{ab}^{i}\mathbf {M}_{aabb} + 2 \displaystyle \sum _{a=1}^3 \sum _{b=1, b\ne a}^3 \displaystyle \frac{\overline{s}^{i}_b-\overline{s}^{i}_a }{{\Lambda }_b-{\Lambda }_a} {\hat{\mathbf {M}}}_{abab} \\ 3. &{} c_{ab}^{i}&{}=&{} \displaystyle \frac{\partial \overline{s}^{i}_a}{\partial {\Lambda }_b} = w^{i}\overline{C}^{i}_{ab} + \overline{W}^{i}_a \overline{S}^{i}_b +\overline{S}^{i}_a \overline{W}^{i}_b + \overline{\psi }^{i}\overline{W}_{ab} \\ 4. &{} \overline{C}^{i}_{ab} &{}=&{} \displaystyle \frac{\partial \overline{S}^{i}_a }{\partial {\Lambda }_b} = \displaystyle \sum _{c=1}^{3} \displaystyle \sum _{d=1}^{3} \displaystyle \frac{\partial ^2 \overline{\psi }^{i}}{\partial \overline{{\lambda }}_c \partial \overline{{\lambda }}_d} \displaystyle \frac{\partial \overline{{\lambda }}_c}{\partial {\Lambda }_a} \displaystyle \frac{\partial \overline{{\lambda }}_d}{\partial {\Lambda }_b} + \displaystyle \sum _{c=1}^{3} \displaystyle \frac{\partial \overline{\psi }^{i}}{\partial \overline{{\lambda }}_c} \left. \displaystyle \frac{\partial ^2 \overline{{\lambda }}_c}{\partial {\Lambda }_a \partial {\Lambda }_b} \right. \\ 5. &{} \overline{W}^{i}_{ab} &{}=&{} \displaystyle \frac{\partial \overline{W}^{i}_a }{\partial {\Lambda }_b} = \displaystyle \sum _{c=1}^{3} \displaystyle \sum _{d=1}^{3} \left. \displaystyle \frac{\partial ^2 w^{i}}{\partial {{\bar{\Lambda }}}_c \partial {{\bar{\Lambda }}}_d} \displaystyle \frac{\partial {{\bar{\Lambda }}}_d}{\partial {\Lambda }_b} \right. \displaystyle \frac{\partial {{\bar{\Lambda }}}_c}{\partial {\Lambda }_a} + \displaystyle \sum _{c=1}^{3} \displaystyle \frac{\partial w^{i}}{\partial {{\bar{\Lambda }}}_c} \left. \displaystyle \frac{\partial ^2 {{\bar{\Lambda }}}_c}{\partial {\Lambda }_b \partial {\Lambda }_a} \right. \end{array} \end{aligned}$$

(28)

where the fourth-order basis tensors $\mathbf {M}_{abcd} = \mathbf {N}_a\otimes \mathbf {N}_b \otimes \mathbf {N}_c\otimes \mathbf {N}_d$ and ${\hat{\mathbf {M}}}_{abab} = \left( \mathbf {M}_{abab} + \mathbf {M}_{abba} \right)$ have been defined. The coefficients ${\partial ^2\overline{\psi }^{i}}/{\partial \overline{{\lambda }}_a \partial \overline{{\lambda }}_c}$ must be obtained for the individual material model. Examples for some classical material models are provided in Appendix B. The derivatives ${\partial \overline{{\lambda }}_a}/{\partial {{\bar{\Lambda }}}_a}$ and $\displaystyle {\partial {{\bar{\Lambda }}}_b}/{\partial {\Lambda }_a}$ are given in Eq. (27). Moreover, the following results are required for evaluation of Eq. (28.4–5):

$$\begin{aligned} \begin{array}{llllll} 1.~~ &{} \displaystyle \frac{\partial ^2 \overline{{\lambda }}_a}{\partial {\Lambda }_b\partial {\Lambda }_c} &{}=&{} \left. \displaystyle \sum _{d=1}^3 \displaystyle \sum _{e=1}^3 \displaystyle \frac{\partial ^2 \overline{{\lambda }}_a}{\partial {{\bar{\Lambda }}}_d\partial {{\bar{\Lambda }}}_e } \frac{\partial {{\bar{\Lambda }}}_e}{\partial {\Lambda }_b} \frac{\partial {{\bar{\Lambda }}}_d}{\partial {\Lambda }_c}\right. + \left. \displaystyle \sum _{d=1}^3 \displaystyle \frac{\partial \overline{{\lambda }}_a}{\partial {{\bar{\Lambda }}}_d} \frac{\partial ^2 {{\bar{\Lambda }}}_d}{\partial {\Lambda }_b \partial {\Lambda }_c }\right. , \quad \text{ where }\\ 2.~~&{} \displaystyle \frac{\partial ^2 \overline{{\lambda }}_a}{\partial {{\bar{\Lambda }}}_b\partial {{\bar{\Lambda }}}_c} &{}=&{} \left\{ \begin{array}{llll} -\displaystyle \frac{1}{4\overline{{\lambda }}_a^3} &{} \text{ for }~ a = b = c \\ 0 &{} \text{ else } \end{array} \right. \quad \qquad \\ 3.~~&{} \displaystyle \frac{\partial ^2 {{\bar{\Lambda }}}_a}{\partial {\Lambda }_b\partial {\Lambda }_c} &{}=&{} -\displaystyle \frac{1}{3} J^{-2/3} \left( \displaystyle \frac{1}{{\Lambda }_c} \left( \delta _{ab} - \displaystyle \frac{1}{3} \displaystyle \frac{{\Lambda }_a}{{\Lambda }_b} \right) + \displaystyle \frac{\delta _{ac}}{{\Lambda }_b} - \displaystyle \frac{{\Lambda }_a}{{\Lambda }_b^2}{\delta _{bc}} \right) . \end{array} \end{aligned}$$

(29)

3.4 Hyperelasticity based on invariants

Alternatively to the principal-stretch-based formulation (25) a strain energy function can be written depending on the invariants of the right Cauchy–Green tensor. A general formulation reads $\overline{\psi }= \overline{\psi }[I_1(\mathbf {C}), I_2 (\mathbf {C}), I_3 (\mathbf {C})]$, which we assume as continuously differentiable with respect to the three invariants $I_A, A = 1,2,2$ in Eq. (4.1) of the right Cauchy–Green strain tensor. In order to account for incompressibility and strain mode-dependent material behavior, the free energy density for the isochoric part in Eq. (9) is now postulated in a mixed formulation as

$$\begin{aligned} \overline{\psi }[\mathbf {C}, \varvec{\kappa }] = \mathop {\sum }\limits _{i=1}^{S} w^{i}[{{\bar{\Lambda }}}_a] \overline{\psi }^{i}[\bar{I}_1[\overline{\mathbf {C}}], {\bar{I}}_2 [\overline{\mathbf {C}}],\varvec{\kappa }^{i}] \end{aligned}$$

(30)

in terms of the eigenvalues ${{\bar{\Lambda }}}_a$ introduced in Eq. (2) and the two invariants ${\bar{I}}_A, A = 1,2$ in Eq. (4.2) of the isochoric right Cauchy–Green strain tensor. Closed-form expressions for the related stresses and tangent moduli of $\overline{\psi }^{i}[{\bar{I}}_A,\varvec{\kappa }^{i}]$ have been derived, e.g., in [21] for a formulation based on invariants, see also [31]. A summary for the second Piola–Kirchhoff stress tensor and the corresponding tangent of Eq. (7) is provided e.g. in [47].

A possible formulation related to the ith strain mode for the energy function in Eq. (25) is given as the Mooney–Rivlin/Saunders model [43]

$$\begin{aligned} \overline{\psi }^{i}[\bar{I}_A, \varvec{\kappa }]&= \displaystyle \sum _{k=0}^{K_i} \sum _{l=0}^{L_i} c^{i}_{kl}(\bar{I}_1 - 3)^k (\bar{I}_2 - 3)^l, \quad i = 1,...,S, \end{aligned}$$

(31)

where the vector of material parameters associated with each strain mode is defined as

$$\begin{aligned} \varvec{\kappa }^{i}&= [ C_{0_i0_i}, \dots , C_{K_i L_i} ], i = 1,...,S. \end{aligned}$$

(32)

A reformulation of the mixed relation (30) purely in terms of the eigenvalues ${\Lambda }_a$ requires a reparametrization of the individual energy functions from an invariant based formulation $\overline{\psi }^{i}[{\bar{I}}_1[\overline{\mathbf {C}}], {\bar{I}}_2 [\overline{\mathbf {C}}],\varvec{\kappa }^{i}]$ to an eigenvalue based formulation $\overline{\psi }^{i}[{{\bar{\Lambda }}}_a,\varvec{\kappa }^{i}]$, which is easily achieved by means of the relations (4.2). Accordingly, a reparametrization of the results for the second Piola-Kirchhoff stress tensor in Eq. (26) is achieved by the chain rule. Consequently, the stress coefficients $\overline{S}^{i}_a$ in Eq. (26.4) become

$$\begin{aligned} \begin{array}{llllll}&\overline{S}^{i}_a= & {} \displaystyle \frac{\partial \overline{\psi }^{i}}{\partial {\Lambda }_a} = \sum _{A=1}^{2} \displaystyle \frac{\partial \overline{\psi }^{i}}{\partial {\bar{I}}_A} \displaystyle \frac{\partial {\bar{I}}_A}{\partial {\Lambda }_a}. \end{array} \end{aligned}$$

(33)

The coefficients ${\partial \overline{\psi }^{i}}/{\partial {\bar{I}}_A}$ must be obtained for the individual material model. Examples for some classical material models are provided in Appendix B. Moreover, the following results are required for evaluation of Eq. (33):

$$\begin{aligned} \begin{array}{lllllllll} 1.&{} \displaystyle \frac{\partial {\bar{I}}_A}{\partial {\Lambda }_a} &{}=&{} \displaystyle \sum _{b=1}^{3} \displaystyle \frac{\partial {\bar{I}}_A}{\partial {{\bar{\Lambda }}}_b} \displaystyle \frac{\partial {{\bar{\Lambda }}}_b}{\partial {\Lambda }_a}, ~A=1,2, \quad \text{ where }\\ 2. &{} \displaystyle \frac{\partial {\bar{I}}_1}{\partial {{\bar{\Lambda }}}_a} &{}=&{} 1, \qquad 3. ~~ \displaystyle \frac{\partial {\bar{I}}_2}{\partial {{\bar{\Lambda }}}_a} = {{\bar{\Lambda }}}_b + {{\bar{\Lambda }}}_c \end{array} \end{aligned}$$

(34)

and where ${\partial {{\bar{\Lambda }}}_b}/{\partial {\Lambda }_a}$ is given according to Eq. (27.3).

Analogously, the results for the corresponding tangent in Eq. (28) are reparametrized from an invariant based formulation to an eigenvalue based formulation. The tangent coefficients $\overline{C}^{i}_{ab}$ in Eq. (28.4) become

$$\begin{aligned} \begin{array}{llllll} \overline{C}^{i}_{ab}= & {} \displaystyle \frac{\partial \overline{S}^{i}_a}{\partial {\Lambda }_b} = \displaystyle \sum _{A=1}^{2} \sum _{B=1}^{2} \displaystyle \frac{\partial ^2 \overline{\psi }^{i}}{\partial {\bar{I}}_A \partial {\bar{I}}_B} \displaystyle \frac{\partial \bar{I}_A}{\partial {\Lambda }_a} \displaystyle \frac{\partial {\bar{I}}_B}{\partial {\Lambda }_b} + \displaystyle \sum _{A=1}^{2} \displaystyle \frac{\partial \overline{\psi }^{i}}{\partial {\bar{I}}_A} \displaystyle \frac{\partial \bar{I}_A^2}{\partial {\Lambda }_a \partial {\Lambda }_b}. \end{array} \end{aligned}$$

(35)

The coefficients ${\partial ^2 \overline{\psi }^{i}}/{\partial {\bar{I}}_A \partial {\bar{I}}_B}$ must be obtained for the individual material model. Examples for some classical material models are provided in Appendix B. The coefficients ${\partial {\bar{I}}_A}/{\partial {{\bar{\Lambda }}}_a}$ are given in Eq. (34). Moreover, the following results are required for evaluation of Eq. (35):

$$\begin{aligned} \begin{array}{lllllllll} 1.~~ &{} \displaystyle \frac{\partial ^2 {\bar{I}}_A}{\partial {\Lambda }_a\partial {\Lambda }_b} &{}=&{} \left. \displaystyle \sum _{d=1}^3 \displaystyle \sum _{e=1}^3 \displaystyle \frac{\partial ^2 {\bar{I}}_A}{\partial {{\bar{\Lambda }}}_d\partial {{\bar{\Lambda }}}_e } \frac{\partial {{\bar{\Lambda }}}_e}{\partial {\Lambda }_a} \frac{\partial {{\bar{\Lambda }}}_d}{\partial {\Lambda }_b}\right. + \left. \displaystyle \sum _{d=1}^3 \displaystyle \frac{\partial {\bar{I}}_A}{\partial {{\bar{\Lambda }}}_d} \frac{\partial ^2 {{\bar{\Lambda }}}_d}{\partial {\Lambda }_b \partial {\Lambda }_a }\right. , A = 1,2 , \quad \text{ where }\\ 2. &{} \displaystyle \frac{\partial ^2 {\bar{I}}_1}{\partial {{\bar{\Lambda }}}_a \partial {{\bar{\Lambda }}}_b} &{}=&{} 0, \qquad 3.~~ \displaystyle \frac{\partial ^2 {\bar{I}}_2}{\partial {{\bar{\Lambda }}}_a \partial {{\bar{\Lambda }}}_b} = \left\{ \begin{array}{llll} 0 &{} \text{ for }~ a = b \\ 1 &{} \text{ else } \end{array} \right. \\ \end{array} \end{aligned}$$

(36)

and where the coefficients ${\partial ^2 {\bar{I}}_A}/{\partial {{\bar{\Lambda }}}_a \partial {{\bar{\Lambda }}}_b}$ are obtained based on (34). Observe the analogous structure of the results (29.1) and (36.1).

The general results (26) and (28) require the coefficients $\overline{W}^{i}_a$ in (26.5) for the stress like coefficients and the coefficients $\overline{W}^{i}_{ab}$ in (28.5) for the corresponding tangent coefficients, which are derived in Appendix A.

4 Aspects of stable parameter identification

4.1 Least-squares minimization problem (inverse problem)

We denote by ${\underline{{\bar{d}}}}\in \mathcal {D}= \mathbb {R}^{n_{\text {d}}}$ a measurement vector of experimental data obtained from laboratory testing. The corresponding vector of $n_{\text {d}}$ simulated data shall be termed ${\underline{d}}[\varvec{\kappa }]$, where as before $\varvec{\kappa }\in \mathcal{K}$ denotes the vector of material parameters of the underlying material model. In general $n_{\text {d}}\ge n_{\text {p}}$, such that the distance between both data types must be minimized by means of a suitable least-squares function $f:\mathcal {D}\times \mathcal {K}\rightarrow \mathbb {R}$, e.g., in the following simple form:

(37)

Occasionally, problem (37) will also be referred as the inverse problem. The first-order necessary and the second-order sufficient optimality condition, respectively, are

$$\begin{aligned} \begin{array}{lllll} 1.~~&\nabla _{\varvec{\kappa }} f[\varvec{\kappa }^*] = {\underline{J}}^T ({\underline{d}}[\varvec{\kappa }^*] -{\underline{{\bar{d}}}}) = {{\underline{0}}}, \qquad 2.&\delta \varvec{\kappa }\nabla ^2_{\varvec{\kappa }^*} f[\varvec{\kappa }]\delta \varvec{\kappa }\ge 0 \quad \forall \delta \varvec{\kappa }\in \mathcal {K}\end{array} \end{aligned}$$

(38)

where

$$\begin{aligned} \begin{array}{lllllllll} 1.~~ &{} {\underline{J}}&{} =&{} \nabla _{\varvec{\kappa }}d[\varvec{\kappa }], \qquad &{} 2. ~~ &{} {{\underline{H}}}&{}=&{} \nabla ^2_{\varvec{\kappa }^*} f[\varvec{\kappa }] = {{\underline{H}}}_{GN}+ {{\underline{M}}}\\ 3.~~ &{} {{\underline{H}}}_{GN}&{}=&{} {\underline{J}}^T {\underline{J}}^{} , &{} 4. ~~ &{} {{\underline{M}}}&{}=&{} \displaystyle \sum _{k=1}^{n_{\text {d}}} \nabla ^2_{\varvec{\kappa }^*}d[\varvec{\kappa }] (d_k[\varvec{\kappa }]-{\bar{d}}_k). \end{array} \end{aligned}$$

(39)

Variational formulations for determination of ${{\underline{M}}}$ are provided e.g. in [28, 50]. Details on solution strategies for the minimization problem (37) are given elsewhere and shall not be considered here, cf. e.g. [27]. At this stage we only point out, that the Jacobian ${\underline{J}}$ and the Gauss–Newton matrix ${{\underline{H}}}_{GN}$ play key roles in the performance of different solution strategies.

The solution $\varvec{\kappa }^*$ of problem (37) might render a satisfactory agreement between simulated and experimental data; however, it might be susceptible to instability, in the sense, that a small perturbation of experimental data, $\delta {\bar{d}}$ say, may lead to a large deviation $\delta \varvec{\kappa }$ for $\varvec{\kappa }^*$. Possible reasons for this undesirable effect [or even non-uniqueness of problem (37)] are two-fold, [27]:

• 1. Deficiency of the material model: Functional terms and/or parameters may lead to (almost) linear dependencies within the model (overparametrization), or

• 2. Deficiency of experimental data: Certain material effects intended by the model are not properly ”activated” (incomplete data).

In the sequel, two different indicators are formulated in order to quantify stability for the solution $\varvec{\kappa }^*$ of the minimization problem (37):

• 1. Stability indicator by correlation matrix

• 2. Stability indicators by I-criteria.

4.2 Stability indicator by correlation matrix

Following, e.g., [38] the coefficients of the correlation matrix are given as

$$\begin{aligned} C_{ij}[\varvec{\kappa }^*] = \left. \displaystyle \frac{\sum _{k=1}^{n_{\text {d}}} \partial d_k[\varvec{\kappa }] /\partial {\kappa _i} \cdot \partial d_k[\varvec{\kappa }] /\partial {\kappa _j} }{\sqrt{\sum \nolimits _{k=1}^{n_{\text {d}}} (\partial d_k[\varvec{\kappa }] /\partial {\kappa _i )^2} \sum \nolimits _{k=1}^{n_{\text {d}}} (\partial d_k[\varvec{\kappa }] /\partial {\kappa _j )^2} }} \right| _{\varvec{\kappa }^*} . \end{aligned}$$

(40)

The correlation coefficient $-1\le C_{ij}\le 1$ is a quantitative measure for the correlation or respectively linear dependence between parameter $\kappa _i$ and $\kappa _j$. Positive correlations occur for $C_{ij} \ge 0$ where an increase of $\kappa _i$ results in an increase of $\kappa _j$. Negative correlations with $C_{ij} < 0$ lead to decreasing $\kappa _j$ for increasing $\kappa _i$ and vice versa. There are no correlations when $C_{ij} = 0$. If $|C_{ij}| = 1, i\ne j$, the correlation is called perfect and ensues

$$\begin{aligned} \begin{array}{llllllll} 1.~~&{} C_{ij} &{}=&{} 1 &{}\Longrightarrow &{} \kappa _i &{}=&{} a\kappa _j+b,\quad \text {with}\quad a>0\\ 2.~~&{} C_{ij} &{}=&{} -1 &{}\Longrightarrow &{} \kappa _i &{}=&{} a\kappa _j+b,\quad \text {with}\quad a<0. \end{array} \end{aligned}$$

(41)

Regarding the results of parameter identification $|C_{ij}|\ll 1$ , $i\ne j$ is desirable for a stable—or respectively a robust—solution vector $\varvec{\kappa }^*$.

4.3 First-order perturbation analysis

In order to perform a first-order perturbation analysis, following [50], let us define a function $F:\mathcal {K}\times \mathcal {D}\rightarrow \mathcal {K}$. The first-order necessary condition Eq. (38) for a given measurement vector ${\underline{{\bar{d}}}}$ becomes

$$\begin{aligned} \begin{array}{lllll} F[\varvec{\kappa }^*,{\underline{{\bar{d}}}}] := {\underline{J}}^T ({\underline{d}}[\varvec{\kappa }^*] -{\underline{{\bar{d}}}}) = {{\underline{0}}}. \end{array} \end{aligned}$$

(42)

The implicit function theorem guaranties the existence of a neighborhood $\mathcal {D}_0\subset \mathcal {D}$ and a continuously differentiable function ${\hat{\varvec{\kappa }}}:$ $\mathcal {D}_0 \rightarrow \mathcal {K}$ such that

$$\begin{aligned} \begin{array}{lllll} F[{\hat{\varvec{\kappa }}}[{\underline{{\bar{d}}}}],{\underline{{\bar{d}}}}] = {{\underline{0}}}\quad \forall ~ {\underline{{\bar{d}}}}\in \mathcal {D}_0 \end{array} \end{aligned}$$

(43)

and where ${\hat{\varvec{\kappa }}}[{\underline{{\bar{d}}}}]$ is a solution of problem (37) for given data ${\underline{{\bar{d}}}}$. The total derivative of $F[{\hat{\varvec{\kappa }}}[{\underline{{\bar{d}}}}],{\underline{{\bar{d}}}}]$ wrt to ${\underline{{\bar{d}}}}$ is

$$\begin{aligned} \begin{array}{lllllll} 1.~~&{}\displaystyle \frac{d F[{\hat{\varvec{\kappa }}}[{\underline{{\bar{d}}}}],{\underline{{\bar{d}}}}]}{d {\underline{{\bar{d}}}}} &{}=&{} \displaystyle \frac{\partial F[{\hat{\varvec{\kappa }}}[{\underline{{\bar{d}}}}],{\underline{{\bar{d}}}}]}{\partial \varvec{\kappa }} \displaystyle \frac{\partial \varvec{\kappa }}{\partial {\underline{{\bar{d}}}}} + \displaystyle \frac{\partial F[{\hat{\varvec{\kappa }}}[{\underline{{\bar{d}}}}],{\underline{{\bar{d}}}}]}{\partial {\underline{{\bar{d}}}}} = {{\underline{H}}}\displaystyle \frac{\partial \varvec{\kappa }}{\partial {\underline{{\bar{d}}}}} - {\underline{J}}^T ={{\underline{0}}}\quad \Longrightarrow \quad \\ 2.~~&{}\displaystyle \frac{\partial \varvec{\kappa }}{\partial {\underline{{\bar{d}}}}} &{}=&{} {{\underline{H}}}^{-1} {\underline{J}}^T. \end{array} \end{aligned}$$

(44)

Here, ${{\underline{H}}}$ and ${\underline{J}}$ are the Hessian and the Jacobian in Eq. (39), respectively, and from Eq. (42) the relation ${\partial F[\varvec{\kappa },{\underline{{\bar{d}}}}]}/{\partial {\underline{{\bar{d}}}}} = -{\underline{J}}^T$ has been used, assuming existence of ${{\underline{H}}}^{-1}$. For a perturbation of data $\delta {\underline{{\bar{d}}}}$ the above function ${\hat{\varvec{\kappa }}}[{\underline{{\bar{d}}}}]$ renders by means of a Taylor series

$$\begin{aligned} \begin{array}{lll} \delta {\hat{\varvec{\kappa }}}= & {} {\hat{\varvec{\kappa }}}[{\underline{{\bar{d}}}}+ \delta {\underline{{\bar{d}}}}] - {\hat{\varvec{\kappa }}}[{\underline{{\bar{d}}}}] = \displaystyle \frac{\partial {\hat{\varvec{\kappa }}}}{\partial {\underline{{\bar{d}}}}} \delta {\underline{{\bar{d}}}}+ \mathcal{O}\left( || \delta {\underline{{\bar{d}}}}||^2_{\mathcal {D}}\right) . \end{array} \end{aligned}$$

(45)

With the result in (44.2) Eq. (45) becomes

$$\begin{aligned} \begin{array}{lll} \delta {\hat{\varvec{\kappa }}}= & {} {{\underline{H}}}^{-1} {\underline{J}}^T \delta {\underline{{\bar{d}}}}+ \mathcal{O}\left( || \delta {\underline{{\bar{d}}}}||^2_{\mathcal {D}}\right) . \end{array} \end{aligned}$$

(46)

Several possibilities can be envisaged to obtain an estimate from Eq. (46); see, e.g., [50]. Neglecting the second-order term $\mathcal{O}\left( || \delta {\underline{{\bar{d}}}}||^2_{\mathcal {D}}\right)$ and taking a selected norm on $\mathcal {K}$, we obtain

$$\begin{aligned} \begin{array}{llllll} ||\delta {\hat{\varvec{\kappa }}}||_{\mathcal {K}}\le & {} ||{{\underline{H}}}^{-1}||_{\mathcal {K}} \ ||{\underline{J}}^T \delta {\underline{{\bar{d}}}}||_{\mathcal {K}}\approx & {} ||{{\underline{H}}}_{GN}^{-1}||_{\mathcal {K}} \ ||{\underline{J}}^T \delta {\underline{{\bar{d}}}}||_{\mathcal {K}} \end{array} \end{aligned}$$

(47)

where in the last term the Hessian ${{\underline{H}}}$ has been approximated by the Gauss–Newton matrix ${{\underline{H}}}_{GN}$. Mathematically, this means, that only first-order information of the functional $F[{\hat{\varvec{\kappa }}}[{\underline{{\bar{d}}}}],{\underline{{\bar{d}}}}]$ is used. This is reasonable for small model errors $d_k[\varvec{\kappa }]- {\bar{d}}_k$ in (39.4), such that the matrix ${{\underline{M}}}$ in (39.4) can be neglected.

For the 2-norm, one obtains

$$\begin{aligned} ||\delta {\hat{\varvec{\kappa }}}||_{2}\le & {} ||{{\underline{H}}}_{GN}^{-1}||_{2} \ ||{\underline{J}}^T \delta {\underline{{\bar{d}}}}||_{2} = \mu _{\max }\ ||{\underline{J}}^T \delta {\underline{{\bar{d}}}}||_{2}. \end{aligned}$$

(48)

Here

$$\begin{aligned} \mu _{\max }:= \underset{1 \le i \le n_{\text {p}}}{\max } \mu _{i} [{{\underline{C}}}], \quad \text{ where }\quad {{\underline{C}}}= {{\underline{H}}}_{GN}^{-1} \end{aligned}$$

(49)

and where $\mu _{i}$ are the eigenvalues of the matrix ${{\underline{C}}}$. Eq. (48) reveals that the eigenvalue $\mu _{\max }$ has the interpretation of an amplification factor for the weighted perturbation of data ${\underline{J}}^T \delta {\underline{{\bar{d}}}}$ to the perturbation of parameters $\delta \varvec{\kappa }$.

4.4 Stability indicators by I-criteria

In addition to the eigenvalue $\mu _{\max }$ defined in Eq. (49), several amplification factors have been introduced in the field of optimum experimental design, subsequently denoted as I-criteria with general structure; see, e.g., [4] and [24]

$$\begin{aligned} \phi _I [\varvec{\kappa }]:= \phi _I [{{\underline{C}}}[\varvec{\kappa }]]. \end{aligned}$$

(50)

Common examples of $\phi _I$ are, see, e.g., [4] and [24]

$$\begin{aligned} \begin{array}{lll} 1.~~&{} \hbox {A-Criterion: } \quad \quad \phi _A[{{\underline{C}}}]:= \displaystyle \frac{1}{n_{\text {p}}} {\text {tr}}[{{\underline{C}}}] = \frac{1}{n_{\text {p}}} \sum _{i=1}^{n_{\text {p}}} \mu _i \\ 2.~~&{} \text{ E-Criterion: } \quad \quad \phi _E [{{\underline{C}}}]: = \mu _{\max }= \underset{1 \le i \le n_{\text {p}}}{\max } \mu _{i} [{{\underline{C}}}] \\ 3.~~&{} \text{ D-Criterion: } \quad \quad \phi _D[{{\underline{C}}}]:= \bigg | {\text {det}}[{{\underline{C}}}]\bigg |^{\frac{1}{n_{\text {p}}}} = \left| \displaystyle \prod _{i=1}^{n_{\text {p}}} \mu _{i} \right| ^{\frac{1}{n_{\text {p}}}}\\ 4.~~&{} \text{ M-Criterion: } \quad \quad \phi _M[{{\underline{C}}}]:= \bigg | \max \left\{ \sqrt{{{\underline{C}}}_{ii}}, i = 1,...,n_{\text {p}}\right\} . \end{array} \end{aligned}$$

(51)

Thus, the E-criterion in Eq. (51.2) is identical to the criterion in Eq. (49). Figure 2 provides geometrical interpretations of all four I-criteria based on the confidence ellipsoid for $n_{\text {p}}= 2$, cf., e.g., [23, 52]. The A-criterion is proportional to the average length of the confidence ellipsoid, the D-criterion to its volume, the E-criterion to its the largest expansion, and the M-criterion to the largest side length of a box around the confidence ellipsoid.

Fig. 2

Visualization of four I-criteria (51) in two dimensions, cf. [23, 52]

The A-criterion in Eq. (51.1) is related to the E-criterion in Eq. (49.2) as

$$\begin{aligned} \begin{array}{lll} \phi _A[{{\underline{C}}}] = \displaystyle \frac{1}{n_{\text {p}}} \sum _{i=1}^{n_{\text {p}}} \mu _i \le \frac{1}{n_{\text {p}}} n_{\text {p}}\mu _{\max }= \mu _{\max }= \phi _E[{{\underline{C}}}]. \end{array} \end{aligned}$$

(52)

A relation between the D-criterion in Eq. (51.3) and the E-criterion in Eq. (49.2) is

$$\begin{aligned} \begin{array}{lll} \phi _D[{{\underline{C}}}]= \bigg | {\text {det}}[{{\underline{C}}}]\bigg |^{\frac{1}{n_{\text {p}}}} = \left| \displaystyle \prod _{i=1}^{n_{\text {p}}} \mu _{i} \right| ^{\frac{1}{n_{\text {p}}}} \le \left\{ \displaystyle \mu _{\max }^{n_{\text {p}}} \right\} ^{\frac{1}{n_{\text {p}}}} = \mu _{\max }= \phi _E[{{\underline{C}}}]. \end{array} \end{aligned}$$

(53)

A general relation between the M-criterion in Eq. (51.4) and the E-criterion in Eq. (49.2) does not exist.

4.4.1 Remarks 4.4

• 1. In the field of optimal control problems, the indicator function $\phi _I [{{\underline{C}}}[\varvec{\kappa }]]$ may be dependent on further design variables such that an optimality problem can be formulated, cf. e.g. [4] and [24]. Then, in summary, two requirements are formulated: The solution vector $\varvec{\kappa }^*$

  • (a) should minimize the least squares function (representing a model error) according to (37)

  • (b) should minimize the confidence criterion according to (50).

• 2. In this work, the generality of the methodology of optimal control problems will not be exploited. Instead, the different criteria in (51) will simply be used, to give an assessment of existing solutions $\varvec{\kappa }^*$ for different well known formulations of the energy density function $\overline{\psi }[\mathbf {C},\varvec{\kappa }]$. The treatment of parameter identification as an optimal design problem dependent on additional design variables will constitute an aspect of future work. To the knowledge of the author, there is no similar work so far which applies A-,E-,D-, and M-criteria in the field of hyperelasticity.

• 3. A mathematical correct definition of stability is given e.g. in [50]. From there, we point out that local stability guarantees local uniqueness but not global uniqueness of the inverse problem (37).

5 A practical guide for model development

In order to account for the criteria of verification, validation and stability by means of the strain mode-dependent weighting functions of Sect. 3, a practical guide for model development is summarized in Table 1. As input for the resulting flowchart, we assume that measurement data ${\underline{{\bar{d}}}}^{i}\in \mathcal {D}^{i}=\mathbb {R}^{n^{i}_{\text {d}}}$ and an initial set of energy functions $\overline{\psi }^{i}$, both related to strain modes ${i}= 1,...,S$, are given.

Step 1: Verification for each mode data set

In this step of Table 1 each set of experimental data ${\underline{{\bar{d}}}}^{i}\in \mathcal {D}^{i}=\mathbb {R}^{n^{i}_{\text {d}}}$, ${i}= 1,...,S$ is used separately to minimize mode data related least squares functionals of the form (37) to obtain

(54)

Step 2: Stability for each mode data set

In order to account for mode data related stability of all solution vectors $\varvec{\kappa }^{i}$, based on the general structure in Eq. (50), in Step 2 of Table 1 we evaluate (at least one of) the following I-criteria:

$$\begin{aligned} \begin{array}{lllllllll} \varphi _I [\varvec{\kappa }^{i}] := \phi _I [{{\underline{C}}}^{i}[\varvec{\kappa }^{i}]], \quad I = A,E,D,M, \quad {i}= 1,...,S. \end{array} \end{aligned}$$

(55)

Here we use ${{\underline{C}}}^{i}= [({\underline{J}}^{i})^T{\underline{J}}^{i}]^{-1}$ with Jacobian ${\underline{J}}^{i}\in \mathbb {R}^{n^{i}_{\text {d}}\times n_{\text {p}}^i}$ according to Eq. (39.1) applied to all modes ${i}= 1,...,S$.

Step 3: Validation for complete data set

In order to check conformity according to Definition 1, in Step 3 of Table 1 each solution ${\hat{\varvec{\kappa }}}^{i}$ of Step 2 is used to simulate the remaining modes ${i}=1,...,S, {j}\ne {i}$. This defines the following complete data related least-squares functional

$$\begin{aligned} F[{\hat{\varvec{\kappa }}}^{i}] := \displaystyle \sum _{{j}=1}^{S}f[{\underline{{\bar{d}}}}^{j},{\hat{\varvec{\kappa }}}^{i}], \quad i = 1,...,S. \end{aligned}$$

(56)

Note, that $f[{\underline{{\bar{d}}}}^{j},{\hat{\varvec{\kappa }}}^{i}], {j}= {i}$ is identical to the functional value in (the last iteration of) the verification step of Eq. (54), whereas the values $f[{\underline{{\bar{d}}}}^{j},{\hat{\varvec{\kappa }}}^{i}]$, ${j}= 1,...,S, {j}\ne {i}$ are obtained by predictive simulation of the ${j}$-th data set with the optimized parameter vector ${\hat{\varvec{\kappa }}}^{i}$.

Step 4: Stability for complete data set

In order to account for complete data related stability in Step 4 of Table 1 based on the general structure in Eq. (50), we evaluate (at least one of) the following I-criteria

$$\begin{aligned} \begin{array}{lllllllll} ~&\Phi _I [{\hat{\varvec{\kappa }}}^{i}] := \phi _I [{{\underline{C}}}[{\hat{\varvec{\kappa }}}^{i}]], \quad I = A,E,D,M, \quad {i}= 1,...,S. \end{array} \end{aligned}$$

(57)

Here we use ${{\underline{C}}}= [{\underline{J}}^T{\underline{J}}]^{-1}$ with Jacobian ${\underline{J}}\in \mathbb {R}^{n_{\text {d}}\times n_{\text {p}}}$ according to Eq. (39.1), and where, contrary to Eq. (55), $n_{\text {d}}= \sum _{{i}=1}^{S} n_{\text {d}}^{i}$ refers to the complete set of available experimental data.

Step 5: Selection of final parameter vector

In Step 5 of Table 1 the final parameter vector is selected as

(58)

Consequently, if this step is reached, there is no need for the strain mode-dependent formulation Eq. (9).

Table 1 Flowchart for model development accounting for verification, validation and stability

Step 6: Weighted mode-related model extension

In case Step 3 on validation and/or Step 4 on stability fail, Step 6 in Table 1 is activated, which makes use of the strain mode-dependent formulation Eq. (9) with verified and stabilized mode-related material parameters ${\hat{\varvec{\kappa }}}^{i}$ as a result of Step 1 and Step 2.

Remarks 5

• 1. The loops in Step 1 and Step 2 in Table 1 render verified and stabilized material parameters ${\hat{\varvec{\kappa }}}^{i}$ related to each mode data set ${\underline{{\bar{d}}}}^{i}$, ${i}= 1,...,S$.

• 2. Provided Step 3 and Step 4 in Table 1 are successful, Step 5 guarantees validated (in the sense of Definition 1) and stabilized set of material parameters $\varvec{\kappa }^{i}$ related to the complete data set.

• 3. Contrary, failure of the validation check in Step 3.b or the stability check in Step 4.b results into the extended weighting formulation in Step 6.

• 4. The selection in Step 5 and respectively Eq. (58) is done from a practical viewpoint, and might be somewhat arbitrary. It could also involve results for the least-squares functions $F[{\hat{\varvec{\kappa }}}^{i}]$, $i=1,...,S$, in Step 3. A further alternative is based on complete data related simultaneous fitting

  

  (59)

  to obtain the final parameter vector.

• 5. Since the strain mode-dependent formulation (9) in Step 6 in Table 1 employs verified and stabilized mode related material parameters ${\hat{\varvec{\kappa }}}^{i}$, $i=1,...,S$, as a result of Step 1 and Step 2, no further optimization is necessary.

• 6. In Step 6, conformity according to Definition 1 cannot be investigated, since all available data ${\underline{{\bar{d}}}}^{i}\in \mathcal {D}^{i}=\mathbb {R}^{n^{i}_{\text {d}}}$, ${i}= 1,...,S$, in Table 1 are exploited. For this purpose, additional measurement data activating different modes are required.

• 7. In practice, the two requirements of Remark 4.4.1 on small model error and stable results might be contradictory, and therefore have to be carefully balanced. Of course, this issue is strongly related to tolerances $tol_f, tol_\phi$ in the input data of Table 1. The issue of concrete choices for $tol_f$ and $tol_\phi$ however has not been investigated so far.

6 Representative examples

6.1 Selection of experimental data and hyperelastic models

In this section, the experimental data on vulcanized rubber published by Treloar [48] are used to demonstrate the steps for model development according to Table 1. Three loading scenarios, that is uniaxial tension (UT), equibiaxial tension (ET) compression and pure torsion (PS), respectively, are considered. The data in [48] are given in pairs of principal stretches ${\lambda }_k$ and principal nominal stresses $P_{Treloar}[{\lambda }_k^{Treloar}]$ for all three loading cases.

Regarding the hyperelastic models, we follow very closely the selection provided by Steinmann et al. in [47]. Here, both phenomenological and micro-mechanically motivated models have been investigated in order to capture the elastic and nearly incompressible effects of rubber-like materials investigated in [48]. The complete list of hyperelastic models investigated in this paper is as follows:

• 1. Neo-Hooke model (1943)

• 2. Mooney–Rivlin model (1940)

• 3. Isihara model (1951)

• 4. Gent–Thomas model (1958)

• 5. Swanson model (1985)

• 6. Yeoh model (1990)

• 7. Arruda–Boyce model (1993) (invariant form)

• 8. Gent model (1996)

• 9. Yeoh–Fleming model (1997)

• 10. Carroll model (2011)

• 11. Ogden model (1972) (K=2)

• 12. Three chain model (1943)

• 13. Eight chain model (1993).

Regarding the extensive literature on the above hyperelastic models we refer also to [47], and therefore shall not be repeated here. As mentioned before, the corresponding isochoric free energy densities related to each strain mode $\overline{\psi }^{i}$ in Eq. (9), the partial derivatives ${\partial \overline{\psi }^{i}}/{\partial \overline{{\lambda }}_b}$ in (26.4) and ${\partial ^2 \overline{\psi }^{i}}/{\partial \overline{{\lambda }}_a\partial \overline{{\lambda }}_c}$ for principle stretch-based formulations, as well as the partial derivatives ${\partial \overline{\psi }^{i}}/{\partial {\bar{I}}_A}$ in (33.3) and ${\partial ^2 \overline{\psi }^{i}}/{\partial {\bar{I}}_A \partial {\bar{I}}_B}$ in (35) for invariant-based formulations, and moreover the corresponding material parameters $\varvec{\kappa }^{i}$ are summarized in compact form in Appendix B of this work.

6.2 Analytical stress formulations for UT, ET, and PS

Assuming an isotropic and incompressible material, an analytical $P^{i}_a[\overline{{\lambda }}_a]$ formulation is provided, e.g., in [19, 47, 54] as

$$\begin{aligned} P^{i}_a = \displaystyle \frac{\partial \overline{\psi }^{i}}{\partial \overline{{\lambda }}_a} - \displaystyle \frac{p}{\overline{{\lambda }}_a},\quad a = 1, 2, 3. \end{aligned}$$

(60)

Our implementation departs slightly from the one in [47] by exploiting a generality for UT, ET, and PS as follows:

• Uniaxial tension (UT): For given deformation gradient according to Eq. (11), the stresses normal to the load directions are zero, that is $P_2^{\text{ UT }}= P_3^{\text{ UT }}=0$. By setting Eq. (60) to zero, for example for $a=3$, and inserting the resulting pressure into Eq. (60) for $a=1$, renders

  $$\begin{aligned} p = {\overline{{\lambda }}_3} \displaystyle \frac{\partial \overline{\psi }^{\text{ UT }}}{\partial \overline{{\lambda }}_3} ~~ \Longrightarrow ~~ \quad P_1^{\text{ UT }}= \displaystyle \frac{\partial \overline{\psi }^{\text{ UT }}}{\partial \overline{{\lambda }}_1} - \displaystyle \frac{\overline{{\lambda }}_3}{\overline{{\lambda }}_1} \displaystyle \frac{\partial \overline{\psi }^{\text{ UT }}}{\partial \overline{{\lambda }}_3}. \end{aligned}$$

  (61)

• Equibiaxial tension (ET): For given deformation gradient according to Eq. (12), here the stresses in the load directions are equal, that is $P_2^{\text{ ET }}= P_3^{\text{ ET }}$, while the third direction is stress-free. Therefore, by setting Eq. (60) to zero for $a=3$, and inserting the resulting pressure into Eq. (60) for $a=1$ and $a=2$, renders

  $$\begin{aligned} p = {\overline{{\lambda }}_3} \displaystyle \frac{\partial \overline{\psi }^{\text{ ET }}}{\partial \overline{{\lambda }}_3} ~~ \Longrightarrow ~~ \quad P_1^{\text{ ET }}= P_2^{\text{ ET }}= \displaystyle \frac{\partial \overline{\psi }^{\text{ ET }}}{\partial \overline{{\lambda }}_1} - \displaystyle \frac{\overline{{\lambda }}_3}{\overline{{\lambda }}_1} \displaystyle \frac{\partial \overline{\psi }^{\text{ ET }}}{\partial \overline{{\lambda }}_3}. \end{aligned}$$

  (62)

  Observe the same rule in Eq. (61) and in Eq. (62), which is due to the above choice $a=3$ for UT.

• Pure shear (PS): For given deformation gradient according to Eq. (13) the stress in the third direction is zero. Therefore, by setting Eq. (60) to zero for $a=3$, and inserting the resulting pressure into Eq. (60) for $a=1$ and $a=2$, renders

  $$\begin{aligned} p = {\overline{{\lambda }}_3} \displaystyle \frac{\partial \overline{\psi }^{\text{ PS }}}{\partial \overline{{\lambda }}_3} ~ \Longrightarrow ~ \quad P_1^{\text{ PS }}= \displaystyle \frac{\partial \overline{\psi }^{\text{ PS }}}{\partial \overline{{\lambda }}_1} - \displaystyle \frac{\overline{{\lambda }}_3}{\overline{{\lambda }}_1} \displaystyle \frac{\partial \overline{\psi }^{\text{ PS }}}{\partial \overline{{\lambda }}_3}, \quad P_2^{\text{ ET }}= \displaystyle \frac{\partial \overline{\psi }^{\text{ PS }}}{\partial \overline{{\lambda }}_2} - \displaystyle \frac{\overline{{\lambda }}_3}{\overline{{\lambda }}_2} \displaystyle \frac{\partial \overline{\psi }^{\text{ PS }}}{\partial \overline{{\lambda }}_3}. \end{aligned}$$

  (63)

  Observe the same rule for $P_1^{\text{ PS }}$ in Eq. (63) as in Eq. (61) and Eq. (62).

Consequently, Eqs. (61), (62) and (63) require ${\partial \overline{\psi }^{i}}/{\partial \overline{{\lambda }}_a}$ for principle stretch-based formulations. In the case of invariant-based models according to the reduced form $\overline{\psi }^{i}[{\bar{I}}_1, {\bar{I}}_2]$ analogously to Eq. (30) and in view of the relations (3), (4) a reparametrization is governed by the chain rule as

$$\begin{aligned} \displaystyle \frac{\partial \overline{\psi }^{i}}{\partial \overline{{\lambda }}_a} = \displaystyle \frac{\partial \overline{\psi }^{i}}{\partial {\bar{I}}_1} \displaystyle \frac{\partial {\bar{I}}_1}{\partial \overline{{\lambda }}_a} + \displaystyle \frac{\partial \overline{\psi }^{i}}{\partial {\bar{I}}_2} \displaystyle \frac{\partial {\bar{I}}_2}{\partial \overline{{\lambda }}_a}, \quad \text{ where }\quad \displaystyle \frac{\partial {\bar{I}}_1}{\partial \overline{{\lambda }}_a} = 2 \overline{{\lambda }}_a, \quad \displaystyle \frac{\partial {\bar{I}}_2}{\partial \overline{{\lambda }}_a} = 2 \overline{{\lambda }}_a (\overline{{\lambda }}_b^2 + \overline{{\lambda }}_c^2) \end{aligned}$$

(64)

for ${i}= UT, ET, PS.$ The partial derivatives ${\partial \overline{\psi }^{i}}/{\partial \overline{{\lambda }}_a}$ in Eq. (60) for principle stretch-based formulations, and the partial derivatives ${\partial \overline{\psi }^{i}}/{\partial {\bar{I}}_A}$ in Eq. (64) for invariant-based formulations, respectively, are summarized for thirteen hyperelastic models in compact form in Appendix B of this work.

In our implementation Eq. (60) is used for the final stress calculation for all three load-cases (UT, ET and PS), by accounting for the case-dependent pressure p. It applies throughout for all phenomenological (invariant-based and stretch-based formulation) and micro-mechanically motivated models of the above list with thirteen models. This unified procedure might be at the expense of some numerical effort, but avoids the implementation of load case-dependent and material-dependent formulations as provided in [47]. With this framework, the material-dependent information provided in Appendix B is sufficient for the subsequent discussions.

6.3 Model development according to Table 1

Subsequently, the steps in the flowchart for model development in Table 1 are applied. An excerpt of additional results for the correlation matrix $C_{ij}[\varvec{\kappa }^*]$ defined in Eq. (40) is provided in Appendix D.

Input: Least-squares functional

Setting $d_k^{i}[\varvec{\kappa }] = P^{i}_1[{\lambda }_k^{Treloar},\varvec{\kappa }]$ and ${\bar{d}}^{i}_k[\varvec{\kappa }] = P^{i}_{Treloar}[{\lambda }_k^{Treloar}]$ in Eq. (37) renders the mode data related least-squares functionals Eq. (54) as

$$\begin{aligned} \begin{array}{lll} f[{\underline{{\bar{d}}}}^{i}, \varvec{\kappa }] = \displaystyle \displaystyle \frac{1}{2}\sum _{k=1}^{n^{i}_{\text {d}}} \left( P^{i}_1[{\lambda }_k^{Treloar},\varvec{\kappa }]-P_{Treloar}^{i}[{\lambda }_k^{Treloar}] \right) ^2, \quad {i}= UT, ET, PS \end{array} \end{aligned}$$

(65)

and where $n_{\text {d}}^{\text{ UT }}= 23, n_{\text {d}}^{\text{ ET }}= 17, n_{\text {d}}^{\text{ PS }}= 13$. Detailed values for the data $P^{i}_{Treloar}[{\lambda }_k^{Treloar}]$, ${i}=$ UT, ET, PS are provided e.g. in [47].

Step 1: Verification for each mode data set

Each set of experimental data for UT, ET and PS is used separately to minimize the mode data related least squares functionals $f[{\underline{{\bar{d}}}}^{i}, \varvec{\kappa }]$ in Eq. (54). We point out, that in our simulations no attempt has been made to modify respectively improve the optimized material parameters obtained in [47]. That is, for evaluation of the above criterion (54), for $\varvec{\kappa }^{\text{ UT }}$, $\varvec{\kappa }^{\text{ ET }}$, $\varvec{\kappa }^{\text{ PS }}$ we exploit directly the results from [47] and also summarized in Eq. (B,$\bullet$,4) in Appendix B of this work. A summary of results for the least-squares functionals $f[{\underline{{\bar{d}}}}^{i}, \varvec{\kappa }^{i}]$, $i=UT, ET,PS$ in Eq. (54) is given in Tables 2, 3 and 4, respectively.

Step 2: Stability for each mode data set

In order to account for stability of all three vectors $\varvec{\kappa }_{i}$, ${i}=UT, ET, PS$ taken from [47], I-criteria $\varphi _I [\varvec{\kappa }], I = A,E,D,M$ according to Eq. (55) are calculated. A summary of related results is also given in Tables 2, 3 and 4, respectively.

Step 3: Validation for complete data set

As in [47], each set of optimal material parameters $\varvec{\kappa }^{\text{ UT }}$, $\varvec{\kappa }^{\text{ ET }}$ and $\varvec{\kappa }^{\text{ PS }}$ which minimize the least squares functionals (54), is used to simulate the remaining two deformation modes. As mentioned before, for evaluation of the criterion (56) we use ${\hat{\varvec{\kappa }}}^{i}= \varvec{\kappa }^{i}$, $i = UT, ET, PS$, according to Eq. (B,$\bullet$,4). This step renders results for the complete data related least-squares functionals (56) in Tables 5, 6 and 7.

Step 4: Stability for complete data set

In order to account for stability, in addition to [47] and based on the general structure in Eq. (50) we distinguish the I-criteria $\Phi _I [{\hat{\varvec{\kappa }}}^{i}], I = A,E,D,M$ in Eq. (57). For this purpose we use ${\hat{\varvec{\kappa }}}^{i}= \varvec{\kappa }^{i}$, $i = UT, ET, PS$, according to Eq. (B,$\bullet$,4). A summary of results for the I-criteria (57) is also given in Tables 5, 6 and 7, respectively.

Fig. 3

Comparative study of all original hyperelastic models on Treloar’s data with parameters $\varvec{\kappa }^{\text{ AL }}$. On corresponding results for least-squares functional $F[{\underline{{\bar{d}}}},\varvec{\kappa }^{\text{ AL }}]$ in Eq. (58) and design functions $\Phi _I [\varvec{\kappa }^{\text{ AL }}]$ in Eq. (50) see Table 8, “simult. fitting”

Note, that in all cases the relations $\phi _A[{{\underline{C}}}] \le \mu _{\max }= \phi _E[{{\underline{C}}}]$ in Eq. (52) and $\phi _D[{{\underline{C}}}] \le \mu _{\max }= \phi _E[{{\underline{C}}}]$ in Eq. (53) are verified, which reveals the eigenvalue $\mu _{\max }= \phi _E[{{\underline{C}}}]$ as a conservative estimate for the amplification of data perturbations. Regarding the M-criterion both cases $\phi _M[{{\underline{C}}}] < \mu _{\max }= \phi _E[{{\underline{C}}}]$ as well as $\phi _M[{{\underline{C}}}] > \mu _{\max }= \phi _E[{{\underline{C}}}]$ do occur.

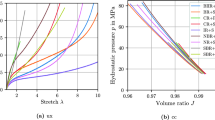
In view of the extensive discussion in [47] on all thirteen models, in this work we restrict a detailed discussion to three representative hyperelastic models, that is the Neo-Hooke model (No. 1 in the list of Sect. 6.1), the Isihara model (No. 3 in the list of Sect. 6.1) and the Caroll model (No. 10 in the list of Sect. 6.1) to Appendix C of this work. The comparative study in Fig. 5 reveals a poor verification quality of the Neo-Hooke model. A good verification quality of the Isihara model with however disappointing validation quality is illustrated in Fig. 6. Figure 7 visualizes a superior model performance of the Carroll model on Treloar’s data, due to both, a perfect fit quality and remarkable predictive results for UT, ET, PS, respectively.

Step 5: Selection of final parameter vector

Here, according to Remark 5.4 we simply select a final parameter set $\varvec{\kappa }^*$ according to Eq. (58), in case Step 4 is successful. In view of the excellent model performance on verification and validation in Fig. 7 as well as on stability in Tables 5, 6 and 7, respectively, this applies only for the Caroll model. Consequently, the parameter vector $\varvec{\kappa }^{\text{ UT }}$ in Eq. (B.10.4) could be selected for $\varvec{\kappa }^*$, which renders lowest value for $\Phi _A [\varvec{\kappa }^{\text{ UT }}]$ according to Table 5. The remaining models would require the weighted mode related model extension according to Step 6.

Fig. 4

Comparative study of all weighted hyperelastic models on Treloar’s data with parameters $\varvec{\kappa }^*= \{\varvec{\kappa }^{i}\}_{i=1}^3$, ${i}= UT,ET,PS$. On corresponding results for least-squares functional $F[{\underline{{\bar{d}}}},\varvec{\kappa }^*]$ in Eq. (58) and design functions $\Phi _I [\varvec{\kappa }^*]$ in Eq. (50) see Table 8, “weighted model”

In order to obtain an overview on the performance of all models, still, results of a fourth optimization step are shown next, that computes material parameters $\varvec{\kappa }^{\text{ AL }}$ under simultaneous consideration of the complete data set set, that is, UT, ET and PS. To this end, as in the previous Sect. 6.3 no attempt has been made to modify and, respectively, improve the optimized material parameters $\varvec{\kappa }^{\text{ AL }}$ obtained in [47] and summarized in Eq. (B,$\bullet$,4) in Appendix B of this work. Clearly, as a consequence no additional data are left for validation.

A comparative study of the verification quality in this step for all original hyperelastic models on Treloar’s data is given in Fig. 3. The corresponding results for the least-squares functional $F[{\underline{{\bar{d}}}},\varvec{\kappa }^{\text{ AL }}]$ in Eq. (58) and the design functions $\Phi _I [\varvec{\kappa }^{\text{ AL }}]$, $I=A,E,D,M$, in Eq. (50) are summarized in Table 8 for each model in the first line.

Contrary to the individual fit capability for single measurement sets, some of the models do not capture the S-shape behavior anymore. This deficiency becomes apparent, e.g., for the Isihara model, if the results in Fig. 6 are compared to those in Fig. 3.3. This illustrative effect is confirmed by the relatively high value for $F[{\underline{{\bar{d}}}},\varvec{\kappa }^{\text{ AL }}]$ in Table 8. The deficiency of the material model of non-uniqueness discussed in Sect. C.2 for the Isihara model has dramatic consequences for almost all design functions $\Phi _I [\varvec{\kappa }]$ in Table 8.

As mentioned before, from the macroscopic models the Carroll model [9] captured very well all three deformation patterns with the lowest least-squares value $F[{\underline{{\bar{d}}}},\varvec{\kappa }^{\text{ AL }}]$ of all models considered here. This positive phenomenon is accompanied by relatively low values for the design functions $\Phi _I [\varvec{\kappa }^{\text{ AL }}]$.

From the microscopic models the eight-parameter model is able to reproduce almost perfectly all deformations. When compared with the Carroll model, higher values for the design functions $\Phi _I [\varvec{\kappa }^{\text{ AL }}]$ confirm the conclusion of [47] of “a questionable sensitivity wrt the initial values”, such that “small changes may already yield a completely different set of values.”

Step 6: Weighted mode-related model extension

All models, except the Carroll model, require a model extension according to Step 6 in Table 1 by means of the strain mode-dependent formulation (9.1). Comparative results are provided in Table 8, where additionally to the results of simultaneously fitting in Step 5 two cases are distinguished for each model:

• The second line in Table 8 of each model corresponds to the weighted model according to Eq. (9). We use material parameters $\varvec{\kappa }^*= \{\varvec{\kappa }^{i}\}_{i=1}^3$, ${i}= UT,ET,PS$ taken from [47] and summarized in compact form in Eq. (B,$\bullet$,4) in Appendix B of this work. The corresponding diagrams are provided in Fig. 4. Apart from the Neo-Hooke model, the Mooney–Rivlin model and the Gent–Thomas model, almost all models show a satisfying up to excellent fitting quality.

• The third line in Table 8 of each model corresponds to Eq. (9.1) with new with material parameters $\varvec{\kappa }^*= \{{\hat{\varvec{\kappa }}}^{i}\}_{i=1}^3$, ${i}= UT,ET,PS$ obtained by model reduction, such that in general ${\hat{n}}^i_{\text {p}}= \dim |{\hat{\varvec{\kappa }}}^{i}| \le \dim | \varvec{\kappa }^{i}|=n_{\text {p}}^i$ holds. The resulting material parameters ${\hat{\varvec{\kappa }}}^{i}$ are summarized in compact form in Eq. (B,$\bullet$,5) in Appendix B of this work. Note, that model reduction has been performed only for some selected models. Table 8 reveals a drastic reduction of the corresponding I-criteria $\Phi _I [\varvec{\kappa }^{i}]$ in Eq. (57) in some cases. E.g. for the Isihara model the total number of material parameters $n_{\text {p}}$ is reduced from 9 to 6, with the same least squares functional $F[\varvec{\kappa }^{i}] = 7.79e$-1 in Eq. (56) but a reduction for the E-criterion $\Phi _E [\varvec{\kappa }]$ in Eq. (57) from $\infty$ to 7.97e-3.

Table 2 Verification and stability investigations for all hyperelastic models on Treloar’s UT-data: Least-squares functional $f[{\underline{{\bar{d}}}}^{\text{ UT }},\varvec{\kappa }^{\text{ UT }}]$ Eq. (54), I-criteria $\varphi _I [\varvec{\kappa }^{\text{ UT }}]$ Eq. (55)

Table 3 Verification and stability investigations for all hyperelastic models on Treloar’s ET-data: Least-squares functional $f[{\underline{{\bar{d}}}}^{\text{ ET }},\varvec{\kappa }^{\text{ ET }}]$ Eq. (54), I-criteria $\varphi _I [\varvec{\kappa }^{\text{ ET }}]$ Eq. (55)

Table 4 Verification and stability investigations for all hyperelastic models on Treloar’s PS-data: Least-squares functional $f[{\underline{{\bar{d}}}}^{\text{ PS }},\varvec{\kappa }^{\text{ PS }}]$ Eq. (54), I-criteria $\varphi _I [\varvec{\kappa }^{\text{ PS }}]$ Eq. (55)

Table 5 Validation and stability investigations for all hyperelastic models on Treloar’s complete data: Least-squares functional $F[{\hat{\varvec{\kappa }}}^{\text{ UT }}]$ Eq. (56), I-criteria $\Phi _I [{\hat{\varvec{\kappa }}}^{\text{ UT }}]$ Eq. (57)

Table 6 Validation and stability investigations for all hyperelastic models on Treloar’s complete data: Least-squares functional $F[{\hat{\varvec{\kappa }}}^{\text{ ET }}]$ Eq. (56), I-criteria $\Phi _I [{\hat{\varvec{\kappa }}}^{\text{ ET }}]$ Eq. (57)

Table 7 Validation and stability investigations for all hyperelastic models on Treloar’s complete data: Least-squares functional $F[{\hat{\varvec{\kappa }}}^{\text{ PS }}]$ Eq. (56), I-criteria $\Phi _I [{\hat{\varvec{\kappa }}}^{\text{ PS }}]$ Eq. (57)

Table 8 Simultaneous fit for all hyperelastic models on Treloar’s data for UT, ET and PS: Least squares functionals and I-criteria. For each model, the first line presents results with parameters $\varvec{\kappa }^*= \varvec{\kappa }^{\text{ AL }}, n_{\text {p}}^*= \dim |\varvec{\kappa }^{\text{ AL }}|$ taken from [47], see also (B,$\bullet$,4). The second line corresponds to the proposed extended formulation (9) including weighting functions. Parameters $\varvec{\kappa }^*= \{\varvec{\kappa }^{i}\}_{i=1}^3, {i}= UT, ET, PS$ are taken from [47], see also (B,$\bullet$,4). Note the relation $n_{\text {p}}^*= \dim |\{\varvec{\kappa }^{i}\}_{i=1}^3| = 3 \dim |\varvec{\kappa }^{\text{ AL }}|$ before model reduction. Any third line corresponds to model reduction of the scheme (9). The new parameters $\varvec{\kappa }^*= \{{\hat{\varvec{\kappa }}}^{i}\}_{i=1}^3, {i}= UT, ET, PS$ are summarized in Eq. (B,$\bullet$,5) in Appendix B, where ${\hat{n_{\text {p}}^*}} = \dim |\{{\hat{\varvec{\kappa }}}^{i}\}_{i=1}^3| \le 3 \dim |\varvec{\kappa }^{\text{ AL }}|$ holds

7 Summary and conclusions

This contribution presents a practical guide for model development accounting for the criteria of verification, validation and stability. As a prerequisite, it requires a set of different data sets, which can be related to different strain modes investigated experimentally in the laboratory.

In case, the validity check on non-conformity according to Definition 1 in this work is not satisfying, an extension of hyperelastic material models is proposed by means of so-called strain mode-dependent weighting functions, as a counterpart to the extension in [26] with stress mode-dependent weighting functions. To this end, an additive decomposition of the strain energy function is assumed into a sum of weighted strain mode related quantities. This approach can easily be combined with techniques of model reduction, in order to obtain more stable material parameters.

In order to account for incompressibility and strain mode-dependent material behavior, the free energy density for the isochoric part has been postulated in a mixed formulation as $\overline{\psi }[\overline{\mathbf {C}}, \varvec{\kappa }] = \sum \nolimits _{i=1}^{S} w^{i}[{{\bar{\Lambda }}}_a] \cdot \overline{\psi }^{i}[\overline{{\lambda }}_a,\varvec{\kappa }^{i}]$ in terms of the eigenvalues ${{\bar{\Lambda }}}_a$ and the principal isochoric stretches $\overline{{\lambda }}_a, a = 1,2,3$, and alternatively as $\overline{\psi }[\mathbf {C}, \varvec{\kappa }] = \sum \nolimits _{i=1}^{S} w^{i}[{{\bar{\Lambda }}}_a] \cdot \overline{\psi }^{i}[\bar{I}_1[\overline{\mathbf {C}}], {\bar{I}}_2 [\overline{\mathbf {C}}],\varvec{\kappa }^{i}]$ in terms of the eigenvalues ${{\bar{\Lambda }}}_a$ and the three invariants ${\bar{I}}_A, A = 1,2,3$ of the isochoric right Cauchy–Green strain tensor. For convenient implementation, including the corresponding tangent operators, a general framework has been presented, which only requires the partial derivatives ${\partial \overline{\psi }^{i}}/{\partial \overline{{\lambda }}_b}$, ${\partial ^2 \overline{\psi }^{i}}/{\partial \overline{{\lambda }}_a\partial \overline{{\lambda }}_b}$ in the first case and respectively the coefficients ${\partial \overline{\psi }^{i}}/{\partial {\bar{I}}_A}$, ${\partial ^2 \overline{\psi }^{i}}/{\partial {\bar{I}}_A \partial {\bar{I}}_B}$ in the second case. The detailed results for these coefficients are provided for thirteen well-known material models in Appendix B.

The approach is successfully applied for all 13 hyperelastic models with regard to the classical experimental data on vulcanized rubber published by Treloar [48], showing quadratic convergence for the finite-element equilibrium iteration as well as excellent fitting capabilties and stable material parameters.

We remark that in the field of optimal control problems, the indicator function $\phi _I [{{\underline{C}}}[\varvec{\kappa }]]$ is used to formulate an optimization criterion, which apart from material parameters may be dependent on further design variables, cf e.g. [4] and [24]. Then, in summary, two requirements become essential: The solution vector

• 1. Should minimize the least-squares functional (representing a model error) according to (37)

• 2. Should minimize the confidence criterion according to (50).

In practice, the above two requirements on small model error and stable results might be contradictory and, therefore, have to be carefully balanced. In this work, the generality of the methodology of optimal control problems has not be exploited and therefore will constitute an aspect of future work.

Appendices

Appendix

Derivatives of weighting functions

The general results (26) and (28) require the coefficients $\overline{W}^{i}_a$ in (26.5) for the stress like coefficients and the coefficients $\overline{W}^{i}_{ab}$ in (28.5) for the corresponding tangent coefficients, which will be derived next. Exploiting the relation (17) the derivative of the strain mode factor $\xi$ with respect to the isochoric eigenvalues ${{\bar{\Lambda }}}_A$ is obtained from Eqs. (16.1) to (17.1–2) as

$$\begin{aligned} \begin{array}{lllll} 1. &{} \displaystyle \frac{\partial \xi }{\partial {{\bar{\Lambda }}}_a} &{}=&{} \displaystyle \frac{\sqrt{27}}{2} \left( \displaystyle \frac{1}{J_2^{1.5}} \displaystyle \frac{\partial {J}_3}{\partial {{\bar{\Lambda }}}_a} - \displaystyle \frac{1.5 {J}_3}{{J}_2^{2.5}} \displaystyle \frac{\partial {J}_2}{\partial {{\bar{\Lambda }}}_a} \right) , ~ \text{ where }\\ 2. &{} \displaystyle \frac{\partial {J}_2}{\partial {{\bar{\Lambda }}}_a} &{}=&{} \displaystyle \frac{\ln {{\bar{\Lambda }}}_a}{{{\bar{\Lambda }}}_a}, \qquad 3. ~~ \displaystyle \frac{\partial {J}_3}{\partial {{\bar{\Lambda }}}_a} = \displaystyle \frac{(\ln {{\bar{\Lambda }}}_a)^2}{\overline{{\lambda }}_a}. \end{array} \end{aligned}$$

(A.1)

Consequently, from the relation (23) the first derivative of the weighting functions becomes

$$\begin{aligned} \begin{array}{rllllll} ~~1. &{} \text{ UT: } &{} \displaystyle \frac{\partial w^{(1)}}{\partial {{\bar{\Lambda }}}_a} &{}=&{} \left\{ \begin{array}{llll} 2 \xi \displaystyle \frac{\partial \xi }{\partial {{\bar{\Lambda }}}_a}, &{} &{}\text{ if } &{} \xi \ge 0 \\ 0, &{} &{} \text{ else } &{} \\ \end{array} \right. \\ ~~2. &{} \text{ ET: } &{} \displaystyle \frac{\partial w^{(2)}}{\partial {{\bar{\Lambda }}}_a} &{}=&{} \left\{ \begin{array}{llll} 0, &{} &{}\text{ if } &{} \xi \le 0 \\ 2 \xi \displaystyle \frac{\partial \xi }{\partial {{\bar{\Lambda }}}_a}, &{} &{} \text{ else } &{} \\ \end{array} \right. \\ ~~3. &{} \text{ PS: } &{} \displaystyle \frac{\partial w^{(3)}}{\partial {{\bar{\Lambda }}}_a} &{}=&{} -2 \xi \displaystyle \frac{\partial \xi }{\partial {{\bar{\Lambda }}}_a} \\ \end{array} \end{aligned}$$

(A.2)

and respectively from (24)

$$\begin{aligned} {{\begin{array}{rllllll} ~~1.&\text{ UT: } \quad \displaystyle \frac{\partial w^{(1)}}{\partial {{\bar{\Lambda }}}_a} = \displaystyle \frac{1}{2}\displaystyle \frac{\partial \xi }{\partial {{\bar{\Lambda }}}_a}, \quad ~~2.&\text{ ET: } \quad \displaystyle \frac{\partial w^{(2)}}{\partial {{\bar{\Lambda }}}_a} = -\displaystyle \frac{1}{2}\displaystyle \frac{\partial \xi }{\partial {{\bar{\Lambda }}}_a}. \end{array}}} \end{aligned}$$

(A.3)

The relations (A.2) and (A.3), respectively, serve to compute the coefficients $\overline{W}^{i}_a = (\displaystyle {1}/{{{\bar{\Lambda }}}_a}) \displaystyle {\partial w^{i}}/{\partial {\Lambda }_a}$ in Eq. (26).

Exploiting the relation (A.1) the second derivative of the strain mode factor $\xi$ with respect to the isochoric eigenvalues ${\Lambda }_A$ is obtained from Eq. (A.1.2–3) as

$$\begin{aligned} \begin{array}{lllll} 1. &{} \displaystyle \frac{\partial ^2 \xi }{\partial {{\bar{\Lambda }}}_a \partial {{\bar{\Lambda }}}_b} &{}=&{} \displaystyle \frac{\sqrt{27}}{2} \left( \displaystyle \frac{1}{J_2^{1.5}} \displaystyle \frac{\partial ^2 {J}_3}{\partial {{\bar{\Lambda }}}_a \partial {{\bar{\Lambda }}}_b} + \displaystyle \frac{1.5 \cdot 2.5 {J}_3}{{J}_2^{3.5}} \displaystyle \frac{\partial {J}_2}{\partial {{\bar{\Lambda }}}_a} \displaystyle \frac{\partial {J}_2}{\partial {{\bar{\Lambda }}}_b} \right. \\ &{}&{} -&{} \left. \displaystyle \frac{1.5 }{{J}_2^{2.5}} \left( \displaystyle \frac{\partial {J}_3}{\partial {{\bar{\Lambda }}}_a} \displaystyle \frac{\partial {J}_2}{\partial {{\bar{\Lambda }}}_b} + \displaystyle \frac{\partial {J}_2}{\partial {{\bar{\Lambda }}}_a} \displaystyle \frac{\partial {J}_3}{\partial {{\bar{\Lambda }}}_b} \right) - \displaystyle \frac{1.5 {J}_3}{{J}_2^{2.5}} \displaystyle \frac{\partial ^2 {J}_2}{\partial {{\bar{\Lambda }}}_a \partial {{\bar{\Lambda }}}_b} \right) , \text{ where }\\ 2. &{} \displaystyle \frac{\partial ^2 {J}_2}{\partial {{\bar{\Lambda }}}_a \partial {{\bar{\Lambda }}}_b} &{}=&{} \left\{ \begin{array}{lll} \displaystyle \frac{1}{{{\bar{\Lambda }}}_a^2} \left( 1 - \ln {{\bar{\Lambda }}}_a \right) &{} \text{ if }~a=b\\ 0 &{}\text{ else } \end{array} \right. , \quad \\ 3. &{} \displaystyle \frac{\partial ^2 {J}_3}{\partial {{\bar{\Lambda }}}_a \partial {{\bar{\Lambda }}}_b} &{}=&{} \left\{ \begin{array}{lll} \displaystyle \frac{1}{{{\bar{\Lambda }}}_a^2} \left( 2 \ln {{\bar{\Lambda }}}_a - (\ln {{\bar{\Lambda }}}_a)^2 \right) &{} \text{ if }~a=b\\ 0 &{}\text{ else } \end{array} \right. , \quad \\ \end{array} \end{aligned}$$

(A.4)

Consequently, from the relations (A.2) the second derivative of the weighting functions becomes

$$\begin{aligned} \begin{array}{rllllll} ~~1. &{} \text{ UT: } &{} \displaystyle \frac{\partial ^2 w^{(1)}}{\partial {{\bar{\Lambda }}}_a \partial {{\bar{\Lambda }}}_b} &{}=&{} \left\{ \begin{array}{llll} \zeta _{aa} &{} \xi \ge 0 \\ 0, &{} &{} \text{ else } &{} \\ \end{array} \right. \\ ~~2. &{} \text{ ET: } &{} \displaystyle \frac{\partial ^2 w^{(2)}}{\partial {{\bar{\Lambda }}}_a \partial {{\bar{\Lambda }}}_b} &{}=&{} \left\{ \begin{array}{llll} 0, &{} &{}\text{ if } &{} \xi \le 0 \\ \zeta _{aa} &{} &{} \text{ else } &{} \\ \end{array} \right. \\ ~~3. &{} \text{ PS: } &{} \displaystyle \frac{\partial ^2 w^{(3)}}{\partial {{\bar{\Lambda }}}_a \partial {{\bar{\Lambda }}}_b} &{}=&{} -\zeta _{aa}, ~~ \text{ where }\\ ~~4. &{} &{} \zeta _{aa} &{}=&{} 2 \displaystyle \frac{\partial \xi }{\partial {{\bar{\Lambda }}}_a} \displaystyle \frac{\partial \xi }{\partial {{\bar{\Lambda }}}_b} + 2 \xi \displaystyle \frac{\partial ^2 \xi }{\partial {{\bar{\Lambda }}}_a \partial {{\bar{\Lambda }}}_b} \end{array} \end{aligned}$$

(A.5)

and respectively from (A.3)

$$\begin{aligned} {{\begin{array}{rllllllllll} ~~1.&\text{ UT: }&\displaystyle \frac{\partial ^2 w^{(1)}}{\partial {{\bar{\Lambda }}}_a \partial {{\bar{\Lambda }}}_b} = \displaystyle \frac{1}{2}\displaystyle \frac{\partial ^2 \xi }{\partial {{\bar{\Lambda }}}_a \partial {{\bar{\Lambda }}}_b} , \quad ~~2.&\text{ ET: }&\displaystyle \frac{\partial ^2 w^{(2)}}{\partial {{\bar{\Lambda }}}_a \partial {{\bar{\Lambda }}}_b} = -\displaystyle \frac{1}{2}\displaystyle \frac{\partial ^2 \xi }{\partial {{\bar{\Lambda }}}_a \partial {{\bar{\Lambda }}}_b}. \end{array}}} \end{aligned}$$

(A.6)

The relations (A.5) and (A.6), respectively, serve to compute the coefficients $\overline{W}^{i}_{ab}$ in Eq. (28)

Survey on hyperelastic models

In this section we summarize basic relations needed for the comparative study in Sect. 6 for the isochoric free energy density, the partial derivatives in (33) and material parameters related to the i-th strain mode: Moreover, we summarize the coefficients ${\partial \overline{\psi }^{i}}/{\partial \overline{{\lambda }}_a}$ and ${\partial ^2 \overline{\psi }^{i}}/{\partial \overline{{\lambda }}_a \partial \overline{{\lambda }}_b}$ for evaluation of the stress coefficients $\overline{S}^{i}_a$ in Eq. (26.4) and the tangent coefficients $\overline{C}^{i}_{ab}$ in Eq. (28.4) for a stretch based formulation, as well as the coefficients ${\partial \overline{\psi }^{i}}/{\partial {\bar{I}}_A}$ and ${\partial ^2 \overline{\psi }^{i}}/{\partial {\bar{I}}_A \partial {\bar{I}}_B}$ for evaluation of the stress coefficients $\overline{S}^{i}_a$ in Eq. (33) and the tangent coefficients $\overline{C}^{i}_{ab}$ in Eq. (35) for an invariant based formulation. Any 5-th equation refers to parameters ${\hat{\varvec{\kappa }}}^{i}$ obtained from "model reduction” according to Step 2.c.i in Table 1.

• 1. Neo-Hooke model (1943)

  

  (B.1)

• 2. Mooney-Rivlin model (1940)

  

  (B.2)

• 3. Isihara model (1951)

  

  (B.3)

• 4. Gent-Thomas model (1958)

  

  (B.4)

• 5. Swanson model (1985)

  

  (B.5)

• 6. Yeoh model (1990)

  

  (B.6)

• 7. Arruda-Boyce model (1993) (invariant form)

  

  (B.7)

• 8. Gent model (1996)

  

  (B.8)

• 9. Yeoh-Fleming model (1997)

  

  (B.9)

• 10. Carroll model (2011)

  

  (B.10)

• 11. Ogden model (1972)

  

  (B.11)

• 12. Three chain model (1943)

  

  (B.12)

• 13. Eight chain model (1993)

  

  (B.13)

Detailed results on verification, validation and stability

1.1 Neo-Hooke model (1943)

The Neo-Hooke model constitutes the simplest specification of the Mooney-Rivlin-Saunders model series since it only considers $c^i_{10}\ne 0$ in Eq. (31), that is, the summation is up to $k = 1, l = 0$ and the additive constant $c^i_{00}$ related to the i-th strain mode is set to zero. The free energy function related to the i-th strain mode with $n_{\text {p}}^i=1, i = UT,ET, PS$, material parameters is given in Eq. (B.1.1) and the partial derivatives in (33) are given in Eq. (B.1.2). Each of the first three sets of material parameters in Eq. (B.1.4) is used to predict the two complementary deformation modes, and results are plotted in Fig. 5. In the following, we will discuss on the three aspects of 1. verification, 2. validation and 3. stability.

• Verification: Comparing the results or $f[\varvec{\kappa }^{i}]$, ${i}= UT,ET,PS$ in Tables 2, 3 and 4, and as already discussed in [47], fitting the PS-data with one curvature renders an acceptable result. However, the characteristic S-shape of ET and PS with two curvatures cannot be captured with the simple model structure. If small small deformations with $\lambda < 1.5$ are of interest, the Neo-Hooke model provides reasonable results for the nonlinear stress-stretch regime, see also [8]. To summarize, the verification capability of the Neo-Hooke model is only acceptable for small deformations with $\lambda < 1.5$. For larger stretches a model extension is indispensable

• Validation: Failing the requirements of verification, the Neo-Hooke model cannot predict Treloars data. The visualization in Fig. 5 of this deficiency is confirmed by the relatively large values for $F[\varvec{\kappa }^{i}]$, $i=UT,ET,PS$ according to Eq. (56) in Tables 5, 6 and 7, respectively.

• Stability: Due to the simple model structure with only $n_{\text {p}}^i=1, i=UT,ET,PS$ material parameters, very stable results for the inverse problem can be expected. This is confirmed by the comparative small values for the I-criteria $\varphi _I [\varvec{\kappa }^{i}], I = A,E,D,M$ of Eq. (55) and listed in Tables 2, 3 and 4, as well as of $\Phi _I [\varvec{\kappa }^{i}], I = A,E,D,M$ of Eq. (57) and listed in Tables 5, 6 and 7, Observe, that indeed all values for $\varphi _I [\varvec{\kappa }^{i}], I = A,E,D$ are identical, which by means of $n_{\text {p}}=1$ can be verified from Eq. (52) and Eq. (53), respectively. To summarize: The model simple structure of the Neo-Hooke model with only one parameter leads to a relatively high stability of the material parameter.

Fig. 5

Performance of the Neo-Hooke model on Treloar’s data. The minimum least squares fits to UT (left) and ET (middle) yield unacceptable results due to the incapability of the model to reproduce the S-shape. The S-shape does not occur for PS (right), which renders an acceptable fit quality in this case. Overall, the verification capability is unacceptable, which excludes validated results for prediction

1.2 Isihara model (1951)

Isihara et al. [20] proposed a model incorporating a non-Gaussian chain theory. It can be derived by linearization of the Mooney-Rivlin/Saunders model in Eq. (31), thus resulting into a simple model with three material parameters and a term, which couples the two invariants ${\bar{I}}_1$ and ${\bar{I}}_2$ in a nonlinear manner. Based in the formulation in [30] the free energy function related to the i-th strain mode is given in Eq. (B.3.1). Each of the first three sets of material parameters in Eq. (B.3.4) is used to predict the two complementary deformation modes, and results are plotted in Fig. 6. In the following, we will discuss on the three aspects of 1. verification, 2. validation and 3. stability.

• Verification: As already discussed in [47], the fit quality is very high for all deformation modes. In particular for ET and PS almost perfect results are obtained. Regarding UT-data, the high initial stiffness is not properly reflected, however (in contrast to the Neo-Hooke model and the Mooney Rivlin model) Isihara’s model can capture the characteristic S-shape at large stretches. Related results for $f[\varvec{\kappa }^{i}]$, ${i}= UT,ET,PS$ are given in Tables 2, 3 and 4. To summarize, the fit capability of Isihara model [20] for Treloa’s data is very good.

• Validation: Regarding the prediction capability, the results are rather disappointing for all three cases. In particular, the material parameters $\varvec{\kappa }^{\text{ ET }}$ obtained from ET-data in the middle graph of Fig. 6 are not able to capture the S-shape curve of UT in the left graph. The same holds e.g. for the material parameters $\varvec{\kappa }^{\text{ UT }}$ obtained from UT-data in the left graph, applied to ET-data in the middle graph. These illustrative results are confirmed by the comparative large values for the least-squares functionals $F[\varvec{\kappa }_{i}], {i}= UT,ET,PS$ defined in Eq. (56) and summarized in Tables 5, 6 and 7. As a consequence, with reference to Definition 1 in the introduction of work we summarize: The conformity between the Treloar data [48] and the Isihara model [20] is very poor.

• Stability: A closer look on Eq. (B.3) reveals the product $c_{20}^i$ and $c_{01}^i$ within the formulation. Obviously, an infinite number of combinations can be constructed to obtain a certain value for any product $c_{20}^i\cdot c_{01}^i$. This property leads to non-uniqueness of the inverse problem (65), and according to Sect. 4.1 is certainly a deficiency of the material model - rather than of the experimental data. These effects are confirmed by the comparative large values for the I-criteria $\varphi _I [\varvec{\kappa }^{i}], I = A,E,D,M$ of Eq. (55) and listed in Tables 2, 3 and 4, as well as of $\Phi _I [\varvec{\kappa }^{i}], I = A,E,D,M$ of Eq. (57) and listed in Tables 5, 6 and 7. To summarize: The stability of the Isihara model [20] is rather poor. A modification of experimental information, in whatever way, cannot account for this undesired property. A model reduction is indispensable.

Fig. 6

Performance of the Isihara model on Treloar’s data. The fit quality is acceptable (UT) to perfect (ET, PS) which renders high verification quality. Contrary, the validation quality is very poor, in particular in the middle graph where unrealistic high stresses are predicted for ET for parameters $\varvec{\kappa }^{\text{ UT }}$ and $\varvec{\kappa }^{\text{ PS }}$, respectively

Fig. 7

Performance of the Carroll model on Treloar’s data. The fit quality is perfect for UT, ET, PS. Also the predictive results show a remarkable model performance

1.3 Carroll model (2011)

Carroll [9] proposed a phenomenological approach based on a successive extension of the free energy. Here the additional terms are chosen such that they reduce the errors that remain in the stress response of the previous terms, compared to measurements, see e.g. [9] on more details. The free energy function related to the i-th strain mode is given in Eq. (B.10.1). Each of the first three sets of material parameters in Eq. (B.10.4) is used to predict the two complementary deformation modes, and results are plotted in Fig. 7. In the following, we will discuss on the three aspects of 1. verification, 2. validation and 3. stability.

• Verification: As already discussed in [47], the fit quality of the parameter sets are very good to perfect. Related results for $f[\varvec{\kappa }^{i}]$, ${i}= UT,ET,PS$ are given in Tables 2, 3 and 4.

• Validation: The corresponding curves on prediction in Fig. 7 and reveal a remarkable model performance. These illustrative results are confirmed by the comparative low values for the least-squares functionals $F[\varvec{\kappa }^{i}], {i}= UT,ET,PS$ defined in Eq. (56) and summarized in Tables 5, 6 and 7. With reference to Definition 1 in the introduction of work we summarize: The conformity between the Treloar data [48] and the Carroll model [9] is very good.

• Stability: A comparative study of the I-criteria $\varphi _I [\varvec{\kappa }^{i}], I = A,E,D,M$ of Eq. (55) and listed in Tables 2, 3 and 4, as well as of $\Phi _I [\varvec{\kappa }^{i}], I = A,E,D,M$ of Eq. (57) and listed in Tables 5, 6 and 7 reveals remarkable stability properties.

The correlation matrix of Isiharas model

This part of the Appendix provides results for the correlation matrix $C_{ij}[\varvec{\kappa }^*]$ defined in Eq. (40). For briefness of presentation, only results for the Isihara model after model reduction are shown.

The comparatively high correlations in Table 10 between some of the material parameters (e.g. within the UT regime -0.9172 between $c_{10}^{UT}$ and $c_{20}^{UT}$) is an indicator for overparameterization, but, no attempt has been made on further reduction. However, the results in Table 10 also demonstrate a clear independence between UT, ET and PS related material parameters. This is regarded as a main advantage of the proposed weighted strain energy in Eq. (9).

Table 9 Isihara model: Correlation matrix between UT, ET and PS

Table 10 Finite-element residual norms for all 13 models in the list of Sect. 6.1

Local check for quadratic convergence

This section intends to verify the results for the isochoric tangent operator in Eq. (28), consistent with the isochoric second Piola-Kirchhoff stress tensor in Eq. (26). Thereby, we are only interested in the convergence performance, such that the checks are performed as one-element tests (rather than for a complex finite element geometry).

The coordinates of the element are $\{x_i, y_i\}, i = 1,...,4$ = $\{0., 0.\}, \{1.2, 0.\}, \{1., 1.\}, \{0., 1.\}$, such that an inhomogeneous strain and stress state is generated. As (Dirichlet) boundary conditions we prescribe $\{u_{yi}\} =\{0\},$ $\{u_{xi}, u_{yi}\} =\{0, 0\}, i = 2,...,3$, and the Neumann boundary condition is $\{f_{xi}\} =\{0.05\}$. The parameters for simultaneous identification summarized in the vectors $\varvec{\kappa }^{i}$ in the survey on hyperelastic models in Sect. B are used. Solutions of the resulting equilibrium problems (not discussed in more detail here) are performed with a Newton method, which iterates on the corresponding finite-element residual of the element.

Table 11 summarizes the final residual norms for all thirteen models in the list of Sect. 6.1. In almost all cases the number of correct digits is doubled in every iteration, that is quadratic convergence is achieved, which verifies correct derivation and implementation of the corresponding tangent operators.